Fuzzy Probability Points Reasoning for 3D Reconstruction Via Deep Deterministic Policy Gradient
-
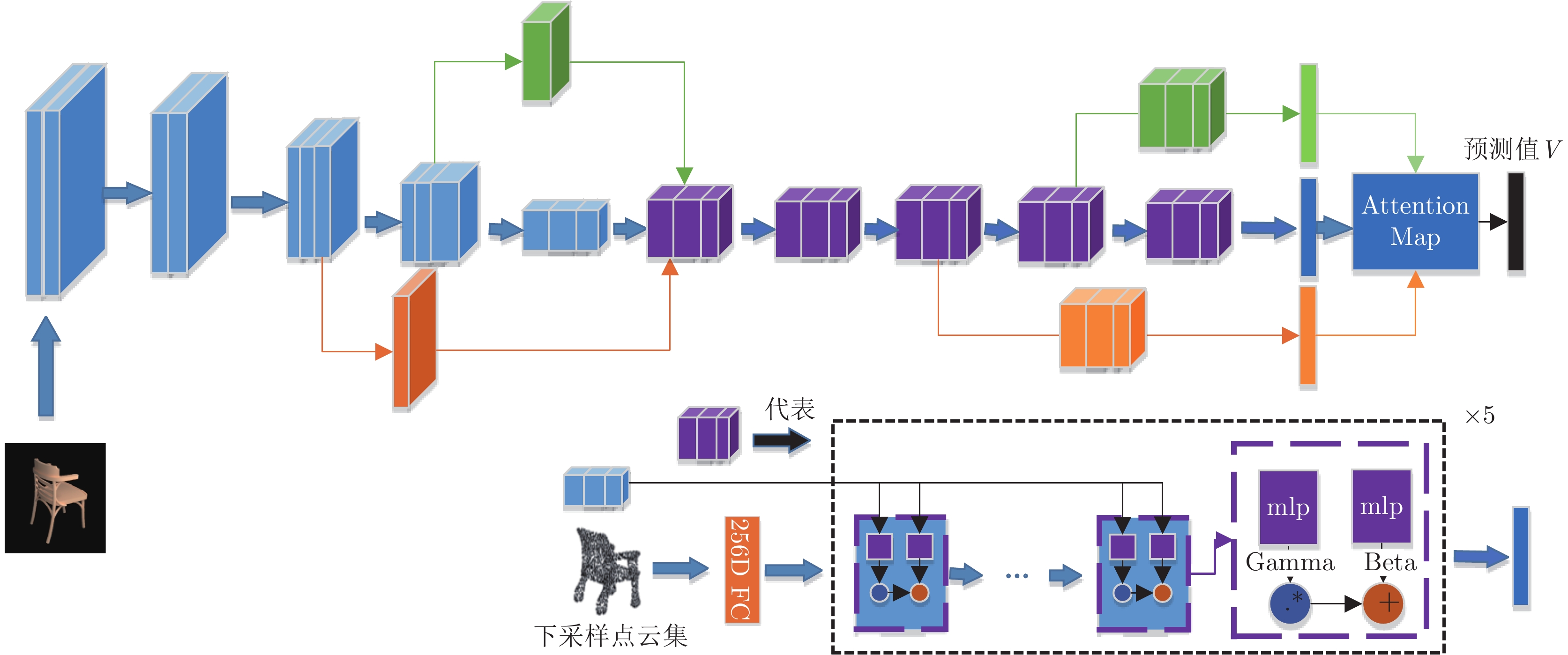
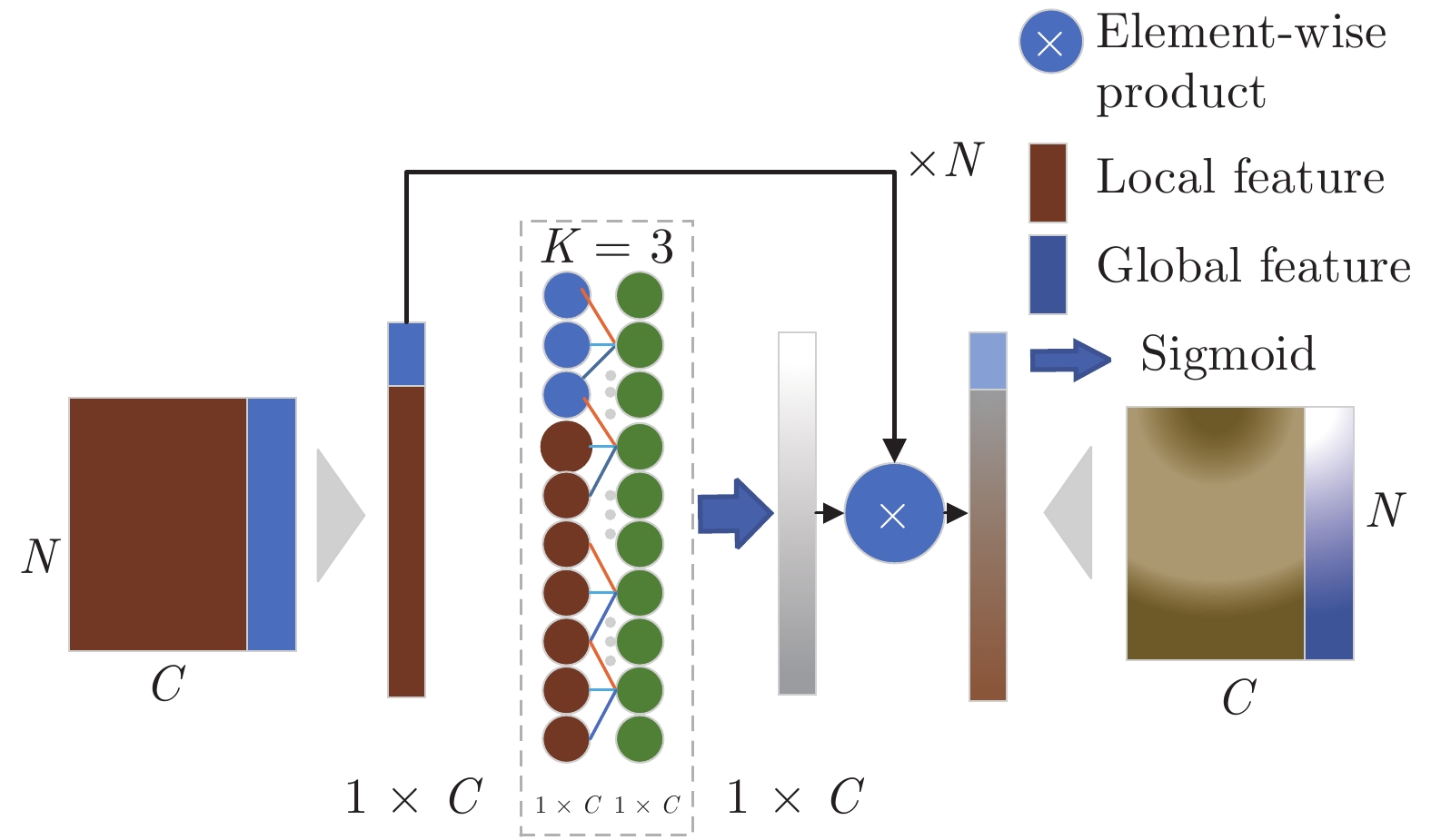
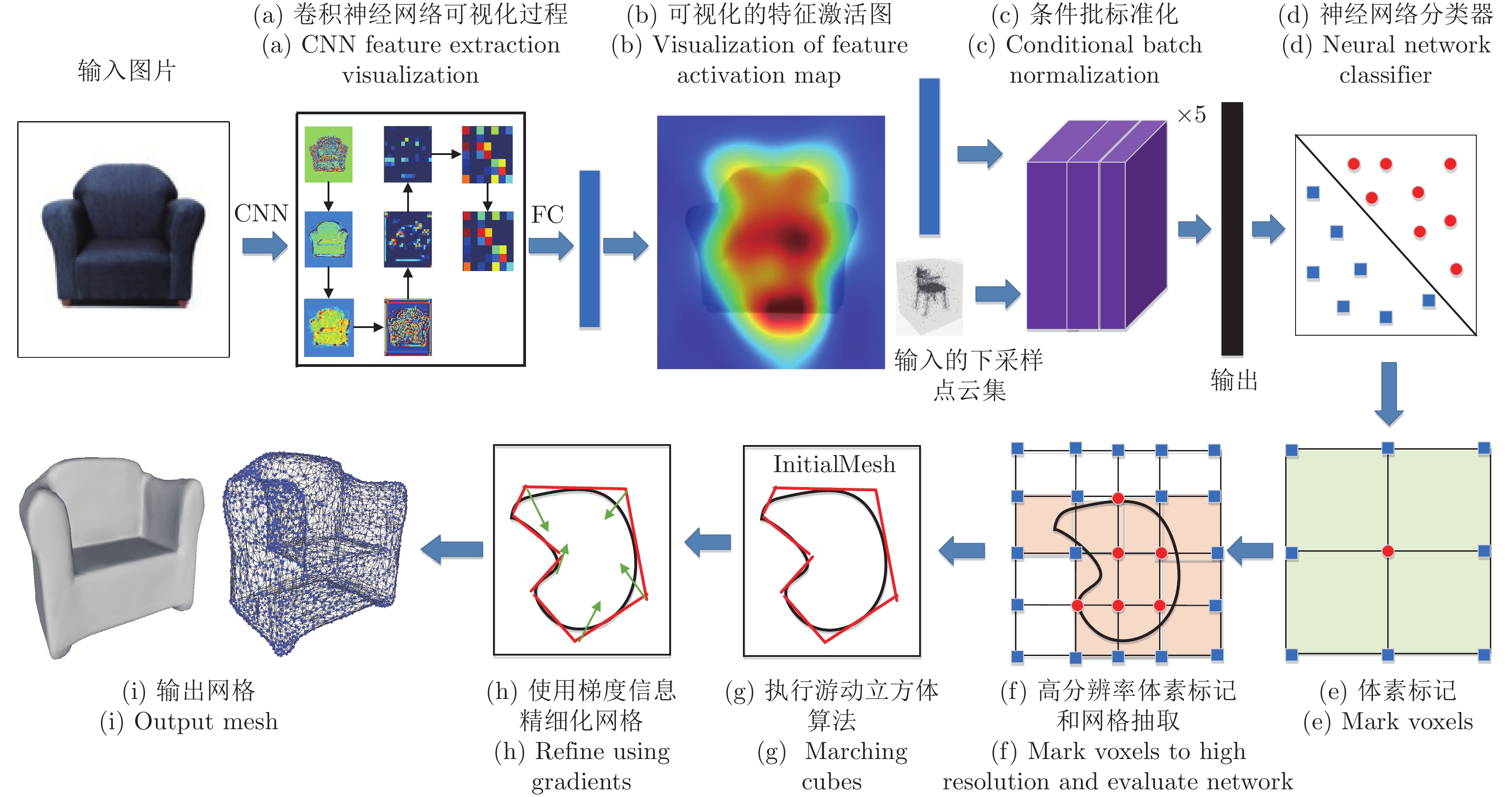
摘要: 单视图物体三维重建是一个长期存在的具有挑战性的问题. 为了解决具有复杂拓扑结构的物体以及一些高保真度的表面细节信息仍然难以准确进行恢复的问题, 本文提出了一种基于深度强化学习算法深度确定性策略梯度 (Deep deterministic policy gradient, DDPG)的方法对三维重建中模糊概率点进行再推理, 实现了具有高保真和丰富细节的单视图三维重建. 本文的方法是端到端的, 包括以下四个部分: 拟合物体三维形状的动态分支代偿网络的学习过程, 聚合模糊概率点周围点的邻域路由机制, 注意力机制引导的信息聚合和基于深度强化学习算法的模糊概率调整. 本文在公开的大规模三维形状数据集上进行了大量的实验证明了本文方法的正确性和有效性. 本文提出的方法结合了强化学习和深度学习, 聚合了模糊概率点周围的局部信息和图像全局信息, 从而有效地提升了模型对复杂拓扑结构和高保真度的细节信息的重建能力.Abstract: 3D object reconstruction from a single-view image is a long-standing challenging problem. In order to address the difficulty of accurately predicting the objects of complex topologies and some high-fidelity surface details, we propose a new method based on DDPG (Deep deterministic policy gradient) to reason the fuzzy probability points in 3D reconstruction and achieve high-quality detail-rich reconstruction result of single-view image. Our method is end-to-end and includes four parts: the dynamic branch compensation network learning process to fit the 3D shape of objects, the neighborhood routing mechanism to aggregate the points around the fuzzy probability points, the attention guidance mechanism to aggregate the information, and the deep reinforcement learning algorithm to perform probabilistic reasoning. Extensive experiments on a large-scale public 3D shape dataset demonstrate the validity and efficiency of our method. Our method combines reinforcement learning and deep learning, aggregates local information around the fuzzy probability points and global information of the image, and effectively improves the model's ability to reconstruct complex topologies and high-fidelity details.
-
表 1 本文的方法在ShapeNet数据集上与最先进方法的交并比(IoU)的定量比较
Table 1 The quantitative comparison of our method with the state-of-the-art methods for IoU on ShapeNet dataset
类别\方法 3D-R2N2 Pix2Mesh AtlasNet ONet Our Airplane 0.426 0.420 — 0.571 0.592 Bench 0.373 0.323 — 0.485 0.503 cabinet 0.667 0.664 — 0.733 0.757 Car 0.661 0.552 — 0.737 0.755 Chair 0.439 0.396 — 0.501 0.542 Display 0.440 0.490 — 0.471 0.548 Lamp 0.281 0.323 — 0.371 0.409 Loudspeaker 0.611 0.599 — 0.647 0.672 Rifle 0.375 0.402 — 0.474 0.500 Sofa 0.626 0.613 — 0.680 0.701 Table 0.420 0.395 — 0.506 0.547 Telephone 0.611 0.661 — 0.720 0.763 Vessel 0.482 0.397 — 0.530 0.569 Mean 0.493 0.480 — 0.571 0.605 表 2 本文的方法在ShapeNet数据集上与最先进方法法线一致性(NC)的定量比较
Table 2 The quantitative comparison of our method with the state-of-the-art methods for NC on ShapeNet dataset
类别\方法 3D-R2N2 Pix2Mesh AtlasNet ONet Our Airplane 0.629 0.759 0.836 0.840 0.847 Bench 0.678 0.732 0.779 0.813 0.818 Cabinet 0.782 0.834 0.850 0.879 0.887 Car 0.714 0.756 0.836 0.852 0.855 Chair 0.663 0.746 0.791 0.823 0.835 Display 0.720 0.830 0.858 0.854 0.871 Lamp 0.560 0.666 0.694 0.731 0.751 Loudspeaker 0.711 0.782 0.825 0.832 0.845 Rifle 0.670 0.718 0.725 0.766 0.781 Sofa 0.731 0.820 0.840 0.863 0.872 Table 0.732 0.784 0.832 0.858 0.864 Telephone 0.817 0.907 0.923 0.935 0.938 Vessel 0.629 0.699 0.756 0.794 0.801 Mean 0.695 0.772 0.811 0.834 0.844 表 3 本文的方法在ShapeNet数据集上与最先进方法倒角距离 (CD)的定量比较
Table 3 The quantitative comparison of our method with the state-of-the-art methods for CD on ShapeNet dataset
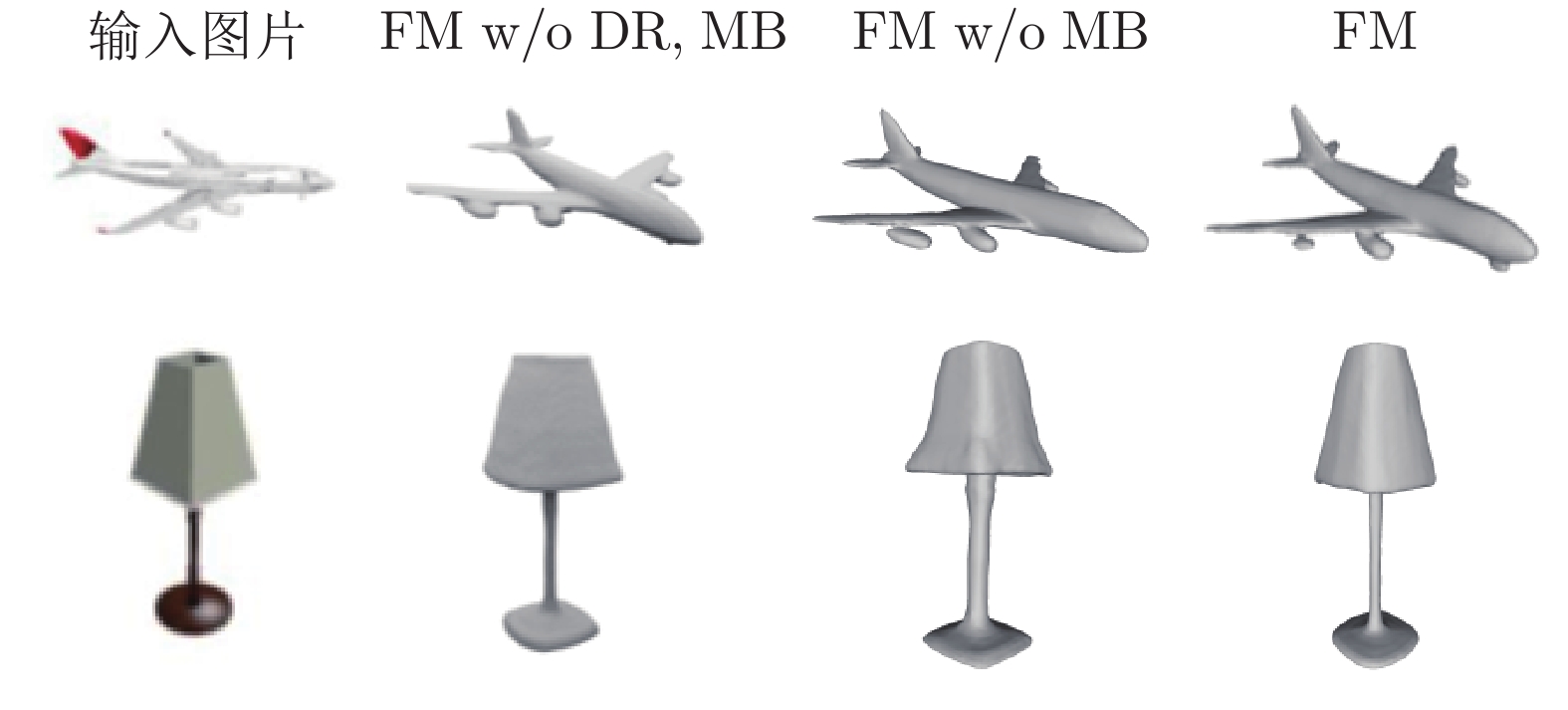
类别\方法 3D-R2N2 Pix2Mesh AtlasNet ONet Our Airplane 0.227 0.187 0.104 0.147 0.130 Bench 0.194 0.201 0.138 0.155 0.149 Cabinet 0.217 0.196 0.175 0.167 0.146 Car 0.213 0.180 0.141 0.159 0.144 Chair 0.270 0.265 0.209 0.228 0.200 Display 0.314 0.239 0.198 0.278 0.220 Lamp 0.778 0.308 0.305 0.479 0.364 Loudspeaker 0.318 0.285 0.245 0.300 0.263 Rifle 0.183 0.164 0.115 0.141 0.130 Sofa 0.229 0.212 0.177 0.194 0.179 Table 0.239 0.218 0.190 0.189 0.170 Telephone 0.195 0.149 0.128 0.140 0.121 Vessel 0.238 0.212 0.151 0.218 0.189 Mean 0.278 0.216 0.175 0.215 0.185 表 4 消融实验
Table 4 Ablation study
模型\指标 IoU NC CD FM w/o DR, MB 0.593 0.840 0.194 FM w/o MB 0.599 0.839 0.194 FM 0.605 0.844 0.185 -
[1] 陈加, 张玉麒, 宋鹏, 魏艳涛, 王煜. 深度学习在基于单幅图像的物体三维重建中的应用. 自动化学报, 2019, 45(4): 657-668Chen Jia, Zhang Yu-Qi, Song Peng, Wei Yan-Tao, Wang Yu. Application of deep learning to 3D object reconstruction from a single image. Acta Automatica Sinica, 2019, 45(4): 657-668 [2] 郑太雄, 黄帅, 李永福, 冯明驰. 基于视觉的三维重建关键技术研究综述. 自动化学报, 2020, 46(4): 631-652Zheng Tai-Xiong, Huang Shuai, Li Yong-Fu, Feng Ming-Chi. Key techniques for vision based 3D reconstruction: A review. Acta Automatica Sinica, 2020, 46(4): 631-652 [3] 薛俊诗, 易辉, 吴止锾, 陈向宁. 一种基于场景图分割的混合式多视图三维重建方法. 自动化学报, 2020, 46(4): 782-795Xue Jun-Shi, Yi Hui, Wu Zhi-Huan, Chen Xiang-Ning. A hybrid multi-view 3D reconstruction method based on scene graph partition. Acta Automatica Sinica, 2020, 46(4): 782-795 [4] Wu J J, Zhang C K, Xue T F, Freeman W T, Tenenbaum J B. Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates, Inc., 2016. 82−90 [5] Choy C B, Xu D F, Gwak J Y, Chen K, Savarese S. 3D-R2N2: A unified approach for single and multi-view 3D object reconstruction. In: Proceedings of the 14th European Conference on Computer Vision. Amsterdam, The Netherlands: Springer, 2016. 628−644 [6] Yao Y, Luo Z X, Li S W, Fang T, Quan L. MVSNet: Depth inference for unstructured multi-view stereo. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 785−801 [7] Wu J J, Wang Y F, Xue T F, Sun X Y, Freeman W T, Tenenbaum J B. MarrNet: 3D shape reconstruction via 2.5D sketches. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates, Inc., 2017. 540−550 [8] Fan H Q, Su H, Guibas L. A point set generation network for 3D object reconstruction from a single image. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, USA: IEEE, 2017. 2463−2471 [9] Wang N Y, Zhang Y D, Li Z W, Fu Y W, Liu W, Jiang Y G. Pixel2Mesh: Generating 3D mesh models from single RGB images. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 55−71 [10] Scarselli F, Gori M, Tsoi A C, Hagenbuchner M, Monfardini G. The graph neural network model. IEEE Transactions on Neural Networks, 2009, 20(1): 61-80 doi: 10.1109/TNN.2008.2005605 [11] Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533-536 doi: 10.1038/323533a0 [12] Roth S, Richter S R. Matryoshka networks: Predicting 3D geometry via nested shape layers. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 1936−1944 [13] Wu J J, Zhang C K, Zhang X M, Zhang Z T, Freeman W T, Tenenbaum J B. Learning shape priors for single-view 3D completion and reconstruction. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 673−691 [14] Groueix T, Fisher M, Kim V G, Russell B C, Aubry M. A Papier-Mache approach to learning 3D surface generation. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 216−224 [15] Kanazawa A, Black M J, Jacobs D W, Malik J. End-to-end recovery of human shape and pose. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 7122−7131 [16] Kong C, Lin C H, Lucey S. Using locally corresponding CAD models for dense 3D reconstructions from a single image. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, USA: IEEE, 2017. 5603−5611 [17] Mescheder L, Oechsle M, Niemeyer M, Nowozin S, Geiger A. Occupancy networks: Learning 3D reconstruction in function space. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, USA: IEEE, 2019. 4455−4465 [18] Lillicrap T P, Hunt J J, Pritzel A, Heess N, Erez T, Tassa Y, et al. Continuous control with deep reinforcement learning [Online], available: https: //arxiv.org/abs/1509. 02971, July 5, 2019 [19] Li D, Chen Q F. Dynamic hierarchical mimicking towards consistent optimization objectives. In: Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle, USA: IEEE, 2020. 7639−7648 [20] Chang A X, Funkhouser T, Guibas L, et al.Shapenet:An information-rich 3d model repository [Online], available: https: //arxiv.org/abs/1512. 03012, December 9, 2015 [21] Durou J D, Falcone M, Sagona M. Numerical methods for shape-from-shading: A new survey with benchmarks. Computer Vision and Image Understanding, 2008, 109(1): 22-43 doi: 10.1016/j.cviu.2007.09.003 [22] Zhang R, Tsai P S, Cryer J E, Shah M. Shape-from-shading: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(8): 690-706 doi: 10.1109/34.784284 [23] Goodfellow I J, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. In: Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2014. 2672−2680 [24] Kingma D P, Welling M. Auto-encoding variational bayes [Online], available: https: //arxiv. org/abs/1312. 6114, May 1, 2014 [25] Kar A, Hane C, Malik J. Learning a multi-view stereo machine. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates, Inc., 2017. 364−375 [26] Tatarchenko M, Dosovitskiy A, Brox T. Octree generating networks: Efficient convolutional architectures for high-resolution 3D outputs. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy: IEEE, 2017. 2107−2115 [27] Wang W Y, Ceylan D, Mech R, Neumann U. 3DN: 3D deformation network. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, USA: IEEE, 2019. 1038−1046 [28] Bernardini F, Mittleman J, Rushmeier H, Silva C, Taubin G. The ball-pivoting algorithm for surface reconstruction. IEEE Transactions on Visualization and Computer Graphics, 1999, 5(4): 349-359 doi: 10.1109/2945.817351 [29] Kazhdan M, Hoppe H. Screened poisson surface reconstruction. ACM Transactions on Graphics, 2013, 32(3): Article No. 29 [30] Calakli F, Taubin G. SSD: Smooth signed distance surface reconstruction. Computer Graphics Forum, 2011, 30(7): 1993-2002 doi: 10.1111/j.1467-8659.2011.02058.x [31] Chen Z Q, Zhang H. Learning implicit fields for generative shape modeling. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, USA: IEEE, 2019. 5932−5941 [32] Wang W Y, Xu Q G, Ceylan D, Mech R, Neumann U. DISN: Deep implicit surface network for high-quality single-view 3D reconstruction. In: Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates, Inc., 2019. Article No. 45 [33] Wang Q L, Wu B G, Zhu P F, Li P H, Zuo W M, Hu Q H. ECA-Net: Efficient channel attention for deep convolutional neural networks. In: Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle, USA: IEEE, 2020. 11531−11539 [34] Selvaraju R R, Cogswell M, Das A, Vedantam R, Parikh D, Batra D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy: IEEE, 2017. 618−626 [35] Garland M, Heckbert P S. Simplifying surfaces with color and texture using quadric error metrics. In: Proceedings of the 1998 Visualization′ 98 (Cat. No.98CB362-76). Research Triangle Park, USA: IEEE, 1998. 263−269 [36] Lorensen W E, Cline H E. Marching cubes: A high resolution 3D surface construction algorithm. ACM SIGGRAPH Computer Graphics, 1987, 21(4): 163-169 doi: 10.1145/37402.37422 [37] Drucker H, Le Cun Y. Improving generalization performance using double backpropagation. IEEE Transactions on Neural Networks, 1992, 3(6): 991-997 doi: 10.1109/72.165600 [38] Oh Song H, Xiang Y, Jegelka S, Savarese S. Deep metric learning via lifted structured feature embedding. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, USA: IEEE, 2016. 4004−4012 [39] Stutz D, Geiger A. Learning 3D shape completion from laser scan data with weak supervision. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 1955−1964 [40] de Vries H, Strub F, Mary J, Larochelle H, Pietquin O, Courville A C. Modulating early visual processing by language. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates, Inc., 2017. 6597−6607 [41] He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, USA: IEEE, 2016. 770−778 [42] Kingma D P, Ba J. Adam: A method for stochastic optimization [Online], available: https: //arxiv. org/abs/1412. 6980, January 30, 2017 [43] Zhu C C, Liu H, Yu Z H, Sun, X H. Towards Omni-supervised face alignment for large scale unlabeled videos. In: Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York, USA: AAAI, 2020. 13090−13097 [44] Zhu C C, Li X Q, Li J D, Ding G T, Tong W Q. Spatial-temporal knowledge integration: Robust self-supervised facial landmark tracking. In: Proceedings of the 28th ACM International Conference on Multimedia. Lisboa, Portugal: ACM, 2020. 4135−4143 -




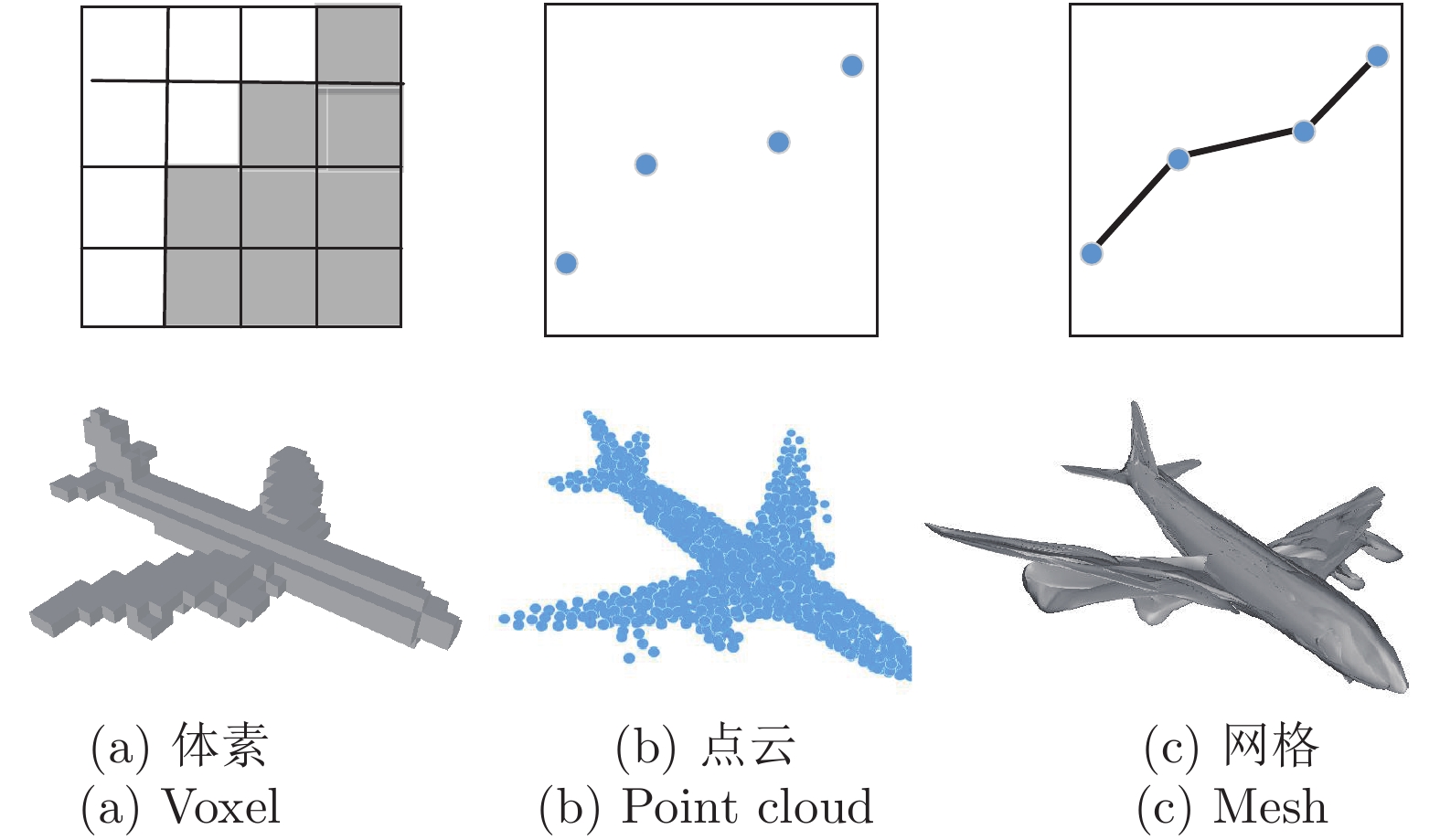
 下载:
下载: