Novel Path Curvature Optimization Algorithm for Intelligent Wheelchair to Smoothly Pass a Narrow Space
-
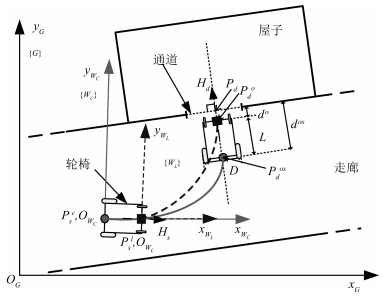
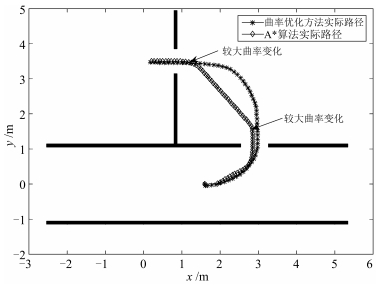
摘要: 为了使用户更感舒适,智能轮椅应该能在具有复杂几何约束的室内环境下平滑地通过狭窄通道.本文提出一个基于路径曲率优化的算法以确保智能轮椅平滑地通过狭窄过道.考虑到路径平滑度取决于路径曲率及其变化率,在通过传感器数据计算出狭窄通道相对于轮椅的位置后,算法以贝塞尔曲线的曲率及其变化率最小为优化目标,以轮椅过通道时的方向及贝塞尔多边形应为凸多边形作为约束,规划出一条平滑的最优路径,然后控制轮椅实时跟踪这条路径.上述过程动态循环运行,实现了智能轮椅平滑通过狭窄通道.仿真中将本文算法同基于A*的路径规划导航算法进行了对比,结果表明本文提出的基于曲率优化的算法可以实现比A*算法路径曲率更小且更加平滑的过狭窄通道过程,并且即使在没有全局地图和定位信息情况下,算法也能控制轮椅平滑地通过狭窄过道.实验中详细阐述了算法的实现过程,实验结果也证实了算法的有效性.Abstract: This paper presents a novel algorithm to address the smooth narrow pass traversing issue, which is based on optimizing the curvature of the wheelchair path. Being aware of the fact that the path smoothness is determined by the path curvature and its change rate, after calculating the position of the narrow pass relative to the base frame of the wheelchair from perception sensor data, the algorithm takes the curvature and its change rate of Bezier curve as the optimal objective, and the wheelchair heading and the condition that the Bezier curve polygon should be convex polygon as constraints, and plans a smooth and optimal path for the controlled wheelchair to follow. This process is iterated dynamically to enable the intelligent wheelchair to traverse the narrow pass smoothly. Simulation is firstly conducted to compare the performances of our method and the A*-based path planning navigation algorithm, which shows that the proposed algorithm is able to achieve more smooth path with smaller curvature when the wheelchair traverses narrow path. Furthermore, the algorithm can control the wheelchair to traverse narrow pass smoothly even without any global map and localization. Real experiment with detailed explanation of algorithm implementation is also given to verify the effectiveness of the proposed algorithm.
-
Key words:
- Intelligent wheelchair /
- curvature optimization /
- Bezier curve /
- pass traversing
1) 本文责任编委 程龙 -
表 1 每条路径的输入参数
Table 1 The input parameters for each path
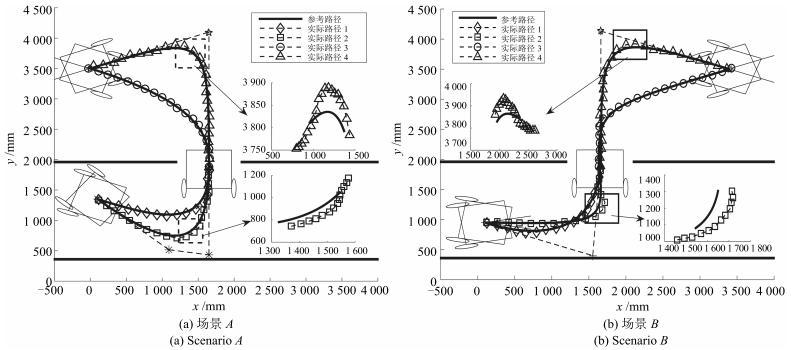
场景 Ps (m) Pd (m) Pt (m) 1 (Hs, Hd) 2 (Hs, Hd) 3 (Hd, Ht) 4 (Hd, Ht) A (0.1, 1.3) (1.6, 1.8) (0.0, 3.5) (-20, 90) (-40, 90) (90, 160) (90, 200) B (0.1, 1.3) (1.6, 1.8) (3.4, 3.5) (-10, 90) (10, 90) (90, 20) (90, -20) -
[1] Elbanhawi M, Simic M, Jazar R N. Continuous path smoothing for car-like robots using B-spline curves. Journal of Intelligent and Robotic Systems, 2015, 80(1):23-56 http://www.academia.edu/15534117/Continuous_Path_Smoothing_for_Car-Like_Robots_Using_B-Spline_Curves [2] Yoon S, Yoon S E, Lee U, Shim D H. Recursive path planning using reduced states for car-like vehicles on grid maps. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5):2797-2813 doi: 10.1109/TITS.2015.2422991 [3] Pan Z, Li J Q, Hu K M, Zhu H. Intelligent vehicle path planning based on improved artificial potential field method. Applied Mechanics and Materials, 2014, 742:349-354 https://www.researchgate.net/publication/276868213_Intelligent_Vehicle_Path_Planning_Based_on_Improved_Artificial_Potential_Field_Method [4] 张浩杰, 龚建伟, 姜岩, 熊光明, 陈慧岩.基于变维度状态空间的增量启发式路径规划方法研究.自动化学报, 2013, 39(10):1602-1610 doi: 10.3724/SP.J.1004.2013.01602Zhang Hao-Jie, Gong Jian-Wei, Jiang Yan, Xiong Guang-Ming, Chen Hui-Yan. Research on incremental heuristic path planner with variable dimensional state space. Acta Automatica Sinica, 2013, 39(10):1602-1610 doi: 10.3724/SP.J.1004.2013.01602 [5] 祖迪, 韩建达, 谈大龙.加速度空间中基于线性规划的移动机器人路径规划方法.自动化学报, 2007, 33(10):1036-1042 http://www.aas.net.cn/CN/abstract/abstract13407.shtmlZu Di, Han Jian-Da, Tan Da-Long. LP-based path planning method in acceleration space for mobile robot. Acta Automatica Sinica, 2007, 33(10):1036-1042 http://www.aas.net.cn/CN/abstract/abstract13407.shtml [6] Park J W, Im W S, Kim D Y, Kim J M. Safe driving algorithm of the electric wheelchair with model following control. In:Proceedings of the 16th European Conference on Power Electronics and Applications. Lappeenranta, Finland:IEEE, 2014. 1-10 [7] Sinyukov D A, Padir T. Adaptive motion control for a differentially driven semi-autonomous wheelchair platform. In:Proceedings of the 2015 International Conference on Advanced Robotics. Istanbul, Turkey:IEEE, 2015. 288-294 [8] Zhang Z Y, Zhao Z P. A multiple mobile robots path planning algorithm based on a-star and Dijkstra algorithm. International Journal of Smart Home, 2014, 8(3):75-86 doi: 10.14257/ijsh [9] Bhadoria A, Singh R K. Optimized angular a star algorithm for global path search based on neighbor node evaluation. International Journal of Intelligent Systems and Applications, 2014, 6(8):46-52 doi: 10.5815/ijisa [10] Seder M, Mostarac P, Petrović I. Hierarchical path planning of mobile robots in complex indoor environments. Transactions of the Institute of Measurement and Control, 2011, 33(3-4):332-358 doi: 10.1177/0142331208100107 [11] BSI. Design of Buildings and Their Approaches to Meet the Needs of Disabled People. Code of Practice. Standard Number BS 8300:2009+A1:2010, ISBN 9780580707308, British Standards Institute, 2009. [12] Cheein F, De La Cruz C, Guimaraes E, Bastos-Filho T, Carelli R. Navigation system for UFES's robotic wheelchair. Devices for Mobility and Manipulation for People with Reduced Abilities. Boca Raton, FL:CRC Press, 2014. 41-93 [13] Peula J M, Urdiales C, Herrero I, Fernandez-Carmona M, Sandoval F. Case-based reasoning emulation of persons for wheelchair navigation. Artificial Intelligence in Medicine, 2012, 56(2):109-121 doi: 10.1016/j.artmed.2012.08.007 [14] Rastelli J R, Lattarulo R, Nashashibi F. Dynamic trajectory generation using continuous-curvature algorithms for door to door assistance vehicles. In:Proceedings of the 2014 IEEE Intelligent Vehicles Symposium. Dearborn, USA:IEEE, 2014. 510-515 [15] Brezak M, Petrović I. Real-time approximation of clothoids with bounded error for path planning applications. IEEE Transactions on Robotics, 2014, 30(2):507-515 doi: 10.1109/TRO.2013.2283928 [16] Chu C H, Hsieh H T, Lee C H, Yan C Y. Spline-constrained tool-path planning in five-axis flank machining of ruled surfaces. The International Journal of Advanced Manufacturing Technology, 2015, 80(9-12):2097-2104 doi: 10.1007/s00170-015-7201-4 [17] Simba K R, Uchiyama N, Sano S. Real-time smooth trajectory generation for nonholonomic mobile robots using Bézier curves. Robotics and Computer-Integrated Manufacturing, 2016, 41(1):31-42 https://www.researchgate.net/publication/297587735_Real-time_smooth_trajectory_generation_for_nonholonomic_mobile_robots_using_Bezier_curves [18] Yang L, Song D L, Xiao J Z, Han J D, Yang L Y, Cao Y. Generation of dynamically feasible and collision free trajectory by applying six-order Bezier curve and local optimal reshaping. In:Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Hamburg, Germany:IEEE, 2015. 643-648 [19] Wu J, Snášel V. A Bézier curve-based approach for path planning in robot soccer. In:Proceedings of the 4th International Conference on Innovations in Bio-inspired Computing and Applications. Ostrava, Czech Republic:Springer International Publishing, 2014. 105-113 [20] 陈成, 何玉庆, 卜春光, 韩建达.基于四阶贝塞尔曲线的无人车可行轨迹规划.自动化学报, 2015, 41(3):486-496 http://www.aas.net.cn/CN/abstract/abstract18627.shtmlChen Cheng, He Yu-Qing, Bu Chun-Guang, Han Jian-Da. Feasible trajectory generation for autonomous vehicles based on quartic Bézier curve. Acta Automatica Sinica, 2015, 41(3):486-496 http://www.aas.net.cn/CN/abstract/abstract18627.shtml [21] Choi J W, Curry R, Elkaim G. Piecewise Bezier curves path planning with continuous curvature constraint for autonomous driving. Machine Learning and Systems Engineering. Netherlands:Springer, 2010. 31-45 [22] Hart P E, Nilsson N J, Raphael B. A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2):100-107 doi: 10.1109/TSSC.1968.300136 [23] Open Source Robotics Foundation (OSRF). Robot operating system[Online], available:http://www.ros.org, May 21, 2016 [24] Open Source Robotics Foundation (OSRF). Gazebo[Online], available:http://www.gazebosim.org/, May 21, 2016 [25] Open Source Robotics Foundation (OSRF). Global planner of navigation stack in ROS[Online], available:http://wiki.ros.org/global_planner?distro=indigo, May 21, 2016 [26] Borges G A, Aldon M J. Line extraction in 2D range images for mobile robotics. Journal of Intelligent and Robotic Systems, 2004, 40(3):267-297 doi: 10.1023/B:JINT.0000038945.55712.65 [27] Duda R O, Hart P E. Pattern Classification and Scene Analysis. New York:Wiley, 1973. -





 下载:
下载: