Continuum Robot Control Based on Varying Parameter Recursive Network and Recursive Least Square
-
摘要: 连续体机器人通常由柔性材料制成, 能够承受大幅度形变, 在各领域具有广阔的应用前景. 然而, 其软体结构和非传统的驱动机制也带来了诸多非线性因素, 使得其状态和运动难以被精确建模. 因此, 为连续体机器人设计了一种无模型控制方案. 该方案一方面通过变参递归神经网络(Varying parameter-recursive neural network, VP-RNN)求解连续体机器人的逆运动学, 以实现高精度运动控制, 另一方面使用递归最小二乘法(Recursive least square, RLS)基于实时数据估计和更新机器人雅可比矩阵伪逆, 以避免机器人的解析建模. 最后, 通过仿真模拟和实物实验验证了所提出控制方案的可行性、精确性和鲁棒性, 并通过一系列对比实验突出了所提出方法的优势. 该方法率先研究基于递归最小二乘法的连续体机器人雅可比矩阵伪逆估计, 对未来的连续体机器人研究具有一定的启示作用.Abstract: Continuum robots are usually made of soft materials and can withstand significant deformation, making them promising for applications in various fields. However, their soft structures and non-traditional actuation mechanisms also bring many nonlinear factors, leading to difficulties in modeling their states and motions precisely. Therefore, this work designs a model-free control scheme for continuum robots. On the one hand, the scheme solves the inverse kinematics of continuum robots through a varying parameter-recursive neural network (VP-RNN) to achieve high-precision motion control. On the other hand, it uses the recursive least square (RLS) method to estimate and update the pseudo-inverse of Jacobian matrix based on real-time data, for the sake of avoiding analytical modeling of robots. Finally, simulations and physical experiments are performed to verify the feasibility, accuracy and robustness of the proposed scheme, and the merits of the proposed method are revealed through a series of comparative experiments. This work pioneers the study of Jacobian matrix pseudo-inverse estimation for continuum robots based on the recursive least square method, which could inspire the future research on continuum robots.
-
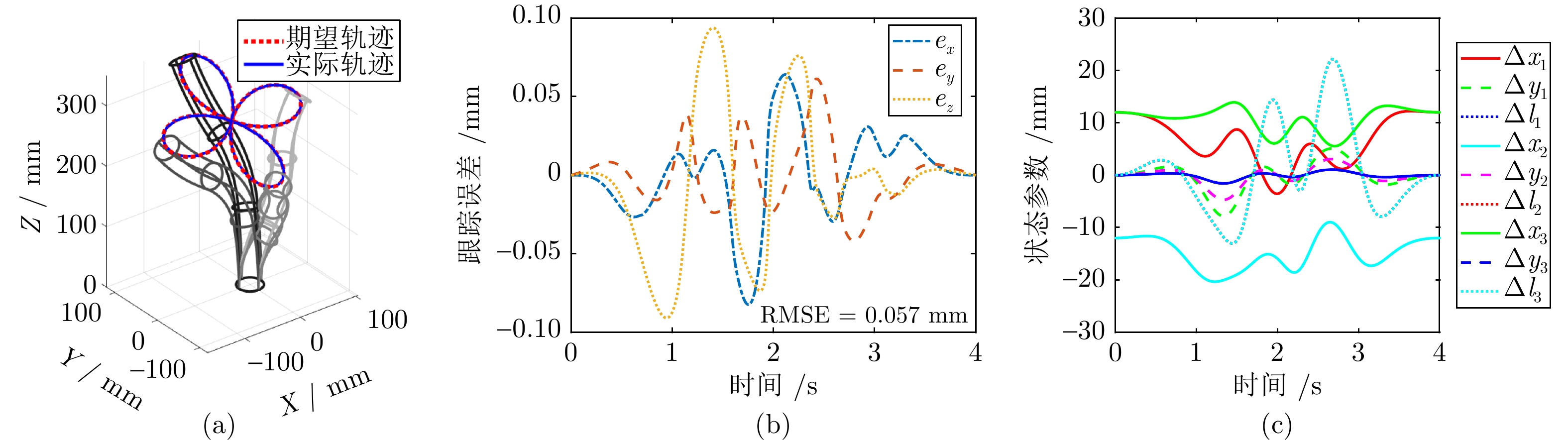
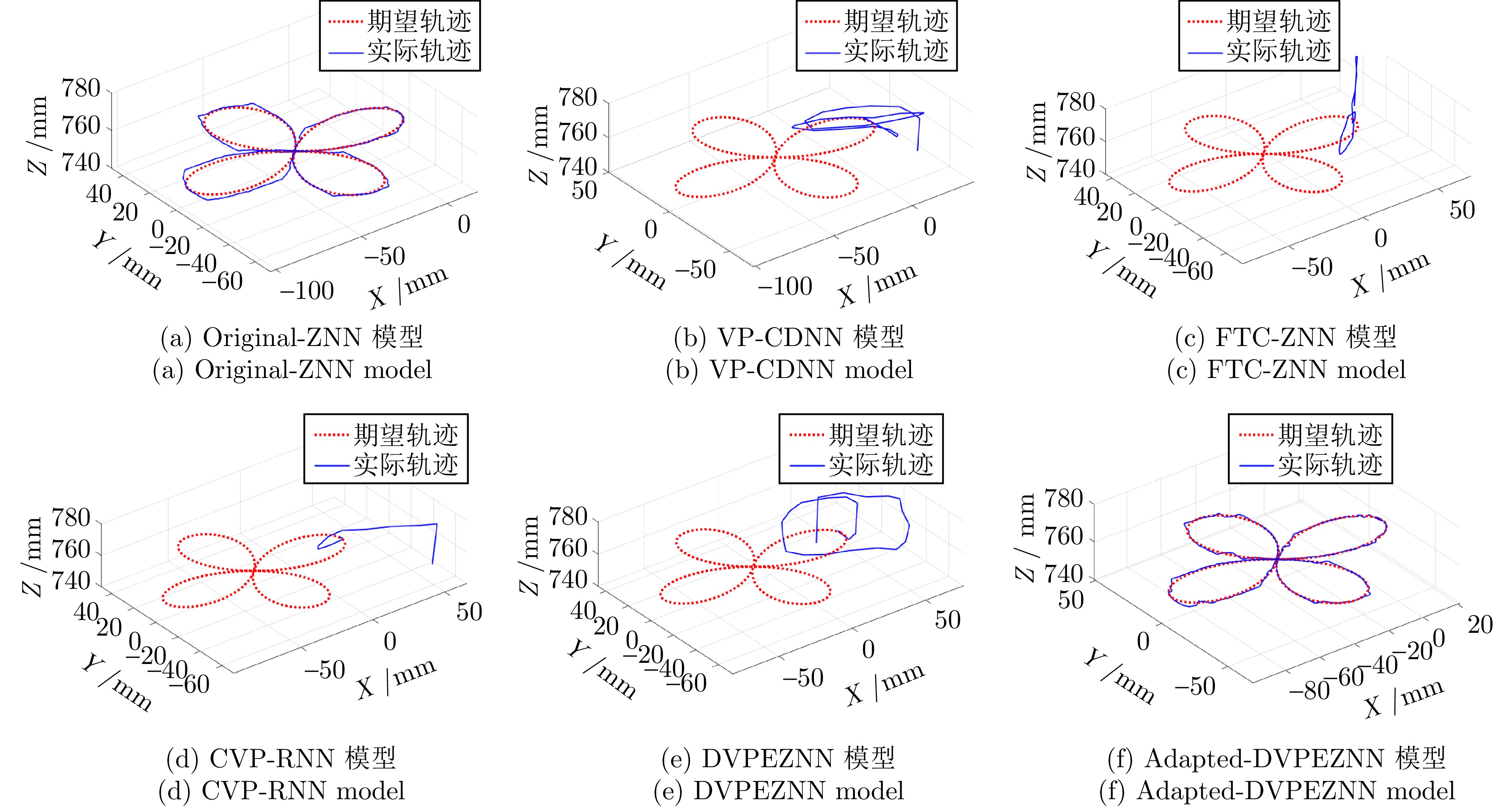
图 3 仿真跟踪结果((a) 采用三段连续体机器人, 利用所提出的基于改进动态变参数增强零化神经网络的控制方案仿真得到的轨迹; (b) 跟踪误差变化$ {\boldsymbol{e}}=[e_x,\; e_y,\; e_z]^{\rm{T}} $; (c) 状态参数q的变化过程)
Fig. 3 Simulation tracking results ((a) Trajectory of the three-segment continuum robot using the proposed control scheme based on Adapted-DVPEZNN; (b) Tracking error $ {\boldsymbol{e}}=[e_x,\; e_y,\; e_z]^{\rm{T}} $; (c) The change of state parameter q)
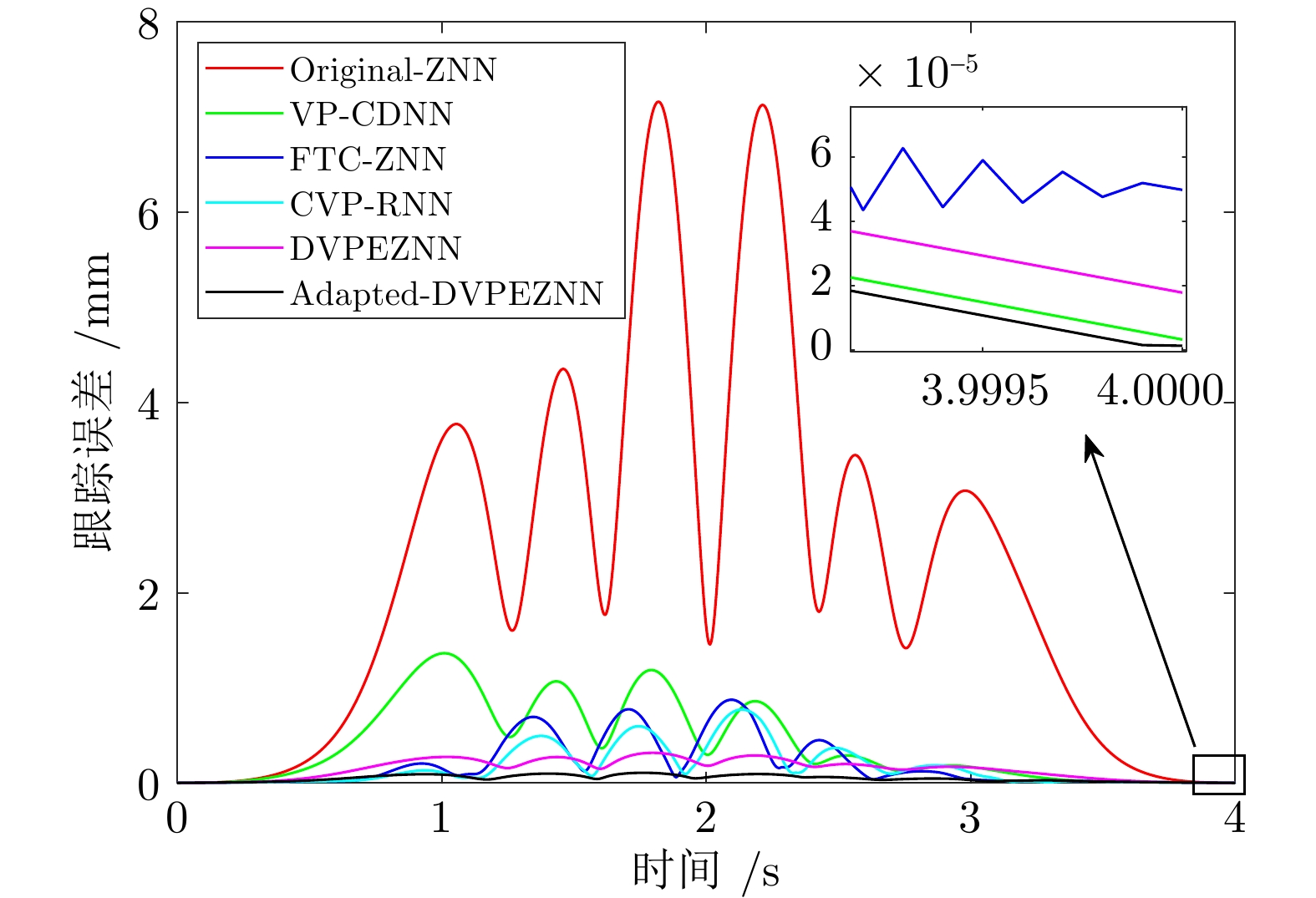
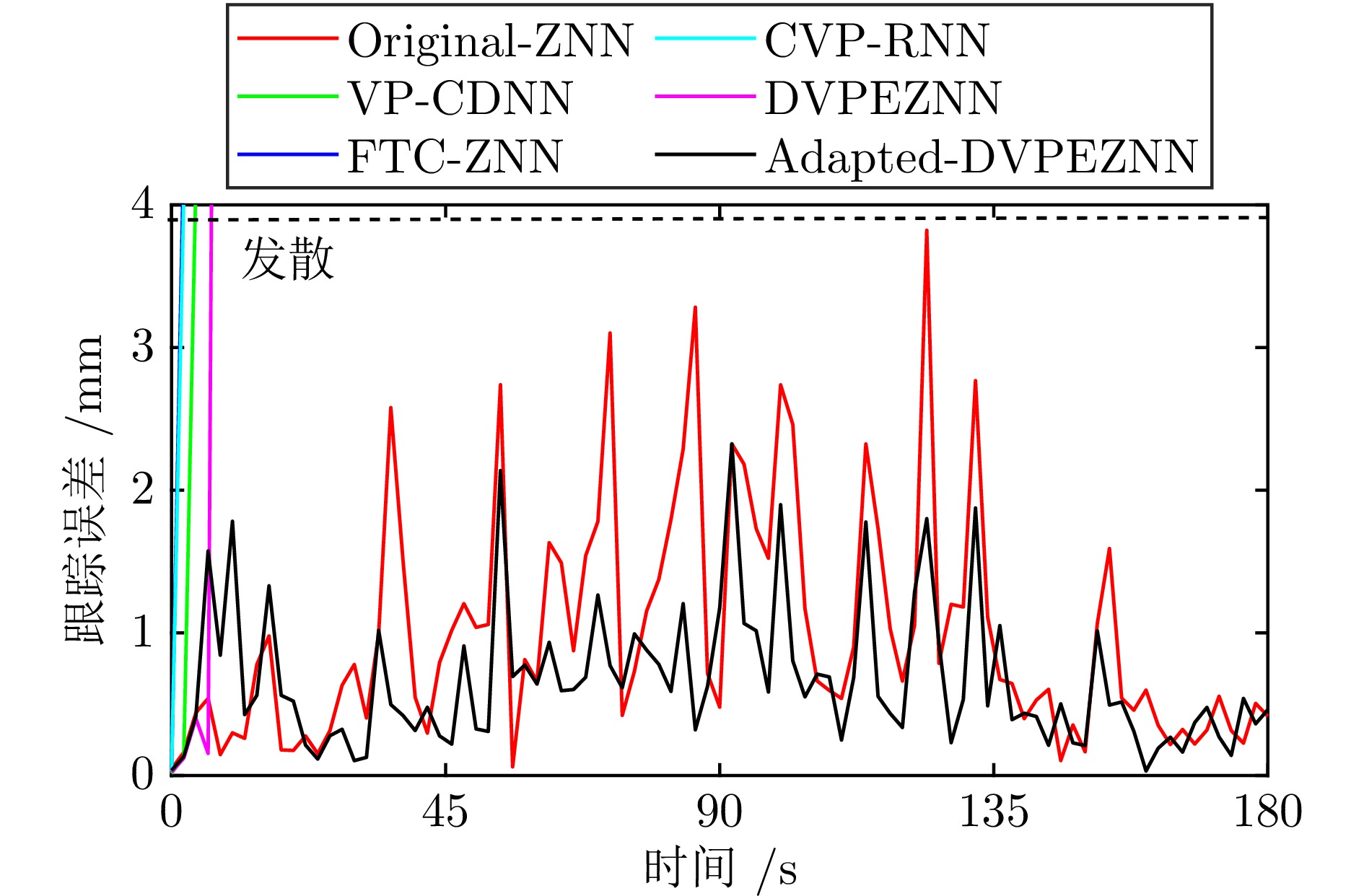
表 1 不同ZNN模型设计公式及激活函数对比
Table 1 Comparison of design formulas and activation functions of different ZNN models
模型 设计公式 激活函数 Original-ZNN[21] $ -\lambda \Phi\left({\boldsymbol{e}}\right) $ $ \phi\left(e\right)=e $ VP-CDNN[24] $ -\lambda \exp(t) \Phi\left({\boldsymbol{e}}\right) $ $ \phi\left(e\right)=e $ FTC-ZNN[25] $ -\lambda \left(P({\boldsymbol{e}})+\displaystyle \int_0^t Q({\boldsymbol{e}}(\tau)){\rm{d}}\tau\right) $ $\left\{ \begin{aligned} &p(e)=(k_1g^\frac{1}{2}(t,\; e)\left|e\right|^\frac{1}{2}+k_2g(t,\; e)\left|e\right|){\rm{sign} }(e)\\&q(e)=(k_3g(t,\; e)+k_4g^2(t,\; e)\left|e\right|){\rm{sign} }(e) \end{aligned} \right.$ CVP-RNN[35] $ -\lambda (t)P({\boldsymbol{e}}(t))-\displaystyle \int_0^t \mu(\tau)Q({\boldsymbol{e}}(\tau)){\rm{d}}\tau $ $ \left\{ \begin{aligned} &p(e)=\frac{1}{\sigma}\exp\left(\left|e\right|^\sigma\right)\psi^{1-\sigma}(e)\\ &q(e)=\frac{1}{\sigma}\exp\left(2\left|e\right|^\sigma\right)\left(\psi^{1-\sigma}(e)+\frac{1-\sigma}{\sigma}\psi^{1-2\sigma}(e)\right) \end{aligned} \right. $ DVPEZNN[36] $ -\lambda\exp\left(\left(\beta^t+\beta\right)\Vert{\boldsymbol{e}}\Vert_2\right)P({\boldsymbol{e}}) $ $ p(e)= \begin{cases} \zeta_1\psi^{r_1}(e)+\zeta_2e\exp\left(\left|e\right|+1\right),\; \left|e\right|\leq1\\\zeta_1\psi^{r_2}(e)+\zeta_2e\exp\left(\left|e\right|+1\right),\; {\text{其他}} \end{cases} $ Adapted-DVPEZNN $\begin{aligned} & -\lambda\bigg(\exp\left(\xi_1\beta^t\Vert{\boldsymbol{e} }\Vert_2\right)P({\boldsymbol{e} })\;+\\ &\displaystyle \int_0^t \exp\left(\xi_2 \tau +\xi_3\right)Q({\boldsymbol{e} }) {\rm{d} }\tau \bigg) \end{aligned}$ $ \left\{\begin{aligned} &p(e)= \begin{cases} \zeta_1\psi^{r_1}(e)+\zeta_2e\exp\left(\zeta_3\left|e\right|+1\right),\; \left|e\right|\leq1\\\zeta_1\psi^{r_2}(e)+\zeta_2e\exp\left(\zeta_3\left|e\right|+1\right),\; {\text{其他}} \end{cases}\\ &q(e)= \begin{cases} \zeta_4\psi^{r_1}(e),\; \left|e\right|\leq1\\\zeta_4\psi^{r_2}(e),\; {\text{其他}} \end{cases} \end{aligned} \right. $ 表 2 ZNN模型在无噪声下的定量分析
Table 2 Quantitative analysis of ZNN models without noise
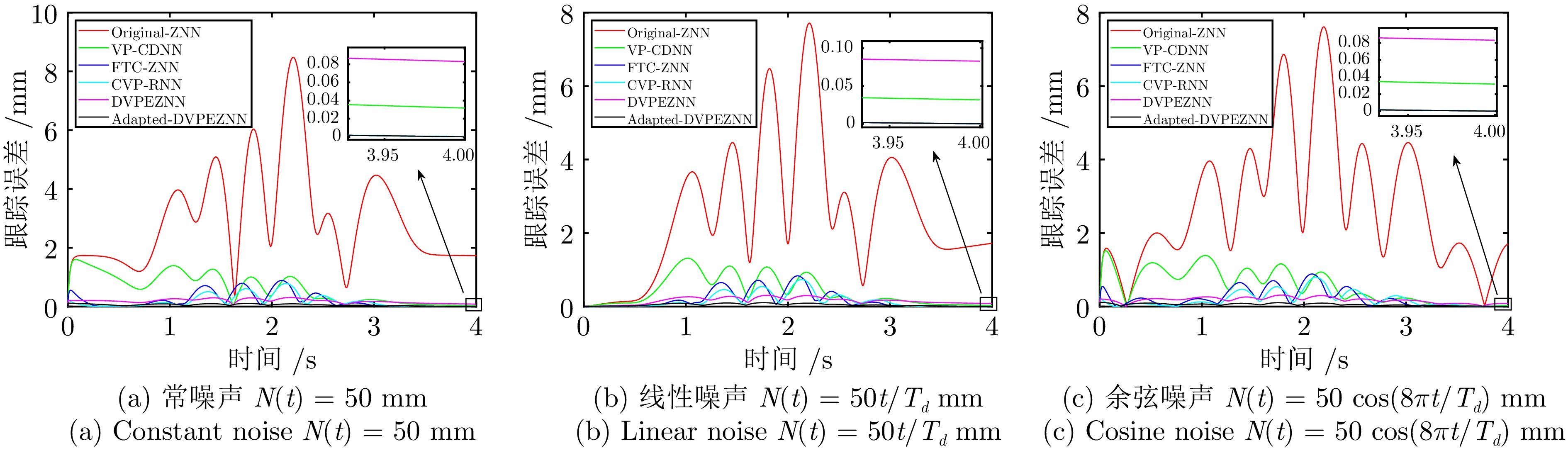
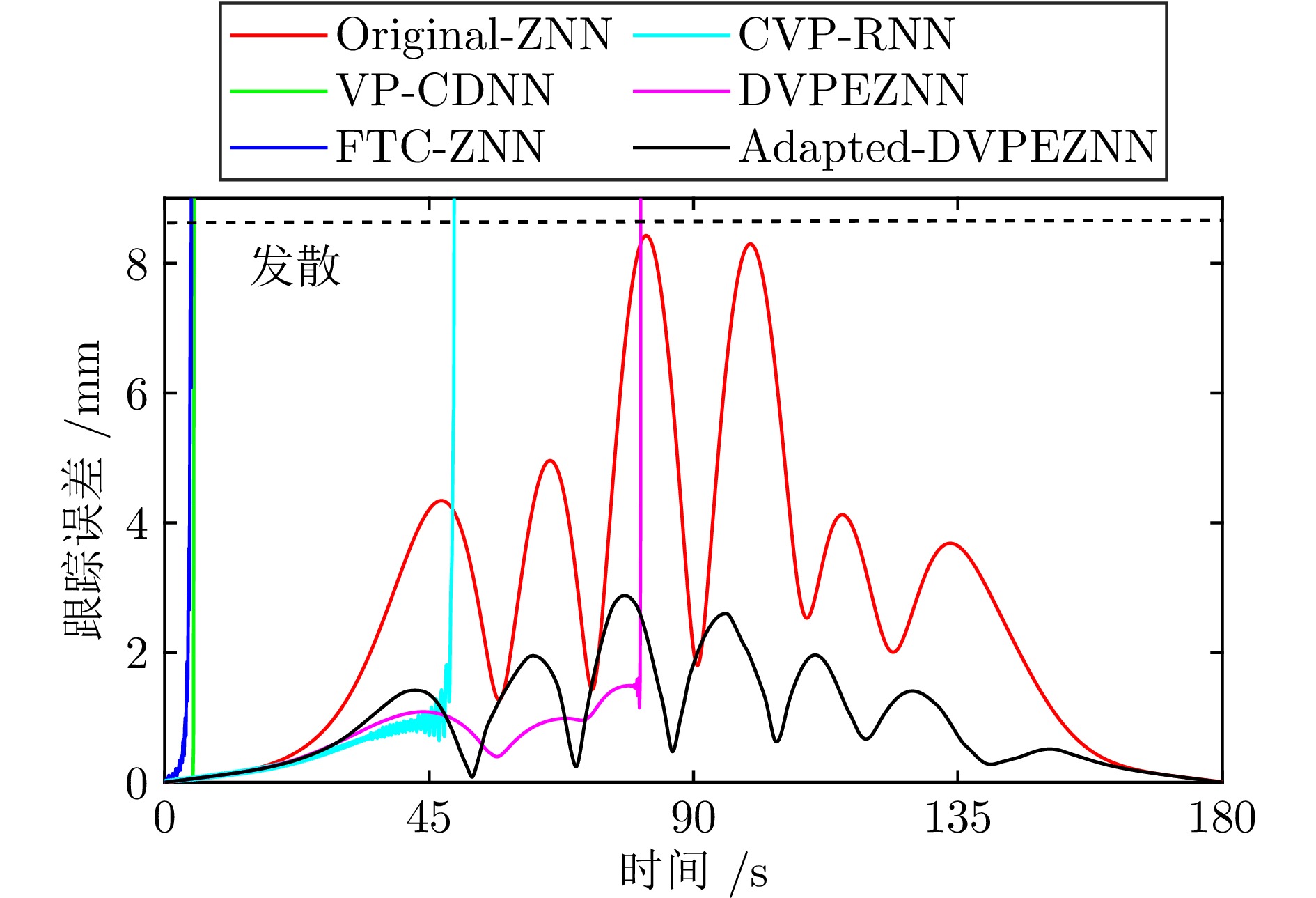
表 3 ZNN模型受噪声影响时的定量分析
Table 3 Quantitative analysis of ZNN models with noise
表 4 参数更新方法的定量分析
Table 4 Quantitative analysis of parameter update methods
方法 跟踪误差(mm) 控制能耗(s) 增量法 0.033 33.658 双模型法 0.058 1 356.239 递归最小二乘法 0.057 7.689 表 5 收敛系数$ \lambda $定量分析
Table 5 Quantitative analysis of convergence factor $ \lambda $
收敛系数$ \lambda $ 跟踪误差(mm) 控制能耗(s) 1 0.150 7.872 3 0.122 7.786 5 0.110 7.830 10 0.093 7.607 30 0.068 7.426 50 0.057 7.382 表 6 遗忘因子$ \gamma $定量分析
Table 6 Quantitative analysis of forgetting factor $ \gamma $
遗忘因子$ \gamma $ 跟踪误差(mm) 控制能耗(s) 0.1 $ 5.762 \times 10^{-2} $ 7.454 0.3 $ 5.757 \times 10^{-2} $ 7.508 0.5 $ 5.759 \times 10^{-2} $ 7.408 0.7 $5.751 \times 10^{-2} $ 7.368 0.9 $ 5.711 \times 10^{-2} $ 7.382 1.0 $5.939 \times 10^{-2} $ 7.779 表 7 不同场景下的跟踪误差定量分析
Table 7 Quantitative analysis of tracking errors in different scenarios
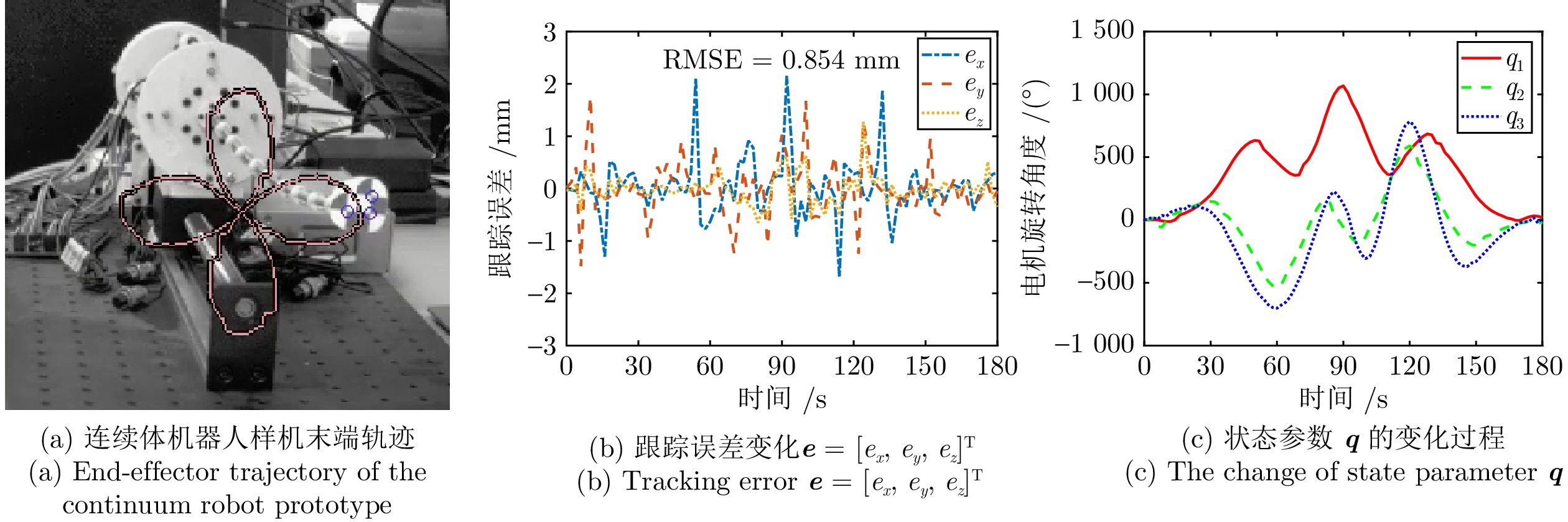
场景设置 跟踪误差 (mm) 无负载无障碍物 0.854 1个负载无障碍物 0.986 2个负载无障碍物 1.208 无负载有障碍物 0.869 -
[1] Yip M C, Camarillo D B. Model-less hybrid position/force control: A minimalist approach for continuum manipulators in unknown, constrained environments. IEEE Robotics and Automation Letters, 2016, 1(2): 844−851 doi: 10.1109/LRA.2016.2526062 [2] Rus D, Tolley M T. Design, fabrication and control of soft robots. Nature, 2015, 521(7553): 467−475 doi: 10.1038/nature14543 [3] Fang G, Tian Y, Yang Z X, Geraedts J M, Wang C C. Effcient Jacobian-based inverse kinematics with sim-to-real transfer of soft robots by learning. IEEE/ASME Transactions on Mechatronics, 2022, 27(6): 5296−5306 doi: 10.1109/TMECH.2022.3178303 [4] Polygerinos P, Wang Z, Galloway K C, Wood R J, Walsh C J. Soft robotic glove for combined assistance and at-home rehabilitation. Robotics and Autonomous Systems, 2015, 73: 135−143 doi: 10.1016/j.robot.2014.08.014 [5] Ranzani T, Gerboni G, Cianchetti M, Menciassi A. A bioinspired soft manipulator for minimally invasive surgery. Bioinspiration & biomimetics, 2015, 10(3): Article No. 035008 [6] El-Atab N, Mishra R B, Al-Modaf F, Joharji L, Alsharif A A, Alamoudi H, et al. Soft actuators for soft robotic applications: A review. Advanced Intelligent Systems, 2020, 2(10): Article No. 2000128 doi: 10.1002/aisy.202000128 [7] Lee C, Kim M, Kim Y J, Hong N, Ryu S, Kim H J, et al. Soft robot review. International Journal of Control, Automation and Systems, 2017, 15: 3−15 doi: 10.1007/s12555-016-0462-3 [8] Kasaei M, Babarahmati K K, Li Z, Khadem M. Data-effcient non-parametric modelling and control of an extensible soft manipulator. In: Proceedings of 2023 IEEE International Conference on Robotics and Automation (ICRA). London, UK: IEEE, 2023. 2641−2647 [9] 徐璠, 王贺升. 软体机械臂水下自适应鲁棒视觉伺服. 自动化学报, 2023, 49(4): 744−753Xu Fan, Wang He-Sheng. Adaptive robust visual servoing control of a soft manipulator in underwater environment. Acta Automatica Sinica, 2023, 49(4): 744−753 [10] Qiu K, Zhang J, Sun D, Xiong R, Lu H, Wang Y. An effcient multi-solution solver for the inverse kinematics of 3-section constant-curvature robots. In: Proceedings of Robotics: Science and Systems (RSS). Daegu, Republic of Korea: RSS Foundation, 2023 [11] Thamo B, Dhaliwal K, Khadem M. Rapid solution of cosserat rod equations via a nonlinear partial observer. In: Proceedings of 2021 IEEE International Conference on Robotics and Automation (ICRA). Xi'an, China: IEEE, 2021. 9433−9438 [12] Xavier M S, Fleming A J, Yong Y K. Finite element modeling of soft fluidic actuators: Overview and recent developments. Advanced Intelligent Systems, 2021, 3(2): Article No. 2000187 doi: 10.1002/aisy.202000187 [13] Yu B, Fernández J d G, Tan T. Probabilistic kinematic model of a robotic catheter for 3D position control. Soft Robotics, 2019, 6(2): 184−194 doi: 10.1089/soro.2018.0074 [14] Jung J, Park M, Kim D, Park Y L. Optically sensorized elastomer air chamber for proprioceptive sensing of soft pneumatic actuators. IEEE Robotics and Automation Letters, 2020, 5(2): 2333−2340 doi: 10.1109/LRA.2020.2970984 [15] Ha X T, Wu D, Lai C F, Ourak M, Borghesan G, Menciassi A, et al. Contact localization of continuum and flexible robot using data-driven approach. IEEE Robotics and Automation Letters, 2022, 7(3): 6910−6917 doi: 10.1109/LRA.2022.3176723 [16] Bern J M, Schnider Y, Banzet P, Kumar N, Coros S. Soft robot control with a learned differentiable model. In: Proceedings of 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft). New Haven, USA: IEEE, 2020. 417−423 [17] Giorelli M, Renda F, Calisti M, Arienti A, Ferri G, Laschi C. Neural network and Jacobian method for solving the inverse statics of a cable-driven soft arm with nonconstant curvature. IEEE Transactions on Robotics, 2015, 31(4): 823−834 doi: 10.1109/TRO.2015.2428511 [18] Thuruthel T G, Falotico E, Manti M, Laschi C. Stable open loop control of soft robotic manipulators. IEEE Robotics and Automation Letters, 2018, 3(2): 1292−1298 doi: 10.1109/LRA.2018.2797241 [19] Thuruthel T G, Shih B, Laschi C, Tolley M T. Soft robot perception using embedded soft sensors and recurrent neural networks. Science Robotics, 2019, 4(26): Article No. eaav1488 doi: 10.1126/scirobotics.aav1488 [20] Jiang H, Wang Z, Jin Y, Chen X, Li P, Gan Y, et al. Hierarchical control of soft manipulators towards unstructured interactions. The International Journal of Robotics Research, 2021, 40(1): 411−434 doi: 10.1177/0278364920979367 [21] Zhang Y, Guo D. Zhang Functions and Various Models. Berlin: Springer-Verlag, 2015. [22] Zhang Y, Jiang D, Wang J. A recurrent neural network for solving Sylvester equation with time-varying coeffcients. IEEE Transactions on Neural Networks, 2002, 13(5): 1053−1063 doi: 10.1109/TNN.2002.1031938 [23] Chen D, Zhang Y, Li S, Ling Y. Robust Zhang neural network for tracking control of parallel robot manipulators with unknown parameters. In: Proceedings of 2019 Chinese Control and Decision Conference (CCDC). Nanchang, China: IEEE, 2019. 3527−3532 [24] Zhang Z, Yan Z. A varying parameter recurrent neural network for solving nonrepetitive motion problems of redundant robot manipulators. IEEE Transactions on Control Systems Technology, 2018, 27(6): 2680−2687 [25] Tan Z, Li W, Xiao L, Hu Y. New varying-parameter ZNN models with finite-time convergence and noise suppression for time-varying matrix Moore-Penrose inversion. IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(8): 2980−2992 [26] Tan N, Yu P, Zhang X, Wang T. Model-free motion control of continuum robots based on a zeroing neurodynamic approach. Neural Networks, 2021, 133: 21−31 doi: 10.1016/j.neunet.2020.10.005 [27] Chen D, Zhang Y, Li S. Tracking control of robot manipulators with unknown models: A Jacobian-Matrix-Adaption method. IEEE Transactions on Industrial Informatics, 2018, 14(7): 3044−3053 doi: 10.1109/TII.2017.2766455 [28] Tan N, Yu P, Ni F, Sun Z. Trajectory tracking of soft continuum robots with unknown models based on varying parameter recurrent neural networks. In: Proceedings of 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Melbourne, Australia: IEEE, 2021. 1035−1041 [29] Hu X, Sun F, Zou Y, Peng H. Online estimation of an electric vehicle Lithium-Ion battery using recursive least squares with forgetting. In: Proceedings of the 2011 American Control Conference. San Francisco, USA: IEEE, 2011. 935−940 [30] Ho H W, Zhou Y. Incremental nonlinear dynamic inversion based optical flow control for flying robots: An effcient data-driven approach. In: Proceedings of Robotics: Science and Systems (RSS). Daegu, Republic of Korea: RSS Foundation, 2023 [31] Webster III R J, Jones B A. Design and kinematic modeling of constant curvature continuum robots: A review. The International Journal of Robotics Research, 2010, 29(13): 1661−1683 doi: 10.1177/0278364910368147 [32] Della Santina C, Bicchi A, Rus D. On an improved state parametrization for soft robots with piecewise constant curvature and its use in model based control. IEEE Robotics and Automation Letters, 2020, 5(2): 1001−1008 doi: 10.1109/LRA.2020.2967269 [33] Zhang Y, Xiao L, Xiao Z, Mao M. Zeroing Dynamics, Gradient Dynamics, and Newton Iterations. Florida: CRC Press, 2016. [34] Liao B, Zhang Y. Different complex ZFs leading to different complex ZNN models for time-varying complex generalized inverse matrices. IEEE Transactions on Neural Networks and Learning Systems, 2013, 25(9): 1621−1631 [35] Tan N, Yu P, Ni F. New varying-parameter recursive neural networks for model-free kinematic control of redundant manipulators with limited measurements. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1−14 [36] Xiao L, Li X, Cao P, He Y, Tang W, Li J, et al. A dynamic-varying parameter enhanced ZNN model for solving time-varying complex-valued tensor inversion with its application to image encryption. IEEE Transactions on Neural Networks and Learning Systems, 35 (10): 13681−13690, 2023 [37] Sherman J, Morrison W J. Adjustment of an inverse matrix corresponding to a change in one element of a given matrix. The Annals of Mathematical Statistics, 1950, 21(1): 124−127 doi: 10.1214/aoms/1177729893 -




 下载:
下载: