Model-free Output Consensus Control for Heterogeneous Nonlinear Multi-agent Systems
-
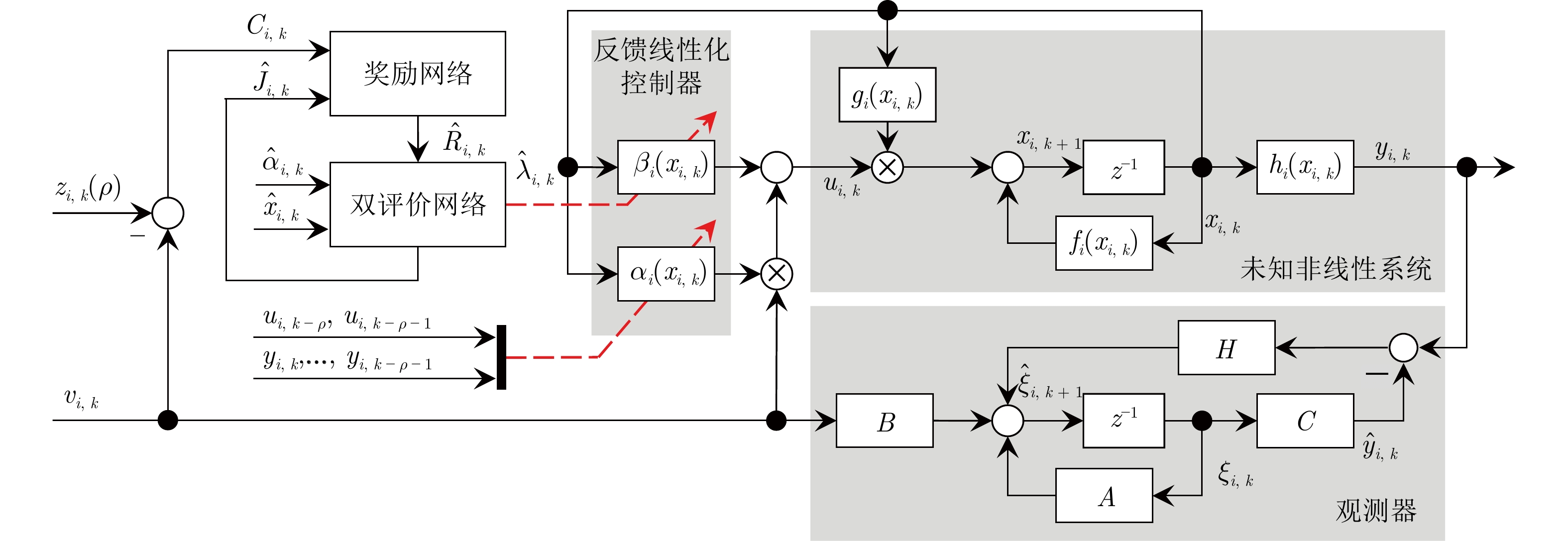
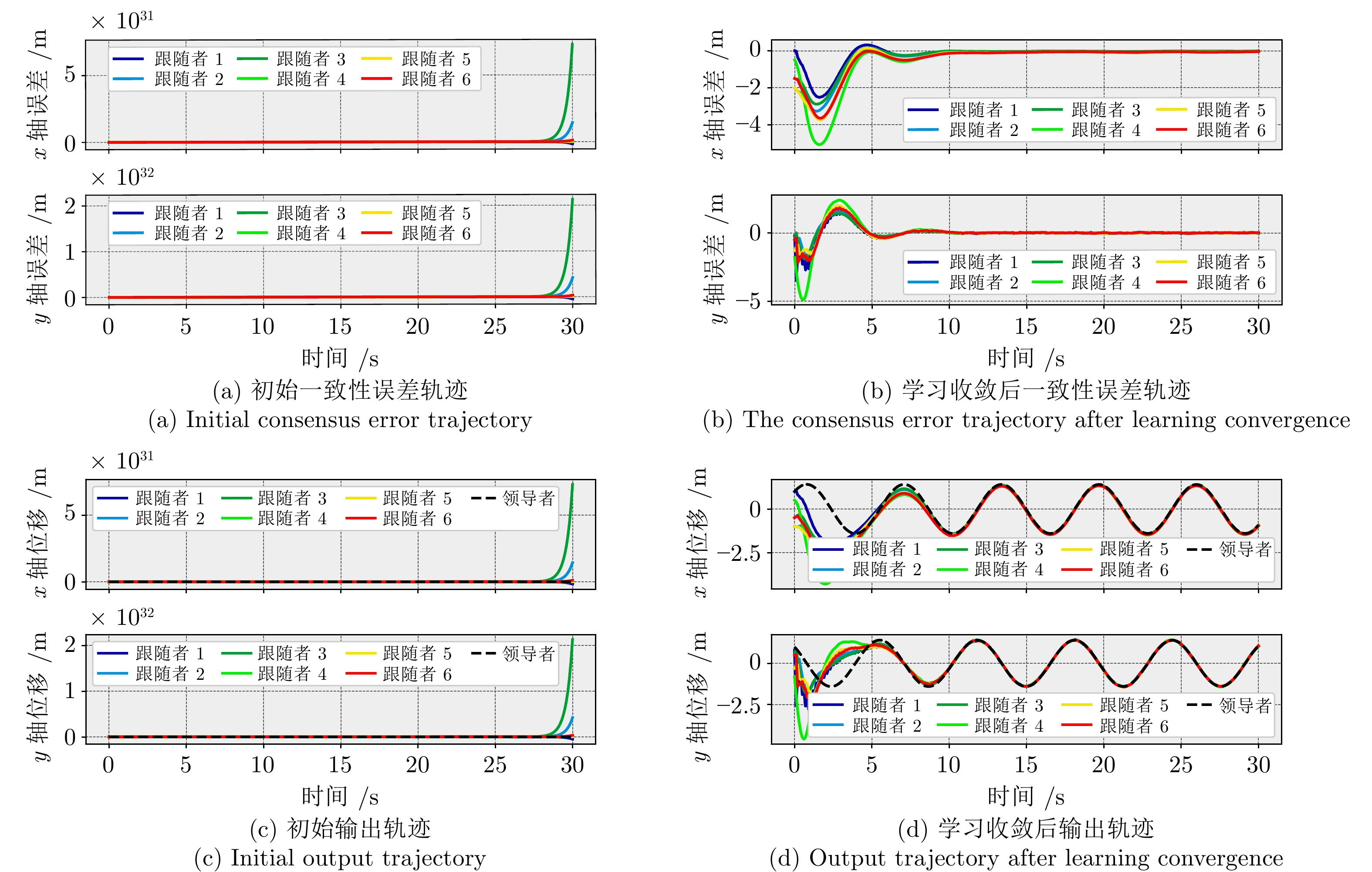
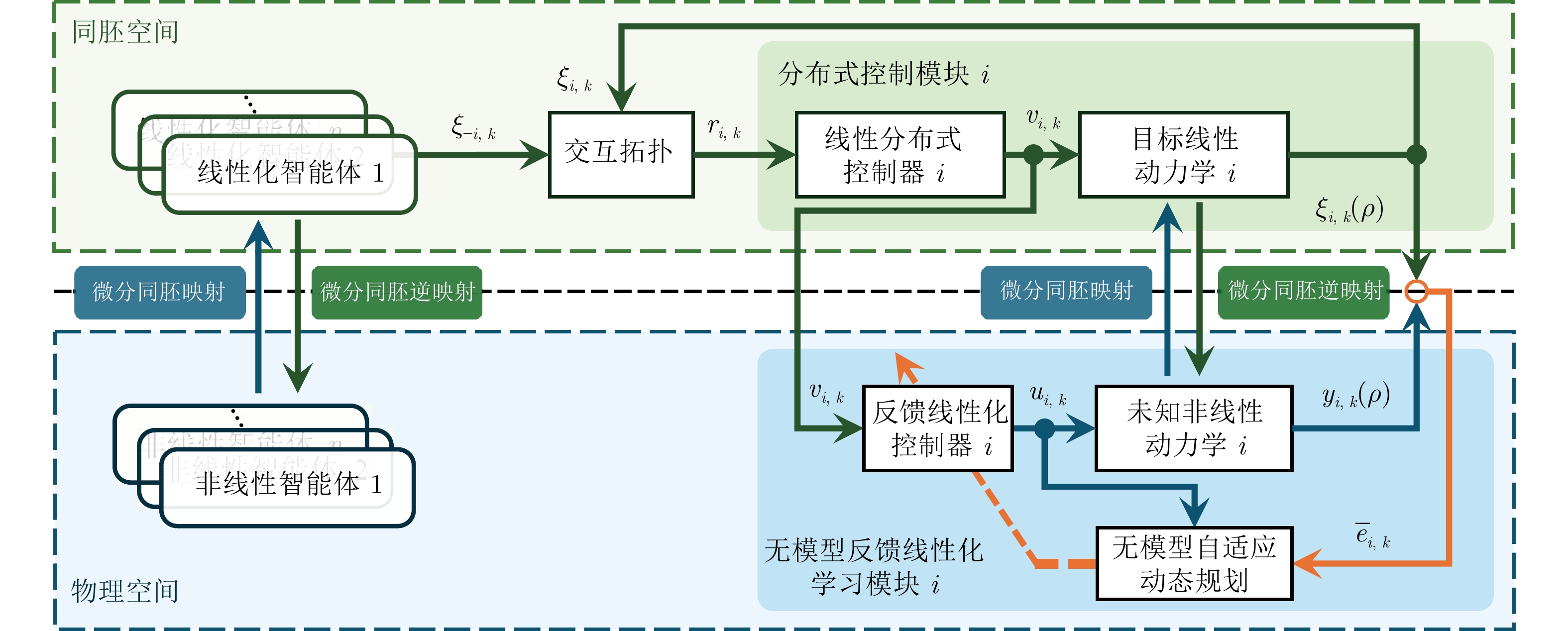
摘要: 针对异构非线性多智能体系统的输出一致性控制难题, 设计了一种基于同胚分布式控制协议的无模型方法. 通过将输出反馈线性化理论与自适应动态规划相结合, 可以在不需要精确系统模型的情况下实现非线性智能体的线性化, 简化分布式控制器的设计复杂性. 具体而言, 通过设计双层分布式控制结构, 在物理空间层通过无模型反馈线性书方法实现未知系统线性化, 在微分同构空间层利用线性控制方法进行分布式共识控制. 通过两个实验验证了所提方法在处理未知异构非线性多智能体系统中的有效性, 将传统的线性分布式控制方法扩展到未知非线性多智能体控制器设计问题.Abstract: A model-free method based on homeomorphic distributed control protocol is proposed to address the output consensus control problem of heterogeneous nonlinear multi-agent systems. By integrating output feedback linearization theory with adaptive dynamic programming, this approach linearizes nonlinear agents without requiring precise system models, simplifying the design of distributed controllers. Specifically, a two-layer distributed control structure is designed: in the physical space layer, model-free feedback linearization is applied to linearize unknown systems, while in the diffeomorphic space layer, linear control techniques are used for distributed consensus control. The effectiveness of the proposed method in handling unknown heterogeneous nonlinear multi-agent systems is validated through two experiments, extending traditional linear distributed control methods to the design of controllers for unknown nonlinear multi-agent systems.
-
图 1 同胚分布式控制协议结构图
Fig. 1 Structure diagram of homeomorphic distributed control protocol
图 4 学习前后输出和一致性误差轨迹对比((a)初始一致性误差轨迹; (b)学习收敛后一致性误差轨迹; (c)初始输出轨迹; (d)学习收敛后输出轨迹)
Fig. 4 The output and output error trajectory comparison before and after learning ((a) initial consensus error trajectory; (b) the consensus error trajectory after learning convergence; (c) initial output trajectory; (d) output trajectory after learning convergence))
图 7 网络更新损失演化轨迹((a)评价网络更新损失; (b)奖励网络更新损失)
Fig. 7 Evolution trajectory of network update loss ((a) Critic network update loss; (b) Reward network update loss)
图 8 学习收敛后输出一致性轨迹切换实验
Fig. 8 Output consensus trajectory switching experiment after learning convergence
表 1 异构多智能体系统参数
Table 1 Heterogeneous multi-agent system parameters
变量 值 (m) 变量 值 (m) 变量 值 (m) $ {m_1} $ 0.04 $ {m_2} $ 0.04 $ {m_3} $ 0.06 $ {h_1} $ 0.06 $ {h_2} $ 0.04 $ {h_3} $ 0.06 $ {m_4} $ 0.06 $ {m_5} $ 0.08 $ {m_6} $ 0.08 $ {h_4} $ 0.04 $ {h_5} $ 0.06 $ {h_6} $ 0.04 
下载: 导出CSV
表 2 学习参数设置
Table 2 Learning parameter
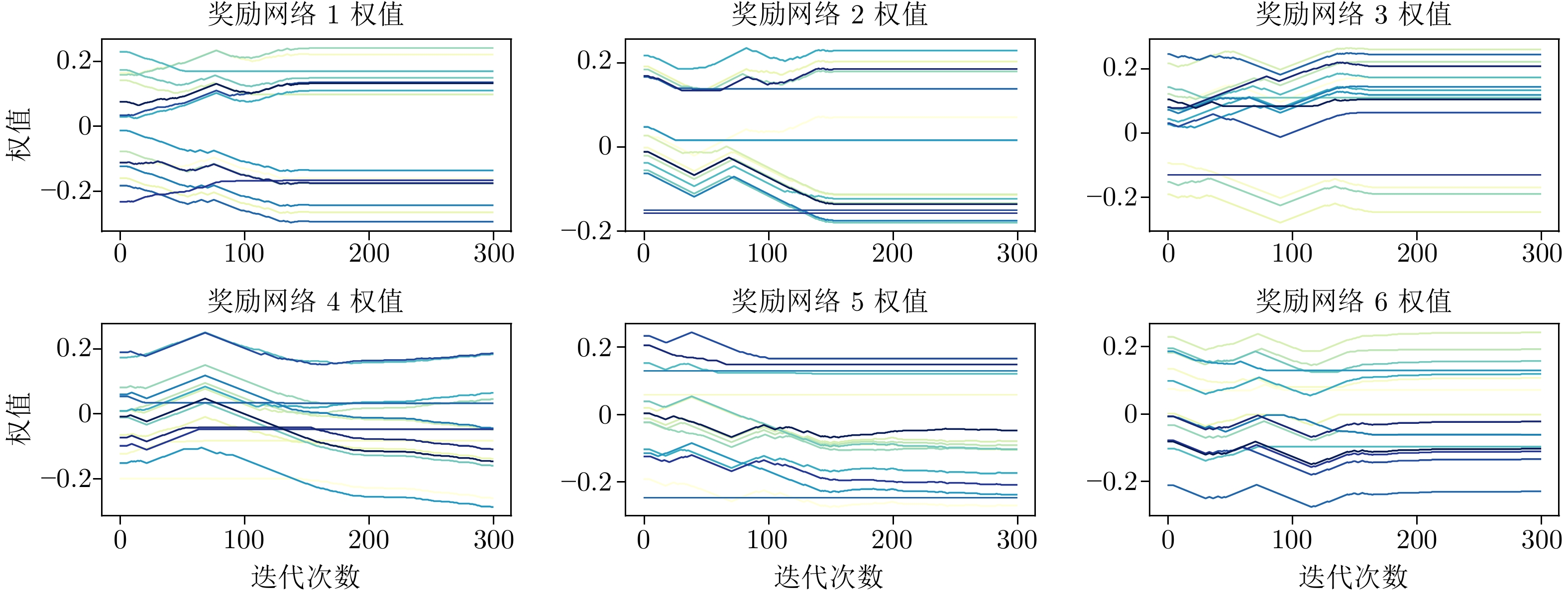
参数 值 参数 值 参数 值 $ {\eta _r} $ 0.05 $ {\eta _c} $ 0.02 $ {\eta _a} $ 0.01 $ \gamma $ 0.9 $ {\mu _j} $ 0.01 $ {\mu _\lambda } $ 0.01 $ \varepsilon_i $ 0.08 $ H $ $ [1,\; 0.2] $
下载: 导出CSV
-
[1] Nair R R and Behera L. Robust adaptive gain higher order sliding mode observer based control-constrained nonlinear model predictive control for spacecraft formation flying. IEEE/CAA Journal of Automatica Sinica, 2016, 5(1): 367−381 [2] Guo X, Wei G, Yao M, and Zhang P. Consensus control for multiple euler-lagrange systems based on high-order disturbance observer: An event-triggered approach. IEEE/CAA Journal of Automatica Sinica, 2022, 9(5): 945−948 doi: 10.1109/JAS.2022.105584 [3] Peng Z, Wang D, Li T, and Han M. Output-feedback cooperative formation maneuvering of autonomous surface vehicles with connectivity preservation and collision avoidance. IEEE Transactions on Cybernetics, 2019, 50(6): 2527−2535 [4] Simões D, Lau N, and Reis L P. Multi-agent actor centralized-critic with communication. Neurocomputing, 2020, 390: 40−56 doi: 10.1016/j.neucom.2020.01.079 [5] Wu J and Lou Y. Efficient centralized traffic grid signal control based on meta-reinforcement learning. IEEE/CAA Journal of Automatica Sinica, 20231−3 [6] Yan B, Shi P, and Lim C-C. Robust formation control for nonlinear heterogeneous multiagent systems based on adaptive event-triggered strategy. IEEE Transactions on Automation Science and Engineering, 2021, 19(4): 2788−2800 [7] Bai C, Yan P, Pan W, and Guo J. Learning-based multi-robot formation control with obstacle avoidance. IEEE Transactions on Intelligent Transportation Systems, 2021, 23(8): 11811−11822 [8] Huang J, Zhou S, Tu H, Yao Y, and Liu Q. Distributed optimization algorithm for multi-robot formation with virtual reference center. IEEE/CAA Journal of Automatica Sinica, 2022, 9(4): 732−734 doi: 10.1109/JAS.2022.105473 [9] Ju Y, Ding D, He X, Han Q-L, and Wei G. Consensus control of multi-agent systems using fault-estimation-in-the-loop: Dynamic event-triggered case. IEEE/CAA Journal of Automatica Sinica, 2021, 9(8): 1440−1451 [10] Yu X, Yang F, Zou C, and Ou L. Stabilization parametric region of distributed PID controllers for general first-order multi-agent systems with time delay. IEEE/CAA Journal of Automatica Sinica, 2019, 7(6): 1555−1564 [11] Bidram A, Lewis F L, and Davoudi A. Synchronization of nonlinear heterogeneous cooperative systems using input-output feedback linearization. Automatica, 2014, 50(10): 2578−2585 doi: 10.1016/j.automatica.2014.08.016 [12] Sun Y, Chen X, He W, Zhang Z. Fukushima E F, and She J, Q-learning based model-free input-output feedback linearization control method. IFAC-PapersOnLine, 2023, 56(2): 9534−9539 doi: 10.1016/j.ifacol.2023.10.253 [13] Li K, Hua C C, You X, and Guan X P. Output feedback-based consensus control for nonlinear time delay multiagent systems. Automatica, 2020, 111: 108669 doi: 10.1016/j.automatica.2019.108669 [14] Wang D, Gao N, Liu D, Li J, and Lewis F L, Recent progress in reinforcement learning and adaptive dynamic programming for advanced control applications[J], IEEE/CAA Journal of Automatica Sinica, 2023. [15] Jiang H and He H. Data-driven distributed output consensus control for partially observable multiagent systems. IEEE Transactions on Cybernetics, 2018, 49(3): 848−858 [16] Jiang Y, Fan J, Gao W, Chai T, and Lewis F L. Cooperative adaptive optimal output regulation of nonlinear discrete-time multi-agent systems. Automatica, 2020, 121: 109149 doi: 10.1016/j.automatica.2020.109149 [17] Lu X and Li H. Consensus of singular linear multiagent systems via hybrid control. IEEE Transactions on Control of Network Systems, 2022, 9(2): 647−656 doi: 10.1109/TCNS.2022.3161193 [18] Wen G, Chen C L P, Feng J, and Zhou N. Optimized multi-agent formation control based on an identifier–actor–critic reinforcement learning algorithm. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 2719−2731 doi: 10.1109/TFUZZ.2017.2787561 -
计量
- 文章访问数: 19
- HTML全文浏览量: 14
- 被引次数: 0
