-
摘要: 针对三维空间中多航天器协同捕获机动目标问题, 提出一种具有终端角度约束和时间一致性约束的设定时间协同制导律, 将视线角误差和齐射攻击的收敛时间作为一个可提前设定的参数, 实现对收敛时间进行设置. 构建三维场景航天器−目标运动学模型, 在沿视线(Line-of-sight, LOS)方向将同时攻击问题转化为一致性问题, 提出一种分布式协同制导律, 设定时间内使得多个航天器剩余飞行时间相等; 在垂直视线方向利用滑模控制方法对制导律进行设计, 使得每个航天器的视线角在设定时间内达到期望值. 上述制导律中, 设计了一种设定时间扩展状态观测器对未知的目标加速度进行估计. 数值仿真结果验证了方法的有效性.Abstract: Aiming at the problem of multi-spacecraft cooperatively capturing the maneuvering target in 3D, a predefined-time cooperative guidance law with terminal angle constraint and time consistency constraint is proposed. The convergence time of line-of-sight (LOS) angle error and salvo attack can be treated as predefined parameters to achieve the setting of the convergence time. Construct a 3D scene spacecraft-target kinematics model. The simultaneous attack problem can be regarded as a consensus problem along the LOS direction, where a distributed cooperative guidance law is presented to make the time-to-go of all spacecrafts equal within the predefined-time. A guidance law is also designed using sliding mode control in the normal direction of the LOS to achieve the desired LOS angles for each spacecraft within the predefined-time. In the above guidance law, a predefined-time extended state observer (PTESO) is developed to estimate the unknown target acceleration. The effectiveness of this method is verified by numerical simulation results.
-
图 10 ${T_s} = 3\,\;\mathrm{s} $沿视线方向目标加速度真值和观测值
Fig. 10 Actual values and observations of target acceleration on the LOS direction when ${T_s} = 3\,\;\mathrm{s} $
图 12 $ {T_s} = 3\,\;\mathrm{s}$视线偏角方向目标加速度真值和观测值
Fig. 12 Actual values and observations of target acceleration on the yaw direction when $ {T_s} = 3\,\;\mathrm{s}$
图 13 ${T_s} = 2\,\;\mathrm{s} $沿视线方向目标加速度真值和观测值
Fig. 13 Actual values and observations of target acceleration on the LOS direction when ${T_s} = 2\,\;\mathrm{s} $
图 15 ${T_s} = 2\,\;\mathrm{s} $视线偏角方向目标加速度真值和观测值
Fig. 15 Actual values and observations of target acceleration on the yaw direction when ${T_s} = 2\,\;\mathrm{s} $
图 11 $ {T_s} = 3\,\;\mathrm{s}$视线倾角方向目标加速度真值和观测值
Fig. 11 Actual values and observations of target acceleration on the pitch direction when $ {T_s} = 3\,\;\mathrm{s}$
图 14 ${T_s} = 2\,\;\mathrm{s} $视线倾角方向目标加速度真值和观测值
Fig. 14 Actual values and observations of target acceleration on the pitch direction when ${T_s} = 2\,\;\mathrm{s} $
图 16 ${T_{fr}} = 8\,\;\mathrm{s} $的航天器剩余飞行时间
Fig. 16 Time-to-go when ${T_{fr}} = 8\,\;\mathrm{s} $
图 17 $ {T_{f\lambda }} = 13\,\;\mathrm{s}$的视线倾角
Fig. 17 LOS angles on the pitch direction when $ {T_{f\lambda }} = 13\,\;\mathrm{s}$
图 18 $ {T_{f\lambda }} = 13\,\;\mathrm{s}$的视线偏角
Fig. 18 LOS angles on the yaw direction when $ {T_{f\lambda }} = 13\,\;\mathrm{s}$
表 1 航天器初始状态
Table 1 Initial state of the spacecrafts
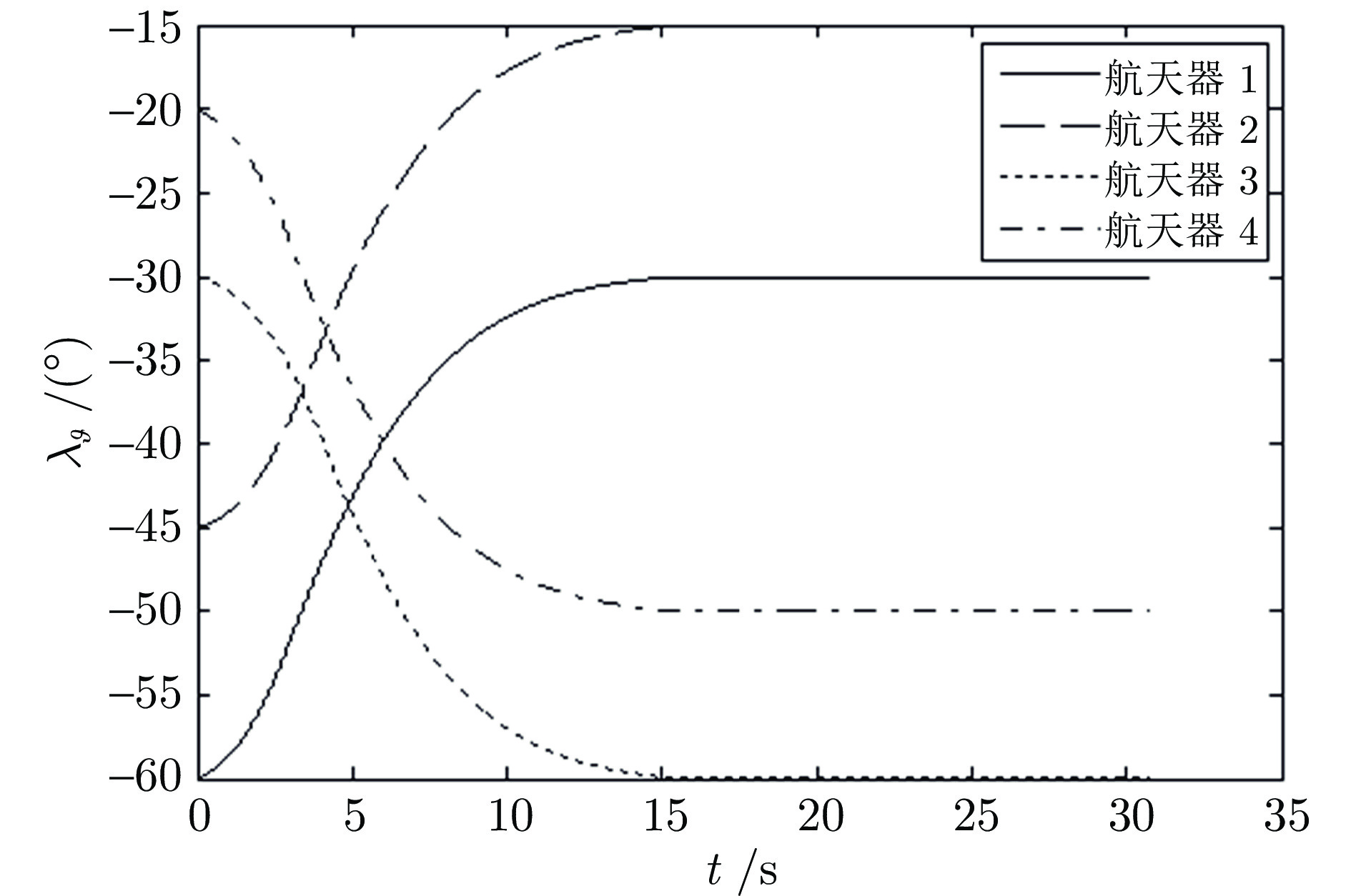
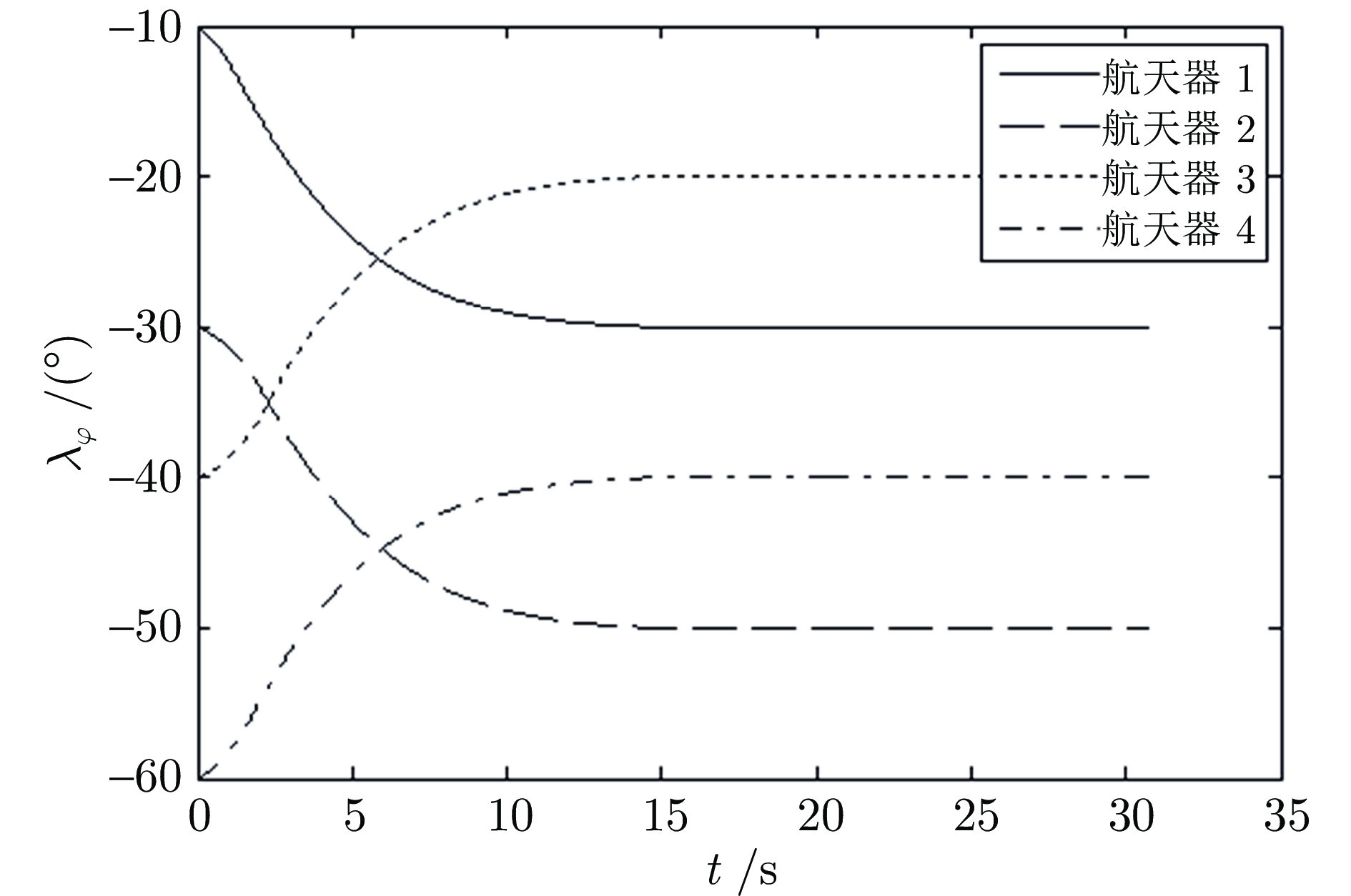
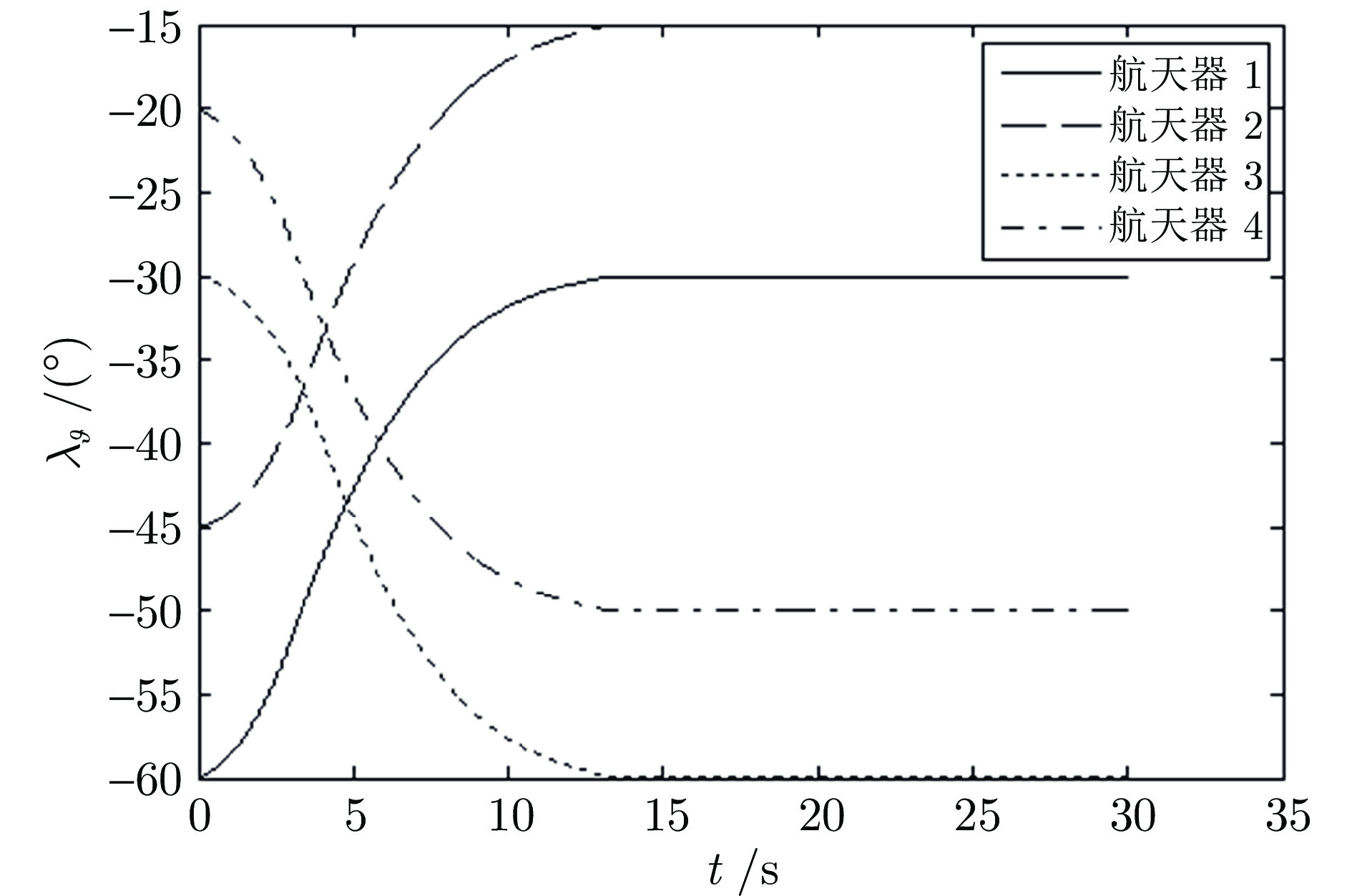
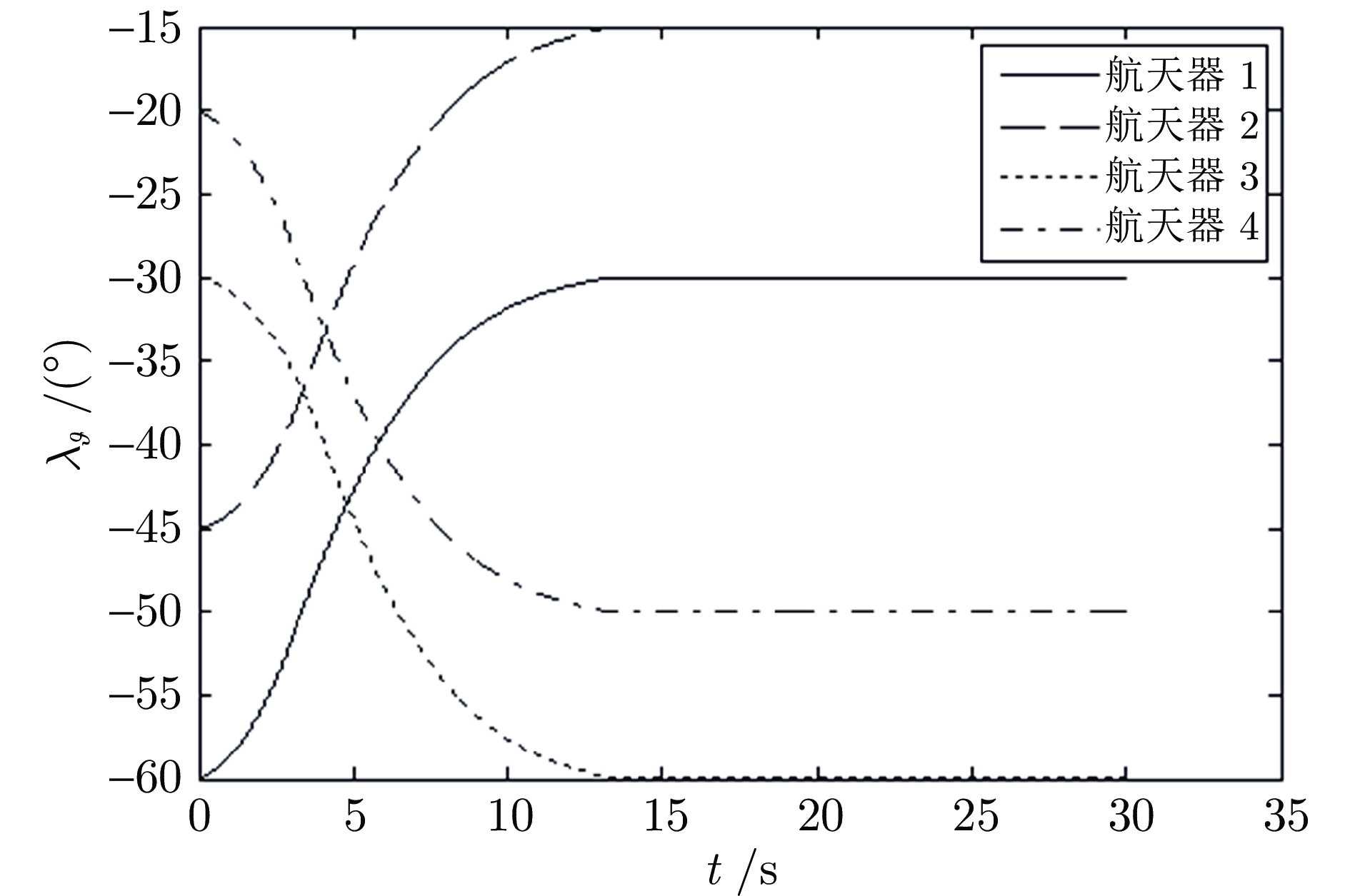
参数名称 参数初始值 序号1 序号2 序号3 序号4 相对距离(km) 11 12 11 9 相对速率(m/s) −320 −400 −380 −350 视线倾角(°) −60 −45 −30 −20 视线偏角(°) 10 30 40 60 视线倾角速率((°)/s) 0.63 0.246 −0.355 −0.779 视线偏角速率((°)/s) 1.404 0.67 −0.521 −0.882 期望视线倾角(°) −30 −15 −60 −50 期望视线偏角(°) 30 50 20 40 
下载: 导出CSV
-
[1] 耿远卓, 袁利, 黄煌, 汤亮. 基于终端诱导强化学习的航天器轨道追逃博弈. 自动化学报, 2023, 49(5): 974−984Geng Yuan-Zhuo, Yuan Li, Huang Huang, Tang Liang. Terminal-guidance based reinforcement-learning for orbital pursuit-evasion game of the spacecraft. Acta Automatica Sinica, 2023, 49(5): 974−984 [2] 路遥. 一种非仿射高超声速飞行器输出反馈控制方法. 自动化学报, 2022, 48(6): 1530−1542Lu Yao. A method of output feedback control for non-affine hypersonic vehicles. Acta Automatica Sinica, 2022, 48(6): 1530−1542 [3] Clark D E. Stochastic multi-object guidance laws for interception and rendezvous problems. IEEE Transactions on Automatic Control, 2021, 67(3): 1482−1489 [4] Jeon I S, Lee J I, Tahk M J. Impact-time-control guidance law for anti-ship missiles. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260−266 doi: 10.1109/TCST.2005.863655 [5] Chen Z, Chen W, Liu X, Cheng J. Three-dimensional fixed-time robust cooperative guidance law for simultaneous attack with impact angle constraint. Aerospace Science and Technology, 2021, 110: Article No. 106523 doi: 10.1016/j.ast.2021.106523 [6] Cho N, Kim Y. Modified pure proportional navigation guidance law for impact time control. Journal of Guidance, Control, and Dynamics, 2016, 39(4): 852−872 doi: 10.2514/1.G001618 [7] Chen X, Wang J. Nonsingular sliding-mode control for field-of-view constrained impact time guidance. Journal of Guidance, Control, and Dynamics, 2018, 41(5): 1214−1222 doi: 10.2514/1.G003146 [8] Lyu T, Guo Y N, Li C J, Ma G F, Zhang H B. Multiple missiles cooperative guidance with simultaneous attack requirement under directed topologies. Aerospace Science and Technology, 2019, 89: 100−110 [9] Nikusokhan M, Nobahari H. Closed-form optimal cooperative guidance law against random step maneuver. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(1): 319−336 doi: 10.1109/TAES.2015.140623 [10] Chen Y D, Wang J N, Shan J Y, Xin M. Cooperative guidance for multiple powered missiles with constrained impact and bounded speed. Journal of Guidance, Control, and Dynamics, 2021, 44(4): 825−841 [11] Dong W, Deng F, Wang C Y, Wang J N. Three-dimensional spatial–temporal cooperative guidance without active speed control. Journal of Guidance, Control, and Dynamics, 2023, 46(10): 1981−1996 doi: 10.2514/1.G007641 [12] Wang C Y, Dong W, Wang J N, Shan J Y, Xin M. Guidance law design with fixed-time convergent error dynamics. Journal of Guidance, Control, and Dynamics, 2021, 44(7): 1389−1398 doi: 10.2514/1.G005833 [13] Moulay E, Léchappé V, Bernuau E, Defoort M, Plestan F. Fixed-time sliding mode control with mismatched disturbances. Automatica, 2022, 136: Article No. 110009 doi: 10.1016/j.automatica.2021.110009 [14] Moulay E, Léchappé V, Bernuau E, Defoort M, Plestan F. Robust fixed-time stability: Application to sliding-mode control. IEEE Transactions on Automatic Control, 2021, 67(2): 1061−1066 [15] You H, Chang X L, Zhao J F, Wang S H, Zhang Y H. Three-dimensional impact-angle-constrained fixed-time cooperative guidance algorithm with adjustable impact time. Aerospace Science and Technology, 2023, 141: Article No. 108574 doi: 10.1016/j.ast.2023.108574 [16] Dong W, Wang C Y, Liu J H, Wang J N, Xin M. Three-dimensional vector guidance law with impact time and angle constraints. Journal of the Franklin Institute, 2023, 360(2): 693−718 doi: 10.1016/j.jfranklin.2022.11.035 [17] Dong W, Wang C Y, Wang J N, Zuo Z Y, Shan J Y. Fixed-time terminal angle-constrained cooperative guidance law against maneuvering target. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(2): 1352−1366 doi: 10.1109/TAES.2021.3113292 [18] Zhang P, Zhang X Y. Multiple missiles fixed-time cooperative guidance without measuring radial velocity for maneuvering targets interception. ISA Transactions, 2022, 126: 388−397 [19] Sánchez-Torres J D, Gómez-Gutiérrez D, López E, Loukianov A G. A class of predefined-time stable dynamical systems. IMA Journal of Mathematical Control and Information, 2018, 35(Supplement_1): i1−i29 doi: 10.1093/imamci/dnx004 [20] Munoz-Vazquez A J, Sánchez-Torres J D, Jimenez-Rodriguez E, Loukianov A G. Predefined-time robust stabilization of robotic manipulators. IEEE/ASME Transactions on Mechatronics, 2019, 24(3): 1033−1040 doi: 10.1109/TMECH.2019.2906289 [21] Sánchez-Torres J D, Defoort M, Munoz-Vázquez A J. Predefined-time stabilisation of a class of nonholonomic systems. International Journal of Control, 2020, 93(12): 2941−2948 doi: 10.1080/00207179.2019.1569262 [22] Wang F, Miao Y, Li C, et al. Attitude control of rigid spacecraft with predefined-time stability. Journal of the Franklin Institute, 2020, 357(7): 4212−4221 doi: 10.1016/j.jfranklin.2020.01.001 [23] Jing L, Wei C Z, Zhang L, Cui N G. Cooperative guidance law with predefined-time convergence for multimissile systems. Mathematical Problems in Engineering, 2021, 2021: 1−13 [24] 池海红, 丁栖航, 张国良. 预定时间多导弹三维协同制导律. 宇航学报, 2023, 44(8): 1238−1250 doi: 10.3873/j.issn.1000-1328.2023.08.012Chi Hai-Hong, Ding Xi-Hang, Zhang Guo-Liang. Three-dimensional cooperative guidance law for multiple missiles with predefined-time convergence. Journal of Astronautics, 2023, 44(8): 1238−1250 doi: 10.3873/j.issn.1000-1328.2023.08.012 [25] Pal A K, Kamal S, Nagar S K, Bandyopadhyay B, Fridman L. Design of controllers with arbitrary convergence time. Automatica, 2020, 112: Article No. 108710 doi: 10.1016/j.automatica.2019.108710 [26] Olfati-Saber R, Murray R M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on Automatic Control, 2004, 49(9): 1520−1533 doi: 10.1109/TAC.2004.834113 [27] Zhang L, Jing L, Ye L H, Gao X. Predefined-time control for a horizontal takeoff and horizontal landing reusable launch vehicle. Aircraft Engineering and Aerospace Technology, 2021, 93(6): 957−970 doi: 10.1108/AEAT-11-2020-0253 [28] Holloway J, Krstic M. Prescribed-time observers for linear systems in observer canonical form. IEEE Transactions on Automatic Control, 2019, 64(9): 3905−3912 [29] Ju X Z, Wei C Z, Xu H C, Wang F. Fractional-order sliding mode control with a predefined-time observer for VTVL reusable launch vehicles under actuator faults and saturation constraints. ISA Transactions, 2022, 129: 55−72 doi: 10.1016/j.isatra.2022.02.003 [30] Zuo Z Y, Song J W, Tian B L, Basin M. Robust fixed-time stabilization control of generic linear systems with mismatched disturbances. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 52(2): 759−768 [31] Wang X, Tan C P, Zhou D. Observer-based PIGC for missiles with impact angle constraint. IEEE Transactions on Aerospace and Electronic Systems, 2018, 55(5): 2226−2240 [32] Hu Q L, Han T, Xin M. Three-dimensional guidance for various target motions with terminal angle constraints using twisting control. IEEE Transactions on Industrial Electronics, 2019, 67(2): 1242−1253 [33] Zhang L, Li D Y, Jing L, Ju X Z, Cui N G. Appointed-time cooperative guidance law with line-of-sight angle constraint and time-to-go control. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(3): 3142−3155 doi: 10.1109/TAES.2022.3221059 [34] 李鹤宇, 王建斌, 张锐, 宋峰, 姚雨晗, 楼朝飞. 具有角度和时间约束的固定时间协同制导律. 宇航学报, 2024, 45(3): 462−468 doi: 10.3873/j.issn.1000-1328.2024.03.013Li He-Yu, Wang Jian-Bin, Zhang Rui, Song Feng, Yao Yu-Han, Lou Chao-Fei. Fixed-time cooperative guidance law with angle and remaining flight time constraints. Journal of Astronautics, 2024, 45(3): 462−468 doi: 10.3873/j.issn.1000-1328.2024.03.013 -
计量
- 文章访问数: 61
- HTML全文浏览量: 29
- PDF下载量: 8
- 被引次数: 0
