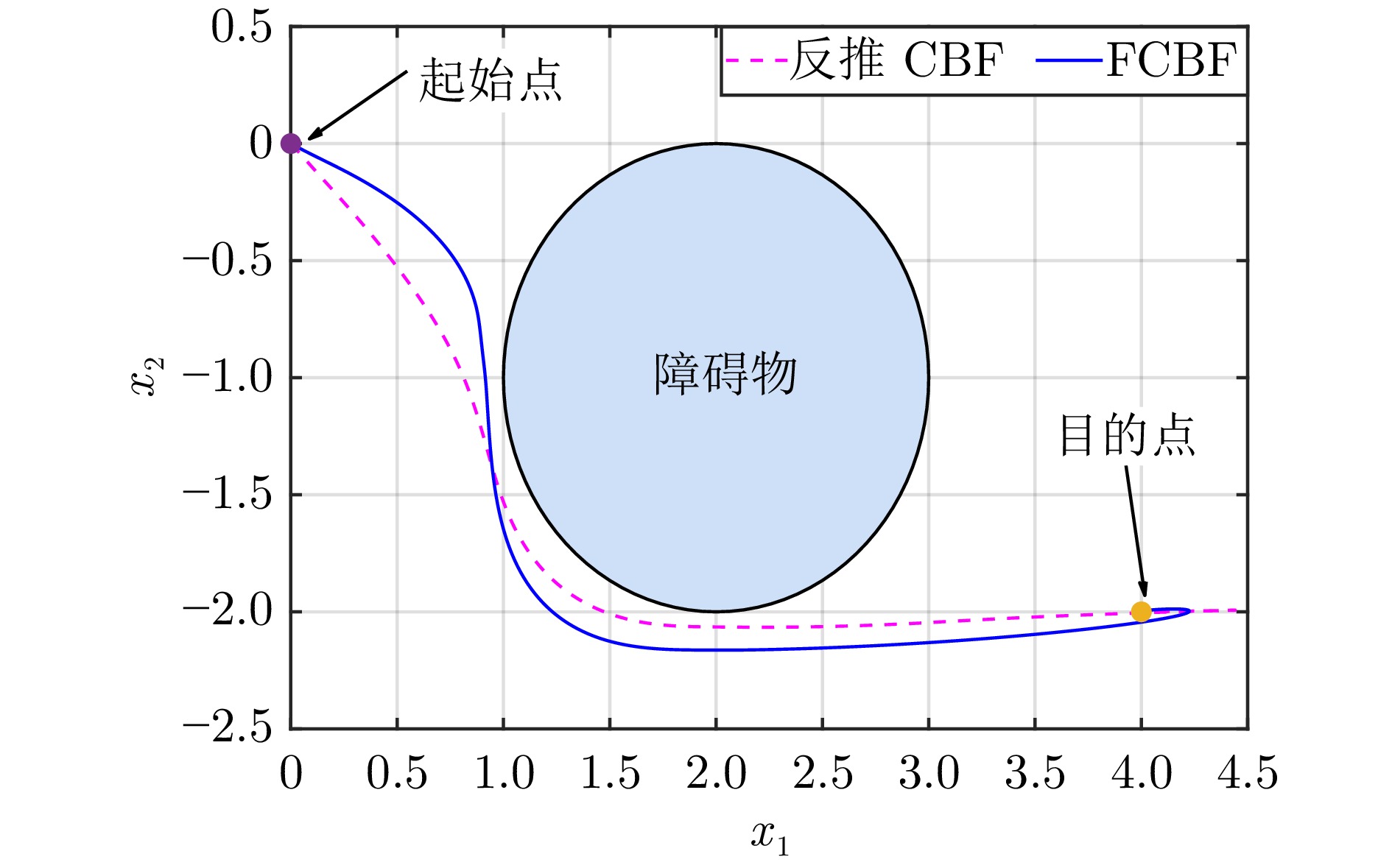
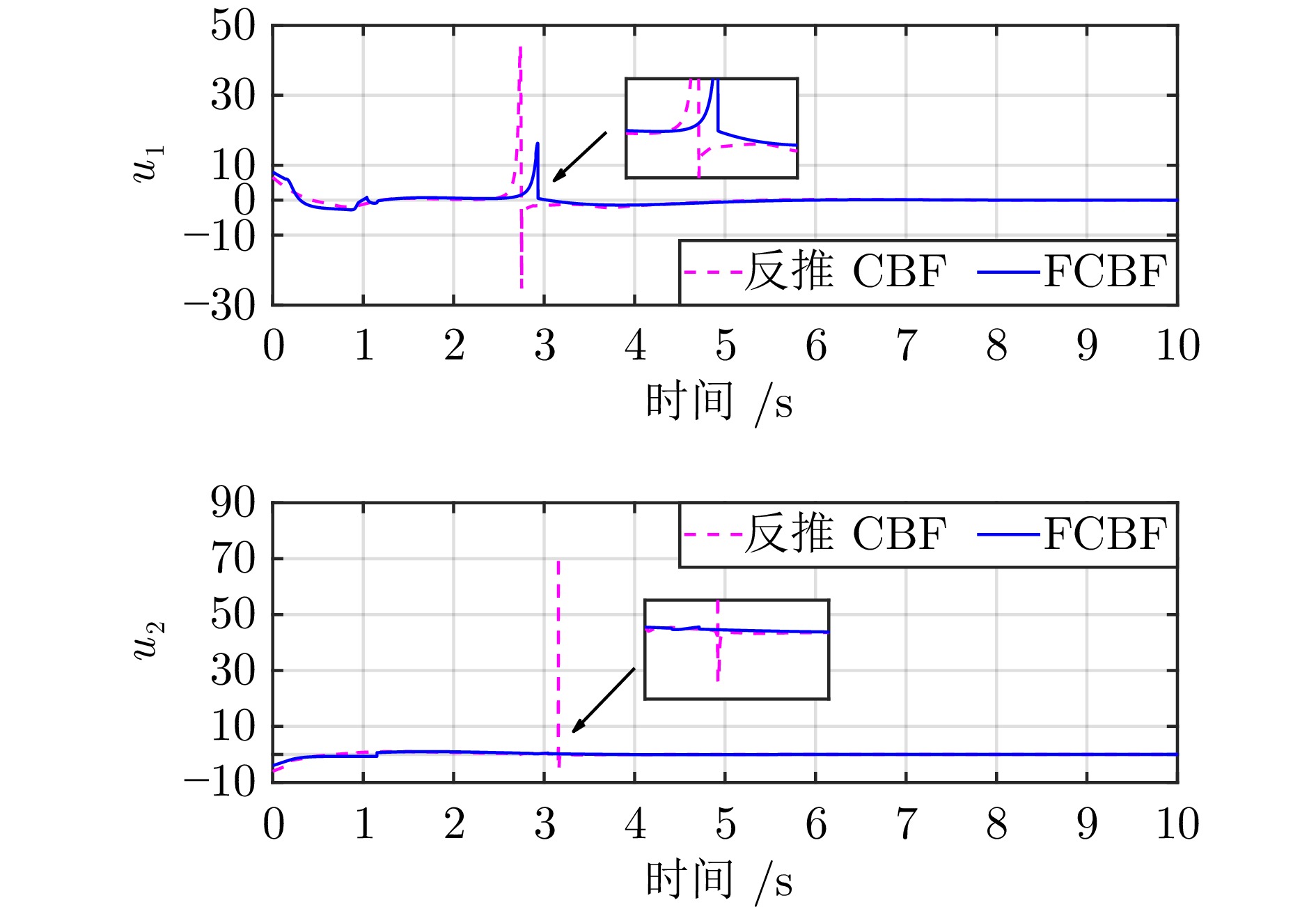
|
[1]
|
Clarke E M, Grumberg O, Peleg D. Model Checking. Cambridge: MIT Press, 1999.
|
|
[2]
|
Tomlin C, Pappas G J, Sastry S. Conflict resolution for airtraffic management: A study in multiagent hybrid systems. IEEE Transactions on Automatic Control, 1998, 43(4): 509−521 doi: 10.1109/9.664154
|
|
[3]
|
Gao Y, Johansson K H, Xie L. Computing probabilistic controlled invariant sets. IEEE Transactions on Automatic Control, 2021, 66(7): 3138−3151 doi: 10.1109/TAC.2020.3018438
|
|
[4]
|
Sun J, Yang J, Zeng Z. Safety-critical control with control barrier function based on disturbance observer. IEEE Transactions on Automatic Control, 2024, 69(7): 4750−4756 doi: 10.1109/TAC.2024.3352707
|
|
[5]
|
Cohen M H, Belta C. Safe exploration in model-based reinforcement learning using control barrier functions. Automatica, 2023, 147: Article No. 110684 doi: 10.1016/j.automatica.2022.110684
|
|
[6]
|
陈杰, 吕梓亮, 黄鑫源, 洪奕光. 非线性系统的安全分析与控制: 障碍函数方法. 自动化学报, 2023, 49(3): 567−579Chen Jie, Lyu Zi-Liang, Huang Xin-Yuan, Hong Yi-Guang. Safety analysis and safety-critical control of nonlinear systems: Barrier function approach. Acta Automatica Sinica, 2023, 49(3): 567−579
|
|
[7]
|
Artstein Z. Stabilization with relaxed controls. Nonlinear Analysis: Theory, Methods and Applications, 1983, 7(11): 1163−1173
|
|
[8]
|
Sontag E D. A ‘universal’ construction of Artstein's theorem on nonlinear stabilization. Systems and Control Letters, 1989, 13(2): 117−123 doi: 10.1016/0167-6911(89)90028-5
|
|
[9]
|
Wieland P, Allgöwer F. Constructive safety using control barrier functions. IFAC Proceedings Volumes, 2007, 40(12): 462−467 doi: 10.3182/20070822-3-ZA-2920.00076
|
|
[10]
|
Ames A D, Grizzle J W, Tabuada P. Control barrier function based quadratic programs with application to adaptive cruise control. In: Proceedings of the 53rd IEEE Conference on Decision and Control (CDC). Los Angeles, USA: IEEE, 2014. 6271−6278
|
|
[11]
|
Xu X, Tabuada P, Grizzle J W, Ames A D. Robustness of control barrier functions for safety-critical control. IFAC-PapersOnLine, 2015, 48(27): 54−61 doi: 10.1016/j.ifacol.2015.11.152
|
|
[12]
|
Ames A D, Xu X, Grizzle J W, Tabuada P. Control barrier function based quadratic programs for safety critical systems. IEEE Transactions on Automatic Control, 2017, 62(8): 3861−3876 doi: 10.1109/TAC.2016.2638961
|
|
[13]
|
Xu Y, Sun Y, Chen Y Y, Tao H F. Safety predefined time tracking control of second-order nonlinear systems. In: Proceedings of the 12th Data Driven Control and Learning Systems Conference (DDCLS). Xiangtan, China: IEEE, 2023. 1320−1324
|
|
[14]
|
Cortez W S, Dimarogonas D V. Correct-by-design control barrier functions for Euler-Lagrange systems with input constraints. In: Proceedings of the American Control Conference (ACC). Denver, USA: IEEE, 2020. 950−955
|
|
[15]
|
Cortez W S, Dimarogonas D V. Safe-by-design conrtrol for Euler-Lagrange systems. Automatica, 2022, 146: Article No. 110620 doi: 10.1016/j.automatica.2022.110620
|
|
[16]
|
Das E, Murray R M. Robust safe control synthesis with disturbance observer-based control barrier functions. In: Proceedings of the 61st Conference on Decision and Control (CDC). Cancun, Mexico: IEEE, 2022. 5566−5573
|
|
[17]
|
Nguyen Q, Sreenath K. Exponential control barrier function for enforcing high relative-degree safety-critical constraints. In: Proceedings of the American Control Conference (ACC). Boston, USA: IEEE, 2016. 322−328
|
|
[18]
|
Xiao W, Belta C. Control barrier functions for systems with high relative degree. In: Proceedings of the 58th IEEE Conference on Decision and Control (CDC). Nice, France: IEEE, 2019. 474−479
|
|
[19]
|
Xiao W, Belta C. High-order control barrier functions. IEEE Transactions on Automatic Control, 2022, 67(7): 3655−3662 doi: 10.1109/TAC.2021.3105491
|
|
[20]
|
Tan X, Cortez W S, Dimarogonas D V. High-order barrier functions: Robustness, safety, and performance-critical control. IEEE Transactions on Automatic Control, 2021, 67(6): 3021−3028
|
|
[21]
|
Wang H, Peng J, Xu J, Zhang F, Wang Y. High-order control barrier functions based optimization control for time-varying nonlinear systems with full-state constraints: A dynamic sub-safe set approach. International Journal of Robust and Nonlinear Control, 2023, 33(8): 4490−4503 doi: 10.1002/rnc.6624
|
|
[22]
|
Zhang D H, Van M, Mcllvanna S, Sun Y, McLoone S. Adaptive safety critical control with uncertainty estimation for human-robot collaboration. IEEE Transactions on Automation Science and Engineering, DOI: 10.1109/TASE.2023.3320873
|
|
[23]
|
Molnar T G, Cosner R K, Singletary A W, Ubellacker W, Ames A D. Model-free safety critical control for robotic systems. IEEE Robotics and Automation Letters, 2022, 7(2): 944−951 doi: 10.1109/LRA.2021.3135569
|
|
[24]
|
Xu J X, Gu N, Wang D, Li T S, Han B, Peng Z H. Safety critical parallel trajectory tracking control of maritime autonomous surface ships based on integral control barrier functions. IEEE Transactions on Intelligent Vehicles, 9 (5): 4979−4988, 2024 doi: 10.1109/TIV.2024.3361477
|
|
[25]
|
Xu X. Constrained control of input-output linearizable systems using control sharing barrier funcions. Automatica, 2018, 87: 195−201 doi: 10.1016/j.automatica.2017.10.005
|
|
[26]
|
Taylor A J, Ong P, Molnar T G, Ames A D. Safe backstepping with control barrier functions. In: Proceedings of the 61st IEEE Conference on Decision and Control (CDC). Cancun, Mexico: IEEE, 2022. 5775−5782
|
|
[27]
|
Abel I, Steeves D, KritićM, JankovićM. Prescribed time safety design for strict-feedback nonlinear systems. IEEE Transactions on Automatic Control, 2024, 69(3): 1464−1479 doi: 10.1109/TAC.2023.3326393
|
|
[28]
|
马知恩, 周义仓, 李承治. 常微分方程定性与稳定性方法. 第2版. 北京: 科学出版社, 2015.Ma Zhi-En, Zhou Yi-Cang, Li Cheng-Zhi. Qualitative and Stability Theory of Ordinary Differential Equations (2nd edition). Beijing: Science Press, 2015.
|
|
[29]
|
Ames A D, Coogan S, Egerstedt M, Notomista G, Sreenath K, Tabuada P. Control barrier functions: Theory and applications. In: Proceedings of the 18th European Control Conference (ECC). Naples, Italy: IEEE, 2019. 3420−3431
|
|
[30]
|
Li L H, Zhao K, Zhang Z Z, Song Y D. Dual-channel event-triggered robust adaptive control of strict-feedback system with flexible prescribed performance. IEEE Transactions on Automatic Control, 2024, 69(3): 1752−1759 doi: 10.1109/TAC.2023.3328167
|
|
[31]
|
Cheng H, Huang X C, Cao H W. Asymptotic tracking control for uncertain nonlinear strict-feedback systems with unknown time-varying delays. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(12): 9821−9831 doi: 10.1109/TNNLS.2022.3160803
|
|
[32]
|
Yip P P, Hedrick J K. Adaptive dynamic surface control: A simplified algorithm for adaptive backstepping control of nonlinear systems. International Journal of Control, 1998, 71(5): 959−979 doi: 10.1080/002071798221650
|
|
[33]
|
Khalil H K. Nonlinear Systems. Upper Saddle River: Prentice Hall, 2002.
|
|
[34]
|
Wang H, Margellos K, Papachristodoulou A. Explicit solutions for safety problems using control barrier functions. In: Proceedings of the 61st IEEE Conference on Decision and Control (CDC). Cancun, Mexico: IEEE, 2022. 5680−5685
|
|
[35]
|
Saviolo A, Loianno G. Learning quadrotor dynamics for precise, safe, and agile flight control. Annual Reviews in Control, 2023, 55: 45−60 doi: 10.1016/j.arcontrol.2023.03.009
|
|
[36]
|
Yuan W, Liu Y H, Su C Y, Zhao F. Whole-body control of an autonomous mobile manipulator using model predictive control and adaptive fuzzy technique. IEEE Transactions on Fuzzy Systems, 2024, 31(3): 799−809
|
|
[37]
|
Yuan W, Liu Y, Liu Y H, Su C Y. Differential flatness-based adaptive robust tracking control for wheeled mobile robots with slippage disturbances. ISA Transactions, 2024, 144: 482−489 doi: 10.1016/j.isatra.2023.11.008
|




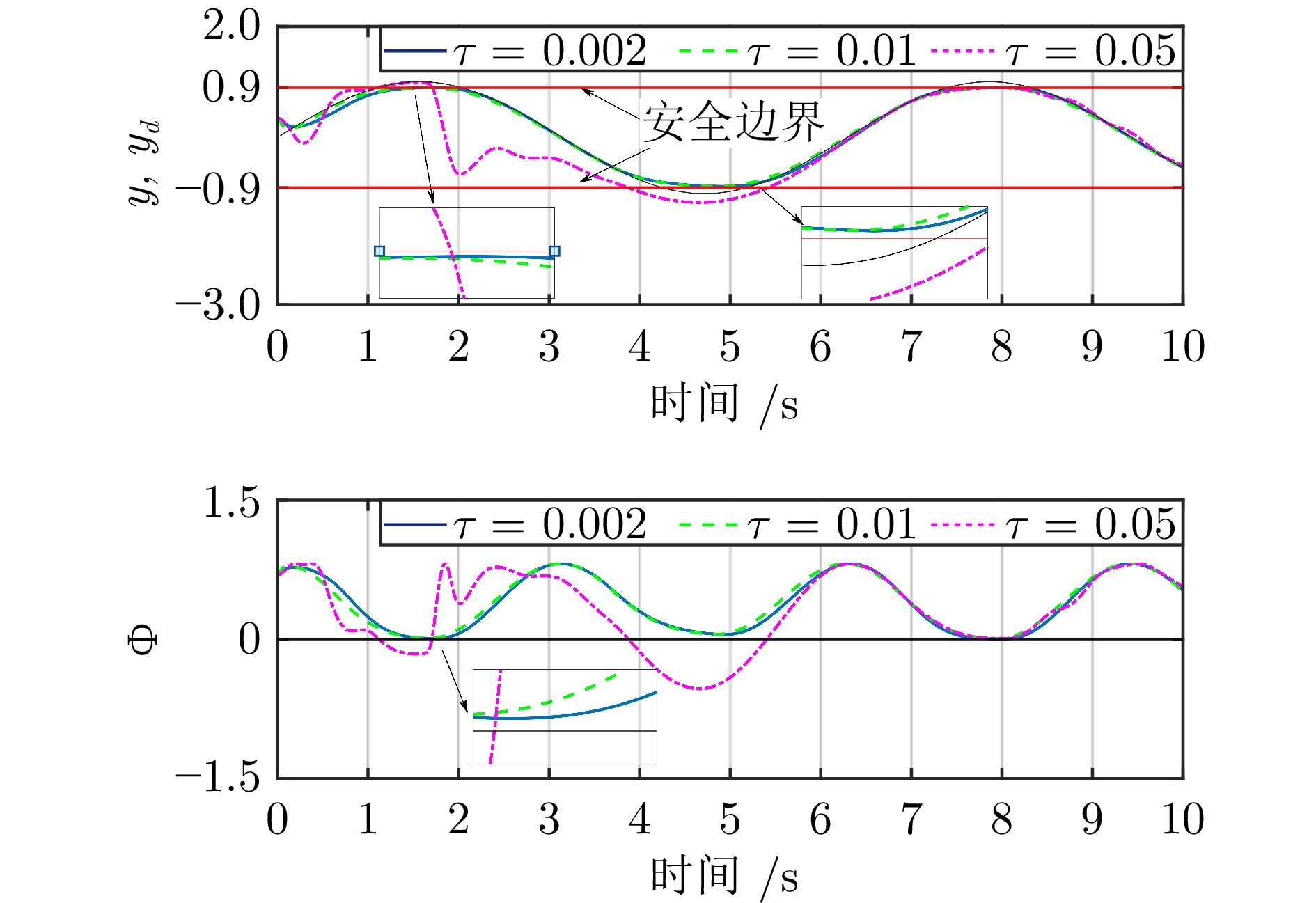
 下载:
下载: