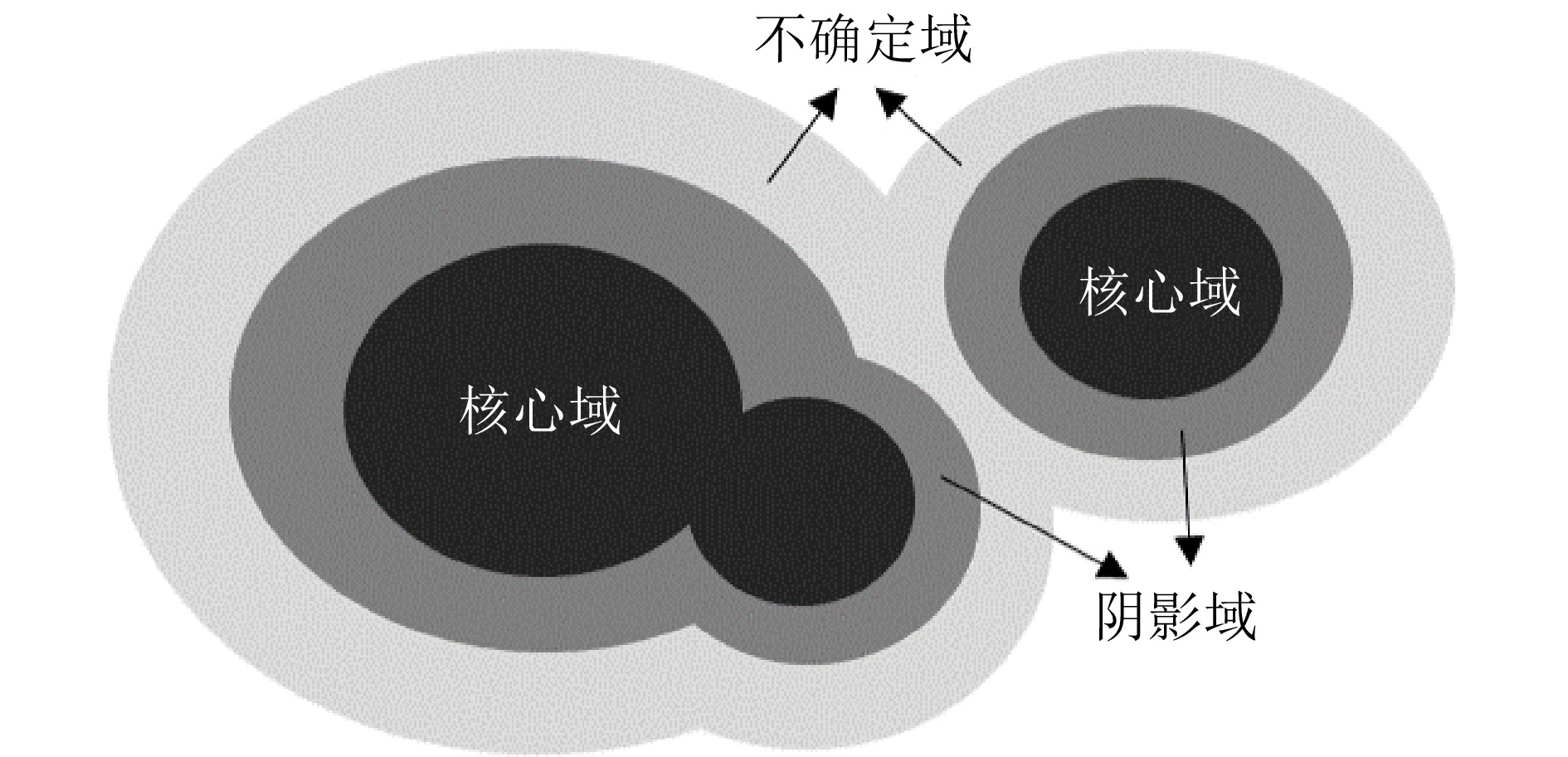
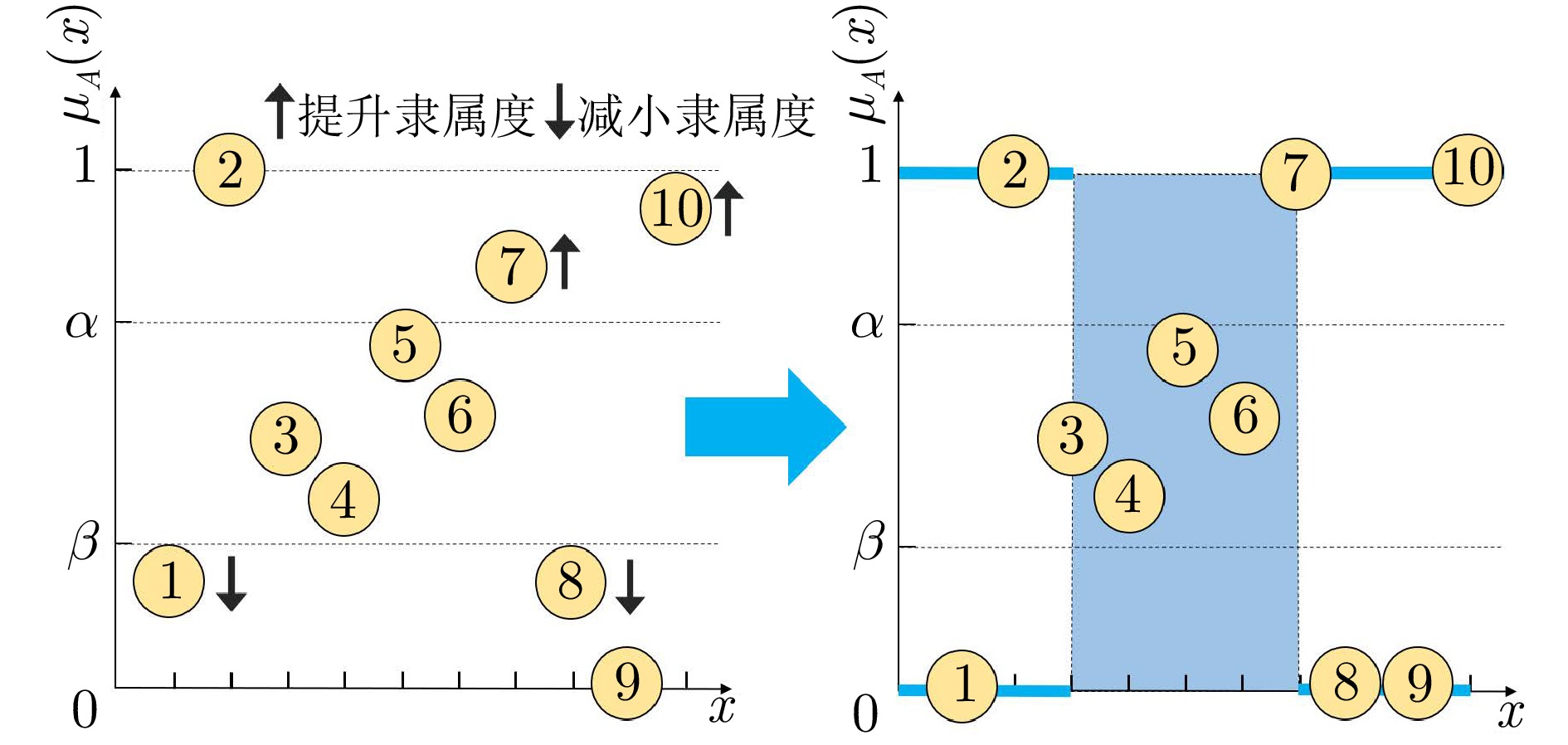
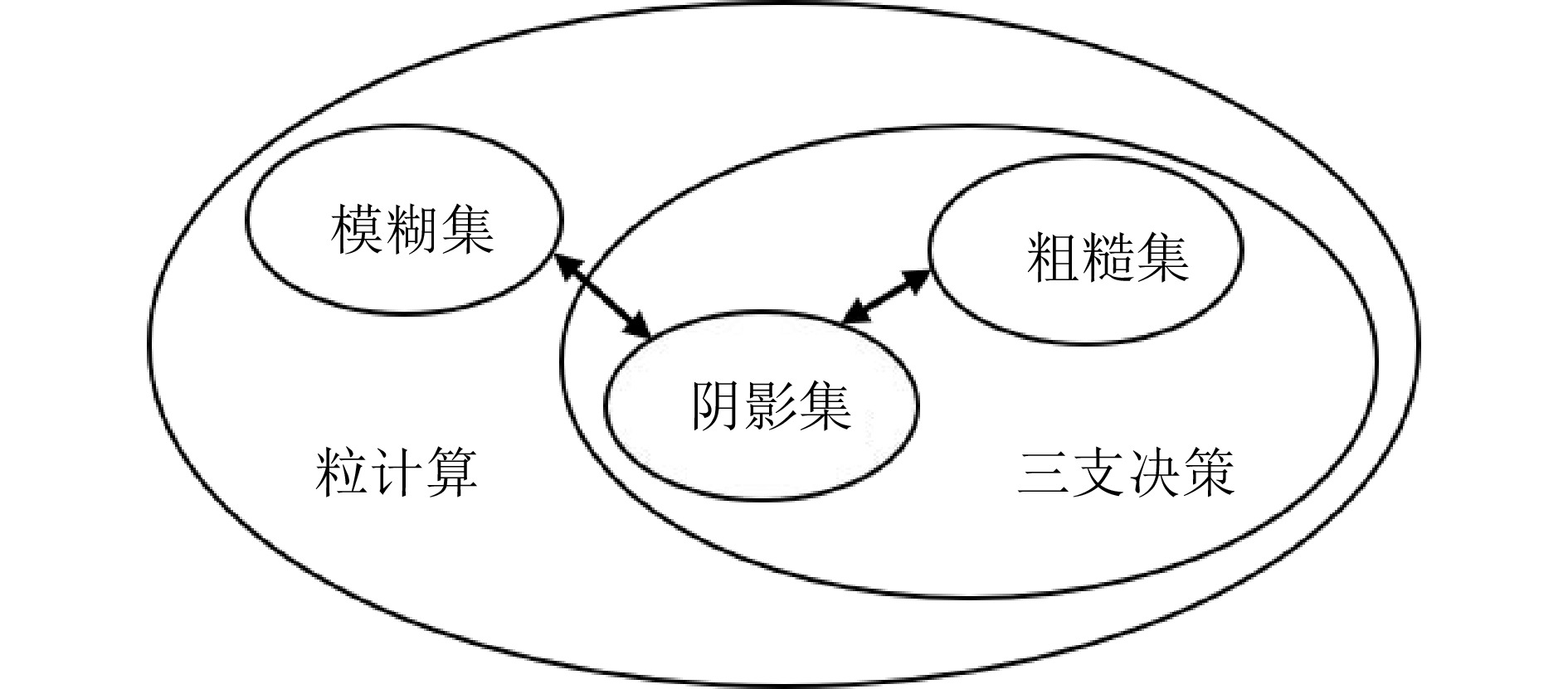
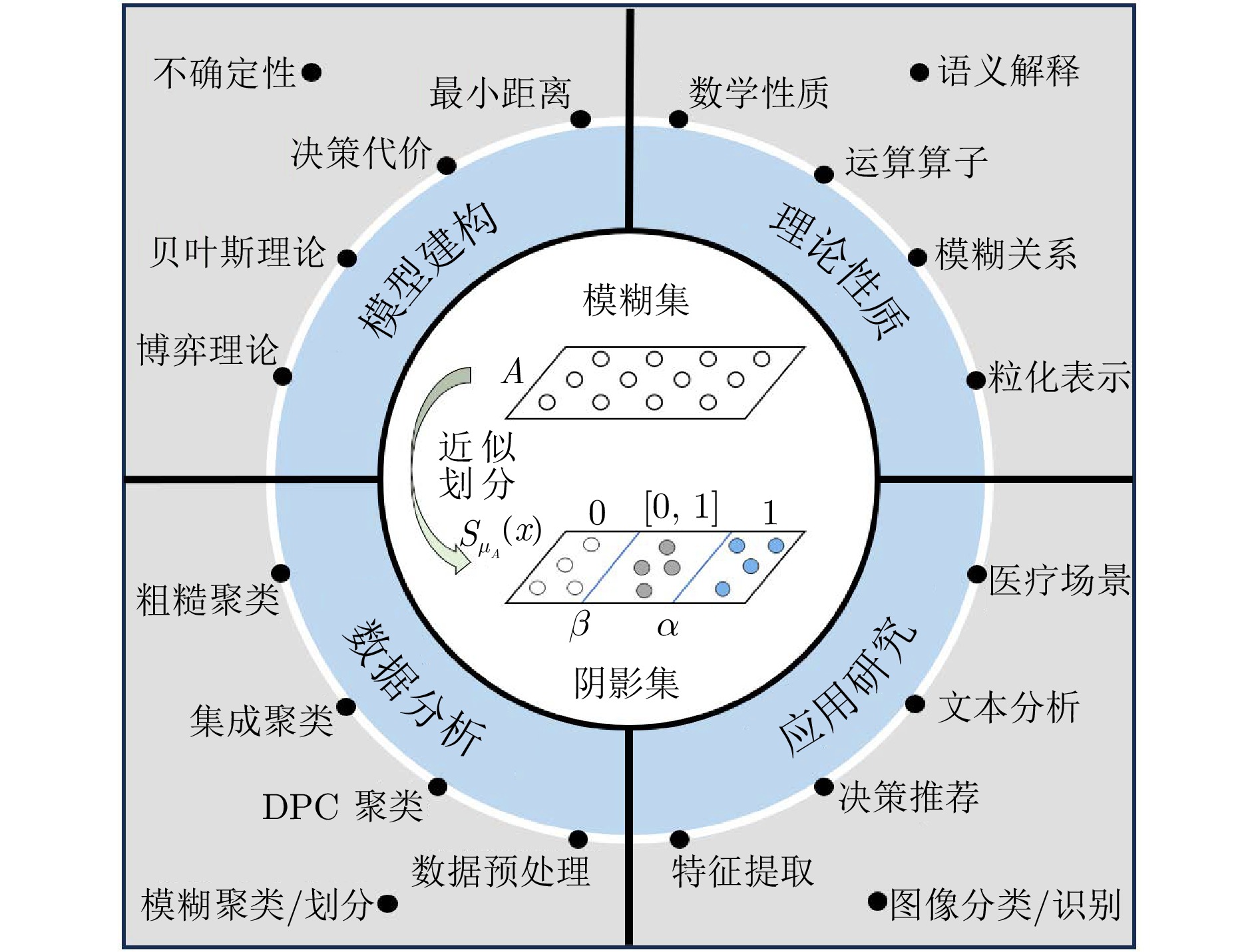
-
摘要: 阴影集(Shadowed set, SS)是一种对模糊集进行三支近似处理的不确定性知识发现模型, 其能够对模糊集中具有精确值的不确定性对象进行有效的近似和划分, 从而减少模糊决策过程中不确定性对象的决策划分成本和计算损耗. 首先, 回顾阴影集的发展历程, 并从四个方面介绍其研究现状及内容, 即阴影集的模型构建、理论性质、数据分析以及应用研究. 通过总结分析它们的核心思想、方法体系、相互关系和区别等, 为该领域的后续研究提供借鉴. 随后, 讨论分析阴影集理论与其他不确定性问题处理理论模型的联系, 尤其是阴影集与模糊集、粗糙集和三支决策理论之间的区别、联系以及互补性. 最后, 围绕上述四个研究方面, 对当前若干具有挑战性的研究问题进行分析和展望.Abstract: Shadowed set (SS) is a kind of uncertain knowledge discovery model which carries out three-way approximate processing on fuzzy sets. It can effectively approximate and partition the uncertain objects with precise values in fuzzy sets, so as to reduce the decision partitioning cost and calculation loss of uncertain objects in fuzzy decision-making process. Firstly, the development of shadowed set is reviewed, and introduces its research status and content from four aspects: Model construction, theoretical properties, data analysis and application research. By summarizing and analyzing their core ideas, methodological systems, interrelationships, and differences, etc., this paper provides reference for subsequent research in this field. Subsequently, the connection between shadowed set theory and other uncertainty problem handling theoretical models is discussed and analyzed, especially the differences, connections and complementarities between shadowed set and fuzzy sets, rough sets, and three-way decision theories. Finally, based on the above four research aspects, some current challenging research problems are analyzed and prospected.
-
Key words:
- Shadowed set (SS) /
- fuzzy sets /
- three-way decision /
- uncertainty /
- granular computing
-
图 4 GTSS中两种隶属度误差随决策阈值的博弈变化
Fig. 4 The game variation of two kinds of membership errors with decision threshold in GTSS
图 5 FE-GTSS中两种模糊熵损失随决策阈值的博弈变化
Fig. 5 The game variation of two fuzzy entropy losses with decision threshold in FE-GTSS
图 6 阴影集在聚类过程中对数据结构的描述
Fig. 6 Shadowed set describe the data structure in the clustering process
图 7 不同粒计算理论模型之间的简要关系图谱
Fig. 7 Brief relationship graph between different granular computing theory models
图 8 基于阴影集思想的模糊集近似划分示意图
Fig. 8 Schematic diagram of fuzzy sets approximation partition based on shadowed set idea
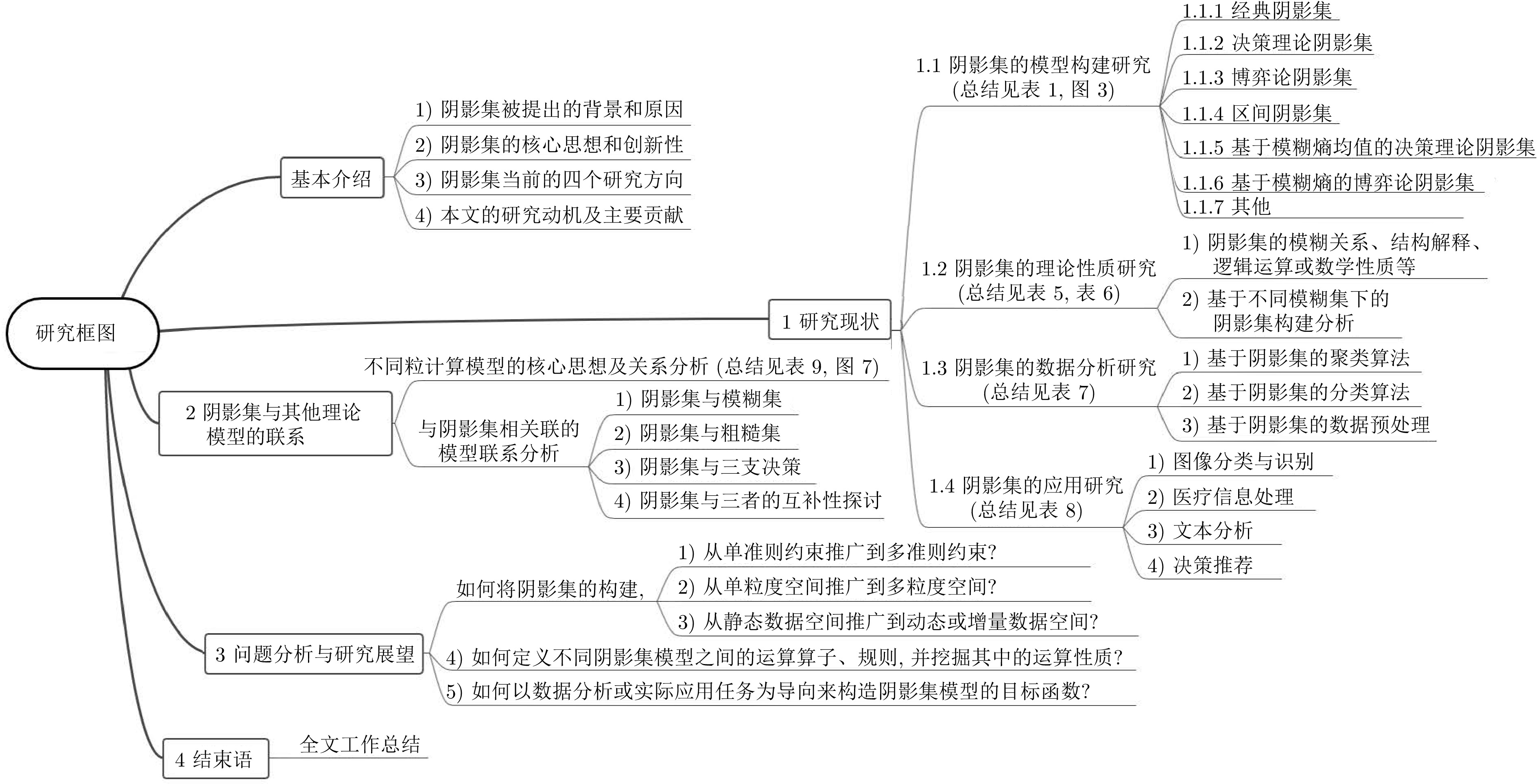
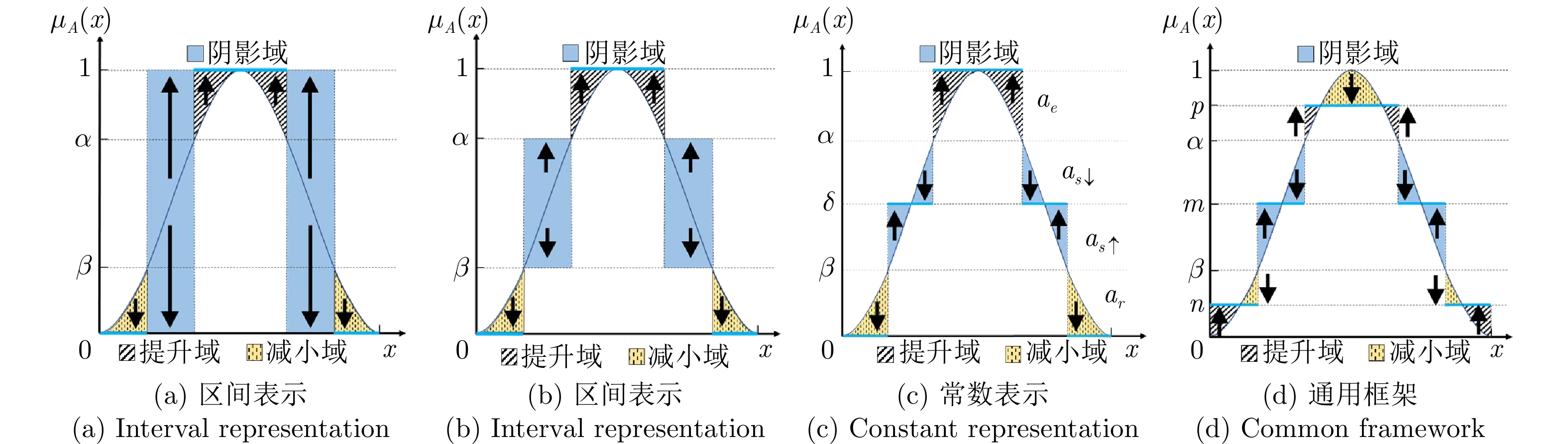
表 1 不同阴影集之间的区别和联系
Table 1 The difference and relation between different shadowed sets
年份 文献 模型 阴影域 构建准则 分析视角 构建方法 人为参数设定 时间复杂度 1998 [2] SS $[ {0,\;1} ]$ 不确定性不变性 不确定性损失 最优化目标函数 — $\mathrm{O}( n )$ 2003 [5−6] 0.5SS 0.5 不确定性不变性 不确定性损失 最优化目标函数 — $\mathrm{O}( n )$ 2013, 2014, 2017 [7−9] MDTSS $\overline \delta $ 最小成本 隶属度误差 决策划分规则推导 ${\lambda _e},\;{\lambda _r},\;{\lambda _{s \downarrow }},\;{\lambda _{s \uparrow }}$ $\mathrm{O}( n )$ 2018, 2020 [10−11] GTSS 0.5 最小成本 隶属度误差 博弈竞争机制 ${c_E},\;{c_R}$ $\mathrm{O}( {{n^2}} )$ 2020 [12] ISS $[ {\beta ,\;\alpha } ]$ 不确定性不变性 不确定性损失 最优化目标函数 — $\mathrm{O}( n )$ 2020 [13] MESS ${\delta ^ * }$ 不确定性不变性 不确定性损失 决策划分规则推导 — $\mathrm{O}( n )$ 2020 [14−15] FE-GTSS 0.5, $\overline \delta $ 不确定性不变性 不确定性损失 博弈竞争机制 ${c_E},\;{c_R}$ $\mathrm{O}( {\mathrm{lo{g_2}}n} )$ 2023 [16] New-ISS $[ {\beta ,\;\alpha } ]$ 不确定性不变性 不确定性损失 最优化目标函数 — $\mathrm{O}( {n\mathrm{lo{g_2}}n} )$ 2023 [17] UC-GTSS 0.5 最小成本,
不确定性不变性隶属度误差,
不确定性损失博弈竞争机制 ${c_E},\;{c_R}$ $\mathrm{O}( n )$ 
下载: 导出CSV
表 2 MDTSS中划分所造成的误差和代价
Table 2 Error and cost caused by partitions in MDTSS
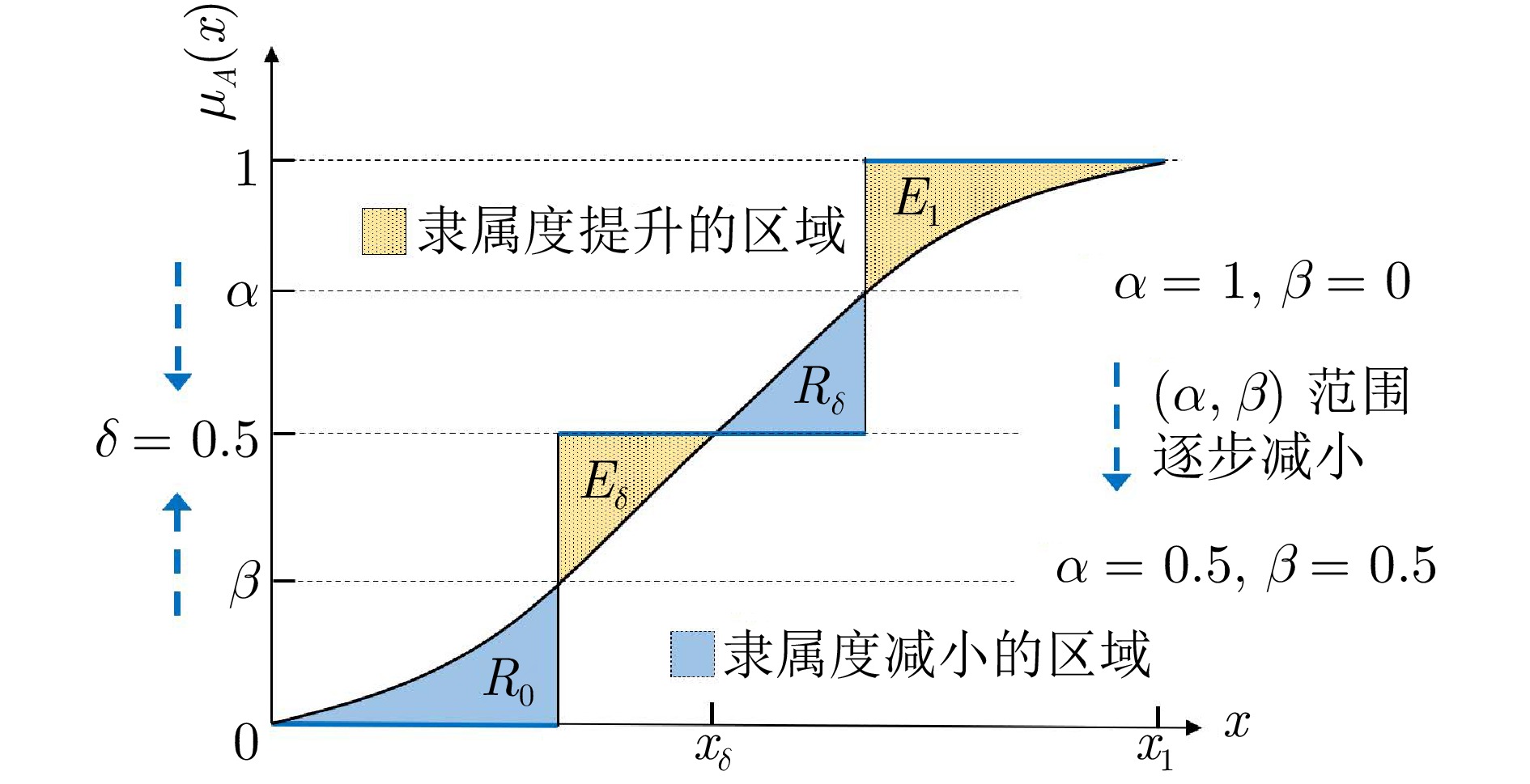
划分操作 模糊集 阴影集 决策误差${E_a}$ 决策代价${\lambda _a}$ ${a_e}$ ${\mu _A}( x )$ 1 $1 - {\mu _A}( x )$ ${\lambda _e}$ ${a_r}$ ${\mu _A}( x )$ 0 ${\mu _A}( x ) - 0$ ${\lambda _r}$ ${a_{s \downarrow }}$ ${\mu _A}( x ) \ge \delta $ $\delta $ ${\mu _A}( x ) - \delta $ ${\lambda _{s \downarrow }}$ ${a_{s \uparrow }}$ ${\mu _A}( x ) < \delta $ $\delta $ $\delta - {\mu _A}( x )$ ${\lambda _{s \uparrow }}$
下载: 导出CSV
表 3 博弈机制下阴影集的博弈收益
Table 3 Game payoff of shadowed set under game mechanism
博弈对象 ${n_2}$ 博弈策略 ${\beta _1}$ ${\beta _2}$ $\cdots $ ${\beta _q}$ ${n_1}$ ${\alpha _1}$ $\left\langle {{P_{{n_1}}}\left( {{\alpha _1},\;{\beta _1}} \right),\;{P_{{n_2}}}\left( {{\alpha _1},\;{\beta _1}} \right)} \right\rangle $ $\left\langle {{P_{{n_1}}}\left( {{\alpha _1},\;{\beta _2}} \right),\;{P_{{n_2}}}\left( {{\alpha _1},\;{\beta _2}} \right)} \right\rangle $ $\cdots $ $\left\langle {{P_{{n_1}}}\left( {{\alpha _1},\;{\beta _q}} \right),\;{P_{{n_2}}}\left( {{\alpha _1},\;{\beta _q}} \right)} \right\rangle $ ${\alpha _2}$ $\left\langle {{P_{{n_1}}}\left( {{\alpha _2},\;{\beta _1}} \right),\;{P_{{n_2}}}\left( {{\alpha _2},\;{\beta _1}} \right)} \right\rangle $ $\left\langle {{P_{{n_1}}}\left( {{\alpha _2},\;{\beta _2}} \right),\;{P_{{n_2}}}\left( {{\alpha _2},\;{\beta _2}} \right)} \right\rangle $ $\cdots $ $\left\langle {{P_{{n_1}}}\left( {{\alpha _2},\;{\beta _q}} \right),\;{P_{{n_2}}}\left( {{\alpha _2},\;{\beta _q}} \right)} \right\rangle $ $ \vdots$ $ \vdots$ $ \vdots$ $ \vdots$ $ \vdots$ ${\alpha _p}$ $\left\langle {{P_{{n_1}}}\left( {{\alpha _p},\;{\beta _1}} \right),\;{P_{{n_2}}}\left( {{\alpha _p},\;{\beta _1}} \right)} \right\rangle $ $\left\langle {{P_{{n_1}}}\left( {{\alpha _p},\;{\beta _2}} \right),\;{P_{{n_2}}}\left( {{\alpha _p},\;{\beta _2}} \right)} \right\rangle $ $\cdots $ $\left\langle {{P_{{n_1}}}\left( {{\alpha _p},\;{\beta _q}} \right),\;{P_{{n_2}}}\left( {{\alpha _p},\;{\beta _q}} \right)} \right\rangle $
下载: 导出CSV
表 4 MESS中划分所造成的熵损失
Table 4 Entropy loss caused by partitions in MESS
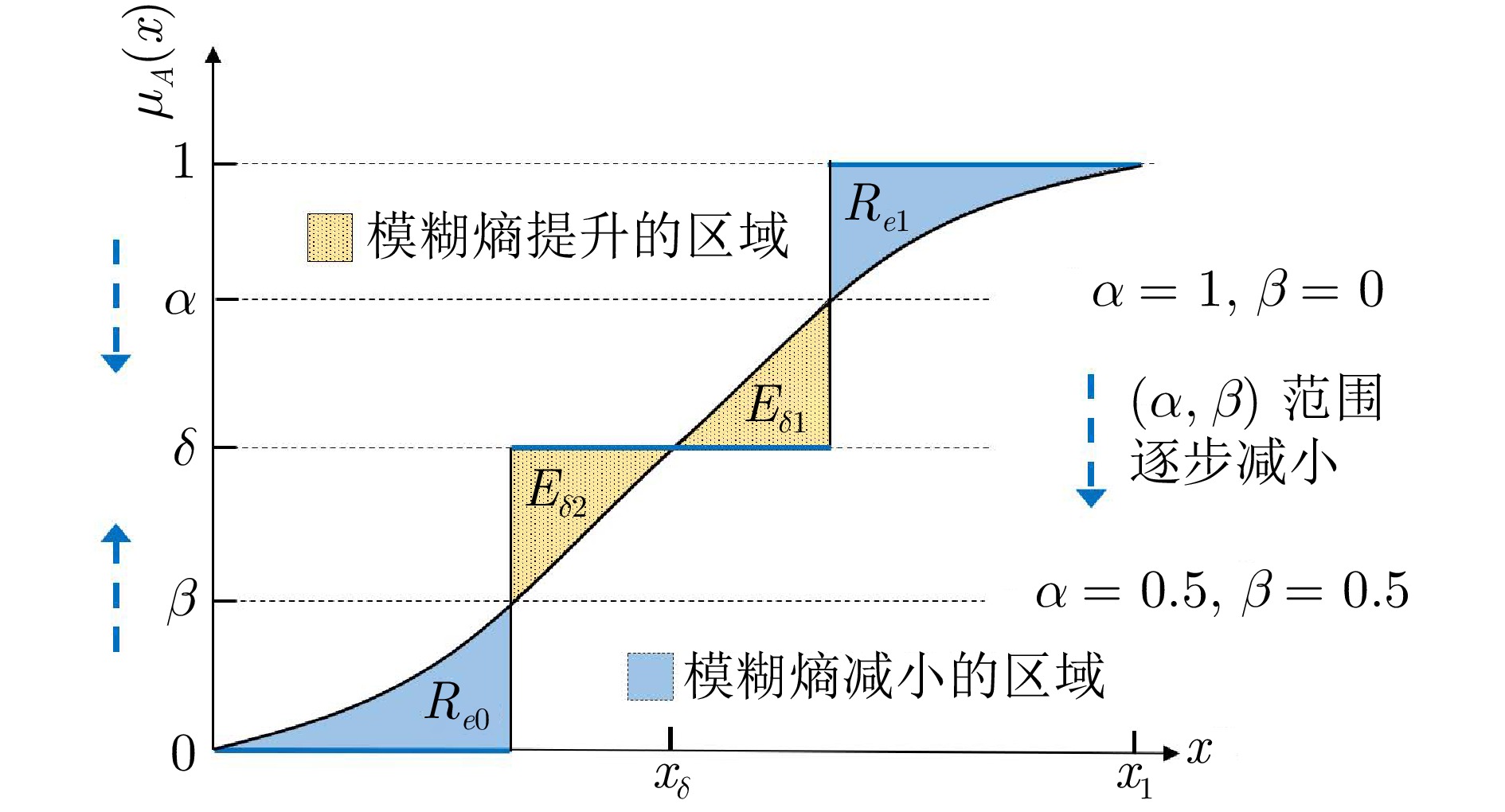
划分动作 模糊集 阴影集 熵损失$El(a| x )$ ${a_e}$ ${\mu _A}( x )$ 1 $El({a_e}| x )$ ${a_r}$ ${\mu _A}( x )$ 0 $El({a_r}| x )$ ${a_{s \downarrow }}$ ${\mu _A}( x ) \ge {\delta ^*}$ ${\delta ^*}$ $El({a_{s \downarrow }}| x )$ ${a_{s \uparrow }}$ ${\mu _A}( x ) < {\delta ^*}$ ${\delta ^*}$ $El({a_{s \uparrow }}| x )$
下载: 导出CSV
表 6 基于不同模糊集的阴影集构建研究总结
Table 6 Research summary of shadowed set construction based on different fuzzy sets
下载: 导出CSV
表 7 基于阴影集的数据分析研究总结
Table 7 Research summary of data analysis based on shadowed set
类别 研究内容 文献 引入阴影集的优势 聚类 基于阴影集的C均值聚类算法(SCM) [38] 实现了阈值自动化求取、数据约减、计算效率的提升 基于多粒度近似区域和阴影集的粗糙可能性C均值聚类算法(MS-RPCM) [39−40] 实现了阈值自动化求取、数据不确定性问题的解决、噪声抑制能力的增强 基于阴影集的粗糙模糊C均值聚类算法(S-RFCM) [41] 实现了阈值自动化求取、异常值的有效识别 基于阴影集的粗糙模糊可能性C均值聚类算法(S-RFPCM) [42] 实现了阈值自动化求取、异常值的有效识别 结合傅立叶随机特征映射和阴影集的粗糙模糊C均值聚类算法(AR-SRFCM) [43] 实现了非球形数据类簇的有效处理、异常值的有效识别 基于增量数据的阴影集集群聚类算法(OSC) [44] 实现了数据的实时处理、噪声样本的有效识别 结合阴影集和粒子群优化算法的模糊C均值聚类算法(SP-FCM) [45] 实现了数据约减、异常值的有效识别、算法效率和精度的提升 结合阴影集和混合蛙跳算法的粗糙模糊C均值聚类算法
(SFLA-SRFCM)[46] 实现了初值敏感、局部最优和参数设置主观性问题的解决 基于阴影集的高维混合属性数据集聚类边界检测算法
(CHASM)[47] 实现了边界检测及噪声抑制能力的增强 基于阴影集和集成学习的模糊聚类算法及应用场景 [48−49] 实现了阈值自动化求取、异常值的有效识别, 算法鲁棒性增强 基于区间阴影集的密度峰值聚类算法(ISS-DPC) [50−51] 实现了错误分类率的减少、抗噪性的增强 基于阴影集的截集式可能性C均值聚类算法(C-PCM) [52] 实现了截集门限的自动化选取 基于阴影集的广义多粒度粗糙模糊C均值聚类算法(MSRFCM) [53−54] 实现了数据拓扑结构的捕捉、数据不确定性问题的解决 基于无监督学习框架下的阴影C均值聚类算法(SCM) [55] 实现了传统SCM算法聚类质量和效率的提升 基于阴影集的多粒度三支聚类集成算法(MTWCES) [59−60] 实现了数据不确定性问题的解决、聚类准确率的提升 分类 基于阴影邻域的三支分类算法(3WC-SNB) [56] 实现了不确定性数据的有效分类、分类风险性的降低 基于半监督阴影集的三支分类算法(3WC-SSN) [57−58] 实现了不确定性数据的有效分类、分类风险性的降低 基于阴影集的快速KNN分类算法(TWC-KNN) [61−62] 实现了数据约减、数据质量的优化、分类效率的提高 数据
预处理基于阴影集的训练数据选择算法 [63−66] 实现了训练数据质量的提升、训练效率和分类器性能的提升 基于阴影集的候选断点集提取算法 [67] 实现了候选断点识别效率和准确率的提高 基于阴影集聚类的离群点检测算法 [68] 实现了聚类离群点检测识别率和识别精度的提高
下载: 导出CSV
表 8 基于阴影集的应用研究总结
Table 8 Summary of application research based on shadowed set
类别 研究内容 文献 引入阴影集的优势 图像分类
与识别基于阴影集的遥感图像分割算法 [69] 解决了遥感图像像素交叠区域的不确定性问题, 并提高了遥感图像分割的准确性和稳定性 基于阴影集的图像信息检索算法 [70] 有效减少了冗余信息, 降低了信息检索的复杂性, 提高了图像检索精度 基于阴影集的图像对比度增强算法 [71] 优化了图像的局部和全局参数, 实现了图像对比度增强的自动化提升 基于阴影集和人脸图像的两阶段性别分类算法 [72] 实现了图像数据的多阶段处理, 大大减少了训练时间损耗以及分类的不确定性, 提高了图像的分类精度 基于阴影集的两阶段图像分类算法 [73] 实现了图像数据的多阶段处理, 大大减少了训练时间损耗以及分类的不确定性, 提高了图像的分类精度 基于阴影集的半监督样本选择网络在噪声标记图像中的分类算法 [74] 实现了干净样本的自适应选取和高质量伪标签样本的有效选取, 减少了训练样本的数量, 并提高了图像分类性能 医疗信息处理 基于阴影集的基因表达聚类问题及基因性质识别 [75] 增强了聚类混淆区域中基因性质识别的有效性和准确率 基于阴影集的乳房X光图像对比度增强及微钙化识别 [76] 增强了图像不确定性区域的对比度以及微钙化的识别率, 提高了乳腺癌的识别率 文本分析 基于阴影集的语言术语建模及其在多属性决策中的应用 [77] 解决了信息丢失或失真所引起的不确定性问题, 提供了更合理和准确的决策结果 基于区间数据驱动的阴影集构建及其在语言词建模中的应用 [78] 实现了以区间数据驱动的阴影集模型构建, 为针对语言词问题的建模提供了一种新视角 基于博弈论阴影集的文本词特征提取算法 [79] 实现了语言词特征的有效提取, 并提高了针对语言词的分类性能和分类效率 决策推荐 基于阴影集的语言信息大规模群体决策算法 [80] 通过阴影集对语言术语进行建模, 实现了对群体决策者意见的综合考虑, 提高了群体决策的效率和有效性 基于阴影集的用户个性化决策推荐算法 [81] 减少了推荐系统推荐过程中的不确定性, 增强了决策推荐质量, 并能够针对不同用户实现个性化推荐
下载: 导出CSV
表 9 粒计算理论的主要模型及核心思想总结
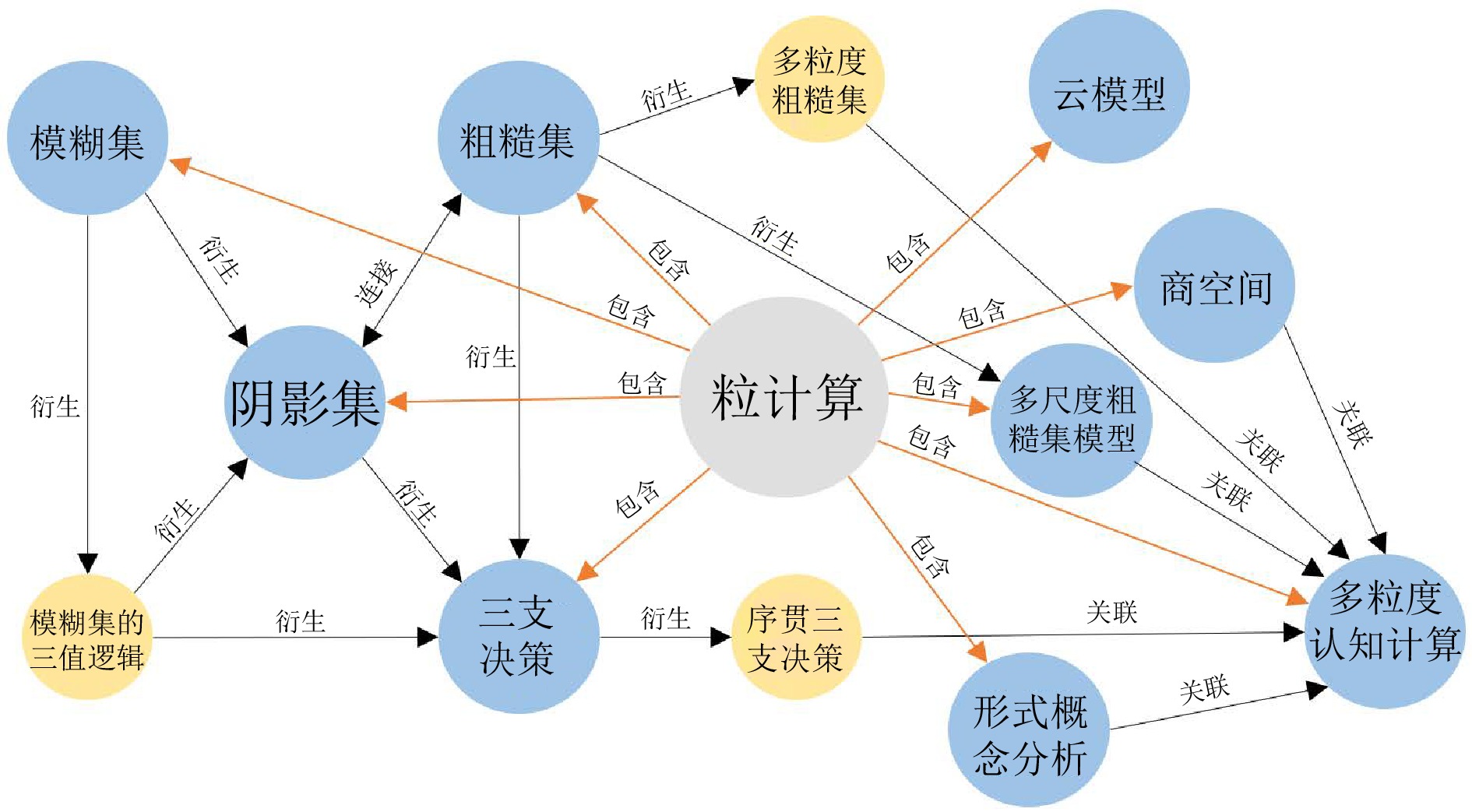
Table 9 Summary of the main models and core ideas of granular computing theory
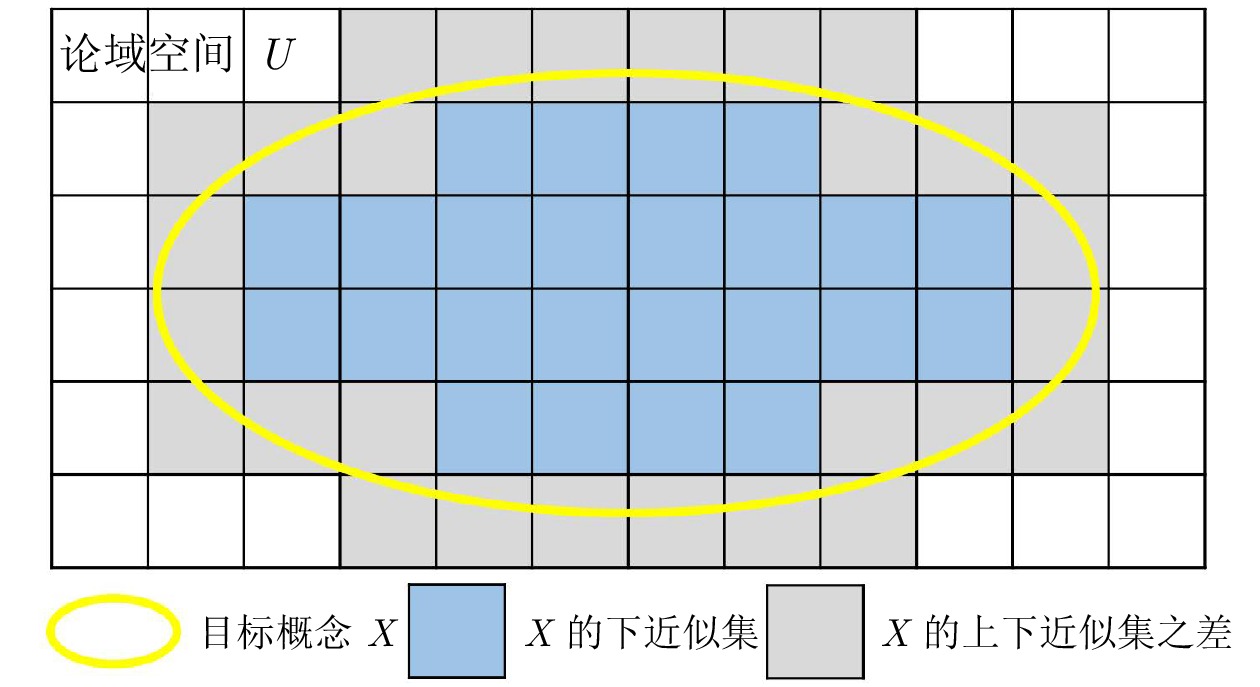
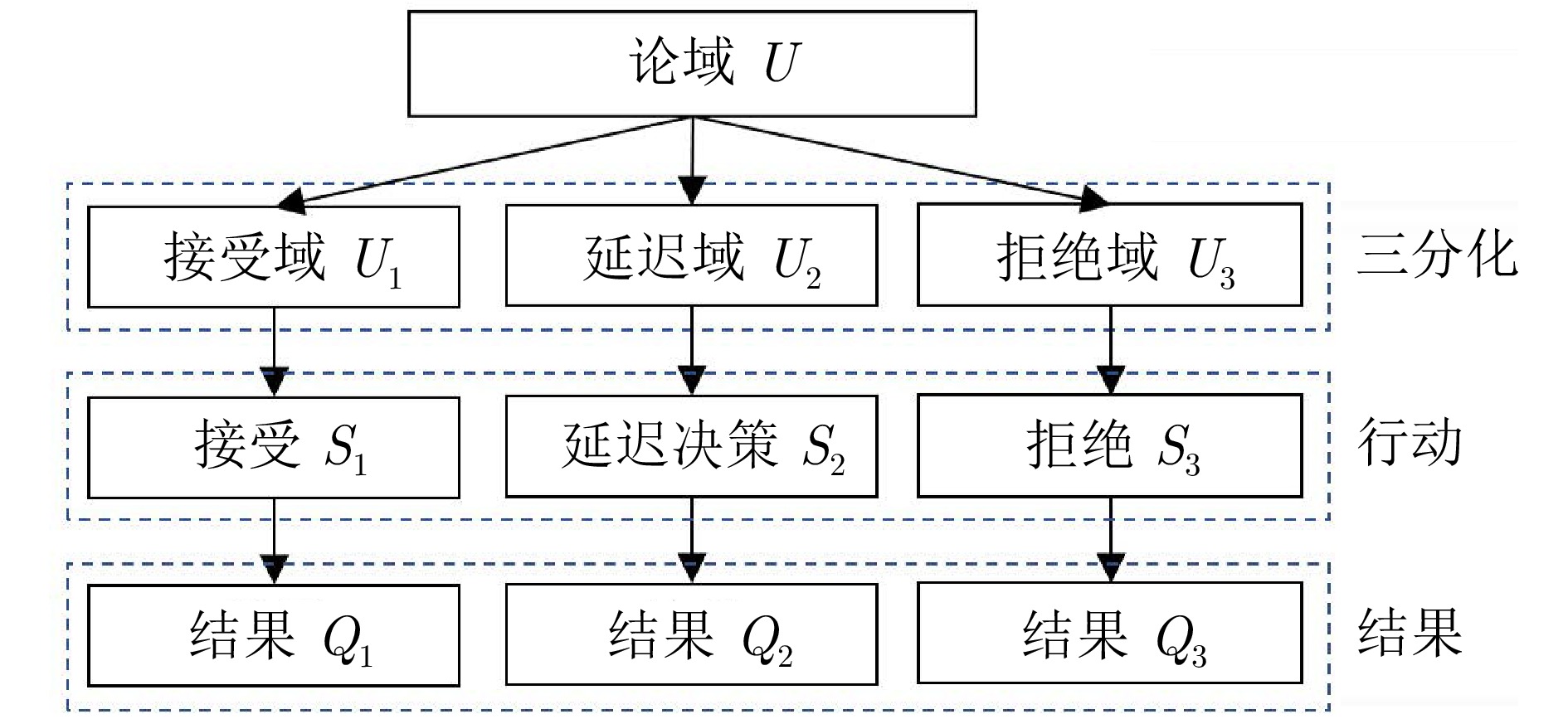
年份 文献 理论模型 核心思想 1965 [1] 模糊集 通过使用隶属度函数来对模糊性概念或不确定性信息进行表示与处理, 并进一步通过取值范围在0到1之间的精确隶属度值来描述一个对象隶属于模糊性概念的程度 1982 [88] 粗糙集 通过利用不可分辨关系构成对象的等价类, 实现对论域空间的近似划分, 并使用具有精确概念的上近似集和下近似集来实现对一个不精确概念的近似表示与度量 1982 [94] 形式概念分析 通过对象集与属性集之间的某种关联关系, 建立由对象集与属性集对所形成的形式概念层次结构, 并利用哈斯图的形式呈现不同粒概念之间的复杂关系, 实现对知识的挖掘和不确定性推理 1992 [89] 商空间 通过将复杂问题表示成不同粗细的粒度空间, 从而构建多粒度分层递阶空间结构, 通过由粗到细或由细到粗的方式在多粒度空间中进行近似逼近, 将多粒度空间中粒的解组合成原问题的解, 从而获得复杂问题的解 1995 [90] 云模型 通过使用期望、熵和超熵三个参数来对不确定性知识进行描述, 融合人类认知过程中随机与模糊这两种不确定性, 实现知识内涵与外延的相互转换 1998 [2] 阴影集 通过一对决策划分阈值来对模糊集进行近似划分处理, 并通过平衡不同划分区域的不确定性来构建阈值求取的目标函数, 利用这种粗糙的近似表达来替换模糊集过于精确的表达, 从而减少模糊决策过程中不确定性对象的决策划分成本和计算损耗 2009, 2010 [91−92] 三支决策 通过“三分而治”的思想将论域划分为三个子集, 即正域、负域和边界域, 并对不同子集采取不同的决策行为或分治策略, 即接受、拒绝和延迟决策, 进而对相应的行为或策略进行评价和反馈, 实现对复杂问题或信息不充分问题的求解 2011 [93] 多尺度粗糙集模型 通过将属性的取值标记为不同尺度(粒度)层次, 进而讨论知识在不同尺度下的关系及变化规律, 以及在给定尺度好坏评价标准的情况下最优尺度层次的选择方法, 实现在最优尺度空间中对知识的表示和获取 2018, 2019,
2022[86, 95−96] 多粒度认知计算 通过数据信息驱动, 融合人类“大范围首先”的认知机制(即“由粗粒度到细粒度”的认知过程)以及计算机的信息处理机制(即“由细粒度到粗粒度”的知识挖掘过程), 实现数据和知识双向驱动的空间变换和智能信息处理, 解决认知计算过程中的“数据与知识分离”问题
下载: 导出CSV
表 10 篮球运动员挑选
Table 10 Selection of basketball players
对象 身高(m) 身高$({S_{{\mu _A}}}( x ))$ 力量 篮球技术 决策 ${x_1}$ 1.95 1 大 好 1 ${x_2}$ 2.00 1 大 一般 1 ${x_3}$ 2.10 1 大 好 1 ${x_4}$ 1.98 1 小 一般 0 ${x_5}$ 1.85 [0, 1] 大 差 0 ${x_6}$ 1.73 0 中 差 0 ${x_7}$ 1.88 [0, 1] 中 好 1 ${x_8}$ 1.70 0 小 好 1
下载: 导出CSV
-
[1] Zadeh L A. Fuzzy sets. Information and Control, 1965, 8(3): 338−353 doi: 10.1016/S0019-9958(65)90241-X [2] Pedrycz W. Shadowed sets: Representing and processing fuzzy sets. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 1998, 28(1): 103−109 doi: 10.1109/3477.658584 [3] Pedrycz W, Vukovich G. Granular computing with shadowed sets. International Journal of Intelligent Systems, 2002, 17(2): 173−197 doi: 10.1002/int.10015 [4] Pedrycz W. From fuzzy sets to shadowed sets: Interpretation and computing. International Journal of Intelligent Systems, 2009, 24(1): 48−61 doi: 10.1002/int.20323 [5] Cattaneo G, Ciucci D. Shadowed sets and related algebraic structures. Fundamenta Informaticae, 2003, 55(3−4): 255−284 [6] Cattaneo G, Ciucci D. An algebraic approach to shadowed sets. Electronic Notes in Theoretical Computer Science, 2003, 82(4): 64−75 doi: 10.1016/S1571-0661(04)80706-0 [7] Deng X F, Yao Y Y. Mean-value-based decision-theoretic shadowed sets. In: Proceedings of the Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS). Edmonton, Canada: IEEE, 2013. 1382−1387 [8] Deng X F, Yao Y Y. Decision-theoretic three-way approximations of fuzzy sets. Information Sciences, 2014, 279: 702−715 doi: 10.1016/j.ins.2014.04.022 [9] Yao Y Y, Wang S, Deng X F. Constructing shadowed sets and three-way approximations of fuzzy sets. Information Sciences, 2017, 412−413: 132−153 doi: 10.1016/j.ins.2017.05.036 [10] Zhang Y, Yao J T. Determining strategies in game-theoretic shadowed sets. In: Proceedings of the 17th International Conference on Information Processing and Management of Uncertainty in Knowledge-based Systems. Cádiz, Spain: Springer, 2018. 736−747 [11] Zhang Y, Yao J T. Game theoretic approach to shadowed sets: A three-way tradeoff perspective. Information Sciences, 2020, 507: 540−552 doi: 10.1016/j.ins.2018.07.058 [12] Zhang Q H, Chen Y H, Yang J, Wang G Y. Fuzzy entropy: A more comprehensible perspective for interval shadowed sets of fuzzy sets. IEEE Transactions on Fuzzy Systems, 2020, 28(11): 3008−3022 doi: 10.1109/TFUZZ.2019.2947224 [13] Gao M, Zhang Q H, Zhao F, Wang G Y. Mean-entropy-based shadowed sets: A novel three-way approximation of fuzzy sets. International Journal of Approximate Reasoning, 2020, 120: 102−124 doi: 10.1016/j.ijar.2020.02.006 [14] Zhang Q H, Gao M, Zhao F, Wang G Y. Fuzzy-entropy-based game theoretic shadowed sets: A novel game perspective from uncertainty. IEEE Transactions on Fuzzy Systems, 2020, 30(3): 597−609 [15] 高满. 基于不确定性分析的阴影集模型研究 [硕士学位论文], 重庆邮电大学, 中国, 2020.Gao Man. Research on Shadowed Sets Model Based on Uncertainty Analysis [Master thesis], Chongqing University of Posts and Telecommunications, China, 2020. [16] Luo Z Q, Hu J, Zhang Q H, Wang G Y. Induction of interval shadowed sets from the perspective of maintaining fuzziness. International Journal of Approximate Reasoning, 2023, 153: 219−238 doi: 10.1016/j.ijar.2022.11.019 [17] Gao M, Zhang Q H, Zhao F, Wu C Y, Wang G Y, Xia D Y. Constructing shadowed set based on game analysis of uncertainty and decision cost. Applied Soft Computing, 2023, 147: Article No. 110762 doi: 10.1016/j.asoc.2023.110762 [18] Vincent T L. Game theory as a design tool. Journal of Mechanical Design, 1983, 105(2): 165−170 [19] Rao S S. Game theory approach for multiobjective structural optimization. Computers & Structures, 1987, 25(1): 119−127 [20] Liu X C. Entropy, distance measure and similarity measure of fuzzy sets and their relations. Fuzzy Sets and Systems, 1992, 52(3): 305−318 doi: 10.1016/0165-0114(92)90239-Z [21] Grzegorzewski P. Fuzzy number approximation via shadowed sets. Information Sciences, 2013, 225: 35−46 doi: 10.1016/j.ins.2012.10.028 [22] Zhou J, Miao D Q, Gao C, Lai Z H, Yue X D. Constrained three-way approximations of fuzzy sets: From the perspective of minimal distance. Information Sciences, 2019, 502: 247−267 doi: 10.1016/j.ins.2019.06.004 [23] Zhang Q H, Xia D Y, Liu K X, Wang G Y. A general model of decision-theoretic three-way approximations of fuzzy sets based on a heuristic algorithm. Information Sciences, 2020, 507: 522−539 doi: 10.1016/j.ins.2018.10.051 [24] 夏德友. 三支决策粗糙集模型及其应用研究 [硕士学位论文], 重庆邮电大学, 中国, 2018.Xia De-You. Research on Three-way Decision-theoretic With Rough Set Models and Its Application [Master thesis], Chongqing University of Posts and Telecommunications, China, 2018. [25] Zhou J, Gao C, Pedrycz W, Lai Z H, Yue X D. Constrained shadowed sets and fast optimization algorithm. International Journal of Intelligent Systems, 2019, 34(10): 2655−2675 doi: 10.1002/int.22170 [26] Zhao X R, Yao Y Y. Three-way fuzzy partitions defined by shadowed sets. Information Sciences, 2019, 497: 23−37 doi: 10.1016/j.ins.2019.05.022 [27] Ciucci D, Yao Y Y. Synergy of granular computing, shadowed sets, and three-way decisions. Information Sciences, 2020, 508: 422−425 doi: 10.1016/j.ins.2019.09.003 [28] Boffa S, Campagner A, Ciucci D, Yao Y Y. Aggregation operators on shadowed sets. Information Sciences, 2022, 595: 313−333 doi: 10.1016/j.ins.2022.02.046 [29] Tahayori H, Sadeghian A, Pedrycz W. Induction of shadowed sets based on the gradual grade of fuzziness. IEEE Transactions on Fuzzy Systems, 2013, 21(5): 937−949 doi: 10.1109/TFUZZ.2012.2236843 [30] Cai M J, Li Q G, Lang G M. Shadowed sets of dynamic fuzzy sets. Granular Computing, 2017, 2(2): 85−94 doi: 10.1007/s41066-016-0029-y [31] Bose A, Mali K. A two threshold model for shadowed set with gradual representation of cardinality. In: Proceedings of the 14th IEEE India Council International Conference (INDICON). Roorkee, India: IEEE, 2017. 1−6 [32] Ibrahim A M, William-West T O. Induction of shadowed sets from fuzzy sets. Granular Computing, 2019, 4(1): 27−38 doi: 10.1007/s41066-018-0083-8 [33] William-West T O, Ibrahim A M, Kana A F D. Shadowed set approximation of fuzzy sets based on nearest quota of fuzziness. Annals of Fuzzy Mathematics and Informatics, 2019, 17(2): 133−145 doi: 10.30948/afmi.2019.17.2.133 [34] William-West T O, Ibrahim M A. Trade-off principle for standard shadowed sets and its generalization to five-regions. Fuzzy Sets and Systems, 2023, 461: Article No. 108373 doi: 10.1016/j.fss.2022.08.005 [35] Campagner A, Dorigatti V, Ciucci D. Entropy-based shadowed set approximation of intuitionistic fuzzy sets. International Journal of Intelligent Systems, 2020, 35(12): 2117−2139 doi: 10.1002/int.22287 [36] Yang J L, Yao Y Y. A three-way decision based construction of shadowed sets from Atanassov intuitionistic fuzzy sets. Information Sciences, 2021, 577: 1−21 doi: 10.1016/j.ins.2021.06.065 [37] Yao Y Y, Yang J L. Granular rough sets and granular shadowed sets: Three-way approximations in Pawlak approximation spaces. International Journal of Approximate Reasoning, 2022, 142: 231−247 doi: 10.1016/j.ijar.2021.11.012 [38] Mitra S, Pedrycz W, Barman B. Shadowed c-means: Integrating fuzzy and rough clustering. Pattern Recognition, 2010, 43(4): 1282−1291 doi: 10.1016/j.patcog.2009.09.029 [39] Zhou J, Pedrycz W, Miao D Q. Shadowed sets in the characterization of rough-fuzzy clustering. Pattern Recognition, 2011, 44(8): 1738−1749 doi: 10.1016/j.patcog.2011.01.014 [40] Zhou J, Lai Z H, Gao C, Miao D Q, Yue X D. Rough possibilistic C-means clustering based on multigranulation approximation regions and shadowed sets. Knowledge-based Systems, 2018, 160: 144−166 doi: 10.1016/j.knosys.2018.07.007 [41] 郭晋华, 苗夺谦, 周杰. 基于阴影集的粗糙聚类阈值选择. 计算机科学, 2011, 38(10): 209−210Guo Jin-Hua, Miao Duo-Qian, Zhou Jie. Shadowed sets based threshold selection in rough clustering. Computer Science, 2011, 38(10): 209−210 [42] 汪海良, 佘堃, 周明天. 基于阴影集的粗糙模糊可能性C均值聚类算法. 计算机科学, 2013, 40(1): 191−194Wang Hai-Liang, She Kun, Zhou Ming-Tian. Shadowed sets-based rough fuzzy possibilistic C-means clustering. Computer Science, 2013, 40(1): 191−194 [43] Kong L N, Chen L. Shadowed set-based rough-fuzzy clustering using random feature mapping. In: Proceedings of the International Conference on Security, Pattern Analysis, and Cybernetics (SPAC). Shenzhen, China: IEEE, 2017. 400−405 [44] Falcon R, Nayak A, Abielmona R. An online shadowed clustering algorithm applied to risk visualization in territorial security. In: Proceedings of the IEEE Symposium on Computational Intelligence for Security and Defence Applications. Ottawa, Canada: IEEE, 2012. 1−8 [45] 李秀馨, 王敬东, 徐烨晔, 温家旺. 基于改进FCM算法的卫星云图聚类方法研究. 红外技术, 2013, 35(3): 150−154Li Xiu-Xin, Wang Jing-Dong, Xu Ye-Ye, Wen Jia-Wang. Satellite image clustering research based on improved FCM algorithm. Infrared Technology, 2013, 35(3): 150−154 [46] 蒙祖强, 胡玉兰, 蒋亮, 常红岩. 基于混合蛙跳与阴影集优化的粗糙模糊聚类算法. 控制与决策, 2015, 30(10): 1766−1772Meng Zu-Qiang, Hu Yu-Lan, Jiang Liang, Chang Hong-Yan. Shuffled frog leaping algorithm and shadowed sets based rough fuzzy clustering algorithm. Control and Decision, 2015, 30(10): 1766−1772 [47] Li X L, Geng P, Qiu B Z. A cluster boundary detection algorithm based on shadowed set. Intelligent Data Analysis, 2016, 20(1): 29−45 doi: 10.3233/IDA-150792 [48] 王丽娜. 基于阴影集和粗糙集的模糊聚类算法研究与应用 [博士学位论文], 南京航空航天大学, 中国, 2016.Wang Li-Na. Research on Fuzzy Clustering Algorithms Based on Shadowed Sets and Rough Sets and Their Applications [Ph. D. dissertation], Nanjing University of Aeronautics and Astronautics, China, 2016. [49] 王丽娜, 王建东, 李涛, 叶枫. 集成粗糙集和阴影集的簇特征加权模糊聚类算法. 系统工程与电子技术, 2013, 35(8): 1769−1776Wang Li-Na, Wang Jian-Dong, Li Tao, Ye Feng. Cluster's feature weighting fuzzy clustering algorithm integrating rough sets and shadowed sets. Systems Engineering and Electronics, 2013, 35(8): 1769−1776 [50] 陈玉洪, 张清华, 杨洁. 基于区间阴影集的密度峰值聚类算法. 模式识别与人工智能, 2019, 32(6): 531−544Chen Yu-Hong, Zhang Qing-Hua, Yang Jie. Density peak clustering algorithm based on interval shadowed sets. Pattern Recognition and Artificial Intelligence, 2019, 32(6): 531−544 [51] 陈玉洪. 基于模糊熵的区间阴影集模型及其应用 [硕士学位论文], 重庆邮电大学, 中国, 2019.Chen Yu-Hong. Interval Shadowed Set Model Based on Fuzzy Entropy and Its Application [Master thesis], Chongqing University of Posts and Telecommunications, China, 2019. [52] 雒僖, 范九伦, 于海燕, 梁丹. 基于阴影集的截集式可能性C-均值聚类截集门限的选取. 计算机科学, 2019, 46(8): 249−254Luo Xi, Fan Jiu-Lun, Yu Hai-Yan, Liang Dan. Selection of cutset threshold for cutset-type possibilistic C-means clustering based on shadowed set. Computer Science, 2019, 46(8): 249−254 [53] Zhou J, Lai Z H, Miao D Q, Gao C, Yue X D. Multigranulation rough-fuzzy clustering based on shadowed sets. Information Sciences, 2020, 507: 553−573 doi: 10.1016/j.ins.2018.05.053 [54] Zhou J, Pedrycz W, Gao C, Lai Z H, Yue X D. Principles for constructing three-way approximations of fuzzy sets: A comparative evaluation based on unsupervised learning. Fuzzy Sets and Systems, 2021, 413: 74−98 doi: 10.1016/j.fss.2020.06.019 [55] William-West T, Kana A F D, Ibrahim M A. Shadowed-set-based three-way clustering methods: An investigation of new optimization-based principles. Information Sciences, 2022, 591: 1−24 doi: 10.1016/j.ins.2022.01.018 [56] Yue X D, Zhou J, Yao Y Y, Miao D Q. Shadowed neighborhoods based on fuzzy rough transformation for three-way classification. IEEE Transactions on Fuzzy Systems, 2020, 28(5): 978−991 doi: 10.1109/TFUZZ.2020.2979365 [57] Yue X D, Liu S W, Qian Q, Miao D Q, Gao C. Semi-supervised shadowed sets for three-way classification on partial labeled data. Information Sciences, 2022, 607: 1372−1390 doi: 10.1016/j.ins.2022.06.062 [58] 刘思雯. 基于不确定阴影原型的分类方法研究 [硕士学位论文], 上海大学, 中国, 2022.Liu Si-Wen. Research on Classification Method With Uncertain Shadowed Prototypes [Master thesis], Shanghai University, China, 2022. [59] 姜春茂, 赵书宝. 基于阴影集的多粒度三支聚类集成. 电子学报, 2021, 49(8): 1524−1532Jiang Chun-Mao, Zhao Shu-Bao. Multi-granulation three-way clustering ensemble based on shadowed sets. Acta Electronica Sinica, 2021, 49(8): 1524−1532 [60] Jiang C M, Li Z C, Yao J T. A shadowed set-based three-way clustering ensemble approach. International Journal of Machine Learning and Cybernetics, 2022, 13(9): 2545−2558 doi: 10.1007/s13042-022-01543-5 [61] 赵书宝, 姜春茂. 一种基于三支聚类的快速KNN算法. 小型微型计算机系统, 2021, 42(9): 1845−1851Zhao Shu-Bao, Jiang Chun-Mao. Fast KNN classification algorithm based on three-way clustering. Journal of Chinese Computer Systems, 2021, 42(9): 1845−1851 [62] 赵书宝. 三支决策视角下的聚类集成与分类研究 [硕士学位论文], 哈尔滨师范大学, 中国, 2021.Zhao Shu-Bao. Clustering Ensemble and Classification Under the Perspective of Three-way Decision [Master thesis], Harbin Normal University, China, 2021. [63] Zhou Y, Su H B, Zhang H T. A novel data selection method based on shadowed sets. Procedia Engineering, 2011, 15: 1410−1415 doi: 10.1016/j.proeng.2011.08.261 [64] 周玉, 钱旭, 王自强. 基于阴影集数据选择的可拓神经网络性能改进. 北京工业大学学报, 2013, 39(3): 430−437Zhou Yu, Qian Xu, Wang Zi-Qiang. Performance improvement of extension neural network using data selection method based on shadowed sets. Journal of Beijing University of Technology, 2013, 39(3): 430−437 [65] 周玉, 朱安福, 周林, 钱旭. 一种神经网络分类器样本数据选择方法. 华中科技大学学报(自然科学版), 2012, 40(6): 39−43Zhou Yu, Zhu An-Fu, Zhou Lin, Qian Xu. Sample data selection method for neural network classifiers. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(6): 39−43 [66] 苏小红, 赵玲玲, 谢琳, 马培军. 阴影集的模糊支持向量机样本选择方法. 哈尔滨工业大学学报, 2012, 44(9): 78−84Su Xiao-Hong, Zhao Ling-Ling, Xie Lin, Ma Pei-Jun. Shadowed sets-based sample selection method for fuzzy support vector machine. Journal of Harbin Institute of Technology, 2012, 44(9): 78−84 [67] 周凡程, 吴孟达, 王丹. 基于Shadowed Sets的连续属性离散化. 模糊系统与数学, 2012, 26(2): 120−128Zhou Fan-Cheng, Wu Meng-Da, Wang Dan. Discretization of continuous attributes based on shadowed sets. Fuzzy Systems and Mathematics, 2012, 26(2): 120−128 [68] 王丹, 毛紫阳, 吴孟达. 融合Shadowed Sets聚类的离群点检测算法. 计算机科学与探索, 2012, 6(11): 985−993Wang Dan, Mao Zi-Yang, Wu Meng-Da. Outlier detection algorithm on shadowed sets clustering. Journal of Frontiers of Computer Science and Technology, 2012, 6(11): 985−993 [69] Mitra S, Kundu P P. Satellite image segmentation with shadowed C-means. Information Sciences, 2011, 181(17): 3601−3613 doi: 10.1016/j.ins.2011.04.027 [70] Zhang H Y, Zhang T, Pedrycz W, Zhao C R, Miao D Q. Improved adaptive image retrieval with the use of shadowed sets. Pattern Recognition, 2019, 90: 390−403 doi: 10.1016/j.patcog.2019.01.029 [71] Alavi M, Kargari M. A novel method for contrast enhancement of gray scale image based on shadowed sets. In: Proceedings of the 6th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS). Mashhad, Iran: IEEE, 2020. 1−7 [72] 杨晨旭, 蔡克参, 张红云, 苗夺谦. 基于人脸图像的二阶段性别分类算法. 计算机科学与探索, 2021, 15(3): 524−532Yang Chen-Xu, Cai Ke-Can, Zhang Hong-Yun, Miao Duo-Qian. Facial image based two-level model for gender classification. Journal of Frontiers of Computer Science and Technology, 2021, 15(3): 524−532 [73] 陈超凡, 张红云, 蔡克参, 苗夺谦. 基于三支决策的二阶段图像分类方法. 模式识别与人工智能, 2021, 34(8): 768−776Chen Chao-Fan, Zhang Hong-Yun, Cai Ke-Can, Miao Duo-Qian. Two-stage image classification method based on three-way decisions. Pattern Recognition and Artificial Intelligence, 2021, 34(8): 768−776 [74] Cai K C, Zhang H Y, Pedrycz W, Miao D Q. SSS-Net: A shadowed-sets-based semi-supervised sample selection network for classification on noise labeled images. Knowledge-based Systems, 2023, 276: Article No. 110732 doi: 10.1016/j.knosys.2023.110732 [75] Bose A, Mali K. Gradual representation of shadowed set for clustering gene expression data. Applied Soft Computing, 2019, 83: Article No. 105614 doi: 10.1016/j.asoc.2019.105614 [76] Bose A, Mali K. Mammogram image enhancement using a two-threshold model of shadowed set with gradual representation of cardinality. In: Proceedings of the IEEE Region 10 Symposium (TENSYMP). Mumbai, India: IEEE, 2022. 1−6 [77] Wang H D, He S F, Pan X H, Li C D. Shadowed sets-based linguistic term modeling and its application in multi-attribute decision-making. Symmetry, 2018, 10(12): Article No. 688 doi: 10.3390/sym10120688 [78] Li C D, Yi J Q, Wang H K, Zhang G Q, Li J Q. Interval data driven construction of shadowed sets with application to linguistic word modelling. Information Sciences, 2020, 507: 503−521 doi: 10.1016/j.ins.2018.11.018 [79] Zhang Y, Zhou Y, Yao J T. Feature extraction with TF-IDF and game-theoretic shadowed sets. In: Proceedings of the 18th International Conference on Information Processing and Management of Uncertainty in Knowledge-based Systems. Lisbon, Portugal: Springer, 2020. 722−733 [80] He S F, Pan X H, Wang Y M. A shadowed set-based TODIM method and its application to large-scale group decision making. Information Sciences, 2021, 544: 135−154 doi: 10.1016/j.ins.2020.07.028 [81] Wu C Y, Zhang Q H, Zhao F, Cheng Y L, Wang G Y. Three-way recommendation model based on shadowed set with uncertainty invariance. International Journal of Approximate Reasoning, 2021, 135: 53−70 doi: 10.1016/j.ijar.2021.04.009 [82] 梁吉业, 钱宇华, 李德玉, 胡清华. 大数据挖掘的粒计算理论与方法. 中国科学: 信息科学, 2015, 45(11): 1355−1369 doi: 10.1360/N112015-00092Liang Ji-Ye, Qian Yu-Hua, Li De-Yu, Hu Qing-Hua. Theory and method of granular computing for big data mining. Scientia Sinica Informationis, 2015, 45(11): 1355−1369 doi: 10.1360/N112015-00092 [83] 徐计, 王国胤, 于洪. 基于粒计算的大数据处理. 计算机学报, 2015, 38(8): 1497−1517Xu Ji, Wang Guo-Yin, Yu Hong. Review of big data processing based on granular computing. Chinese Journal of Computers, 2015, 38(8): 1497−1517 [84] Zadeh L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets and Systems, 1997, 90(2): 111−127 doi: 10.1016/S0165-0114(97)00077-8 [85] Yao J T, Vasilakos A V, Pedrycz W. Granular computing: Perspectives and challenges. IEEE Transactions on Cybernetics, 2013, 43(6): 1977−1989 doi: 10.1109/TSMCC.2012.2236648 [86] 王国胤, 李帅, 杨洁. 知识与数据双向驱动的多粒度认知计算. 西北大学学报(自然科学版), 2018, 48(4): 488−500Wang Guo-Yin, Li Shuai, Yang Jie. A multi-granularity cognitive computing model bidirectionally driven by knowledge and data. Journal of Northwest University (Natural Science Edition), 2018, 48(4): 488−500 [87] 王国胤, 张清华, 马希骜, 杨青山. 知识不确定性问题的粒计算模型. 软件学报, 2011, 22(4): 676−694 doi: 10.3724/SP.J.1001.2011.03954Wang Guo-Yin, Zhang Qing-Hua, Ma Xi-Ao, Yang Qing-Shan. Granular computing models for knowledge uncertainty. Journal of Software, 2011, 22(4): 676−694 doi: 10.3724/SP.J.1001.2011.03954 [88] Pawlak Z. Rough sets. International Journal of Computer & Information Sciences, 1982, 11(5): 341−356 [89] Zhang B, Zhang L. Theory and Applications of Problem Solving. New York: Elsevier Science Inc., 1992. [90] 李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器. 计算机研究与发展, 1995, 32(6): 15−20Li De-Yi, Meng Hai-Jun, Shi Xue-Mei. Membership clouds and membership cloud generators. Journal of Computer Research and Development, 1995, 32(6): 15−20 [91] Yao Y Y. Three-way decision: An interpretation of rules in rough set theory. In: Proceedings of the 4th International Conference Rough Sets and Knowledge Technology. Gold Coast, Australia: Springer, 2009. 642−649 [92] Yao Y Y. Three-way decisions with probabilistic rough sets. Information Sciences, 2010, 180(3): 341−353 doi: 10.1016/j.ins.2009.09.021 [93] Wu W Z, Leung Y. Theory and applications of granular labelled partitions in multi-scale decision tables. Information Sciences, 2011, 181(18): 3878−3897 doi: 10.1016/j.ins.2011.04.047 [94] Wille R. Restructuring lattice theory: An approach based on hierarchies of concepts. In: Proceedings of the NATO Advanced Study Institute. Banff, Canada: Springer, 1982. 445−470 [95] 王国胤, 于洪. 多粒度认知计算——一种大数据智能计算的新模型. 数据与计算发展前沿, 2019, 1(2): 75−85Wang Guo-Yin, Yu Hong. Multi-granularity cognitive computing——A new model for big data intelligent computing. Frontiers of Data & Computing, 2019, 1(2): 75−85 [96] 王国胤, 傅顺, 杨洁, 郭毅可. 基于多粒度认知的智能计算研究. 计算机学报, 2022, 45(6): 1161−1175Wang Guo-Yin, Fu Shun, Yang Jie, Guo Yi-Ke. A review of research on multi-granularity cognition based intelligent computing. Chinese Journal of Computers, 2022, 45(6): 1161−1175 [97] 刘盾, 梁德翠. 广义三支决策与狭义三支决策. 计算机科学与探索, 2017, 11(3): 502−510Liu Dun, Liang De-Cui. Generalized three-way decisions and special three-way decisions. Journal of Frontiers of Computer Science and Technology, 2017, 11(3): 502−510 [98] Yao Y Y. The geometry of three-way decision. Applied Intelligence, 2021, 51(9): 6298−6325 doi: 10.1007/s10489-020-02142-z [99] Yao Y Y. An outline of a theory of three-way decisions. In: Proceedings of the 8th International Conference on Rough Sets and Current Trends in Computing. Chengdu, China: Springer, 2012. 1−17 [100] Yao Y Y. Three-way decisions and cognitive computing. Cognitive Computation, 2016, 8(4): 543−554 doi: 10.1007/s12559-016-9397-5 [101] Yao Y Y. The Dao of three-way decision and three-world thinking. International Journal of Approximate Reasoning, 2023, 162: Article No. 109032 doi: 10.1016/j.ijar.2023.109032 [102] 刘盾, 李天瑞, 杨新, 梁德翠. 三支决策——基于粗糙集与粒计算研究视角. 智能系统学报, 2019, 14(6): 1111−1120 doi: 10.11992/tis.201905039Liu Dun, Li Tian-Rui, Yang Xin, Liang De-Cui. Three-way decisions: Research perspectives for rough sets and granular computing. CAAI Transactions on Intelligent Systems, 2019, 14(6): 1111−1120 doi: 10.11992/tis.201905039 [103] Liu D, Yang X, Li T R. Three-way decisions: Beyond rough sets and granular computing. International Journal of Machine Learning and Cybernetics, 2020, 11(5): 989−1002 doi: 10.1007/s13042-020-01095-6 [104] 刘盾, 叶晓庆, 李天瑞. 三支决策——基于可解释研究视角. 西北大学学报(自然科学版), 2023, 53(6): 991−1003Liu Dun, Ye Xiao-Qing, Li Tian-Rui. Three-way decision based on the interpretability research perspective. Journal of Northwest University (Natural Science Edition), 2023, 53(6): 991−1003 [105] Azam N, Yao J T. Multiple criteria decision analysis with game-theoretic rough sets. In: Proceedings of the 7th International Conference on Rough Sets and Knowledge Technology. Chengdu, China: Springer, 2012. 399−408 [106] Zhang Y, Yao J T. Multi-criteria based three-way classifications with game-theoretic rough sets. In: Proceedings of the 23rd International Symposium on Foundations of Intelligent Systems. Warsaw, Poland: Springer, 2017. 550−559 [107] Qian Y H, Liang J Y, Yao Y Y, Dang C Y. MGRS: A multi-granulation rough set. Information Sciences, 2010, 180(6): 949−970 doi: 10.1016/j.ins.2009.11.023 [108] 王君宇, 李言, 李丽红. 动态三支决策研究综述及展望. 数字技术与应用, 2021, 39(9): 174−176Wang Jun-Yu, Li Yan, Li Li-Hong. Summary and prospect of the research on dynamic three-way decisions. Digital Technology & Application, 2021, 39(9): 174−176 [109] Zhang Q H, Liu K X, Feng L. Research on rough equality and rough inclusion of sets in multi-granulation spaces. Journal of Intelligent & Fuzzy Systems, 2019, 36(3): 2793−2806 -
图(11) / 表(10)
计量
- 文章访问数: 554
- HTML全文浏览量: 75
- PDF下载量: 116
- 被引次数: 0
