Modeling and Fixed-time Prescribed Performance Control for Hypersonic Morphing Vehicle
-
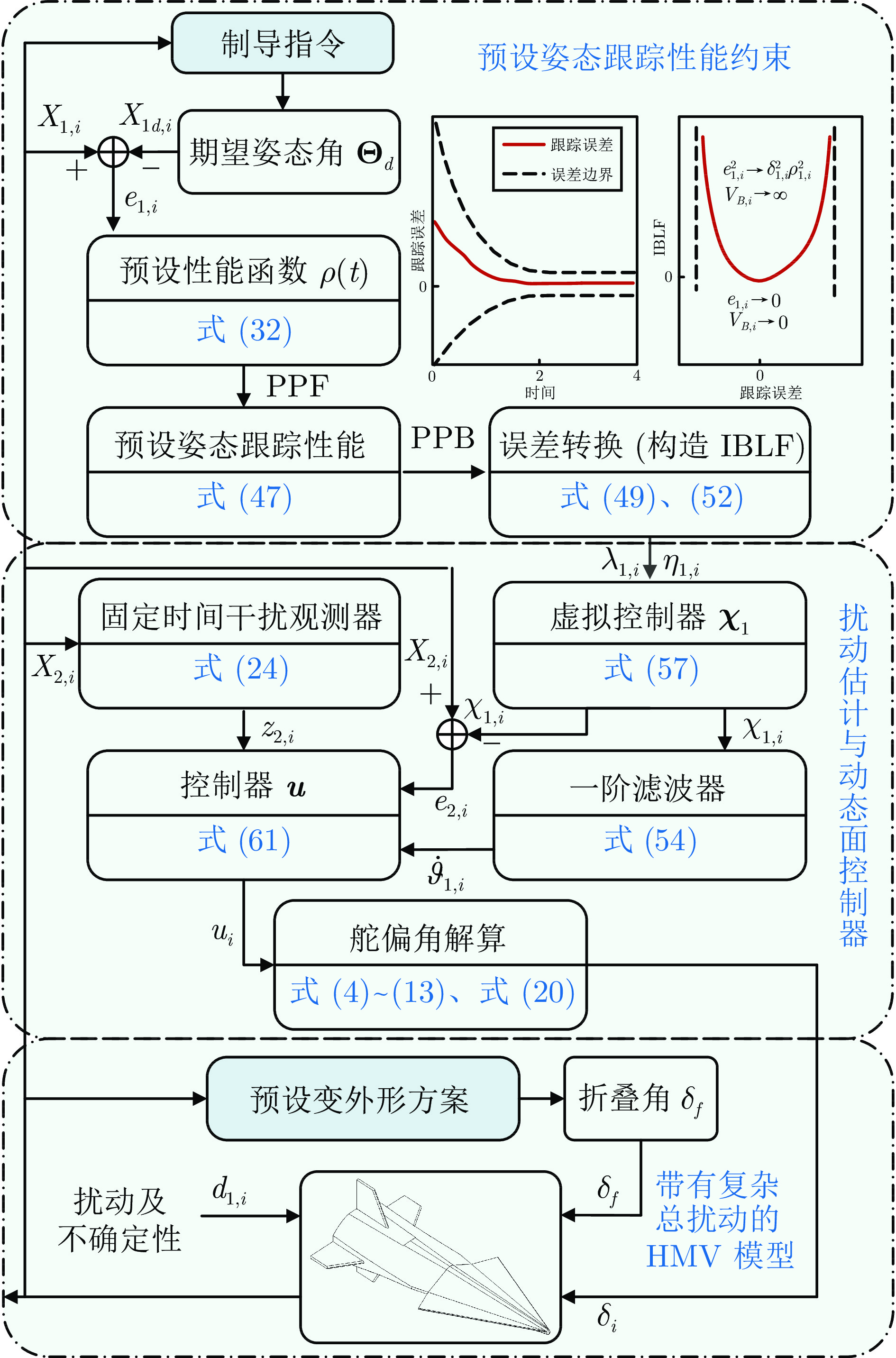
摘要: 以一种折叠式高超声速变外形飞行器(Hypersonic morphing vehicle, HMV)为研究对象, 综合考虑变形引起的气动特性、动力学特性的动态变化和模型不确定性、外部干扰的影响, 开展飞行器建模与固定时间预设性能控制方法研究. 首先, 建立高超声速变外形飞行器的运动模型和姿态控制模型; 然后, 采用固定时间干扰观测器实现对模型不确定性和外部干扰构成的复合总扰动的精确估计, 并设计一种新型固定时间预设性能函数以定量描述期望性能约束, 在此基础上, 基于预设性能控制架构并结合动态面控制技术设计预设性能姿态控制器, 利用Lyapunov稳定性理论证明闭环系统的固定时间稳定性; 最后, 通过数值仿真验证所提出方法的有效性和鲁棒性.
-
关键词:
- 高超声速变外形飞行器 /
- 固定时间 /
- 预设性能 /
- 干扰观测器 /
- 动态面控制
Abstract: Taking a folding hypersonic morphing vehicle (HMV) as the research object, comprehensively considering dynamic changes caused by the deformation of aerodynamic characteristics and kinetics characteristics, as well as the influence of model uncertainties and external disturbances, the research on vehicle motion modeling and fixed-time prescribed performance control method is carried out. Firstly, the motion model and attitude control model of hypersonic morphing vehicle are established. Then, a fixed-time disturbance observer is established to accurately estimate the complex disturbance composed of model uncertainties and external disturbances, a novel fixed-time prescribed performance function is designed to quantitatively describe the expected performance constraints, the attitude controller is designed by integrating the dynamic surface control technique into the prescribed performance control framework, and the fixed-time stability of the closed-loop system is proved by Lyapunov stability theory. Finally, the numerical simulation is carried out to verify the effectiveness and robustness of the proposed method. -
图 1 高超声速变外形飞行器气动外形及变形过程示意图
Fig. 1 Aerodynamic shape and morphing process of hypersonic morphing vehicle
图 5 滚转力矩系数随折叠角变化曲线
Fig. 5 Curves of rolling moment coefficient varying with folding angle
图 6 偏航力矩系数随折叠角变化曲线
Fig. 6 Curves of yawing moment coefficient varying with folding angle
图 7 俯仰力矩系数随折叠角变化曲线
Fig. 7 Curves of pitching moment coefficient varying with folding angle
图 8 飞行器固定时间预设性能控制方案框图
Fig. 8 Flowchart of fixed-time prescribed performance control for HMV
图 14 仿真1气动力和附加力变化曲线 (0 ~ 3 s)
Fig. 14 Curves of aerodynamic force and additional force in Simulation 1 (0 ~ 3 s)
图 15 仿真1气动力和附加力变化曲线 (5 ~ 9 s)
Fig. 15 Curves of aerodynamic force and additional force in Simulation 1 (5 ~ 9 s)
图 16 仿真1气动力和附加力变化曲线 (11 ~ 16 s)
Fig. 16 Curves of aerodynamic force and additional force in Simulation 1 (11 ~ 16 s)
图 17 仿真1气动力矩和附加力矩变化曲线 (0 ~ 3 s)
Fig. 17 Curves of aerodynamic torque and additional torque in Simulation 1 (0 ~ 3 s)
图 18 仿真1气动力矩和附加力矩变化曲线 (5 ~ 9 s)
Fig. 18 Curves of aerodynamic torque and additional torque in Simulation 1 (5 ~ 9 s)
图 19 仿真1气动力矩和附加力矩变化曲线 (11 ~ 16 s)
Fig. 19 Curves of aerodynamic torque and additional torque in Simulation 1 (11 ~ 16 s)
图 23 仿真2总扰动及其观测误差曲线
Fig. 23 Curves of total disturbance and its observation error in Simulation 2
表 1 气动模型状态量范围
Table 1 State quantity range of aerodynamics model
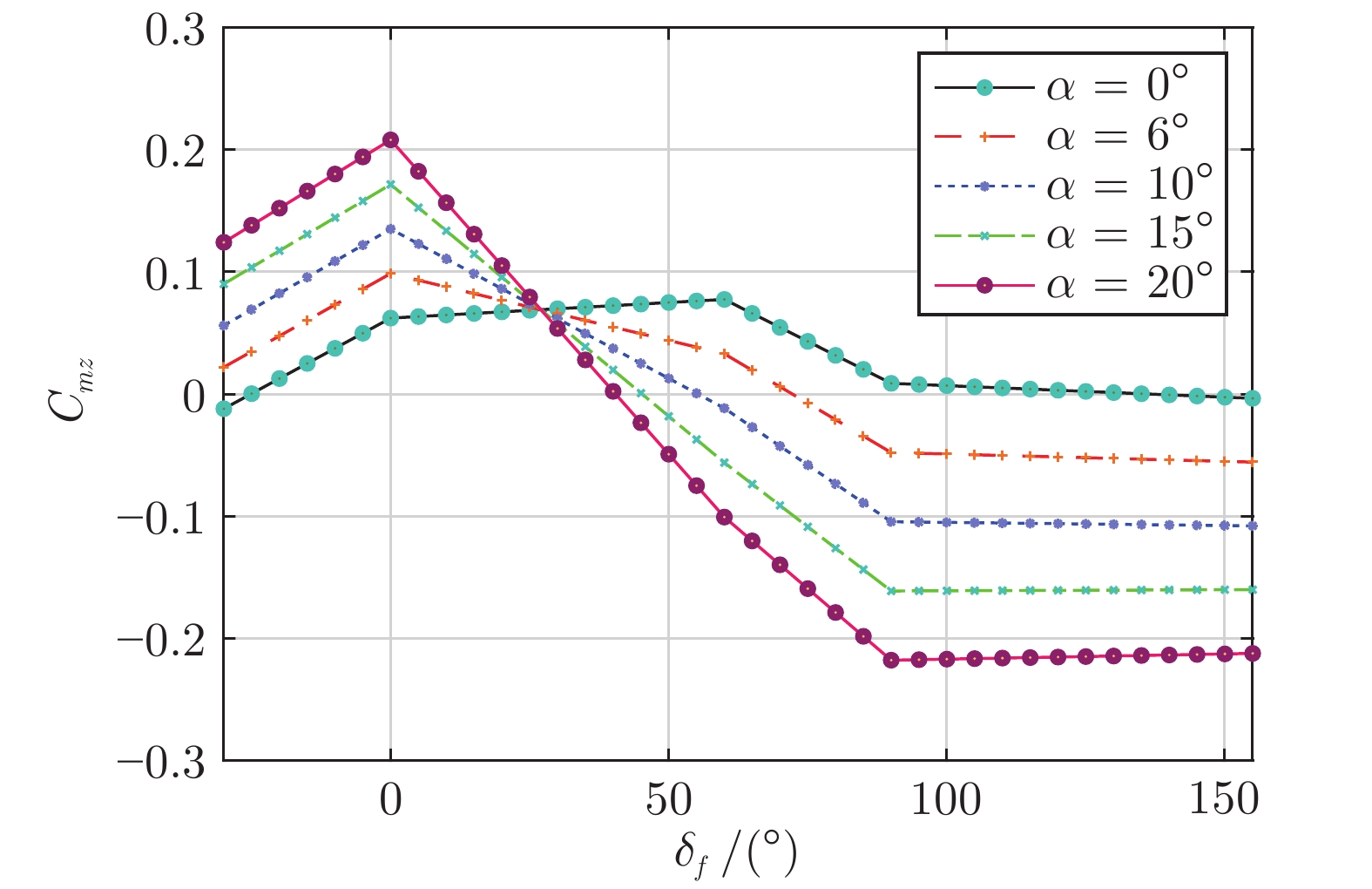
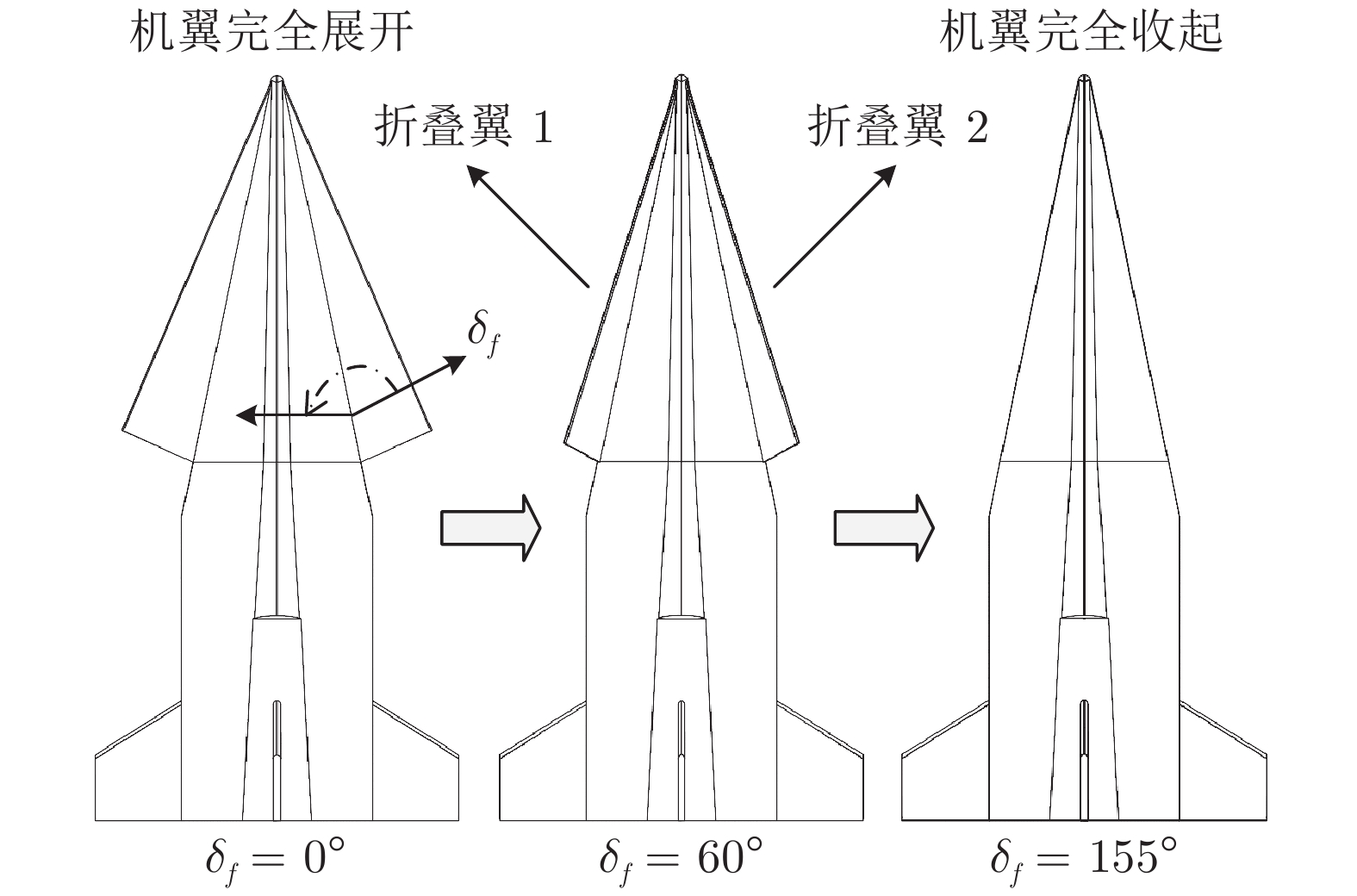
状态量 符号 取值范围 马赫数 Ma $\left [ 2,18 \right ]$ 攻角 $\alpha $ $\left [ 0^{\circ},20^{\circ} \right ]$ 侧滑角 $\beta $ $\left [ -2^{\circ},2^{\circ} \right ] $ 滚转舵偏角 $\delta_x$ $ \left [ -20^{\circ},20^{\circ} \right ] $ 偏航舵偏角 $\delta_y$ $ \left [ -20^{\circ},20^{\circ} \right ] $ 俯仰舵偏角 $\delta_z$ $ \left [ -20^{\circ},20^{\circ} \right ] $ 折叠角 $\delta_f$ $\left [ -30^{\circ},155^{\circ} \right ]$ 
下载: 导出CSV
表 2 高超声速变外形飞行器机体参数
Table 2 Body parameters of HMV
参量 符号 数值 单位 机身质量 $m_f$ 2950 kg 折叠翼质量 $m_1, m_2$ 55 kg $x$主轴转动惯量 $I_{xx}$ $\left [ 283,298 \right ] $ kg·m2 $y$主轴转动惯量 $I_{yy}$ $\left [ 2\;679,2\;722 \right ]$ kg·m2 $z$主轴转动惯量 $I_{zz}$ $\left [ 2\;528,2\;630 \right ]$ kg·m2 惯量积 $I_{xy}$ $\left [ 163,169 \right ] $ kg·m2 参考面积 $S_r$ 1.8 m2 参考气动弦长 $c_A$ 2.4 m 参考气动展长 $b_A$ 1.1 m
下载: 导出CSV
表 3 仿真参数设置
Table 3 Setting of simulation parameters
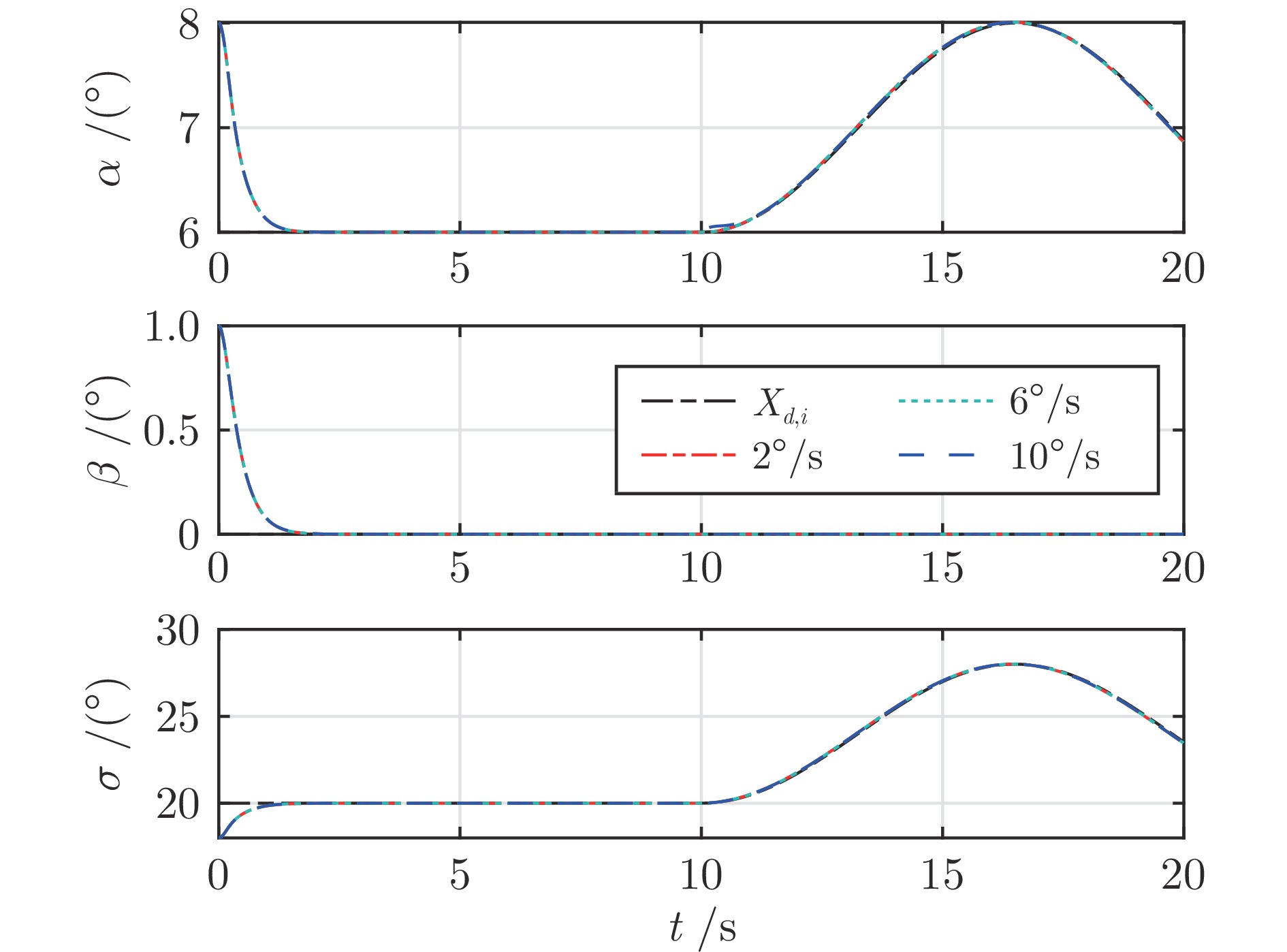
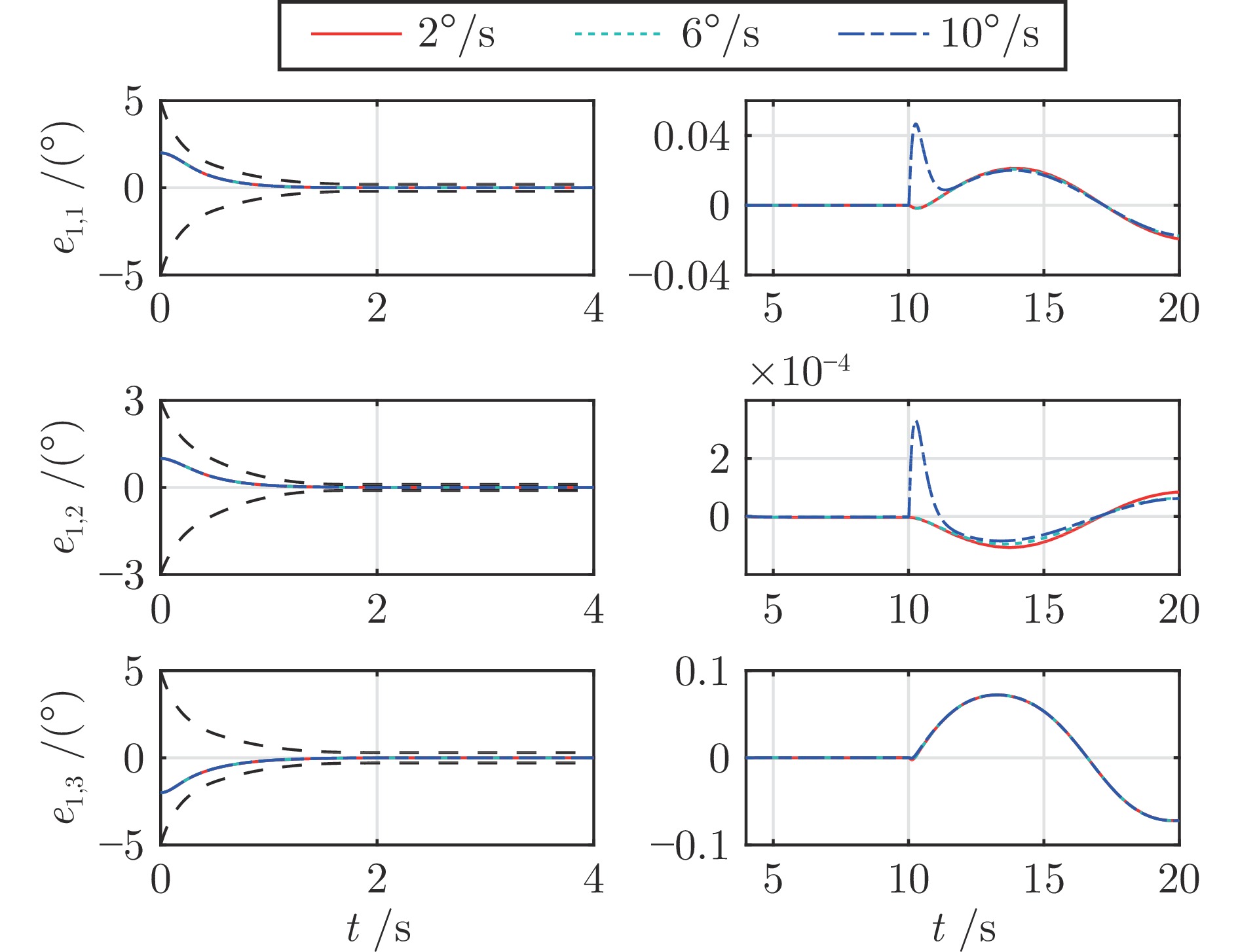
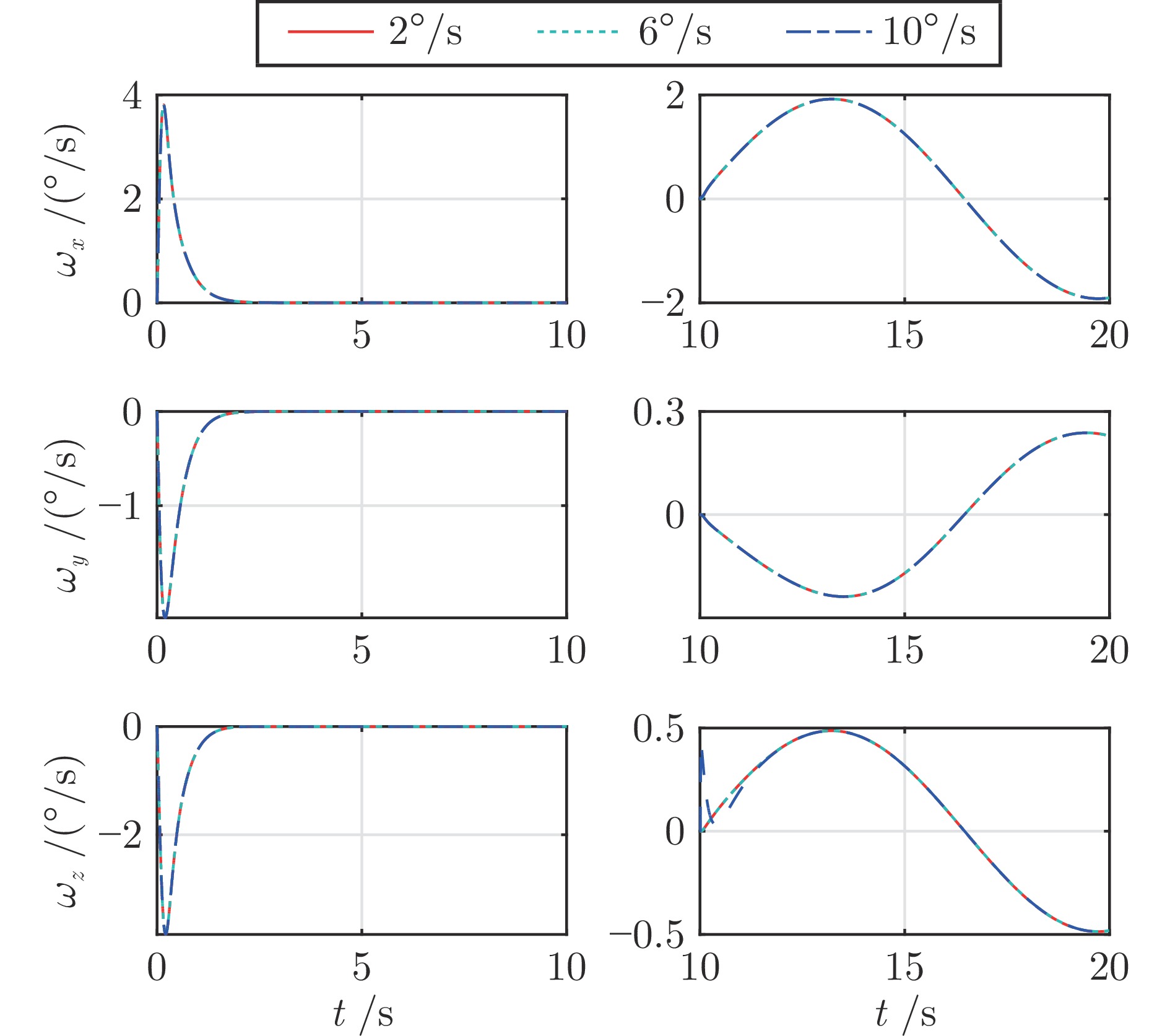
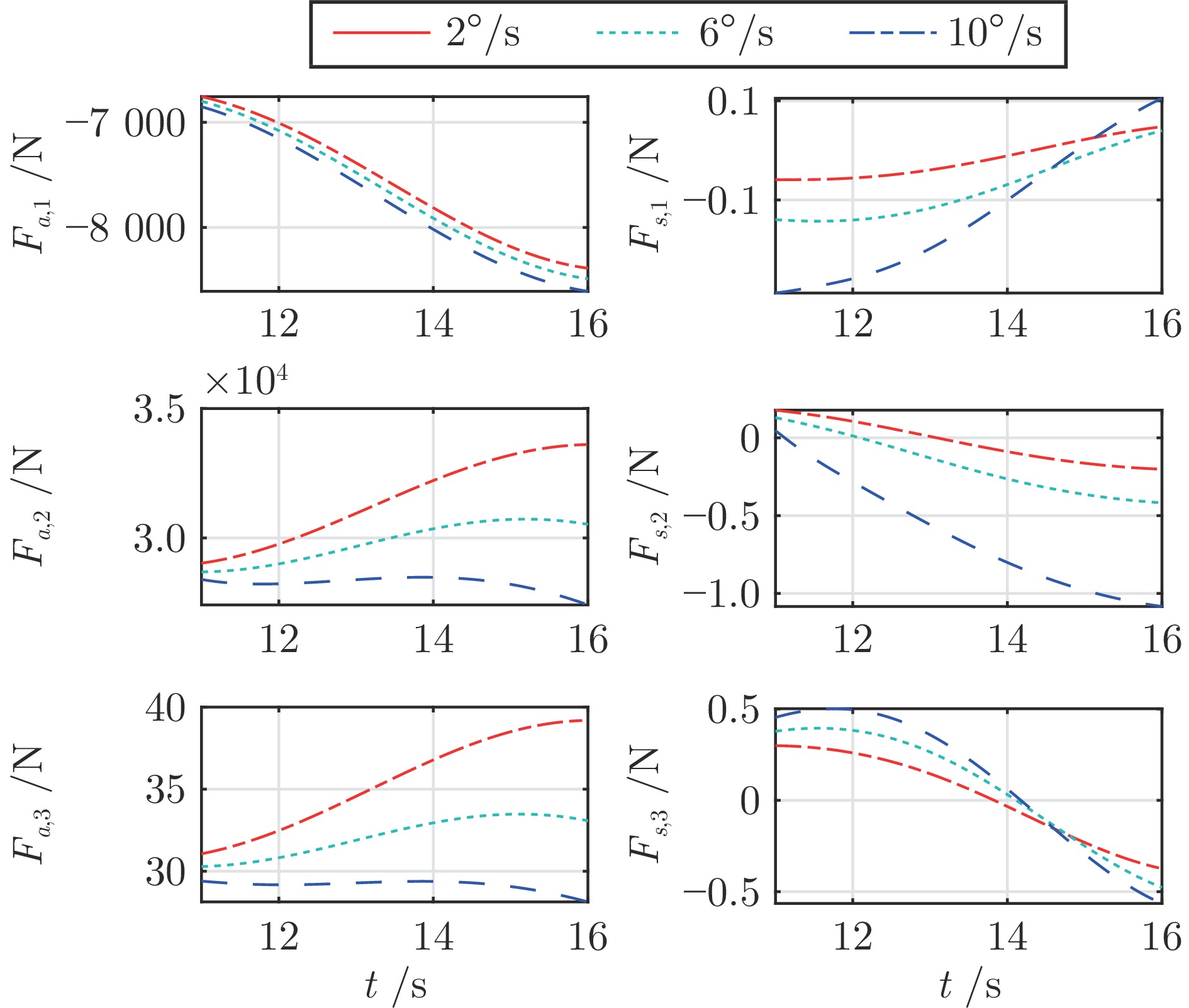
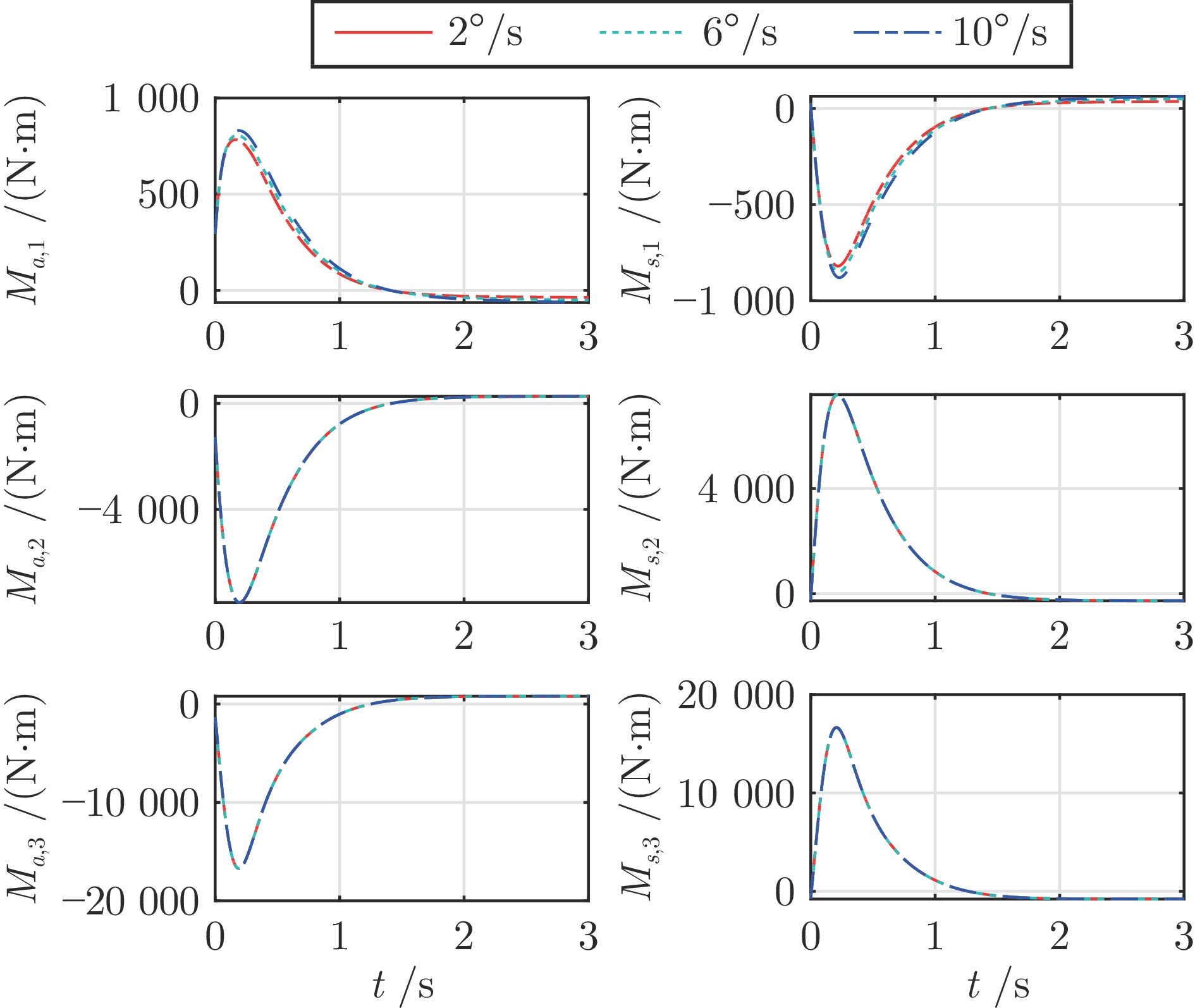
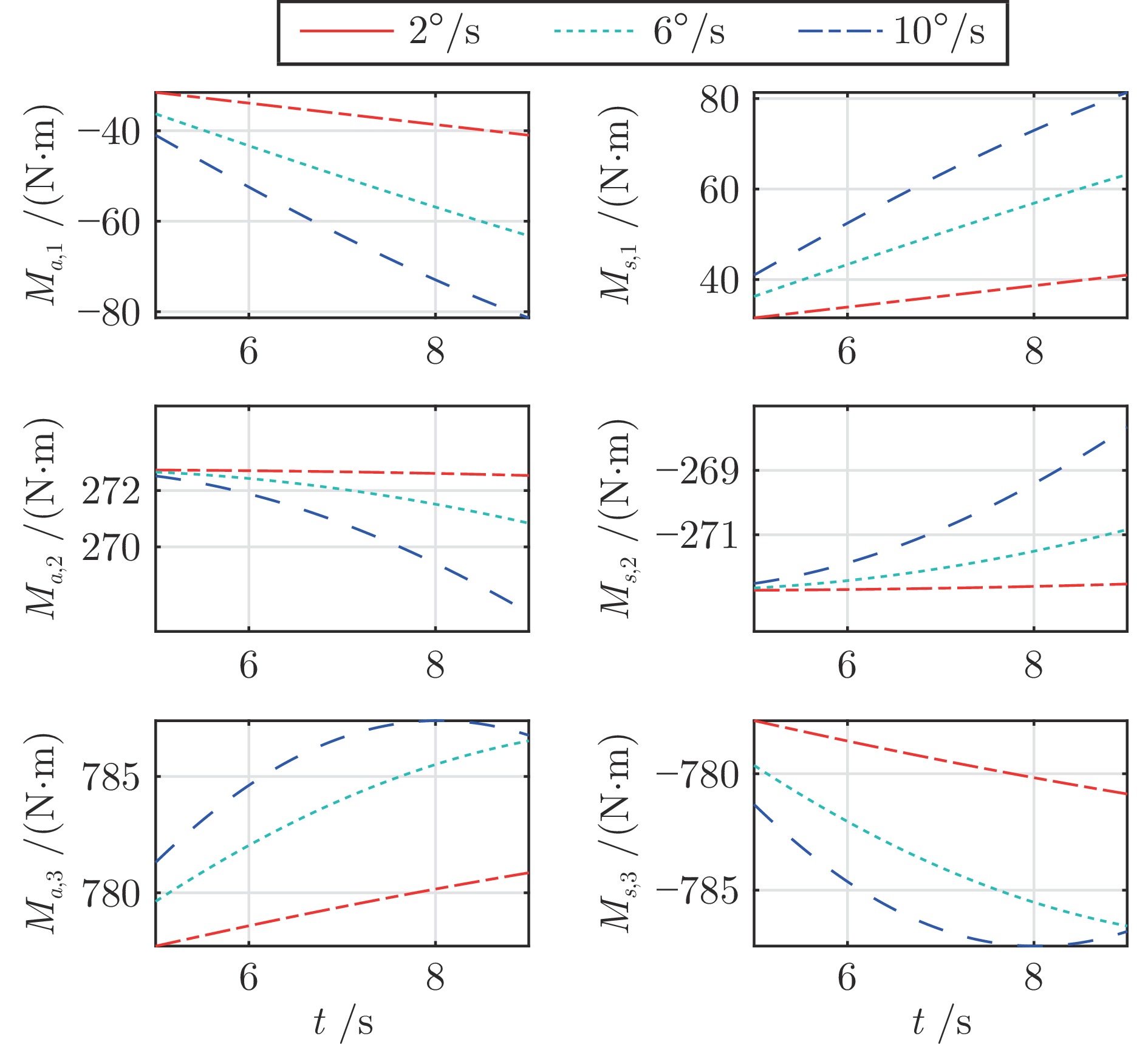
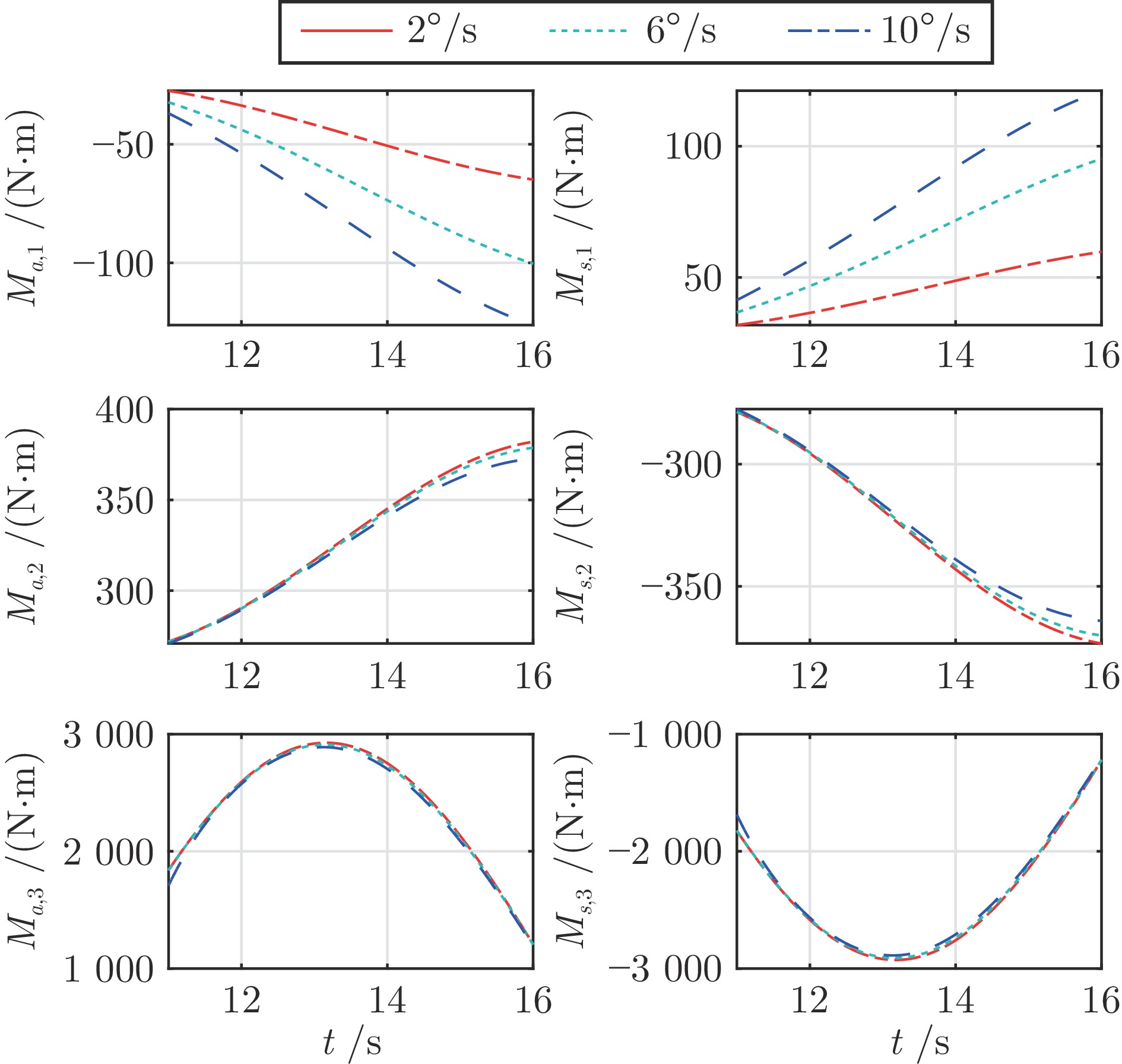
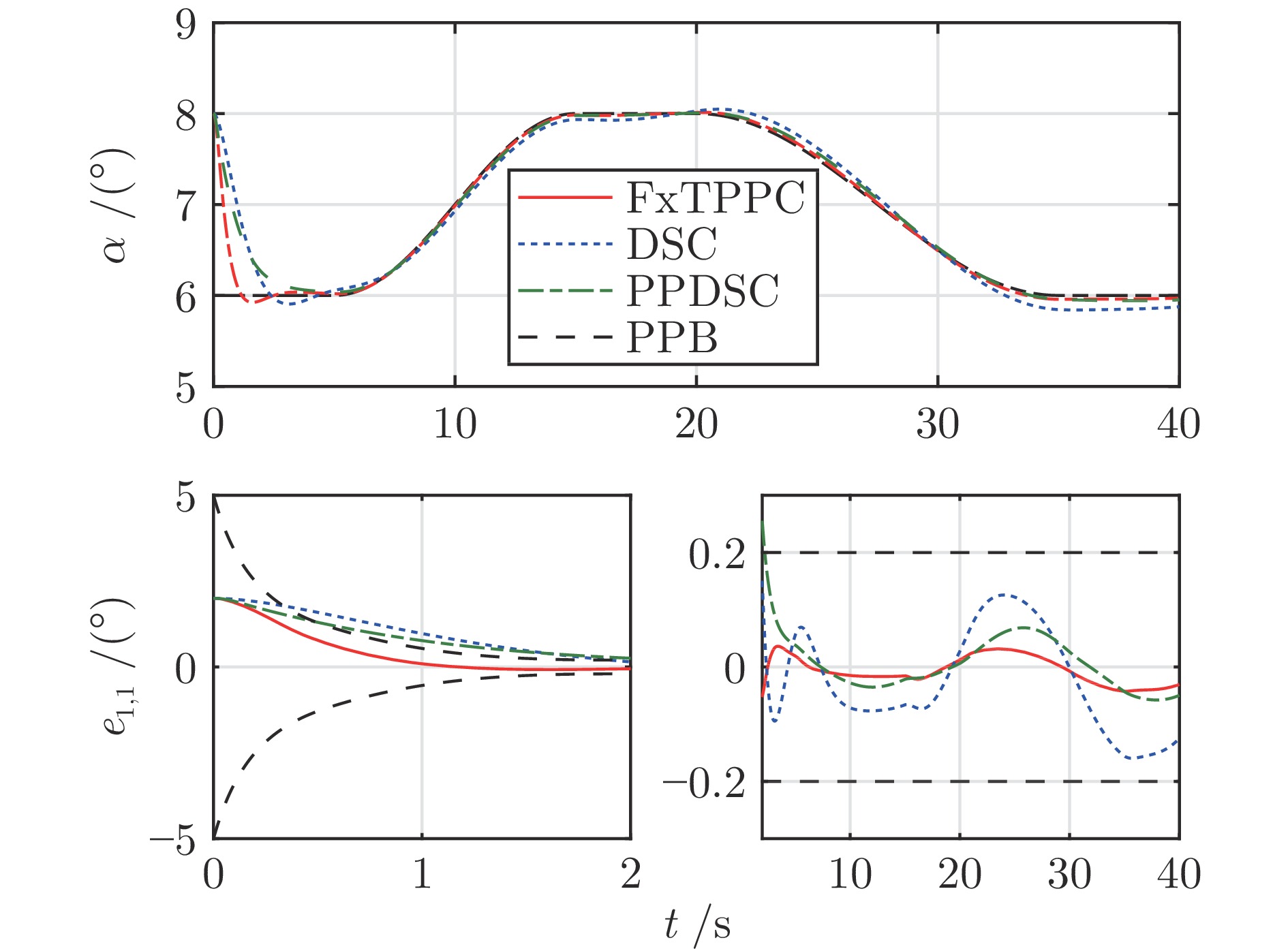
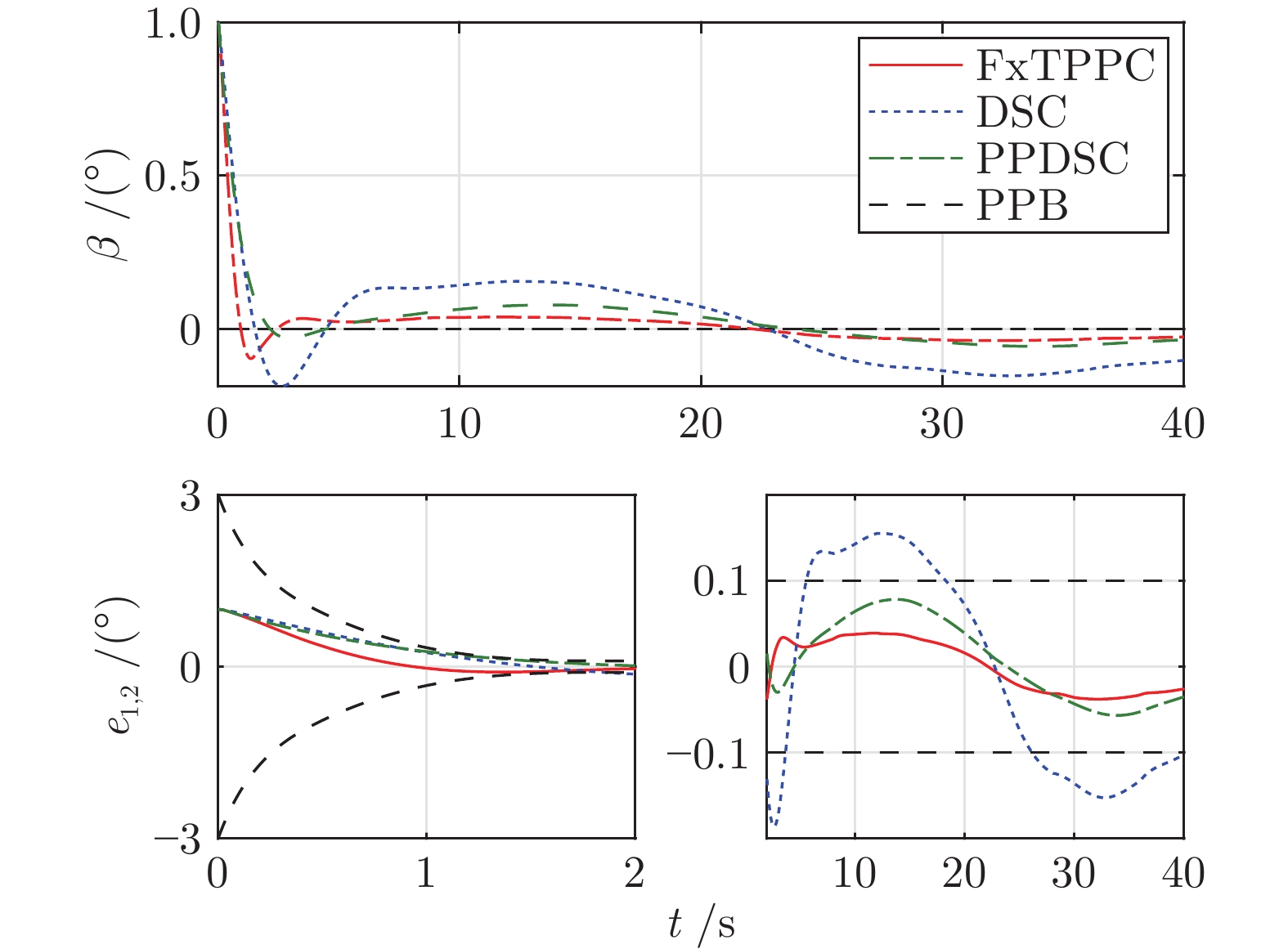
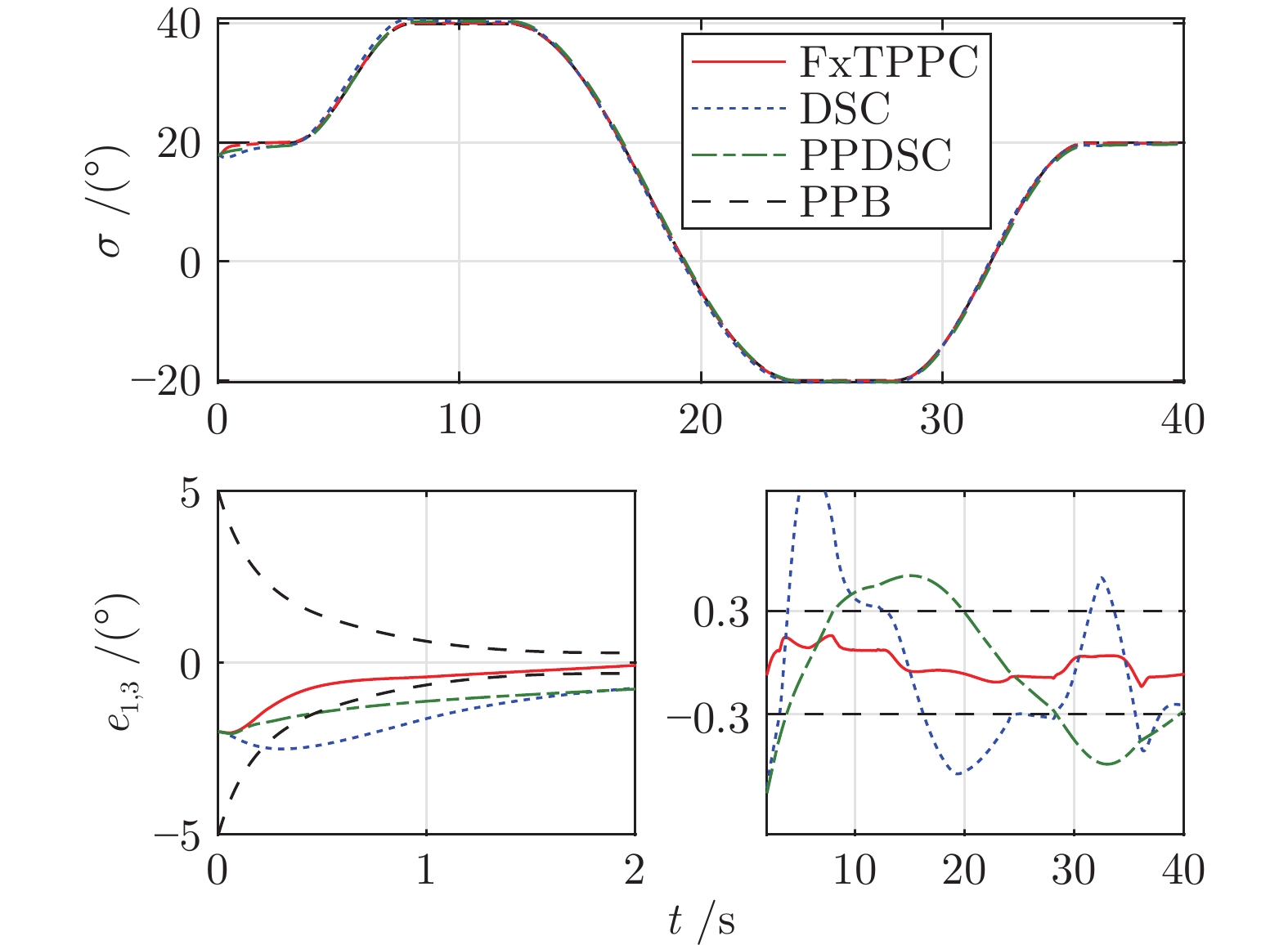
参数类型 参数值 初始状态参数 $H=35$ km, $V=3\;200$ m/s $\lambda ={{120}^{\circ }}$, $\phi ={{20}^{\circ}}$, $\theta=-{{1}^{\circ}}$, ${{\psi}_{v}}={{10}^{\circ}}$ $\alpha={{8}^{\circ}}$, $\beta={{1}^{\circ}}$, $\sigma={{18}^{\circ}}$ ${{\omega}_{x}}={{\omega}_{y}}={{\omega}_{z}}=0$, ${{\delta}_{x}}={{\delta}_{y}}={{\delta}_{z}}=0$ 控制参数 ${{\boldsymbol{\rho }}_{0}}={{\left[ {{\rho }_{0,1}},{{\rho }_{0,2}},{{\rho }_{0,3}} \right]}^{\text{T}}}={{\left[ 5,3,5 \right]}^{\text{T}}}$ ${{\boldsymbol{\rho }}_{\infty }}={{\left[ {{\rho }_{\infty ,1}},{{\rho }_{\infty ,2}},{{\rho }_{\infty ,3}} \right]}^{\text{T}}}={{\left[ 0.2,0.1,0.3 \right]}^{\text{T}}}$ ${{m}_{1,i}}=3$, ${{m}_{2,i}}=5$, ${{n}_{1,i}}=5$, ${{n}_{2,i}}=7$ ${{\alpha }_{01,i}}=0.15$, ${{\alpha }_{02,i}}=0.2$, ${{\delta }_{1,i}}={{\delta }_{2,i}}=1$ ${{k}_{1,i}}={{k}_{2,i}}=2$, $\text{ }{{k}_{3,i}}={{k}_{4,i}}=4$ ${{\varepsilon }_{1,i}}=0.02$, ${{\gamma }_{1,i}}=0.6$, ${{\gamma }_{2,i}}=1.4$ ${{k}_{z1,i}}=4$, ${{k}_{z2,i}}=4$, ${{\varepsilon }_{0,i}}=0.2$ 仿真步长 d$t$= 0.01 s 外部干扰项 $\Delta {{d}_{1,1}}=500\left( -\cos ({\pi t}/{20})+\sin ({\pi t}/{40}) \right)\;\text{N}\cdot \text{m}$ $\Delta {{d}_{1,2}}=300\left( -\cos ({\pi t}/{30})+\sin ({\pi t}/{60}) \right)\;\text{N}\cdot \text{m}$ $\Delta {{d}_{1,3}}=1\;000\cos ({\pi t}/{30})\sin ({\pi t}/{20})\;\text{N}\cdot \text{m}$ 模型不确定项 $\Delta{{C}_{L}}=\Delta{{C}_{D}}=\Delta{{C}_{Y}}=\pm20\%$ $\Delta{{C}_{mx}}=\Delta{{C}_{my}}=\Delta{{C}_{mz}}=\pm20\%$ $\Delta{{I}_{xx}}=\Delta{{I}_{yy}}=\Delta{{I}_{zz}}=\Delta{{I}_{xy}}=\pm20\%$ $\Delta{{S}_{r}}=\Delta{{b}_{A}}=\Delta{{c}_{A}}=\pm5\%$
下载: 导出CSV
-
[1] 宋慧心, 金磊. 折叠翼飞行器的动力学建模与稳定控制. 力学学报, 2020, 52(6): 1548-1559 doi: 10.6052/0459-1879-20-115Song Hui-Xin, Jin Lei. Dynamic modeling and stability control of folding wing aircraft. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1548-1559 doi: 10.6052/0459-1879-20-115 [2] 张远, 黄万伟, 路坤锋, 白文艳, 于江龙. 高超声速变外形飞行器建模与有限时间控制. 北京航空航天大学学报, 2022, 48(10): 1979-1993 doi: 10.13700/j.bh.1001-5965.2021.0701Zhang Yuan, Huang Wan-Wei, Lu Kun-Feng, Bai Wen-Yan, Yu Jiang-Long. Modeling and finite-time control for hypersonic morphing flight vehicle. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(10): 1979-1993 doi: 10.13700/j.bh.1001-5965.2021.0701 [3] Bao C Y, Wang P, He R Z, Tang G J. Observer-based optimal control method combination with event-triggered strategy for hypersonic morphing vehicle. Aerospace Science and Technology, 2023, 136: 108219 doi: 10.1016/j.ast.2023.108219 [4] Liang X H, Wang Q, Xu B, Dong C Y. Back-stepping fault-tolerant control for morphing aircraft based on fixed-time observer. International Journal of Control, Automation and Systems, 2021, 19(12): 3924-3936 doi: 10.1007/s12555-020-0764-3 [5] 张康康, 周彬, 蔡光斌, 侯明哲. 高超声速飞行器指定时间时变高增益反馈跟踪控制. 自动化学报, DOI: 10.16383/j.aas.c210895Zhang Kang-Kang, Zhou Bin, Cai Guang-Bin, Hou Ming-Zhe. Prescribed-time tracking control of hypersonic vehicles by time-varying high-gain feedback. Acta Automatica Sinica, DOI: 10.16383/j.aas.c210895 [6] Bu X W, Jiang B X, Lei H M. Nonfragile quantitative prescribed performance control of waverider vehicles with actuator saturation. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 3538-3548 doi: 10.1109/TAES.2022.3153429 [7] Ding Y B, Yue X K, Chen G S, et al. Review of control and guidance technology on hypersonic vehicle. Chinese Journal of Aeronautics, 2022, 35(7): 1-18 doi: 10.1016/j.cja.2021.10.037 [8] Tian B L, Li Z Y, Zhao X P, Zong Q. Adaptive multivariable reentry attitude control of rlv with prescribed performance. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(10): 6674-6678 doi: 10.1109/TSMC.2022.3145508 [9] 罗世彬, 吴瑕, 魏才盛. 可重复使用飞行器的保性能姿态跟踪控制方法. 航空学报, 2021, 42(11): 415-426Luo Shi-Bin, Wu Xia, Wei Cai-Sheng. A novel attitude tracking control with guaranteed performance for reusable launch vehicle. Acta Aeronautica et Astronautica Sinica, 2021, 42(11): 415-426 [10] Wang F, Wen L Z, Zhou C, Hua C H. Adaptive preassigned-time controller design for a hypersonic vehicle with improved performance and uncertainties. ISA Transactions, 2023, 132: 309-328 doi: 10.1016/j.isatra.2022.05.040 [11] Chu L L, Li Q, Gu F, Du X T, He Y Q, Deng Y C. Design, modeling, and control of morphing aircraft: A review. Chinese Journal of Aeronautics, 2022, 35(5): 220-246 doi: 10.1016/j.cja.2021.09.013 [12] 王鹏, 陈浩岚, 鲍存余, 汤国建. 变形飞行器建模及控制方法研究综述. 宇航学报, 2022, 43(7): 853-865 doi: 10.3873/j.issn.1000-1328.2022.07.002Wang Peng, Chen Hao-Lan, Bao Cun-Yu, Tang Guo-Jian. Review on modeling and control methods of morphing vehicle. Journal of Astronautics, 2022, 43(7): 853-865 doi: 10.3873/j.issn.1000-1328.2022.07.002 [13] 李新凯, 张宏立, 范文慧. 非匹配扰动下变体无人机预设性能控制. 航空学报, 2022, 43(2): 382-397 doi: 10.7527/j.issn.1000-6893.2022.2.hkxb202202031Li Xin-Kai, Zhang Hong-Li, Fan Wen-Hui. Prescribed performance control for morphing aerospace vehicle under mismatched disturbances. Acta Aeronautica et Astronautica Sinica, 2022, 43(2): 382-397 doi: 10.7527/j.issn.1000-6893.2022.2.hkxb202202031 [14] Xu D, Hui Z, Liu Y Q, Chen G. Morphing control of a new bionic morphing UAV with deep reinforcement learning. Aerospace science and technology, 2019, 92: 232-243 doi: 10.1016/j.ast.2019.05.058 [15] Bao C Y, Wang P, Tang G J. Integrated method of guidance, control and morphing for hypersonic morphing vehicle in glide phase. Chinese Journal of Aeronautics, 2021, 34(5): 535-553 doi: 10.1016/j.cja.2020.11.009 [16] Song, M S, Zhang, F, Huang, B X, Huang, P F. Anti-disturbance control for tethered aircraft system with deferred output constraints. IEEE-CAA Journal of Automatica Sinica, 2023, 10(2): 474-485 doi: 10.1109/JAS.2023.123222 [17] 王宁, 高颖, 王仁慧. 状态测量不确定和动力学未知的无人艇固定时间容错控制. 自动化学报, 2023, 49(5): 1050-1061 doi: 10.16383/j.aas.c220482Wang Ning, Gao Ying, Wang Ren-Hui. Fixed-time fault-tolerance control of an unmanned surface vehicle with uncertain measurements and unknown dynamics. Acta Automatica Sinica, 2023, 49(5): 1050-1061 doi: 10.16383/j.aas.c220482 [18] 李小华, 胡利耀. 一类p规范型非线性系统预设性能有限时间H∞跟踪控制. 自动化学报, 2021, 47(12): 2870-2880Li Xiao-Hua, Hu Li-Yao. Prescribed performance finite-time H∞ tracking control for a class of p-normal form nonlinear systems. Acta Automatica Sinica, 2021, 47(12): 2870-2880 [19] 陈辰. 基于扰动补偿的高超声速飞行器再入姿态控制研究[博士学位论文], 哈尔滨工业大学, 中国, 2018.Chen Chen. Research on Reentry Attitude Control for Hypersonic Vehicle Based on Disturbance Compensation [Ph.D. dissertation], Harbin Institute of Technology, China, 2018. [20] 杨炳尉. 标准大气参数的公式表示. 宇航学报, 1983(1): 83-86.Yang Bing-Wei. Formulization of standard atmospheric parameters. Journal of Astronautics, 1983(1): 83-86 [21] Zipfel P H. Modeling and Simulation of Aerospace Vehicle Dynamics, Third Edition. Reston: AIAA Education Series, 2014. [22] 文利燕, 陶钢, 姜斌, 杨杰. 非线性动态突变系统的多模型自适应执行器故障补偿设计. 自动化学报, 2022, 48(1): 207-222Wen Li-Yan, Tao Gang, Jiang Bin, Yang Jie. A multiple-model based adaptive actuator failure compensation scheme for nonlinear systems with dynamic mutations. Acta Automatica Sinica, 2022, 48(1): 207-222 [23] Tee K P, Ge S S, Tay E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica, 2009, 45(4): 918-927 doi: 10.1016/j.automatica.2008.11.017 [24] Ge S S, Wang C. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Transactions Neural Networks, 2004, 15(3): 674-692 doi: 10.1109/TNN.2004.826130 [25] Ren B B, Ge S S, Tee K P, Lee T H. Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Transactions on Neural Networks, 2010, 21(8): 1339-1345 doi: 10.1109/TNN.2010.2047115 [26] Wu R, Wei C Z, Yang F, Cui N G, Zhang L. FxTDO-based non-singular terminal sliding mode control for second-order uncertain systems. IET Control Theory and Applications, 2018, 12(18): 2459-2467 doi: 10.1049/iet-cta.2018.5455 [27] Yu L, He G, Wang X K, Zhao S L. Robust fixed-time sliding mode attitude control of tilt trirotor UAV in helicopter mode. IEEE Transactions on Industrial Electronics, 2021, 10(69): 10322-10332 doi: 10.1109/TIE.2021.3118556 [28] Fu M Y, Zhang T, Ding F G, Wang D S. Appointed-time integral barrier Lyapunov function-based trajectory tracking control for a hovercraft with performance constraints. Applied Sciences, 2020, 10(20): 1-21 [29] Liu W, Fei S Q, Ma Q, et al. Prescribed performance dynamic surface control for nonlinear systems subject to partial and full state constraints. Applied Mathematics and Computation, 2022, 431: 127318: 1-14 doi: 10.1016/j.amc.2022.127318 [30] Yin Z Y, Luo J J, Wei C S. Quasi fixed-time fault-tolerant control for nonlinear mechanical systems with enhanced performance. Applied Mathematics and Computation, 2019, 352: 157-173 doi: 10.1016/j.amc.2019.01.068 [31] 刘晓东, 黄万伟, 禹春梅. 含扩张状态观测器的高超声速飞行器动态面姿态控制. 宇航学报, 2015, 36(8): 916-922Liu Xiao-Dong, Huang Wan-Wei, Yu Chun-Mei. Dynamic surface attitude control for hypersonic vehicle containing ex-tended state observer. Journal of Astronautics, 2015, 36(8): 916-922 [32] Shen Z P, Li F, Cao X M, Guo C. Prescribed performance dynamic surface control for trajectory tracking of quadrotor UAV with uncertainties and input constraints. International Journal of Control, 2020, 94(11): 2945-2955 -
计量
- 文章访问数: 1359
- HTML全文浏览量: 382
- PDF下载量: 303
- 被引次数: 0
