面向复杂物流配送场景的车辆路径规划多任务辅助进化算法

李坚强; 蔡俊创; 孙涛; 朱庆灵; 林秋镇

doi:10.16383/j.aas.c230043

面向复杂物流配送场景的车辆路径规划多任务辅助进化算法

doi: 10.16383/j.aas.c230043

李坚强^{1, 2,},
蔡俊创^1,,
孙涛^1,,
朱庆灵^1,,
林秋镇^1,

1.
深圳大学计算机与软件学院深圳 518060
2.
深圳大学大数据系统计算技术国家工程实验室深圳 518060

基金项目: 国家自然科学基金 (62325307, 62073225, 62203134, 62376163, 62203308),广东省自然科学基金 (2023B1515120038, 2019B151502018), 深圳市科技计划项目(20220809141216003), 深圳大学科学仪器开发项目 (2023YQ019) 资助

详细信息

作者简介:
李坚强：深圳大学计算机与软件学院教授. 2008年获华南理工大学博士学位. 主要研究方向为嵌入式系统和物联网. E-mail: lijq@szu.edu.cn

蔡俊创：深圳大学计算机与软件学院博士研究生. 主要研究方向为进化计算及其在物流领域中的应用. E-mail: caijunchuang2020@email.szu.edu.cn

孙涛：中兴通讯股份有限公司工程师. 2022年获深圳大学硕士学位. 主要研究方向为进化计算和路径规划. E-mail: 1910272020@email.szu.edu.cn

朱庆灵：深圳大学计算机与软件学院博士后. 2021年获香港城市大学博士学位. 主要研究方向为进化多目标优化和机器学习. E-mail: zhuqingling@szu.edu.cn

林秋镇：深圳大学计算机与软件学院副教授. 2014年获香港城市大学博士学位. 主要研究方向为人工免疫系统,多目标优化和动态系统. 本文通信作者. E-mail: qiuzhlin@szu.edu.cn

计量
- 文章访问数: 667
- HTML全文浏览量: 196
- PDF下载量: 243
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-10
- 录用日期: 2023-08-07
- 网络出版日期: 2024-02-19
- 刊出日期: 2024-03-29

Multitask-based Assisted Evolutionary Algorithm for Vehicle Routing Problems inComplex Logistics Distribution Scenarios

1.
College of Computer Science and Software Engineering, Shenzhen University, Shenzhen 518060
2.
National Engineering Laboratory for Big Data System Computing Technology, Shenzhen University, Shenzhen 518060

Funds: Supported by National Natural Science Foundation of China(62325307, 62073225, 62203134, 62376163, 62203308), Natural ScienceFoundation of Guangdong Province (2023B1515120038, 2019B151502018), Shenzhen Science and Technology Program (20220809141216003), and the Scientific Instrument Developing Project of Shenzhen University (2023YQ019)

More Information

Author Bio:
LI Jian-Qiang　Professor at the College of Computer Science and Software Engineering, Shenzhen University. He received his Ph.D. degree from South China University of Technology in 2008. His research interest covers embedded systems and internet of things

CAI Jun-Chuang　Ph.D. candidate at the College of Computer Science and Software Engineering, Shenzhen University. His research interest covers evolutionary computation and its applications in the field of logistics

SUN Tao　Engineer at ZTE Corporation. He received his master degree from Shenzhen University in 2022. His research interest covers evolutionary computation and path planning

ZHU Qing-Ling　Postdoctor at the College of Computer Science and Software Engineering, Shenzhen University. He received his Ph.D. degree from the City University of Hong Kong in 2021. His research interest covers evolutionary multiobjective optimization and machine learning

LIN Qiu-Zhen　Associate professor at the College of Computer Science and Software Engineering, Shenzhen University. He received his Ph.D. degree from the City University of Hong Kong in 2014. His research interest covers artificial immune system, multiobjective optimization, and dynamic system. Corresponding author of this paper

摘要

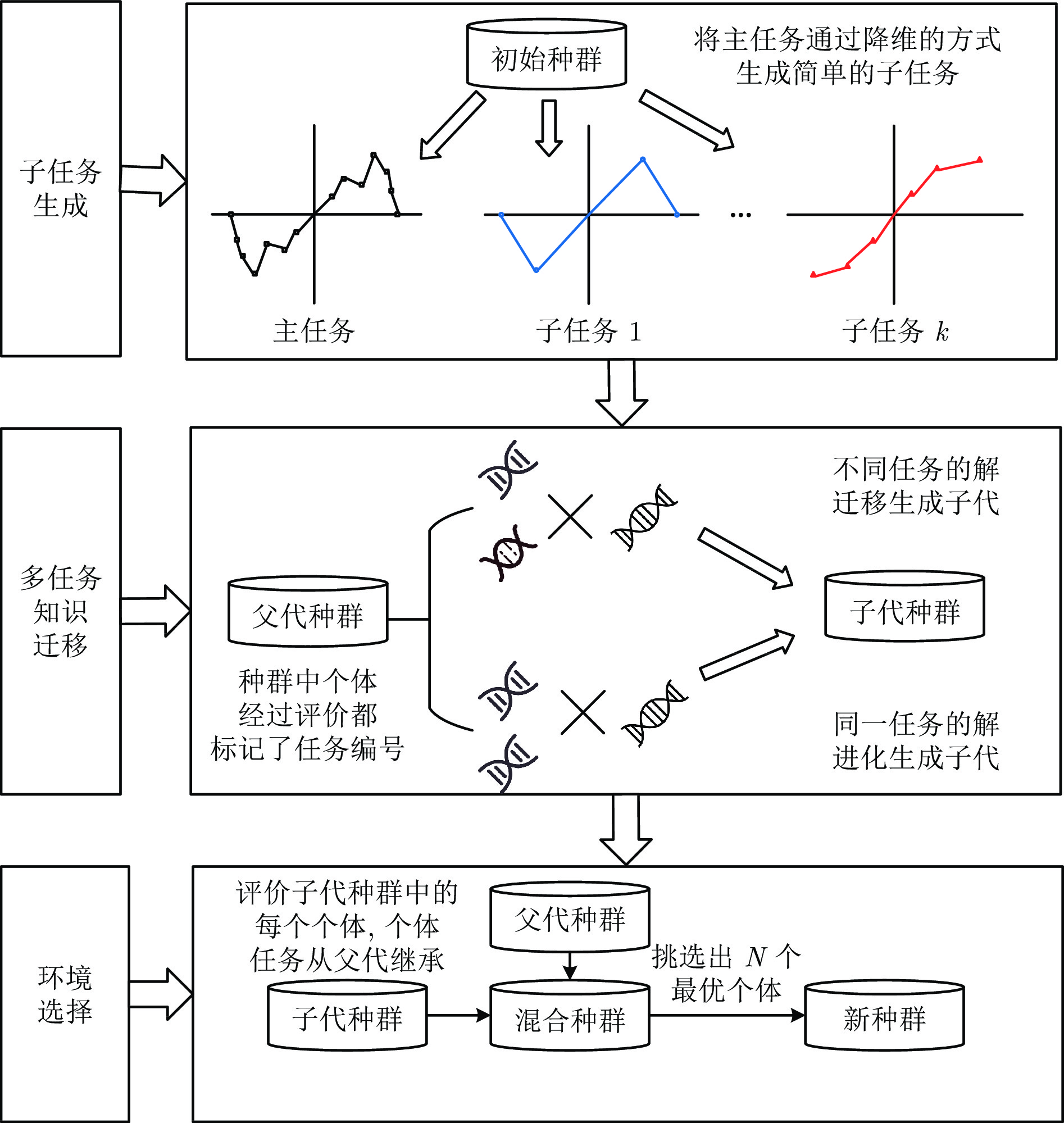
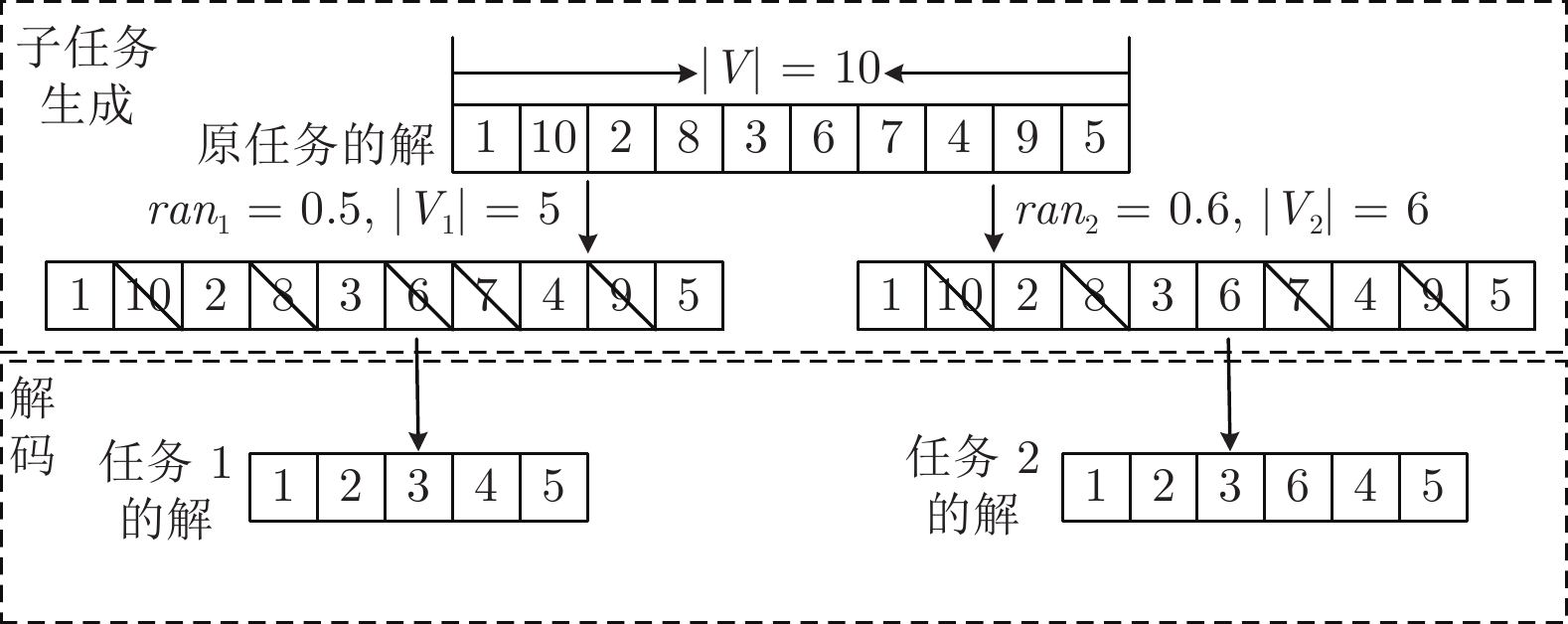
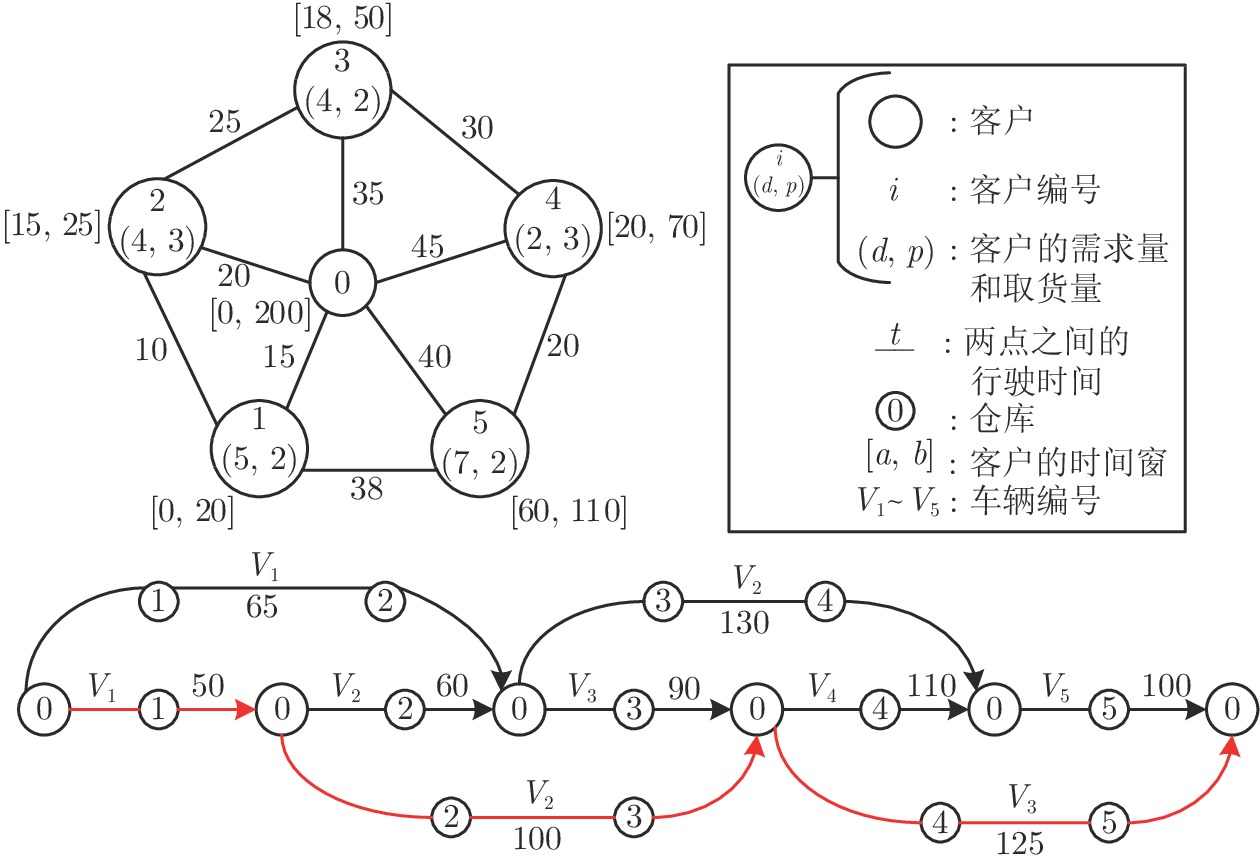
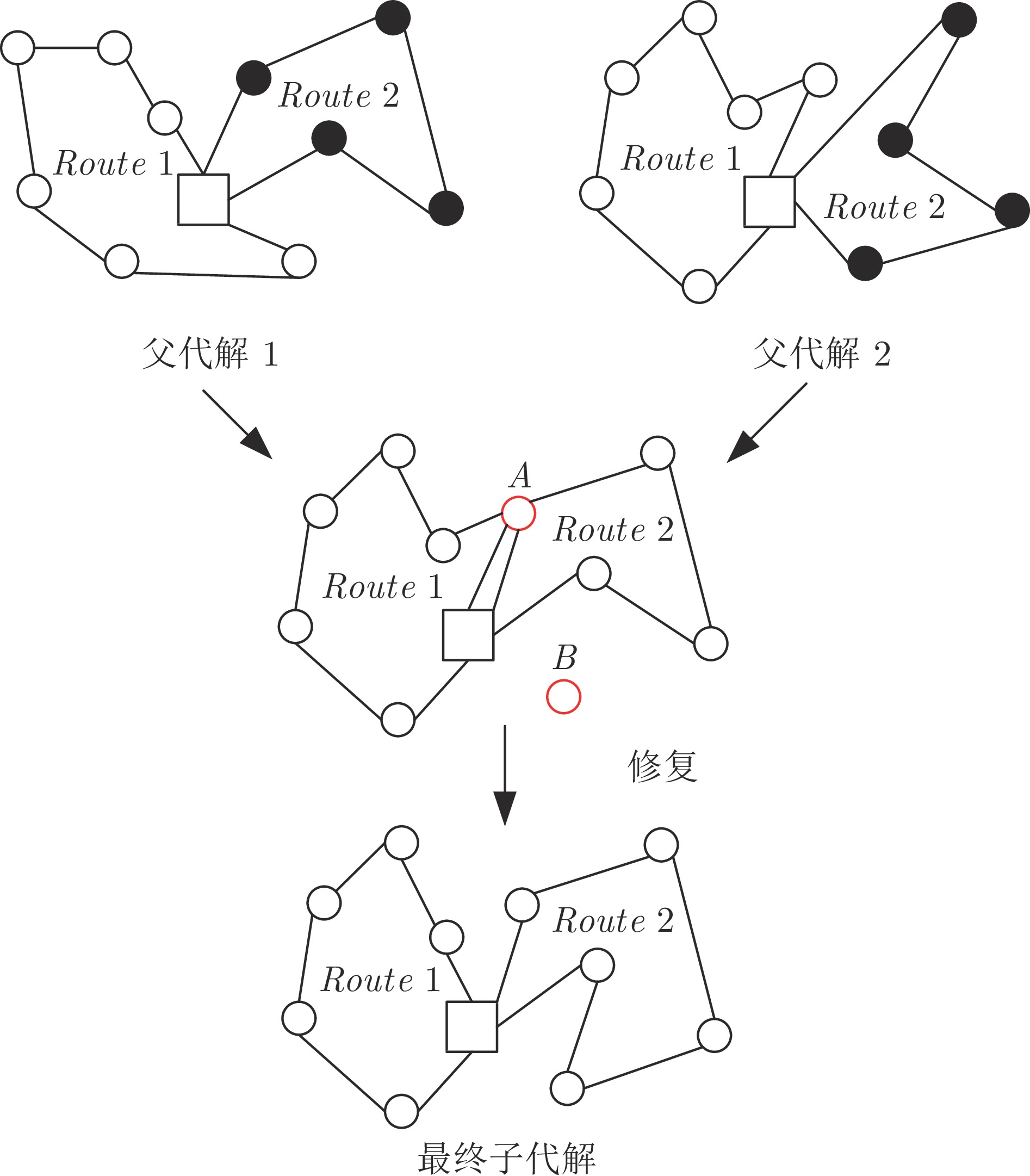
摘要: 在现代社会中, 复杂物流配送场景的车辆路径规划问题(Vehicle routing problem, VRP)一般带有时间窗约束且需要提供同时取送货的服务. 这种复杂物流配送场景的车辆路径规划问题是NP-难问题. 当其规模逐渐增大时, 一般的数学规划方法难以求解, 通常使用启发式方法在限定时间内求得较优解. 然而, 传统的启发式方法从原大规模问题直接开始搜索, 无法利用先前相关的优化知识, 导致收敛速度较慢. 因此, 提出面向复杂物流配送场景的车辆路径规划多任务辅助进化算法(Multitask-based assisted evolutionary algorithm, MBEA), 通过使用迁移优化方法加快算法收敛速度, 其主要思想是通过构造多个简单且相似的子任务用于辅助优化原大规模问题. 首先从原大规模问题中随机选择一部分客户订单用于构建多个不同的相似优化子任务, 然后使用进化多任务(Evolutional multitasking, EMT)方法用于生成原大规模问题和优化子任务的候选解. 由于优化子任务相对简单且与原大规模问题相似, 其搜索得到的路径特征可以通过任务之间的知识迁移辅助优化原大规模问题, 从而加快其求解速度. 最后, 提出的算法在京东物流公司快递取送货数据集上进行验证, 其路径规划效果优于当前最新提出的路径规划算法.
- 车辆路径规划问题 /
- 时间窗约束 /
- 同时取送货 /
- 进化算法 /
- 迁移优化
Abstract: In complex logistics, addressing the vehicle routing problem (VRP) with simultaneous pickup and delivery and time windows, an NP-hard problem, becomes increasingly challenging as the scale expands. Traditional heuristic methods, often unable to leverage prior optimization knowledge, result in slow convergence. To address this, we introduce a multitask-based evolutionary algorithm (MBEA), which assists the optimization of the original large-scale problem by constructing multiple simple and similar subtasks and utilizing transfer learning to accelerate convergence speed. First, a subset of orders is randomly selected from the original problem to construct various subtasks, and then a multitask evolutionary approach is applied to generate candidate solutions for the original problem and subtasks. Given that the subtasks are simpler yet similar to the original problem, useful routing traits can be shared through knowledge transfer among the tasks, thereby speeding up its evolutionary search. To validate MBEA＇s efficacy, empirical studies were conducted on a large-scale express dataset from Jingdong, and the results demonstrate that MBEA outperforms recently proposed vehicle routing algorithms.
- Vehicle routing problem (VRP) /
- time windows constraint /
- simultaneous pickup and delivery /
- evolutionary algorithm /
- transfer optimization

HTML全文

图 1 VRPPDT模型

Fig. 1 The model of the VRPPDT

下载: 全尺寸图片幻灯片

图 2 MBEA总体框架图

Fig. 2 The overall framework diagram of MBEA

下载: 全尺寸图片幻灯片

图 3 一个个体的编码方法

Fig. 3 The coding method of an individual

下载: 全尺寸图片幻灯片

图 4 子任务生成及解码过程

Fig. 4 The generation and decoding process of the subtask

下载: 全尺寸图片幻灯片

图 5 一个解的切分过程

Fig. 5 The splitting process of a solution

下载: 全尺寸图片幻灯片

图 6 基于路径的交叉过程

Fig. 6 The operation process of the route-based crossover

下载: 全尺寸图片幻灯片

图 7 顺序交叉操作过程

Fig. 7 The operation process of the order crossover

下载: 全尺寸图片幻灯片

图 8 本文提出的方法和对比算法的平均搜索收敛轨迹

Fig. 8 Averaged search convergence traces of the proposed method and the compared algorithms

下载: 全尺寸图片幻灯片

表 1 京东数据集的特性

Table 1 Properties of Jingdong dataset

问题	\|V\|	C	J	$ {u_1} $	$ {u _2} $
F201 ~ F204	200	2.5	500	300	0.014
F401 ~ F404	400	2.5	500	300	0.014
F601 ~ F604	600	2.5	500	300	0.014
F801 ~ F804	800	2.5	500	300	0.014
F1001 ~ F1004	1 000	2.5	500	300	0.014

下载: 导出CSV

表 2 MBEA算法参数设置

Table 2 Parameter settings in MBEA

参数	含义	值
Evaluation	算法总评价次数	18 000
TE	每阶段的评价次数	3 600
N	种群大小	36
N_re	阶段数	5
N_be	保留个体的数量	18
k	子任务个数	1
lower	子任务维度最低占比	0.7

下载: 导出CSV

表 3 MBEA和5种对比算法在京东数据集对比实验结果

Table 3 Comparative experimental results of MBEA and five compared algorithms on Jingdong dataset

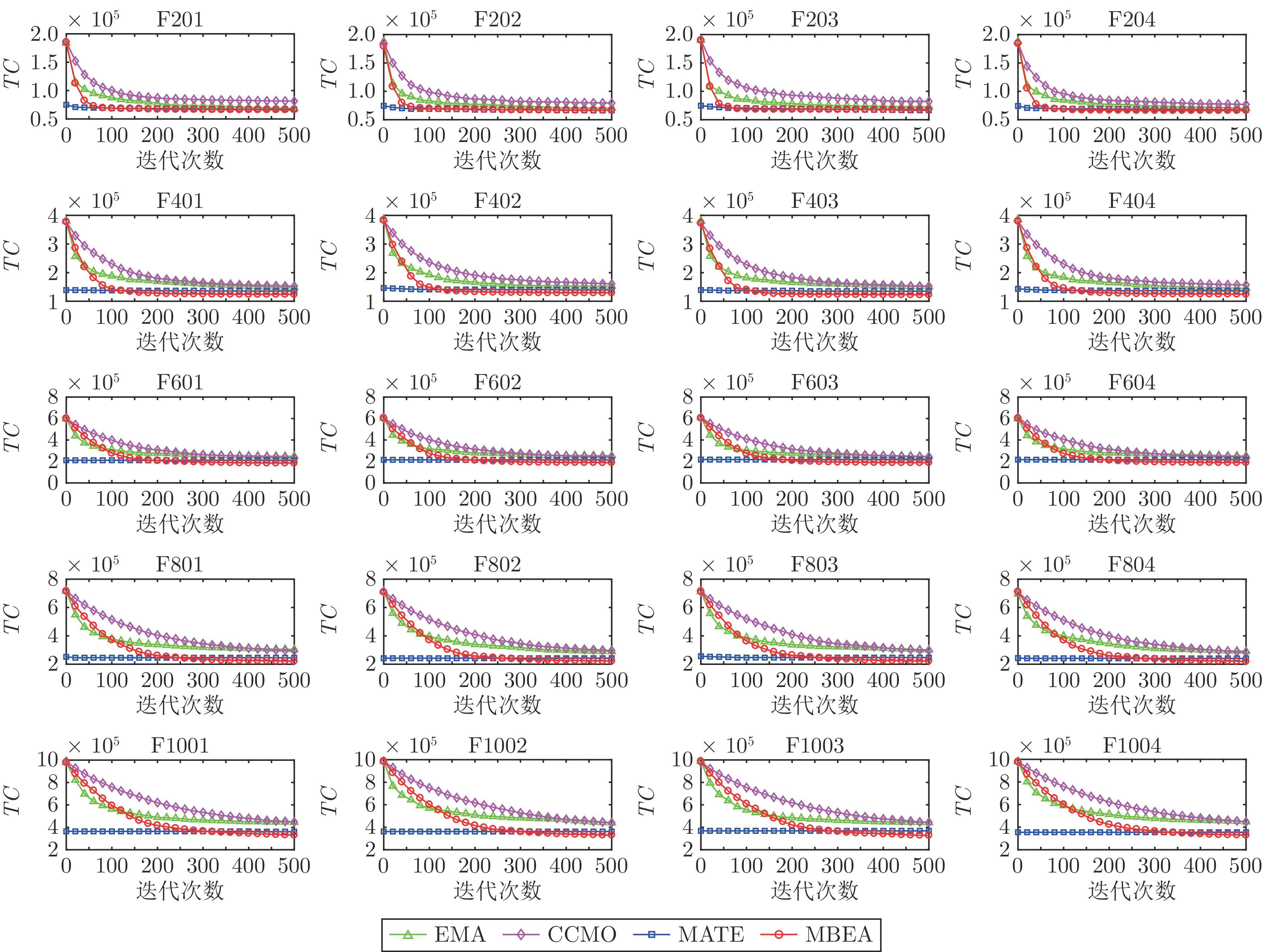
问题	MBEA				EMA				MATE				CCMO				GVNS				VNSME
问题	NV	TD	TC	运行时间 (s)	NV	TD	TC	运行时间 (s)	NV	TD	TC	运行时间 (s)	NV	TD	TC	运行时间 (s)	NV	TD	TC	运行时间 (s)	NV	TD	TC	运行时间 (s)
F201	43	53 851	66 751	3 291	45	54 918	68 418	4 252	42	53 997	66 597	8 712	51	66 099	81 399	2 976	52	84 808	100 408	81	50	60 494	75 494	3
F202	44	53 155	66 355	3 270	47	56 288	70 388	4 340	43	53 649	66 609	14 194	52	63 782	79 382	2 839	53	67 756	83 656	252	49	59 728	74 428	2
F203	43	54 899	67 679	3 356	46	59 009	72 809	5 416	42	54 544	67 024	13 635	49	67 608	82 308	2 881	51	83 079	98 379	103	51	65 951	81 251	2
F204	43	53 311	66 211	2 983	46	56 456	70 256	3 986	43	54 398	67 238	9 929	48	62 329	76 729	2 970	52	74 571	90 171	300	51	60 415	75 715	2
F401	81	99 380	123 620	11 538	93	120 041	147 941	2 567	84	109 863	135 123	16 852	94	124 412	152 612	8 580	98	144 757	174 157	1 229	96	112 942	141 742	15
F402	84	103 091	128 351	13 338	101	122 636	152 936	2 535	87	113 871	139 971	10 742	100	130 655	160 655	7 923	101	160 822	191 122	268	98	117 970	147 370	12
F403	80	98 175	122 055	12 119	95	122 289	150 789	2 731	84	109 212	134 412	10 154	97	123 599	152 699	8 364	98	160 018	189 418	420	93	111 171	139 071	15
F404	83	99 809	124 649	12 656	95	116 269	144 769	2 694	86	110 555	136 295	13 709	100	127 209	157 209	8 154	101	136 483	166 783	651	94	110 775	138 975	17
F601	118	149 868	185 148	15 779	153	202 915	248 816	2 663	126	174 424	212 344	17 795	148	192 176	236 576	15 623	144	240 941	284 141	702	138	171 997	213 397	41
F602	121	153 129	189 429	19 571	164	204 772	253 972	2 656	129	177 851	216 551	18 839	146	199 278	243 078	15 505	141	227 723	270 023	1 624	143	175 068	217 968	49
F603	120	153 681	189 741	16 090	151	202 985	248 285	2 922	128	176 806	215 146	17 636	151	198 996	244 296	15 032	143	219 879	262 779	395	142	171 057	213 657	37
F604	122	153 477	190 137	18 569	157	204 541	251 641	2 886	128	176 943	215 403	18 789	154	196 028	242 228	15 201	145	204 293	247 793	757	141	172 956	215 256	33
F801	159	175 009	222 709	11 565	200	244 506	304 506	3 679	164	196 076	245 156	20 421	200	234 549	294 549	25 467	189	278 179	334 879	1 654	178	189 502	242 902	82
F802	157	173 598	220 577	13 077	210	226 736	289 736	3 657	164	194 325	243 465	20 835	199	236 794	296 494	25 879	184	271 798	326 998	1 153	179	192 243	245 943	107
F803	159	173 474	221 173	14 682	206	240 358	302 158	3 355	165	195 539	244 919	24 212	201	236 025	296 325	25 387	186	231 297	287 097	1 130	180	188 245	242 245	71
F804	156	171 956	218 756	12 743	213	227 247	291 147	3 324	161	191 853	240 033	21 884	198	226 353	285 753	25 707	181	231 743	286 043	1 490	174	186 214	238 414	81
F1001	212	265 385	329 044	9 698	275	363 035	445 535	3 874	222	293 298	359 838	25 957	279	364 136	447 836	34 957	239	391 293	462 993	1 236	232	278 192	347 792	154
F1002	211	264 034	327 213	8 655	279	356 200	439 900	3 858	225	291 180	358 740	27 482	284	354 899	440 099	34 582	240	352 092	424 092	2 847	234	278 465	348 665	126
F1003	212	265 409	329 008	8 910	275	358 768	441 268	3 917	227	295 806	363 786	26 217	283	359 276	444 176	33 748	243	408 770	481 670	554	231	274 553	343 853	126
F1004	212	262 117	325 656	10 331	285	362 496	447 996	3 914	223	289 035	355 815	26 180	289	360 481	447 181	33 515	234	348 460	418 660	890	233	276 896	346 796	123
最佳/ 全部			18/20				0/20				2/20				0/20				0/20				0/20

下载: 导出CSV

表 4 RBX和OX的消融实验结果

Table 4 Ablation experiment results of RBX and OX

问题	RBX	OX	RBX + OX
F201	66 517	67 966	66 751
F202	66 365	67 744	66 355
F203	68 948	71 718	67 679
F204	66 970	69 372	66 211
F401	124 851	148 685	123 620
F402	128 798	146 954	128 351
F403	123 550	149 781	122 055
F404	125 247	155 403	124 649
F601	187 048	246 299	185 148
F602	192 623	253 252	189 429
F603	193 915	247 466	189 741
F604	193 410	245 400	190 137
F801	224 758	298 889	222 709
F802	228 345	296 430	220 577
F803	226 138	302 783	221 173
F804	220 988	294 788	218 756
F1001	342 544	442 939	329 044
F1002	339 143	440 007	327 213
F1003	341 946	446 173	329 008
F1004	336 077	445 518	325 656
最佳/全部	1/20	0/20	19/20

下载: 导出CSV

表 5 MBEA中参数lower的敏感性分析

Table 5 Sensitivity analysis of lower in MBEA

问题	TC (0.7)	TC (0.5)	TC (0.6)	TC (0.8)	TC (0.9)
F201	66 751	66 664	66 926	66 895	66 971
F202	66 355	66 587	66 597	66 677	66 751
F203	67 679	68 206	67 919	68 027	67 783
F204	66 211	66 215	65 920	66 209	66 150
F401	123 620	123 826	123 103	122 861	122 672
F402	128 351	127 154	127 696	127 771	127 986
F403	122 055	122 428	122 703	122 343	122 270
F404	124 649	124 771	125 365	125 138	124 936
F601	185 148	185 831	186 163	185 579	186 371
F602	189 429	190 317	190 661	190 363	190 731
F603	189 741	189 160	189 740	189 986	189 683
F604	190 137	189 300	189 128	189 743	188 712
F801	222 709	221 057	221 905	221 221	220 910
F802	220 577	221 957	220 655	219 998	220 951
F803	221 173	222 172	222 227	221 495	221 377
F804	218 756	218 002	216 628	217 680	218 297
F1001	329 044	330 379	330 059	330 929	329 632
F1002	327 213	327 346	327 565	326 923	327 199
F1003	329 008	329 596	326 035	328 369	327 482
F1004	325 656	325 790	325 812	326 352	327 106
最佳/全部	9/20	3/20	3/20	2/20	3/20

下载: 导出CSV

表 6 MBEA中参数k的敏感性分析

Table 6 Sensitivity analysis of parameter k in MBEA

问题	TC (1)	TC (0)	TC (2)	TC (3)
F201	66 751	67 985	66 298	66 731
F202	66 355	67 920	67 002	67 111
F203	67 679	68 180	67 917	67 680
F204	66 211	66 621	66 524	65 730
F401	123 620	124 871	124 825	123 839
F402	128 351	127 377	128 292	127 603
F403	122 055	123 494	122 305	121 883
F404	124 649	126 338	124 959	125 486
F601	185 148	187 055	185 004	187 381
F602	189 429	192 343	192 178	189 516
F603	189 741	190 448	190 047	190 610
F604	190 137	191 208	189 940	189 096
F801	222 709	223 158	223 670	224 248
F802	220 577	222 758	223 576	225 523
F803	221 173	222 456	223 684	223 939
F804	218 756	218 393	217 485	220 373
F1001	329 044	330 374	331 387	332 643
F1002	327 213	329 829	329 525	326 603
F1003	329 008	331 877	330 099	329 200
F1004	325 656	330 725	326 082	331 858
最佳/全部	12/20	1/20	3/20	4/20

下载: 导出CSV

参考文献(70)

[1]	Hu M, Liu W D, Peng K, Ma X Q, Cheng W Q, Liu J C, et al. Joint routing and scheduling for vehicle-assisted multidrone surveillance. IEEE Internet of Things Journal, 2019, 6(2): 1781-1790 doi: 10.1109/JIOT.2018.2878602
[2]	杨培颖, 唐加福, 于洋, 裴金翔. 面向最小碳排放量的接送机场服务的车辆路径与调度. 自动化学报, 2013, 39(4): 424-432 doi: 10.1016/S1874-1029(13)60042-7 Yang Pei-Ying, Tang Jia-Fu, Yu Yang, Pei Jin-Xiang. Minimizing carbon emissions for vehicle routing and scheduling in picking up and delivering customers to airport service. Acta Automatica Sinica, 2013, 39(4): 424-432 doi: 10.1016/S1874-1029(13)60042-7
[3]	韩月起, 张凯, 宾洋, 秦闯, 徐云霄, 李小川, 等. 基于凸近似的避障原理及无人驾驶车辆路径规划模型预测算法. 自动化学报, 2020, 46(1): 153-167 Han Yue-Qi, Zhang Kai, Bin Yang, Qin Chuang, Xu Yun-Xiao, Li Xiao-Chuan, et al. Convex approximation based avoidance theory and path planning MPC for driver-less vehicles. Acta Automatica Sinica, 2020, 46(1): 153-167
[4]	徐杨, 陆丽萍, 褚端峰, 黄子超. 无人车辆轨迹规划与跟踪控制的统一建模方法. 自动化学报, 2019, 45(4): 799-807 Xu Yang, Lu Li-Ping, Chu Duan-Feng, Huang Zi-Chao. Unified modeling of trajectory planning and tracking for unmanned vehicle. Acta Automatica Sinica, 2019, 45(4): 799-807
[5]	吴伟, 刘洋, 刘威, 吴国弘, 马万经. 自动驾驶环境下交叉口车辆路径规划与最优控制模型. 自动化学报, 2020, 46(9): 1971-1985 Wu Wei, Liu Yang, Liu Wei, Wu Guo-Hong, Ma Wan-Jing. A novel autonomous vehicle trajectory planning and control model for connected-and-autonomous intersections. Acta Automatica Sinica, 2020, 46(9): 1971-1985
[6]	Abbatecola L, Fanti M P, Pedroncelli G, Ukovich W. A distributed cluster-based approach for pick-up services. IEEE Transactions on Automation Science and Engineering, 2019, 16(2): 960-971 doi: 10.1109/TASE.2018.2879875
[7]	王素欣, 高利, 崔小光, 曹宏美. 多需求点车辆调度模型及其群体智能混合求解. 自动化学报, 2008, 34(1): 102-104 Wang Su-Xin, Gao Li, Cui Xiao-Guang, Cao Hong-Mei. Study on multi-requirement points vehicle scheduling model and its swarm mix algorithm. Acta Automatica Sinica, 2008, 34(1): 102-104
[8]	曾正洋, 许维胜, 徐志宇. 开放式两级车辆路径问题建模与多起始点变邻域下降法求解. 计算机科学, 2014, 41(10): 232-237 Zeng Zheng-Yang, Xu Wei-Sheng, Xu Zhi-Yu. Modeling and multi-start variable neighborhood descent solution of two-echelon open vehicle routing problem. Computer Science, 2014, 41(10): 232-237
[9]	Kheirkhah A, Navidi H, Bidgoli M M. An improved benders decomposition algorithm for an arc interdiction vehicle routing problem. IEEE Transactions on Engineering Management, 2016, 63(2): 259-273 doi: 10.1109/TEM.2016.2542849
[10]	胡蓉, 李洋, 钱斌, 金怀平, 向凤红. 结合聚类分解的增强蚁群算法求解复杂绿色车辆路径问题. 自动化学报, 2022, 48(12): 3006-3023 Hu Rong, Li Yang, Qian Bin, Jin Huai-Ping, Xiang Feng-Hong. An enhanced ant colony optimization combined with clustering decomposition for solving complex green vehicle routing problem. Acta Automatica Sinica, 2022, 48(12): 3006-3023
[11]	Xiao J H, Zhang T, Du J G, Zhang X Y. An evolutionary multiobjective route grouping-based heuristic algorithm for large-scale capacitated vehicle routing problems. IEEE Transactions on Cybernetics, 2021, 51(8): 4173-4186 doi: 10.1109/TCYB.2019.2950626
[12]	Lin C H, Choy K L, Ho G T S, Chung S H, Lam H Y. Survey of green vehicle routing problem: Past and future trends. Expert Systems With Applications, 2014, 41(4): 1118-1138 doi: 10.1016/j.eswa.2013.07.107
[13]	Kassem S, Chen M Y. Solving reverse logistics vehicle routing problems with time windows. The International Journal of Advanced Manufacturing Technology, 2013, 68(1-4): 57-68 doi: 10.1007/s00170-012-4708-9
[14]	Min H. The multiple vehicle routing problem with simultaneous delivery and pick-up points. Transportation Research Part A: General, 1989, 23(5): 377-386 doi: 10.1016/0191-2607(89)90085-X
[15]	Dethloff J. Vehicle routing and reverse logistics: The vehicle routing problem with simultaneous delivery and pick-up. OR-Spektrum, 2001, 23(1): 79-96 doi: 10.1007/PL00013346
[16]	Berbeglia G, Cordeau J F, Laporte G. Dynamic pickup and delivery problems. European Journal of Operational Research, 2010, 202(1): 8-15 doi: 10.1016/j.ejor.2009.04.024
[17]	Wang H F, Chen Y Y. A genetic algorithm for the simultaneous delivery and pickup problems with time window. Computers and Industrial Engineering, 2012, 62(1): 84-95 doi: 10.1016/j.cie.2011.08.018
[18]	Eksioglu B, Vural A V, Reisman A. The vehicle routing problem: A taxonomic review. Computers and Industrial Engineering, 2009, 57(4): 1472-1483 doi: 10.1016/j.cie.2009.05.009
[19]	范厚明, 刘鹏程, 刘浩, 侯登凯. 多中心联合配送模式下集货需求随机的VRPSDP问题. 自动化学报, 2021, 47(7): 1646-1660 Fan Hou-Ming, Liu Peng-Cheng, Liu Hao, Hou Deng-Kai. The multi-depot vehicle routing problem with simultaneous deterministic delivery and stochastic pickup based on joint distribution. Acta Automatica Sinica, 2021, 47(7): 1646-1660
[20]	陈萍, 黄厚宽, 董兴业. 求解卸装一体化的车辆路径问题的混合启发式算法. 计算机学报, 2008, 31(4): 565-73 Chen Ping, Huang Hou-Kuan, Dong Xing-Ye. A hybrid heuristic algorithm for the vehicle routing problem with simultaneous delivery and pickup. Chinese Journal of Computers, 2008, 31(4): 565-573
[21]	Gupta A, Heng C K, Ong Y S, Tan P S, Zhang A N. A generic framework for multi-criteria decision support in eco-friendly urban logistics systems. Expert Systems with Applications, 2017, 71: 288-300 doi: 10.1016/j.eswa.2016.09.033
[22]	Wang J H, Weng T Y, Zhang Q F. A two-stage multiobjective evolutionary algorithm for multiobjective multidepot vehicle routing problem with time windows. IEEE Transactions on Cybernetics, 2019, 49(7): 2467-2478 doi: 10.1109/TCYB.2018.2821180
[23]	Wang C, Mu D, Zhao F, Sutherland J W. A parallel simulated annealing method for the vehicle routing problem with simultaneous pickup-delivery and time windows. Computers & Industrial Engineering, 2015, 83: 111-122
[24]	Mingyong L, Erbao C. An improved differential evolution algorithm for vehicle routing problem with simultaneous pickups and deliveries and time windows. Engineering Applications of Artificial Intelligence, 2010, 23(2): 188-195 doi: 10.1016/j.engappai.2009.09.001
[25]	黄务兰, 张涛. 基于改进全局人工鱼群算法的VRPSPDTW研究. 计算机工程与应用, 2016, 52(21): 21-29 Huang Wu-Lan, Zhang Tao. Vehicle routing problem with simultaneous pick-up and delivery and time-windows based on improved global artificial fish swarm algorithm. Computer Engineering and Applications, 2016, 52(21): 21-29
[26]	Shi Y, Zhou Y J, Boudouh T, Grunder O. A lexicographic-based two-stage algorithm for vehicle routing problem with simultaneous pickup-delivery and time window. Engineering Applications of Artificial Intelligence, 2020, 95: Article No. 103901
[27]	Hof J, Schneider M. An adaptive large neighborhood search with path relinking for a class of vehicle-routing problems with simultaneous pickup and delivery. Networks, 2019, 74(3): 207-250 doi: 10.1002/net.21879
[28]	Iqbal M, Xue B, Al-Sahaf H, Zhang M J. Cross-domain reuse of extracted knowledge in genetic programming for image classification. IEEE Transactions on Evolutionary Computation, 2017, 21(4): 569-587 doi: 10.1109/TEVC.2017.2657556
[29]	Di S, Zhang H G, Li C G, Mei X, Prokhorov D, Ling H B. Cross-domain traffic scene understanding: A dense correspondence-based transfer learning approach. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(3): 745-757 doi: 10.1109/TITS.2017.2702012
[30]	Chalmers E, Contreras E B, Robertson B, Luczak A, Gruber A. Learning to predict consequences as a method of knowledge transfer in reinforcement learning. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(6): 2259-2270 doi: 10.1109/TNNLS.2017.2690910
[31]	Gupta A, Ong Y S, Feng L. Multifactorial evolution: Toward evolutionary multitasking. IEEE Transactions on Evolutionary Computation, 2016, 20(3): 343-357 doi: 10.1109/TEVC.2015.2458037
[32]	Gupta A, Ong Y S, Feng L, Tan K C. Multiobjective multifactorial optimization in evolutionary multitasking. IEEE Transactions on Cybernetics, 2017, 47(7): 1652-1665 doi: 10.1109/TCYB.2016.2554622
[33]	Bali K K, Ong Y S, Gupta A, Tan P S. Multifactorial evolutionary algorithm with online transfer parameter estimation: MFEA-Ⅱ. IEEE Transactions on Evolutionary Computation, 2020, 24(1): 69-83 doi: 10.1109/TEVC.2019.2906927
[34]	Hao X X, Qu R, Liu J. A unified framework of graph-based evolutionary multitasking hyper-heuristic. IEEE Transactions on Evolutionary Computation, 2021, 25(1): 35-47 doi: 10.1109/TEVC.2020.2991717
[35]	Feng L, Zhou L, Gupta A, Zhong J H, Zhu Z X, Tan K C, et al. Solving generalized vehicle routing problem with occasional drivers via evolutionary multitasking. IEEE Transactions on Cybernetics, 2021, 51(6): 3171-3184 doi: 10.1109/TCYB.2019.2955599
[36]	Feng L, Huang Y X, Zhou L, Zhong J H, Gupta A, Tang K, et al. Explicit evolutionary multitasking for combinatorial optimization: A case study on capacitated vehicle routing problem. IEEE Transactions on Cybernetics, 2021, 51(6): 3143-3156 doi: 10.1109/TCYB.2019.2962865
[37]	Feng L, Zhou L, Zhong J H, Gupta A, Ong Y S, Tan K C, et al. Evolutionary multitasking via explicit autoencoding. IEEE Transactions on Cybernetics, 2019, 49(9): 3457-3470 doi: 10.1109/TCYB.2018.2845361
[38]	Feng L, Huang Y X, Tsang I W, Gupta A, Tang K, Tan K C, et al. Towards faster vehicle routing by transferring knowledge from customer representation. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(2): 952-965 doi: 10.1109/TITS.2020.3018903
[39]	Shang Q X, Huang Y X, Wang Y, Li M, Feng L. Solving vehicle routing problem by memetic search with evolutionary multitasking. Memetic Computing, 2022, 14(1): 31-44. doi: 10.1007/s12293-021-00352-7
[40]	Braekers K, Ramaekers K, Van Nieuwenhuyse I. The vehicle routing problem: State of the art classification and review. Computers & Industrial Engineering, 2016, 99: 300-313
[41]	Huang M F, Hu X P. Large scale vehicle routing problem: An overview of algorithms and an intelligent procedure. International Journal of Innovative Computing, Information and Control, 2012, 8(8): 5809-5819
[42]	Shin K, Han S Y. A centroid-based heuristic algorithm for the capacitated vehicle routing problem. Computing and Informatics, 2011, 30(4): 721-732
[43]	Angelelli E, Mansini R. The vehicle routing problem with time windows and simultaneous pick-up and delivery. Quantitative Approaches to Distribution Logistics and Supply Chain Management. Berlin: Springer, 2002. 249−267
[44]	Dell'Amico M, Righini G, Salani M. A branch-and-price approach to the vehicle routing problem with simultaneous distribution and collection. Transportation Science, 2006, 40(2): 235-247 doi: 10.1287/trsc.1050.0118
[45]	Rieck J, Zimmermann J. Exact solutions to the symmetric and asymmetric vehicle routing problem with simultaneous delivery and pick-up. Business Research, 2013, 6(1): 77-92 doi: 10.1007/BF03342743
[46]	Subramanian A, Uchoa E, Pessoa A A, Ochi L S. Branch-cut-and-price for the vehicle routing problem with simul-taneous pickup and delivery. Optimization Letters, 2013, 7(7): 1569-1581 doi: 10.1007/s11590-012-0570-9
[47]	Cao W J, Yang W S. A survey of vehicle routing problem. MATEC Web of Conferences, 2017, 100: Article No. 01006
[48]	Elshaer R, Awad H. A taxonomic review of metaheuristic algorithms for solving the vehicle routing problem and its variants. Computers and Industrial Engineering, 2020, 140: Article No. 106242
[49]	Yu V F, Redi A A N P, Hidayat Y A, Wibowo O J. A simulated annealing heuristic for the hybrid vehicle routing problem. Applied Soft Computing, 2017, 53: 119-132 doi: 10.1016/j.asoc.2016.12.027
[50]	Schermer D, Moeini M, Wendt O. A hybrid VNS/Tabu search algorithm for solving the vehicle routing problem with drones and en route operations. Computers & Operations Research, 2019, 109: 134-158
[51]	Ribeiro G M, Laporte G. An adaptive large neighborhood search heuristic for the cumulative capacitated vehicle routing problem. Computers & Operations Research, 2012, 39(3): 728-735
[52]	Avci M, Topaloglu S. A hybrid metaheuristic algorithm for heterogeneous vehicle routing problem with sim-ultaneous pickup and delivery. Expert Systems with Applications, 2016, 53: 160-171 doi: 10.1016/j.eswa.2016.01.038
[53]	Zhou Y, Kong L J, Cai Y Q, Wu Z Y, Liu S P, Hong J M, et al. A decomposition-based local search for large-scale many-objective vehicle routing problems with simultaneous delivery and pickup and time windows. IEEE Systems Journal, 2020, 14(4): 5253-5264 doi: 10.1109/JSYST.2019.2959664
[54]	Baker B M, Ayechew M A. A genetic algorithm for the vehicle routing problem. Computers & Operations Research, 2003, 30(5): 787-800
[55]	Mohammed M A, Abd Ghani M K, Hamed R I, Mostafa S A, Ahmad M S, Ibrahim D A. Solving vehicle routing problem by using improved genetic algorithm for optimal solution. Journal of Computational Science, 2017, 21: 255-262 doi: 10.1016/j.jocs.2017.04.003
[56]	Sabar N R, Bhaskar A, Chung E, Turky A, Song A. An adaptive memetic approach for heterogeneous vehicle routing problems with two-dimensional loading constraints. Swarm and Evolutionary Computation, 2020, 58: Article No. 100730
[57]	Ouaddi K, Mhada F, Benadada Y. Memetic algorithm for multi-tours dynamic vehicle routing problem with overtime (MDVRPOT). International Journal of Industrial Engineering Computations, 2020, 11(4): 643-662
[58]	Zhang X Y, Duan H B. An improved constrained differential evolution algorithm for unmanned aerial vehicle global route planning. Applied Soft Computing, 2015, 26: 270-284 doi: 10.1016/j.asoc.2014.09.046
[59]	Venkatesan S R, Logendran D, Chandramohan D. Optimization of capacitated vehicle routing problem using PSO. International Journal of Engineering Science and Technology, 2011, 3(10): 7469-7477
[60]	Yu B, Yang Z Z, Yao B Z. An improved ant colony optimization for vehicle routing problem. European Journal of Operational Research, 2009, 196(1): 171-176 doi: 10.1016/j.ejor.2008.02.028
[61]	Lee C Y, Lee Z J, Lin S W, Ying K C. An enhanced ant colony optimization (EACO) applied to capacitated vehicle routing problem. Applied Intelligence, 2010, 32(1): 88-95 doi: 10.1007/s10489-008-0136-9
[62]	Liu S C, Tang K, Yao X. Memetic search for vehicle routing with simultaneous pickup-delivery and time windows. Swarm and Evolutionary Computation, 2021, 66: Article No. 100927
[63]	Ma Y F, Li Z M, Yan F, Feng C Y. A hybrid priority-based genetic algorithm for simultaneous pickup and delivery problems in reverse logistics with time windows and multiple decision-makers. Soft Computing, 2019, 23(15): 6697-6714 doi: 10.1007/s00500-019-03754-5
[64]	Wang J H, Zhou Y, Wang Y, Zhang J, Chen C L P, Zheng Z B. Multiobjective vehicle routing problems with simultaneous delivery and pickup and time windows: Formulation, instances, and algorithms. IEEE Transactions on Cybernetics, 2016, 46(3): 582-594 doi: 10.1109/TCYB.2015.2409837
[65]	Lagos C, Guerrero G, Cabrera E, Moltedo A, Johnson F, Paredes F. An improved particle swarm optimization algorithm for the VRP with simultaneous pickup and delivery and time windows. IEEE Latin America Transactions, 2018, 16(6): 1732-1740 doi: 10.1109/TLA.2018.8444393
[66]	Potvin J Y, Bengio S. The vehicle routing problem with time windows Part Ⅱ: Genetic search. INFORMS Journal on Computing, 1996, 8(2): 165-172 doi: 10.1287/ijoc.8.2.165
[67]	Oliver I M, Smith D J, Holland J R C. A study of permutation crossover operators on the traveling salesman problem. In: Proceedings of the Second International Conference on Genetic Algorithms on Genetic Algorithms and Their Application. Cambridge, USA: L. Erlbaum Associates Inc., 1987.
[68]	Tian Y, Zhang T, Xiao J H, Zhang X Y, Jin Y C. A coevolutionary framework for constrained multiobjective opti-mization problems. IEEE Transactions on Evolutionary Computation, 2021, 25(1): 102-116 doi: 10.1109/TEVC.2020.3004012
[69]	Fleszar K, Osman I H, Hindi K S. A variable neighbourhood search algorithm for the open vehicle routing problem. European Journal of Operational Research, 2009, 195(3): 803-809 doi: 10.1016/j.ejor.2007.06.064
[70]	Cai J C, Zhu Q L, Lin Q Z. Variable neighborhood search for a new practical dynamic pickup and delivery problem. Swarm and Evolutionary Computation, 2022, 75: Article No. 101182