状态测量不确定和动力学未知的无人艇固定时间容错控制

王宁; 高颖; 王仁慧

doi:10.16383/j.aas.c220482

状态测量不确定和动力学未知的无人艇固定时间容错控制

doi: 10.16383/j.aas.c220482

王宁^1,,
高颖^2,,
王仁慧^2,

1.
大连海事大学轮机工程学院大连 116026
2.
大连海事大学船舶电气工程学院大连 116026

基金项目: 国家自然科学基金 (52271306), 船舶总体性能创新研究开放基金 (31422120) 资助

详细信息

作者简介:
王宁：大连海事大学轮机工程学院教授. 主要研究方向为自主系统与控制, 智能绿色船舶, 海洋人工智能. 本文通信作者. E-mail: n.wang@ieee.org

高颖：大连海事大学船舶电气工程学院博士研究生. 主要研究方向为无人船优化控制, 强化学习. E-mail: lutyinggao2013@163.com

王仁慧：大连海事大学船舶电气工程学院硕士研究生. 主要研究方向为水面无人艇轨迹跟踪控制. E-mail: wrh1744754029@163.com

计量
- 文章访问数: 774
- HTML全文浏览量: 250
- PDF下载量: 301
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-10
- 录用日期: 2022-10-29
- 网络出版日期: 2023-01-05
- 刊出日期: 2023-05-20

Fixed-time Fault-tolerance Control of an Unmanned Surface Vehicle With Uncertain Measurements and Unknown Dynamics

1.
Marine Engineering College, Dalian Maritime University, Dalian 116026
2.
Marine Electrical Engineering College, Dalian Maritime University, Dalian 116026

Funds: Supported by National Natural Science Foundation of China (52271306) and Open Foundation for Innovative Research on Ship General Performance (31422120)

More Information

Author Bio:
WANG Ning　Professor at Marine Engineering College, Dalian Maritime University. His research interest covers autonomous systems and control, intelligent green ships, and marine artificial intelligence. Corresponding author of this paper

GAO Ying　Ph.D. candidate at Marine Electrical Engineering College, Dalian Maritime University. Her research interest covers unmanned vehicle optimization control and reinforcement learning

WANG Ren-Hui　Master student at Marine Electrical Engineering College, Dalian Maritime University. His main research interest is trajectory tracking control of unmanned surface vehicles

摘要

摘要: 针对含有推进器故障和状态测量不确定的无人艇(Unmanned surface vehicle, USV)系统, 提出一种基于双扰动观测器的固定时间容错跟踪控制(Double disturbance observer-based fixed-time fault-tolerance control, DDO-FxFC)方法. 设计两个固定时间扰动观测器, 分别估计状态测量不确定性产生的非匹配干扰和包含推进器故障的集总非线性, 同时自适应实时补偿未知观测误差; 采用测量位姿跟踪误差及其动态, 设计快速非奇异终端滑模面, 构建DDO-FxFC框架; 理论分析证明DDO-FxFC方法能够确保跟踪误差固定时间收敛, 其中收敛时间的上界独立于系统初始状态; 针对原型USV的仿真结果和综合对比验证所提出DDO-FxFC技术的有效性和优越性.
- 无人艇 /
- 测量不确定性 /
- 未知动力学 /
- 固定时间控制 /
- 容错控制
Abstract: In this paper, a double disturbance observer-based fixed-time fault-tolerance control (DDO-FxFC) scheme is developed for an unmanned surface vehicle (USV) in the presence of thruster faults and measurement uncertainties. To be specific, two fixed-time disturbance observers are devised to estimate the mismatching disturbances generated by measurement uncertainties and the lumped nonlinearities including thruster faults, respectively, while unknown estimation errors are compensated in an adaptively real-time manner. Furthermore, a fast nonsingular terminal sliding-mode using measurement tracking errors and their dynamics is deployed to build up the DDO-FxFC framework. Theoretical analysis proves that the DDO-FxFC scheme can ensure fixed-time convergence of tracking errors, whereby the upper bound of convergence time is independent of initial states. Simulation results and comprehensive comparisons on a prototype USV demonstrate the remarkable effectiveness and superiority of the proposed DDO-FxFC scheme.
- Unmanned surface vehicle (USV) /
- measurement uncertainty /
- unknown dynamics /
- fixed-time control /
- fault-tolerance control

HTML全文

图 1 轨迹跟踪

Fig. 1 Trajectory tracking

下载: 全尺寸图片幻灯片

图 2 位姿跟踪误差

Fig. 2 Position tracking errors

下载: 全尺寸图片幻灯片

图 3 速度跟踪误差

Fig. 3 Velocity tracking errors

下载: 全尺寸图片幻灯片

图 4 控制输入

Fig. 4 Control inputs

下载: 全尺寸图片幻灯片

图 5 集总扰动观测

Fig. 5 The observation of lumped disturbances

下载: 全尺寸图片幻灯片

图 6 自适应增益变化

Fig. 6 The variation of adaptive gain

下载: 全尺寸图片幻灯片

表 1 Cybership II水动力参数

Table 1 Hydrodynamic parameters of the Cybership II

参数	取值	参数	取值	参数	取值
$ m $	23.800	$ Y_v $	−0.8612	$ X_{\dot{u}} $	−2.0
$ I_z $	1.760	$ Y_{\|v\|v} $	−36.2823	$ Y_{\dot{v}} $	−10.0
$ x_g $	0.046	$ Y_r $	0.1079	$ Y_{\dot{r}} $	0
$ X_u $	−0.7225	$ N_v $	0.1052	$ N_{\dot{v}} $	0
$ X_{\|u\|u} $	−1.3274	$ N_{\|v\|v} $	5.0437	$ N_{\dot{r}} $	−1.0
$ X_{uuu} $	1.255

下载: 导出CSV

表 2 4种控制方案下积分绝对误差

Table 2 Integrated absolute errors of the four controllers

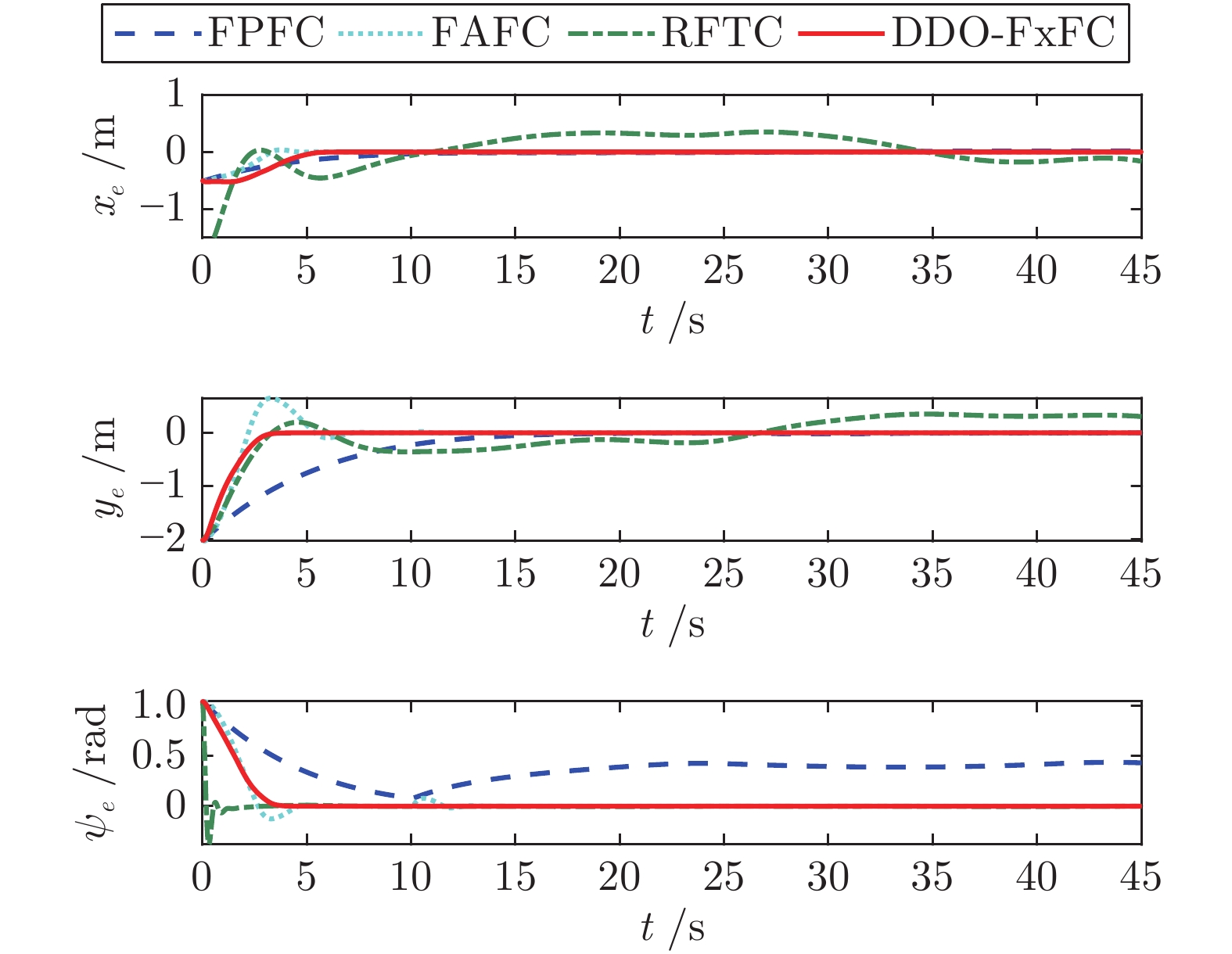
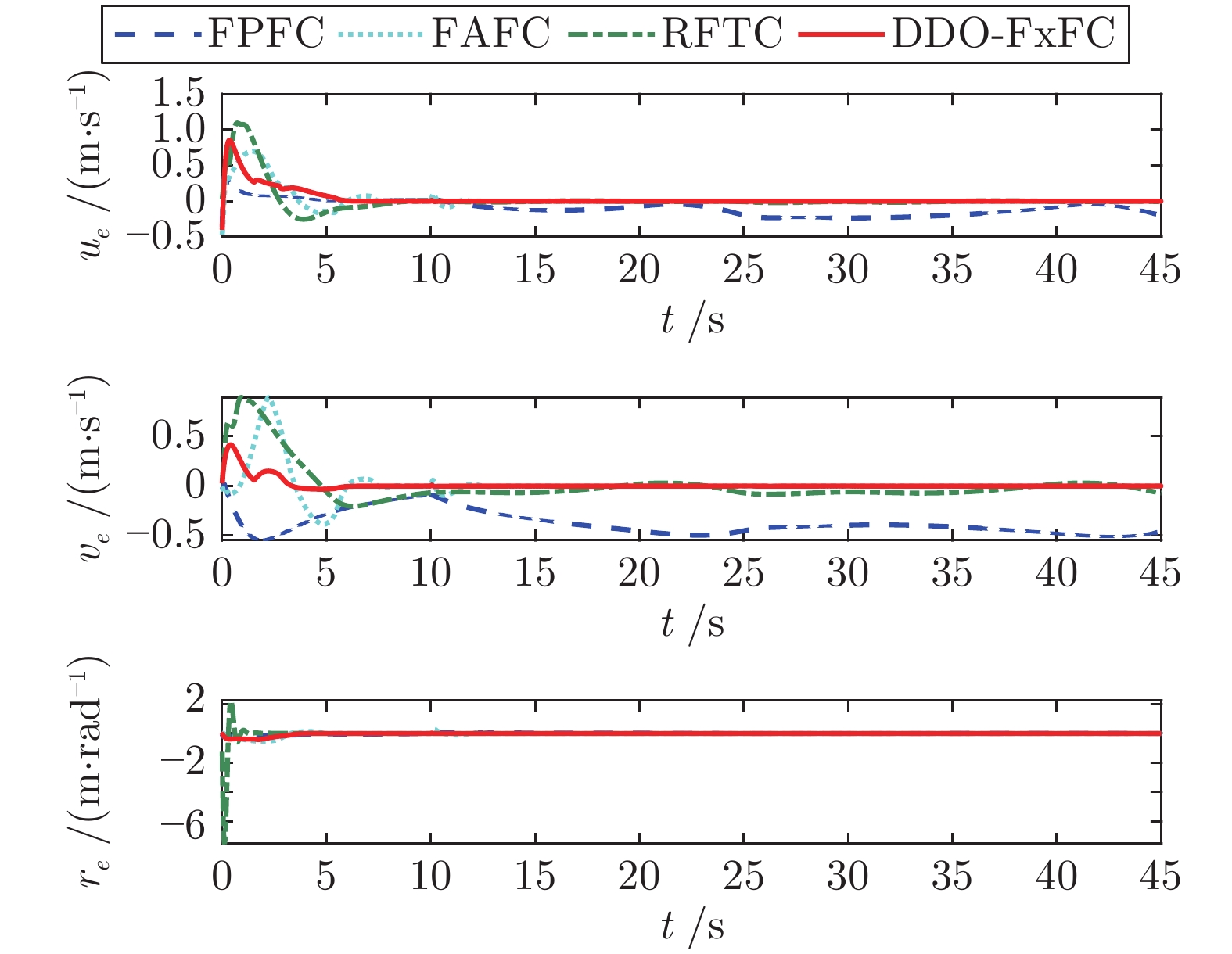
	$ {\rm IAE}_x $	$ {{\rm IAE}}_y $	$ {{\rm IAE}}_{\psi} $	$ {{\rm IAE}}_u $	$ {{\rm IAE}}_v $	$ {{\rm IAE}}_r $
FPFC	2.32	9.69	17.23	5.27	17.07	1.41
FAFC	1.07	4.13	1.92	1.96	2.09	1.54
RFTC	11.52	13.64	0.34	2.67	4.69	1.54
DDO-FxFC	1.79	2.53	1.61	1.50	0.64	2.08

下载: 导出CSV

表 3 4种控制方案下积分时间绝对误差

Table 3 Integrated time absolute errors ofthe four controllers

	$ {\rm ITAE}_x $	$ {\rm ITAE}_y $	$ {\rm ITAE}_{\psi} $	$ {\rm ITAE}_u $	$ {\rm ITAE}_v $	$ {\rm ITAE}_r $
FPFC	17.12	44.49	39.26	23.20	42.91	11.64
FAFC	1.51	7.65	3.16	5.32	7.61	5.25
RFTC	10.97	26.48	1.95	11.79	5.62	1.11
DDO-FxFC	3.42	2.35	1.72	3.05	1.28	2.01

下载: 导出CSV

参考文献(48)

[1]	张卫东, 刘笑成, 韩鹏. 水上无人系统研究进展及其面临的挑战. 自动化学报, 2020, 46(5): 847-857 Zhang Wei-Dong, Liu Xiao-Cheng, Han Peng. Progress and challenges of overwater unmanned systems. Acta Automatica Sinica, 2020, 46(5): 847-857
[2]	Wang N, Xie G M, Pan X X, Su S F. Full-state regulation control of asymmetric underactuated surface vehicles. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8741-8750 doi: 10.1109/TIE.2018.2890500
[3]	林安辉, 蒋德松, 曾建平. 具有输入饱和的欠驱动船舶编队控制. 自动化学报, 2018, 44(8): 1496-1504 Lin An-Hui, Jiang De-Song, Zeng Jian-Ping. Underactuated ship formation control with input saturation. Acta Automatica Sinica, 2018, 44(8): 1496-1504
[4]	Wang N, Karimi H R. Successive waypoints tracking of an underactuated surface vehicle. IEEE Transactions on Industrial Informatics, 2020, 16(2): 898-908 doi: 10.1109/TII.2019.2922823
[5]	王宁, 王仁慧, 鲁挺. 推进器饱和约束的水面无人艇固定时间精准跟踪控制. 控制理论与应用, DOI: 10.7641/CTA.2022.10778 Wang Ning, Wang Ren-Hui, Lu Ting. Fixed-time precision tracking control of an unmanned surface vehicle constrained by thruster saturations. Control Theory & Applications, DOI: 10.7641/CTA.2022.10778
[6]	Zhou B, Huang B, Su Y M, Zheng Y X, Zheng S. Fixed-time neural network trajectory tracking control for underactuated surface vessels. Ocean Engineering, 2021, 236: Article No. 109416 doi: 10.1016/j.oceaneng.2021.109416
[7]	Chen L P, Cui R X, Yang C G, Yan W S. Adaptive neural network control of underactuated surface vessels with guaranteed transient performance: Theory and experimental results. IEEE Transactions on Industrial Electronics, 2020, 67(5): 4024-4035 doi: 10.1109/TIE.2019.2914631
[8]	Du B, Lin B, Zhang C M, Dong B T, Zhang W D. Safe deep reinforcement learning-based adaptive control for USV interception mission. Ocean Engineering, 2022, 246: Article No. 110477 doi: 10.1016/j.oceaneng.2021.110477
[9]	Wang N, He H K. Dynamics-level finite-time fuzzy monocular visual servo of an unmanned surface vehicle. IEEE Transactions on Industrial Electronics, 2020, 67(11): 9648-9658 doi: 10.1109/TIE.2019.2952786
[10]	Esfahani H N, Szlapczynski R. Model predictive super-twisting sliding mode control for an autonomous surface vehicle. Polish Maritime Research, 2019, 26(3): 163-171 doi: 10.2478/pomr-2019-0057
[11]	Roy S, Roy S B, Kar I N. Adaptive-robust control of Euler-Lagrange systems with linearly Parametrizable uncertainty bound. IEEE Transactions on Control Systems Technology, 2018, 26(5): 1842-1850 doi: 10.1109/TCST.2017.2739107
[12]	Wang N, Gao Y, Zhao H, Ahn C K. Reinforcement learning-based optimal tracking control of an unknown unmanned surface vehicle. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(7): 3034-3045 doi: 10.1109/TNNLS.2020.3009214
[13]	Wang N, Gao Y, Zhang X F. Data-driven performance-prescribed reinforcement learning control of an unmanned surface vehicle. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(12): 5456-5467 doi: 10.1109/TNNLS.2021.3056444
[14]	Chen Z, Zhang Y G, Nie Y, Tang J Z, Zhu S Q. Adaptive sliding mode control design for nonlinear unmanned surface vessel using RBFNN and disturbance-observer. IEEE Access, 2020, 8: 45457-45467 doi: 10.1109/ACCESS.2020.2977609
[15]	Qiao L, Zhang W D. Adaptive second-order fast nonsingular terminal sliding mode tracking control for fully actuated autonomous underwater vehicles. IEEE Journal of Oceanic Engineering, 2019, 44(2): 363-385 doi: 10.1109/JOE.2018.2809018
[16]	Gonzalez-Garcia A, Castañeda H. Guidance and control based on adaptive sliding mode strategy for a USV subject to uncertainties. IEEE Journal of Oceanic Engineering, 2021, 46(4): 1144-1154 doi: 10.1109/JOE.2021.3059210
[17]	Shen Z P, Wang Y, Yu H M, Guo C. Finite-time adaptive tracking control of marine vehicles with complex unknowns and input saturation. Ocean Engineering, 2020, 198: Article No. 106980 doi: 10.1016/j.oceaneng.2020.106980
[18]	付德祥, 康伟, 朱瑾. 基于参考模型的电力推进船舶航向滑模控制器设计. 控制工程, 2013, 20(S1): 35-38 Fu De-Xiang, Kang Wei, Zhu Jin. Sliding-model control based on model reference for electric propulsion ship course tracking control. Control Engineering of China, 2013, 20(S1): 35-38
[19]	沈智鹏, 张晓玲. 基于非线性增益递归滑模的船舶轨迹跟踪动态面自适应控制. 自动化学报, 2018, 44(10): 1833-1841 Shen Zhi-Peng, Zhang Xiao-Ling. Recursive sliding-mode dynamic surface adaptive control for ship trajectory tracking with nonlinear gains. Acta Automatica Sinica, 2018, 44(10): 1833-1841
[20]	Cao L, Xiao B, Golestani M. Robust fixed-time attitude stabilization control of flexible spacecraft with actuator uncertainty. Nonlinear Dynamics, 2020, 100(3): 2505-2519
[21]	Mustafa A, Dhar N K, Verma N K. Event-triggered sliding mode control for trajectory tracking of nonlinear systems. IEEE/CAA Journal of Automatica Sinica, 2020, 7(1): 307-314 doi: 10.1109/JAS.2019.1911654
[22]	Yu Z F, Zhao F, Ding S H, Chen X Y. Adaptive pre-assigned finite-time control of uncertain nonlinear systems with unknown control gains. Applied Mathematics and Computation, 2022, 417: Article No. 126784 doi: 10.1016/j.amc.2021.126784
[23]	Su S, Han L G, Li S K. Finite-time event-triggered consensus control for high-speed train with gradient resistance. Journal of the Franklin Institute, 2022, 359(2): 1144-1175 doi: 10.1016/j.jfranklin.2021.11.012
[24]	王宁, 吕帅林. 基于有限时间扰动观测器的无人水面艇精确航迹跟踪控制. 控制与决策, 2019, 34(11): 2491-2497 Wang Ning, Lü Shuai-Lin. Finite-time disturbance observer based accurate trajectory tracking control of an unmanned surface vehicle. Control and Decision, 2019, 34(11): 2491-2497
[25]	付明玉, 刘佳, 吴宝奇. 基于扰动观测器的动力定位船终端滑模航迹跟踪控制. 中国造船, 2015, 56(4): 33-45 Fu Ming-Yu, Liu Jia, Wu Bao-Qi. Terminal sliding mode tracking control with disturbance observer of dynamic positioning vessel. Shipbuilding of China, 2015, 56(4): 33-45
[26]	Wang N, Deng Z C. Finite-time fault estimator based fault-tolerance control for a surface vehicle with input saturations. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1172-1181 doi: 10.1109/TII.2019.2930471
[27]	Wang N, Zhu Z B, Qin H D, Deng Z C, Sun Y C. Finite-time extended state observer-based exact tracking control of an unmanned surface vehicle. International Journal of Robust and Nonlinear Control, 2021, 31(5): 1704-1719 doi: 10.1002/rnc.5369
[28]	Yang G C, Wang H, Chen J, Zhang H. Command filtered robust control of nonlinear systems with full-state time-varying constraints and disturbances rejection. Nonlinear Dynamics, 2020, 101(4): 2325-2342 doi: 10.1007/s11071-020-05921-y
[29]	Polyakov A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Transactions on Automatic Control, 2012, 57(8): 2106-2110 doi: 10.1109/TAC.2011.2179869
[30]	Yao Q J. Robust fixed-time trajectory tracking control of marine surface vessel with feedforward disturbance compensation. International Journal of Systems Science, 2022, 53(4): 726-742 doi: 10.1080/00207721.2021.1972354
[31]	Zhang J Q, Yu S H, Yan Y. Fixed-time velocity-free sliding mode tracking control for marine surface vessels with uncertainties and unknown actuator faults. Ocean Engineering, 2020, 201: Article No. 107107 doi: 10.1016/j.oceaneng.2020.107107
[32]	Sun J J, Wang J, Yang P, Guo S J. Model-free prescribed performance fixed-time control for wearable exoskeletons. Applied Mathematical Modelling, 2021, 90: 61-77 doi: 10.1016/j.apm.2020.09.010
[33]	Wang T Q, Liu Y T, Zhang X F. Extended state observer-based fixed-time trajectory tracking control of autonomous surface vessels with uncertainties and output constraints. ISA Transactions, 2022, 128: 174-183 doi: 10.1016/j.isatra.2021.09.005
[34]	Song S, Park J H, Zhang B Y, Song X N. Event-triggered adaptive practical fixed-time trajectory tracking control for unmanned surface vehicle. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(1): 436-440 doi: 10.1109/TCSII.2020.3001314
[35]	Fan Y S, Qiu B B, Liu L, Yang Y. Global fixed-time trajectory tracking control of underactuated USV based on fixed-time extended state observer. ISA Transactions, DOI: 10.1016/j.isatra.2022.06.011
[36]	Rauh A, Wirtensohn S, Hoher P, Reuter J, Jaulin L. Reliability assessment of an unscented kalman filter by using ellipsoidal enclosure techniques. Mathematics, 2022, 10(16): Article No. 3011 doi: 10.3390/math10163011
[37]	Cui J W, Sun H B. Fixed-time trajectory tracking control of autonomous surface vehicle with model uncertainties and disturbances. Complexity, 2020, 2020: Article No. 3281368
[38]	Zhang J Q, Yu S H, Yan Y, Wu D F. Fixed-time output feedback sliding mode tracking control of marine surface vessels under actuator faults with disturbance cancellation. Applied Ocean Research, 2020, 104: Article No. 102378 doi: 10.1016/j.apor.2020.102378
[39]	王元慧, 王海滨, 张晓云. 动力定位船轨迹跟踪鲁棒自适应容错控制. 控制理论与应用, 2021, 38(2): 287-300 Wang Yuan-Hui, Wang Hai-Bin, Zhang Xiao-Yun. Robust adaptive fault-tolerant tracking control for dynamic positioning vessel. Control Theory & Applications, 2021, 38(2): 287-300
[40]	Wang Y Y, Jiang B, Wu Z G, Xie S R, Peng Y. Adaptive sliding mode fault-tolerant fuzzy tracking control with application to unmanned marine vehicles. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(11): 6691-6700 doi: 10.1109/TSMC.2020.2964808
[41]	Zhang G Q, Chu S J, Huang J S, Zhang W D. Robust adaptive fault-tolerant control for unmanned surface vehicle via the multiplied event-triggered mechanism. Ocean Engineering, 2022, 249: Article No. 110755 doi: 10.1016/j.oceaneng.2022.110755
[42]	Liu K, Wang R J, Zheng S J, Dong S F, Sun G W. Fixed-time disturbance observer-based robust fault-tolerant tracking control for uncertain quadrotor UAV subject to input delay. Nonlinear Dynamics, 2022, 107(3): 2363-2390 doi: 10.1007/s11071-021-07080-0
[43]	Gao C, Guo Y J, Zhong M J, Liang X F, Wang H D, Yi H. Reliability analysis based on dynamic Bayesian networks: A case study of an unmanned surface vessel. Ocean Engineering, 2021, 240: Article No. 109970 doi: 10.1016/j.oceaneng.2021.109970
[44]	Chen M, Jiang B, Cui R X. Actuator fault-tolerant control of ocean surface vessels with input saturation. International Journal of Robust and Nonlinear Control, 2016, 26(3): 542-564 doi: 10.1002/rnc.3324
[45]	Hao L Y, Yu Y, Li H. Fault tolerant control of UMV based on sliding mode output feedback. Applied Mathematics and Computation, 2019, 359: 433-455 doi: 10.1016/j.amc.2019.04.069
[46]	Hao L Y, Zhang H, Yue W, Li H. Fault-tolerant compensation control based on sliding mode technique of unmanned marine vehicles subject to unknown persistent ocean disturbances. International Journal of Control, Automation and Systems, 2020, 18(3): 739-752 doi: 10.1007/s12555-019-0112-7
[47]	Guo G, Zhang P F. Asymptotic stabilization of USVs with actuator dead-zones and yaw constraints based on fixed-time disturbance observer. IEEE Transactions on Vehicular Technology, 2020, 69(1): 302-316 doi: 10.1109/TVT.2019.2955020
[48]	Yao Q J. Adaptive finite-time sliding mode control design for finite-time fault-tolerant trajectory tracking of marine vehicles with input saturation. Journal of the Franklin Institute, 2020, 357(18): 13593-13619 doi: 10.1016/j.jfranklin.2020.10.015