考虑全局和局部帕累托前沿的多模态多目标优化算法

李文桦; 明梦君; 张涛; 王锐; 黄生俊; 王凌

doi:10.16383/j.aas.c220476

考虑全局和局部帕累托前沿的多模态多目标优化算法

doi: 10.16383/j.aas.c220476

李文桦^1,,
明梦君^1,,
张涛^{1, 2,},
王锐^{1, 2,},
黄生俊^{1, 2,},
王凌^3,

1.
国防科技大学系统工程学院长沙 410073
2.
多能源系统智慧互联技术湖南省重点实验室长沙 410073
3.
清华大学自动化系北京 100084

基金项目: 国家优秀青年科学基金 (62122093), 国家自然科学基金 (72071205, 62273193) 资助

详细信息

作者简介:
李文桦：国防科技大学系统工程学院博士研究生. 2020年获得国防科技大学硕士学位. 主要研究方向为多目标优化及其应用. E-mail: liwenhua1030@aliyun.com

明梦君：国防科技大学系统工程学院讲师. 2022年获得国防科技大学博士学位. 主要研究方向为约束优化, 多目标优化和微电网调度优化. E-mail: mmengjun@gmail.com

张涛：国防科技大学系统工程学院教授. 2004年获得国防科技大学博士学位. 主要研究方向为能源互联网优化调度, 数据挖掘和优化方法. E-mail: zhangtao@nudt.edu.cn

王锐：国防科技大学系统工程学院副研究员. 2013年获得英国谢菲尔德大学博士学位. 主要研究方向为进化计算, 多目标优化及其应用. 本文通信作者. E-mail: ruiwangnudt@gmail.com

黄生俊：国防科技大学系统工程学院副教授. 2018年获得加拿大阿尔伯塔大学博士学位. 主要研究方向为混合整数线性规划, 鲁棒优化算法, 大规模电力系统和微电网集群. E-mail: huangshengjun@nudt.edu.cn

王凌：清华大学自动化系教授. 1999年获得北京清华大学控制理论和控制工程博士学位. 主要研究方向为智能优化, 生产调度. E-mail: wangling@tsinghua.edu.cn

中图分类号: 10.16383/j.aas.c220476
计量
- 文章访问数: 5180
- HTML全文浏览量: 4976
- PDF下载量: 2886
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-08
- 录用日期: 2022-08-15
- 网络出版日期: 2022-09-21
- 刊出日期: 2023-01-07

Multimodal Multi-objective Evolutionary Algorithm Considering Global and Local Pareto Fronts

LI Wen-Hua^1
,,
MING Meng-Jun^1
,,
ZHANG Tao^{1, 2
,},
WANG Rui^{1, 2
,},
HUANG Sheng-Jun^{1, 2
,},
WANG Ling^3
,

1.
College of Systems Engineering, National University of Defense Technology, Changsha 410073
2.
Hunan Key Laboratory of Multi-energy System Intelligent Interconnection Technology, Changsha 410073
3.
Department of Automation, Tsinghua University, Beijing 100084

Funds: Supported by National Science Fund for Outstanding Young Scholars (62122093) and National Natural Science Foundation of China (72071205, 62273193)

More Information

Author Bio:
LI Wen-Hua　Ph.D. candidate at the College of Systems Engineering, National University of Defense Technology. He received his master degree from National University of Defense Technology in 2020. His research interest covers multi-objective optimization and applications

MING Meng-Jun　Lecturer at the College of Systems Engineering, National University of Defense Technology. She received her Ph.D. degree from National University of Defense Technology in 2022. Her research interest covers constrained optimization, multi-objective optimization, and microgrid dispatch optimization

ZHANG Tao　Professor at the College of Systems Engineering, National University of Defense Technology. He received his Ph.D. degree from National University of Defense Technology in 2004. His research interest covers energy internet scheduling optimization, data mining, and optimization methods

WANG Rui　Associate researcher at the College of Systems Engineering, National University of Defense Technology. He received his Ph.D. degree from the University of Sheffield, UK, in 2013. His research interest covers evolutionary computation, multi-objective optimization, and the development of algorithms applicable in practice. Corresponding author of this paper

HUANG Sheng-Jun　Associate professor at the College of Systems Engineering, National University of Defense Technology. He received his Ph.D. degree from the University of Alberta, Canada, in 2018. His research interest covers mixed-integer linear programming, robust optimization algorithms, large-scale power systems, and microgrid clusters

WANG Ling　Professor in the Department of Automation, Tsinghua University. He received his Ph.D. degree in control theory and control engineering from Tsinghua University in 1999. His research interest covers intelligent optimization and production scheduling

摘要

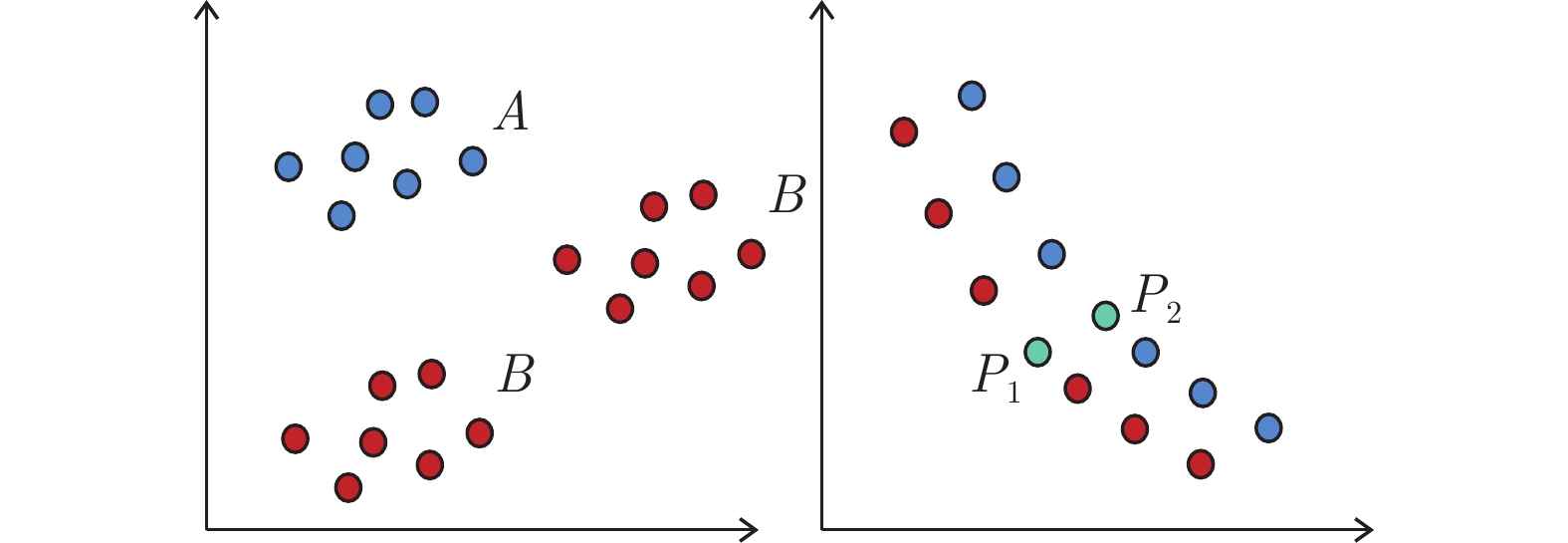
摘要: 多模态多目标优化问题 (Multimodal multi-objective optimization problems, MMOPs)是指具有多个全局或局部Pareto解集(Pareto solution sets, PSs)的多目标优化问题 (Multi-objective optimization problems, MOPs). 在这类问题中, Pareto前沿(Pareto front, PF)上相距很近的目标向量, 可能对应于决策空间中相距较远的不同解. 在实际应用中全局或局部最优解的缺失可能导致决策者缺乏对问题的整体认识, 造成不必要的困难或经济损失. 大部分多模态多目标进化算法 (Multimodal multi-objective evolutionary algorithms, MMEAs) 仅关注获取尽可能多的全局最优解集, 而忽略了对局部最优解集的搜索. 为了找到局部最优解集并提高多模态优化算法的性能, 首先提出了一种局部收敛性指标 ($ I_{LC}$), 并设计了一种基于该指标和改进种群拥挤度的环境选择策略. 基于此提出了一种用于获取全局和局部最优解集的多模态多目标优化算法. 经实验验证, 该算法在对比的代表性算法中性能较好.
- 多模态多目标优化 /
- 局部收敛性 /
- 进化算法 /
- 种群多样性
Abstract: Multimodal multi-objective optimization problems (MMOPs) refer to problems with multiple global or local Pareto solution sets (PSs). Different solutions far apart in the decision space may correspond to objective vectors in the Pareto front (PF) that are closed. The lack of global or local optimal solutions in practical applications may lead to the lack of overall understanding of the problem for decision-makers, resulting in unnecessary difficulties or economic losses. Most of the multimodal multi-objective evolutionary algorithms (MMEAs) mainly focus on obtaining the global optimal solution sets and pay little attention to the local optimal solutions. In order to find the local optimal solution sets and improve the performance of MMEAs, this paper proposes a local convergence indicator ($ I_{LC}$) and designs an environment selection strategy. Then, a multimodal multi-objective optimization algorithm for obtaining global and local optimal solution sets is proposed. Experiments show that the performance of the proposed algorithm is better than that of the compared representative algorithms.
- Multimodal multi-objective optimization /
- local convergence /
- evolutionary algorithms /
- population diversity

HTML全文

图 1 两目标两决策变量多模态问题示意图 (左图和右图分别表示问题的决策空间和目标空间)

Fig. 1 Diagram of a two-objective two-decision-variable MMOP (the left figure and right figure are decision space and objective space respectively)

下载: 全尺寸图片幻灯片

图 2 具有局部帕累托前沿的两目标多模态问题 (左图和右图分别表示问题的决策空间和目标空间)

Fig. 2 A two-objective MMOP with local Pareto front (the left figure and right figure are decision space and objective space respectively)

下载: 全尺寸图片幻灯片

图 3 MMF12 (左)和MMF15 (右)问题的PF和PS示意图

Fig. 3 Diagram of PF and PS for MMF12 (left) and MMF15 (right)

下载: 全尺寸图片幻灯片

图 4 局部收敛性指标示意图

Fig. 4 Diagram of local convergence indicator

下载: 全尺寸图片幻灯片

图 5 目标空间和决策空间的分布均匀性

Fig. 5 Distribution uniformity in the objective space and the decision space

下载: 全尺寸图片幻灯片

图 6 不同算法在IDMPM3T4问题上获得的PS和PF

Fig. 6 PS and PF obtained by different algorithms on IDMPM3T4 problem

下载: 全尺寸图片幻灯片

图 7 不同算法在IDMPM4T3问题上获得的PS (蓝色实线) 和真实PS (红色虚线)

Fig. 7 True PS (red dotted lines) and obtained PS (blue solid lines) by different algorithms on IDMPM4T3 problem

下载: 全尺寸图片幻灯片

图 8 不同算法在MMF11问题 (前两行) 和MMF12问题 (后两行) 上获得的PS和PF

Fig. 8 PS and PF obtained by different algorithms on MMF11 (first two rows) and MMF12 (last two rows) problems

下载: 全尺寸图片幻灯片

图 9 不同算法在不同目标个数测试问题上的计算时间

Fig. 9 Computational time of different algorithms on test problems with different number of objectives

下载: 全尺寸图片幻灯片

表 1 不同算法在IDMP测试问题上31次独立运行的IGDX平均值和方差

Table 1 Mean and variance of 31 independent runs of IGDX for different algorithms on IDMP test problems

测试问题	Omni-optimizer	DN-NSGAII	MO_Ring_ PSO_SCD	DNEA-L	CPDEA	MMOEA/DC	MMEA-WI	$I_{LC}$-MMEA
IDMPM2T1	3.88×10⁻¹	2.84×10⁻¹	5.90×10⁻²	1.27×10⁻³	1.03×10⁻³	8.76×10⁻⁴	9.32×10⁻⁴	6.55×10⁻⁴
IDMPM2T1	3.31×10⁻¹	3.24×10⁻¹	1.67×10⁻¹	2.39×10⁻³	5.41×10⁻⁴	1.15×10⁻⁴	7.13×10⁻⁵	2.30×10⁻⁹
IDMPM2T2	2.99×10⁻¹	2.99×10⁻¹	5.58×10⁻³	1.75×10⁻³	9.55×10⁻⁴	1.03×10⁻³	1.12×10⁻³	8.65×10⁻⁴
IDMPM2T2	3.33×10⁻¹	3.34×10⁻¹	2.91×10⁻³	1.39×10⁻³	1.33×10⁻⁴	1.14×10⁻⁴	8.61×10⁻⁵	4.71×10⁻⁹
IDMPM2T3	1.19×10⁻¹	1.19×10⁻¹	3.35×10⁻³	2.65×10⁻³	3.70×10⁻³	1.85×10⁻³	1.99×10⁻³	1.42×10⁻³
IDMPM2T3	2.57×10⁻¹	2.55×10⁻¹	4.22×10⁻⁴	1.62×10⁻³	1.47×10⁻³	1.92×10⁻⁴	2.49×10⁻⁴	8.51×10⁻⁹
IDMPM2T4	5.44×10⁻¹	6.10×10⁻¹	8.67×10⁻²	1.30×10⁻²	2.32×10⁻²	9.06×10⁻²	4.58×10⁻²	6.12×10⁻⁴
IDMPM2T4	2.63×10⁻¹	1.94×10⁻¹	2.00×10⁻¹	2.16×10⁻²	1.23×10⁻¹	2.32×10⁻¹	1.71×10⁻¹	7.82×10⁻¹⁰
IDMPM3T1	3.50×10⁻¹	3.49×10⁻¹	1.19×10⁻¹	3.26×10⁻²	1.53×10⁻²	8.41×10⁻³	7.48×10⁻³	8.67×10⁻³
IDMPM3T1	2.30×10⁻¹	2.42×10⁻¹	1.47×10⁻¹	7.42×10⁻²	4.42×10⁻²	3.97×10⁻⁴	1.78×10⁻⁴	1.68×10⁻⁸
IDMPM3T2	6.00×10⁻¹	6.14×10⁻¹	1.45×10⁻¹	2.78×10⁻²	7.23×10⁻³	8.17×10⁻³	7.69×10⁻³	8.73×10⁻³
IDMPM3T2	2.29×10⁻¹	2.90×10⁻¹	1.25×10⁻¹	6.21×10⁻²	2.56×10⁻⁴	2.71×10⁻⁴	2.01×10⁻⁴	1.51×10⁻⁸
IDMPM3T3	3.71×10⁻¹	4.75×10⁻¹	2.65×10⁻²	3.65×10⁻²	2.65×10⁻²	1.01×10⁻²	2.55×10⁻²	9.66×10⁻³
IDMPM3T3	2.03×10⁻¹	2.32×10⁻¹	4.34×10⁻²	7.41×10⁻²	6.09×10⁻²	6.01×10⁻⁴	6.29×10⁻²	5.89×10⁻⁸
IDMPM3T4	8.24×10⁻¹	8.13×10⁻¹	2.64×10⁻¹	8.16×10⁻²	5.71×10⁻²	1.84×10⁻²	1.54×10⁻¹	8.43×10⁻³
IDMPM3T4	2.16×10⁻¹	2.27×10⁻¹	1.82×10⁻¹	1.08×10⁻¹	9.87×10⁻²	3.13×10⁻²	1.52×10⁻¹	1.91×10⁻⁸
IDMPM4T1	7.94×10⁻¹	6.36×10⁻¹	9.36×10⁻¹	1.07×10⁻¹	7.03×10⁻¹	4.44×10⁻²	2.68×10⁻²	9.15×10⁻³
IDMPM4T1	3.07×10⁻¹	3.33×10⁻¹	2.75×10⁻¹	1.50×10⁻¹	2.89×10⁻¹	7.50×10⁻²	6.77×10⁻²	2.40×10⁻⁶
IDMPM4T2	9.72×10⁻¹	9.24×10⁻¹	5.59×10⁻¹	2.89×10⁻¹	5.47×10⁻¹	2.62×10⁻²	3.62×10⁻¹	4.45×10⁻²
IDMPM4T2	2.28×10⁻¹	2.37×10⁻¹	2.64×10⁻¹	2.51×10⁻¹	2.36×10⁻¹	5.25×10⁻²	2.81×10⁻¹	2.79×10⁻³
IDMPM4T3	7.44×10⁻¹	7.25×10⁻¹	8.04×10⁻²	1.32×10⁻¹	4.07×10⁻¹	1.66×10⁻²	4.16×10⁻¹	1.82×10⁻²
IDMPM4T3	3.18×10⁻¹	3.05×10⁻¹	8.42×10⁻²	1.59×10⁻¹	2.56×10⁻¹	1.33×10⁻³	2.92×10⁻¹	9.53×10⁻⁴
IDMPM4T4	1.08	1.11	6.86×10⁻¹	1.70×10⁻¹	7.94×10⁻¹	3.87×10⁻²	7.28×10⁻¹	2.86×10⁻²
IDMPM4T4	1.68×10⁻¹	1.53×10⁻¹	3.44×10⁻¹	2.38×10⁻¹	3.19×10⁻¹	6.08×10⁻²	3.28×10⁻¹	3.95×10⁻³
+/−/=	0/10/2	0/12/0	0/12/0	0/11/1	1/10/1	1/7/4	1/8/3

下载: 导出CSV

表 2 不同算法在具有局部PS测试问题上31次独立运行的IGDX平均值和方差

Table 2 Mean and variance of 31 independent runs of IGDX for different algorithms on MMOPs with local PS

测试问题	Omni-optimizer	DN-NSGAII	MO_Ring_ PSO_SCD	DNEA-L	CPDEA	MMOEA/DC	MMEA-WI	$ I_{LC}$-MMEA
MMF10	1.76×10⁻¹	1.48×10⁻¹	1.69×10⁻¹	1.76×10⁻²	2.01×10⁻¹	1.55×10⁻²	1.99×10⁻¹	1.40×10⁻²
MMF10	3.11×10⁻²	2.97×10⁻²	8.40×10⁻³	2.03×10⁻²	4.68×10⁻⁵	3.18×10⁻²	8.00×10⁻³	2.64×10⁻³
MMF11	2.50×10⁻¹	2.50×10⁻¹	2.10×10⁻¹	9.08×10⁻³	2.49×10⁻¹	7.51×10⁻³	2.48×10⁻¹	7.26×10⁻³
MMF11	3.63×10⁻⁴	4.16×10⁻⁴	2.49×10⁻²	9.42×10⁻⁴	3.24×10⁻⁴	3.33×10⁻⁴	2.17×10⁻³	1.05×10⁻⁷
MMF12	2.45×10⁻¹	2.47×10⁻¹	1.90×10⁻¹	3.01×10⁻²	2.45×10⁻¹	3.21×10⁻³	2.44×10⁻¹	2.88×10⁻³
MMF12	9.24×10⁻³	5.35×10⁻⁴	4.29×10⁻²	3.22×10⁻²	2.11×10⁻⁴	2.01×10⁻⁴	3.62×10⁻⁴	2.83×10⁻⁸
MMF13	2.86×10⁻¹	2.86×10⁻¹	2.35×10⁻¹	2.59×10⁻¹	2.53×10⁻¹	8.85×10⁻²	2.52×10⁻¹	8.08×10⁻²
MMF13	9.28×10⁻³	9.59×10⁻³	1.57×10⁻²	2.31×10⁻³	7.32×10⁻⁴	1.59×10⁻²	7.26×10⁻⁴	1.94×10⁻⁵
MMF15	2.44×10⁻¹	2.26×10⁻¹	1.51×10⁻¹	6.69×10⁻²	2.31×10⁻¹	5.36×10⁻²	2.58×10⁻¹	5.54×10⁻²
MMF15	2.05×10⁻²	2.38×10⁻²	1.04×10⁻²	4.36×10⁻³	1.78×10⁻²	1.56×10⁻³	9.91×10⁻⁴	1.00×10⁻⁶
+/–/ =	0/5/0	0/5/0	0/5/0	0/4/1	0/5/0	0/3/2	0/5/0

下载: 导出CSV

参考文献(41)

[1]	公茂果, 焦李成, 杨咚咚, 马文萍. 进化多目标优化算法研究. 软件学报, 2009, 20(2): 271-289 doi: 10.3724/SP.J.1001.2009.00271 Gong Mao-Guo, Jiao Li-Cheng, Yang Dong-Dong, Ma Wen-Ping. Research on evolutionary multi-objective optimization Algorithms. Journal of Software, 2009, 20(2): 271-289 doi: 10.3724/SP.J.1001.2009.00271
[2]	冀俊忠, 邹爱笑, 刘金铎. 基于功能磁共振成像的人脑效应连接网络识别方法综述. 自动化学报, 2021, 47(2): 278-296 doi: 10.16383/j.aas.c190491 Ji Jun-Zhong, Zou Ai-Xiao, Liu Jin-Duo. An overview of identification methods on human brain effective connectivity networks based on functional magnetic resonance imaging. Acta Automatica Sinica, 2021, 47(2): 278-296 doi: 10.16383/j.aas.c190491
[3]	Ouyang T C, Su Z X, Gao B X, Pan M Z, Chen N, Huang H Z. Design and modeling of marine diesel engine multistage waste heat recovery system integrated with flue-gas desulfurization. Energy Conversion and Management, 2019, 196: 1353-68 doi: 10.1016/j.enconman.2019.06.065
[4]	Ma L B, Cheng S, Shi M L, Guo Y N. Angle-based multi-objective evolutionary algorithm based on pruning-power indicator for game map generation. IEEE Transactions on Emerging Topics in Computational Intelligence, 2021, 6(2): 341-354
[5]	岳彩通, 梁静, 瞿博阳, 于坤杰, 王艳丽, 胡毅. 多模态多目标优化综述. 控制与决策, 2021, 36(11): 2577-2588 doi: 10.13195/j.kzyjc.2020.1509 Yue Cai-Tong, Liang Jing, Qu Bo-Yang, Yu Kun-Jie, Wang Yan-Li, Hu Yi. A survey on multimodal multiobjective optimization. Control and Decision, 2021, 36(11): 2577-2588 doi: 10.13195/j.kzyjc.2020.1509
[6]	Schutze O, Vasile M, Coello C A C. Computing the set of Epsilon-efficient solutions in multiobjective space mission design. Journal of Aerospace Computing, Information, and Communication, 2011, 8(3): 53-70 doi: 10.2514/1.46478
[7]	王丽芳, 曾建潮. 基于微粒群算法与模拟退火算法的协同进化方法. 自动化学报, 2006, 32(4): 630-635 doi: 10.16383/j.aas.2006.04.019 Wang Li-Fang, Zeng Jian-Chao. A cooperative evolutionary algorithm based on particle swarm optimization and simulated annealing algorithm. Acta Automatica Sinica, 2006, 32(4): 630-635 doi: 10.16383/j.aas.2006.04.019
[8]	马永杰, 陈敏, 龚影, 程时升, 王甄延. 动态多目标优化进化算法研究进展. 自动化学报, 2020, 46(11): 2302-2318 doi: 10.16383/j.aas.c190489 Ma Yong-Jie, Chen Min, Gong Ying, Cheng Shi-Sheng, Wang Zhen-Yan. Research progress of dynamic multi-objective optimization evolutionary algorithm. Acta Automatica Sinica, 2020, 46(11): 2302-2318 doi: 10.16383/j.aas.c190489
[9]	Tanabe R, Ishibuchi H. A review of evolutionary multimodal multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2019, 24(1): 193-200
[10]	Liu Y P, Ishibuchi H, Nojima Y, Masuyama N, Han Y Y. Searching for local Pareto optimal solutions: A case study on polygon-based problems. In: Proceedings of the IEEE Congress on Evolutionary Computation (CEC). Wellington, New Zealand: IEEE, 2019. 896−903
[11]	Gong W Y, Liao Z W, Mi X Y, Wang L, Guo Y Y. Nonlinear equations solving with intelligent optimization algorithms: A survey. Complex System Modeling and Simulation, 2021, 1(1): 15-32 doi: 10.23919/CSMS.2021.0002
[12]	Lin C M, Tian D X, Duan X T, Zhou J S. 3D environmental perception modeling in the simulated autonomous-driving systems. Complex System Modeling and Simulation, 2021, 1(1): 45-54 doi: 10.23919/CSMS.2021.0004
[13]	Deb K, Tiwari S. Omni-optimizer: A generic evolutionary algorithm for single and multi-objective optimization. European Journal of Operational Research, 2008, 185(3): 1062-87 doi: 10.1016/j.ejor.2006.06.042
[14]	Deb K, Pratap A, Agarwal S, Meyarivan TA. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-97 doi: 10.1109/4235.996017
[15]	Shir O M, Preuss M, Naujoks B, Emmerich M. Enhancing decision space diversity in evolutionary multiobjective algorithms. In: Proceedings of the 5th International Conference on Evolutionary Multi-Criterion Optimization. Nantes, France: Springer, 2009. 95−109
[16]	Liu Y P, Ishibuchi H, Nojima Y, Masuyama N, Shang K. A double-niched evolutionary algorithm and its behavior on polygon-based problems. In: Proceedings of the 15th International Conference on Parallel Problem Solving from Nature. Coimbra, Portugal: Springer, 2018. 262−273
[17]	Liang J J, Yue C T, Qu B Y. Multimodal multi-objective optimization: A preliminary study. In: Proceedings of the IEEE Congress on Evolutionary Computation (CEC). Vancouver, Canada: IEEE, 2016. 2454−2461
[18]	Liang J, Guo Q Q, Yue C T, Qu B Y, Yu K J. A self-organizing multi-objective particle swarm optimization algorithm for multimodal multi-objective problems. In: Proceedings of the 9th International Conference on Swarm Intelligence. Shanghai, China: Springer, 2018. 550−560
[19]	Yue C T, Qu B Y, Liang J. A multiobjective particle swarm optimizer using ring topology for solving multimodal multiobjective problems. IEEE Transactions on Evolutionary Computation, 2017, 22(5): 805-17
[20]	Wang D S, Tan D P, Liu L. Particle swarm optimization algorithm: An overview. Soft Computing, 2018, 22(2): 387-408 doi: 10.1007/s00500-016-2474-6
[21]	Bilal, Pant M, Zaheer H, Garcia-Hernandez L, Abraham A. Differential evolution: A review of more than two decades of research. Engineering Applications of Artificial Intelligence, 2020, 90: Article No. 103479
[22]	Liang J, Xu W W, Yue C T, Yu K J, Song H, Crisalle O D, et al. Multimodal multiobjective optimization with differential evolution. Swarm and Evolutionary Computation, 2019, 44: 1028-59 doi: 10.1016/j.swevo.2018.10.016
[23]	Li Z H, Shi L, Yue C T, Shang Z G, Qu B Y. Differential evolution based on reinforcement learning with fitness ranking for solving multimodal multiobjective problems. warm and Evolutionary Computation, 2019, 49: 234-44 doi: 10.1016/j.swevo.2019.06.010
[24]	Liu Y P, Ishibuchi H, Yen G G, Nojima Y, Masuyama N. Handling imbalance between convergence and diversity in the decision space in evolutionary multimodal multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2019, 24(3): 551-65
[25]	Li W H, Zhang T, Wang R, Ishibuchi H. Weighted indicator-based evolutionary algorithm for multimodal multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2021, 25(6): 1064-78 doi: 10.1109/TEVC.2021.3078441
[26]	Fan Q Q, Ersoy O K. Zoning search with adaptive resource allocating method for balanced and imbalanced multimodal multi-objective optimization. IEEE/CAA Journal of Automatica Sinica, 2021, 8(6): 1163-1176 doi: 10.1109/JAS.2021.1004027
[27]	Li H, Deng J D, Zhang Q F, Sun J Y. Adaptive epsilon dominance in decomposition-based multiobjective evolutionary algorithm. Swarm and Evolutionary Computation, 2019, 45: 52-67 doi: 10.1016/j.swevo.2018.12.007
[28]	Hu Y, Wang J, Liang J, Yu K J, Song H, Guo Q Q, et al. A self-organizing multimodal multi-objective pigeon-inspired optimization algorithm. Science China Information Sciences, 2019, 62(7): 1-7
[29]	Tanabe R, Ishibuchi H. A framework to handle multimodal multiobjective optimization in decomposition-based evolutionary algorithms. IEEE Transactions on Evolutionary Computation, 2019, 24(4): 720-34
[30]	Ulrich T, Bader J, Thiele L. Defining and optimizing indicator-based diversity measures in multiobjective search. In: Proceedings of the 11th International Conference on Parallel Problem Solving from Nature. Krakov, Poland: Springer, 2010. 707−717
[31]	Liang J, Qu B Y, Gong D W, Yue C T. Problem Definitions and Evaluation Criteria for the CEC 2019 Special Session on Multimodal Multiobjective Optimization, Technical Report, School of Electrical Engineering, Zhengzhou University, China, 2019
[32]	Lin Q Z, Lin W, Zhu Z X, Gong M G, Li J Q, Coello C A C. Multimodal multiobjective evolutionary optimization with dual clustering in decision and objective spaces. IEEE Transactions on Evolutionary Computation, 2020, 25(1): 130-44
[33]	Li W H, Yao X Y, Zhang T, Wang R, Wang L. Hierarchy ranking method for multimodal multi-objective optimization with local Pareto fronts. IEEE Transactions on Evolutionary Computation, DOI: 10.1109/TEVC.2022.3155757
[34]	Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm, Technical Report, Department of Electrical Engineering, Swiss Federal Institute of Technology, Switzerland, 2001
[35]	Wang H D, Jiao L C, Yao X. Two_Arch2: An improved two-archive algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2015, 19(4): 524-541 doi: 10.1109/TEVC.2014.2350987
[36]	Tian Y, Cheng R, Zhang X Y, Jin Y C. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization[educational forum]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87 doi: 10.1109/MCI.2017.2742868
[37]	Bader J, Zitzler E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary computation, 2011, 19(1): 45-76 doi: 10.1162/EVCO_a_00009
[38]	Riquelme N, Lücken C V, Baran B. Performance metrics in multi-objective optimization. In: Proceedings of the Latin American Computing Conference (CLEI). Arequipa, Peru: IEEE, 2015. 1−11
[39]	Zhou A M, Zhang Q F, Jin Y C. Approximating the set of Pareto-optimal solutions in both the decision and objective spaces by an estimation of distribution algorithm. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 1167-89 doi: 10.1109/TEVC.2009.2021467
[40]	Liang J, Yue C T, Li G P, Qu B Y, Suganthan P N, Yu K J. Problem Definitions and Evaluation Criteria for the CEC 2021 on Multimodal Multiobjective Path Planning Optimization, Technical Report, School of Electrical Engineering, Zhengzhou University, China, 2020
[41]	Yao X Y, Li W H, Pan X G, Wang R. Multimodal multi-objective evolutionary algorithm for multiple path planning. Computers & Industrial Engineering, 2022, 169: Article No. 108145