基于Petri网的组合设备建模与调度综述

袁凤连; 黄波; 王际鹏; 潘春荣

doi:10.16383/j.aas.c210951

基于Petri网的组合设备建模与调度综述

doi: 10.16383/j.aas.c210951

1.
南京理工大学计算机科学与工程学院南京 210094
2.
湖北工业大学机械工程学院武汉 430068
3.
江西理工大学机电工程学院赣州 341000

详细信息

作者简介:
袁凤连：南京理工大学计算机科学与工程学院博士研究生. 主要研究方向为离散事件系统, Petri网和晶圆制造系统. E-mail: yuanfenglian@njust.edu.cn

黄波：南京理工大学计算机科学与工程学院教授. 主要研究方向为离散事件系统, Petri网, 智能制造和机器人系统. 本文通信作者. E-mail: huangbo@njust.edu.cn

王际鹏：湖北工业大学机械工程学院讲师. 主要研究方向为晶圆制造系统, 智能制造, 离散事件系统和Petri网. E-mail: wangjipeng.tpk@gmail.com

潘春荣：江西理工大学机电工程学院教授. 主要研究方向为制造系统的建模, 仿真, 调度与控制. E-mail: mailto:crpan@jxust.edu.cn

计量
- 文章访问数: 1303
- HTML全文浏览量: 503
- PDF下载量: 415
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-08
- 录用日期: 2022-06-07
- 网络出版日期: 2022-07-22
- 刊出日期: 2023-05-20

A Survey of Modeling and Scheduling of Cluster Tools Based on Petri Nets

1.
School of Computer Science and Engineering, Nanjing University of Science and Technology, Nanjing 210094
2.
School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068
3.
School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000

More Information

Author Bio:
YUAN Feng-Lian　Ph.D. candidate at the School of Computer Science and Engineering, Nanjing University of Science and Technology. Her research interest covers discrete event systems, Petri nets, and wafer fabrication system

HUANG Bo　Professor at the School of Computer Science and Engineering, Nanjing University of Science and Technology. His research interest covers discrete event systems, Petri nets, intelligent manufacturing, and robotic systems. Corresponding author of this paper

WANG Ji-Peng　Lecturer at the School of Mechanical Engineering, Hubei University of Technology. His research interest covers wafer fabrication system, intelligent manufacturing, discrete event systems, and Petri nets

PAN Chun-Rong　Professor at the School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology. His research interest covers modeling, simulation, scheduling, and control of manufacturing systems

摘要

摘要: 组合设备是半导体晶圆制造的核心装备, 其调度与控制优化是半导体制造领域极具挑战性的课题. Petri网因其强大的建模能力和简约的图形化表达优势, 被广泛地应用于组合设备的建模与调度. 对基于Petri网的组合设备建模与调度方法进行综述, 归纳总结了组合设备的结构类型、晶圆流模式、调度策略及Petri网建模方法, 并系统阐述组合设备的7类典型调度问题, 包括驻留时间约束、作业时间波动、晶圆重入加工、多品种晶圆加工、加工模块(Process module, PM)故障、PM清洗和组合设备群. 最后, 讨论了当前组合设备调度存在的挑战及后续可能的研究方向.
- 晶圆制造 /
- Petri网 /
- 组合设备 /
- 建模 /
- 调度
Abstract: Cluster tools are the core equipment of semiconductor wafer manufacturing. Their scheduling and controlling are challenging topics in the field of semiconductor manufacturing. Petri nets have the advantages of powerful modeling capacity and simple graphical descriptions. They are thus widely used in modeling and scheduling of cluster tools. This paper summarizes the research on cluster tools modeling and scheduling based on Petri nets. It presents structures and types of cluster tools, wafer flow patterns, scheduling strategy, and Petri net-based methods. It also addresses seven typical scheduling problems of cluster tools, including wafer residency time constraints, activity time variation, wafer revisiting, multi-type wafer flow patterns, process module (PM) failure, PM cleaning, and multi-cluster tools. Finally, the challenges existing in the cluster tools scheduling field and some possible future research directions are given.
- Wafer fabrication /
- Petri net /
- cluster tool /
- modeling /
- scheduling

HTML全文

图 1 组合设备示意图

Fig. 1 Sketch of cluster tools

下载: 全尺寸图片幻灯片

图 2 线型混合组合设备群

Fig. 2 Linear hybrid multi-cluster tools

下载: 全尺寸图片幻灯片

图 3 树型单臂组合设备群

Fig. 3 Tree-like single-arm multi-cluster tools

下载: 全尺寸图片幻灯片

图 4 组合设备不同晶圆流模式

Fig. 4 Different wafer flow patterns for cluster tools

下载: 全尺寸图片幻灯片

图 5 晶圆流为(1, 1, 1, 1)的拉式策略

Fig. 5 Backward strategy for wafer flow pattern (1, 1, 1, 1)

下载: 全尺寸图片幻灯片

图 6 晶圆流为(1, 1, 1, 1)的交换策略

Fig. 6 Swap strategy for wafer flow pattern (1, 1, 1, 1)

下载: 全尺寸图片幻灯片

图 7 不同晶圆流的POPN模型

Fig. 7 POPN models for different wafer flow patterns

下载: 全尺寸图片幻灯片

图 8 混合2-组合设备的POPN模型

Fig. 8 The POPN model for a hybrid 2-cluster tools

下载: 全尺寸图片幻灯片

图 9 单臂组合设备的ROPN模型

Fig. 9 The ROPN model for a single-arm cluster tool

下载: 全尺寸图片幻灯片

图 10 双臂组合设备的ROPN模型

Fig. 10 The ROPN model for a dual-arm cluster tool

下载: 全尺寸图片幻灯片

图 11 邻接组合设备ROPN模型

Fig. 11 The ROPN model of adjacent cluster tools

下载: 全尺寸图片幻灯片

表 1 拉式与交换策略在组合设备的应用

Table 1 Backward and swap strategy in cluster tools

调度问题	拉式/改进拉式	交换/改进交换
驻留时间约束	文献[16, 19–21, 25, 34–35]	文献[11–12, 17]
作业时间波动	文献[30, 34–36]	文献[29–33]
晶圆重入加工	文献[14, 36, 38–40, 47]	文献[41–46, 48–50]
多品种晶圆	文献[53, 56, 59, 62–63, 66, 72]	文献[54–57, 62–63]
PM故障	文献[76–77]	文献[78–79]
PM清洗	文献[69–70, 72–73]	文献[68, 70–71]

下载: 导出CSV

表 2 组合设备的典型问题及调度方法

Table 2 Typical problems and scheduling methods of cluster tools

调度问题	相关文献	系统特征	Petri网类型	调度方法	调度目标
驻留时间约束	[11]	双臂	POPN	变迁发射顺序	最小周期时间
	[12]	双臂	POPN	变迁发射顺序	可调度性分析
	[13]	单/双臂	POPN	TM无干涉序列	最小周期时间
	[14]	单/双臂	POPN	变迁发射顺序	最小周期时间
	[15]	双臂	POPN	混合整数规划	优化最坏情况下$k$-晶圆周期
	[16–17]	单/双臂, 加工主导	ROPN	TM等待时间	最优1-晶圆周期
	[19–21]	单臂, 暂态过程, 加工主导	ROPN	TM等待时间	优化暂态过程
	[18, 25]	单臂, 传输与加工主导	ROPN	TM等待时间	最小周期时间
作业时间波动	[26]	单/双臂, 驻留时间约束	POPN	延迟TM发射时间	稳态运行
	[27]	单臂	POPN	延迟TM发射时间	恢复到稳态
	[28]	单/双臂, 驻留时间约束	POPN	反馈控制法	最小周期时间
	[29]	双臂, 驻留时间约束	POPN	TM变迁发射顺序	可调度的充分必要条件
	[30]	单/双臂, 驻留时间约束	POPN	自适应调度	最小周期时间
	[31–36]	单/双臂, 驻留时间约束	ROPN	实时调度	最小周期时间
晶圆重入加工	[38]	单臂	POPN	库所不变量分析	稳态的性能分析
	[39]	单臂, 不同晶圆流	POPN	变迁发射顺序	最小周期时间
	[40–44]	单/双臂	ROPN	TM等待时间	最小周期时间
	[45–48]	单/双臂, 驻留时间约束	ROPN	TM等待时间	最小周期时间
	[49–50]	单/双臂, 驻留时间约束和作业时间波动	ROPN	实时调度	最小周期时间
多品种晶圆	[56]	单/双臂, 混流, PM共享	POPN	启发式调度	最小周期时间
	[57]	双臂, 混流, PM共享	POPN	变迁发射顺序	最小周期时间
	[58]	双臂/混流, 并行, 驻留时间约束	POPN	变迁发射顺序	晶圆延迟最少
	[59]	单臂/混流, 驻留时间约束	ROPN	虚拟加工	可调度性
	[53]	单臂/混流	POPN	自循环控制法	系统无死锁运行
	[62]	单/双臂, 切换, 驻留时间约束	POPN	混合整数规划	最少完成时间
	[63]	单/双臂, 切换	POPN	混合整数规划	最少完成时间
PM清洗	[68]	双臂, $m\geq 1$	POPN	启发式调度	最小周期时间
	[69–70]	单/双臂, $m=1$	POPN	部分加载	最小周期时间
	[71]	双臂, $m=1$	POPN	部分加载	最小晶圆延迟
	[72]	单臂, $m=1$, 驻留时间约束	ROPN	线性规划	最小周期时间
	[73]	单臂, $m=1$, 驻留时间约束, 暂态	ROPN	线性规划	优化暂态过程
PM故障	[76–77]	单臂, 驻留时间约束	ROPN	故障响应策略	可行调度
PM故障	[79]	双臂, 重入, 驻留时间约束	ROPN	虚拟晶圆	优化暂态过程

下载: 导出CSV

表 3 不同组合设备群及调度方法

Table 3 Different multi-cluster tools and scheduling methods

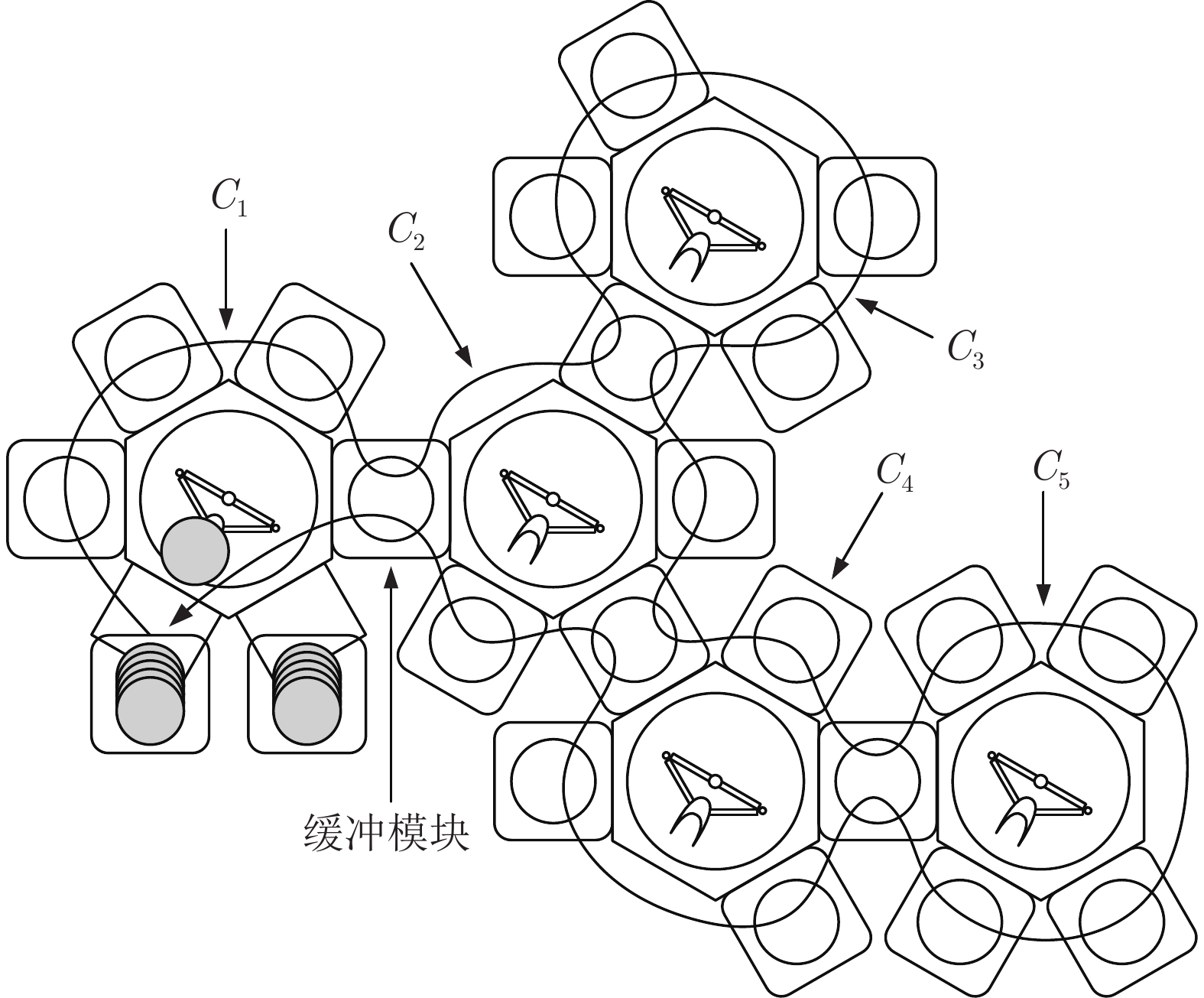
相关文献	拓扑结构	系统特征	缓冲模块容量	运行状态	调度策略	模型方法	调度目标
[80, 82]	线型	单臂	1或2	加工主导	拉式	ROPN	最优1-晶圆周期
[81]	线型	单臂	1	传输主导	拉式	ROPN	最优1-晶圆周期
[83]	线型	单臂	1或2	加工主导	拉式	ROPN	最优缓冲模块配置
[84]	线型	混合	1	加工主导	拉式/交换	ROPN	最优1-晶圆周期
[85]	树型	单臂	1	加工主导	拉式	ROPN	最优1-晶圆周期
[86–87]	树型	混合	1	加工主导	拉式/交换	ROPN	最优1-晶圆周期
[88]	线型	单/双臂	1	无固定	无固定	POPN	最优k-晶圆周期
[89]	线型	混合	1或2	无固定	拉式/交换	分解法	最优k-晶圆周期
[91]	树型	单臂	1或2	无固定	拉式	递归与分解法	最小周期
[92]	线型	单臂, 驻留时间约束	2	加工主导	拉式	ROPN	最优1-晶圆周期
[93]	线型	混合, 驻留时间约束	1	加工主导	拉式/交换	ROPN	最优1-晶圆周期
[94]	线型	单臂, 驻留时间约束	2	无固定	无固定	启发式	最小化最大完工时间
[95]	线型	单/双臂, 驻留时间约束, 暂态	1	加工主导	拉式/交换	线性规划	最优1-晶圆周期
[96]	线型	双臂, 驻留时间约束, 作业时间波动	1	加工主导	交换	实时调度	最优1-晶圆周期
[97]	线型	单/双臂, 驻留时间约束	2	无固定	无固定	改进动态规划	最优Pareto
[98]	线型	单/双臂/混合, 驻留时间约束	2	无固定	无固定	POPN	最优1-晶圆周期

下载: 导出CSV

参考文献(122)

[1]	Bader M E, Hall R P, Strasser G. Integrated processing equipment. Solid State Technology, 1990, 33(5): 149-154
[2]	Burggraaf P. Coping with the high cost of wafer fabs. Semiconductor International, 1995, 38(3): 45-50
[3]	Singer P. The driving forces in cluster tools development. Semiconductor International, 1995, 18(8): 113-118
[4]	Mönch L, Fowler J W, Dauzère-Pérès S, Mason S J, Rose, O. A survey of problems, solution techniques, and future challenges in scheduling semiconductor manufacturing operations. Journal of Scheduling, 2011, 14(6): 583-599
[5]	Huang B, Zhou M C. Supervisory Control and Scheduling of Resource Allocation Systems: Reachability Graph Perspective. New Jersey: John Wiley & Sons, 2020.
[6]	Chen H, Wu N Q, Zhou M C. A novel method for deadlock prevention of AMS by using resource-oriented Petri nets. Information Sciences, 2016, 363: 178-189 doi: 10.1016/j.ins.2015.08.016
[7]	Wu N Q, Zhou M C. System Modeling and Control With Resource-oriented Petri Nets. New York: CRC Press, Taylor & Francis Group, 2009.
[8]	Lee T E. A review of scheduling theory and methods for semiconductor manufacturing cluster tools. In: Proceedings of the Winter Simulation Conference. Miami, USA: IEEE, 2008. 2127−2135
[9]	Pan C R, Zhou M C, Qiao Y, Wu, N Q. Scheduling cluster tools in semiconductor manufacturing: recent advances and challenges. IEEE Transactions on Automation Science and Engineering, 2018, 15(2): 586-601 doi: 10.1109/TASE.2016.2642997
[10]	潘春荣, 王际鹏. 组合设备调度及其优化控制. 长沙: 中南大学出版社, 2020. Pan Chun-Rong, Wang Ji-Peng. Cluster Tool Scheduling and Its Optimal Control. Changsha: Central South University Press, 2020.
[11]	Kim J H, Lee T E, Lee H Y, Park D B. Scheduling analysis of time-constrained dual-armed cluster tools. IEEE Transactions on Semiconductor Manufacturing, 2003, 16(3): 521-534 doi: 10.1109/TSM.2003.815203
[12]	Lee T E, Park S H. An extended event graph with negative places and tokens for time window constraints. IEEE Transactions on Automation Science and Engineering, 2005, 2(4): 319-332 doi: 10.1109/TASE.2005.851236
[13]	Lim Y, Yu T S, Lee T E. A new class of sequences without interferences for cluster tools with tight wafer delay constraints. IEEE Transactions on Automation Science and Engineering, 2019, 16(1): 392-405 doi: 10.1109/TASE.2018.2815157
[14]	Jung C, Lee T E. An efficient mixed integer programming model based on timed Petri nets for diverse complex cluster tool scheduling problems. IEEE Transactions on Semiconductor Manufacturing, 2012, 25(2): 186-199 doi: 10.1109/TSM.2011.2180547
[15]	Roh D H, Lee T G, Lee T E. K-cyclic schedules and the worst-case wafer delay in a dual-armed cluster tool. IEEE Transactions on Semiconductor Manufacturing, 2019, 32(2): 236-249 doi: 10.1109/TSM.2019.2910399
[16]	Wu N Q, Chu C, Chu F, Zhou M C. A Petri net method for schedulability and scheduling problems in single-arm cluster tools with wafer residency time constraints. IEEE Transactions on Semiconductor Manufacturing, 2008, 21(2): 224−236
[17]	Wu N Q, Zhou M C. A closed-form solution for schedulability and optimal scheduling of dual-arm cluster tools with wafer residency time constraint based on steady schedule analysis. IEEE Transactions on Automation Science and Engineering, 2010, 7(2): 303-315 doi: 10.1109/TASE.2008.2008633
[18]	Yang F J, Wu N Q, Qiao Y, Su R, Qu T. Modeling and optimal cyclic scheduling of time-constrained single-robot-arm cluster tools via Petri nets and linear programming. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 50(3): 871-883 doi: 10.1109/TSMC.2017.2755599
[19]	Qiao Y, Zhou M, Wu N Q, Zhu Q H. Scheduling and control of startup process for single-arm cluster tools with residency time constraints. IEEE Transactions on Control Systems Technology, 2017, 25(4): 1243-1256 doi: 10.1109/TCST.2016.2598762
[20]	Zhu Q H, Zhou M C, Qiao Y, Wu N Q. Petri net modeling and scheduling of a close-down process for time-constrained single-arm cluster tools. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(3): 389-400 doi: 10.1109/TSMC.2016.2598303
[21]	Yang F J, Qiao Y, Gao K Z, Wu N Q, Zhu Y T, Ware S I, et al. Efficient approach to scheduling of transient processes for time-constrained single-arm cluster tools with parallel chambers. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 50(10): 3646-3657 doi: 10.1109/TSMC.2018.2852724
[22]	Qiao Y, Zhou M C, Wu N Q, Li Z W, Zhu Q H. Closing-down optimization for single-arm cluster tools subject to wafer residency time constraints. IEEE Transactions on Systems, Man and Cybernetics, 2021, 51(11): 6792-6807 doi: 10.1109/TSMC.2020.2964032
[23]	Zhu Q H, Zhou M C, Qiao Y, Wu N Q, Hou Y. Multiobjective scheduling of dual-blade robotic cells in wafer fabrication. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 50(12): 5015-5023 doi: 10.1109/TSMC.2019.2944866
[24]	Zhu Q H, Zhou M C, Qiao Y, Wu N Q, Hou Y. Post-processing time-aware optimal scheduling of single robotic cluster tools. IEEE/CAA Journal of Automatica Sinica, 2020, 7(2): 597-608 doi: 10.1109/JAS.2020.1003069
[25]	Xiong W Q, Pan C R, Qiao Y, Wu N Q, Hsieh P H. Reducing wafer delay time by robot idle time regulation for single-arm cluster tools. IEEE Transactions on Automation Science and Engineering, 2021, 18(4): 1653-1667 doi: 10.1109/TASE.2020.3014078
[26]	Kim J H, Lee T E. Schedule stabilization and robust timing control for time-constrained cluster tools. In: Proceedings of the IEEE International Conference on Robotics and Automation. Taipei, China: IEEE, 2003. 1039−1044
[27]	Kim J H, Zhou M C, Lee T E. Schedule restoration for single-armed cluster tools. IEEE Transactions on Semiconductor Manufacturing, 2014, 27(3): 388-399 doi: 10.1109/TSM.2014.2315871
[28]	Kim C, Lee T E. Feedback control of cluster tools for regulating wafer delays. IEEE Transactions on Automation Science and Engineering, 2016, 13(2): 1189-1199 doi: 10.1109/TASE.2015.2404921
[29]	Kim J H, Lee TE. Schedulability analysis of time-constrained cluster tools with bounded time variation by an extended Petri net. IEEE Transactions on Automation Science and Engineering, 2008, 5(3): 490-503 doi: 10.1109/TASE.2007.912716
[30]	Lim Y, Yu T S, Lee T E. Adaptive scheduling of cluster tools with wafer delay constraints and process time variation. IEEE Transactions on Automation Science and Engineering, 2020, 17(1): 375-388 doi: 10.1109/TASE.2019.2930046
[31]	Wu N Q, Zhou M C. Analysis of wafer sojourn time in dual-arm cluster tools with residency time constraint and activity time variation. IEEE Transactions on Semiconductor Manufacturing, 2010, 23(1): 53-64 doi: 10.1109/TSM.2009.2039243
[32]	Wu N Q, Zhou M C. Schedulability analysis and optimal scheduling of dual-arm cluster tools with residency time constraint and activity time variation. IEEE Transactions on Automation Science and Engineering, 2012, 9(1): 203-209 doi: 10.1109/TASE.2011.2160452
[33]	Wu N Q, Zhou M C. Modeling, analysis and control of dual-arm cluster tools with residency time constraint and activity time variation based on Petri nets. IEEE Transactions on Automation Science and Engineering, 2012, 9(2): 446-454 doi: 10.1109/TASE.2011.2178023
[34]	Qiao Y, Wu N Q, Zhou M C. Petri net modeling and wafer sojourn time analysis of single-arm cluster tools with residency time constraints and activity time variation. IEEE Transactions on Semiconductor Manufacturing, 2012, 25(3): 432-446 doi: 10.1109/TSM.2012.2199338
[35]	Qiao Y, Wu N Q, Zhou M C. Real-time scheduling of single-arm cluster tools subject to residency time constraints and bounded activity time variation. IEEE Transactions on Automation Science and Engineering, 2012, 9(3): 564-577 doi: 10.1109/TASE.2012.2192476
[36]	Pan C R, Qiao Y, Wu N Q, Zhou M C. A novel algorithm for wafer sojourn time analysis of single-arm cluster tools with wafer residency time constraints and activity time variation. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45(5): 805-818 doi: 10.1109/TSMC.2014.2368995
[37]	Yang F J, Tang X, Wu N Q, Zhang C J, Gao L. Wafer residency time analysis for time-constrained single-robot-arm cluster tools with activity time variation. IEEE Transactions on Control Systems Technology, 2020, 28(4): 1177-1188 doi: 10.1109/TCST.2019.2902329
[38]	Zuberek W M. Cluster tools with chamber revisiting-modeling and analysis using timed Petri nets. IEEE Transactions on Semiconductor Manufacturing, 2004, 17(3): 333-344 doi: 10.1109/TSM.2004.831524
[39]	Lee H Y, Lee T E. Scheduling single-armed cluster tools with reentrant wafer flows. IEEE Transactions on Semiconductor Manufacturing, 2006, 19(2): 226-239 doi: 10.1109/TSM.2006.873402
[40]	Wu N Q, Chu F, Chu C B, Zhou M C. Petri net-based scheduling of single-arm cluster tools with reentrant atomic layer deposition processes. IEEE Transactions on Automation Science and Engineering, 2011, 8(1): 42-55 doi: 10.1109/TASE.2010.2046736
[41]	Wu N Q, Chu F, Chu C B, Zhou M C. Petri net modeling and cycle-time analysis of dual-arm cluster tools with wafer revisiting. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 2013, 43(1): 196-207 doi: 10.1109/TSMCA.2012.2187890
[42]	Qiao Y, Wu N Q, Zhu Q H, Bai L P. Cycle time analysis of dual-arm cluster tools for wafer fabrication processes with multiple wafer revisiting times. Computers & Operations Research, 2015, 53: 252-260
[43]	Wu N Q, Zhou M C, Chu F, Chu C B. A Petri net-based scheduling strategy for dual-arm cluster tools with wafer revisiting. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2013, 43(5): 1182-1194 doi: 10.1109/TSMCA.2012.2230440
[44]	Qiao Y, Wu N Q, Zhou M C. A Petri net-based novel scheduling approach and its cycle time analysis for dual-arm cluster tools with wafer revisiting. IEEE Transactions on Semiconductor Manufacturing, 2013, 26(1): 100-110 doi: 10.1109/TSM.2012.2222945
[45]	Qiao Y, Wu N Q, Zhou M C. Scheduling of dual-arm cluster tools with wafer revisiting and residency time constraints. IEEE Transactions on Industrial Informatics, 2014, 10(1): 286-300 doi: 10.1109/TII.2013.2272702
[46]	Qiao Y, Wu N Q, Zhou M C. Schedulability and scheduling analysis of dual-arm cluster tools with wafer revisiting and residency time constraints based on a novel schedule. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45(3): 472-484 doi: 10.1109/TSMC.2014.2347928
[47]	Yang F J, Wu N Q, Qiao Y, Zhou M C, Li Z W. Scheduling of single-arm cluster tools for an atomic layer deposition process with residency time constraints. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(3): 502-516 doi: 10.1109/TSMC.2015.2507140
[48]	伍乃骐, 乔岩. 应用离散事件系统控制理论求解生产调度的新方法. 控制理论与应用, 2021, 38(11): 1809-1818 doi: 10.7641/CTA.2021.10748 Wu Nai-Qi, Qiao Yan. A novel production scheduling methodology by using discrete event system control theories. Control Theory & Applications, 2021, 38(11): 1809-1818 doi: 10.7641/CTA.2021.10748
[49]	Qiao Y, Wu N Q, Yang F J, Zhou M C, Zhu Q H. Wafer sojourn time fluctuation analysis of time-constrained dual-arm cluster tools with wafer revisiting and activity time variation. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(4): 622-636 doi: 10.1109/TSMC.2016.2600583
[50]	Qiao Y, Wu N Q, Yang F J, Zhou M C, Zhu Q H. Robust scheduling of time-constrained dual-arm cluster tools with wafer revisiting and activity time disturbance. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(6): 1228-1240 doi: 10.1109/TSMC.2017.2721979
[51]	潘春荣, 黎良. 晶圆重入加工的组合设备终止暂态的调度与分析. 控制理论与应用, 2015, 32(5): 655-664 doi: 10.7641/CTA.2015.40780 Pan Chun-Rong, Li Liang. Scheduling and analysis of final transient process for cluster tools with wafer revisiting. Control Theory and Applications, 2015, 32(5): 655-664 doi: 10.7641/CTA.2015.40780
[52]	Pan C R, Qiao Y, Zhou M C, Wu N Q. Scheduling and analysis of start-up transient processes for dual-arm cluster tools with wafer revisiting. IEEE Transactions on Semiconductor Manufacturing, 2015, 28(2): 160-170 doi: 10.1109/TSM.2015.2390644
[53]	Lu Y J, Qiao Y, Pan C R, Chen Y F, Wu N Q, Li Z W, et al. Modeling and control for deadlock-free operation of single-arm cluster tools with concurrently processing multiple wafer types via Petri net. IEEE Access, 2021, 9: 70868-70882 doi: 10.1109/ACCESS.2021.3077503
[54]	Kim H J, Lee J H, Jung C, Lee T E. Closed-form expressions on lot completion time for dual-armed cluster tools with parallel processing modules. IEEE Transactions on Automation Science and Engineering, 2019, 16(2): 898-907 doi: 10.1109/TASE.2018.2874664
[55]	Lee J H, Kim H J, Lee T E. Scheduling cluster tools for concurrent processing of two wafer types. IEEE Transactions on Automation Science and Engineering, 2014, 11(2): 525-536 doi: 10.1109/TASE.2013.2296855
[56]	Lee J H, Kim H J, Lee T E. Scheduling cluster tools for concurrent processing of two wafer types with PM sharing. International Journal of Production Research, 2015, 53(19): 6007-6022 doi: 10.1080/00207543.2015.1035813
[57]	Ko S G, Yu T S, Lee T E. Scheduling dual-armed cluster tools for concurrent processing of multiple wafer types with identical job flows. IEEE Transactions on Automation Science and Engineering, 2019, 16(3): 1058-1070 doi: 10.1109/TASE.2018.2868004
[58]	Ko S G, Yu T S, Lee T E. Wafer delay analysis and workload balancing of parallel chambers for dual-armed cluster tools with multiple wafer types. IEEE Transactions on Automation Science and Engineering, 2021, 18(3): 1516-1526 doi: 10.1109/TASE.2021.3061140
[59]	潘春荣, 王际鹏. 具有多品种晶圆混合加工的单臂组合设备调度. 控制理论与应用, 2016, 33(9): 1171-1181 doi: 10.7641/CTA.2016.60104 Pan Chun-Rong, Wang Ji-Peng. Scheduling for single-armed cluster tools with mixed-processing of multi-variety wafers. Control Theory and Applications, 2016, 33(9): 1171-1181 doi: 10.7641/CTA.2016.60104
[60]	Wang J P, Pan C R, Hu H S, Li L, Zhou Y. A cyclic scheduling approach to single-arm cluster tools with multiple wafer types and residency time constraints. IEEE Transactions on Automation Science and Engineering, 2019, 16(3): 1373-1386 doi: 10.1109/TASE.2018.2878063
[61]	Wang J P, Hu H S, Pan C R, Zhou Y, Li L. Scheduling dual-arm cluster tools with multiple wafer types and residency time constraints. IEEE/CAA Journal of Automatica Sinica, 2020, 7(3): 776-789 doi: 10.1109/JAS.2020.1003150
[62]	Kim H J, Lee J H, Jung C, Lee T E. Scheduling cluster tools with ready time constraints for consecutive small lots. IEEE Transactions on Automation Science and Engineering, 2013, 10(1): 145-159 doi: 10.1109/TASE.2012.2220355
[63]	Lee J H, Kim H J, Lee T E. Scheduling lot switching operations for cluster tools. IEEE Transactions on Semiconductor Manufacturing, 2013, 26(4): 592-601 doi: 10.1109/TSM.2013.2281083
[64]	Nishi T and Matsumoto I. Petri net decomposition approach to deadlock-free and non-cyclic scheduling of dual-armed cluster tools. IEEE Transactions on Automation Science and Engineering, 2015, 12(1):281-294 doi: 10.1109/TASE.2013.2292572
[65]	Lee J H, Kim H J. Makespan analysis of lot switching period in cluster tools. IEEE Transactions on Semiconductor Manufacturing, 2016, 29(2): 127-136 doi: 10.1109/TSM.2016.2530810
[66]	Lee J H, Kim H J. Completion time analysis of wafer lots in single-armed cluster tools with parallel processing modules. IEEE Transactions on Automation Science and Engineering, 2017, 14(4): 1622-1633 doi: 10.1109/TASE.2017.2690443
[67]	Qiao Y, Lu Y J, Li J, Zhang S W, Wu N Q, Liu B. An efficient binary integer programming model for residency time-constrained cluster tools with chamber cleaning requirements. IEEE Transactions on Automation Science and Engineering, 2022, 19(3): 1757−1771
[68]	Kim H, Kim H J, Lee J H, Lee T E. Scheduling dual-armed cluster tools with cleaning processes. International Journal of Production Research, 2013, 51(12): 3671-3687 doi: 10.1080/00207543.2012.758392
[69]	Yu T S, Kim H J, Lee T E. Scheduling single-armed cluster tools with chamber cleaning operations. IEEE Transactions on Automation Science and Engineering, 2018, 15(2): 705-716 doi: 10.1109/TASE.2017.2682271
[70]	Yu T S, Lee T E. Scheduling dual-armed cluster tools with chamber cleaning operations. IEEE transactions on automation science and engineering, 2019, 16(1): 218-228 doi: 10.1109/TASE.2017.2764105
[71]	Yu T S, Lee T E. Wafer delay analysis and control of dual-armed cluster tools with chamber cleaning operations. International Journal of Production Research, 2020, 58(2): 434-447 doi: 10.1080/00207543.2019.1593547
[72]	Yang F J, Wu N Q, Gao K Z, Zhang C J, Zhu Y T, Su R, et al. Efficient approach to cyclic scheduling of single-Arm cluster tools with chamber cleaning operations and wafer residency time constraint. IEEE Transactions on Semiconductor Manufacturing, 2018, 31(2): 196-205 doi: 10.1109/TSM.2018.2811125
[73]	潘春荣, 郭文有. 具有清洗工艺的单臂组合设备终止暂态调度. 控制理论与应用, 2021, 38(6): 784-794 doi: 10.7641/CTA.2021.00603 Pan Chun-Rong, Guo Wen-You. Scheduling of closed-down process for single-arm cluster tools with chamber cleaning operations. Control Theory and Applications, 2021, 38(6): 784-794 doi: 10.7641/CTA.2021.00603
[74]	Li C, Yang F J, Lu Z. Efficient scheduling approaches to time-constrained single-armed cluster tools with condition-based chamber cleaning operations. International Journal of production research, 2022, 60(11), 3555-3568 doi: 10.1080/00207543.2021.1926568
[75]	Yao X, Michael E F-G, Fu M C, Marcus S I. Optimal preventive maintenance scheduling in semiconductor manufacturing. IEEE Transactions on Semiconductor Manufacturing, 2004, 17(3): 345-356 doi: 10.1109/TSM.2004.831948
[76]	Qiao Y, Wu N Q, Pan C, Zhou M C. How to respond to process module failure in residency time-constrained single-arm cluster tools. IEEE Transactions on Semiconductor Manufacturing, 2014, 27(4): 462-474 doi: 10.1109/TSM.2014.2340858
[77]	Qiao Y, Pan C R, Wu N Q, Zhou M C. Response policies to process module failure in single-arm cluster tools subject to wafer residency time constraints. IEEE Transactions on Automation Science and Engineering, 2015, 12(3): 1125-1139 doi: 10.1109/TASE.2014.2312823
[78]	Qiao Y, Zhang S, Wu N Q, Zhou M C, Qu T. Efficient approach to failure response of process module in dual-arm cluster tools with wafer residency time constraints. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(3): 1612-1629 doi: 10.1109/TSMC.2019.2899590
[79]	潘春荣, 付锦超. 基于Petri网的可重入双臂组合设备故障响应策略. 计算机集成制造系统, 2019, 25(12): 3235-3245 doi: 10.13196/j.cims.2019.12.025 Pan Chun-Rong, Fu Jin-Chao. Faiure response policy revisting dual-arm cluster tools based on Petri nets. Computer Integrated Manufacturing Systems, 2019, 25(12): 3235-3245 doi: 10.13196/j.cims.2019.12.025
[80]	Zhu Q H, Wu N Q, Qiao Y, Zhou M C. Petri net-based optimal one-wafer scheduling of single-arm multi-cluster tools in semiconductor manufacturing. IEEE Transactions on Semiconductor Manufacturing, 2013, 26(4): 578-591 doi: 10.1109/TSM.2013.2278378
[81]	Yang F J, Wu N Q, Qiao Y, Zhou M C, Su R, Qu T. Petri net-based efficient determination of optimal schedules for transport-dominant single-arm multi-cluster tools. IEEE Access, 2018, 6: 355-365 doi: 10.1109/ACCESS.2017.2763778
[82]	Yang F J, Wu N Q, Qiao Y, Zhou M C. Optimal one-wafer cyclic scheduling of single-arm multi-cluster tools with two-space buffering modules. IEEE Transactions on Systems, Man and Cybernetics: systems, 2014, 44(12): 1584-1597 doi: 10.1109/TSMC.2014.2327051
[83]	Bai P L, Wu N Q, Li Z W, Zhou M C. Optimal one-wafer cyclic scheduling and buffer space configuration for single-arm multi-cluster tools with linear topology. IEEE Transactions on Systems, Man and Cybernetics, 2016, 46(10): 1456-1467 doi: 10.1109/TSMC.2015.2501232
[84]	Yang F J, Wu N Q, Qiao Y, Zhou M C. Petri net-based polynomially complex approach to optimal one-wafer cyclic scheduling of hybrid multi-cluster tools in semiconductor manufacturing. IEEE Transactions on Systems, Man and Cybernetics, 2014, 44 (12): 1598-1610 doi: 10.1109/TSMC.2014.2318679
[85]	Zhu Q H, Wu N Q, Qiao Y, Zhou M C. Optimal scheduling of complex multi-cluster tools based on timed resource-oriented Petri nets. IEEE Access, 2016, 4: 2096-2109 doi: 10.1109/ACCESS.2016.2549546
[86]	Yang F J, Wu N Q, Qiao Y, Zhou M C. Optimal one-wafer cyclic scheduling of hybrid multirobot cluster tools with tree topology. IEEE Transactions on Systems, Man and Cybernetics, 2018, 48(2):289-298 doi: 10.1109/TSMC.2016.2587697
[87]	Yang F J, Wu N Q, Qiao Y, Su R. Polynomial approach to optimal one-wafer cyclic scheduling of treelike hybrid multi-cluster tools via Petri nets. IEEE/CAA Journal of Automatica Sinica, 2018, 5(1): 270-280 doi: 10.1109/JAS.2017.7510772
[88]	Ding S, Yi J, Zhang M T. Multicluster tools scheduling: an integrated event graph and network model approach. IEEE Transactions on Semiconductor Manufacturing, 2006, 19(3): 339-351 doi: 10.1109/TSM.2006.879414
[89]	Yi J G, Ding S W, Song D Z, Zhang M T. Steady-state throughput and scheduling analysis of multicluster tools: a decomposition approach. IEEE Transactions on Automation Science and Engineering, 2008, 5(2): 321-336 doi: 10.1109/TASE.2007.906678
[90]	Chan W K V, Yi J, Ding S. Optimal scheduling of multicluster tools with constant robot moving times, part I: Two-cluster analysis. IEEE Transactions on Automation Science and Engineering, 2011, 8(1): 5-16 doi: 10.1109/TASE.2010.2046891
[91]	Chan W K V, Ding S W, Yi J G, Song D Z. Optimal scheduling of multicluster tools with constant robot moving times, part Ⅱ: tree-like topology configurations. IEEE Transactions on Automation Science and Engineering, 2011, 8(1): 17-28 doi: 10.1109/TASE.2010.2046893
[92]	Zhu Q H, Wu N Q, Qiao Y, Zhou M C. Scheduling of single-arm multi-cluster tools with wafer residency time constraints in semiconductor manufacturing. IEEE Transactions on Semiconductor Manufacturing, 2015, 28(1): 117-125 doi: 10.1109/TSM.2014.2375880
[93]	Yang F J, Wu N Q, Qiao Y, Zhou M C. Optimal one-wafer cyclic scheduling of time-constrained hybrid multicluster tools via Petri nets. IEEE Transactions on Systems, Man and Cybernetics, 2017, 47(11): 2920-2932 doi: 10.1109/TSMC.2016.2531697
[94]	Liu M X, Zhou B H. Modelling and scheduling analysis of multi-cluster tools with residency constraints based on time constraint sets. International Journal of Production Research, 2013, 51(16): 4835-485 doi: 10.1080/00207543.2013.774490
[95]	Zhu Q H, Qiao Y, Wu N Q. Optimal integrated schedule of entire process of dual-blade multi-cluster tools from start-up to close-down. IEEE/CAA Journal of Automatica Sinica, 2019, 6(2): 553-565 doi: 10.1109/JAS.2019.1911411
[96]	Yang F J, Wu N Q, Qiao Y, Su R, Zhang C J. Wafer sojourn time fluctuation analysis for time-constrained dual-arm multi-cluster tools with activity time variation. International Journal of Computer Integrated Manufacturing, 2021, 34(7−8): 734−751
[97]	Yan Y, Wang H G, Tao Q H, Fan W H, Lin T Y, Xiao Y Y. Noncyclic scheduling of multi-cluster tools with residency constraints based on pareto optimization. IEEE Transactions on Semiconductor Manufacturing, 2020, 33(3): 476-486 doi: 10.1109/TSM.2020.2998734
[98]	Bao T P, Wang H G. Cyclic scheduling of multi-cluster tools based on mixed integer programming. IEEE Transactions on Semiconductor Manufacturing, 2017, 30(4): 515-525 doi: 10.1109/TSM.2017.2733559
[99]	Nishi T, Watanabe Y and Sakai M. An efficient deadlock prevention policy for noncyclic scheduling of multicluster tools. IEEE Transactions on Automation Science and Engineering, 2018, 15(4): 1677-1691 doi: 10.1109/TASE.2017.2771751
[100]	López M J, Wood S C. Systems of multiple cluster tools: configuration, reliability, and performance. IEEE Transactions on Semiconductor Manufacturing, 2003, 16(2): 170-178 doi: 10.1109/TSM.2003.810936
[101]	Dawande M, Sriskandarajah C, Sethi S. On throughput maximization in constant travel-time robotic cell. Manufacturing and Service Operations Management, 2002, 4(4): 296-312 doi: 10.1287/msom.4.4.296.5731
[102]	Venkatesh S, Davenport R, Foxhoven P, Nulman J. A steady-state throughput analysis of cluster tools: dual-blade versus single-blade robots. IEEE Transactions on Semiconductor Manufacturing, 1997, 10(4): 418-424 doi: 10.1109/66.641483
[103]	Sethi, S P, Sidney J B, Sriskandarajah C. Scheduling in dual gripper robotic cell for productivity gains. IEEE Transactions on Robotics & Automation, 2001, 17(3): 324-341
[104]	Kim H J, Lee J H, Lee T E. Time-feasible reachability tree for noncyclic scheduling of timed Petri nets. IEEE Transactions on Automation Science and Engineering, 2015, 12(3): 1007-1016 doi: 10.1109/TASE.2014.2313979
[105]	Jung C, Kim H J, Lee T E. A branch and bound algorithm for cyclic scheduling of timed Petri nets. IEEE Transactions on Automation Science and Engineering, 2015, 12(1): 309-323 doi: 10.1109/TASE.2013.2285221
[106]	Kim H J, Lee J H, Lee T E. Noncyclic scheduling of cluster tools with a branch and bound algorithm. IEEE Transactions on Automation Science and Engineering, 2015, 12(2): 690-700 doi: 10.1109/TASE.2013.2293552
[107]	马永杰, 陈敏, 龚影, 程时升, 王甄延. 动态多目标优化进化算法研究进展. 自动化学报, 2020, 46(11): 2302-2318 doi: 10.16383/j.aas.c190489 Ma Yong-Jie, Chen Min, Gong Ying, Chen Shi-Sheng, Wang Zhen-Yan. Research progress of dynamic multi-objective optimization evolutionnary algorithm. Acta Automatica Sinica, 2020, 46(11): 2302-2318 doi: 10.16383/j.aas.c190489
[108]	Kim H J, Lee J H. Scheduling of dual-gripper robotic cells with reinforcement learning. IEEE Transactions on Automation Science and Engineering, 2022, 19(2): 1120-1136 doi: 10.1109/TASE.2020.3047924
[109]	Huang B, Zhou M C, Abusorrah A, Sedraoui K. Scheduling robotic cellular manufacturing systems with timed Petri net, A$.$ search, and admissible heuristic function. IEEE Transactions on Automation Science and Engineering*, 2022, 19(1): 243-250
[110]	Huang B, Zhou M C. Symbolic scheduling of robotic cellular manufacturing systems with timed Petri nets. IEEE Transactions on Control Systems Technology, 2022,19(1) - 243～250 doi: 10.1109/TASE.2020.3026351
[111]	Han L B, Xing K Y, Chen X, Xiong F L. A Petri net-based particle swarm optimization approach for scheduling deadlock-prone flexible manufacturing systems. Journal of Intelligent Manufacturing, 2018, 29(5): 1083-1096 doi: 10.1007/s10845-015-1161-2
[112]	Feng Y X, Xing K Y, Liu H X, Wu Y C. Two-stage design method of robust deadlock control for automated manufacturing systems with a type of unreliable resources. Information Sciences, 2019, 484: 286-301 doi: 10.1016/j.ins.2019.01.061
[113]	Chen Y F and Li Z W. Design of a maximally permissive liveness enforcing supervisor with a compressed supervisory structure for flexible manufacturing systems. Automatica, 2011, 47(5): 1028-1034 doi: 10.1016/j.automatica.2011.01.070
[114]	Huang B, Zhou M C, Wang C, Abusorrah A, Al-Turki A. Deadlock-free supervisor design for robotic manufacturing cells with uncontrollable and unobservable events. IEEE/CAA Journal of Automatica Sinica, 2021, 8(3): 597-605 doi: 10.1109/JAS.2020.1003207
[115]	Huang B, Zhou M C, Huang Y S, Yang Y W. Supervisor synthesis for FMS based on critical activity places. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(5): 881-890 doi: 10.1109/TSMC.2017.2732442
[116]	Huang B, Zhou M C, Zhang P Y, Yang J. Speedup techniques for multiobjective integer programs in designing optimal and structurally simple supervisors of AMS. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(1): 77-88 doi: 10.1109/TSMC.2016.2587671
[117]	Huang B, Zhou M C, Zhang G X, Ammari A C, Ahmed A, Fayoumi A G. Lexicographic multiobjective integer programming for optimal and structurally minimal Petri net supervisors of automated manufacturing systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45(11): 1459-1470 doi: 10.1109/TSMC.2015.2415765
[118]	Huang B, Zhou M C, Zhang G X. Synthesis of Petri net supervisors for FMS via redundant constraint elimination. Automatica, 2015, 61: 156-163 doi: 10.1016/j.automatica.2015.08.011
[119]	Rui L l, Chen X S, Gao Z P, Li W J, Qiu X S, Meng L M. Petri net-based reliability assessment and migration optimization strategy of SFC. IEEE Transactions on Network and Service Management, 2021, 18(1): 167-181 doi: 10.1109/TNSM.2020.3045705
[120]	Luo J C, Zhou M C, Wang J Q. A place-timed Petri net-based method to avoid deadlock and conflict in railway networks. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(8): 10763−10772
[121]	李勇, 李坤成, 孙柏青, 张秋豪, 王义娜, 杨俊友. 智能体Petri网融合的多机器人多任务协调框架. 自动化学报, 2021, 47(8): 2029-2049 Li Yong, Li Kun-Cheng, Sun Bai-Qing, Zhang Qiu-Hao, Wang Yi-Na, Yang Jun-You. Multi-robot-multi-task coordination framework based on the integration of intelligent agent and Petri net. Acta Automatica Sinica, 2021, 47(8): 2029-2049
[122]	Zhang S W, Wu N Q, Li Z W, Qu T, Li C D. Petri net-based approach to short-term scheduling of crude oil operations with less tank requirement. Information Sciences, 2017, 417: 247-261 doi: 10.1016/j.ins.2017.07.009