考虑输出约束的冗余驱动绳索并联机器人预设性能控制

陈正升; 程玉虎; 王雪松

doi:10.16383/j.aas.c210949

考虑输出约束的冗余驱动绳索并联机器人预设性能控制

doi: 10.16383/j.aas.c210949

陈正升^{1, 2,},
程玉虎^{1, 2,},
王雪松^{1, 2,}

1.
地下空间智能控制教育部工程研究中心徐州 221116
2.
中国矿业大学信息与控制工程学院徐州 221116

基金项目: 国家自然科学基金(61903347, 61976215, 62176259), 江苏省自然科学基金(BK20200086)资助

详细信息

作者简介:
陈正升：中国矿业大学信息与控制工程学院讲师. 2016年获得哈尔滨工业大学博士学位. 主要研究方向为机器人动力学建模与控制. E-mail: chenzhengsheng@cumt.edu.cn

程玉虎：中国矿业大学信息与控制工程学院教授. 2005年获得中国科学院自动化研究所博士学位. 主要研究方向为机器学习, 智能优化与控制. E-mail: chengyuhu@163.com

王雪松：中国矿业大学信息与控制工程学院教授. 2002年获得中国矿业大学博士学位. 主要研究方向为机器学习, 模式识别. 本文通信作者. E-mail: wangxuesongcumt@163.com

计量
- 文章访问数: 908
- HTML全文浏览量: 122
- PDF下载量: 298
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-08
- 录用日期: 2022-01-11
- 网络出版日期: 2022-05-06
- 刊出日期: 2022-07-01

Prescribed Performance Control of Redundantly-actuated Cable Driving Parallel Robots Subjected to Output Constraint

CHEN Zheng-Sheng^{1, 2
,},
CHENG Yu-Hu^{1, 2
,},
WANG Xue-Song^{1, 2
,}

1.
Engineering Research Center of Intelligent Control for Underground Space, Ministry of Education, Xuzhou 221116
2.
School of Information and Control Engineering, China University of Mining and Technology, Xuzhou 221116

Funds: Supported by National Natural Science Foundation of China (61903347, 61976215, 62176259) and Natural Science Foundation of Jiangsu Province (BK20200086)

More Information

Author Bio:
CHEN Zheng-Sheng　Lecturer at the School of Information and Control Engineering, China University of Mining and Technology. He received his Ph.D. degree from Harbin Institute of Technology in 2016. His main research interest is dynamic modeling and control of robotics

CHENG Yu-Hu　Professor at the School of Information and Control Engineering, China University of Mining and Technology. He received his Ph.D. degree from the Institute of Automation, Chinese Academy of Sciences in 2005. His research interest covers machining learning, intelligent optimization and control

WANG Xue-Song　Professor at the School of Information and Control Engineering, China University of Mining and Technology. She received her Ph.D. degree from China University of Mining and Technology in 2002. Her research interest covers machine learning and pattern recognition. Corresponding author of this paper

摘要

摘要: 提出一种考虑输出约束的冗余驱动绳索并联机器人(Redundantly-actuated cable driving parallel robots, RCDPRs)预设性能有限时间控制算法. 首先, 采用Newton-Euler方程推导系统动力学模型, 并建立绳索拉力优化模型保证系统正常工作; 其次, 将输出约束问题转化为位置跟踪误差的坐标变换问题, 设计给定时间衰减函数与非对称变换函数, 将约束形式的跟踪误差转化为无约束变量, 实现给定时间的输出约束; 然后, 针对滑模控制的抖振问题, 在预设性能控制中采用模型不确定与扰动估计器进行扰动估计, 并通过自适应方法对扰动估计误差进行补偿; 以此为基础, 提出一种基于精度驱动且在分段点处三阶连续的终端滑模面进行控制算法设计; 最后, 采用Lyapunov函数证明算法的有限时间收敛特性, 并以7自由度冗余驱动绳索并联机器人为控制对象进行仿真研究, 对算法进行验证.
- 滑模控制 /
- 有限时间收敛 /
- 输出约束 /
- 给定时间预设性能控制 /
- 冗余驱动绳索并联机器人
Abstract: This paper proposed a prescribed performance finite-time control algorithm of redundantly-actuated cable driving parallel robots (RCDPRs) considering output constraint. Firstly, the Newton-Euler equation is employed to establish the dynamic model of the system, and the optimization model for all cables was constructed to guarantee properly operation. Then, the output constraint problem is transformed into coordinate transformation problem of the position tracking errors, also the appointed time decay function and the asymmetric transformation function are designed to transform the tracking errors into unconstraint variables, thus the output constraint is realized. Meanwhile, aiming at the chattering problem, the uncertainty and disturbance estimator is proposed, and the adaptive algorithm is designed to compensate the estimation error, on the basis of which, the accuracy-driven terminal sliding mode surface with three-order continuity on the segment point is proposed and applied in controller design. Finally, the Lyapunov function is used to prove that the proposed algorithm has finite-time convergence characteristics, and a seven-degrees-of-freedom RCDPR is used as the control object for simulation research to demonstrate the effectiveness of the proposed controller.
- Sliding mode control /
- finite-time convergence /
- output constraint /
- appointed time prescribed performance control /
- redundantly-actuated cable driving parallel robots (RCDPRs)

HTML全文

图 1 冗余驱动绳索并联机器人结构原理图

Fig. 1 Structural schematic diagram of the RCDPR

下载: 全尺寸图片幻灯片

图 2 带有7个驱动绳索的RCDPR

Fig. 2 The RCDPR with 7 driving cables

下载: 全尺寸图片幻灯片

图 3 位置与角度跟踪误差

Fig. 3 Positional and angular tracking errors

下载: 全尺寸图片幻灯片

图 4 速度跟踪误差

Fig. 4 Velocity tracking error

下载: 全尺寸图片幻灯片

图 5 冗余驱动绳索并联机器人驱动力矩及其差值

Fig. 5 Torques and torque deviations of the RCDPR

下载: 全尺寸图片幻灯片

图 6 采用本文算法时RCDPR各绳索拉力

Fig. 6 RCDPR＇s pull forces of the proposed controller

下载: 全尺寸图片幻灯片

图 7 采用本文算法时自适应项系数

Fig. 7 Adaptive coefficients of the proposed controller

下载: 全尺寸图片幻灯片

图 8 采用ASTUDESMC时自适应项系数

Fig. 8 Adaptive coefficients of ASTUDESMC

下载: 全尺寸图片幻灯片

图 9 基于跟踪误差e的滑模面数值

Fig. 9 Sliding mode surface for tracking error e

下载: 全尺寸图片幻灯片

图 10 基于跟踪误差z的滑模面数值

Fig. 10 Sliding mode surface for tracking error z

下载: 全尺寸图片幻灯片

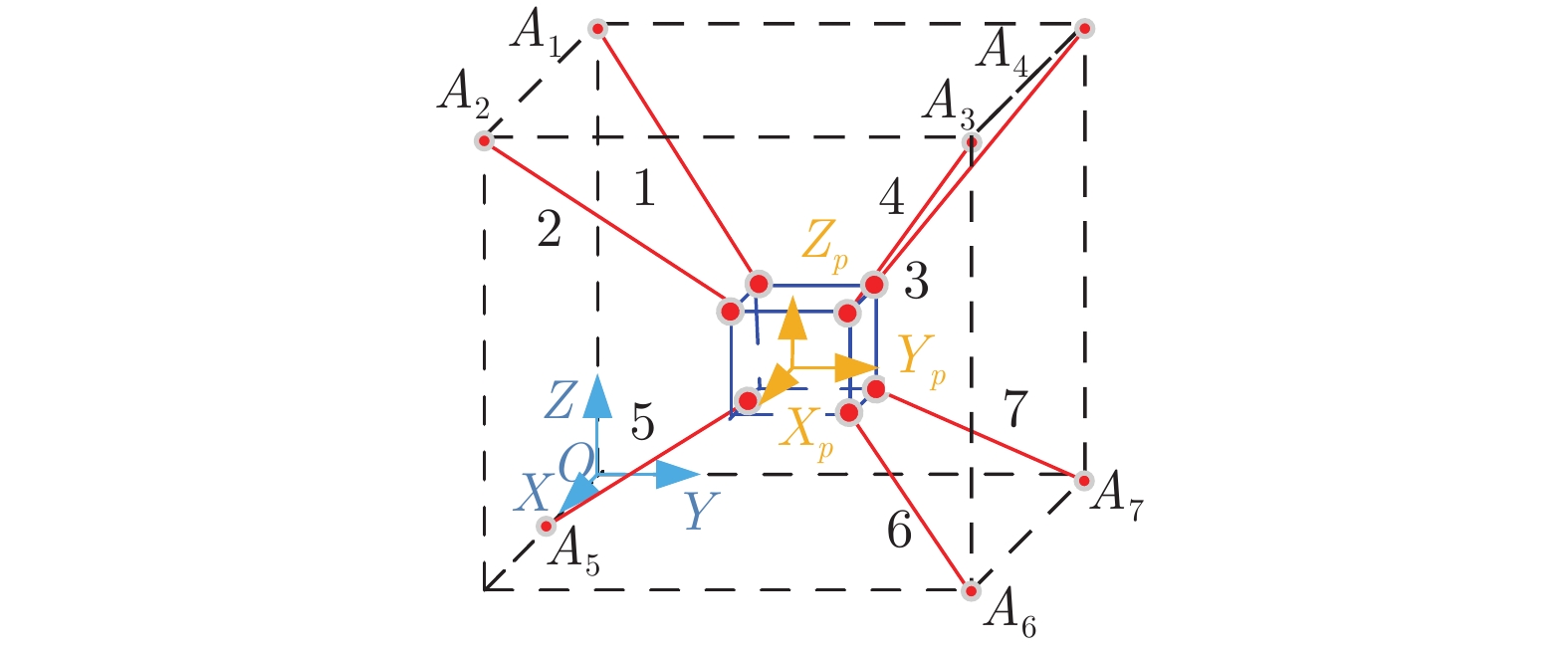
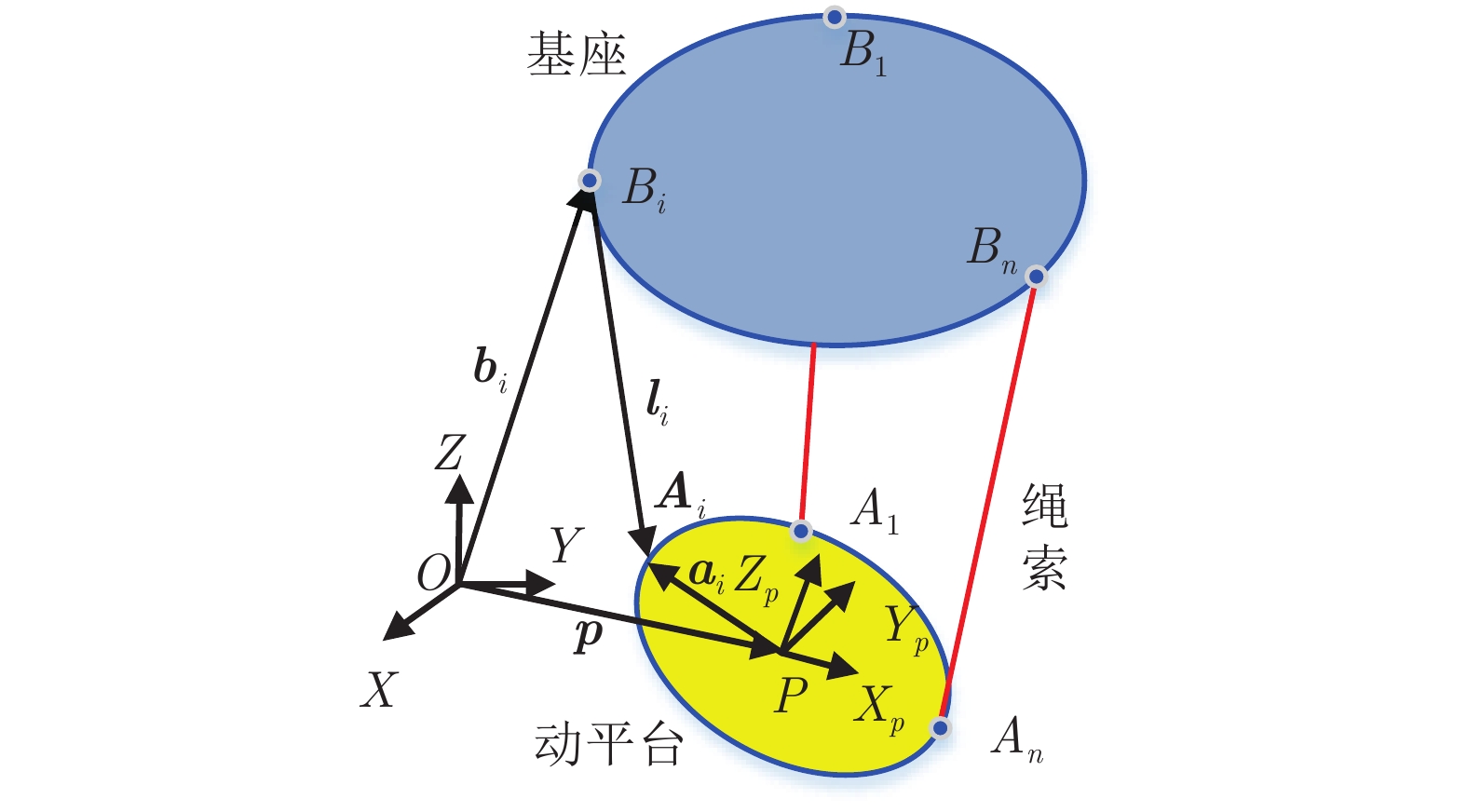
表 1 RCDPR运动学参数(mm)

Table 1 Kinematic parameters of the RCDPR (mm)

参数	数值	参数	数值
b₁	[0, 0, 1000]	a₁	[−150, −100, 50]
b₂	[100, 0, 1000]	a₂	[150, −100, 50]
b₃	[1000, 1000, 1000]	a₃	[150, 100, 50]
b₄	[0, 1000, 1000]	a₄	[−150, 100, 50]
b₅	[500, 0, 0]	a₅	[0, −100, −50]
b₆	[1000, 1000, 0]	a₆	[150, 100, −50]
b₇	[0, 1000, 0]	a₇	[−150, 100, 50]
r	20

下载: 导出CSV

表 2 RCDPR惯性参数

Table 2 Inertial parameters of the RCDPR

参数	描述	数值
m_p	动平台质量	1.67 kg
I_p	动平台转动惯量矩阵	diag{2.78×10⁴, 5.56×10⁴, 7.26×10⁴} kg·mm²
I_b	滑轮转动惯量	1.2×10⁴kg·mm²

下载: 导出CSV

表 3 各控制器参数

Table 3 Parameters of all controllers

控制器	参数	值
PPSMC	K₁, K₂, α₁, α₂, α₃, Δ₁₁, Δ₁₂, Δ₁₃, Δ₁₄, Δ₁₅, Δ₁₆, β₄, β₅, K₃, γ₀, T, λ₁, λ₂, T_e, ε_1i, ε_2i, μ₀, μ_∞, k	100I₆, 50I₆, 0.5, 1.5, 1.8, 0.01, 0.01, 0.01, 0.001, 0.001, 0.001, 5, 5, 10I₆, 10, 0.001 s, 0.001, 0.01, 0.2 s, 0.5, 1, [0.2, 0.2, 0.2, 0.02, 0.02, 0.02]^T, 0.002[1, 1, 1, 0.01, 0.01, 0.01]^T, 30
ASTUDESMC	k₁, k₂, α_i, T, ε, $ {\omega _1}\sqrt {{{{\gamma _1}} \mathord{\left/ {\vphantom {{{\gamma _1}} 2}} \right. } 2}} $, λ+4ε²	100I₆, 50I₆, 0.5, 0.001 s, 0.5, 500, 10
TDENFTSMC	ρ₁, ρ₂, α_1i, α_2i, k₁, k₂, L	100I₆, 50I₆, 0.5, 1.8, 0.001 s
UDESMC	c, 1/a, k	160, 0.001 s, 20

下载: 导出CSV

参考文献(38)

[1]	Begey J, Cuvillon L, Lesellier M, Gouttefarde M, Gangloff J. Dynamic control of parallel robots driven by flexible cables and actuated by position-controlled winches. IEEE Transactions on Robotics, 2019, 35(1): 286-293 doi: 10.1109/TRO.2018.2875415
[2]	姜雷杰, 高丙团, 刘传德, 朱振宇. 2-DOF绳索驱动并联机构轨迹跟踪控制. 控制与决策, 2019, 34(5): 1103-1108 Jiang Lei-Jie, Gao Bing-Tuan, Liu Chuan-De, Zhu Zhen-Yu. Trajectory tracking control of a 2-DOF cable-driven parallel mechanism. Control and Decision, 2019, 34(5): 1103-1108
[3]	Asl HJ, Janabi-Sharifi F. Adaptive neural network control of cable-driven parallel robots with input saturation. Engineering Applications of Artificial Intelligence, 2017, 65: 252-260 doi: 10.1016/j.engappai.2017.05.011
[4]	Chellal R, Cuvillon L, Laroche E. Model identification and vision-based H-infinity position control of 6-DoF cable-driven parallel robots. International Journal of Control, 2017, 90(4): 684-701 doi: 10.1080/00207179.2016.1220623
[5]	黄攀峰, 胡永新, 王东科, 孟中杰, 刘正雄. 空间绳系机器人目标抓捕鲁棒自适应控制器设计. 自动化学报, 2017, 43(4): 538-547 Huang Pan-Feng, Hu Yong-Xin, Wang Dong-Ke, Meng Zhong-Jie, Liu Zheng-Xiong. Capturing the target for a tethered space robot using robust adaptive controller. Acta Automatica Sinica, 2017, 43(4): 538−547
[6]	Wang Y, Liu L, Wang D, Ju F, Chen B. Time-delay control using a novel nonlinear adaptive law for accurate trajectory tracking of cable-driven robots. IEEE Transactions on Industrial Informatics, 2020, 16(8): 5234-5243 doi: 10.1109/TII.2019.2951741
[7]	Chen Z, Wang X, Cheng Y. Adaptive finite-time disturbance observer-based recursive fractional-order sliding mode control of redundantly actuated cable driving parallel robots under disturbances and input saturation. Journal of Vibration and Control, DOI: 10.1177/10775463211051460
[8]	Man Z, Paplinski AP, Wu HR. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Transactions on Automatic Control, 1994, 39(12): 2464-2469 doi: 10.1109/9.362847
[9]	Zheng N J, Zhang Y, Guo Y B, Zhang X H. Hierarchical fast terminal sliding mode control for a self-balancing two-wheeled robot on uneven terrains. In: Proceedings of the 36th Chinese Control Conference (CCC). Dalian, China: IEEE, 2017. 4762−4767
[10]	Feng Y, Yu XH, Man ZH. Non-singular terminal sliding mode control of rigid manipulators. Automatica, 2002, 38(12): 2159-2167 doi: 10.1016/S0005-1098(02)00147-4
[11]	张国庆, 黄晨峰, 吴晓雪, 张显库. 考虑伺服系统增益不确定的船舶动力定位自适应有限时间控制. 自动化学报, 2018, 44(10): 1907-1912 Zhang Guo-Qing, Huang Chen-Feng, Wu Xiao-Xue, Zhang Xian-Ku. Adaptive finite time dynamic positioning control of fully-actuated ship with servo system uncertainties. Acta Automatica Sinica, 2018, 44(10): 1907−1912
[12]	Van M, Ge SS, Ren HL. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Transactions on Cybernetics, 2017, 47(7): 1681-1693 doi: 10.1109/TCYB.2016.2555307
[13]	Zhai JY, Song ZB. Adaptive sliding mode trajectory tracking control for wheeled mobile robots. International Journal of Control, 2019, 92(10): 2255-2262 doi: 10.1080/00207179.2018.1436194
[14]	Wang Y, Zhu K, Chen B, Jin M. Model-free continuous nonsingular fast terminal sliding mode control for cable-driven manipulators. ISA transactions, 2020, 98: 483-495 doi: 10.1016/j.isatra.2019.08.046
[15]	李德昀, 徐德刚, 桂卫华. 基于时间延时估计和自适应模糊滑模控制器的双机械臂协同阻抗控制. 控制与决策, 2021, 36(6): 1311-1323 Li D-Y, Xu D-G, Gui W-H. Coordinated impedance control for dual-arm robots based on time delay estimation and adaptive fuzzy sliding mode controller. Control and Decision, 2021, 36(6): 1311-1323
[16]	李中奇, 金柏, 杨辉, 谭畅, 付雅婷. 高速动车组强耦合模型的分布式滑模控制策略. 自动化学报, 2020, 46(3): 495−508 Li Zhong-Qi, Jin Bai, Yang Hui, Tan Chang, Fu Ya-Ting. Distributed sliding mode control strategy for high-speed EMU strong coupling model. Acta Automatica Sinica, 2020, 46(3): 495-508
[17]	Patre BM, Londhe PS, Waghmare LM, Mohan S. Disturbance estimator based non-singular fast fuzzy terminal sliding mode control of an autonomous underwater vehicle. Ocean Engineering, 2018, 159: 372-387 doi: 10.1016/j.oceaneng.2018.03.082
[18]	李繁飙, 黄培铭, 阳春华, 廖力清, 桂卫华. 基于非线性干扰观测器的飞机全电刹车系统滑模控制设计. 自动化学报, 2021, 47(11): 2557-2569 Li Fan-Biao, Huang Pei-Ming, Yang Chun-Hua, Liao Li-Qing, Gui Wei-Hua. Sliding mode control design of aircraft electric brake system based on nonlinear disturbance observer. Acta Automatica Sinica, 2021, 47(11): 2557−2569
[19]	Wang P, Zhang D, Lu B. ESO based sliding mode control for the welding robot with backstepping. International Journal of Control, 2020, 94(12): 3322-3331
[20]	Wang Y, Yan F, Chen J, Ju F, Chen B. A new adaptive time-delay control scheme for cable-driven manipulators. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3469-3481 doi: 10.1109/TII.2018.2876605
[21]	刘凡, 杨洪勇, 杨怡泽, 李玉玲, 刘远山. 带有不匹配干扰的多智能体系统有限时间积分滑模控制. 自动化学报, 2019, 45(4): 749-758 Liu Fan, Yang Hong-Yong, Yang Yi-Ze, Li Yu-Ling, Liu Yuan-Shan. Finite-time integral sliding-mode control for multi-agent systems with mismatched disturbances. Acta Automatica Sinica, 2019, 45(4): 749−758
[22]	Kolhe JP, Shaheed M, Chandar TS, Talole SE. Robust control of robot manipulators based on uncertainty and disturbance estimation. International Journal of Robust and Nonlinear Control, 2013, 23(1): 104-122 doi: 10.1002/rnc.1823
[23]	Lu Q, Ren BB, Parameswaran S. Uncertainty and disturbance estimator-based global trajectory tracking control for a quadrotor. IEEE/ASME Transactions on Mechatronics, 2020, 25(3): 1519-1530 doi: 10.1109/TMECH.2020.2978529
[24]	Dong YT, Ren BB. UDE-based variable impedance control of uncertain robot systems. IEEE Transactions on Systems Man Cybernetics-Systems, 2019, 49(12): 2487-2498 doi: 10.1109/TSMC.2017.2767566
[25]	Nam Y J. Comparison study of time delay control (TDC) and uncertainty and disturbance estimation (UDE) based control. In: Proceedings of the 16th International Conference on Control, Automation and Systems (ICCAS). Gyeongju, South Korea: IEEE, 2016. 749−756
[26]	Zhou Z, Zhu F, Xu D, Guo S, Liu T, Li X. Robust free‐time‐stable fault tolerant control for rigid satellite attitude system with output constraint. International Journal of Robust and Nonlinear Control, 2021, 31(16): 7587–7760 doi: 10.1002/rnc.5703
[27]	李新凯, 张宏立, 范文慧. 基于时变障碍李雅普诺夫函数的变体无人机有限时间控制. 自动化学报, 2022, 48(6): 1530−1542 Li Xin-Kai, Zhang Hong-Li, Fan Wen-Hui. Finite-time control for morphing aerospace vehicle based on time-varying barrier Lyapunov function. Acta Automatica Sinica, 2022, 48(6): 1530−1542
[28]	Wu Y Y, Zhang Y, Wu A G. Preassigned finite-time attitude control for spacecraft based on time-varying barrier Lyapunov functions. Aerospace Science and Technology, 2021, 108: Article No. 106331
[29]	Wu X, Zheng W, Zhou X, Shao S. Adaptive dynamic surface and sliding mode tracking control for uncertain QUAV with time-varying load and appointed-time prescribed performance. Journal of the Franklin Institute, 2021, 358(8): 4178-4208 doi: 10.1016/j.jfranklin.2021.03.018
[30]	Shabana A A. Dynamics of Multibody Systems. Cambridge: Cambridge University Press, 2020.
[31]	Merlet J P. Parallel Robots. Dordrecht: Springer Science & Business Media, 2005.
[32]	Wu Y, Li G, Zuo Z, Liu X, Xu P. Practical Fixed-time Position Tracking Control of Permanent Magnet DC Torque Motor Systems. IEEE/ASME Transactions on Mechatronics, 2021, 26(1): 563-573
[33]	Yu J, Shi P, Zhao L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica, 2018, 92: 173-180 doi: 10.1016/j.automatica.2018.03.033
[34]	Kuperman A, Zhong Q-C. Robust control of uncertain nonlinear systems with state delays based on an uncertainty and disturbance estimator. International Journal of Robust and Nonlinear Control, 2011, 21(1): 79-92 doi: 10.1002/rnc.1578
[35]	Tian Z, Zhong Q-C, Ren B, Yuan J. Stabilisability analysis and design of UDE-based robust control. IET Control Theory and Applications, 2019, 13(10): 1445-1453 doi: 10.1049/iet-cta.2018.6012
[36]	Zheng Z, Feroskhan M. Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances. IEEE/ASME Transactions on Mechatronics, 2017, 22(6): 2564-2575 doi: 10.1109/TMECH.2017.2756110
[37]	Shtessel Y B, Moreno J A, Plestan F, Fridman L M, Poznyak A S. Super-twisting adaptive sliding mode control: A Lyapunov design. In: Proceedings of the 2010 IEEE Conference on Decision and Control (CDC). Atlanta, GA, USA: IEEE, 2010. 5109−5113
[38]	Tian Z, Lyu Z, Yuan J, Wang C. UDE-based sliding mode control of DC–DC power converters with uncertainties. Control Engineering Practice, 2019, 83: 116-128 doi: 10.1016/j.conengprac.2018.10.019