Combustion States Recognition Method of MSWI Process Based on Mixed Data Enhancement
-
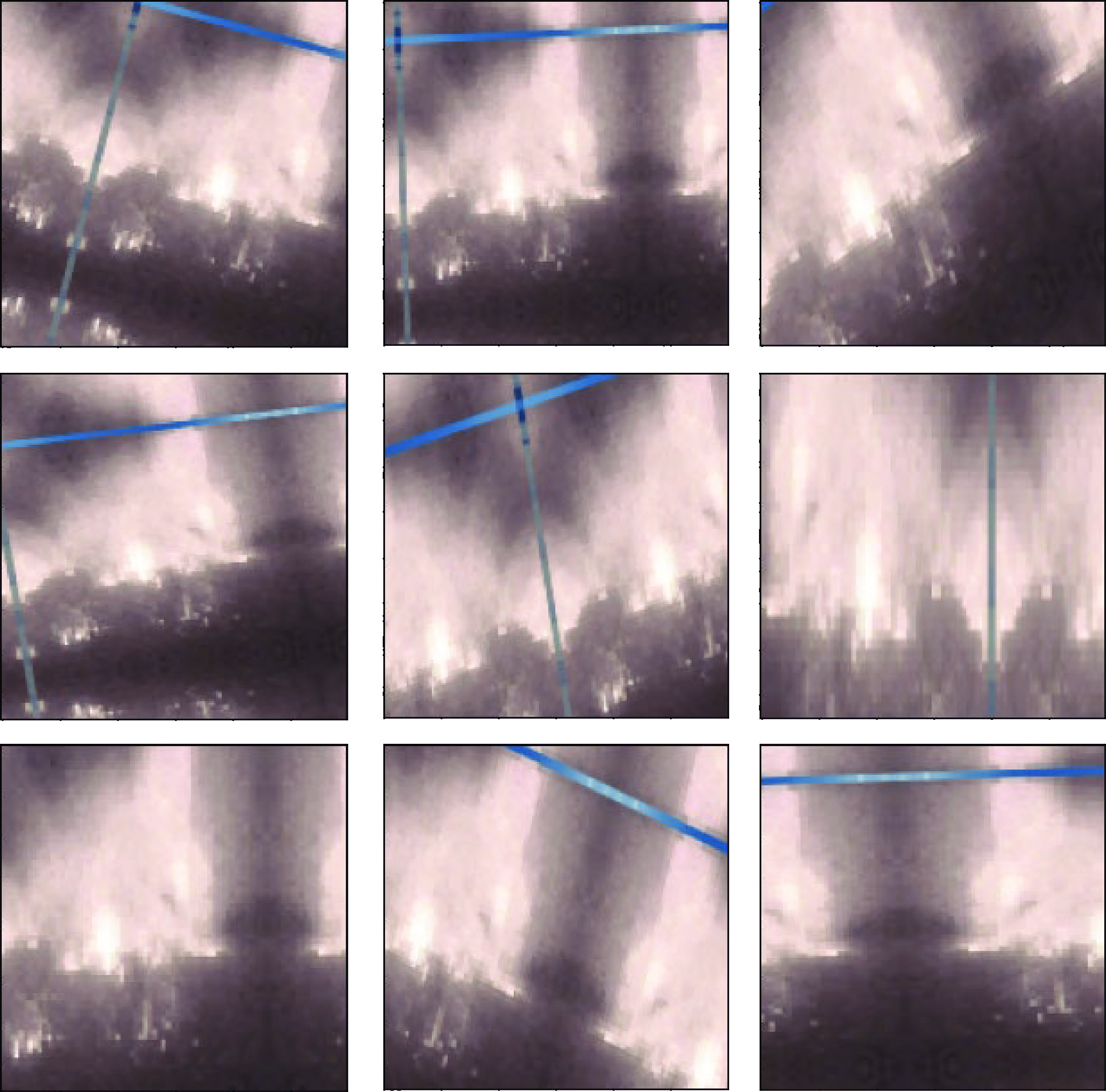
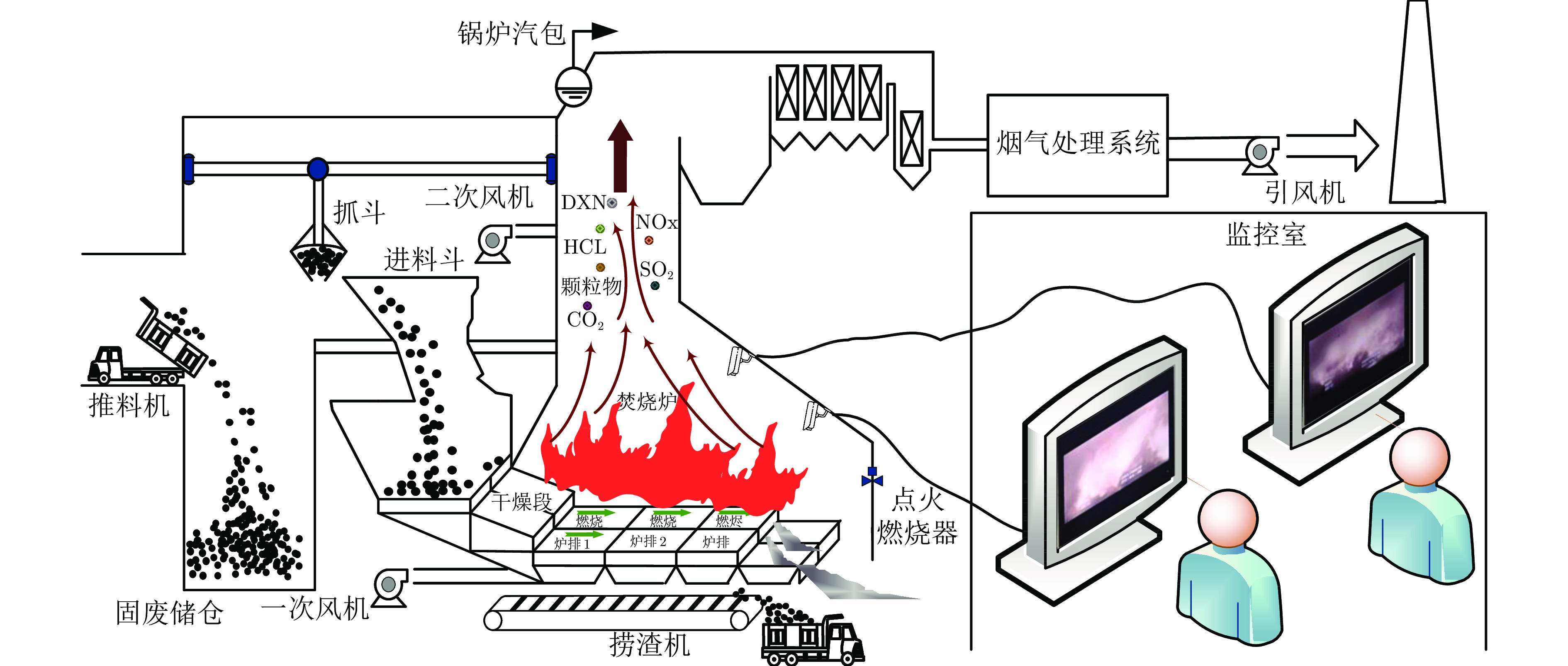
摘要: 国内城市固废焚烧(Municipal solid waste incineration, MSWI)过程通常依靠运行专家观察炉内火焰识别燃烧状态后再结合自身经验修正控制策略以维持稳定燃烧, 存在智能化水平低、识别结果具有主观性与随意性等问题. 由于MSWI过程的火焰图像具有强污染、多噪声等特性, 并且存在异常工况数据较为稀缺等问题, 导致传统目标识别方法难以适用. 对此, 提出一种基于混合数据增强的MSWI过程燃烧状态识别方法. 首先, 结合领域专家经验与焚烧炉排结构对燃烧状态进行标定; 接着, 设计由粗调和精调两级组成的深度卷积生成对抗网络(Deep convolutional generative adversarial network, DCGAN)以获取多工况火焰图像; 然后, 采用弗雷歇距离(Fréchet inception distance, FID)对生成式样本进行自适应选择; 最后, 通过非生成式数据增强对样本进行再次扩充, 获得混合增强数据构建卷积神经网络以识别燃烧状态. 基于某MSWI电厂实际运行数据实验, 表明该方法有效地提高了识别网络的泛化性与鲁棒性, 具有良好的识别精度.
-
关键词:
- 城市固废焚烧 /
- 深度卷积生成对抗网络 /
- 燃烧状态识别 /
- 非生成式数据增强 /
- 混合数据增强
Abstract: The municipal solid waste incineration (MSWI) process usually relies on operating experts to observe the flame inside furnace for recognizing the combustion states. Then, by combining the experts＇ own experience to modify the control strategy to maintain the stable combustion. Thus, this manual mode has disadvantages of low intelligence and the subjectivity and randomness recognition results. The traditional methods are difficult to apply to the MSWI process, which has the characteristics of strong pollution, multiple noise, and scarcity of samples under abnormal conditions. To solve the above problems, a combustion states recognition method of MSWI process based on mixed data enhancement is proposed. Firstly, combustion states are labeled by combining the experience of domain experts and the design structure of furnace grate. Next, a deep convolutional generative adversarial network (DCGAN) consisting of two levels of coarse and fine-tuning was designed to acquire multi-situation flame images. Then, the Fréchet inception distance (FID) is used to adaptively select generated samples. Finally, the sample features are enriched at the second time by using non-generative data enhancement strategy, and a convolutional neural network is constructed based on the mixed enhanced data to recognize the combustion state. Experiments based on actual operating data of a MSWI plant show that this method effectively improves the generalization and robustness of the recognition network and has good recognition accuracy. -
图 2 基于DCGAN数据增强的燃烧状态识别策略
Fig. 2 Strategy of combustion state recognition based on DCGAN data enhancement
图 10 粗调DCGAN迭代过程中FID对生成燃烧状态图像的评估结果
Fig. 10 Assessment of FID for generating combustion state images during rough DCGAN iteration
图 16 不同生成模型生成的燃烧状态图像
Fig. 16 Combustion state images generated by different generation models
表 1 数据集划分
Table 1 Dataset partition
数据集 划分方式 训练集 验证集 测试集 A 时间次序 9 × 8 9 × 1 9 × 1 B 随机抽样 9 × 8 9 × 1 9 × 1 
下载: 导出CSV
表 2 不同生成模型生成数据的评估结果
Table 2 Evaluation results of data generated by different generation models
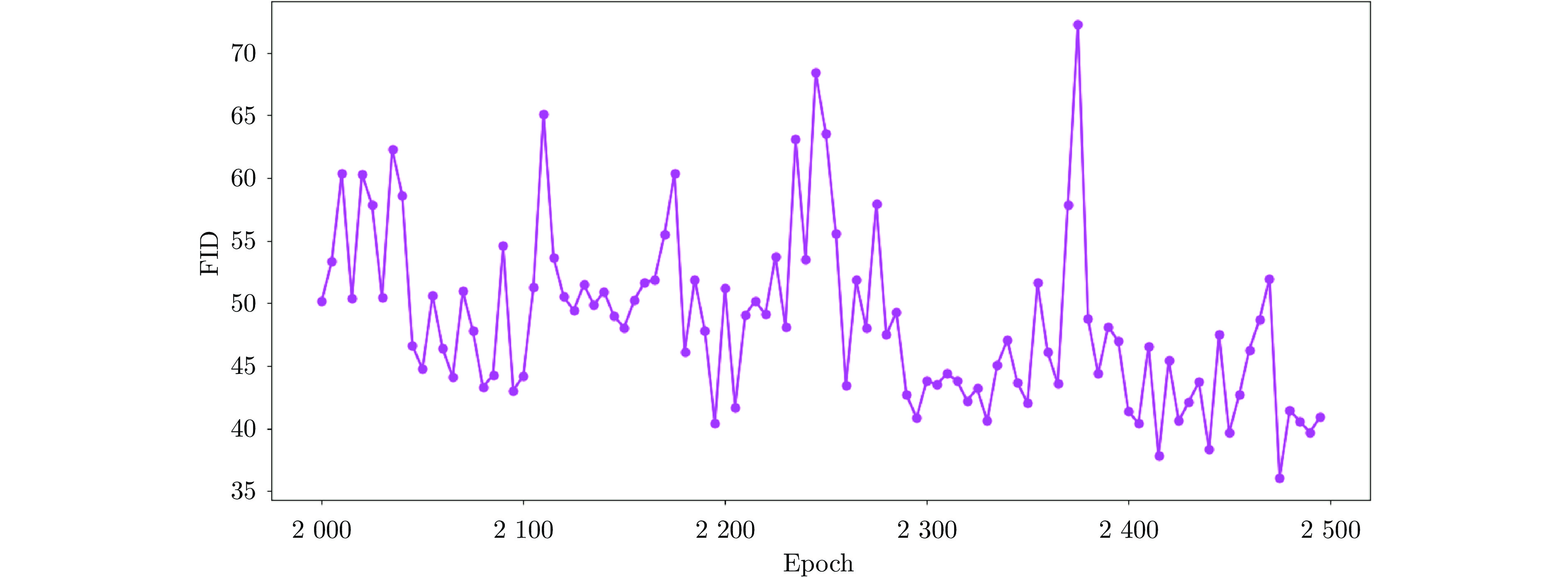
方法 评价指标 FIDmin FIDaverage Epoch GAN 250.00 254.50 10000 LSGAN 58.56 51.94 3000 DCGAN 43.81 49.67 2500 本文方法 36.10 48.51 2500
下载: 导出CSV
表 3 识别模型的性能对比
Table 3 Performance comparison of recognition models
方法 测试集准确率 测试集损失 验证集准确率 验证集损失 方式A CNN 0.7518±0.00245 0.6046±0.02882 0.6115±0.00212 1.6319±0.11640 非生成式数据增强+CNN 0.8272±0.00206 0.6504±0.04038 0.7830±0.00183 0.9077±0.03739 DCGAN数据增强+CNN 0.8000±0.00098 0.8776±0.01063 0.5885±0.00396 1.9024±0.11050 本文方法 0.8482±0.00105 0.5520±0.01006 0.7269±0.00377 0.9768±0.05797 方式B CNN 0.8926±0.00105 0.2298±0.00309 0.8519±0.00061 0.2519±0.00167 非生成式数据增强+CNN 0.9371±0.00184 0.1504±0.00825 0.9704±0.00055 0.1093±0.01037 DCGAN数据增强+CNN 0.9000±0.00123 0.3159±0.01150 0.8445±0.00207 0.2913±0.00396 本文方法 0.9407±0.00367 0.2019±0.01498 0.9741±0.00044 0.0699±0.00195
下载: 导出CSV
A1 符号及含义
A1 Symbols and their descriptions
符号 符号含义 D 判别器 G 生成器 $ V(D,G)$ GAN 原始的目标函数 ${\boldsymbol{z}} $ 潜在空间的随机噪声 $ D^*$ 固定G 参数, 在$\mathop {\max }\nolimits_D V \left({D,G} \right)$过程中, D 的最优解 ${D_{{\text{JS}}}}$ JS 散度 ${R_{jk}}$ 图像中经过卷积核扫描后的第 j 行第 k 列的结果 ${H_{j - u,k - v}}$ 卷积核 ${F_{u,v}}$ 图像 $X$ 燃烧状态数据集, 包含前移、正常和后移的数据集, 即燃烧图像粗调 DCGAN 中判别网络输入值集合$[ { {\boldsymbol{x} }_{{1} } };{ {\boldsymbol{x} }_{{2} } }; $ ${ {\boldsymbol{x} }_{{3} } }; \cdots ;{ {\boldsymbol{x} }_{\rm{a}}} \cdots ]$, 即$ \left[ {{X_{{\rm{real}}}};{X_{{\rm{false}}}}} \right]$ $ X_{{\rm{FW}}}$ 燃烧线前移数据集 $ X_{{\rm{NM}}}$ 燃烧线正常数据集 $ X_{{\rm{BC}}}$ 燃烧线后移数据集 $ X'_{{\rm{FW}}}$ 训练集燃烧线前移数据集 $ X'_{{\rm{NM}}}$ 训练集燃烧线正常数据集 $ X'_{{\rm{BC}}}$ 训练集燃烧线后移数据集 $ X''_{{\rm{FW}}}$ 测试、验证燃烧线前移数据集 $ X''_{{\rm{NM}}}$ 测试、验证燃烧线正常数据集 $ X''_{{\rm{BC}}}$ 测试、验证燃烧线后移数据集 $ {D_t}(\cdot, \cdot )$ 燃烧图像粗调 DCGAN 子模块中, 判别网络参数为${\theta _{D,t}}$时, 判别网络预测值集合 $ {D_{t+1}}(\cdot, \cdot )$ 燃烧图像粗调 DCGAN 子模块中, 判别网络参数为${\theta _{D,t+1}}$时, 判别网络预测值集合 $ Y_{D,t}$ 在燃烧图像粗调 DCGAN 子模块中第 t 次博弈训练判别网络的真实值集合 $ Y_{G,t}$ 在燃烧图像粗调 DCGAN 子模块中第 t 次博弈训练生成网络的真实值集合 $ loss_{D,t}$ 在燃烧图像粗调 DCGAN 子模块中第 t 次博弈更新判别网络的损失值 $ loss_{G,t}$ 在燃烧图像粗调 DCGAN 子模块中第 t 次博弈更新生成网络的损失值 $ X_{{\rm{real}}}$ 在燃烧图像粗调 DCGAN 子模块中参加博弈的真实数据 $ X_{{\rm{false}},t}$ 在燃烧图像粗调 DCGAN 子模块中参加第 t 次博弈的生成的数据 $ G_t({\boldsymbol{z}})$ 在燃烧图像粗调 DCGAN 子模块第 t 次博弈中由随机噪声经过生成网络得到的虚拟样本 ${S_{D,t}}$ 燃烧图像粗调 DCGAN 中获得的判别网络的结构参数 ${S_{G,t}}$ 燃烧图像粗调 DCGAN 中获得的生成网络的结构参数 ${\theta _{D,t}}$ 在燃烧图像粗调 DCGAN 子模块中第 t 次博弈判别网络更新前的网络参数 ${\theta _{G,t}}$ 在燃烧图像粗调 DCGAN 子模块中第 t 次博弈生成网络更新前的网络参数 $ X_{{\rm{real}}}^{{\rm{FW}}}$ 燃烧线前移精调 DCGAN 子模块中参加博弈的真实数据 $ X_{{\rm{false}},t}^{{\rm{FW}}}$ 在燃烧线前移精调 DCGAN 子模块中参加第 t 次博弈的生成数据 $ X_{{\rm{real}}}^{{\rm{NM}}}$ 燃烧线正常精调 DCGAN 子模块中参加博弈的真实数据 $ X_{{\rm{false}},t}^{{\rm{NM}}}$ 在燃烧线正常精调 DCGAN 子模块中参加第 t 次博弈的生成数据 $ X_{{\rm{real}}}^{{\rm{BC}}}$ 燃烧线后移精调 DCGAN 子模块中参加博弈的真实数据 $ X_{{\rm{false}},t}^{{\rm{BC}}}$ 在燃烧线后移精调 DCGAN 子模块中参加第 t 次博弈的生成数据 $ D_t^{{\rm{FW}}}(\cdot, \cdot )$ 在燃烧线前移精调 DCGAN 子模块中判别网络参数为参数$\theta _{D,t}^{{\text{FW}}}$时, 判别网络预测值集合 $ D_t^{{\rm{NM}}}(\cdot, \cdot )$ 在燃烧线正常精调 DCGAN 子模块中判别网络参数为参数$\theta _{D,t}^{{\text{NM}}}$时, 判别网络预测值集合 $ {D}_{t}^{\text{BC}}(\cdot, \cdot ) $ 在燃烧线后移精调 DCGAN 子模块中判别网络参数为参数$\theta _{D,t}^{{\text{BC}}}$时, 判别网络预测值集合 $ D_{t+1}^{{\rm{FW}}}(\cdot, \cdot )$ 在燃烧线前移精调 DCGAN 子模块中判别网络参数为参数$\theta _{D,t + 1}^{{\text{FW}}}$时, 判别网络预测值集合 $ D_{t+1}^{{\rm{NM}}}(\cdot, \cdot )$ 在燃烧线正常精调 DCGAN 子模块中判别网络参数为参数$\theta _{D,t + 1}^{{\text{NM}}}$时, 判别网络预测值集合 $ D_{t+1}^{{\rm{BC}}}(\cdot, \cdot )$ 在燃烧线后移精调 DCGAN 子模块中判别网络参数为参数$\theta _{D,t + 1}^{{\text{BC}}}$时, 判别网络预测值集合 $ Y_{D,t}^{{\rm{FW}}}$ 燃烧线前移精调 DCGAN 子模块中第 t 次博弈训练 D 的真实值集合 $ Y_{G,t}^{{\rm{FW}}}$ 燃烧线前移精调 DCGAN 子模块中第 t 次博弈训练G的真实值集合 $ Y_{D,t}^{{\rm{NM}}}$ 燃烧线正常精调 DCGAN 子模块中第 t 次博弈训练 D 的真实值集合 $ Y_{G,t}^{{\rm{NM}}}$ 燃烧线正常精调 DCGAN 子模块中第 t 次博弈训练G的真实值集合 $ Y_{D,t}^{{\rm{BC}}}$ 燃烧线后移精调 DCGAN 子模块中第 t 次博弈训练 D 的真实值集合 $ Y_{G,t}^{{\rm{BC}}}$ 燃烧线后移精调 DCGAN 子模块中第 t 次博弈训练G的真实值集合 $ loss_{D,t}^{{\rm{FW}}}$ 燃烧线前移精调 DCGAN 子模块中第 t 次博弈更新 D 的损失值 $ loss_{G,t}^{{\rm{FW}}}$ 燃烧线前移精调 DCGAN 子模块中第 t 次博弈更新G的损失值 $ loss_{D,t}^{{\rm{NM}}}$ 燃烧线正常精调 DCGAN 子模块中第 t 次博弈更新 D 的损失值 $ loss_{G,t}^{{\rm{NM}}}$ 燃烧线正常精调 DCGAN 子模块中第 t 次博弈更新 G 的损失值 $ loss_{D,t}^{{\rm{BC}}}$ 燃烧线后移精调 DCGAN 子模块中第 t 次博弈更新 D 的损失值 $ loss_{G,t}^{{\rm{BC}}}$ 燃烧线后移精调 DCGAN 子模块中第 t 次博弈更新G的损失值 $\theta _{D,t}^{{\text{FW}}}$ 燃烧线前移 DCGAN 子模块中第 t 次博弈判别网络更新前的网络参数 $\theta _{G,t}^{{\text{FW}}}$ 燃烧线前移 DCGAN 子模块中第 t 次博弈生成网络更新前的网络参数 $\theta _{D,t}^{{\text{NM}}}$ 燃烧线正常 DCGAN 子模块中第 t 次博弈判别网络更新前的网络参数 $\theta _{G,t}^{{\text{NM}}}$ 燃烧线正常 DCGAN 子模块中第 t 次博弈生成网络更新前的网络参数 $\theta _{D,t}^{{\text{BC}}}$ 燃烧线后移 DCGAN 子模块中第 t 次博弈判别网络更新前的网络参数 $\theta _{G,t}^{{\text{BC}}}$ 燃烧线后移 DCGAN 子模块中第 t 次博弈生成网络更新前的网络参数 ${\widehat Y_{{\text{ CNN }},t}}$ 燃烧状态识别模块第 t 次更新 CNN 模型预测值集合 $los{s_{{\text{ CNN }},t}}$ 燃烧状态识别模块第 t 次更新 CNN 的损失 $ \theta _{{\rm{ CNN }},t}$ 燃烧状态识别模块第 t 次更新 CNN 的网络更新参数 $ loss$ 神经网络的损失 ${\boldsymbol{x} }_{{a} }$ 神经网络第 a 幅输入图像 $y_a $ 第 a 幅输入图像输入神经网络后的输出值 $ D_t(X)$ 判别网络预测值集合, 即$ {D_t}(\cdot, \cdot )$ $L $ 损失函数 $\delta_i $ 第 i 层的误差 $O_i $ 第 i 层输出 $W_i$ 第 i 层的所有权重参数 $B_i $ 第 i 层的所有偏置参数 $ {\nabla _{{W_{i - 1}}}}$ 第$i-1 $层的权重的当前梯度 $ {\nabla _{{B_{i - 1}}}}$ 第$i-1 $层的偏置的当前梯度 $ {\theta _{D,t}}$ 第 t 次判别网络的参数 $ {m _{D,t}}$ 第 t 次判别网络一阶动量 $ {v _{D,t}}$ 第 t 次判别网络的二阶动量 $\alpha $ 学习率 $\gamma $ 很小的正实数 $ {\nabla _{D,t}}$ 第 t 次判别网络参数的梯度 $\beta_1 $ Adam 超参数 $\beta_2 $ Adam 超参数 $ {\eta _{D,t}}$ 计算第 t 次的下降梯度 $ {\widehat m_{D,t}}$ 初始阶段判别网络的第 t 次一阶动量 $ {\widehat v_{D,t}}$ 初始阶段判别网络的第 t 次的二阶动量 $Y $ 神经网络真值集合 $ f(X)$ 神经网络预测值集合 $p $ 概率分布 ${p_{\text{r}}}$ 真实图像的概率分布 ${p_{\text{g}}}$ 生成图像的概率分布 ${p_{\boldsymbol{z}}}$ z 所服从的正态分布 Cov 协方差矩阵
下载: 导出CSV
-
[1] 乔俊飞, 郭子豪, 汤健. 面向城市固废焚烧过程的二噁英排放浓度检测方法综述. 自动化学报, 2020, 46(6): 1063-1089Qiao Jun-Fei, Guo Zi-Hao, Tang Jian. Dioxin emission concentration measurement approaches for municipal solid wastes incineration process: A survey. Acta Automatica Sinica, 2020, 46(6): 1063-1089 [2] Lu J W, Zhang S K, Hai J, Lei M. Status and perspectives of municipal solid waste incineration in China: A comparison with developed regions. Waste Management, 2017, 69: 170-186 doi: 10.1016/j.wasman.2017.04.014 [3] Kalyani K A, Pandey K K. Waste to energy status in India: A short review. Renewable and Sustainable Energy Reviews, 2014, 31: 113-120 doi: 10.1016/j.rser.2013.11.020 [4] 汤健, 乔俊飞. 基于选择性集成核学习算法的固废焚烧过程二噁英排放浓度软测量. 化工学报, 2018, 70(2): 696-706Tang Jian, Qiao Jun-Fei. Dioxin emission concentration soft measuring approach of municipal solid waste incineration based on selective ensemble kernel learning algorithm. CIESC Journal, 2019, 70(2): 696-706 [5] 汤健, 王丹丹, 郭子豪, 乔俊飞. 基于虚拟样本优化选择的城市固废焚烧过程二噁英排放浓度预测. 北京工业大学学报, 2021, 47(5): 431-443Tang Jian, Wang Dan-Dan, Guo Zi-Hao, Qiao Jun-Fei. Prediction of dioxin emission concentration in the municipal solid waste incineration process based on optimal selection of virtual samples. Journal of Beijing University of Technology, 2021, 47(5): 431-443 [6] 汤健, 乔俊飞, 徐喆, 郭子豪. 基于特征约简与选择性集成算法的城市固废焚烧过程二噁英排放浓度软测量. 控制理论与应用, 2021, 38(1): 110-120Tang Jian, Qiao Jun-Fei, Xu Zhe, Guo Zi-Hao. Soft measuring approach of dioxin emission concentration in municipal solid waste incineration process based on feature reduction and selective ensemble algorithm. Control Theory & Applications, 2021, 38(1): 110-120 [7] Kolekar K A, Hazra T, Chakrabarty S N. A review on prediction of municipal solid waste generation models. Procedia Environmental Sciences, 2016, 35: 238-244 doi: 10.1016/j.proenv.2016.07.087 [8] Li X M, Zhang C M, Li Y Z, Zhi Q. The status of municipal solid waste incineration (MSWI) in China and its clean development. Energy Procedia, 2016, 104: 498-503 doi: 10.1016/j.egypro.2016.12.084 [9] 乔俊飞, 段滈杉, 汤健, 蒙西. 基于火焰图像颜色特征的MSWI燃烧工况识别. 控制工程, 2022, 29(7): 1153-1161Qiao Jun-Fei, Duan Hao-Shan, Tang Jian, Meng Xi. Recognition of MSWI combustion conditions based on color features of flame images. Control Engineering of China, 2022, 29(7): 1153-1161 [10] 高济, 何志均. 基于规则的联想网络. 自动化学报, 1989, 15(4): 318-323Gao Ji, He Zhi-Jun. The associative network based on rules. Acta Automatica Sinica, 1989, 15(4): 318-323 [11] Roy S K, Krishna G, Dubey S R, Chaudhuri B B. HybridSN: Exploring 3-D-2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geoscience and Remote Sensing Letters, 2020, 17(2): 277-281 doi: 10.1109/LGRS.2019.2918719 [12] Ahammad S H, Rajesh V, Rahman Z U, Lay-Ekuakille A. A hybrid CNN-based segmentation and boosting classifier for real time sensor spinal cord injury data. IEEE Sensors Journal, 2020, 20(17): 10092-10101 doi: 10.1109/JSEN.2020.2992879 [13] Sun Y, Xue B, Zhang M J, Yen G G, Lv J C. Automatically designing CNN architectures using the genetic algorithm for image classification. IEEE Transactions on Cybernetics, 2020, 50(9): 3840-3854 doi: 10.1109/TCYB.2020.2983860 [14] Zhou P, Gao B H, Wang S, Chai T Y. Identification of abnormal conditions for fused magnesium melting process based on deep learning and multisource information fusion, IEEE Transactions on Industrial Electronics, 2022, 69(3): 3017-3026 doi: 10.1109/TIE.2021.3070512 [15] 张震, 汪斌强, 李向涛, 黄万伟. 基于近邻传播学习的半监督流量分类方法. 自动化学报, 2013, 39(7): 1100-1109Zhang Zhen, Wang Bin-Qiang, Li Xiang-Tao, Huang Wan-Wei. Semi-supervised traffic identification based on affinity propagation. Acta Automatica Sinica, 2013, 39(7): 1100-1109 [16] 王松涛, 周真, 靳薇, 曲寒冰. 基于贝叶斯框架融合的RGB-D图像显著性检测. 自动化学报, 2020, 46(4): 695-720Wang Song-Tao, Zhou Zhen, Jin Wei, Qu Han-Bing. Saliency detection for RGB-D images under Bayesian framework. Acta Automatica Sinica, 2020, 46(4): 695-720 [17] 陶剑文, 王士同. 领域适应核支持向量机. 自动化学报, 2012, 38(5): 797-811 doi: 10.3724/SP.J.1004.2012.00797Tao Jian-Wen, Wang Shi-Tong. Kernel support vector machine for domain adaptation. Acta Automatica Sinica, 2012, 38(5): 797-811 doi: 10.3724/SP.J.1004.2012.00797 [18] 李强, 王正志. 基于人工神经网络和经验知识的遥感信息分类综合方法. 自动化学报, 2000, 26(2): 233-239Li Qiang, Wang Zheng-Zhi. Remote sensing information classification based on artificial neural network and knowledge. Acta Automatica Sinica, 2000, 26(2): 233-239 [19] 罗珍珍, 陈靓影, 刘乐元, 张坤. 基于条件随机森林的非约束环境自然笑脸检测. 自动化学报, 2018, 44(4): 696-706Luo Zhen-Zhen, Chen Jing-Ying, Liu Le-Yuan, Zhang Kun. Conditional random forests for spontaneous smile detection in unconstrained environment. Acta Automatica Sinica, 2018, 44(4): 696-706 [20] 郝红卫, 王志彬, 殷绪成, 陈志强. 分类器的动态选择与循环集成方法. 自动化学报, 2011, 37(11): 1290-1295Hao Hong-Wei, Wang Zhi-Bin, Yin Xu-Cheng, Chen Zhi-Qiang. Dynamic selection and circulating combination for multiple classifier systems. Acta Automatica Sinica, 2011, 37(11): 1290-1295 [21] 常亮, 邓小明, 周明全, 武仲科, 袁野, 杨硕, 等. 图像理解中的卷积神经网络. 自动化学报, 2016, 42(9): 1300-1312Chang Liang, Deng Xiao-Ming, Zhou Ming-Quan, Wu Zhong-Ke, Yuan Ye, Yang Shuo, et al. Convolutional neural networks in image understanding. Acta Automatica Sinica, 2016, 42(9): 1300-1312 [22] Bai W D, Yan J H, Ma Z Y. Method of flame identification based on support vector machine. Power Engingeering, 2004, 24(4): 548-551 [23] Sun D, Lu G, Zhou H, Yan Y, Liu S. Quantitative assessment of flame stability through image processing and spectral analysis. IEEE Transactions on Instrumentation and Measurement, 2015, 64(12): 3323-3333 doi: 10.1109/TIM.2015.2444262 [24] Khan A, Sohail A, Zahoora U, Qureshi A S. A survey of the recent architectures of deep convolutional neural networks. Artificial Intelligence Review, 2020, 53(8): 5455-5516 doi: 10.1007/s10462-020-09825-6 [25] 冯晓硕, 沈樾, 王冬琦. 基于图像的数据增强方法发展现状综述. 计算机科学与应用, 2021, 11(2): 370-382 doi: 10.12677/CSA.2021.112037Feng Xiao-Shuo, Shen Yue, Wang Dong-Qi. A survey on the development of image data augmentation. Computer Science and Application, 2021, 11(2): 370-382 doi: 10.12677/CSA.2021.112037 [26] Goodfellow I J, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. In: Proceedings of the 27th International Conference on Neural Information Processing Systems. Montréal, Canada: MIT Press, 2014. 2672−2680 [27] 唐贤伦, 杜一铭, 刘雨微, 李佳歆, 马艺玮. 基于条件深度卷积生成对抗网络的图像识别方法. 自动化学报, 2018, 44(5): 855-864Tang Xian-Lun, Du Yi-Ming, Liu Yu-Wei, Li Jia-Xin, Ma Yi-Wei. Image recognition with conditional deep convolutional generative adversarial networks. Acta Automatica Sinica, 2018, 44(5): 855-864 [28] 刘建伟, 谢浩杰, 罗雄麟. 生成对抗网络在各领域应用研究进展. 自动化学报, 2020, 46(12): 2500-2536Liu Jian-Wei, Xie Hao-Jie, Luo Xiong-Lin. Research progress on application of generative adversarial networks in various fields. Acta Automatica Sinica, 2020, 46(12): 2500-2536 [29] 王坤峰, 苟超, 段艳杰, 林懿伦, 郑心湖, 王飞跃. 生成式对抗网络GAN的研究进展与展望. 自动化学报, 2017, 43(3): 321-332Wang Kun-Feng, Gou Chao, Duan Yan-Jie, Lin Yi-Lun, Zheng Xin-Hu, Wang Fei-Yue. Generative adversarial networks: The state of the art and beyond. Acta Automatica Sinica, 2017, 43(3): 321-332 [30] Yang L, Liu Y H, Peng J Z. An automatic detection and identification method of welded joints based on deep neural network. IEEE Access, 2019, 7: 164952-164961 doi: 10.1109/ACCESS.2019.2953313 [31] Lian J, Jia W K, Zareapoor M, Zheng Y J, Luo R, Jain D K, et al. Deep-learning-based small surface defect detection via an exaggerated local variation-based generative adversarial network. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1343-1351 doi: 10.1109/TII.2019.2945403 [32] Niu S L, Li B, Wang X G, Lin H. Defect image sample generation with GAN for improving defect recognition. IEEE Transactions on Automation Science and Engineering, 2020, 17(3): 1611-1622 [33] Wu X J, Qiu L T, Gu X D, Long Z L. Deep learning-based generic automatic surface defect inspection (ASDI) with pixelwise segmentation. IEEE Transactions on Instrumentation and Measurement, 2021, 70: Article No. 5004010 [34] Bichler M, Fichtl M, Heidekrüger S, Kohring N, Sutterer P. Learning equilibria in symmetric auction games using artificial neural networks. Nature Machine Intelligence, 2021, 3(8): 687-695 doi: 10.1038/s42256-021-00365-4 [35] Heusel M, Ramsauer H, Unterthiner T, Nessler B, Hochreiter S. GANs trained by a two time-scale update rule converge to a local Nash equilibrium. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 6629−6640 [36] Lucic M, Kurach K, Michalski M, Bousquet O, Gelly S. Are GANs created equal? A large-scale study. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, Canada: Curran Associates Inc., 2018. 698−707 [37] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. In: Proceedings of the 4th International Conference on Learning Representations. San Juan, Puerto Rico: 2016. [38] Suárez P L, Sappa A D, Vintimilla B X. Infrared image colorization based on a triplet DCGAN architecture. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, USA: IEEE, 2017. 18−23 [39] Yeh R A, Chen C, Lim T Y, Schwing A G, Hasegawa-Johnson M, Do M N. Semantic image inpainting with deep generative models. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 5485−5493 [40] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. In: Proceedings of the 26th Annual Conference on Neural Information Processing Systems. Lake Tahoe, USA: Curran Associates Inc., 2012. 1106−1114 [41] Zeiler M D, Fergus R. Visualizing and understanding convolutional networks. In: Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland: Springer, 2014. 818−833 [42] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition [Online], available: http://arxiv.org/abs/1409.1556, April 10, 2015 [43] Szegedy C, Liu W, Jia Y Q, Sermanet P, Reed S, Anguelov D, et al. Going deeper with convolutions. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA: IEEE, 2015. 1−9 [44] He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016. 770−778 [45] 林景栋, 吴欣怡, 柴毅, 尹宏鹏. 卷积神经网络结构优化综述. 自动化学报, 2020, 46(1): 24-37Lin Jing-Dong, Wu Xin-Yi, Chai Yi, Yin Hong-Peng. Structure optimization of convolutional neural networks: A survey. Acta Automatica Sinica, 2020, 46(1): 24-37 [46] Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533-536 doi: 10.1038/323533a0 [47] Kingma D P, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv: 1412.6980, 2017. [48] Mao X D, Li Q, Xie H R, Lau R Y K, Wang Z, Smolley S P. Least squares generative adversarial networks. In: Proceedings of the IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017. 2813−2821 -
图(16) / 表(4)
计量
- 文章访问数: 909
- HTML全文浏览量: 465
- PDF下载量: 161
- 被引次数: 0
