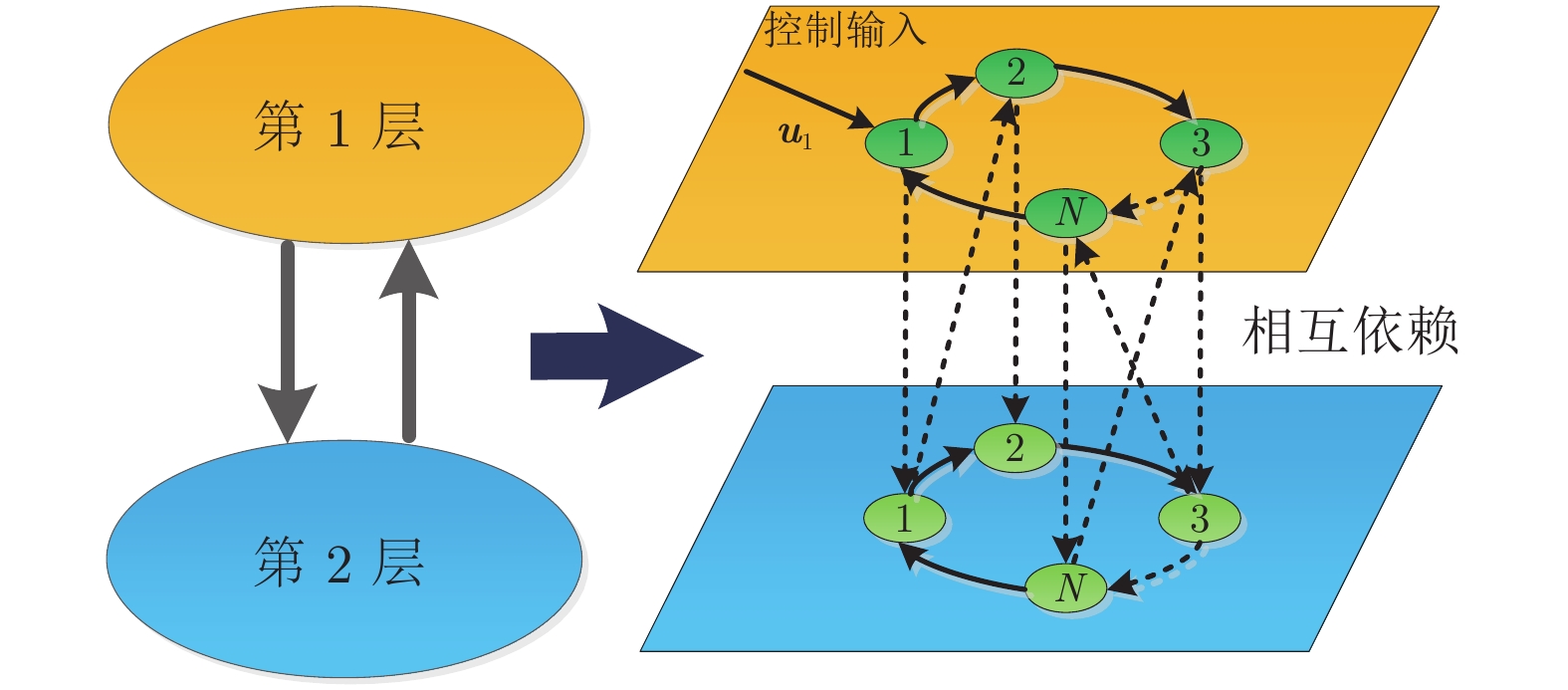
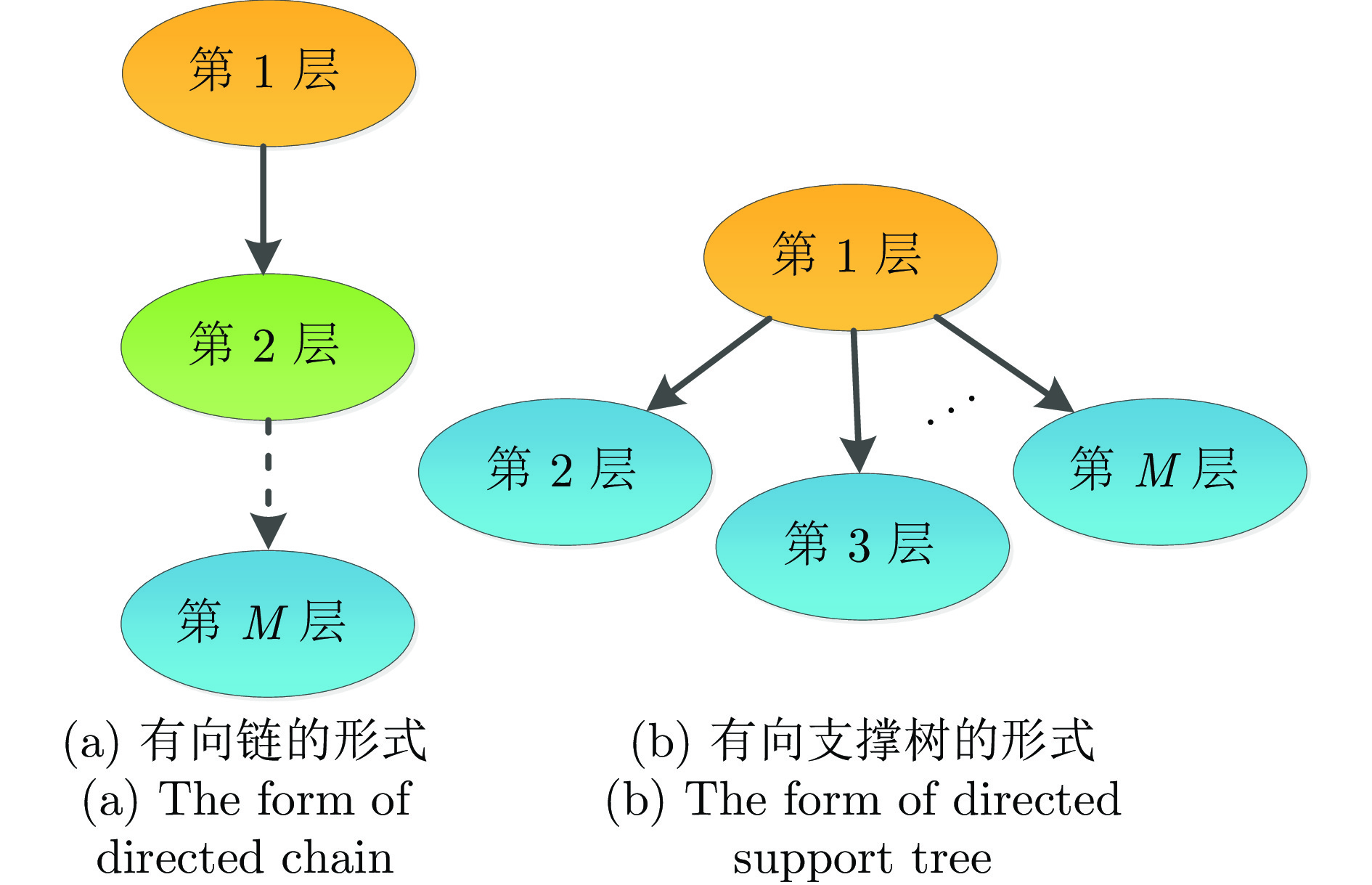
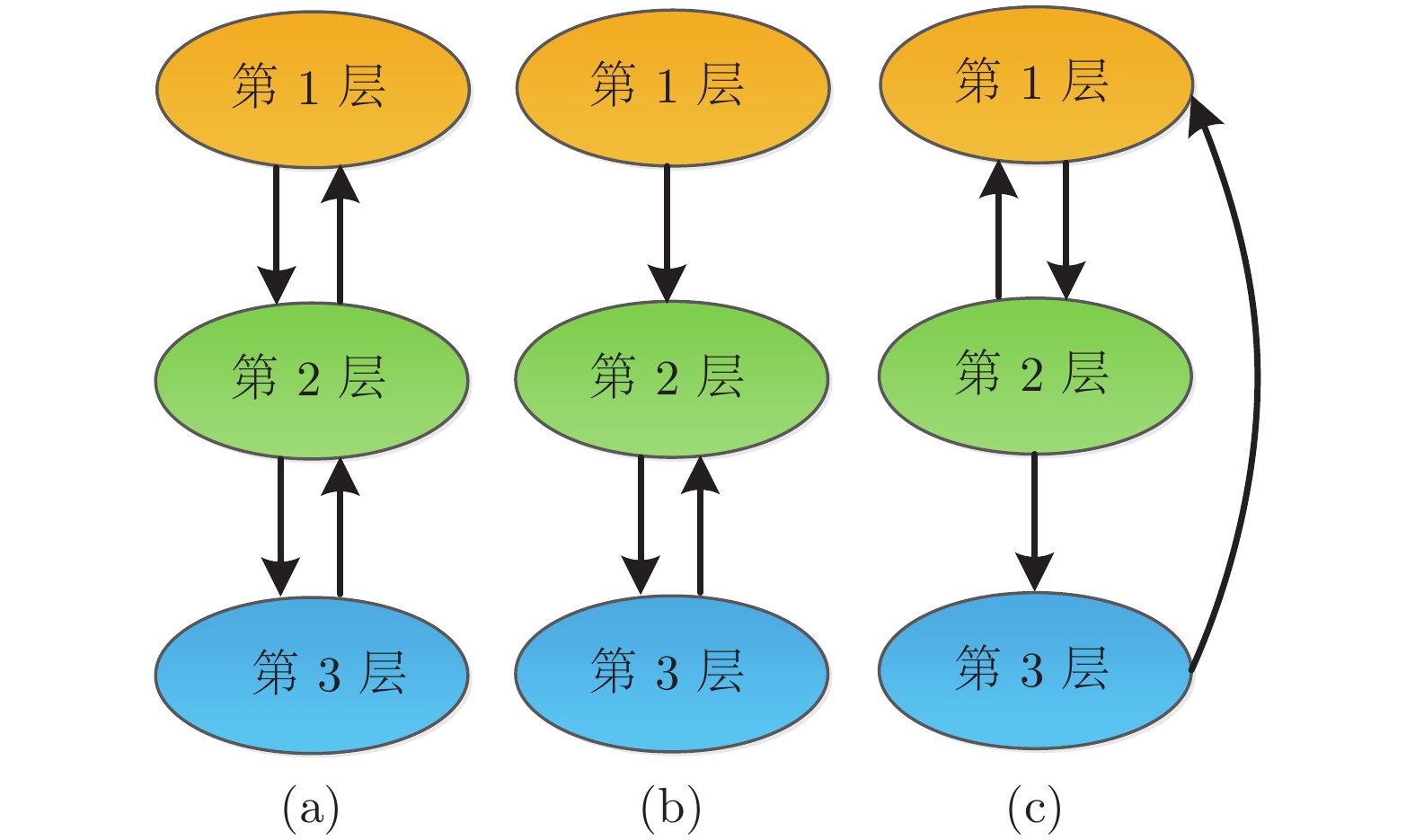
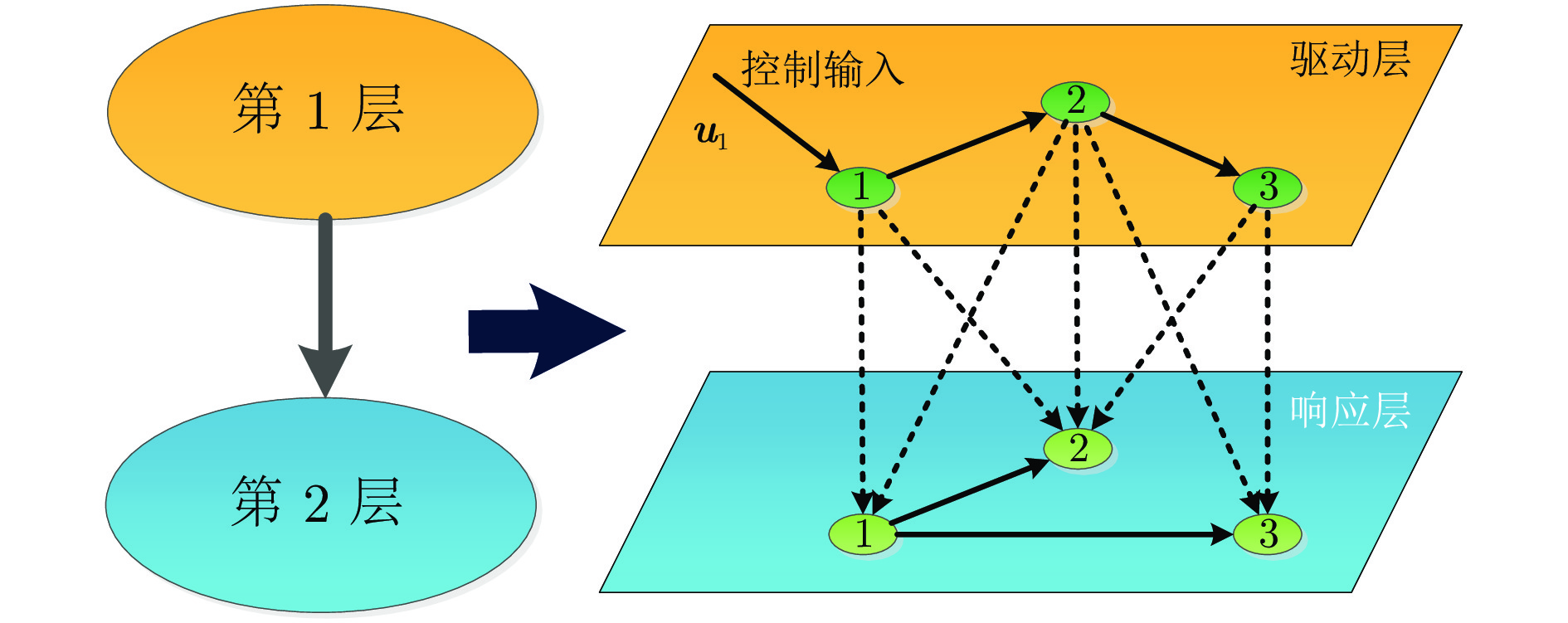
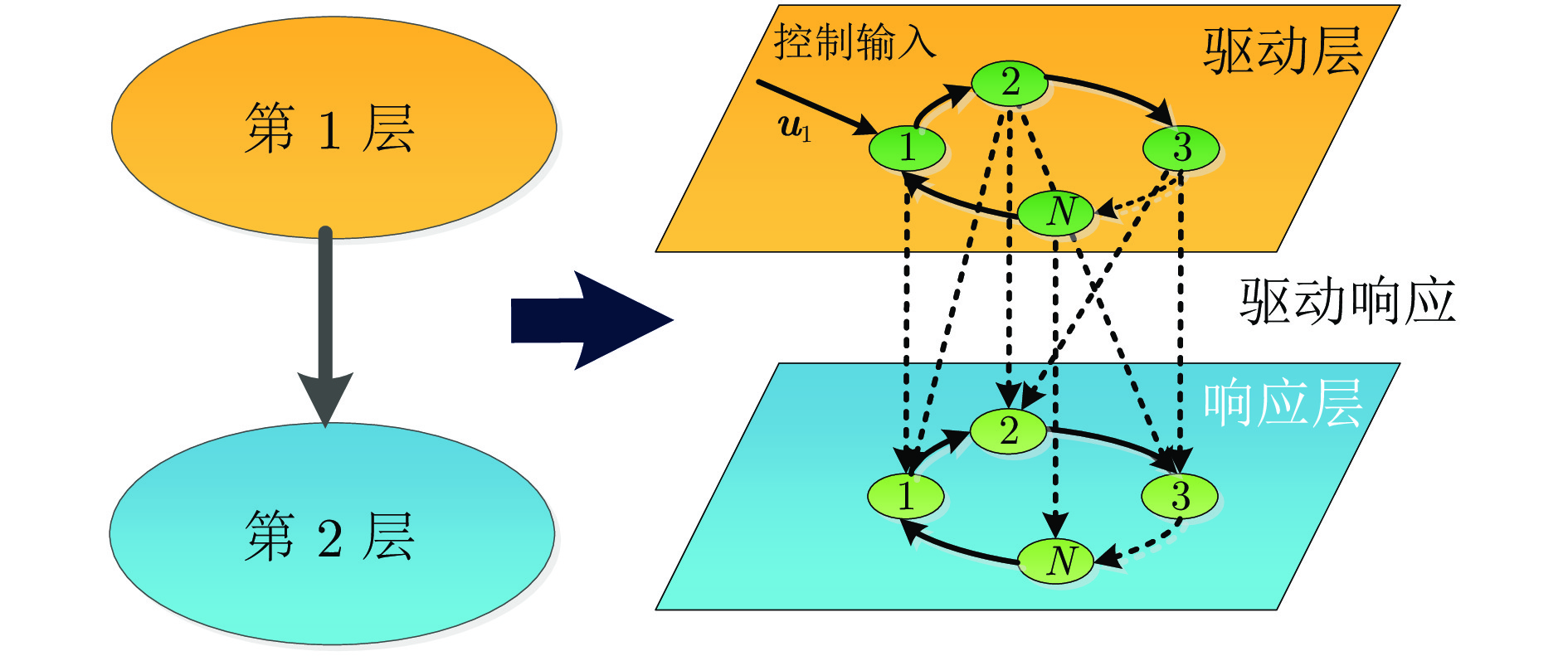
-
摘要: 研究了节点状态为高维的多层复杂网络系统的能控性问题. 讨论了节点的异质性、层间耦合和层内耦合对网络能控性的影响. 研究发现当节点状态由同质变为异质、内耦合矩阵由相同变为不同时, 对网络能控性均有影响(网络可以由能控变为不能控, 反之亦然). 对层间耦合模式为驱动响应模式和相互依赖模式, 分别给出了网络系统能控的充分条件或必要条件. 相比于直接应用经典的能控性判据, 这些条件更易于验证, 且驱动响应模式比相互依赖模式实现系统完全能控所需的条件更弱.Abstract: This paper studies the controllability of multi-layer complex network systems with high-dimensional node states. We discuss the influence of node heterogeneity, inter-layer coupling, and intra-layer coupling on the controllability of the network. It is found that when the state of the node changes from homogeneous to heterogeneous or the inner-coupling matrix changes from identical to nonidentical, both have an impact on the controllability of the network (the network can be changed from controllable to uncontrollable, and vice versa). The sufficient or necessary conditions for the controllability of the networked system when the inter-layer coupling mode is the drive response mode and the interdependence mode are given, respectively. These conditions are easier to verify than using the classic controllability criteria directly, and the conditions that the drive response mode to achieve fully controllability are weaker than the conditions for the interdependence mode.
-
图 1 层间耦合为驱动响应模式的两层网络
Fig. 1 Two-layer networks with the inter-layer drive-response couplings
图 2 层间耦合为相互依赖模式的两层网络
Fig. 2 Two-layer networks with the inter-layer interdependent couplings
图 3 层间耦合为驱动响应模式的M层网络结构示意图
Fig. 3 The illustration of M-layer networks with the inter-layer drive-response couplings
图 4 层间耦合为相互依赖模式的3层网络结构示意图
Fig. 4 The illustration of three-layer networks with the inter-layer interdependent couplings
图 5 驱动层为链网络、响应层为星形网络的两层网络
Fig. 5 Two-layer networks with the topology of the drive-layer is a chain network, and the response layer is a star network
表 1 本文模型中所用的特殊符号
Table 1 Special notations used in the model of this paper
特殊符号 含义 ${\boldsymbol{A}}_i^K$ 第$ K $层网络的第$ i $个节点的状态矩阵 ${\boldsymbol{B}}_i^K$ 第$ K $层网络的第$ i $个节点的输入矩阵 ${\boldsymbol{C}}_i^K$ 第$ K $层网络的第$ i $个节点的输出矩阵 ${\boldsymbol{H}}_i^K$ 第$ K $层网络的第$ i $个节点与该层其他节点之间的内耦合矩阵 ${\boldsymbol{H}}_i^{KJ}$ 第$ J $层网络的第$ i $个节点与第$ K $层网络的其他节点之间的内耦合矩阵 ${{\boldsymbol{W}}^K}$ 第$ K $层的网络拓扑 ${{\boldsymbol{D}}^{KJ} }$ 第$ J $层到第$ K $层的网络拓扑 ${\boldsymbol{x}}$ 整个网络系统的状态 ${{\boldsymbol{x}}^K}$ 第$ K $层网络的状态 ${\boldsymbol{u}}$ 整个网络系统的输入 ${{\boldsymbol{u}}^K}$ 第$ K $层网络的输入 ${\boldsymbol{ \Phi}}$ 整个网络系统的状态矩阵 ${{\boldsymbol{\Phi}} _{KK} }$ 第$ K $层网络的状态矩阵 ${{\boldsymbol{\Phi}} _{KJ} }$ 第$ J $层到第$ K $层网络的状态矩阵 ${\boldsymbol{\Psi}}$ 整个网络系统的输入矩阵 ${\boldsymbol{ \Xi}}$ 整个网络系统的输出矩阵 ${{\boldsymbol{\Lambda}} ^K}$ 以${\boldsymbol{A}}_1^K,\cdots,{\boldsymbol{A}}_N^K$为对角元的分块对角矩阵 ${\boldsymbol{ \Delta}}$ 对角矩阵${ {\text{diag} } } \{ {{\boldsymbol{\Delta}} ^1},\cdots,{{\boldsymbol{\Delta}} ^M}\}$ ${{\boldsymbol{\Delta}} ^K}$ 对角矩阵${ {\text{diag} } } \{ \delta _1^K,\cdots,\delta _N^K\}$ 
下载: 导出CSV
-
[1] Chen G R, Wang X F, Li X. Fundamentals of Complex Networks: Models, Structures, and Dynamics. Singapore: Wiley, 2015. 69−82 [2] Kalman R E. Canonical structure of linear dynamical systems. Proceedings of the National Academy of Sciences of the United States of America, 1962, 48(4): 596−600 [3] Kalman R E. Algebraic structure of linear dynamical systems, I. The module of $ {\Sigma} $. Proceedings of the National Academy of Sciences of the United States of America, 1965, 54(6): 1503−1508 [4] Hautus M L J. Controllability and observability conditions of linear autonomous systems. Indagationes Mathematicae (Proceedings), 1969, 72(5): 443−448 [5] Lin C T. Structural controllability. IEEE Transactions on Automatic Control, 1974, 19(3): 201−208 doi: 10.1109/TAC.1974.1100557 [6] Hosoe S, Matsumoto K. On the irreducibility condition in the structural controllability theorem. IEEE Transactions on Automatic Control, 1979, 24(6): 963−966 doi: 10.1109/TAC.1979.1102192 [7] 段广仁. 高阶系统方法——II. 能控性与全驱性. 自动化学报, 2020, 46(8): 1571−1581Duan Guang-Ren. High-order system approaches: II. Controllability and full-actuation. Acta Automatica Sinica, 2020, 46(8): 1571−1581 [8] Liu Y Y, Slotine J J, Barabási A L. Controllability of complex networks. Nature, 2011, 473(7346): 167−173 doi: 10.1038/nature10011 [9] Liu Y Y, Slotine J J, Barabási A L. Control centrality and hierarchical structure in complex networks. PLoS One, 2012, 7(9): Article No. e44459 doi: 10.1371/journal.pone.0044459 [10] Pequito S, Kar S, Aguiar A P. A framework for structural input/output and control configuration selection in large-scale systems. IEEE Transactions on Automatic Control, 2016, 61(2): 303−318 doi: 10.1109/TAC.2015.2437525 [11] Hsu S P. A necessary and sufficient condition for the controllability of single-leader multi-chain systems. International Journal of Robust and Nonlinear Control, 2017, 27(1): 156−168 doi: 10.1002/rnc.3566 [12] Wang X C, Xi Y G, Huang W Z, Jia S. Deducing complete selection rule set for driver nodes to guarantee network' structural controllability. IEEE/CAA Journal of Automatica Sinica, 2019, 6(5): 1152−1165 doi: 10.1109/JAS.2017.7510724 [13] Bai T, Li S Y, Zou Y Y, Yin X. Block-based minimum input design for the structural controllability of complex networks. Automatica, 2019, 107: 68−76 doi: 10.1016/j.automatica.2019.05.006 [14] Wang B B, Gao L, Gao Y, Deng Y, Wang Y. Controllability and observability analysis for vertex domination centrality in directed networks. Scientific Reports, 2014, 4(1): Article No. 5399 doi: 10.1038/srep05399 [15] Menara T, Bassett D S, Pasqualetti F. Structural controllability of symmetric networks. IEEE Transactions on Automatic Control, 2019, 64(9): 3740−3747 doi: 10.1109/TAC.2018.2881112 [16] Commault C, van der Woude J. A classification of nodes for structural controllability. IEEE Transactions on Automatic Control, 2019, 64(9): 3877−3882 doi: 10.1109/TAC.2018.2886181 [17] Xue M R, Roy S. Structural controllability of linear dynamical networks with homogeneous subsystems. IFAC-PapersOnLine, 2019, 52(3): 25−30 doi: 10.1016/j.ifacol.2019.06.005 [18] Joseph G, Murthy C R. Controllability of linear dynamical systems under input sparsity constraints. IEEE Transactions on Automatic Control, 2021, 66(2): 924−931 doi: 10.1109/TAC.2020.2989245 [19] Pan Y J, Li X. Structural controllability and controlling centrality of temporal networks. PLoS One, 2014, 9(4): Article No. e94998 doi: 10.1371/journal.pone.0094998 [20] Hou B Y, Li X, Chen G R. Structural controllability of temporally switching networks. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(10): 1771−1781 doi: 10.1109/TCSI.2016.2583500 [21] Yao P, Hou B Y, Pan Y J, Li X. Structural controllability of temporal networks with a single switching controller. PLoS One, 2017, 12(1): Article No. e0170584 doi: 10.1371/journal.pone.0170584 [22] Cui Y L, He S B, Wu M C, Zhou C W, Chen J M. Improving the controllability of complex networks by temporal segmentation. IEEE Transactions on Network Science and Engineering, 2020, 7(4): 2765−2774 doi: 10.1109/TNSE.2020.2991056 [23] Mousavi S S, Haeri M, Mesbahi M. Strong structural controllability of networks under time-invariant and time-varying topological perturbations. IEEE Transactions on Automatic Control, 2021, 66(3): 1375−1382 doi: 10.1109/TAC.2020.2992439 [24] Wang L, Chen G R, Wang X F, Tang W K S. Controllability of networked MIMO systems. Automatica, 2016, 69: 405−409 doi: 10.1016/j.automatica.2016.03.013 [25] Wang L, Wang X F, Chen G R. Controllability of networked higher-dimensional systems with one-dimensional communication. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2017, 375(2088): Article No. 20160215 doi: 10.1098/rsta.2016.0215 [26] Hao Y Q, Duan Z S, Chen G R. Further on the controllability of networked MIMO LTI systems. International Journal of Robust and Nonlinear Control, 2018, 28(5): 1778−1788 doi: 10.1002/rnc.3986 [27] Hao Y Q, Duan Z S, Chen G R, Wu F. New controllability conditions for networked, identical LTI systems. IEEE Transactions on Automatic Control, 2019, 64(10): 4223−4228 doi: 10.1109/TAC.2019.2893899 [28] Hao Y Q, Wang Q Y, Duan Z S. Some necessary and sufficient conditions on the controllability of star networks. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(11): 2582−2586 [29] Hao Y Q, Duan Z S, Chen G R. Decentralised fixed modes of networked MIMO systems. International Journal of Control, 2018, 91(4): 859−873 doi: 10.1080/00207179.2017.1295318 [30] Cai N, Khan M J. On generalized controllability canonical form with multiple input variables. International Journal of Control, Automation and Systems, 2017, 15(1): 169−177 doi: 10.1007/s12555-015-0142-8 [31] Trumpf J, Trentelman H L. Controllability and stabilizability of networks of linear systems. IEEE Transactions on Automatic Control, 2019, 64(8): 3391−3398 doi: 10.1109/TAC.2018.2882713 [32] Yuan Z Z, Zhao C, Di Z R, Wang W X, Lai Y C. Exact controllability of complex networks. Nature Communications, 2013, 4(1): Article No. 2447 doi: 10.1038/ncomms3447 [33] Commault C, Kibangou A. Generic controllability of networks with identical SISO dynamical nodes. IEEE Transactions on Control of Network Systems, 2020, 7(2): 855−865 doi: 10.1109/TCNS.2019.2950587 [34] 陆君安. 从单层网络到多层网络——结构、动力学和功能. 现代物理知识, 2015, 27(4): 3−8Lu Jun-An. From single-layer networks to multi-layer networks: Structure, dynamics and function. Modern Fhysics, 2015, 27(4): 3−8 [35] Zhang Y, Garas A, Schweitzer F. Value of peripheral nodes in controlling multilayer scale-free networks. Physical Review E, 2016, 93(1): Article No. 012309 [36] Pósfai M, Gao J X, Cornelius S P, Barabási A L, D'Souza R M. Controllability of multiplex, multi-time-scale networks. Physical Review E, 2016, 94(3): Article No. 032316 [37] Wang D J, Zou X F. Control energy and controllability of multilayer networks. Advances in Complex Systems, 2017, 20(4−5): Article No. 1750008 doi: 10.1142/S0219525917500084 [38] Nacher J C, Ishitsuka M, Miyazaki S, Akutsu T. Finding and analysing the minimum set of driver nodes required to control multilayer networks. Scientific Reports, 2019, 9(1): Article No. 576 doi: 10.1038/s41598-018-37046-z [39] Doostmohammadian M, Khan U A. Minimal sufficient conditions for structural observability/controllability of composite networks via Kronecker product. IEEE Transactions on Signal and Information Processing Over Networks, 2020, 6: 78−87 doi: 10.1109/TSIPN.2019.2960002 [40] Song K, Li G Q, Chen X M, Deng L, Xiao G X, Zeng F, et al. Target controllability of two-layer multiplex networks based on network flow theory. IEEE Transactions on Cybernetics, 2021, 51(5): 2699−2711 doi: 10.1109/TCYB.2019.2906700 [41] Chapman A, Nabi-Abdolyousefi M, Mesbahi M. Controllability and observability of network-of-networks via Cartesian products. IEEE Transactions on Automatic Control, 2014, 59(10): 2668−2679 doi: 10.1109/TAC.2014.2328757 [42] Hao Y Q, Wang Q Y, Duan Z S, Chen G R. Controllability of Kronecker product networks. Automatica, 2019, 110: Article No. 108597 doi: 10.1016/j.automatica.2019.108597 [43] Chen C, Surana A, Bloch A M, Rajapakse I. Controllability of hypergraphs. IEEE Transactions on Network Science and Engineering, 2021, 8(2): 1646−1657 doi: 10.1109/TNSE.2021.3068203 [44] Wu J N, Li X. Interlayer impacts to deep-coupling dynamical networks: A snapshot of equilibrium stability. Chaos, 2019, 29(7): Article No. 073104 [45] Wu J N, Li X, Chen G R. Controllability of deep-coupling dynamical networks. IEEE Transactions on Circuits and Systems I: Regular Papers, 2020, 67(12): 5211−5222 doi: 10.1109/TCSI.2020.2999451 [46] Jiang L X, Tang L K, Lv J H. Controllability of multilayer networks. Asian Journal of Control, 2022, 24(4): 1517−1527 doi: 10.1002/asjc.2561 [47] Xiang L Y, Zhu J J H, Chen F, Chen G R. Controllability of weighted and directed networks with nonidentical node dynamics. Mathematical Problems in Engineering, 2013, 2013: Article No. 405034 [48] Wang P R, Xiang L Y, Chen F. Controllability of heterogeneous networked MIMO systems. In: Proceedings of the International Workshop on Complex Systems and Networks. Doha, Qatar: IEEE, 2017. 45−49 [49] Xiang L Y, Wang P R, Chen F, Chen G R. Controllability of directed networked MIMO systems with heterogeneous dynamics. IEEE Transactions on Control of Network Systems, 2020, 7(2): 807−817 doi: 10.1109/TCNS.2019.2948994 -
图(5) / 表(1)
计量
- 文章访问数: 1234
- HTML全文浏览量: 535
- PDF下载量: 133
- 被引次数: 0
