-
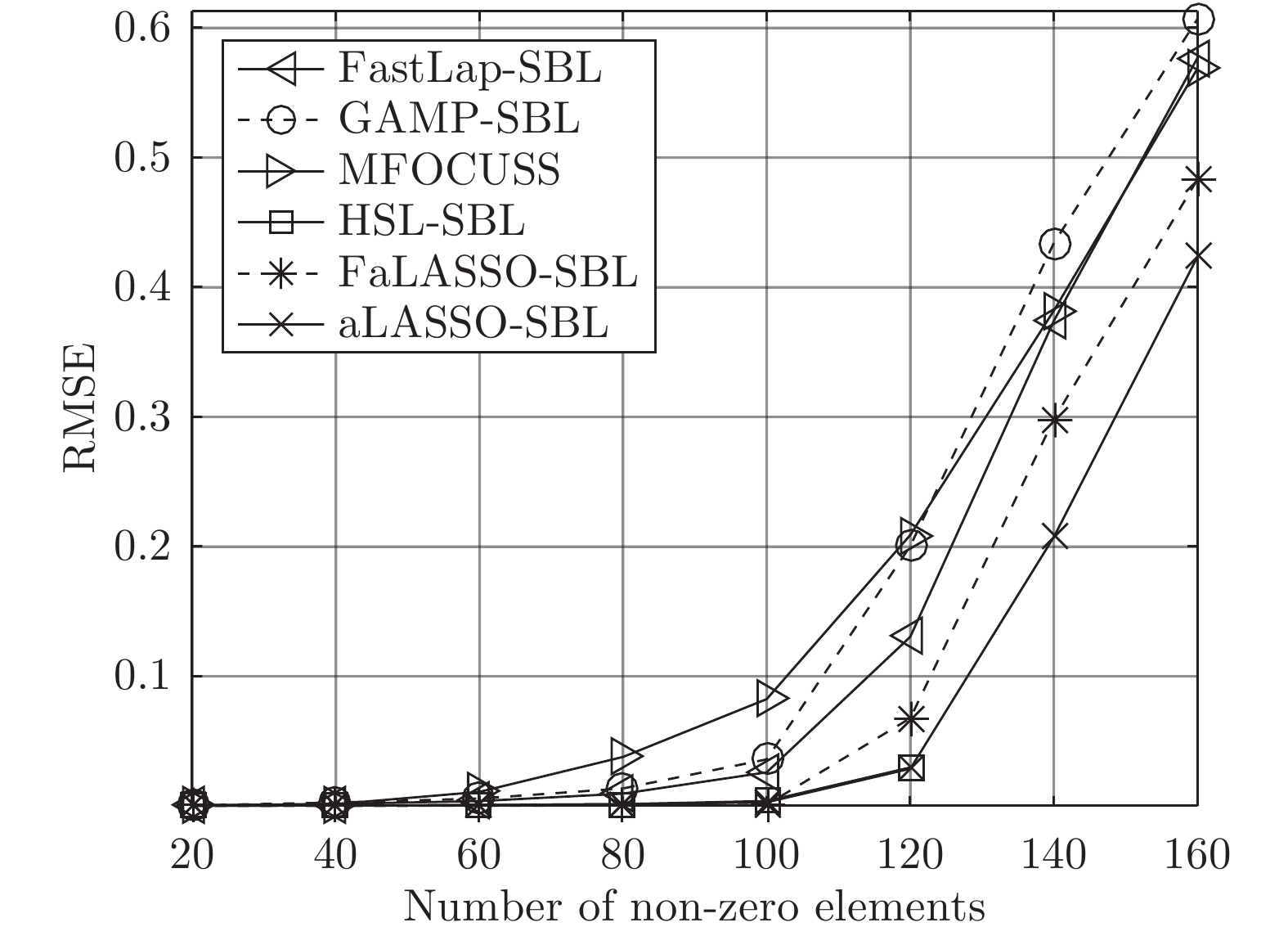
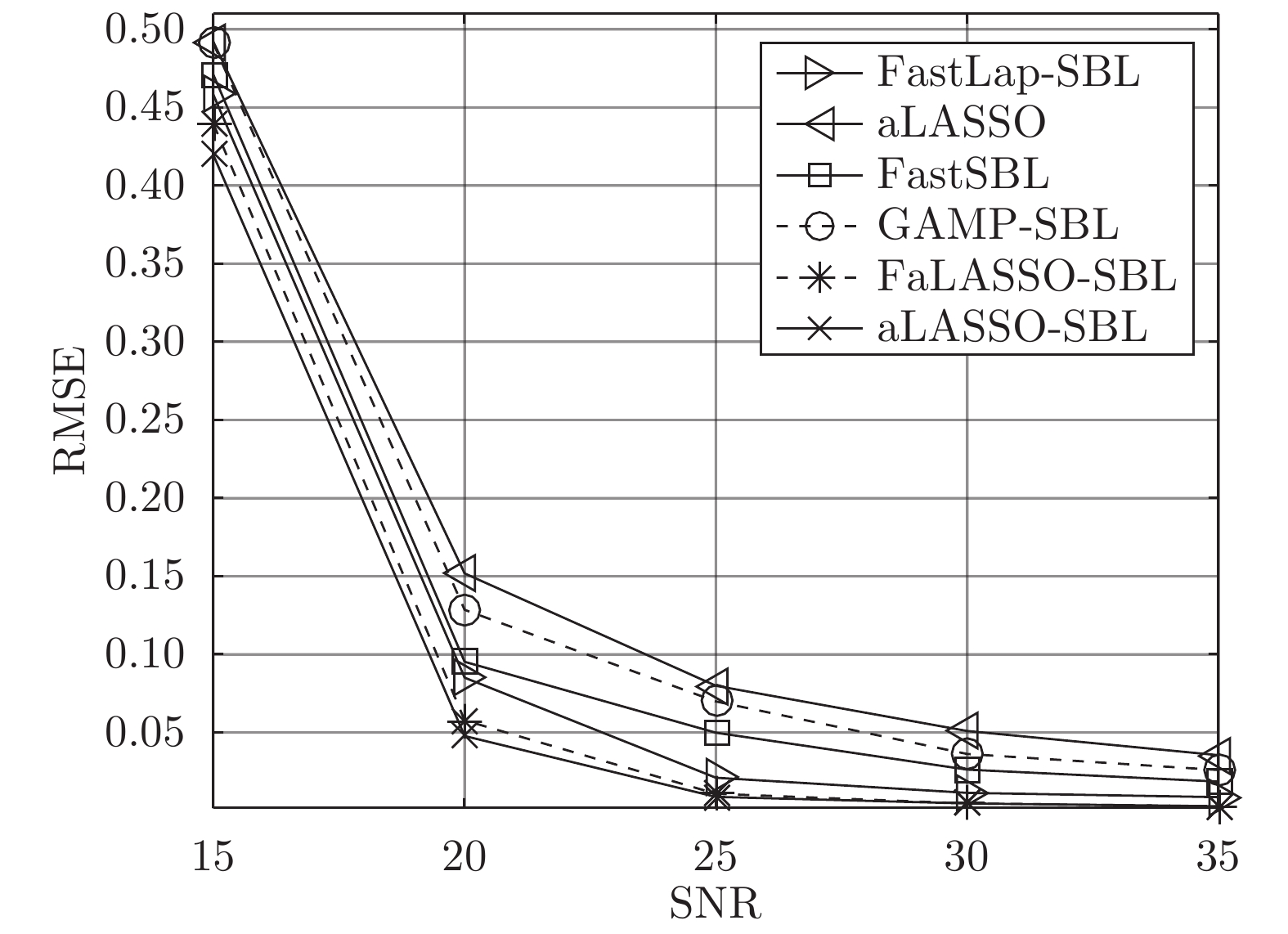
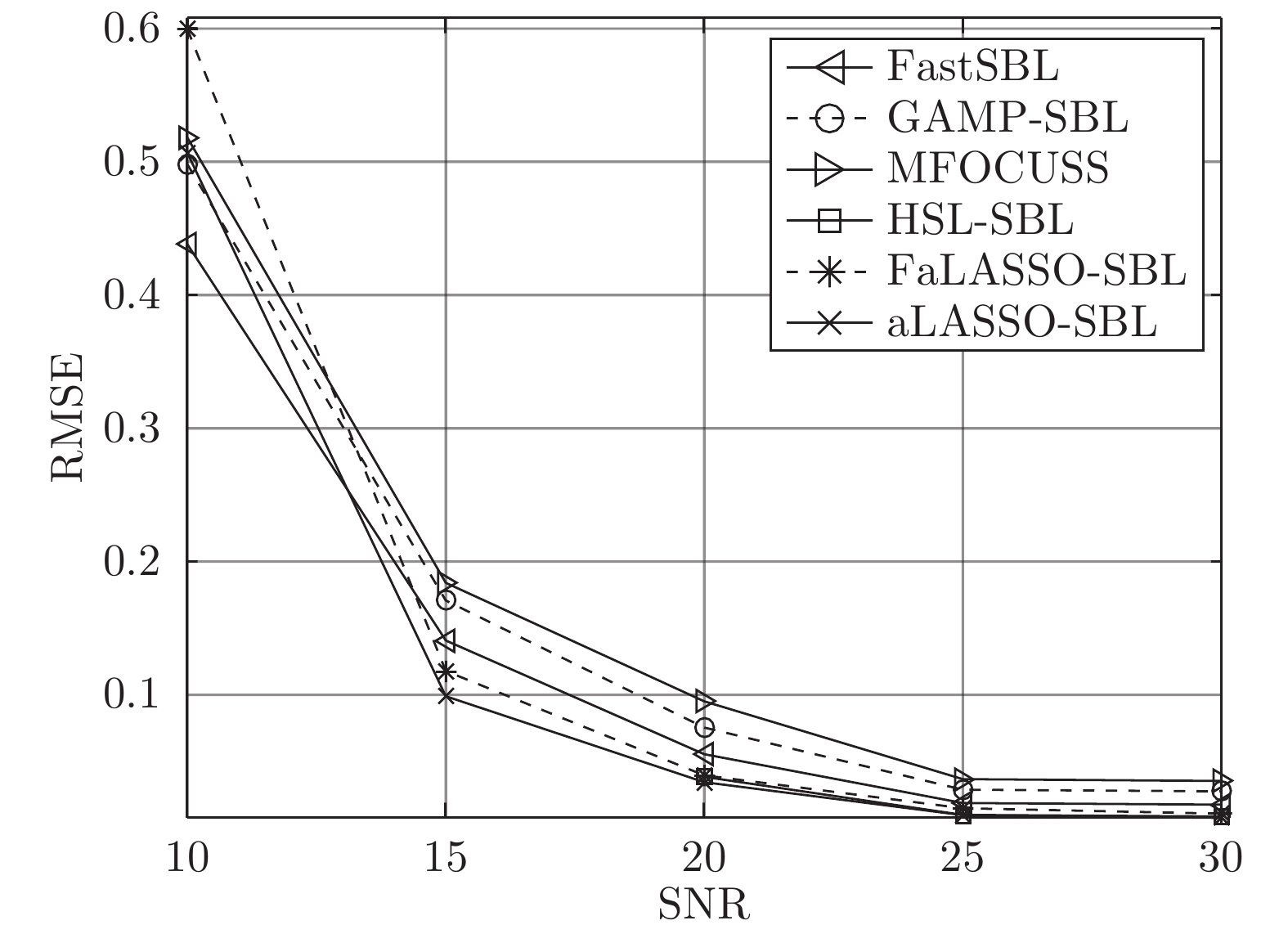
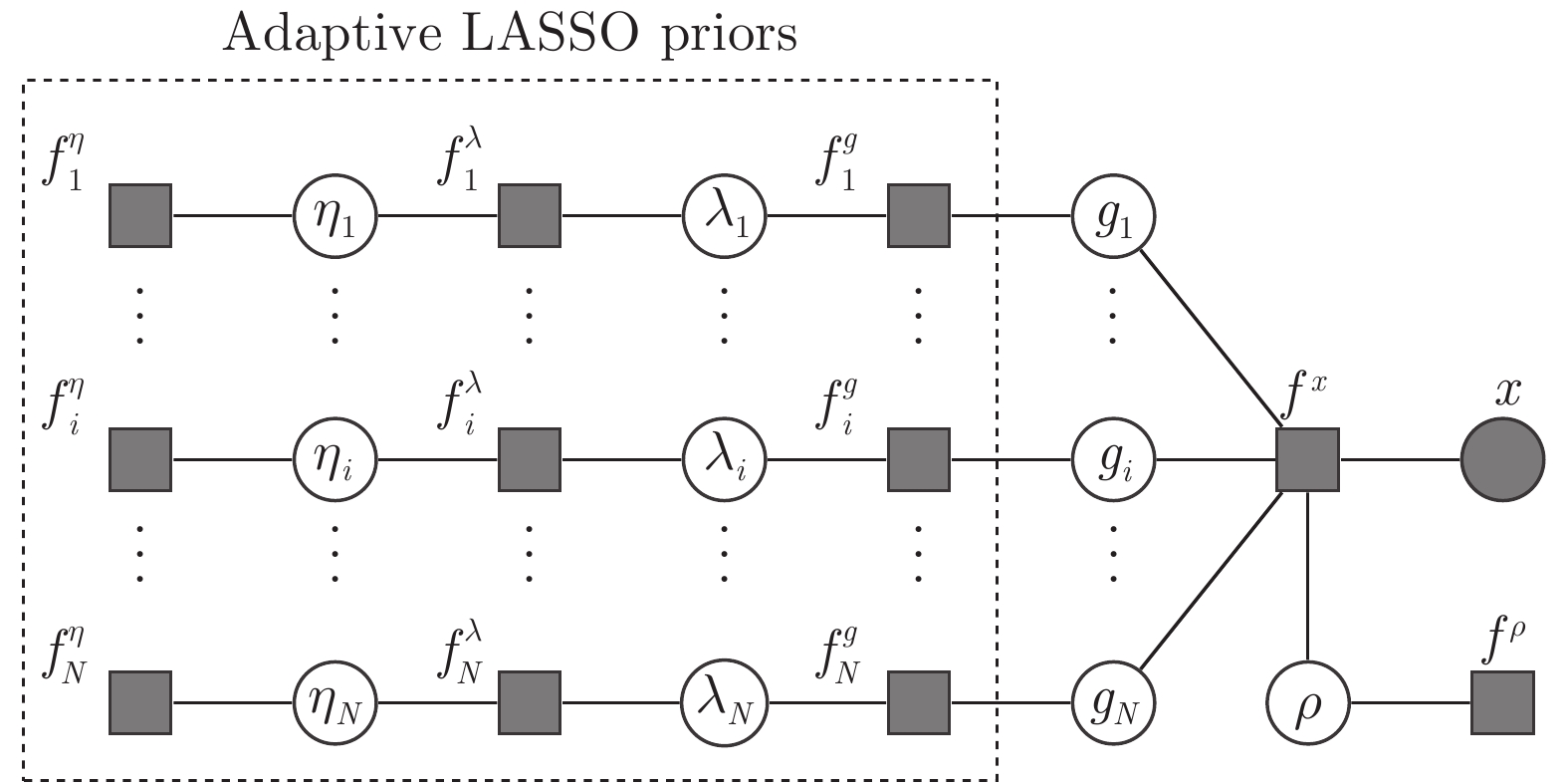
摘要: 为了提高稀疏信号恢复的准确性, 开展了基于自适应套索算子(Least absolute shrinkage and selection operator, LASSO)先验的稀疏贝叶斯学习(Sparse Bayesian learning, SBL)算法研究. 1) 在稀疏贝叶斯模型构建阶段, 构造了一种新的多层贝叶斯框架, 赋予信号中元素独立的LASSO先验. 该先验比现有稀疏先验更有效地鼓励稀疏并且该模型中所有参数更新存在闭合解. 然后在该多层贝叶斯框架的基础上提出了一种基于自适应LASSO先验的SBL算法. 2) 为降低提出的算法的计算复杂度, 在贝叶斯推断阶段利用空间轮换变元方法对提出的算法进行改进, 避免了矩阵求逆运算, 使参数更新快速高效, 从而提出了一种基于自适应LASSO先验的快速SBL算法. 本文提出的算法的稀疏恢复性能通过实验进行了验证, 分别针对不同大小测量矩阵的稀疏信号恢复以及单快拍波达方向(Direction of arrival, DOA)估计开展了实验. 实验结果表明: 提出基于自适应LASSO先验的SBL算法比现有算法具有更高的稀疏恢复准确度; 提出的快速算法的准确度略低于提出的基于自适应LASSO先验的SBL算法, 但计算复杂度明显降低.
-
关键词:
- 稀疏信号恢复 /
- 稀疏贝叶斯学习 /
- 自适应LASSO先验 /
- 贝叶斯推断
Abstract: To improve the recovery accuracy of sparse signal, we study on sparse Bayesian learning (SBL) algorithm using adaptive least absolute shrinkage and selection operator (LASSO) priors. First, a hierarchical Bayesian framework is built for Bayesian model. Each elements of the weights is assigned with hierarchical priors, resulting in adaptive LASSO priors. Compared with other priors, the proposed adaptive LASSO priors encourage sparsity more efficiently and all the variables in the proposed model can be updated using close form solution. Thus, a SBL algorithm using adaptive LASSO priors is proposed. Second, the space alternating approach is integrated into the proposed algorithm to reduce the computational complexity by avoiding matrix inverse operation. In this way, the parameters can be updated efficiently and a fast SBL algorithm using adaptive LASSO priors is proposed. The accuracy performance of the proposed algorithms are verified using numerical simulations versus different size of measurement matrix and single snapshot direction-of-arrival (DOA) estimation, respectively. The experiments show that the root mean square error (RMSE) of the proposed adaptive LASSO priors based SBL method is lower than state-of-the-art methods. Besides, the RMSE of proposed fast algorithm is slightly lower than the proposed adaptive LASSO priors based SBL method but achieves lower computational complexity performance.1) 1 Oracle特性具体包括模型选择相和性和参数估计渐进正态性. 其含义为, 在一些变量不是提前已知的情况下, 如果算法具有Oracle特性, 那么它能够筛选出正确的预测的概率为1而且能够有效而正确地估计非零估计量. -
表 1 各算法单次运行时间
Table 1 Time consumptions of different algorithms
实值信号模型 复值信号模型 算法 用时(s) 算法 用时(s) FastLaplace 0.11 FastSBL 1.54 aLASSO 1.94 GAMP-SBL 0.51 FastSBL 0.40 MFOCUSS 0.21 GAMP-SBL 0.07 HSL-SBL 3.16 FaLASSO-SBL 0.26 FaLASSO-SBL 0.74 aLASSO-SBL 0.98 aLASSO-SBL 2.33 表 2 恢复高维信号时各算法单次运行时间
Table 2 Time consumptions of different algorithms when the dimension of signal is high
实值信号模型 复值信号模型 算法 用时(s) 算法 用时(s) FastLaplace 0.83 FastSBL 6.95 aLASSO 5.71 GAMP-SBL 2.17 FastSBL 3.40 MFOCUSS 2.86 GAMP-SBL 0.69 HSL-SBL 15.73 FaLASSO-SBL 1.06 FaLASSO-SBL 4.61 aLASSO-SBL 8.38 aLASSO-SBL 17.41 表 3 单快拍DOA估计实验各算法单次运行时间
Table 3 Time consumptions of different algorithms for single snapshot DOA estimation
算法 用时(s) 算法 用时(s) SS-ESPRIT 0.37 HSL-SBL 0.85 SURE-IR 1.64 FaLASSO-SBL 0.47 L1-SR 0.91 aLASSO-SBL 0.83 OGSBL 0.69 -
[1] Wang L, Zhao L F, Bi G A,, Wan C R, Zhang L R, Zhang H J. Novel wideband DOA estimation based on sparse Bayesian learning with dirichlet process priors. IEEE Transactions on Signal Processing. 2016, 64(2): 275-289. doi: 10.1109/TSP.2015.2481790 [2] Xenaki A, Boldt J B, Christensen M G. Sound source localization and speech enhancement with sparse Bayesian learning beamforming. The Journal of the Acoustical Society of America. 2018, 143(6): 3912-3921 doi: 10.1121/1.5042222 [3] Bai Z L, Sun J W, Jensen J R, Christensen M G. Indoor sound source localization based on sparse Bayesian learning and compressed data. In: Proceedings of the 27th European Signal Processing Conference. A Coruna, Spain: IEEE, 2019. 1−5 [4] Zheng Y L, Fraysse A, Rodet T. Efficient variational Bayesian approximation method based on subspace optimization. IEEE Transactions on Image Processing. 2015, 24(2): 681-693 doi: 10.1109/TIP.2014.2383321 [5] 兰诚栋, 林宇鹏, 方大锐, 陈建. 多视点稀疏测量的图像绘制方法. 自动化学报, 2021, 47(4): 882-890Lan Cheng-Dong, Lin Yu-Peng, Fang Da-Rui, Chen Jian. Multi-view sparse measurement for image-based rendering method. Acta Automatica Sinica. 2021, 47(4): 882-890 [6] Zhang M C, Yuan X J, He Z Q. Variance state propagation for structured sparse Bayesian learning. IEEE Transactions on Signal Processing. 2020, 68: 2386-2400 doi: 10.1109/TSP.2020.2983827 [7] Liu S H, Huang Y M, Wu H, Tan C, Jia J B. Efficient multitask structure-aware sparse Bayesian learning for frequency-difference electrical impedance tomography. IEEE Transactions on Industrial Informatics. 2021, 17(1): 463-472 doi: 10.1109/TII.2020.2965202 [8] 郭俊锋, 李育亮. 基于学习字典的机器人图像稀疏表示方法. 自动化学报, 2020, 46(4): 820-830Guo Jun-Feng, Li Yu-Liang. Sparse representation of robot image based on dictionary learning algorithm. Acta Automatica Sinica. 2020, 46(4): 820-830 [9] 张芳, 王萌, 肖志涛, 吴骏, 耿磊, 童军, 王雯. 基于全卷积神经网络与低秩稀疏分解的显著性检测. 自动化学报, 2019, 45(11): 2148-2158Zhang Fang, Wang Meng, Xiao Zhi-Tao, Wu Jun, Geng Lei, Tong Jun, Wang Wen. Saliency detection via full convolution neural network and low rank sparse decomposition. Acta Automatica Sinica. 2019, 45(11): 2148-2158 [10] Ojeda A, Kenneth K D, Mullen T. Fast and robust block-sparse Bayesian learning for EEG source imaging. NeuroImage. 2018, 174: 449-462 doi: 10.1016/j.neuroimage.2018.03.048 [11] Jiao Y, Zhang Y, Chen X, Yin E W, Jin J, Wang X Y, Cichocki A. Sparse group representation model for motor imagery EEG classification. IEEE Journal of Biomedical and Health Informatics. 2019, 23(2): 631-641 doi: 10.1109/JBHI.2018.2832538 [12] Niu H Q, Gerstoft P, Ozanich E, Li Z L, Zhang R H, Gong Z X, Wang H B. Block sparse Bayesian learning for broadband mode extraction in shallow water from a vertical array. The Journal of the Acoustical Society of America 2020, 147(6): 3729-3739 doi: 10.1121/10.0001322 [13] Zheng R, Xu X, Ye Z F, Dai J S. Robust sparse Bayesian learning for DOA estimation in impulsive noise environments. Signal Processing. 2020, 171(107500): 1-6 [14] 曹娜, 王永利, 孙建红, 赵宁, 宫小泽. 基于字典学习和拓展联合动态稀疏表示的SAR目标识别. 自动化学报, 2020, 46(12): 2638-2646CAO Na, WANG Yong-Li, SUN Jian-Hong, ZHAO Ning, GONG Xiao-Ze. SAR target recognition based on dictionary learning and extended joint dynamic sparse representation. Acta Automatica Sinica. 2020, 46(12): 2638-2646 [15] Yang Z, Li J, Stoica P, Xie L H. Sparse methods for direction-of-arrival estimation. Academic Press Library in Signal Processing. London: Academic Press, 2018. 509-581 [16] Tipping M E, Smola A. Sparse Bayesian learning and the relevance vector machine. The Journal of Machine Learning Research. 2001, 59(1): 211-244 [17] Babacan S D, Molina R, Katsaggelos A K. Bayesian compressive sensing using laplace priors. IEEE Transactions on Image Processing. 2010, 19(1): 53-63 doi: 10.1109/TIP.2009.2032894 [18] Zhao L F, Wang L, Bi G A, Yang L. An autofocus technique for high-resolution inverse synthetic aperture radar imagery. IEEE Transactions on Geoscience and Remote Sensing. 2014, 52(10): 6392-6403 doi: 10.1109/TGRS.2013.2296497 [19] Yang J, Yang Y. Sparse Bayesian DOA estimation using hierarchical synthesis lasso priors for off-grid signals. IEEE Transactions on Signal Processing. 2020, 68: 872-884 doi: 10.1109/TSP.2020.2967665 [20] Zou H. The adaptive lasso and its oracle properties. Journal of the American Statistical Association. 2006, 101(476): 1418-1429 doi: 10.1198/016214506000000735 [21] Tipping M E, Faul A C. Fast marginal likelihood maximisation for sparse Bayesian models. In: Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics. Florida, USA: Springer, 2003. 3−6 [22] Duan H, Yang L, Fang J, Li H. Fast inverse-free sparse Bayesian learning via relaxed evidence lower bound maximization. IEEE Signal Processing Letters. 2017, 24(6): 774-778 doi: 10.1109/LSP.2017.2692217 [23] Shoukairi M A, Rao B D. Sparse Bayesian learning using approximate message passing. In: Proceedings of the 48th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, USA: IEEE, 2014. 1957−1961 [24] Shoukairi M A, Schniter P, Rao B D. A gamp-based low complexity sparse Bayesian learning algorithm. IEEE Transactions on Signal Processing. 2018, 66(2): 294-308 doi: 10.1109/TSP.2017.2764855 [25] Thomas C K, Slock D. Save - space alternating variational estimation for sparse Bayesian learning. In: Proceedings of IEEE Data Science Workshop. Lausanne, Switzerland: IEEE, 2018. 11−15 [26] Worley B. Scalable mean-field sparse Bayesian learning. IEEE Transactions on Signal Processing. 2019, 67(24): 6314-6326 doi: 10.1109/TSP.2019.2954504 [27] Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory. 2006, 52(2): 489-509 doi: 10.1109/TIT.2005.862083 [28] Wipf D P, Rao B D, Nagarajan S. Latent variable Bayesian models for promoting sparsity. IEEE Transactions on Information Theory. 2011, 57(9): 6236-6255 doi: 10.1109/TIT.2011.2162174 [29] Figueiredo M A T, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE Journal of Selected Topics in Signal Processing. 2007, 1(4): 586-597 doi: 10.1109/JSTSP.2007.910281 [30] Xenaki A, Gerstoft P, Mosegaard K. Compressive beamforming. Journal of the Acoustical Society of America. 2014, 136(1): 260-271 doi: 10.1121/1.4883360 [31] Bishop C M. Pattern recognition and machine learning. New York, USA: Springer-Verlag, 2006. 152−169 [32] Tzikas D G, Likas A C, Galatsanos N P. The variational approximation for Bayesian inference. IEEE Signal Processing Magazine. 2008, 25(6): 131-146 doi: 10.1109/MSP.2008.929620 [33] Higham N J. Accuracy and stability of numerical algorithms. Society for Industrial and Applied Mathematics. Philadelphia, USA: Springer, 2002. 67−93 [34] Pati Y C, Rezaiifar R, Krishnaprasad P S. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. In: Proceesdings of the Conference on Signals, Systems and Computers. Pacific Grove, USA: IEEE, 2002. 1−5 [35] Cotter S F, Rao B D, Engan K, Delgado K K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Transactions on Signal Processing. 2005, 53(7): 2477-2488 doi: 10.1109/TSP.2005.849172 [36] Thakre A, Haardt M, Giridhar K. Single snapshot spatial smoothing with improved effective array aperture. IEEE Signal Processing Letters. 2009, 16(6): 505-508 doi: 10.1109/LSP.2009.2017573 [37] Raj A G, Mcclellan J H. Single snapshot super-resolution DOA estimation for arbitrary array geometries. IEEE Signal Processing Letters. 2019, 26(1): 119-123 doi: 10.1109/LSP.2018.2881927 [38] Fang J, Wang F, Shen Y, Li H, Blum R S. Super-resolution compressed sensing for line spectral estimation: An iterative reweighted approach. IEEE Transactions on Signal Processing. 2016, 64(18): 4649-4662 doi: 10.1109/TSP.2016.2572041 [39] Yang Z, Xie L H, Zhang C. Off-grid direction of arrival estimation using sparse Bayesian inference. IEEE Transactions on Signal Processing. 2013, 61(1): 38-43 doi: 10.1109/TSP.2012.2222378 -




 下载:
下载: