-
摘要: 代理模型能够辅助进化算法在计算资源有限的情况下加快找到问题的最优解集, 因此建立高效的代理模型辅助多目标进化搜索逐渐受到了重视. 然而随着目标数量的增加, 对每个目标分别建立高斯过程模型时个体整体估值的不确定度会随之增加. 因此通过对模型最优解集的搜索探索原问题潜在的非支配解集, 并基于个体的收敛性, 种群的多样性和估值的不确定度, 提出了一种新的期望提高计算方法, 用于辅助从潜在的非支配解集中选择使用真实目标函数计算的个体, 从而更新代理模型, 能够在有限的计算资源下更有效地辅助优化算法找到好的非支配解集. 在7个DTLZ 基准测试问题上的实验对比结果表明, 该算法在求解计算费时高维多目标优化问题上是有效的, 且具有较强的竞争力.Abstract: Surrogate models have attracted increasing attention in assisting evolutionary many-objective optimization when the computational budget is limited since a surrogate model can assist to accelerate the search for a set of Pareto solutions. However, the approximation uncertainty of an individual on the objective approximated values will be increased when the number of objectives increases in the case that a surrogate model is trained for each objective. Therefore, we propose to explore the potential non-dominated solutions of the original optimization problem by searching for the optimal solutions of the surrogate models, and a new expected improvement in this paper, which takes into account on the convergence of the solution, the diversity of the population, and the uncertainty of the approximation, for assisting selecting solutions from the potential non-dominated solutions to be evaluated using the exact expensive objective function. The surrogate model will be updated using the new evaluated solutions and is expected to assist the optimization algorithms to efficiently find a good set of non-dominated solutions within a limited computational budget. The experimental results on seven DTLZ test problems show that our proposed method is efficient and competitive to solve expensive many-objective problems.
-
表 1 SAExp-EMO和ParEGO在3个和4个目标函数的DTLZ测试问题上获得的平均IGD统计结果
Table 1 Average IGD statistical results of SAExp-EMO and ParEGO on DTLZ test problems of 3 and 4 objective functions
测试问题 目标数 ParEGO SAExp-EMO DTLZ1 3 $4.84\times 10^{1}(8.51\times 10^{0})$− $\bf{1.09\times10^{1}(4.16\times 10^{0})}$ 4 $5.49\times10^{1}(1.09\times10^{1})$− $\bf{1.25\times10^{1}(5.06\times10^{1})}$ DTLZ2 3 $4.76\times10^{-1}(3.63\times10^{-2})$− $\bf{1.72\times10^{-1}(4.60\times10^{-2})} $ 4 $5.77\times10^{-1}(2.98\times10^{-2})$− $\bf{3.65\times10^{-1}(4.40\times10^{-1})}$ DTLZ3 3 $4.61\times10^{0}(5.38\times10^{1})$− $\bf{1.65\times10^{2}(6.07\times10^{1})} $ 4 $4.45\times10^{2}(7.57\times10^{1})$− $\bf{2.40\times10^{2}(1.19\times10^{2})}$ DTLZ4 3 $7.80\times10^{-1}(7.38\times10^{-2})$$\approx$ $\bf{5.59\times10^{-1}(4.80\times10^{-2})}$ 4 $8.92\times10^{-1}(9.00\times10^{-1})$− $\bf{7.12\times10^{-1}(1.48\times10^{\rm{-}1})} $ DTLZ5 3 $3.74\times10^{-1}(7.78\times10^{-2})$− $\bf{4.01\times10^{-2}(7.00\times10^{-2})}$ 4 $4.09\times10^{-1}(4.52\times10^{-2})$− $\bf{7.80\times10^{-2}(0.00\times10^{0})}$ DTLZ6 3 $8.04\times10^{0}(2.44\times10^{-1})$− $\bf{3.63\times10^{0}(2.61\times10^{0})}$ 4 $8.16\times10^{0}(2.52\times10^{-1})$− $\bf{3.84\times10^{0}(4.61\times10^{-1})}$ DTLZ7 3 $7.28\times10^{0}(2.16\times10^{0})$− $\bf{7.70\times10^{-1}(1.35\times10^{-1})}$ 4 $ 1.11\times10^{1}(7.97\times10^{-1})$− $\bf{1.09\times10^{0}(3.18\times10^{-1})}$ +/−/≈ 0/13/1 表 2 SAExp-EMO、RVEA、K-RVEA和CSEA得到的平均IGD值
Table 2 Average IGD values obtained by SAExp-EMO, RVEA, K-RVEA and CSEA
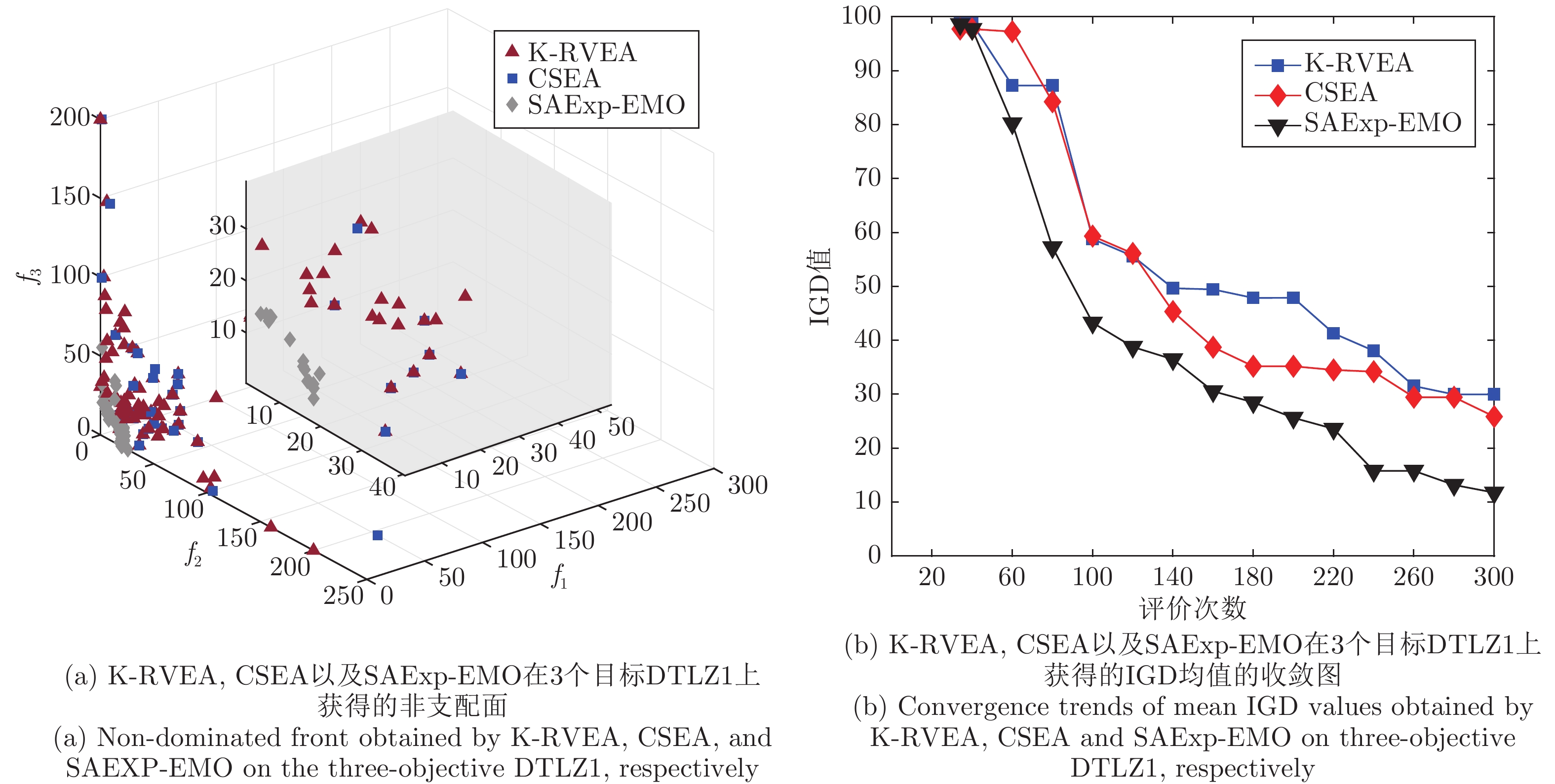
测试问题 目标数 RVEA K-RVEA CSEA SAExp-EMO DTLZ1 3 $3.65\times10^{1}(1.10\times10^{1})$− $2.48\times10^{1}(8.56\times10^{0})$− $1.97\times10^{1}(5.82\times10^{0})$− $\bf{1.33\times10^{1}(4.53\times10^{0})} $ 4 $3.18\times10^{1}(1.03\times10^{1})$− $3.01\times10^{1}(1.18\times10^{1})$− $1.71\times10^{1}(5.31\times10^{0})$− $\bf{1.35\times10^{1}(5.03\times10^{0})} $ 6 $2.96\times10^{1}(8.16\times10^{0})$− $3.18\times10^{1}(6.94\times10^{0})$− $1.43\times10^{1}(6.68\times10^{0})$− $\bf{1.15\times10^{1}(6.29\times10^{0})}$ 8 $2.00\times10^{1}(9.31\times10^{0})$− $3.22\times10^{1}(1.12\times10^{1})$$\approx$ $1.44\times10^{1}(6.01\times10^{0})$− $\bf{1.17\times10^{1}(4.46\times10^{0})} $ 10 $2.15\times10^{1}(8.45\times10^{0})$− $2.48\times10^{1}(9.28\times10^{0})$− $1.45\times10^{1}(5.70\times10^{0})$− $\bf{1.28\times10^{1}(5.45\times10^{0})}$ DTLZ2 3 $4.09\times10^{-1}(3.22\times10^{-2})$− $2.66\times10^{-1}(4.88\times10^{-2})$− $2.69\times10^{-1}(1.13\times10^{-1})$− $\bf{1.38\times10^{-1}(6.13\times10^{-2} )}$ 4 $5.16\times10^{-1}(3.61\times10^{-2})$− $3.95\times10^{-1}(4.94\times10^{-2})$− $4.76\times10^{-1}(1.04\times10^{-1})$− $\bf{3.27\times10^{-1}(5.53\times10^{-2})}$ 6 $6.97\times10^{-1}(6.73\times10^{-2})$− $5.93\times10^{-1}(4.96\times10^{-2})$− $\bf{5.76\times10^{-1}(4.01\times10^{-2})}$$\approx$ ${6.15\times10^{-1}(4.93\times10^{-2})}$ 8 $7.93\times10^{-1}(3.69\times10^{-2})$− $6.54\times10^{-1}(4.95\times10^{-2})$− $7.57\times10^{-1}(3.52\times10^{-2})$− $\bf{5.45\times10^{-1}(2.42\times10^{-1})}$ 10 $9.54\times10^{-1}(5.16\times10^{-2})$− $7.36\times10^{-1}(4.59\times10^{-2})$− $8.44\times10^{-1}(5.65\times10^{-2})$− $\bf{6.08\times10^{-1}(3.09\times10^{-1})}$ DTLZ3 3 $4.18\times10^{2}(6.66\times10^{1})$− $3.38\times10^{2}(7.51\times10^{1})$− $2.12\times10^{2}(4.37\times10^{1})$− $\bf{1.13\times10^{2}(2.96\times10^{1})}$ 4 $4.17\times10^{2}(7.54\times10^{1})$− $3.56\times10^{2}(7.56\times10^{1})$− $2.17\times10^{2}(4.94\times10^{1})$− $\bf{1.26\times10^{2}(6.16\times10^{1})}$ 6 $3.85\times10^{2}(7.05\times10^{1})$− $3.45\times10^{2}(7.90\times10^{1})$− $2.09\times10^{2}(5.44\times10^{1})$− $\bf{1.46\times10^{2}(7.89\times10^{1})}$ 8 $3.57\times10^{2}(7.05\times10^{1})$− $3.38\times10^{2}(5.74\times10^{1})$− $2.08\times10^{2}(5.09\times10^{1})$− $\bf{1.49\times10^{2}(7.88\times10^{1} )}$ 10 $3.77\times10^{2}(1.02\times10^{2})$− $3.24\times10^{2}(7.92\times10^{1})$− $2.18\times10^{2}(5.85\times10^{1})$ $\approx$ $\bf{1.10\times10^{2}(2.87\times10^{1})}$ DTLZ4 3 $5.58\times10^{-1}(6.90\times10^{-2})$− $\bf{4.17\times10^{-1}(1.12\times10^{-1})}$ $\approx$ $7.22\times10^{-1}(1.53\times10^{-1})$− $4.81\times10^{-1}(1.40\times10^{-1})$ 4 $6.96\times10^{-1}(8.80\times10^{-2})$ $\approx$ $5.46\times10^{-1}(1.13\times10^{-1})$+ $\bf{5.43\times10^{-1}(1.02\times10^{-1})}$+ $6.64\times10^{-1}(1.45\times10^{-1})$ 6 $8.53\times10^{-1}(8.13\times10^{-2})$− $6.84\times10^{-1}(8.64\times10^{-2})$+ $\bf{5.74\times10^{-1}(1.01\times10^{-1})}$ $\approx$ $8.52\times10^{-1}(8.99\times10^{-2})$ 8 $9.32\times10^{-1}(7.75\times10^{-2})$− $8.34\times10^{-1}(9.14\times10^{-2})$+ $\bf{7.39\times10^{-1}(3.42\times10^{-2})}$+ $8.36\times10^{-1}(1.76\times10^{-1})$ 10 $1.03\times10^{0}(7.03\times10^{-2})$− $8.89\times10^{-1}(6.96\times10^{-2})$ $\approx$ $\bf{8.12\times10^{-1}(4.54\times10^{-2})}$+ $8.17\times10^{-1}(2.43\times10^{-1})$ DTLZ5 3 $3.45\times10^{-1}(4.41\times10^{-2})$− $1.81\times10^{-1}(4.44\times10^{-2})$− $1.46\times10^{-1}(4.29\times10^{-2})$− $\bf{3.84\times10^{-2}(8.64\times10^{-3})}$ 4 $3.79\times10^{-1}(7.42\times10^{-2})$− $1.90\times10^{-1}(3.12\times10^{-2})$− $2.00\times10^{-1}(4.29\times10^{-2})$− $\bf{6.98\times10^{-2}(1.43\times10^{-2})}$ 6 $4.28\times10^{-1}(6.52\times10^{-2})$− $2.29\times10^{-1}(3.40\times10^{-1})$ $\approx$ $2.17\times10^{-1}(7.87\times10^{-1})$− $\bf{1.30\times10^{-1}(4.04\times10^{-2})}$ 8 $4.26\times10^{-1}(5.83\times10^{-2})$− $2.19\times10^{-1}(4.87\times10^{-2})$− $2.43\times10^{-1}(6.08\times10^{-2})$− $\bf{8.31\times10^{-2}(2.32\times10^{-2})}$ 10 $4.06\times10^{-1}(1.02\times10^{-1})$− $2.23\times10^{-1}(5.87\times10^{-2})$ $\approx$ $2.54\times10^{-1}(5.35\times10^{-2})$− $\bf{9.97\times10^{-2}(4.07\times10^{-2})} $ DTLZ6 3 $7.94\times10^{0}(2.75\times10^{-1})$− $4.42\times10^{0}(5.40\times10^{-1})$− $4.54\times10^{0}(5.84\times10^{-1})$− $\bf{3.07\times10^{0}(7.11\times10^{-1})}$ 4 $8.02\times10^{0}(2.61\times10^{-1})$− $4.35\times10^{0}(4.66\times10^{-1})$− $6.99\times10^{0}(7.87\times10^{-1})$− $\bf{3.46\times10^{0}(4.82\times10^{-1})}$ 6 $8.19\times10^{0}(3.42\times10^{-1})$− $4.58\times10^{0}(7.79\times10^{-1})$− $7.11\times10^{0}(1.76\times10^{-1})$− $\bf{4.19\times10^{0}(6.93\times10^{-1})} $ 8 $8.18\times10^{0}(2.75\times10^{-1})$− $5.78\times10^{0}(4.49\times10^{-1})$− ${7.21\times10^{0}(5.28\times10^{-1})}$$\approx$ $\bf{3.60\times10^{0}(5.11\times10^{-1})}$ 10 $8.22\times10^{0}(4.07\times10^{-1})$− $6.32e\times10^{0}(6.35\times10^{-1})$ $\approx$ $7.44\times10^{0}(4.18\times10^{-1})$ $\approx$ $\bf{3.95\times10^{0}(1.16\times10^{0})}$ DTLZ7 3 $6.85\times10^{0}(7.29\times10^{-1})$− $1.15\times10^{0}(1.69\times10^{0})$− $4.02\times10^{0}(4.82\times10^{0})$− $\bf{5.36\times10^{-1}(2.26\times10^{-1})}$ 4 $8.81\times10^{0}(1.31\times10^{0})$− $2.14\times10^{0}(3.24\times10^{0})$ $\approx$ $7.54\times10^{0}(9.33\times10^{-1})$ $\approx$ $\bf{6.92\times10^{-1}(1.37\times10^{-1})}$ 6 $1.29\times10^{1}(1.44\times10^{0})$− $3.49\times10^{0}(2.76\times10^{0})$− $1.36\times10^{1}(1.65\times10^{0})$− $ \bf{1.13\times10^{0}(2.42\times10^{-1})}$ 8 $1.72\times10^{1}(2.18\times10^{0})$− $4.18\times10^{0}(2.18\times10^{0})$− $2.26\times10^{1}(2.27\times10^{0})$− $\bf{6.82\times10^{-1}(1.38\times10^{-1})}$ 10 $2.18\times10^{1}(3.56\times10^{0})$− $7.83\times10^{0}(3.32\times10^{0})$− $2.86\times10^{1}(2.30\times10^{0})$− $\bf{1.19\times10^{0}(5.68\times10^{-1})} $ +/−/≈ 0/34/1 3/25/7 3/26/6 -
[1] 张晗, 杨继斌, 张继业, 宋鹏云, 徐晓惠. 燃料电池有轨电车能量管理Pareto多目标优化. 自动化学报, 2019, 45(12): 2378-2392Zhang Han, Yang Ji-Bin, Zhang Ji-Ye, Song Peng-Yun, Xu Xiao-Hui. Pareto-based multi-objective optimization of energy management for fuel cell tramway. Acta Automatica Sinica, 2019, 45(12): 2378-2392 [2] Coello Coello C A, Brambila G, Figueroa Gamboa S, Gamboa J F, Tapia M G C, Gómez R H. Evolutionary multiobjective optimization: open research areas and some challenges lying ahead. Complex & Intelligent Systems, 2020, 6(1), 221-236 [3] 王柳静, 张贵军, 周晓根. 基于状态估计反馈的策略自适应差分进化算法. 自动化学报, 2020, 46(4): 752-766.Wang Liu-Jing, Zhang Gui-Jun, Zhou Xiao-Gen. Strategy self-adaptive differential evolution algorithm based on state estimation feedback. Acta Automatica Sinica, 2020, 46(4): 752-766 [4] 封文清, 巩敦卫. 基于在线感知pareto前沿划分目标空间的多目标进化优化. 自动化学报, 2020, 46(8): 1628-1643Feng Wen-Qing, Gong Dun-Wei. Multi-objective evolutionary optimization with objective space partition based on online perception of pareto front. Acta Automatica Sinica, 2020, 46(8): 1628-1643 [5] Deb K, Pratap A, Genetic K, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGAII. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197 doi: 10.1109/4235.996017 [6] 栗三一, 王延峰, 乔俊飞, 黄金花. 一种基于区域局部搜索的NSGAII算法. 自动化学报, 2020, 46(12): 2617-2627Li San-Yi, Wang Yan-Feng, Qiao Jun-Fei, Huang Jin-Hua. A regional local search strategy for NSGAII algorithm. Acta Automatica Sinica, 2020, 46(12): 2617-2627 [7] Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the performance of the strength pareto evolutionary algorithm. Technical Report Gloriastrasse, 2001, 3242(4): 742-751 [8] Zhang Q, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731 doi: 10.1109/TEVC.2007.892759 [9] Cheng R, Jin Y, Olhofer M, Sendhoff B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2006, 20(5): 773-791 [10] Zitzler E, Künzli S. Indicator-based selection in multi-objective search. In Proceedings of: International Conference on Parallel Problem Solving from Nature, Berlin, Heidelberg, 2004. 832−842 [11] Bader J, Zitzler E. HYPE: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary Computation, 2011, 19(1): 45-76 doi: 10.1162/EVCO_a_00009 [12] Li K, Deb K, Zhang Q, Kwong S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Transactions on Evolutionary Computation, 2015, 19(5): 694-716 doi: 10.1109/TEVC.2014.2373386 [13] Li M, Yang S, Liu X. Bi-goal evolution for many-objective optimization problems. Artificial Intelligence, 2015, 228: 45-65 doi: 10.1016/j.artint.2015.06.007 [14] 柳强, 焦国帅. 基于Kriging模型和NSGA-II的航空发动机管路卡箍布局优化. 智能系统学报, 2019, 14(2): 281-287Liu Qiang, Jiao Guo-Shuai. Layout optimization of aero-engine pipe clamps based on kriging model and NSGAII. CAAI Transactions on Intelligent Systems, 2019, 14(2): 281-287 [15] Akhtar T, Shoemaker C A. Multi objective optimization of computationally expensive multi-modal functions with RBF surrogates and multi-rule selection. Journal of Global Optimization, 2016, 64(1): 17-32 doi: 10.1007/s10898-015-0270-y [16] Zhang Q, Liu W, Tsang E, Virginas B. Expensive multiobjective optimization by MOEA/D with Gaussian process model. IEEE Transactions on Evolutionary Computation, 2010, 14(3): 456-474 doi: 10.1109/TEVC.2009.2033671 [17] Chugh T, Jin Y, Miettinen K, Hakanen J, Sindhya K. A surrogate-assisted reference vector guided evolutionary algorithm for computationally expensive many-objective optimization. IEEE Transactions on Evolutionary Computation, 2016, 22(1): 129-142 [18] Wang X, Jin Y, Schmitt S, et al. An adaptive bayesian approach to surrogate-assisted evolutionary multi-objective optimization. Information Sciences, 2020, 519: 317-331 doi: 10.1016/j.ins.2020.01.048 [19] Yang C, Ding J, Jin Y, Chai T. Off-line data-driven multi-objective optimization: knowledge transfer between surrogates and generation of final solutions. IEEE Transactions on Evolutionary Computation, 2020, 24(3): 409-423 [20] Yang C, Ding J, Jin Y, Wang C, Chai T. Multi-tasking multi-objective evolutionary operational indices optimization of beneficiation processes. IEEE Transactions on Automation Science and Engineering, 2019, 16(3): 1046-1057 doi: 10.1109/TASE.2018.2865593 [21] Zhao Y, Sun C, Zeng J, Tan Y, Zhang G. A surrogate-ensemble assisted expensive many-objective optimization. Knowledge-Based Systems, 2020, 211: 106520 [22] Knowles J. ParEGO: A hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems. IEEE Transactions on Evolutionary Computation, 2006, 14(1): 50-66 [23] Pan L, He C, Tian Y, Wang H, Zhang X, Jin Y. A classification based surrogate-assisted evolutionary algorithm for expensive many-objective optimization. IEEE Transactions on Evolutionary Computation, 2019, 23(1): 74-88 doi: 10.1109/TEVC.2018.2802784 [24] Zhang J, Zhou A, Zhang G. A classification and pareto domination based multiobjective evolutionary algorithm; In: Proceedings of the 2015 IEEE Congress on Evolutionary Computation. Sendai, Japan: 2015. 2883−2890 [25] Freeny A. Empirical model-building and response surfaces. Technometrics, 1987, 30(2): 229-231 [26] Yang H, Liu J. An adaptive RBF neural network control method for a class of nonlinear systems. IEEE/CAA Journal of Automatica Sinica, 2018, 5(4): 457-462 [27] Sun C, Jin Y, Cheng R, Ding J, Zeng J. Surrogate-assisted cooperative swarm optimization of high-dimensional expensive problems. IEEE Transactions on Evolutionary Computation, 2017, 21(4): 644-660 doi: 10.1109/TEVC.2017.2675628 [28] 何志昆, 刘光斌, 赵曦晶, 王明昊. 高斯过程回归方法综述. 控制与决策, 2013, 28(8): 1121-1129He Zhi-Kun, Liu Guang-Bin, Zhao Xi-Jing, Wang Ming-Hao. Overview of gaussian process regression. Control and Decision, 2013, 28(8): 1121-1129 [29] Nelson D, Wang J. Introduction to artificial neural systems. Neurocomputing, 1992, 4(6): 328-330 doi: 10.1016/0925-2312(92)90018-K [30] Cortes C, Vapnik V N. Support-vector networks. Machine Learning, 1995, 20(3): 273-293 [31] Liao P, Sun C, Zhang G, Jin Y. Multi-surrogate multi-tasking optimization of expensive problems. Knowledge-Based Systems, 2020, 205(6): 106262 [32] 田杰, 孙超利, 谭瑛, 曾建潮. 基于多点加点准则的代理模型辅助社会学习微粒群算法. 控制与决策, 2020, 35(1): 131-138Tian Jie, Sun Chao-Li, Tan Ying, Zeng Jian-Chao. Similarity-based multipoint infill criterion for surrogate-assisted social learning particle swarm optimization. Control and Decision, 2020, 35(1): 131-138 [33] Guo D, Jin Y, Ding J, Chai T. A multiple surrogate assisted decomposition based evolutionary algorithm for expensive multi/many-objective optimization. IEEE Transactions on Cybernetics, 2018, 49(3): 1012-1025 [34] Deb K, Thiele L, Laumanns M, Zitzler E. Scalable multi-objective optimization test problems. In: Proceedings of the 2002 IEEE Congress on Evolutionary Computation. Honolulu, USA: 2002. 1: 825−830 [35] Habib A, Singh H K, Chugh T, Ray T, Mettinen K. A multiple surrogate assisted decomposition based evolutionary algorithm for expensive multi/many-objective optimization. IEEE Transactions on Evolutionary Computation, 2019, 23(6): 1000-1004 doi: 10.1109/TEVC.2019.2899030 -




 下载:
下载: