-
摘要:
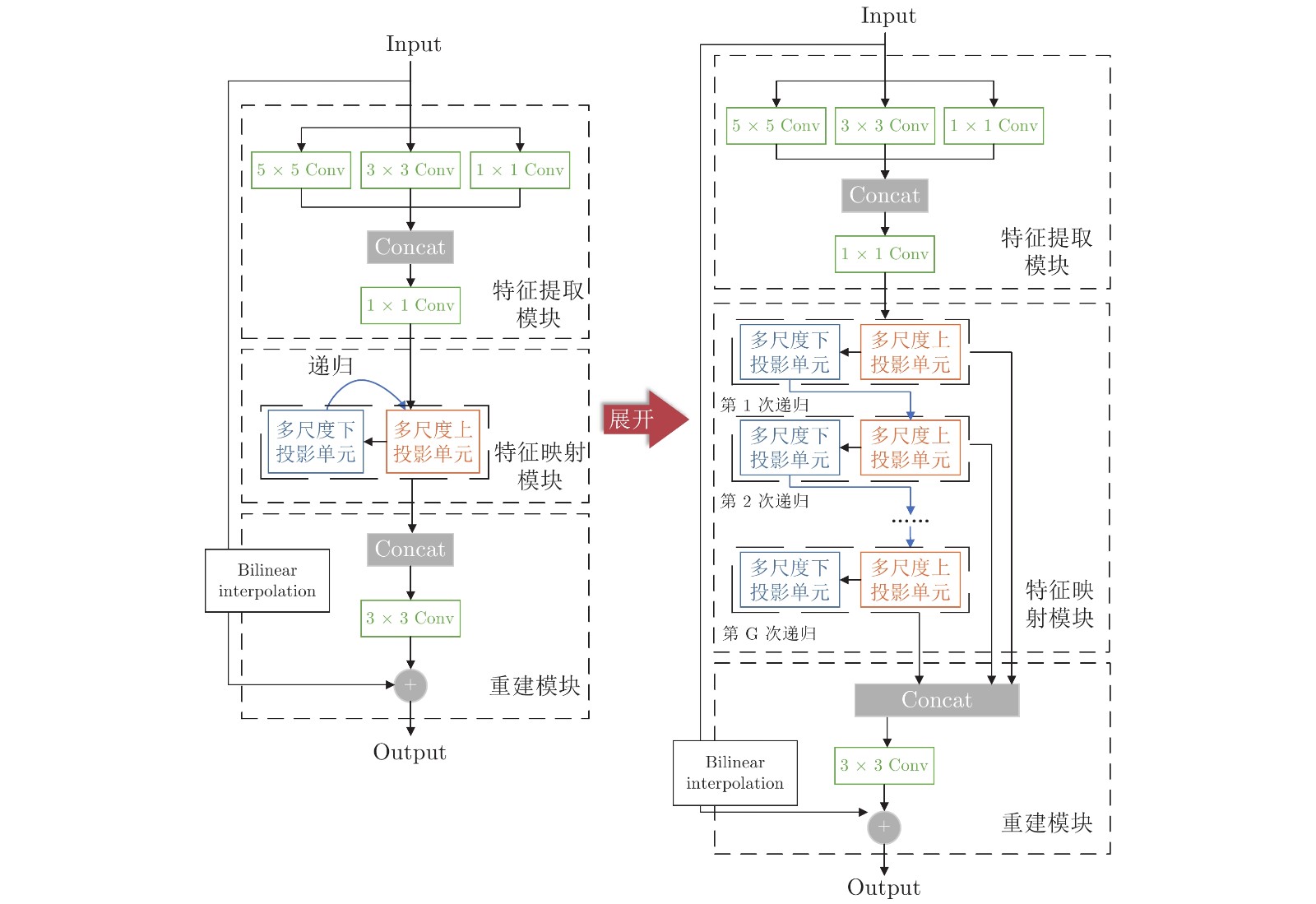
针对现有图像超分辨率重建方法恢复图像高频细节能力较弱、特征利用率不足的问题, 提出了一种多尺度特征融合反投影网络用于图像超分辨率重建. 该网络首先在浅层特征提取层使用多尺度的卷积核提取不同维度的特征信息, 增强跨通道信息融合能力; 然后,构建多尺度反投影模块通过递归学习执行特征映射, 提升网络的早期重建能力; 最后,将局部残差反馈结合全局残差学习促进特征的传播和利用, 从而融合不同深度的特征信息进行图像重建. 对图像进行×2 ~ ×8超分辨率的实验结果表明, 本方法的重建图像质量在主观感受和客观评价指标上均优于现有图像超分辨率重建方法, 超分辨率倍数大时重建性能相比更优秀.
Abstract:Aiming at the problems that existing image super-resolution reconstruction methods have weak ability to restore image high-frequency details and insufficient feature utilization, a multi-scale feature fusion back projection network is proposed for image super-resolution reconstruction. The network first uses multi-scale convolution kernels in the shallow feature extraction layer to extract feature information of different dimensions to enhance cross-channel information fusion; then builds a multi-scale back projection module to perform feature mapping through recursive learning to improve the early reconstruction capabilities of the network; Finally, local residual feedback is combined with global residual learning to promote the spread and utilization of features, thereby fusing feature information of different depths for image reconstruction. The experimental results of ×2 ~ ×8 SR on the images show that the quality of SR image of this method is better than the existing image super-resolution method in subjective perception and objective evaluation index, and the reconstruction performance is relatively better when the scale factors is large.
-
Key words:
- Image super-resolution /
- multi-scale convolution /
- feature fusion /
- back-projection
-
图 2 8倍放大下对特征提取模块卷积核大小的分析
Fig. 2 Analysis of kernel size in the feature extraction module on ×8 enlargement
图 3 主流重建算法在Set5数据集上对于×8 SR的平均PSNR和参数数量对比
Fig. 3 Comparison of the average PSNR and the number of parameters of the mainstream reconstruction algorithm for ×8 SR on Set5
图 9 在Manga109上×8 SR的可视化结果(TouyouKidan)
Fig. 9 Visualized results of ×8 SR on Manga109 (TouyouKidan)
图 8 在Urban100上×8 SR的可视化结果(img005)
Fig. 8 Visualized results of ×8 SR on Urban100 (img005)
表 1 输入块大小、参数数量和网络超参数设置
Table 1 The settings of input patch size, number of parameters and network hyperparameters
放大倍数 × 2 × 3 × 4 × 8 参数数量 5016211 6490771 8161939 16812691 输入块尺寸 60 × 60 50 × 50 40 × 40 20 × 20 特征提取模块 特征提取层 ${f_{1 \times 1}}$: Conv(128, 1, 1, 0); ${f_{{\rm{3}} \times {\rm{3}}}}$: Conv (128, 3, 1, 1); ${f_{{\rm{5}} \times {\rm{5}}}}$: Conv(128, 5, 1, 2) 特征融合层 Conv(128×3, 1, 1, 1) 特征映射模块 支路1 Conv1(64, 6, 2, 2) Conv1(64, 7, 3, 2) Conv1(64, 8, 4, 2) Conv1(64, 12, 8, 2) 支路2 Conv2(64, 8, 2, 3) Conv2(64, 9, 3, 3) Conv2(64, 10, 4, 3) Conv2(64, 14, 8, 3) 重建模块 Conv(64×7, 3, 1, 1) 递归次数 7 深度 73 注: Conv(C, K, S, P): C表示通道数, K表示卷积核大小, S表示步长, P表示填充. 
下载: 导出CSV
表 2 对特征提取模块卷积核大小的分析
Table 2 Analysis of the kernel size of the feature extraction module
Scale Method Set5 PSNR/SSIM Set14 PSNR/SSIM BSD100 PSNR/SSIM Urban100 PSNR/SSIM Manga109 PSNR/SSIM ×8 Ours_135 27.13/0.7819 25.02/0.6445 24.86/0.5992 22.59/0.6231 24.85/0.7885 Ours_357 27.09/0.7806 25.03/0.6437 24.86/0.5986 22.57/0.6219 24.78/0.7859
下载: 导出CSV
表 3 对多尺度投影单元的卷积核大小分析
Table 3 Analysis of the kernel size of the multi-scale projection unit
Scale (卷积核尺寸、步长、填充) PSNR (dB) 支路1 支路2 Set5 Set14 BSD100 Urban100 Manga109 ×8 (8, 8, 0) (10, 8, 1) 27.00 24.95 24.82 22.45 24.68 (10, 8, 1) (12, 8, 2) 27.08 24.99 24.84 22.53 24.77 (12, 8, 2) (14, 8, 3) 27.13 25.02 24.86 22.59 24.85
下载: 导出CSV
表 4 ×8模型在Set5和Set14测试集上的深度分析
Table 4 The depth analysis of the ×8 model on Set5 and Set14 datasets
递归次数 网络层数 参数数量 PSNR (dB) Set5 Set14 1 13 16802323 26.50 24.53 3 33 16805779 26.98 24.89 4 43 16807507 27.03 24.94 5 53 16809235 27.05 24.96 6 63 16810963 27.07 24.98 7 73 16812691 27.13 25.02 8 83 16814419 27.13 25.02
下载: 导出CSV
表 5 不同SR算法在×2、×3和×4上的定量评估
Table 5 Quantitative comparison of different algorithms on ×2, ×3, and ×4
Scale Method Set5 PSNR/SSIM Set14 PSNR/SSIM BSD100 PSNR/SSIM Urban100 PSNR/SSIM Manga109 PSNR/SSIM × 2 1. Bicubic 33.68/0.9304 30.24/0.8691 29.56/0.8435 26.88/0.8405 31.05/0.9350 × 2 2. SRCNN 36.66/0.9542 32.45/0.9067 31.36/0.8879 29.51/0.8946 35.72/0.9680 × 2 3. ESPCN 37.00/0.9559 32.75/0.9098 31.51/0.8939 29.87/0.9065 36.21/0.9694 × 2 4. FSRCNN 37.06/0.9554 32.76/0.9078 31.53/0.8912 29.88/0.9024 29.88/0.9024 × 2 5. VDSR 37.53/0.9587 33.05/0.9127 31.90/0.8960 30.77/0.9141 37.16/0.9740 × 2 6. DRCN 37.63/0.9588 33.06/0.9121 31.85/0.8942 30.76/0.9133 37.57/0.9730 × 2 7. LapSRN 37.52/0.9591 32.99/0.9124 31.80/0.8949 30.41/0.9101 37.53/0.9740 × 2 8. DRRN 37.74/0.9591 33.23/0.9136 32.05/0.8973 31.23/0.9188 37.92/0.9760 × 2 9. DBPN-R64-7 37.57/0.9589 33.09/0.9132 31.83/0.8951 30.75/0.9133 37.65/0.9747 × 2 10. IDN 37.83/0.9600 33.30/0.9148 32.08/0.8985 31.27/0.9196 38.02/0.9749 × 2 11. SRMDNF 37.79/0.9601 33.32/0.9159 32.05/0.8985 31.33/0.9204 38.07/0.9761 × 2 12. DRFN 37.71/0.9595 33.29/0.9142 32.02/0.8979 31.08/0.9179 33.42/0.9123 × 2 13. MRFN 37.98/0.9611 33.41/0.9159 32.14/0.8997 31.45/0.9221 38.29/0.9759 × 2 Ours 37.82/0.9599 33.35/0.9156 32.04/0.8980 31.49/0.9218 38.23/0.9762 × 3 1. Bicubic 30.40/0.8686 27.54/0.7741 27.21/0.7389 24.46/0.7349 26.95/0.8560 × 3 2. SRCNN 32.75/0.9090 29.29/0.8215 28.41/0.7863 26.24/0.7991 30.48/0.9120 × 3 3. ESPCN 33.02/0.9135 29.49/0.8271 28.50/0.7937 26.41/0.8161 30.79/0.9181 × 3 4. FSRCNN 33.20/0.9149 29.54/0.8277 28.55/0.7945 26.48/0.8175 30.98/0.9212 × 3 5. VDSR 33.66/0.9213 29.78/0.8318 28.83/0.7976 27.14/0.8279 32.01/0.9340 × 3 6. DRCN 33.82/0.9226 29.77/0.8314 28.80/0.7963 27.15/0.8277 32.31/0.9360 × 3 7. LapSRN 33.82/0.9227 29.79/0.8320 28.82/0.7973 27.07/0.8271 32.21/0.9350 × 3 8. DRRN 34.03/0.9244 29.96/0.8349 28.95/0.8004 27.53/0.8377 32.74/0.9390 × 3 9. DBPN-R64-7 33.90/0.9236 29.99/0.8353 28.87/0.7991 27.35/0.8336 32.59/0.9373 × 3 10. IDN 34.11/0.9253 29.99/0.8354 28.95/0.8013 27.42/0.8359 32.69/0.9378 × 3 11. SRMDNF 34.12/0.9254 30.04/0.8382 28.97/0.8025 27.57/0.8398 33.00/0.9403 × 3 12. DRFN 34.01/0.9234 30.06/0.8366 28.93/0.8010 27.43/0.8359 30.59/0.8539 × 3 13. MRFN 34.21/0.9267 30.03/0.8363 28.99/0.8029 27.53/0.8389 32.82/0.9396 × 3 Ours 34.31/0.9265 30.29/0.8408 29.05/0.8035 27.94/0.8472 33.37/0.9433 × 4 1. Bicubic 28.43/0.8109 26.00/0.7023 25.96/0.6678 23.14/0.6574 25.15/0.7890 × 4 2. SRCNN 30.48/0.8628 27.50/0.7513 26.9/0.7103 24.52/0.7226 27.66/0.8580 × 4 3. ESPCN 30.66/0.8646 27.71/0.7562 26.98/0.7124 24.60/0.7360 27.70/0.8560 × 4 4. FSRCNN 30.73/0.8601 27.71/0.7488 26.98/0.7029 24.62/0.7272 27.90/0.8517 × 4 5. VDSR 31.35/0.8838 28.02/0.7678 27.29/0.7252 25.18/0.7525 28.82/0.8860 × 4 6. DRCN 31.53/0.8854 28.03/0.7673 27.24/0.7233 25.14/0.7511 28.97/0.8860 × 4 7. LapSRN 31.54/0.8866 28.09/0.7694 27.32/0.7264 25.21/0.7553 29.09/0.8900 × 4 8. DRRN 31.68/0.8888 28.21/0.7720 27.38/0.7284 25.44/0.7638 29.46/0.8960 × 4 9. DBPN-R64-7 31.92/0.8915 28.41/0.7770 27.42/0.7304 25.59/0.7681 29.92/0.9003 × 4 10. IDN 31.82/0.8903 28.25/0.7730 27.41/0.7297 25.41/0.7632 — × 4 11. SRMDNF 31.96/0.8925 28.35/0.7787 27.49/0.7337 25.68/0.7731 30.09/0.9024 × 4 12. DRFN 31.55/0.8861 28.30/0.7737 27.39/0.7293 25.45/0.7629 28.99/0.8106 × 4 13. MRFN 31.90/0.8916 28.31/0.7746 27.43/0.7309 25.46/0.7654 29.57/0.8962 × 4 Ours 32.31/0.8963 28.71/0.7843 27.66/0.7383 26.30/0.7922 30.84/0.9126
下载: 导出CSV
表 6 不同SR算法在×8上的定量评估
Table 6 Quantitative comparison of different algorithms on ×8
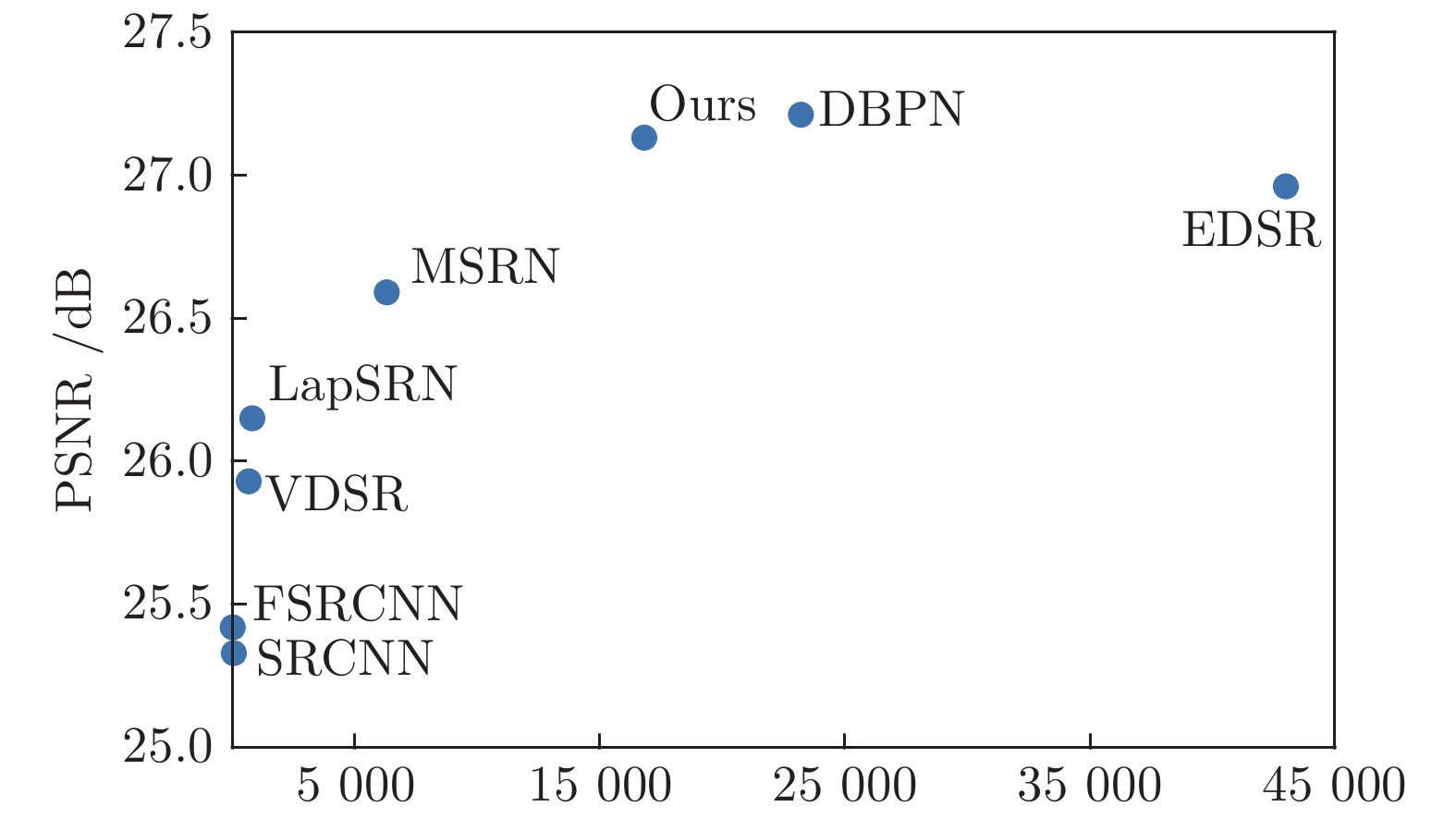
Scale Method Set5 PSNR/SSIM Set14 PSNR/SSIM BSD100 PSNR/SSIM Urban100 PSNR/SSIM Manga109 PSNR/SSIM × 8 1. Bicubic 24.40/0.6580 23.10/0.5660 23.67/0.5480 20.74/0.5160 21.47/0.6500 × 8 2. SRCNN 25.33/0.6900 23.76/0.5910 24.13/0.5660 21.29/0.5440 22.46/0.6950 × 8 3. ESPCN 25.75/0.6738 24.21/0.5109 24.37/0.5277 21.59/0.5420 22.83/0.6715 × 8 4. FSRCNN 25.42/0.6440 23.94/0.5482 24.21/0.5112 21.32/0.5090 22.39/0.6357 × 8 5. VDSR 25.93/0.7240 24.26/0.6140 24.49/0.5830 21.70/0.5710 23.16/0.7250 × 8 6. LapSRN 26.15/0.7380 24.35/0.6200 24.54/0.5860 21.81/0.5810 23.39/0.7350 × 8 7. DRFN 26.22/0.7400 24.57/0.6250 24.60/0.5870 — — × 8 8. MSRN 26.59/0.7254 24.88/0.5961 24.70/0.5410 22.37/0.5977 24.28/0.7517 × 8 9. DBPN-R64-7 26.82/0.7700 24.77/0.6346 24.72/0.5928 22.22/0.6033 24.19/0.7664 × 8 10. EDSR 26.96/0.7762 24.91/0.6420 24.81/0.5985 22.51/0.6221 24.69/0.7841 × 8 Ours 27.13/0.7819 25.02/0.6445 24.86/0.5992 22.59/0.6231 24.85/0.7885
下载: 导出CSV
-
[1] 张宁, 王永成, 张欣, 徐东东. 基于深度学习的单幅图片超分辨率重构研究进展. 自动化学报, 2020, 46(12): 2479−2499Zhang Ning, Wang Yong-Cheng, Zhang Xin, Xu Dong-Dong. A review of single image super-resolution based on deep learning. Acta Automatica Sinica, 2020, 46(12): 2479−2499 [2] 张毅锋, 刘袁, 蒋程, 程旭. 用于超分辨率重建的深度网络递进学习方法. 自动化学报, 2020, 46(2): 274−282Zhang Yi-Feng, Liu Yuan, Jiang Cheng, Cheng Xu. A curriculum learning approach for single image super resolution. Acta Automatica Sinica, 2020, 46(2): 274−282 [3] Tan Y, Cai J, Zhang S, Zhong W, Ye L. Image compression algorithms based on super-resolution reconstruction technology. In: Proceedings of the 2019 IEEE 4th International Conference on Image, Vision and Computing (ICIVC), 2019. 162−166 [4] You C, Li G, Zhang Y Zhang, X, Shan H, Li M, Ju S, Zhao Z, Zhang Z, Cong W, Vannier M W, Saha P K, Hoffman E A, Wang G. CT super-resolution GAN constrained by the identical, residual, and cycle learning ensemble (GAN-CIRCLE). IEEE Transactions on Medical Imaging, 2020, 39(1): 188−203 doi: 10.1109/TMI.2019.2922960 [5] Pang Y, Cao J, Wang J, Han J. JCS-Net: Joint classification and super-resolution network for small-scale pedestrian detection in surveillance images. IEEE Transactions on Information Forensics and Security, 2019, 14(12): 3322−3331 doi: 10.1109/TIFS.2019.2916592 [6] 周登文, 赵丽娟, 段然, 柴晓亮. 基于递归残差网络的图像超分辨率重建. 自动化学报, 2019, 45(6): 1157−1165Zhou Deng-Wen, Zhao Li-Juan, Duan Ran, Chai Xiao-Liang. Image super-resolution based on recursive residual networks. Acta Automatica Sinica, 2019, 45(6): 1157−1165 [7] 孙旭, 李晓光, 李嘉锋, 卓力. 基于深度学习的图像超分辨率复原研究进展. 自动化学报, 2017, 43(5): 697−709Sun Xu, Li Xiao-Guang, Li Jia-Feng, Zhuo Li. Review on deep learning based image super-resolution restoration algorithms. Acta Automatica Sinica, 2017, 43(5): 697−709 [8] Dong C, Loy C C, He K, Tang X. Image super-resolution using deep convolutional networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295−307 doi: 10.1109/TPAMI.2015.2439281 [9] Dong C, Loy C C, He K, Tang X. Learning a deep convolutional network for image super-resolution. In: Proceedings of the 2014 European Conference on Computer Vision (ICCV), Springer, Cham, 2014. 184−199 [10] 刘建伟, 赵会丹, 罗雄麟, 许鋆. 深度学习批归一化及其相关算法研究进展. 自动化学报, 2020, 46(6): 1090−1120Liu Jian-Wei, Zhao Hui-Dan, Luo Xiong-Lin, Xu Jun. Research progress on batch normalization of deep learning and its related algorithms. Acta Automatica Sinica, 2020, 46(6): 1090−1120 [11] Kim J, Kwon Lee J, Mu Lee K. Accurate image super-resolution using very deep convolutional networks. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016. 1646–1654 [12] B. Lim, S. Son, H. Kim, S. Nah, and K. M. Lee. Enhanced deep residual networks for single image super-resolution. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, 2017. 136–144 [13] K. He, X. Zhang, S. Ren and J. Sun. Deep residual learning for image recognition. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016, 770−778 [14] Tong T, Li G, Liu X, Gao Q. Image super-resolution using dense skip connections. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, 2017. 4809−4817 [15] Zhang Y, Tian Y, Kong Y, Zhong B, Fu Y. Residual dense network for image super-resolution. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, 2018. 2472−2481 [16] Haris M, Shakhnarovich G, Ukita N. Deep back-projection networks for single image super-resolution. IEEE Transactions on Pattern Analysis and Machine Intelligence, DOI: 10.1109/TPAMI.2020.3002836, 2020. [17] Huang G, Liu Z, Van Der Maaten L, Weinberger K Q, Densely connected convolutional networks. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, 2017. 2261−2269 [18] Kim J, Lee J K, Lee K M. Deeply-recursive convolutional network for image super-resolution. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016. 1637−1645 [19] Tai Y, Yang J, Liu X. Image super-resolution via deep recursive residual network. In: Proceeding of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, 2017. 2790−2798 [20] Dong C, Loy C C, Tang X. Accelerating the super-resolution convolutional neural network. In: Proceedings of the European Conference on Computer Vision, Springer, Cham, 2016. 391–407 [21] Shi W, Caballero J, Huszár F, Totz J, Aitken A P, Bishop R, Rueckert D, Wang Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016. 1874−1883 [22] Li Jun-Cheng, Fang Fa-Ming, Mei Kang-Fu, Zhang Gui-Xu. Multiscale residual network for image super-resolution. In: Proceedings of the European Conference on Computer Vision, Springer, Cham, 2018. 527−542 [23] Lai W, Huang J, Ahuja N, Yang M. Deep Laplacian pyramid networks for fast and accurate super-resolution. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, 2017. 5835−5843 [24] Agustsson E, Timofte R. NTIRE 2017 challenge on single image super-resolution: Dataset and study. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, 2017. 1122−1131 [25] Deng J, Dong W, Socher R, Li L, Li Kai and Li Fei-Fei. ImageNet: A large-scale hierarchical image database. In: Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 2009. 248−255 [26] Szegedy C, Liu Wei, Jia Yang-Qing, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 2015. 1−9 [27] Bevilacqua M, Roumy A, Guillemot C, Alberi-Morel M L, Low-complexity single image super-resolution based on nonnegative neighbor embedding. In: Proceedings of the British Machine Vision Conference, 2012. 1–10 [28] Zeyde R, Elad M, Protter M. On single image scale-up using sparse-representations. In: Proceedings of the International Conference on Curves and Surfaces, Springer, Berlin, Heidelberg, 2010. 711–730 [29] Arbeláez P, Maire M, Fowlkes C, Malik J. Contour detection and hierarchical image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898−916 doi: 10.1109/TPAMI.2010.161 [30] Huang J, Singh A, Ahuja N. Single image super-resolution from transformed self-exemplars. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 2015. 5197−5206 [31] Matsui Y, Ito K, Aramaki Y, Fujimoto A, Ogawa T, Yamasaki T, Aizawa K. Sketch-based manga retrieval using Manga109 dataset. Multimedia Tools & Applications, 2017, 76(20): 21811−21838 [32] Zhou Wang, Bovik A C, Sheikh H R, Simoncelli E P. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600−612 [33] He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In: Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 2015. 1026−1034 [34] Kingma D P, Ba J. Adam: A method for stochastic optimization, arXiv preprint, arXiv: 1412.6980, 2014. [35] 毕敏敏. 基于深度学习的图像超分辨率技术研究[硕士学位论文]. 哈尔滨工业大学, 中国, 2020.Bi Min-Min. Research on image super-resolution technology based on deep learning [Master thesis]. Harbin Institute of Technology, China, 2020. [36] 李彬, 喻夏琼, 王平, 傅瑞罡, 张虹. 基于深度学习的单幅图像超分辨率重建综述. 计算机工程与科学, 2021, 43(01): 112−124Li Bin, Yu Xia-Qiong, Wang Ping, Fu Rui-Gang, Zhang Hong. A survey of single image super-resolution reconstruction based on deep learning. Computer Engineering and Science, 2021, 43(01): 112−124 [37] Yang X, Mei H, Zhang J, Xu K, Yin B, Zhang Q, Wei X. DRFN: Deep recurrent fusion network for single-image super-resolution with large factors. IEEE Transactions on Multimedia, 2019, 21(2): 328−337 doi: 10.1109/TMM.2018.2863602 [38] Hui Z, Wang X, Gao X. Fast and accurate single image super-resolution via information distillation network. In: Proceeding of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, 2018.723−731 [39] Zhang K, Zuo W, Zhang L. Learning a single convolutional super-resolution network for multiple degradations. In: Proceeding of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, 2018. 3262−3271 [40] He Z, Cao Y, Du L, Xu B, Yang J, Cao Y, Tang S, Zhuang Y. MRFN: Multi-receptive-field network for fast and accurate single image super-resolution. IEEE Transactions on Multimedia, 2020, 22(4): 1042−1054 doi: 10.1109/TMM.2019.2937688 -
计量
- 文章访问数: 1497
- HTML全文浏览量: 473
- PDF下载量: 278
- 被引次数: 0
