Finite-time Control for Morphing Aerospace Vehicle Based on Time-varying Barrier Lyapunov Function
-
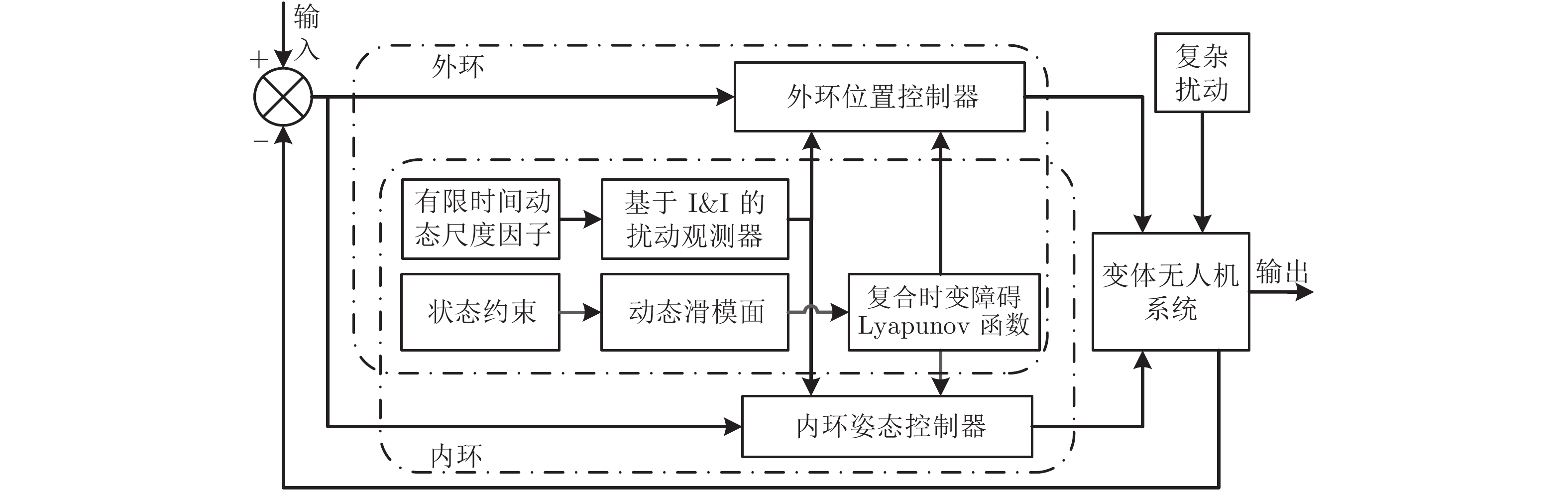
摘要: 针对复杂扰动下可执行多种任务的复合式变体无人机, 提出了一种基于浸入与不变(Immersion and invariance, I&I)理论和隐含系统状态受限条件的复合时变障碍Lyapunov函数(Composite time-varying barrierLyapunov function, CTV-BLF)的控制方案. 设计了一种基于浸入与不变理论的扰动观测器, 构建了一种基于监督因子的有限时间动态尺度因子(Finite-time dynamic scaling factor, FT-DSF)调节器. 在此基础上, 设计了一种基于复合时变障碍Lyapunov函数和动态滑模面的控制器, 保证系统状态始终在约束条件之内. 通过衍生定理证明轨迹跟踪误差是有限时间稳定的. 最终仿真结果验证了所提方案的有效性.
-
关键词:
- 变体无人机 /
- 浸入与不变 /
- 动态尺度因子 /
- 监督因子 /
- 障碍Lyapunov函数
Abstract: A control scheme based on immersion and invariance (I&I) theory and a composite time-varying barrier Lyapunov function (CTV-BLF) with implied system state constraint conditions is proposed for the morphing aerospace vehicle which can perform multiple tasks under complex disturbances. A disturbance observer based on I&I theory is designed, in which a finite-time dynamic scaling factor (FT-DSF) regulator based on supervision factor is constructed. On this basis, a controller based on CTV-BLF and dynamic sliding surface is designed to guarantee that the constraints are always not violated. The derivative theorem proves that the trajectory tracking error is stable in finite-time. Final simulation results verify the effectiveness of the proposed scheme. -
图 2 变体无人机机体受力及坐标示意图
Fig. 2 Schematic diagram of body force and coordinates of the morphing aerospace vehicle
图 6 算例1中2种基于I&I理论扰动观测器的扰动观测误差
Fig. 6 Disturbances observation errors of two observers based on I&I theory in case 1
图 9 算例 2中3种方法轨迹跟踪误差及箱线图分析
Fig. 9 Trajectory tracking errors and boxplot analysis of the three methods in case 2
图 10 算例 2中3种方法姿态角跟踪误差及箱线图分析
Fig. 10 Attitude tracking errors and boxplot analysis of the three methods in case 2
图 12 算例2中3种方法的控制输入信号响应
Fig. 12 Control input signal responses of the three methods in case 2
图 13 算例2中3种方法的虚拟控制输入信号响应
Fig. 13 Virtual control input signal responses of the three methods in case 2
图 11 算例2中3种方法对外部扰动的估计效果
Fig. 11 Estimation effects on external disturbances of the three methods in case 2
图 15 算例2测试周期中本文方法机翼与机身夹角
${\theta _f}$ 与机体速度变化的对应过程Fig. 15 The corresponding process of the angle
${\theta _f}$ between wing and fuselage, and the change of airframe velocity of the proposed method in case 2
图 14 算例2测试周期中机翼与机身夹角
${\theta _f}$ 自适应响应过程Fig. 14 The adaptive response of the angle
${\theta _f}$ between wing and fuselage during the test period in case 2
图 16
${\alpha _i} = 2$ 时6个控制通道FT-DSF自适应过程Fig. 16 FT-DSF adaptive process of six control channels when
${\alpha _i} = 2$ 
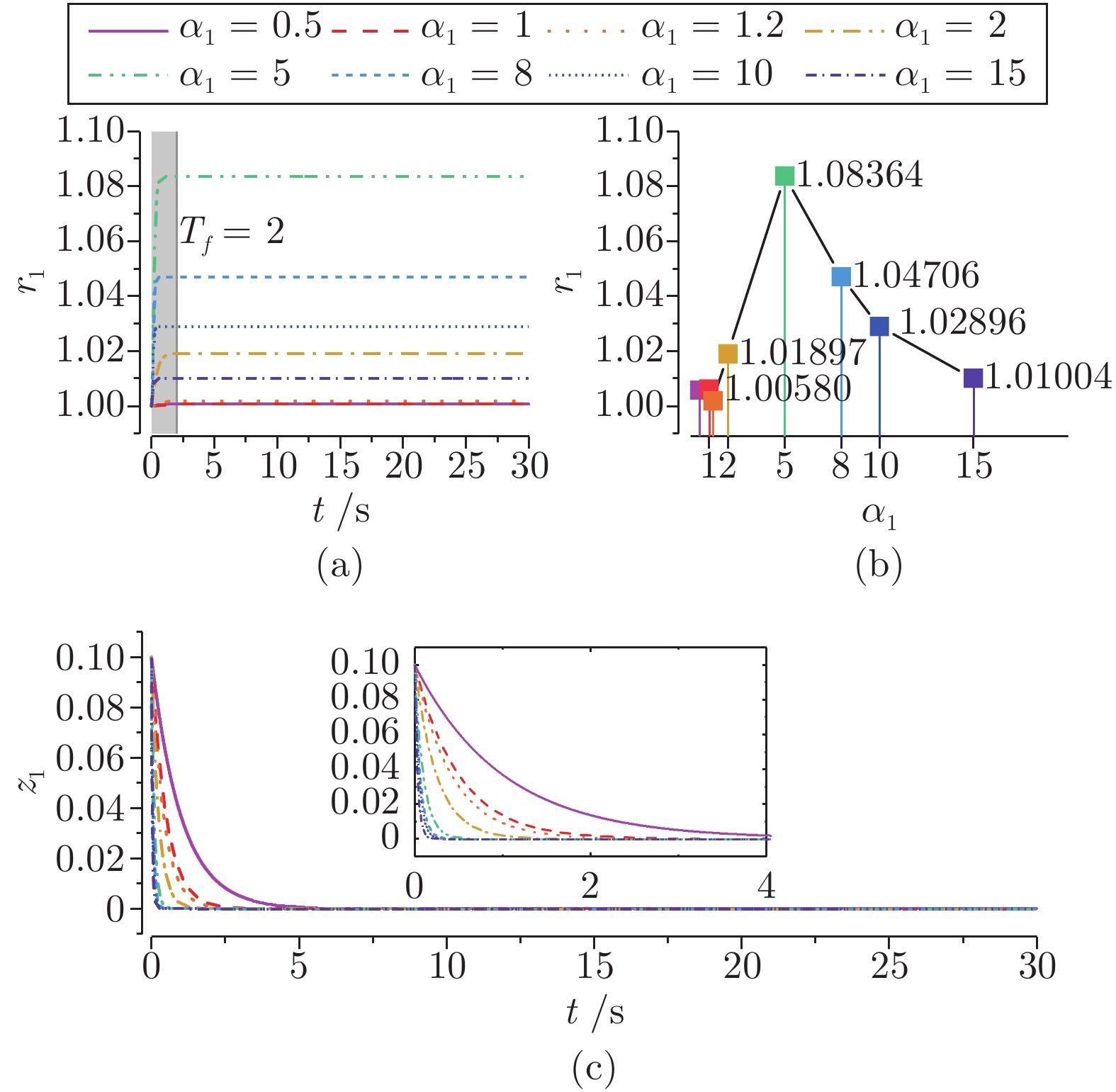
图 17 监督因子
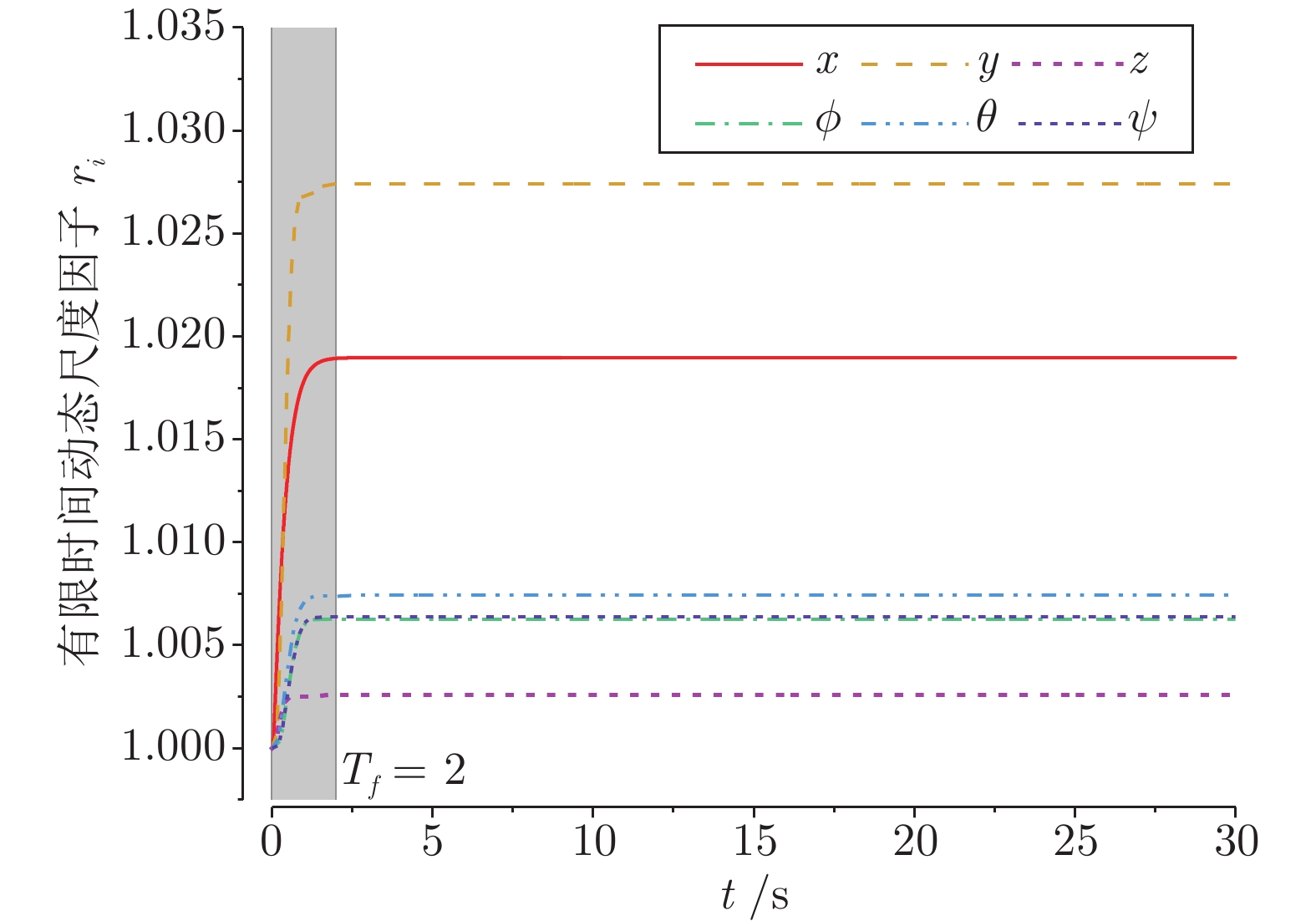
${\alpha _1}$ 的变化对FT-DSF${r_1}$ 及动态尺度误差${z_1}$ 的响应过程(以$x$ 子系统为例) ((a) 随着${\alpha _1}$ 不同取值${r_1}$ 的自适应收敛响应; (b)${\alpha _1}$ 不同取值对应${r_1}$ 的最终收敛值的变化趋势; (c) 随着${\alpha _1}$ 不同取值${z_1}$ 的自适应收敛响应)Fig. 17 The responses of FT-DSF
${r_1}$ and dynamic scaling error${z_1}$ in response to the supervision factor${\alpha _1}$ (take the$x$ subsystem as an example) ((a) Adaptive convergent response of${r_1}$ with different values of${\alpha _1}$ ; (b) Different values of${\alpha _1}$ correspond to the change trend of the final convergence value of${r_1}$ ; (c) Adaptive convergent response of${z_1}$ with different values of${\alpha _1}$ ) -
[1] Totoki H, Ochi Y, Sato M, et al. Design and testing of a low-order flight control system for Quad-tilt-wing UAV. Journal of Guidance, Control, and Dynamics, 2016, 39(10): 2426–2433. doi: 10.2514/1.G001577 [2] Tran A T, Sakamoto N, Sato M, et al. Control augmentation system design for quad-tilt-wing unmanned aerial vehicle via robust output regulation method. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 357–369. doi: 10.1109/TAES.2017.2650618 [3] Ritz R, D＇Andrea R. A Global Strategy for Tailsitter Hover Control. Cham: Springer International Publishing AG, 2018. 21−37 [4] Wang K, Ke Y, Chen B M. Autonomous reconfigurable hybrid tail-sitter UAV U-Lion. Science China Information Sciences, 2017, 60(3): 033201. doi: 10.1007/s11432-016-9002-x [5] 李斌斌, 马磊, 孙小通, 等. 一种多旋翼飞行器的设计及实验验证. 机器人, 2020, 42(03): 257–266.Li Bin-Bin, Ma Lei, Sun Xiao-Tong, et al. Design and experimental verification of a multirotor aircraft. Robot, 2020, 42(3): 257–266 (in Chinese). [6] 卢凯文, 杨忠, 张秋雁, 等. 推力矢量可倾转四旋翼自抗扰飞行控制方法. 控制理论与应用, 2020, 37(6): 1377–1387.Lu Kai-Wen, Yang Zhong, Zhang Qiu-Yan, et al. Active disturbance rejection flight control method for thrust-vectored quadrotor with tiltable rotors. Control Theory & Applications, 2020, 37(6): 1377–1387. [7] 钱辰, 方勇纯, 李友朋. 面向扑翼飞行控制的建模与奇异摄动分析. 自动化学报, 2022, 48(2): 434−443Qian Chen, Fang Yong-Chun, Li You-Peng. Control oriented modeling and singular perturbation analysis in flapping-wing flight. Acta Automatica Sinica, 2022, 48(2): 434−443 [8] Astolfi A, Ortega R. Immersion and invariance: a new tool for stabilization and adaptive control of nonlinear systems. IEEE Transactions on Automatic Control, 2003, 48(4): 590–606. doi: 10.1109/TAC.2003.809820 [9] Hu J, Zhang H. Immersion and invariance based command-filtered adaptive backstepping control of VTOL vehicles. Automatica, 2013, 49(7): 2160–2167. doi: 10.1016/j.automatica.2013.03.019 [10] Li J, Chen S, Li C, et al. Adaptive control of underactuated flight vehicles with moving mass. Aerospace Science and Technology, 2019, 85: 75–84. doi: 10.1016/j.ast.2018.12.003 [11] Zou Y, Meng Z. Immersion and invariance-based adaptive controller for quadrotor systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 49(11): 2288-2297. [12] Karagiannis D, Sassano M, Astolfi A. Dynamic scaling and observer design with application to adaptive control. Automatica, 2009, 45(12): 2883–2889. doi: 10.1016/j.automatica.2009.09.013 [13] Hu J, Zhang H. Bounded output feedback of rigid-body attitude via angular velocity observers. Journal of Guidance, Control, and Dynamics, 2013, 36(4): 1240–1248. doi: 10.2514/1.57187 [14] Lee K W, Singh S N. Quaternion-based adaptive attitude control of asteroid-orbiting spacecraft via immersion and invariance. Acta Astronautica, 2020, 167: 164–180. doi: 10.1016/j.actaastro.2019.10.031 [15] Zhang B, Cai Y. Immersion and invariance based adaptive backstepping control for body-fixed hovering over an asteroid. IEEE Access, 2019, 7: 34850–34861. doi: 10.1109/ACCESS.2019.2904590 [16] Yang S, Akella M R, Mazenc F. Immersion and invariance observers for gyro-free attitude control systems. Journal of Guidance, Control, and Dynamics, 2016: 2570–2577. [17] Shao X, Wang L, Li J, et al. High-order ESO based output feedback dynamic surface control for quadrotors under position constraints and uncertainties. Aerospace Science and Technology, 2019, 89: 288–298. doi: 10.1016/j.ast.2019.04.003 [18] Ngo K B, Mahony R, Jiang Z P. Integrator backstepping using barrier functions for systems with multiple state constraints. In: Proceedings of the 44th IEEE Conference on Decision and Control. Seville, Spain: IEEE, 2005. 8306–8312 [19] Tee K P, Ge S S, Tay E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica, 2009, 45(4): 918–927. doi: 10.1016/j.automatica.2008.11.017 [20] Tee K P, Ge S S. Control of nonlinear systems with partial state constraints using a barrier Lyapunov function. International Journal of Control, 2011, 84(12): 2008–2023. doi: 10.1080/00207179.2011.631192 [21] Liu N, Shao X, Li J, et al. Attitude restricted back-stepping anti-disturbance control for vision based quadrotors with visibility constraint. ISA transactions, 2020, 100: 109-125. doi: 10.1016/j.isatra.2019.11.004 [22] Yuan Y, Wang Z, Guo L, Liu H. Barrier Lyapunov functions-based adaptive fault tolerant control for flexible hypersonic flight vehicles with full state constraints. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018: 1–10 [23] Xu B, Shi Z, Sun F, et al. Barrier Lyapunov function based learning control of hypersonic flight vehicle with AOA constraint and actuator faults. IEEE transactions on cybernetics, 2018, 49(3): 1047–1057. [24] Liu Y J, Lu S, Tong S, et al. Adaptive control-based barrier Lyapunov functions for a class of stochastic nonlinear systems with full state constraints. Automatica, 2018, 87: 83–93. doi: 10.1016/j.automatica.2017.07.028 [25] Kim B S, Yoo S J. Approximation-based adaptive tracking control of nonlinear pure-feedback systems with time-varying output constraints. International Journal of Control, Automation and Systems, 2015, 13(2): 257–265. doi: 10.1007/s12555-014-0084-6 [26] Liu Y J, Ma L, Liu L, Tong S C, Chen L. Adaptive neural network learning controller design for a class of nonlinear systems with time-varying state constraints. IEEE Transactions on Neural Networks and Learning Systems, 2019: 1–10 [27] Tang L, Chen A, Li D. Time-varying Tan-type barrier Lyapunov function-based adaptive fuzzy control for switched systems with unknown dead zone. IEEE Access, 2019, 7: 110928–110935 [28] Wang H, Bai W, Liu P X. Finite-time adaptive fault-tolerant control for nonlinear systems with multiple faults. IEEE/CAA Journal of Automatica Sinica, 2019, 6(6): 1417–1427. doi: 10.1109/JAS.2019.1911765 [29] 王璐, 郭毓, 吴益飞. SGCMGs 驱动的挠性航天器有限时间自适应鲁棒控制. 自动化学报, 2021, 47(3): 641−651Wang Lu, Guo Yu, Wu Yi-Fei. Finite-time adaptive robust control for SGCMGs-based flexible spacecraft. Acta Automatica Sinica, 2021, 47(3): 641−651 [30] Tian B, Liu L, Lu H, Zuo Z Y. Multivariable finite time attitude control for quadrotor UAV: Theory and experimentation. IEEE Transactions on Industrial Electronics, 2017, 65(3): 2567–2577 [31] 张春燕, 戚国庆, 李银伢, 等. 一种基于有限时间稳定的环绕控制器设计. 自动化学报, 2018, 44(11): 2056–2067.Zhang Chun-Yan, Qi Guo-Qing, Li Yin-Ya, et al. Standoff tracking control with respect to moving target via finite-time stabilization. Acta Automatica Sinica, 2018, 44(11): 2056–2067 (in Chinese). [32] Hu Q, Jiang B, Zhang Y. Observer-based output feedback attitude stabilization for spacecraft with finite-time convergence. IEEE Transactions on Control Systems Technology, 2017, 27(2): 781–789. [33] Jacobs E N, Sherman A. Airfoil section characteristics as affected by variations of the Reynolds number. NACA report, 1937, 586: 227–264. -
下载:
计量
- 文章访问数: 2547
- HTML全文浏览量: 735
- PDF下载量: 549
- 被引次数: 0
