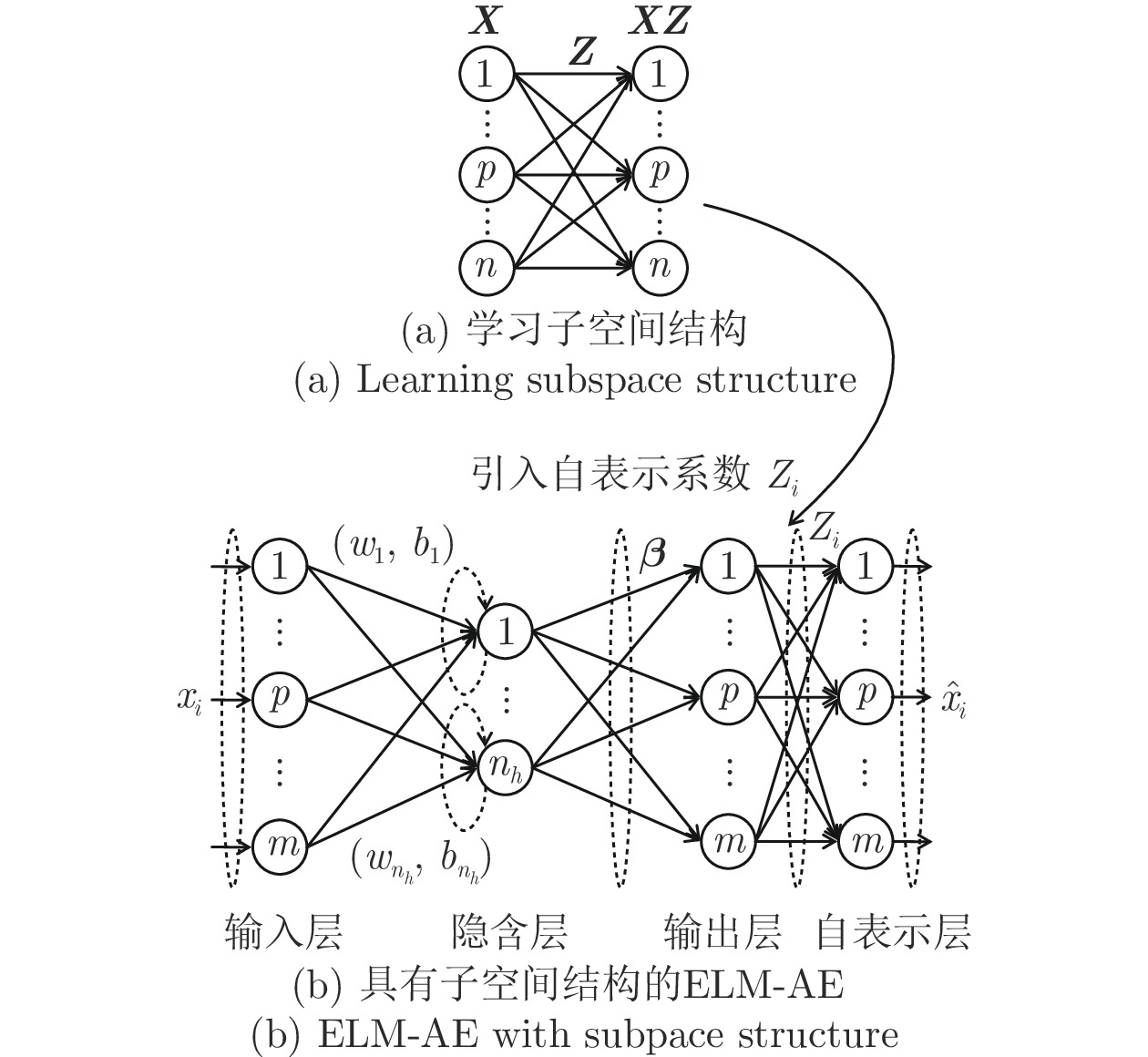
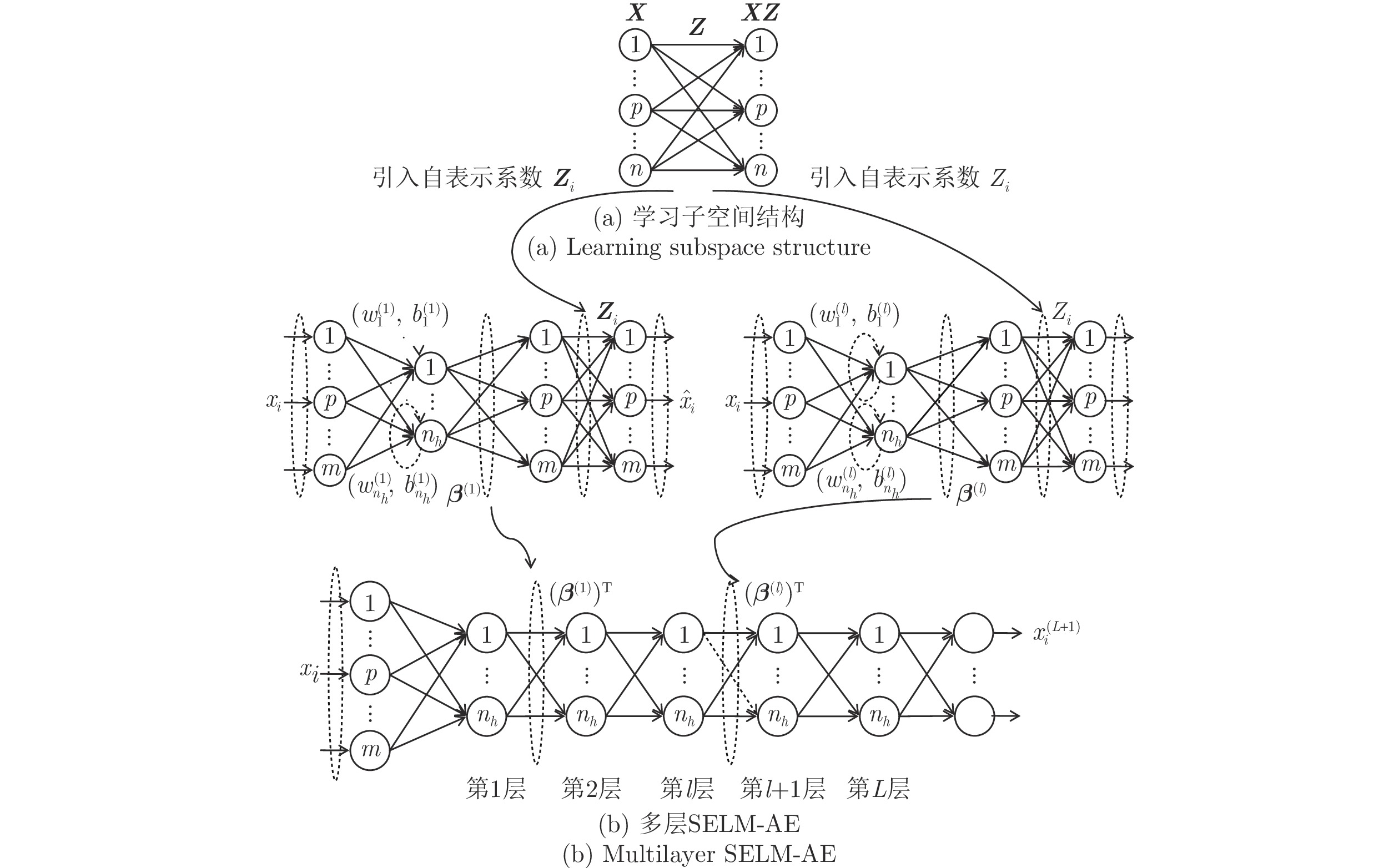
Multi-layer Extreme Learning Machine Autoencoder With Subspace Structure Preserving
-
摘要: 处理高维复杂数据的聚类问题, 通常需先降维后聚类, 但常用的降维方法未考虑数据的同类聚集性和样本间相关关系, 难以保证降维方法与聚类算法相匹配, 从而导致聚类信息损失. 非线性无监督降维方法极限学习机自编码器(Extreme learning machine, ELM-AE)因其学习速度快、泛化性能好, 近年来被广泛应用于降维及去噪. 为使高维数据投影至低维空间后仍能保持原有子空间结构, 提出基于子空间结构保持的多层极限学习机自编码器降维方法(Multilayer extreme learning machine autoencoder based on subspace structure preserving, ML-SELM-AE). 该方法在保持聚类样本多子空间结构的同时, 利用多层极限学习机自编码器捕获样本集的深层特征. 实验结果表明, 该方法在UCI数据、脑电数据和基因表达谱数据上可以有效提高聚类准确率且取得较高的学习效率.Abstract: To deal with the clustering problem of high-dimensional complex data, it is usually reguired to reduce the dimensionality and then cluster, but the common dimensional reduction method does not consider the clustering characteristic of the data and the correlation between the samples, so it is difficult to ensure that the dimensional reduction method matches the clustering algorithm, which leads to the loss of clustering information. The nonlinear unsupervised dimensionality reduction method extreme learning machine autoencoder (ELM-AE) has been widely used in dimensionality reduction and denoising in recent years because of its fast learning speed and good generalization performance. In order to maintain the original subspace structure when high-dimensional data is projected into a low-dimensional space, the dimensional reduction method ML-SELM-AE is proposed. This method captures the deep features of the sample set by using the multi-layer extreme learning machine autoencoder while maintaining multi-subspace structure of clustered samples by self-representation model. Experimental results show that the method can effectively improve the clustering accuracy and achieve higher learning efficiency on UCI data, EEG data and gene expression data.
-
表 1 数据集描述
Table 1 The data set description
数据集 维数 样本数 类别数 IRIS 4 150 3 Data set IIb 1440 504 2 Data set II 2400 1020 2 DLBCL 5469 77 2 Colon 2 000 62 2 Prostate0 6033 102 2 表 2 传统降维方法的聚类准确率(%) (方差, 维数)
Table 2 Comparison of clustering accuracy of traditional methods (%) (variance, dimension)
数据集 k-means 传统算法 PCA LPP NPE IRIS 89.13 (0.32) 89.07 (0.34, 4) 90.27 (0.84, 2) 88.67 (0.00, 2) Data set IIb 86.47 (2.53) 88.21 (0.61, 4) 88.69 (7.33, 4) 89.58 (6.32, 256) Data set II 72.38 (8.94) 79.31 (4.39, 2) 82.26 (0.13, 512) 82.62 (0.71, 256) DLBCL 68.83 (0.00) 68.83 (0.00, 2) 63.55 (1.86, 8) 69.09 (0.82, 32) Colon 54.84 (0.00) 54.84 (0.00, 2) 54.84 (0.00, 2) 56.45 (0.00, 2) Prostate0 56.86 (0.00) 56.83 (0.00, 2) 56.86 (0.00, 2) 56.86 (0.00, 4) 表 3 ELM降维方法聚类准确率(%) (方差, 维数)(参数)
Table 3 Comparison of clustering accuracy of ELM methods (%) (variance, dimension)(parameters)
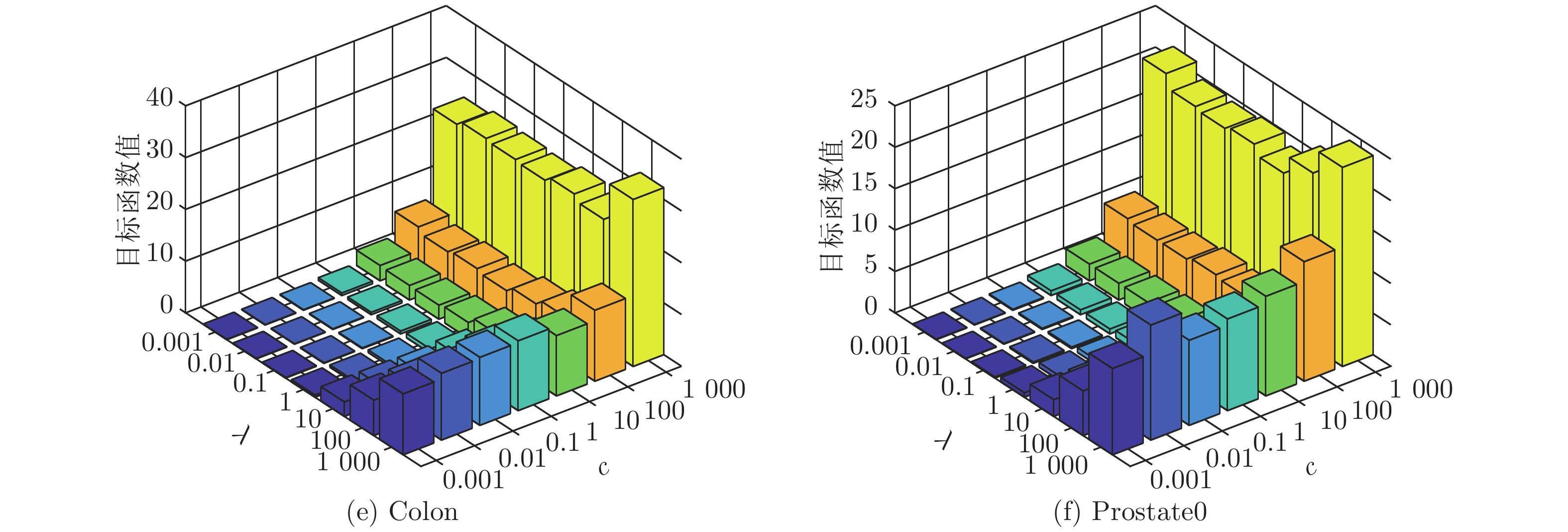
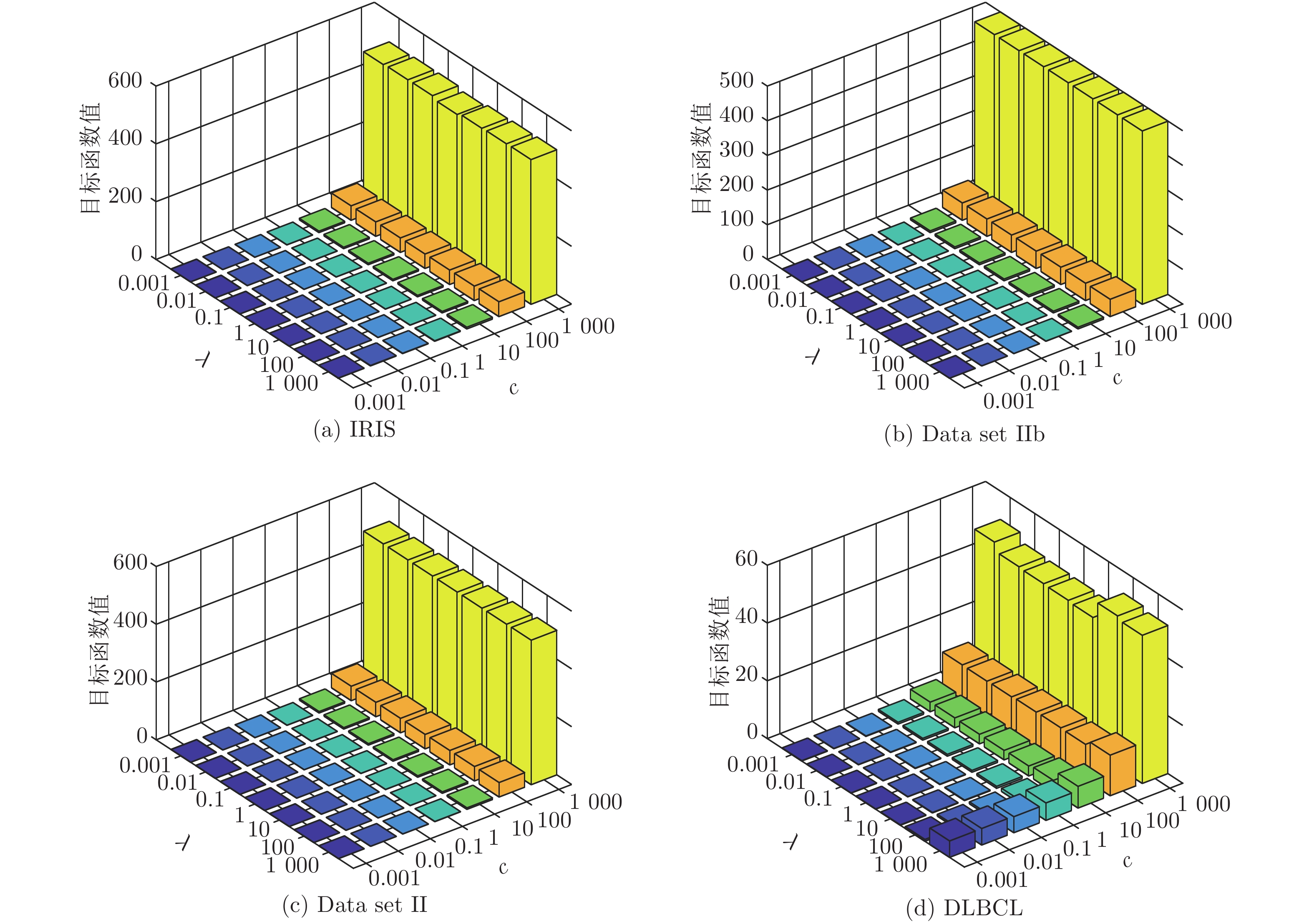
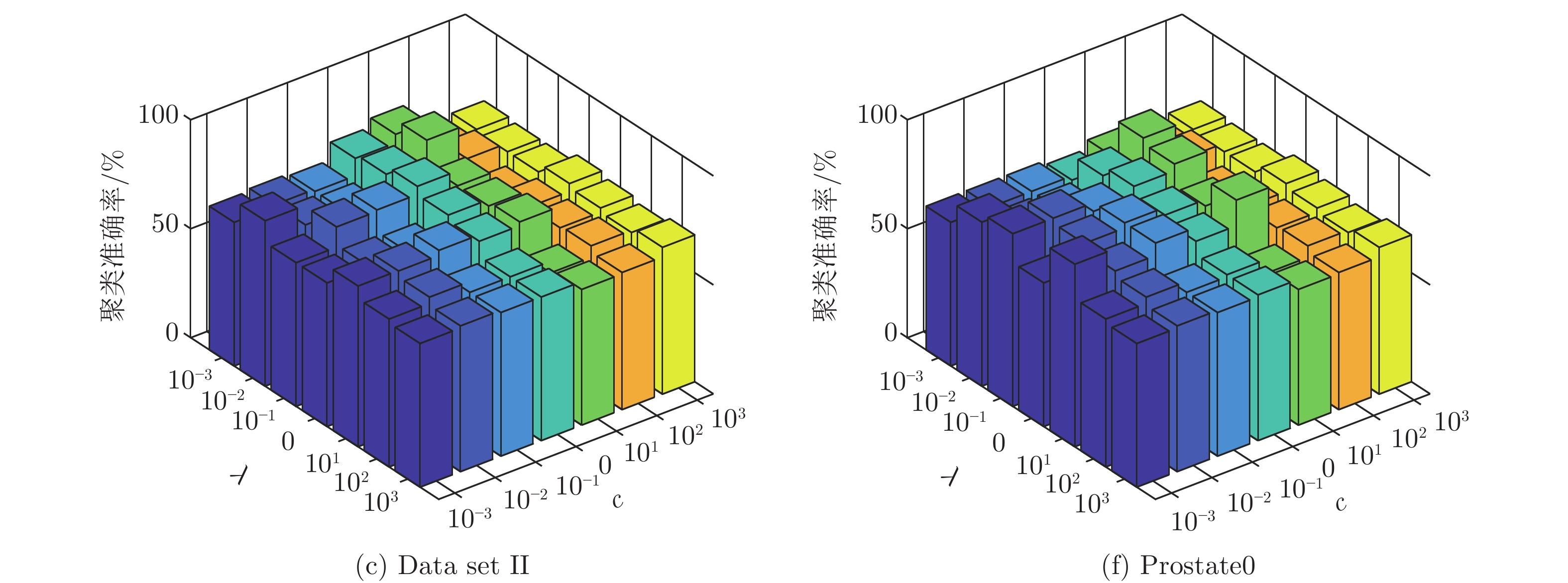
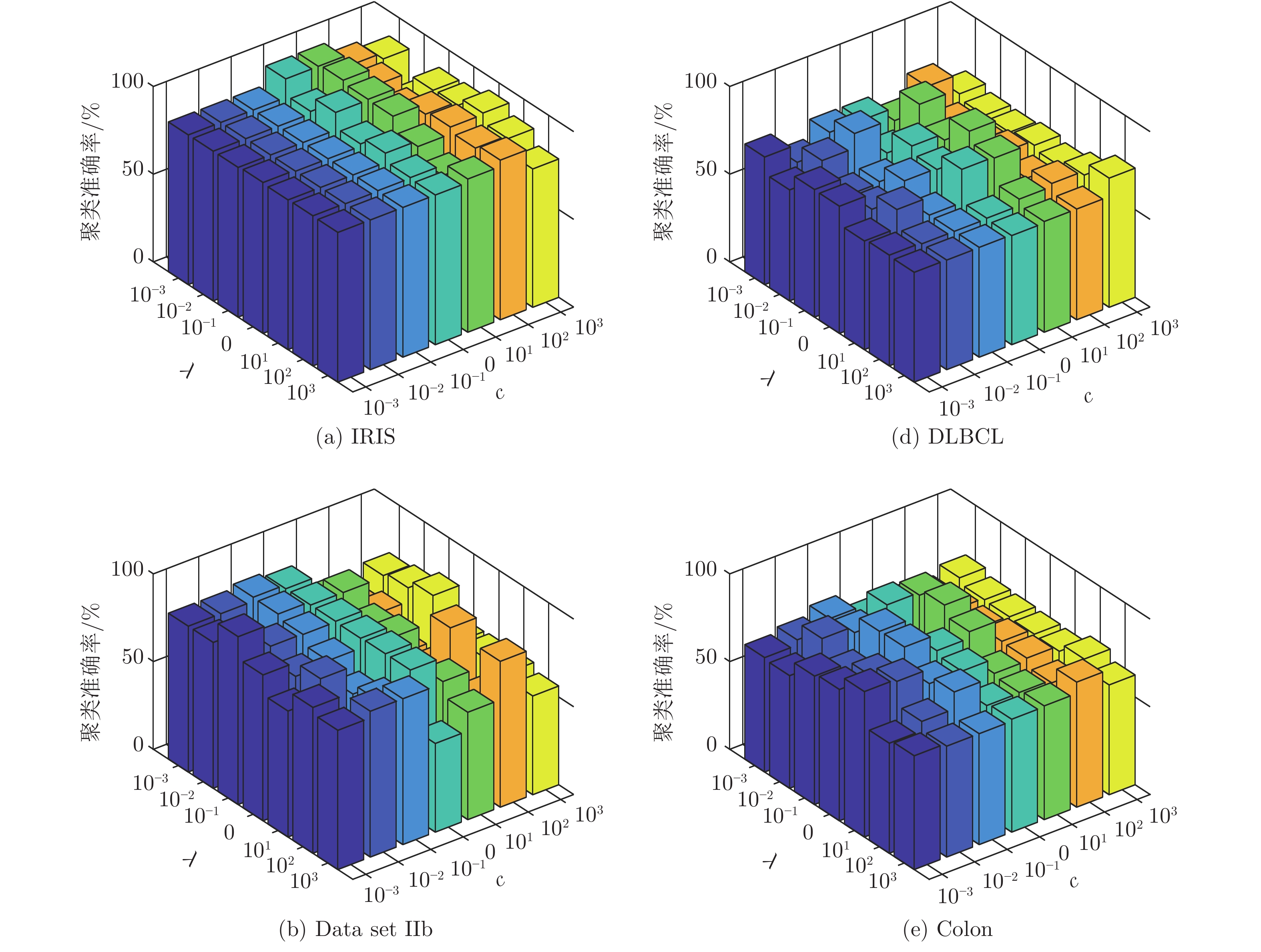
数据集 k-means Unsupervised ELM Subspace + unsupervised ELM US-ELM(λ) ELM-AE(c) ML-ELM-AE (c) SNP-ELM(λ,η,δ) SELM-AE(c, λ) ML-SELM-AE(c, λ) IRIS 89.13
(0.32)93.87
(13.78, 2)
(0.1)93.93
(1.19, 2)
(10)95.20
(1.05, 2)
(0.01)98.46
(0.32, 2)
(10, 0.6, −1)98.00
(0.00, 2)
(10, 0.01)98.40
(0.56, 2)
(10, 0.01)Data set IIb 86.47
(2.53)91.59
(4.25, 4)
(0.1)91.98
(0.25, 4)
(0.1)92.46
(0.08, 16)
(1)92.06
(0.13, 16)
(0.001, 0.8, 0.2)95.29
(0.06, 8)
(0.001, 1)96.63
(0.00, 8)
(0.001, 0.1)Data set II 72.38
(8.94)83.18
(0.32, 256)
(10)82.84
(0.00, 2)
(0.001)83.03
(0.00, 2)
(0.1)83.92
(1.65, 2)
(10, 0.2, −0.2)83.14
(0.00, 2)
(0.01, 1)84.22
(0.00, 2)
(0.001, 10)DLBCL 68.83
(0.00)76.62
(0.00, 32)
(0.001)78.05
(0.73, 2)
(0.001)82.46
(0.68, 2)
(0.001)86.34
(1.78, 8)
(0.001, -0.2, 0.6)83.63
(2.51, 2)
(10, 0.1)86.71
(3.48, 2)
(10, 1)Colon 54.84
(0.00)67.06
(4.19, 32)
(0.001)69.35
(0.00, 2)
(0.001)80.32
(1.02, 2)
(0.001)85.95
(3.69, 8)
(0.001, −0.8, 1)83.87
(0.00, 4)
(10, 0.1)85.97
(0.78, 2)
(10, 0.1)Prostate0 56.86
(0.00)64.09
(5.83, 2)
(0.01)75.98
(0.51, 2)
(0.01)79.61
(1.01, 2)
(0.01)82.92
(2.19, 128)
(0.1, 0.2, 0.8)84.31
(0.00, 2)
(10, 1)85.29
(0.00, 2)
(10, 0.01)表 4 运行时间对比(s)
Table 4 Comparison of running time (s)
数据集 SNP-ELM SELM-AE ML-SELM-AE IRIS 4.58 0.02 0.02 Data set IIb 4.64×103 0.16 0.33 Data set II 8.24×103 0.65 0.76 DLBCL 7.77 0.04 0.06 Colon 3.44×102 0.03 0.11 Prostate0 1.15×102 0.07 0.13 表 5 ML-SELM-AE降维前后数据的聚类准确率(%) (方差)
Table 5 Clustering accuracy before and after ML-SELM-AE dimensionality reduction (%) (variance)
数据集 k-means LSR LRR LatLRR 未降维 已降维 未降维 已降维 未降维 已降维 未降维 已降维 IRIS 89.13 (0.32) 98.40 (0.00) 82.40 (0.69) 97.33 (0.00) 90.87 (0.00) 94.00 (0.83) 81.27 (1.03) 97.33 (0.00) Data set IIb 86.47 (2.53) 93.25 (0.00) 83.13 (0.00) 86.59 (0.19) 83.13 (0.00) 86.11 (0.00) 83.13 (0.00) 86.48 (0.25) Data set II 72.38 (8.94) 84.22 (0.00) 83.24 (0.08) 83.29 (0.05) 83.24 (0.00) 83.24 (0.00) 83.24 (0.00) 83.33 (0.00) DLBCL 68.83 (0.00) 86.71 (3.48) 76.62 (0.00) 81.43 (0.63) 76.62 (0.00) 78.57 (0.68) 74.03 (0.00) 78.18 (3.23) Colon 54.84 (0.00) 85.97 (0.78) 67.74 (0.00) 74.19 (0.00) 63.39 (0.00) 69.35 (0.00) 66.13 (1.67) 75.65 (4.06) Prostate0 56.86 (0.00) 85.29 (0.00) 63.82 (1.37) 70.59 (0.00) 57.84 (0.00) 63.73 (0.00) 55.88 (0.00) 74.51 (0.00) 表 6 三层极限学习机自编码器隐层节点数与聚类准确率(%) (方差)
Table 6 The number of hidden layer nodes and clustering accuracy for three-layer extreme learning machine autoencoder (%) (variance)
数据集 ML-ELM-AE (Multilayer ELM-AE) ML-SELM-AE (Multilayer SELM-AE) 500-100-2 500-100-10 500-100-50 500-100-100 500-100-2 500-100-10 500-100-50 500-100-100 Data set IIb 88.69 (0.00) 91.98 (0.25) 90.89 (0.06) 87.66 (0.20) 95.44 (0.00) 94.92 (0.17) 95.44 (0.00) 94.80 (0.33) Data set II 82.94 (0.00) 82.94 (0.00) 82.94 (0.00) 82.94 (0.00) 83.14 (0.00) 83.04 (0.00) 83.04 (0.00) 83.04 (0.00) DLBCL 74.03 (0.00) 72.99 (3.29) 72.73 (0.00) 69.22 (0.88) 80.52 (0.00) 80.52 (0.00) 78.57 (2.05) 76.62 (0.00) Colon 73.87 (1.67) 59.68 (0.00) 69.52 (7.35) 59.03 (0.83) 78.55 (2.53) 75.97 (7.81) 76.13 (9.46) 70.48 (4.37) Prostate0 66.67 (0.00) 60.78 (0.00) 59.80 (0.00) 62.75 (0.00) 77.16 (0.47) 82.35 (0.00) 78.33 (6.51) 80.39 (0.00) 数据集 2-2-2 10-10-10 50-50-50 100-100-100 2-2-2 10-10-10 50-50-50 100-100-100 Data set IIb 92.46 (0.08) 90.48 (0.00) 90.16 (0.17) 90.40 (0.25) 96.63 (0.00) 95.83 (0.00) 95.44 (0.00) 94.84 (0.00) Data set II 83.04 (0.00) 83.04 (0.00) 83.04 (0.00) 82.94 (0.00) 84.22 (0.00) 83.14 (0.00) 83.04 (0.00) 83.04 (0.00) DLBCL 83.12 (0.00) 77.01 (0.63) 68.83 (0.00) 68.70 (0.41) 86.75 (4.23) 80.52 (0.00) 78.96 (0.82) 76.62 (0.00) Colon 80.64 (0.00) 60.00 (2.50) 70.00 (1.36) 62.90 (0.00) 85.97 (0.78) 68.23 (0.78) 80.65 (0.00) 76.61 (9.48) Prostate0 80.39 (0.00) 57.45 (0.83) 64.41 (0.47) 63.73 (0.00) 85.29 (0.00) 69.61 (0.00) 79.12 (6.67) 84.31 (0.00) -
[1] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507. doi: 10.1126/science.1127647 [2] 田娟秀, 刘国才, 谷珊珊, 鞠忠建, 刘劲光, 顾冬冬. 医学图像分析深度学习方法研究与挑战. 自动化学报, 2018, 44(3): 401-424.Tian Juan-Xiu, Liu Guo-Cai, Gu Shan-Shan, Ju Zhong-Jian, Liu Jin-Guang, Gu Dong-Dong. Deep learning in medical image analysis and its challenges. Acta Automatica Sinica, 2018, 44(3): 401-424. [3] Rik D, Ekta W. Partition selection with sparse autoencoders for content based image classification. Neural Computing and Applications, 2019, 31(3): 675-690. doi: 10.1007/s00521-017-3099-0 [4] Shao H D, Jiang H K, Zhao H W. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mechanical Systems and Signal Processing, 2017, 95: 187-204. doi: 10.1016/j.ymssp.2017.03.034 [5] Chiang H T, Hsieh Y Y, Fu S W, Hung K H, Tsao Y, Chien S Y. Noise reduction in ECG signals using fully convolutional denoising autoencoders. IEEE Access, 2019, 7: 60806-60813. doi: 10.1109/ACCESS.2019.2912036 [6] Yildirim O, Tan R S, Acharya U R. An efficient compression of ECG signals using deep convolutional autoencoders. Cognitive Systems Research, 2018, 52: 198-211. doi: 10.1016/j.cogsys.2018.07.004 [7] Liu W F, Ma T Z, Xie Q S, Tao D P, Cheng J. LMAE: a large margin auto-encoders for classification. Signal Processing, 2017, 141: 137-143. doi: 10.1016/j.sigpro.2017.05.030 [8] Ji P, Zhang T, Li H, Salzmann M, Reid L. Deep subspace clustering networks. In: Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, USA, 2017. 23−32 [9] Kasun L L C, Yang Y, Huang G B, Zhang ZH Y. Dimension reduction with extreme learning machine. IEEE Transactions on Image Processing, 2016, 25(8): 3906-3918. doi: 10.1109/TIP.2016.2570569 [10] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: A new learning scheme of feedforward neural networks. In: Proceedings of Internatinaol Joint Conference on Neural Networks. Budapest, Hungary: IEEE, 2004. 985−990 [11] 许夙晖, 慕晓冬, 柴栋, 罗畅. 基于极限学习机参数迁移的域适应算法. 自动化学报, 2018, 44(2): 311-317.Xu Su-Hui, Mu Xiao-Dong, Chai Dong, Luo Chang. Domain adaption algorithm with ELM parameter transfer. Acta Automatica Sinica, 2018, 44(2): 311-317. [12] Huang G, Song S J, Gupta J N D. Semi-supervised and Unsupervised Extreme Learning Machines. IEEE Transactions on Cybernetics, 2014, 44(12): 2405-2417. doi: 10.1109/TCYB.2014.2307349 [13] 陈晓云, 廖梦真. 基于稀疏和近邻保持的极限学习机降维. 自动化学报, 2019, 45(2): 325-333.Chen Xiao-Yun, Liao Meng-Zhen. Dimensionality reduction with extreme learning machine based on sparsity and neighborhood preserving. Acta Automatica Sinica, 2019, 45(2): 325-333. [14] Lu C Y, Min H, Zhao Z Q. Robust and efficient subspace segmentation via least squares regression. In: Proceedings of the 12th European Conference on Computer Vision. Berlin, Germany: Springer, 2012. 347−360 [15] Ji P, Salzmann M, Li H D. Efficient dense subspace clustering. In: Proceedings of Winter Conference on Applications of Computer Vision. Steamboat Springs, CO, USA: IEEE, 2014.461−468 [16] Sun K, Zhang J S, Z C X, Hu J Y. Generalized extreme learning machine autoencoder and a new deep neural network. Neurocomputing, 2017, 230: 374-381. doi: 10.1016/j.neucom.2016.12.027 [17] Ma J, Yuan Y Y. Dimension reduction of image deep feature using PCA. Journal of Visual Communication and Image Representatio, 2019, 63: 1-8. [18] Wang S J, Xie D Y, Chen F, Gao Q X. Dimensionality reduction by LPP-L21. IET Computer Vision, 2018, 12(5): 659-665. doi: 10.1049/iet-cvi.2017.0302 [19] Kong D D, Chen Y J, Li N, Duan C Q, Lu L X, Chen D X. Tool wear estimation in end milling of titanium alloy using NPE and a novel WOA-SVM model. IEEE Transactions on Instrumentation and Measurement, 2020, 69(7): 5219-5232. doi: 10.1109/TIM.2019.2952476 [20] UCI Machine Learning Repository. [Online], available: http://archive.ics.uci.edu, September 8, 2020 [21] NYS Department of Health. [Online], available: http://www.bbci.de/competition/, September 8, 2020 [22] Gene Expression Model Selector. [Online], available: http://www.gems-system.org, September 8, 2020 [23] Kaper M, Ritter H. Generalizing to new subject in brain-computer interfacing. In: Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. San Francisco, USA: IEEE, 2004. 4363−4366 [24] Chen X Y, Jian C R. Gene expression data clustering based on graph regularized subspace segmentation. Neurocomputing, 2014, 143: 44-50. doi: 10.1016/j.neucom.2014.06.023 [25] Liu G C, Lin Z C, Yu Y. Robust subspace segmentation by low-rank representation. In: the 27th International Conference on Machine Learning. Haifa, Israel, 2010. 663−670 [26] Liu G, Yan S. Latent low-rank representation for subspace segmentation and feature extraction. In: Proceedings of International Conference on Computer Vision. Barcelona, Spain: IEEE, 2011. 1615−1622 -
 AAS-CN-2020-0684数据.zip
AAS-CN-2020-0684数据.zip

-





 下载:
下载: