Remaining Useful Life Prediction for Mixed Stochastic Deteriorating Equipment Based on Fractional Brownian Motion Process
-
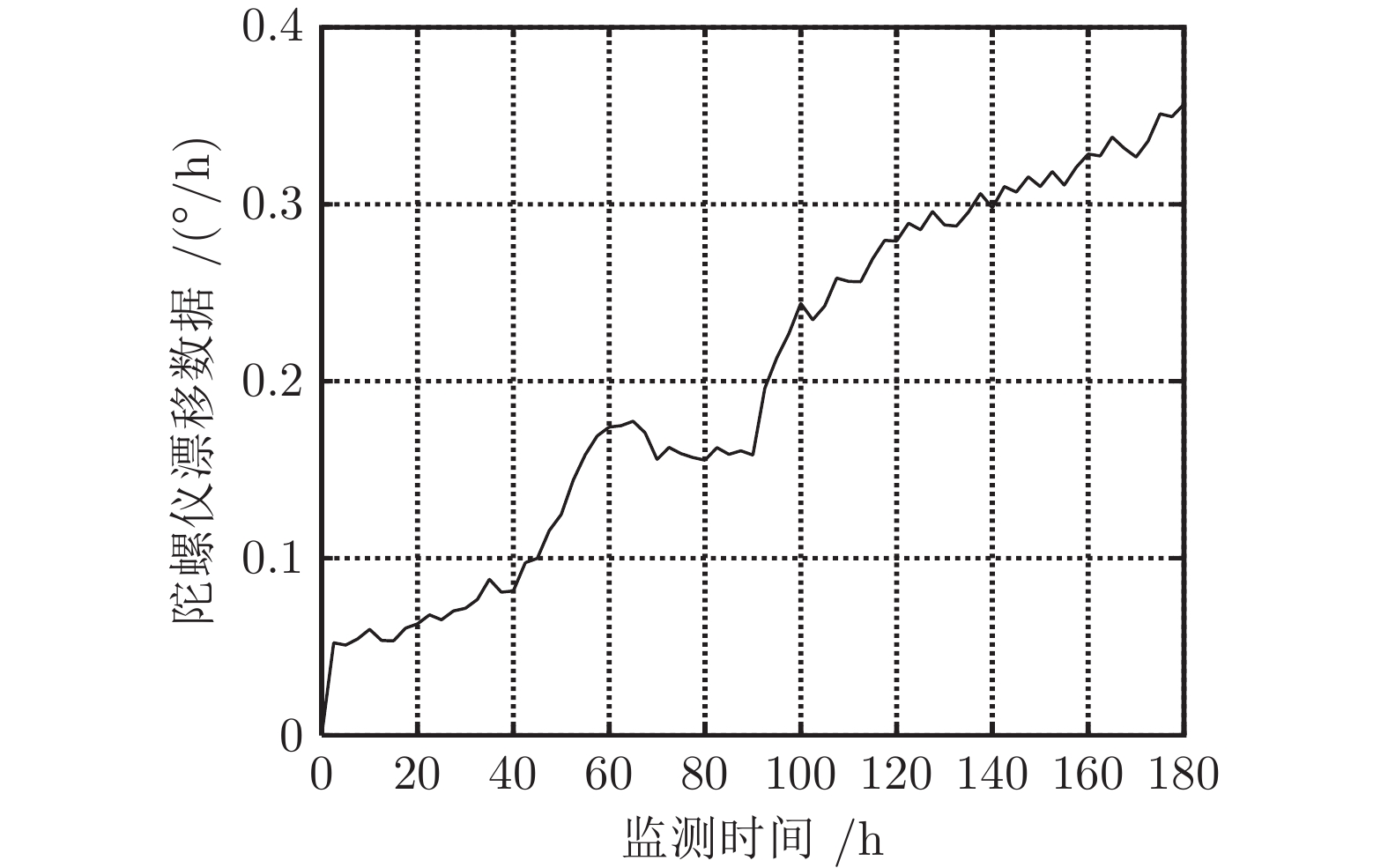
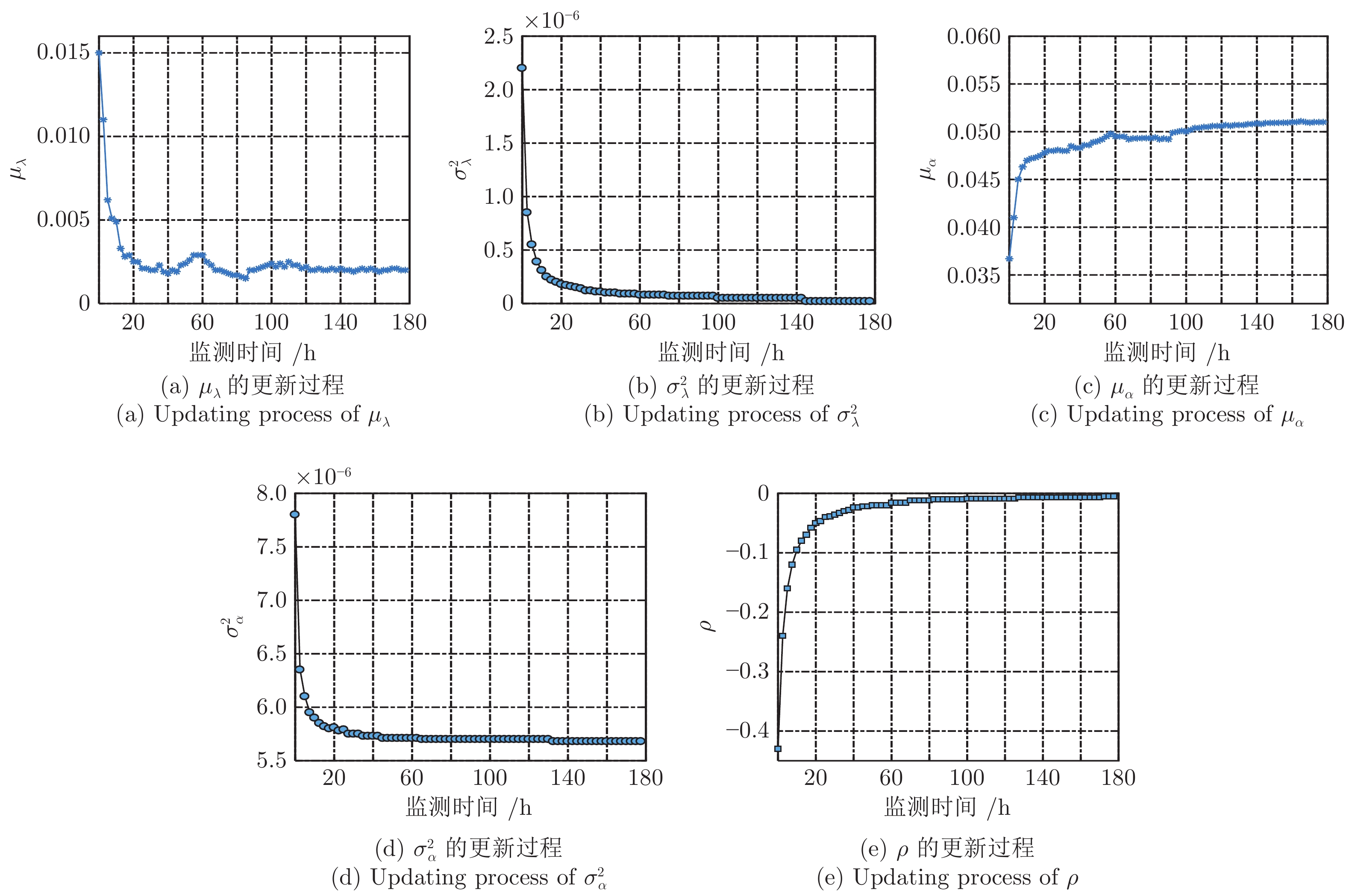
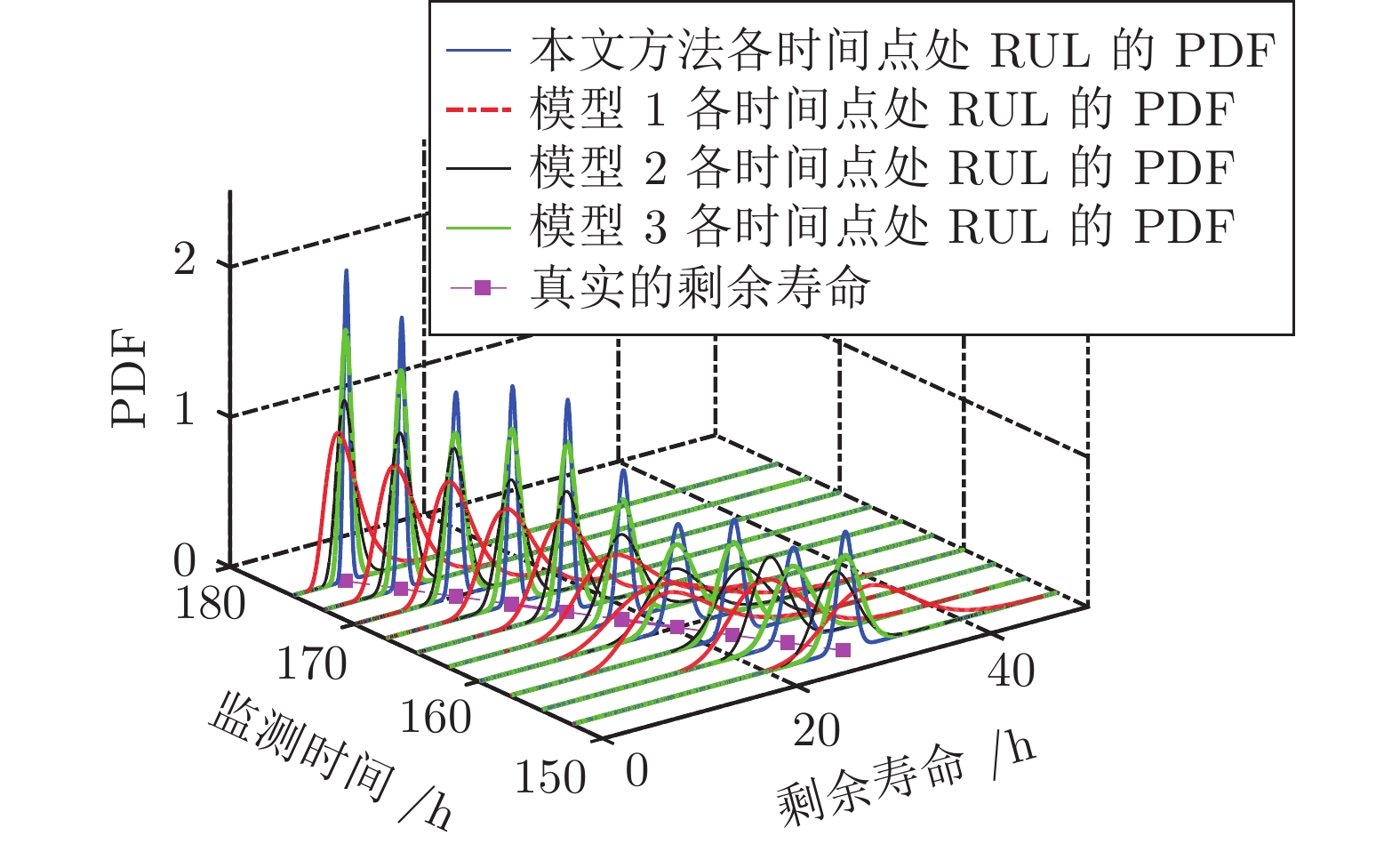
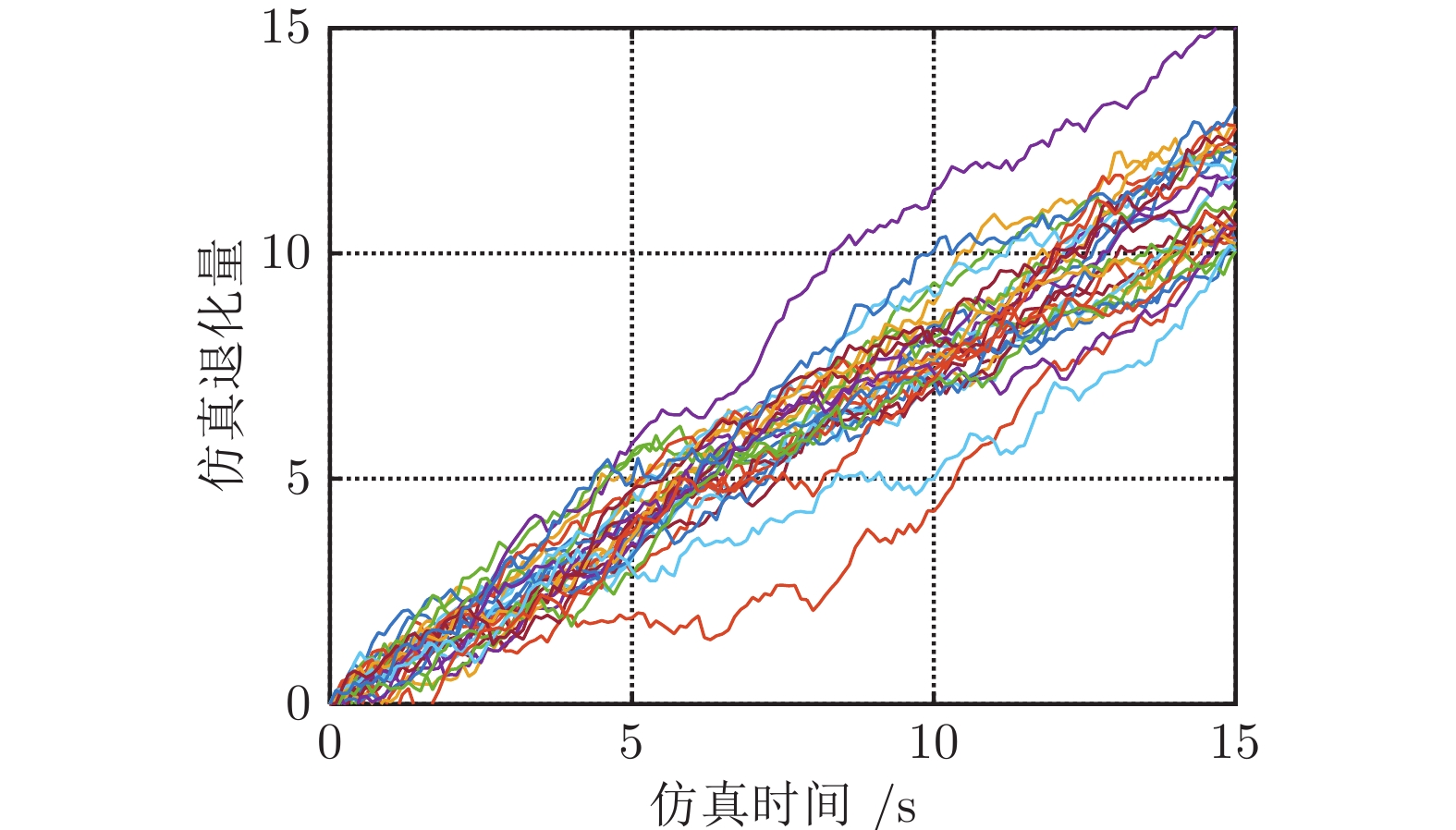
摘要: 在实际工程中, 设备往往是由多个不同类型元件或部件构成的集合体, 其总体性能退化程度是由内部多种随机退化过程综合影响下的结果. 不同于现有文献主要采用无记忆效应的单一线性或非线性形式随机过程模型来描述设备的真实退化, 首先建立一种基于分数布朗运动(Fractional Brownian motion, FBM)的混合随机退化模型, 用以刻画退化过程中的记忆效应与长期依赖性; 进一步, 在退化模型里同时引入双随机效应, 用以描述不同设备之间的退化差异性, 并基于弱收敛性理论推导得到首达时间(First hitting time, FHT)意义下剩余寿命(Remaining useful life, RUL)概率密度函数(Probability density function, PDF)的近似解析表达形式; 然后, 给出一种共性参数离线估计和随机参数实时更新的策略, 进而实现了剩余寿命的实时预测; 最后, 通过数值仿真例子和陀螺仪的实际退化数据, 验证了该方法的有效性和具有潜在的工程应用价值.Abstract: As a result of the interactive influence of a variety of internal random degradation processes, the overall performance of industrial equipment composed of multiple types of components usually deteriorates with its usage. Unlike most of the existing methods which describe the actual degradation of equipment via a single linear or nonlinear stochastic process model without memory effect, a new mixed stochastic degradation model based on Fractional Brownian motion (FBM) is proposed in this paper. Firstly, FBM is adopted to reflect the memory effect and long-term dependence of the degradation process. Then, double random effects are integrated into the degradation model to depict the variability between different units. Under the concept of the first hitting time (FHT), an approximate analytical expression of the probability density function (PDF) of the remaining useful life (RUL) is derived based on the weak convergence theory. Besides, a strategy of offline estimation of universal parameters and online update of random parameters is given to further realize real-time RUL prediction. Finally, numerical simulation examples and a case study of the degradation data of the gyroscope are provided to verify the effectiveness and potential engineering application value of the proposed method.
-
图 2 待预测设备实时监测退化数据
Fig. 2 Real-time monitoring degradation data of the equipment for prediction
图 4 4种方法在各个时间点处RUL预测的对比
Fig. 4 Comparison of RUL prediction by four methods at each time
图 5 四种方法在第5、8、11、13个时间点RUL预测结果的对比
Fig. 5 Comparison of RUL prediction by four methods at 5, 8, 11, 13th time
图 7 陀螺仪退化模型随机参数的实时更新过程
Fig. 7 Real-time updating process of random parameters of gyroscope degradation model
图 8 在不同时间点处四种方法预测RUL的PDF对比
Fig. 8 Comparison of RUL＇s PDFs by four prediction methods at each time
表 1 四种模型参数的先验估计值
Table 1 The parameters＇ prior estimates ofthe four models
参数 本文方法 模型1 模型2 模型3 ${\mu _\lambda }$ 1.0754 2.0251 — — ${\mu _\alpha }$ 0.2547 — 3.1547 3.3643 $\sigma _\lambda ^2$ $4.56\times10^{-4}$ 0.1618 — — $\sigma _\alpha ^2$ $3.47\times10^{-4}$ — 0.0176 0.0103 $\rho$ −0.4793 — — — ${\sigma ^2}$ 0.53362 0.51362 0.58362 0.54112 $\beta$ 0.1547 — 0.6035 0.6101 $H$ 0.8472 — — 0.8130 $\ln L\left( \Theta \right)$ 57.462 46.328 48.633 51.278 ${\rm{AIC}}$ −98.924 −86.656 −89.266 −92.556 ${\rm{BIC}}$ −87.724 −82.456 −83.666 −85.556 
下载: 导出CSV
表 2 陀螺仪退化模型参数的先验估计值
Table 2 A parameters＇ prior estimate of the gyroscope degradation model
参数 本文方法 模型1 模型2 模型3 ${\mu _\lambda }$ 0.0151 0.1348 — — ${\mu _\alpha }$ 0.0373 — 0.1503 0.1671 $\sigma _\lambda ^2$ $2.34\times 10^{-6}$ 0.0028 — — $\sigma _\alpha ^2$ $7.82 \times 10^{-6}$ — $5.76\times 10^{-4}$ $4.76\times 10^{-4}$ $\rho$ $-0.4503$ — — — ${\sigma ^2}$ 0.00192 0.00582 0.00422 0.00272 $\beta$ 0.2114 — 0.1342 0.1742 $H$ 0.8011 — — 0.7903 $\ln L\left( \Theta \right)$ 41.871 31.013 34.337 38.699 ${\rm{AIC}}$ −67.742 −56.026 −60.674 −67.398 ${\rm{BIC}}$ −70.942 −57.226 −62.274 −69.398
下载: 导出CSV
-
[1] 周东华, 魏慕恒, 司小胜. 工业过程异常检测、寿命预测与维修决策的研究进展[J]. 自动化学报, 2013, 39(6): 711-722.Zhou D H, 2 Wei M H, Si X S. A survey on anomaly detection, life prediction and maintenance decision for industrial processes[J]. ACTA AUTOMATICA SINICA, 2013, 39(6): 711-722. [2] Wang W. A two-stage prognosis model in condition based maintenance[J]. European Journal of Operational Research, 2007, 182(3): 1177-1187. doi: 10.1016/j.ejor.2006.08.047 [3] Si X S, Wang W, Hu C H. Remaining useful life estimation with three-level variability in degradation modeling[J]. IEEE Transactions on Reliability, 2014, 63(1): 167-190. doi: 10.1109/TR.2014.2299151 [4] Huang Z Y, Xu Z G. Remaining useful life prediction for hidden wiener process with an adaptive drift[J]. IEEE International Conference, 2013, 15(2): 1396-1400. [5] 王玺, 胡昌华, 裴洪. 新研发光电产品的剩余寿命自适应预测方法[J]. 光学学报, 2019, 39(12): 1223003. doi: 10.3788/AOS201939.1223003Wang X, Hu C H, Pei H. Adaptive remaining useful life prediction method for newly developed photoelectric products[J]. Acta Optica Sinica, 2019, 39(12): 1223003. doi: 10.3788/AOS201939.1223003 [6] Si X S, Wang W, Hu C H, Zhou D H, Pecht M. Remaining useful life estimation based on a nonlinear diffusion degradation process[J], IEEE Transactions on Reliability, 2012, 61(1): 50-67. doi: 10.1109/TR.2011.2182221 [7] 司小胜, 胡昌华, 周东华. 带测量误差的非线性退化过程建模与剩余寿命估计[J]. 自动化学报, 2013, 39(5): 530-541.Si X S, Hu C H, Zhou D H. Nonlinear degradation process modeling and remaining useful life estimation subject to measurement error[J]. ACTA AUTOMATICA SINICA, 2013, 39(5): 530-541. [8] 郑建飞, 胡昌华, 司小胜等. 考虑不确定测量和个体差异的非线性随机退化系统剩余寿命估计[J]. 自动化学报, 2017, 43(02): 259-270.Zheng Jian-fei, Hu Chang-Hua, Si Xiao-Sheng, Zhang Zheng-Xin, Zhang Xin. Remaining useful life estimation for nonlinear stochastic degrading systems with uncertain measurement and unit-to-unit variabilit. Acta Automatica Sinica, 2017, 43(02): 259-270 [9] Cai Z Y, Guo J S, Chen Y X, et al. Remaining lifetime online prediction based on step-stress accelerated degradation modeling[J]. Systems Engineering and Electronics, 2018, 40(11): 218-223. [10] Zhang H, Chen M, Xi X, et al. Remaining useful life prediction for degradation processeswith long-range dependence[J]. IEEE Transactions on Reliability, 2017, 66(4): 1368-1379. doi: 10.1109/TR.2017.2720752 [11] Xi X, Chen M, Zhou D. Remaining useful life prediction for degradation processes with memory effects[J]. IEEE Transactions on Reliability, 2017, 66(3): 751-760. doi: 10.1109/TR.2017.2717488 [12] Zhang H W, Zhou D H, Chen M Y. FBM-based remaining useful life prediction for degradation processes with long-range dependence and multiple modes[J]. IEEE Transactions on Reliability, 2019, 68(3): 1021-1033. doi: 10.1109/TR.2018.2877643 [13] Xi X P, Chen M Y, Zhang H W, et al. An improved non-Markovian degradation model with long-term dependency and item-to-item uncertainty[J]. Mechanical Systems and Signal Processing, 2018, 105(1): 467-480. [14] Zhang H W, Zhou D H. FBM-Based Remaining useful life prediction for degradation processes with long-range dependence and multiple modes[J]. IEEE TRANSACTIONS on RELIABILITY. 2018, 67(4): 1318-1335. [15] Wang Z Q, Hu C H, Wang W B, et al. An additive Wiener process-based prognostic model for hybrid deteriorating systems[J]. IEEE Transactions on Reliability, 2014, 63(1): 208-222. doi: 10.1109/TR.2014.2299155 [16] Mathew S, Das D, Osterman M, et al. Virtual remaining life assessment of electronic hardware subjected to shock and random vibration life cycle loads[J], Journal of the Institute of Environmental Sciences and Technology, 2007, 50(1): 86-97. [17] Chakraborty S, Gebraeel NZ, Lawley M, et al. Residual-life estimation for components with non-symmetric priors[J]. IIE Transactions, 2009, 41(4): 372-387. doi: 10.1080/07408170802369409 [18] Ye ZS, Wang Y, Tsui KL, et al. Degradation data analysis using Wiener processes with measurement errors[J]. IEEE Transactions on Reliability, 2013, 62(4): 772-780. doi: 10.1109/TR.2013.2284733 [19] Park C, Padgett WJ. Accelerated degradation models for failure based on geometric Brownian motion and gamma processes[J]. LifetimeData Analysis, 2005, 11(4): 511-527. [20] Mandelbrot B B, John W V. Fractional Brownian motions, fractional noises and applications[J]. Society for Industial and Applied Mathematics, 1968, 10(4): 422-437. [21] Xu L P, Li Z, Luo J W. Global attracting set and exponential decay of second-order neutral stochastic functional differential equations driven by fBm [J]. Advances in Difference Equations., 2017, 134: 1-16. doi: 10.1186/s13662-017-1186-2 [22] Lau W C, Erramilli A, Wang J L, et al. Self-similar traffic generation: the random midpoint displacement algorithm and its properties[J]. IEEE International Conference on Communications, 1995, 32(3): 66-472. [23] Abry P, Sellan F. The wavelet-based synthesis for fractional Brownian motion[J]. Applied and Computational Harmonic Analysis, 1996, 3(4): 377-383. doi: 10.1006/acha.1996.0030 [24] 余征. 混合分数布朗运动的性质及其在金融中的应用 [博士论文], 东华大学, 中国, 2009Yu Zheng. The Property of Mixed Fractional Brownian Motion and the Application in Finance [Ph.D. dissertation], Donghua University, China, 2009 [25] Si X, Wang W, Hu C, et al. Remaining useful life estimation-A review on the statistical data driven approaches[J]. European Journal of Operational Research, 2011, 213(1): 1-14. doi: 10.1016/j.ejor.2010.11.018 [26] Konstantopoulos T, Sakhanenko A. Convergence and convergence rate to fractional Brownian motion for weighted random sums[J]. Siberian Electronic Mathematical Reports. 2004, 1(4): 47-63. [27] Wang X, Balakrishnan N, Guo B. Residual life estimation based on a generalized Wiener degradation process[J]. Reliability Engineering and System Safety, 2014, 124(3): 13-23. [28] Akaike H. A new look at the statistical model identification[J]. IEEE Transactions Automatical Control, 1974, 19(6): 716-723. doi: 10.1109/TAC.1974.1100705 [29] Schwarz G. Estimating the dimension of a model[J]. Annals of Applied Statistics, 1978, 6(2): 461-464. [30] 周绍华,胡昌华,司小胜,方世鹏,裴洪.融合非线性加速退化模型与失效率模型的产品寿命预测方法[J].电子学报,2017,45(5):1084-1089Zhou Shao-Hua, Hu Chang-Hua, Si Xiao-Sheng. Life prediction approach by integrating nonlinear accelerated degradation model and hazard rate model[J]. Acta Electronica Sinica, 2017, 45(5): 1084-1089. -
图(8) / 表(2)
计量
- 文章访问数: 459
- HTML全文浏览量: 127
- PDF下载量: 162
- 被引次数: 0
