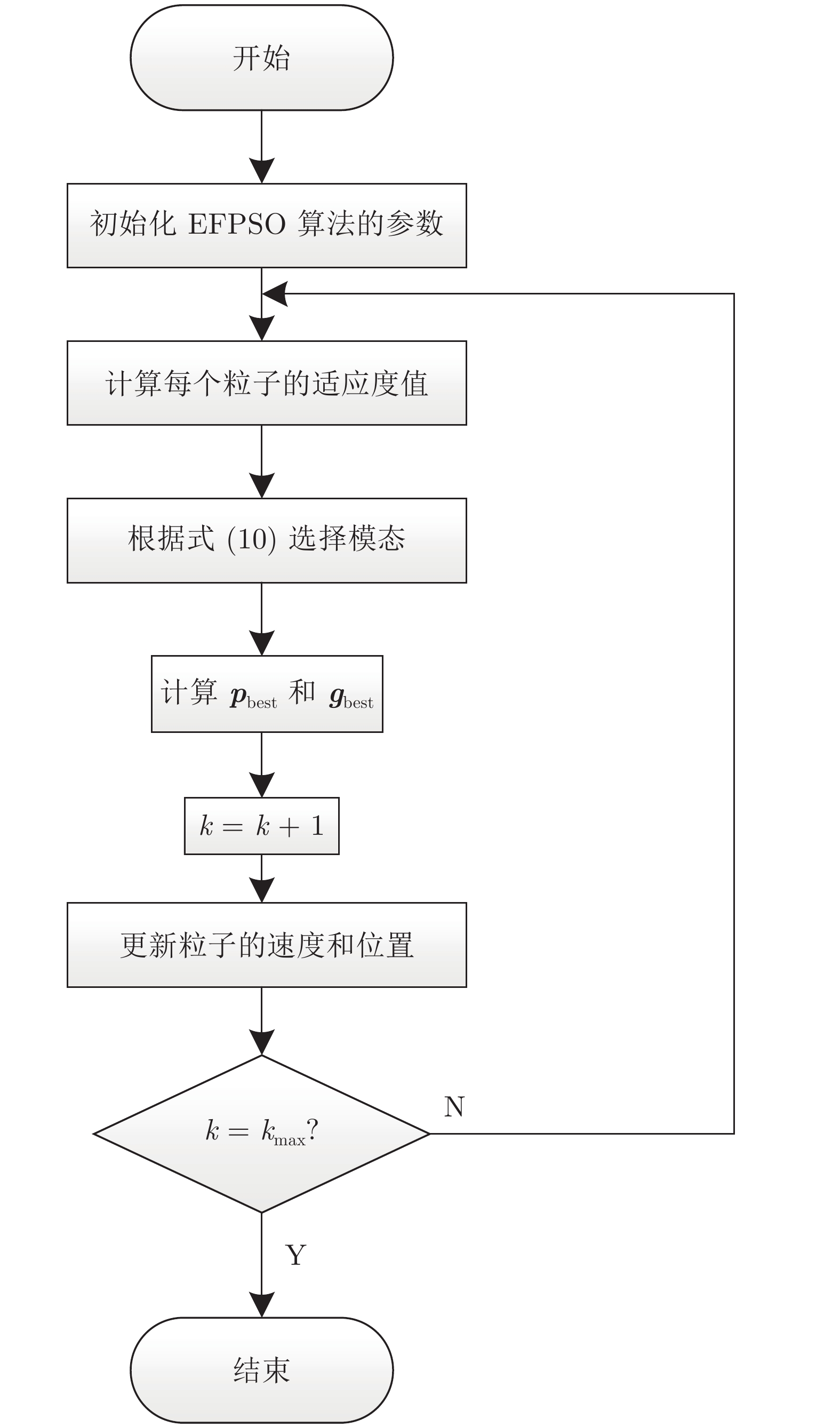
Full-information Particle Swarm Optimizer Based on Event-triggering Strategy and Its Applications
-
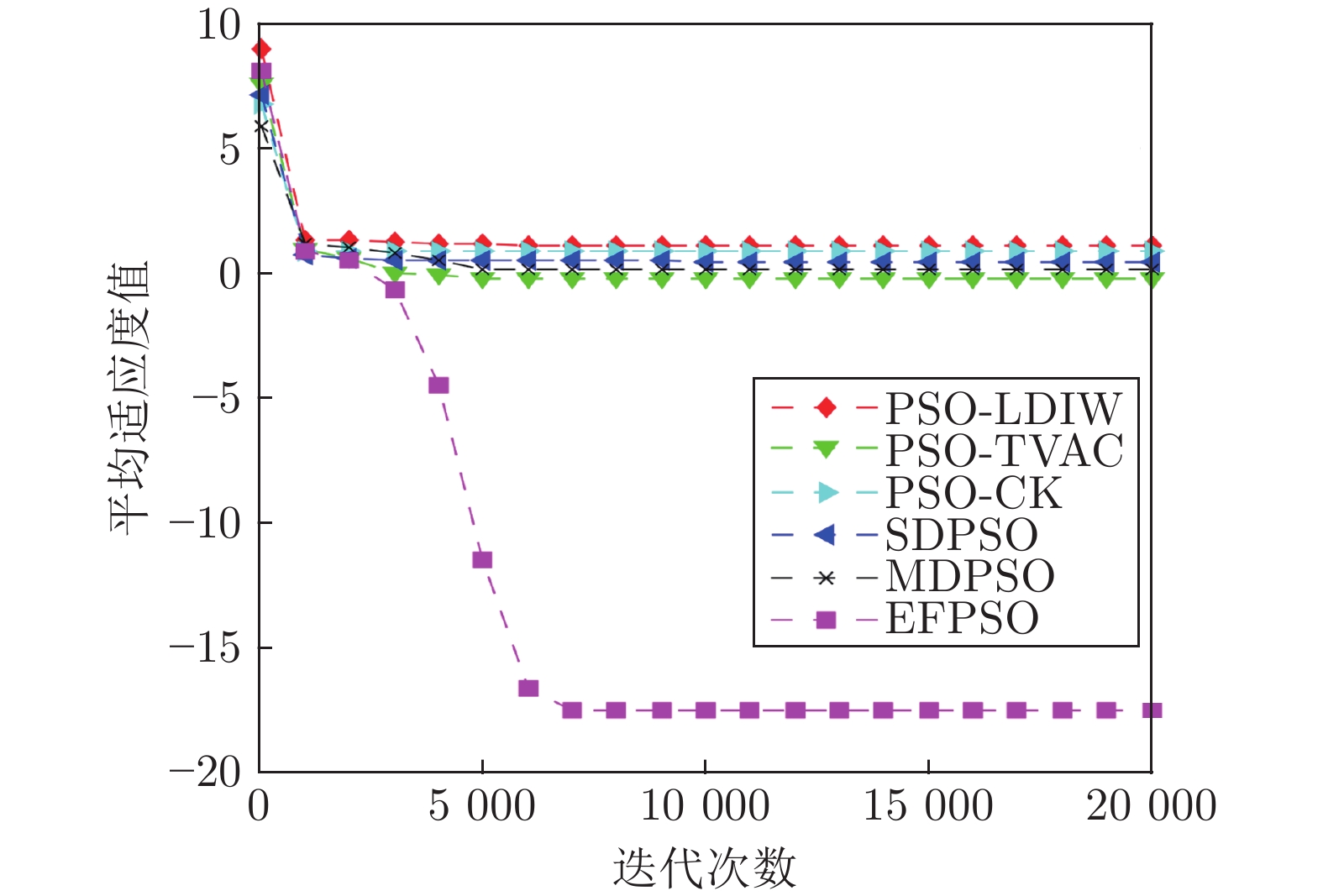
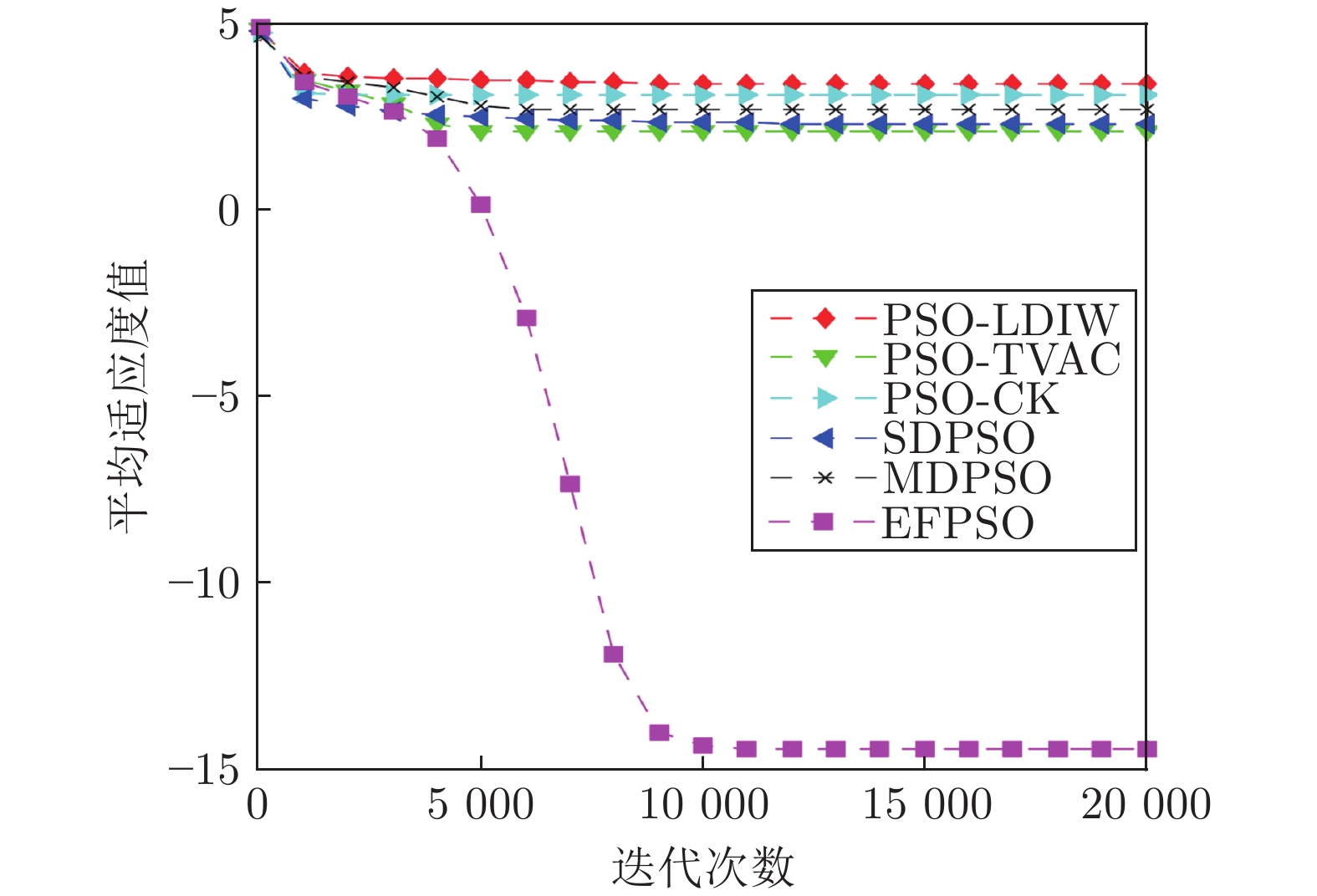
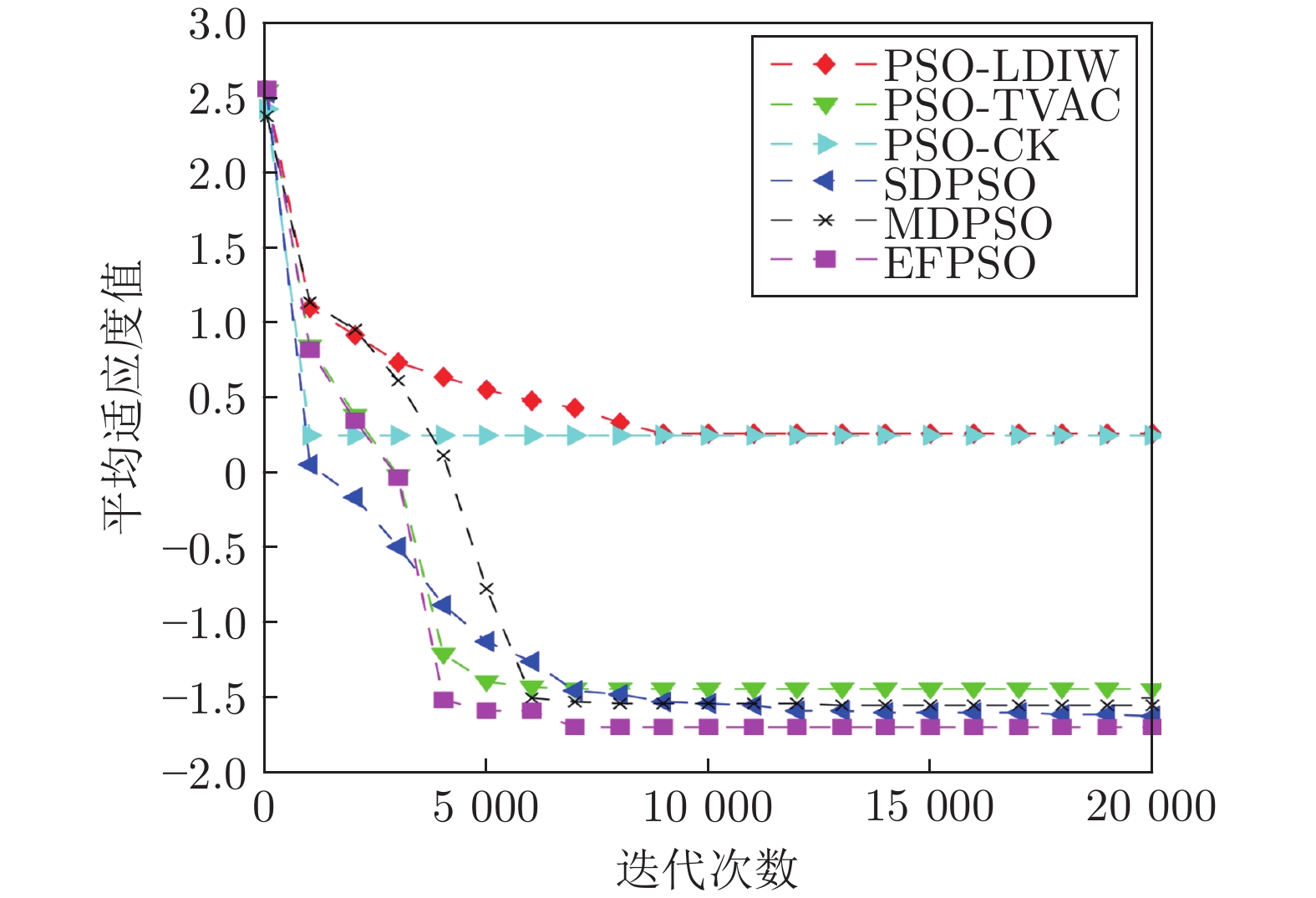
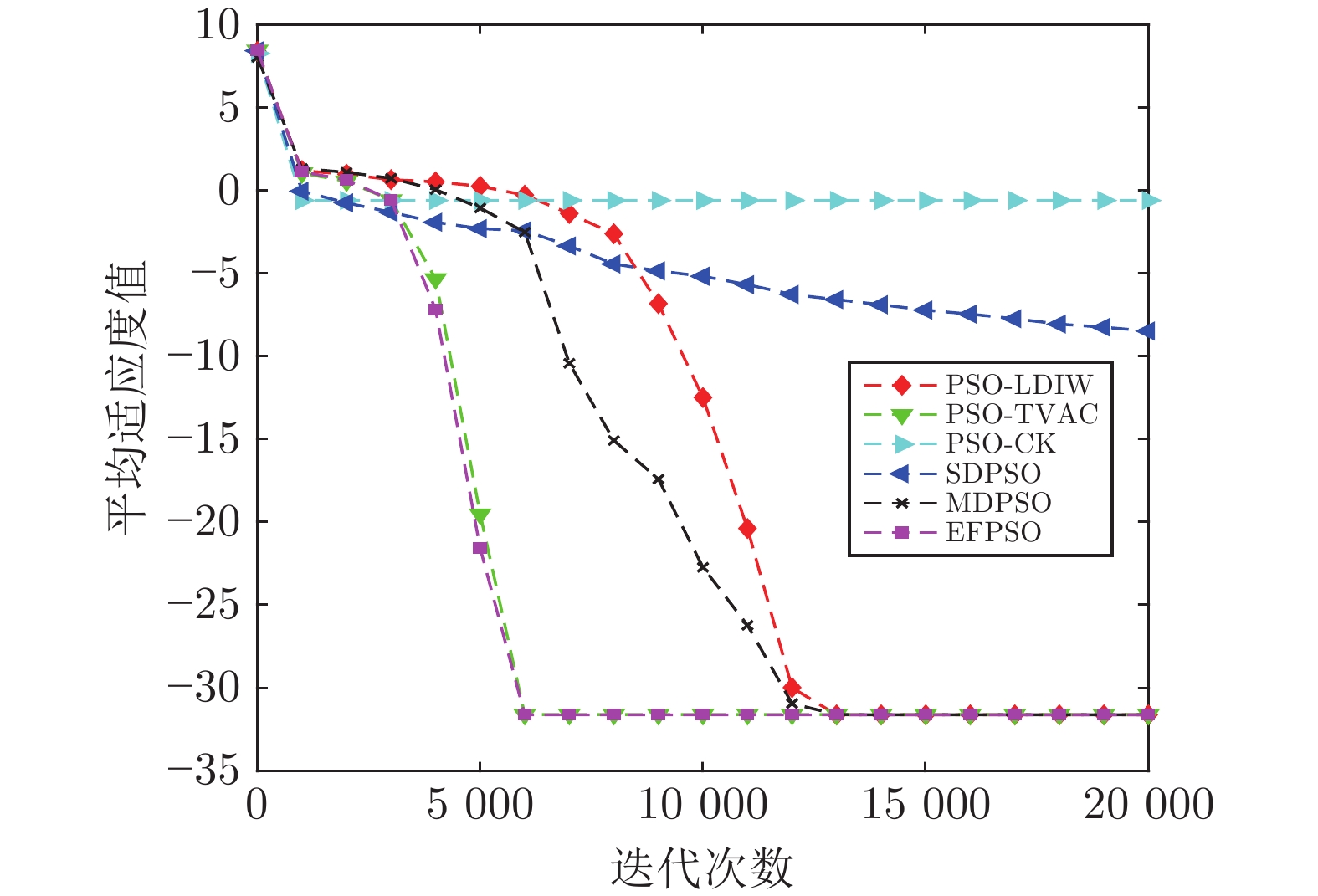
摘要: 针对标准粒子群优化算法存在早熟收敛和容易陷入局部最优的问题, 本文提出了一种基于事件触发的全信息粒子群优化算法(Event-triggering-based full-information particle swarm optimization, EFPSO). 首先, 引入一类基于粒子空间特性的事件触发策略实现粒子群优化算法(Particle swarm optimization, PSO) 的模态切换, 更好地维持了算法搜索和收敛能力之间的动态平衡. 然后, 鉴于引入历史信息能够降低算法陷入局部最优的可能性, 提出一种全信息策略来克服PSO算法搜索能力不足的缺陷. 数值仿真实验表明, EFPSO算法在种群多样性、收敛率、成功率方面优于其他改进的PSO算法. 最后, 应用EFPSO算法对变分模态分解(Variational mode decomposition, VMD)去噪算法进行改进, 并在现场管道信号去噪取得了很好的效果.Abstract: In this paper, an event-triggering-based full-information particle swarm optimization algorithm (EFPSO) is proposed with the purpose of decreasing the possibility of premature convergence and local optimization. First of all, an event-triggering strategy is employed to achieve the mode switching of the particle swarm optimization (PSO) algorithms in terms of the spatial properties of the particles, which better maintains a dynamic balance between the convergence and population diversity. Next, a full-information strategy is introduced to overcome the defect, i.e., the poor exploration ability of the PSO algorithm, where the historical information is considered to reduce the possibility of falling into the local optimum. Experiment results demonstrate the superiority of the proposed EFPSO algorithm over existing popular PSO algorithms in terms of population diversity, convergence rate, and success ratio. Finally, an EFPSO-optimized variational mode decomposition (VMD) denoising algorithm is designed and applied successfully in the field pipeline signal denoising.
-
表 1 基准函数配置
Table 1 The benchmark function configuration
函数 名称 搜索范围 维数 阈值 最优值 $f_{1}(x)$ Sphere [−100 100] 20 0.01 0 $f_{2}(x)$ Ackley [−32 32] 20 0.01 0 $f_{3}(x)$ Rastrigin [−5.12 5.12] 20 50 0 $f_{4}(x)$ Schwefe 2.22 [−10 10] 20 0.01 0 $f_{5}(x)$ Schwefe 1.2 [−100 100] 20 0.01 0 $f_{6}(x)$ Griewank [−600 600] 20 0.01 0 $f_{7}(x)$ Penalized 1 [−100 100] 20 0.01 0 $f_{8}(x)$ Step [−100 100] 20 0.01 0 表 2 6种PSO算法测试结果统计
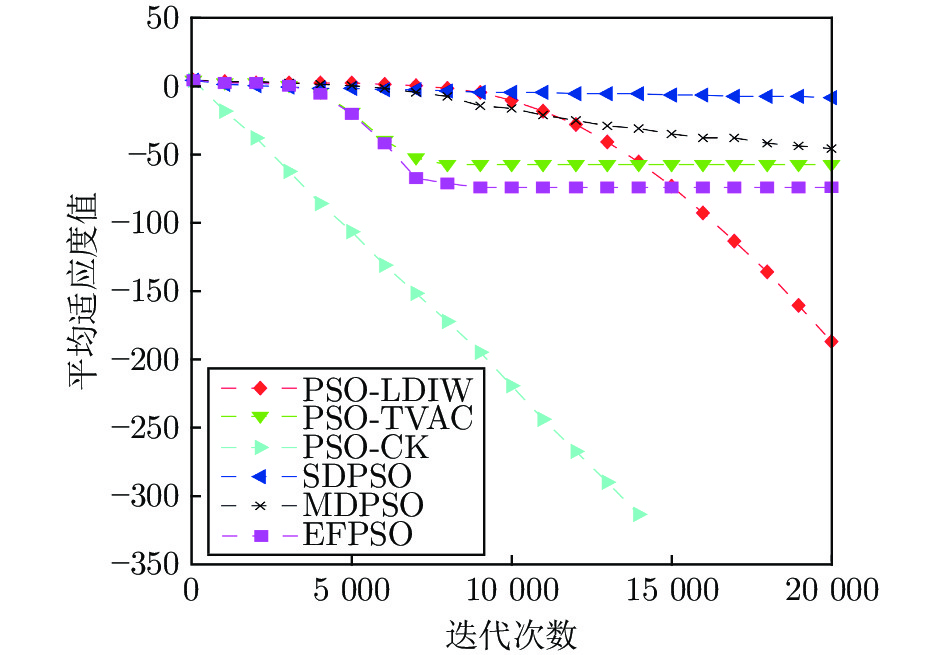
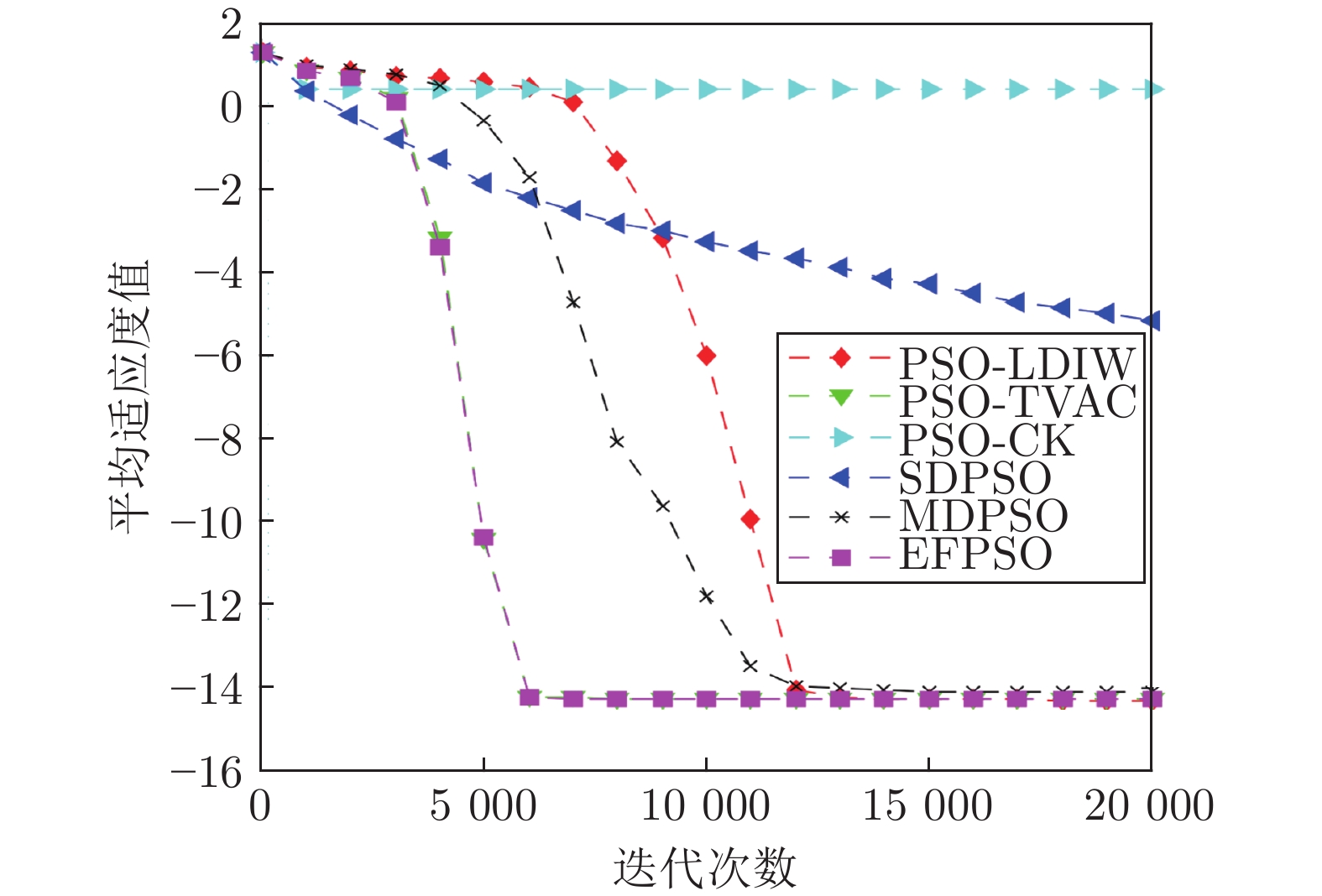
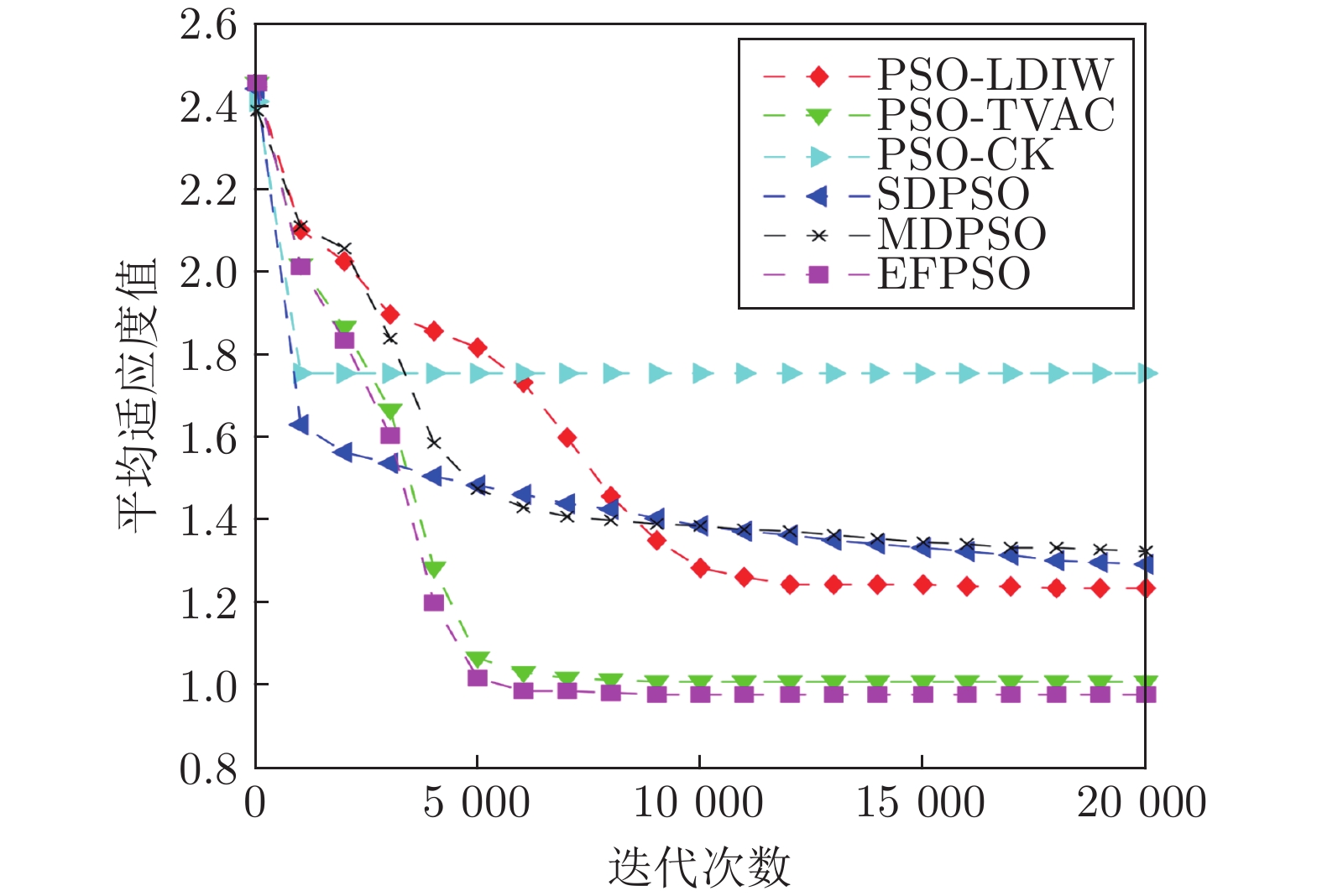
Table 2 Six PSO algorithms test results statistics
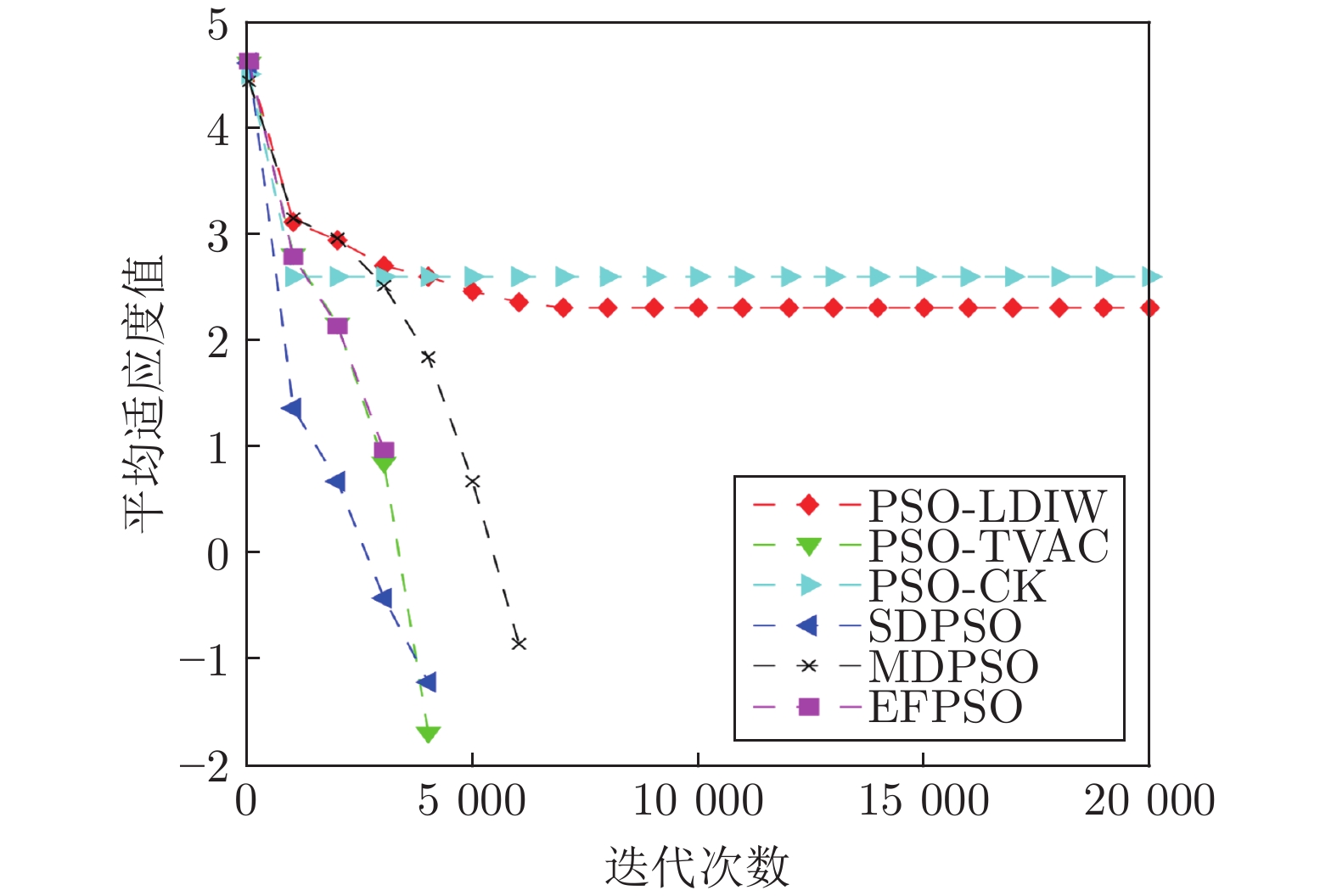
PSO-LDIW PSO-TVAC PSO-CK SDPSO MDPSO EFPSO $f_{1}(x)$ 最小值 $2.44\times10^{-202}$ $8.44\times10^{-152}$ 0 $6.85\times10^{-13}$ $7.57\times10^{-68}$ $1.60\times10^{-139}$ 均值 $1.90\times10^{-188}$ $3.49\times10^{-58}$ 0 $4.26\times10^{-9}$ $2.99\times10^{-46}$ $1.63\times10^{-75}$ 标准差 0 $2.47\times10^{-57}$ 0 $9.72\times10^{-9}$ $1.89\times10^{-45}$ $7.32\times10^{-75}$ 成功率(%) 100 100 100 100 100 100 $f_{2}(x)$ 最小值 $2.66\times10^{-15}$ $2.66\times10^{-15}$ $2.66\times10^{-15}$ $4.09\times10^{-7}$ $2.66\times10^{-15}$ $2.66\times10^{-15}$ 均值 $5.15\times10^{-15}$ $5.50\times10^{-15}$ $2.72$ $7.14\times10^{-6}$ $8.06\times10^{-15}$ $5.50\times10^{-15}$ 标准差 $1.64\times10^{-15}$ $1.43\times10^{-15}$ $4.00$ $5.89\times10^{-6}$ $3.22\times10^{-15}$ $1.45\times10^{-15}$ 成功率(%) 100 100 20 100 100 100 $f_{3}(x)$ 最小值 $3.97$ $2.98$ $20.8$ $3.99$ $5.96$ $4.97$ 均值 $17.1$ $10.2$ $56.3$ $19.5$ $21.1$ $ 9.50$ 标准差 $15.3$ $4.10$ $22.6$ $12.7$ $12.3$ $2.44$ 成功率(%) 96 100 50 94 98 100 $f_{4}(x)$ 最小值 $5.09\times10^{-119}$ $1.07\times10^{-37}$ $6.60\times10^{-65}$ $2.46\times10^{-8}$ $4.37\times10^{-34}$ $1.99\times10^{-32}$ 均值 $12.6$ $6.00\times10^{-1}$ $3.11\times10^{-3}$ $3.00$ $1.40$ $2.96\times10^{-18}$ 标准差 $11.9$ $2.39$ $8.40$ $5.05$ $3.50$ $1.32\times10^{-17}$ 成功率(%) 28 94 44 72 86 100 $f_{5}(x)$ 最小值 $4.31\times10^{-27}$ $4.15\times10^{-33}$ $2.70\times10^{-104}$ $9.40\times10^{-2}$ $1.92\times10^{-21}$ $6.56\times10^{-26}$ 均值 $2.56\times10^{3}$ 133 $1.33\times10^{3}$ 204 533 $3.32\times10^{-15}$ 标准差 $3.91\times10^{3}$ 942 $2.49\times10^{3}$ 988 $1.63\times10^{3}$ $1.12\times10^{-14}$ 成功率(%) 64 98 76 0 90 100 $f_{6}(x)$ 最小值 0 0 0 $2.98\times10^{-13}$ 0 0 均值 $1.84$ $3.69\times10^{-2}$ $1.82$ $2.43\times10^{-2}$ $2.82\times10^{-2}$ $2.03\times10^{-2}$ 标准差 $12.7$ $2.92\times10^{-2}$ $12.7$ $2.08\times10^{-2}$ $2.80\times10^{-2}$ $2.35\times10^{-2}$ 成功率(%) 12 14 28 34 36 40 $f_{7}(x)$ 最小值 $2.35\times10^{-32}$ $2.35\times10^{-32}$ $2.35\times10^{-32}$ $3.77\times10^{-16}$ $2.35\times10^{-32}$ $2.35\times10^{-32}$ 均值 $2.35\times10^{-32}$ $2.43\times10^{-32}$ $2.60\times10^{-1}$ $3.46\times10^{-9}$ $2.37\times10^{-32}$ $ 2.35\times10^{-32}$ 标准差 $2.73\times10^{-34}$ $4.49\times10^{-33}$ $5.17\times10^{-1}$ $1.70\times10^{-8}$ $1.09\times10^{-33}$ $2.80\times10^{-48}$ 成功率(%) 100 100 52 100 100 100 $f_{8}(x)$ 最小值 0 0 0 0 0 0 均值 200 0 401 0 0 0 标准差 $1.41\times10^{3}$ 0 $1.97\times10^{3}$ 0 0 0 成功率(%) 98 100 62 100 100 100 表 3 不同
$\gamma_i(k)$ 的EFPSO算法统计结果比较Table 3 The statistical results of the EFPSO algorithm with different
$\gamma_i(k)$ are compared$\gamma_i(k)=0.2$ $\gamma_i(k)=0.3$ $\gamma_i(k)=0.4$ $\gamma_i(k)=0.5$ $\gamma_i(k)=0.6$ $\gamma_i(k)=0.7$ $f_{1}(x)$ 最小值 $1.42\times10^{-25}$ $2.31\times10^{-101}$ $1.69\times10^{-139}$ $6.03\times10^{-90}$ $7.91\times10^{-53}$ $5.14\times10^{-30}$ 均值 $5.14\times10^{-35}$ $3.34\times10^{-60}$ $1.63\times10^{-75}$ $4.32\times10^{-65}$ $2.24\times10^{-32}$ $7.98\times10^{-7}$ 标准差 $3.21\times10^{-35}$ $3.95\times10^{-60}$ $7.32\times10^{-75}$ $3.98\times10^{-65}$ $3.41\times10^{-32}$ $5.31\times10^{-7}$ 成功率(%) 100 100 100 100 100 100 $f_{2}(x)$ 最小值 $2.60\times10^{-15}$ $2.66\times10^{-15}$ $2.66\times10^{-15}$ $2.66\times10^{-15}$ $3.45\times10^{-12}$ $2.97\times10^{-7}$ 均值 $3.91\times10^{-14}$ $6.29\times10^{-15}$ $5.50\times10^{-15}$ $7.14\times10^{-14}$ $3.63\times10^{-10}$ $5.48\times10^{-7}$ 标准差 $4.32\times10^{-14}$ $8.91\times10^{-15}$ $1.45\times10^{-15}$ $8.93\times10^{-14}$ $2.97\times10^{-10}$ $6.92\times10^{-7}$ 成功率(%) 100 100 100 100 100 100 $f_{3}(x)$ 最小值 $9.01$ $12.6$ $4.97$ $9.12$ $13.1$ $11.1$ 均值 $18.3$ $17.2$ $9.50$ $12.9$ $20.0$ $13.8$ 标准差 $6.59$ $3.33$ $2.44$ $3.39$ $8.18$ $2.23$ 成功率(%) 100 100 100 100 100 100 $f_{4}(x)$ 最小值 $1.69\times10^{-24}$ $1.59\times10^{-24}$ $1.99\times10^{-32}$ $2.24\times10^{-40}$ $2.41\times10^{-35}$ $5.71\times10^{-20}$ 均值 $5.38\times10^{-16}$ $1.78\times10^{-16}$ $2.96\times10^{-18}$ $2.56\times10^{-32}$ $7.98\times10^{-22}$ $6.94\times10^{-7}$ 标准差 $7.69\times10^{-17}$ $0.97\times10^{-16}$ $1.32\times10^{-17}$ $1.68\times10^{-32}$ $6.54\times10^{-22}$ $3.89\times10^{-7}$ 成功率(%) 100 100 100 100 100 100 $f_{5}(x)$ 最小值 $2.31\times10^{-28}$ $7.34\times10^{-30}$ $6.56\times10^{-26}$ $7.19\times10^{-20}$ $5.34\times10^{-20}$ $1.53\times10^{-9}$ 均值 $5.46\times10^{-15}$ $3.84\times10^{-15}$ $3.32\times10^{-15}$ $7.34\times10^{-9}$ $8.91\times10^{-9}$ $8.72\times10^{-5}$ 标准差 $2.49\times10^{-15}$ $2.96\times10^{-15}$ $1.12\times10^{-14}$ $1.36\times10^{-9}$ $6.37\times10^{-9}$ $6.54\times10^{-5}$ 成功率(%) 100 100 100 100 100 100 $f_{6}(x)$ 最小值 $2.72\times10^{-7}$ $1.31\times10^{-7}$ 0 $5.18\times10^{-7}$ $9.07\times10^{-7}$ $1.01\times10^{-6}$ 均值 $1.54\times10^{-2}$ $1.19\times10^{-2}$ $2.03\times10^{-2}$ $4.45\times10^{-3}$ $1.03\times10^{-2}$ $2.40\times10^{-2}$ 标准差 $3.04\times10^{-2}$ $9.57\times10^{-3}$ $2.35\times10^{-2}$ $6.16\times10^{-3}$ $1.05\times10^{-2}$ $3.15\times10^{-2}$ 成功率(%) 30 40 40 42 38 36 $f_{7}(x)$ 最小值 $2.35\times10^{-32}$ $2.35\times10^{-32}$ $2.35\times10^{-32}$ $2.35\times10^{-32}$ $4.67\times10^{-20}$ $2.37\times10^{-16}$ 均值 $2.43\times10^{-32}$ $2.35\times10^{-32}$ $2.35\times10^{-32}$ $2.35\times10^{-32}$ $8.96\times10^{-20}$ $ 8.91\times10^{-9}$ 标准差 $3.71\times10^{-34}$ $3.69\times10^{-33}$ $2.80\times10^{-48}$ $4.96\times10^{-33}$ $7.69\times10^{-20}$ $7.34\times10^{-8}$ 成功率(%) 100 100 100 100 100 100 $f_{8}(x)$ 最小值 0 0 0 0 0 0 均值 0 0 0 0 0 0 标准差 0 0 0 0 0 0 成功率(%) 100 100 100 100 100 100 表 4 测试算法的信噪比和均方误差
Table 4 SNR and MSE of test algorithm
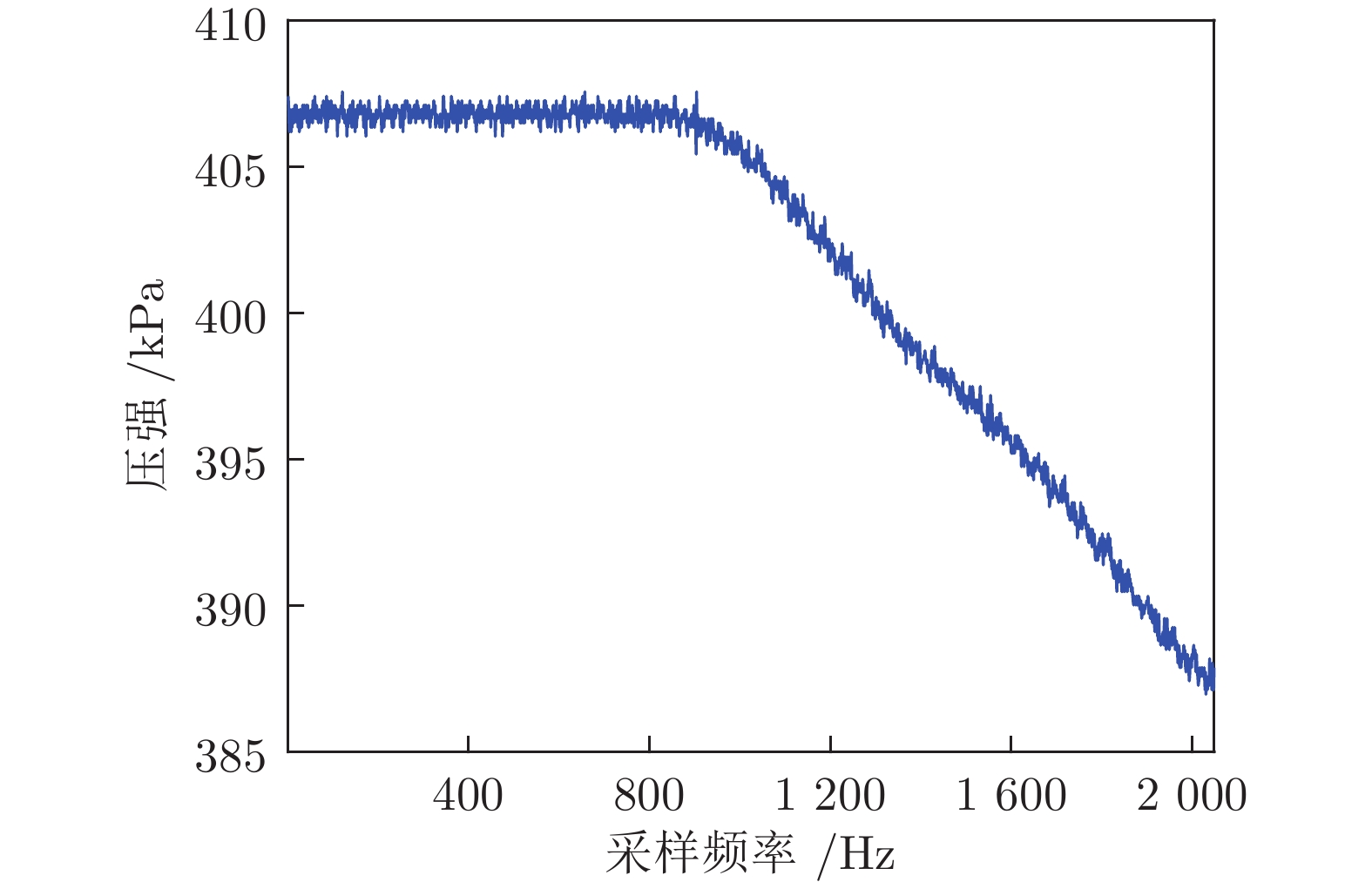
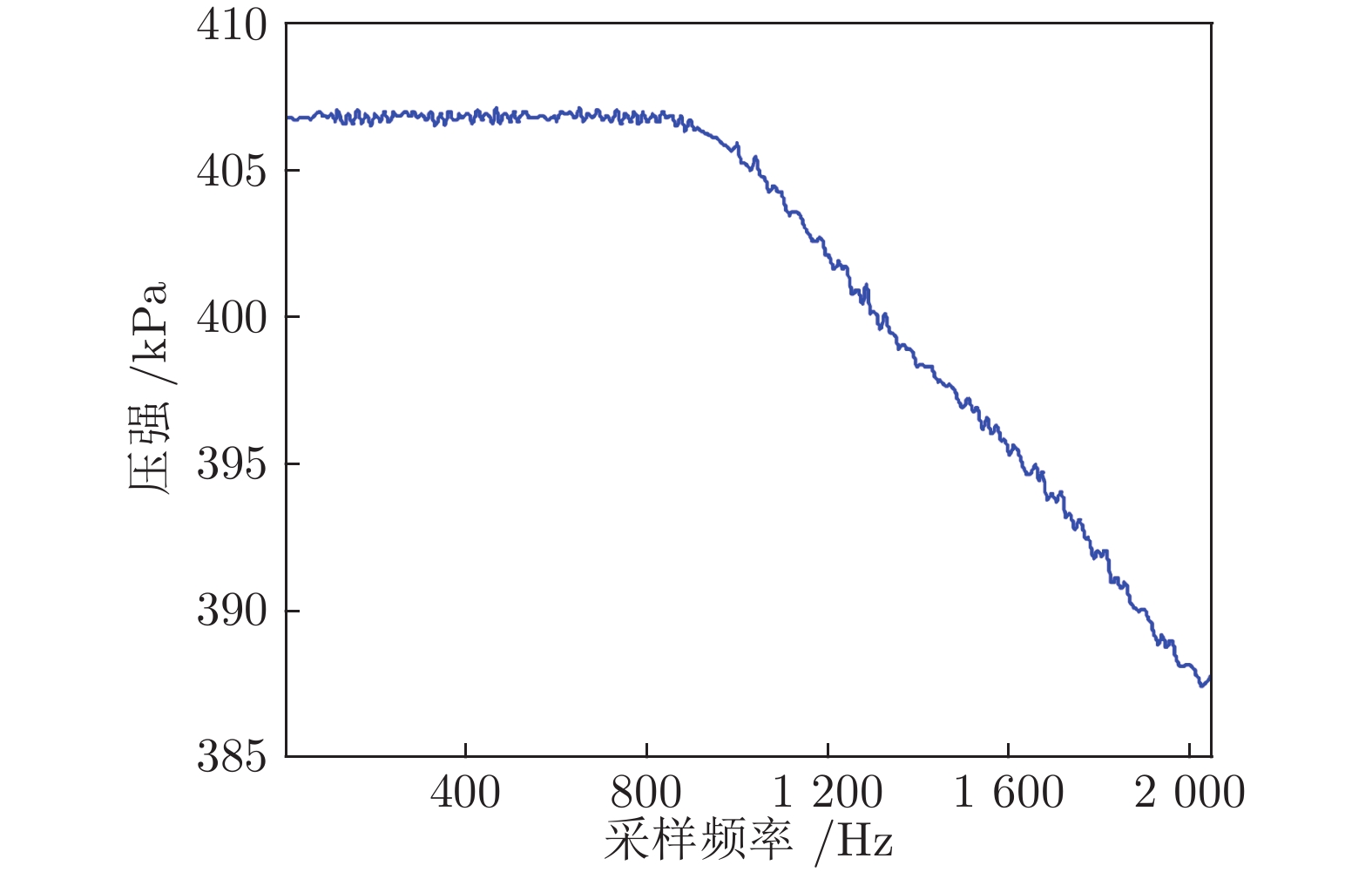
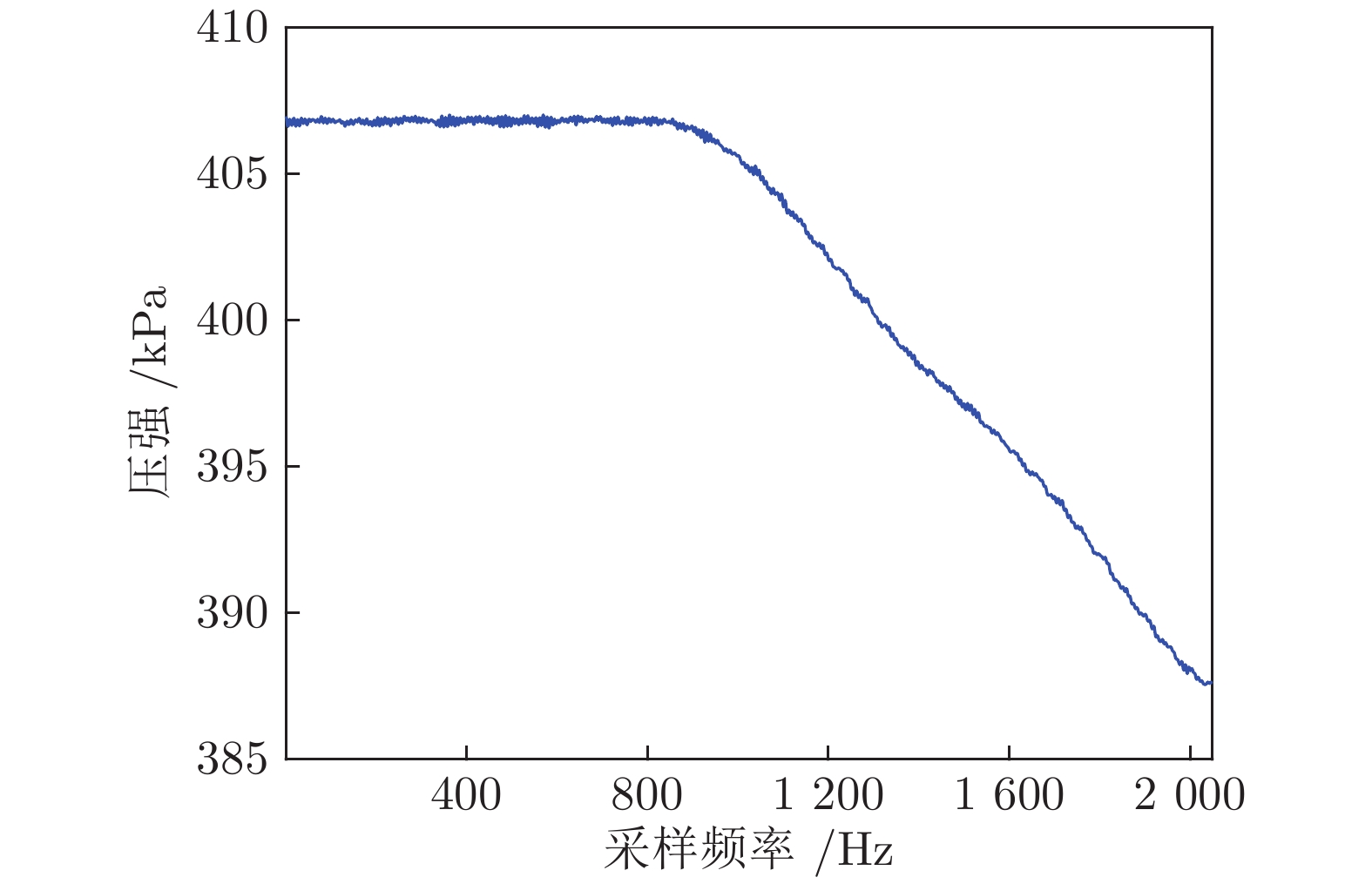
算法 信噪比 (dB) 均方误差 EMD 28.3163 0.2429 VMD 28.4436 0.2394 PSO-VMD 28.4799 0.2384 本文算法 28.6010 0.2351 -
[1] Wang C, Han F, Zhang Y, Lu J Y. An SAE-based resampling SVM ensemble learning paradigm for pipeline leakage detection. Neurocomputing, 2020, 403: 237-246 doi: 10.1016/j.neucom.2020.04.105 [2] 王东风, 孟丽. 粒子群优化算法的性能分析和参数选择. 自动化学报, 2016, 42(10): 1552-1561Wang Dong-Feng, Meng Li. Performance analysis and parameter selection of PSO algorithms. Acta Automatica Sinica, 2016, 42(10): 1552-1561 [3] Shi Y H, Eberhart R C. Parameter selection in particle swarm optimization. In: Proceedings of the 7th International Conference on Evolutionary Programming. San Diego, USA: ACM, 1998. 591−600 [4] Ratnaweera A, Halgamuge S K, Watson H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 240-255 doi: 10.1109/TEVC.2004.826071 [5] Liu W B, Wang Z D, Yuan Y, Zeng N Y, Hone K, Liu X H. A novel Sigmoid-function-based adaptive weighted particle swarm optimizer. IEEE Transactions on Cybernetics, 2019, 1-10 [6] Jana B, Mitra S, Acharyya S. Repository and mutation based particle swarm optimization (RMPSO): A new PSO variant applied to reconstruction of gene regulatory network. Applied Soft Computing, 2019, 74: 330-355 doi: 10.1016/j.asoc.2018.09.027 [7] Liu B, Wang L, Jin Y H, Tang F, Huang D X. Improved particle swarm optimization combined with chaos. Chaos, Solitons & Fractals, 2005, 25(5): 1261-1271 [8] Kennedy J, Mendes R. Population structure and particle swarm performance. In: Proceedings of the Congress on Evolutionary Computation. Honolulu, HI, USA: IEEE, 2002. 1671−1676 [9] Zeng N Y, Wang Z D, Liu W B, Zhang H, Hone K, Liu X H. A dynamic neighborhood-based switching particle swarm optimization algorithm. IEEE Transactions on Cybernetics, 2022, 52(9): 9290−9301 [10] Dong H L, Hou N, Wang Z D, Ren W J. Variance-constrained state estimation for complex networks with randomly varying topologies. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(7): 2757-2768 [11] Dong H L, Hou N, Wang Z D. Fault estimation for complex networks with randomly varying topologies and stochastic inner couplings. Automatica, 2020, 112: Article No. 108734 [12] Moslehi F, Haeri A, Martínez-Álvarez F. A novel hybrid GA-PSO framework for mining quantitative association rules. Soft Computing, 2020, 24: 4645–4666 doi: 10.1007/s00500-019-04226-6 [13] Wu Z H, Wu Z C, Zhang J. An improved FCM algorithm with adaptive weights based on SA-PSO. Neural Computing and Applications, 2017, 28(10): 3113-3118 doi: 10.1007/s00521-016-2786-6 [14] Liu W B, Wang Z D, Liu X H, Zeng N Y, Bell D. A novel particle swarm optimization approach for patient clustering from emergency departments. IEEE Transactions on Evolutionary Computation, 2018, 23(4): 632-644 [15] Zeng N Y, Wang Z D, Zhang H, Alsaadi F E. A novel switching delayed PSO algorithm for estimating unknown parameters of lateral flow immunoassay. Cognitive Computation, 2016, 8(2): 143-152 doi: 10.1007/s12559-016-9396-6 [16] Song B Y, Wang Z D, Zou L. On global smooth path planning for mobile robots using a novel multimodal delayed PSO algorithm. Cognitive Computation, 2017, 9(1): 5-17 doi: 10.1007/s12559-016-9442-4 [17] Dragomiretskiy K, Zosso D. Variational mode decomposition. IEEE Transactions on Signal Processing, 2013, 62(3): 531-544 [18] Kennedy J, Eberhart R C. Particle swarm optimization. In: Proceedings of the IEEE International Conference on Neural Networks. Perth, Australia: IEEE, 1995. 1942−1948 [19] Shi Y H, Eberhart R C. Empirical study of particle swarm optimization. In: Proceedings of the IEEE Congress on Evolutionary Computation. Washington, DC, USA: ACM, 1999. 1945−1950 [20] Li J H, Dong H L, Wang Z D, Bu X Y. Partial-neurons-based passivity-guaranteed state estimation for neural networks with randomly occurring time-delays, IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(9): 3747-3753 doi: 10.1109/TNNLS.2019.2944552 [21] Dong H L, Wang Z D, Shen B, Ding D R. Variance-constrained H∞ control for a class of nonlinear stochastic discrete time-varying systems: The event-triggered design. Automatica, 2016, 72, 28-36 doi: 10.1016/j.automatica.2016.05.012 [22] Wang C, Zhang Y, Song J B, Liu Q Q, Dong H L. A novel optimized SVM algorithm based on PSO with saturation and mixed time-delays for classification of oil pipeline leak detection. Systems Science & Control Engineering, 2019, 7(1): 75-88 [23] Clerc M, Kennedy J. The particle swarm: explosion, stability, and convergence in a multi-dimensional complex space. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73 doi: 10.1109/4235.985692 [24] 刘建昌, 权贺, 于霞, 何侃, 李镇华. 基于参数优化VMD和样本熵的滚动轴承故障诊断. 自动化学报, 2020, 1-12Liu Jian-Chang, Quan He, Yu Xia, He Kan, Li Zhen-Hua. Rolling bearing fault diagnosis based on parameter optimization VMD and sample entropy. Acta Automatica Sinica, 2020, 1-12 [25] 何潇, 郭亚琦, 张召, 贾繁林, 周东华. 动态系统的主动故障诊断技术. 自动化学报, 2020, 46(08): 1557-1570He Xiao, Guo Ya-Qi, Zhang Zhao, Jia Fan-Lin, Zhou Dong-Hua. Active fault diagnosis for dynamic systems. Acta Automatica Sinica, 2020, 46(08): 1557-1570 [26] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用. 西安交通大学学报, 2015, 49(5): 73−81Tang Gui-Ji, Wang Xiao-Long. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing. Journal of Xi'an Jiaotong University, 2015, 49(5): 73−81 -




 下载:
下载: