-
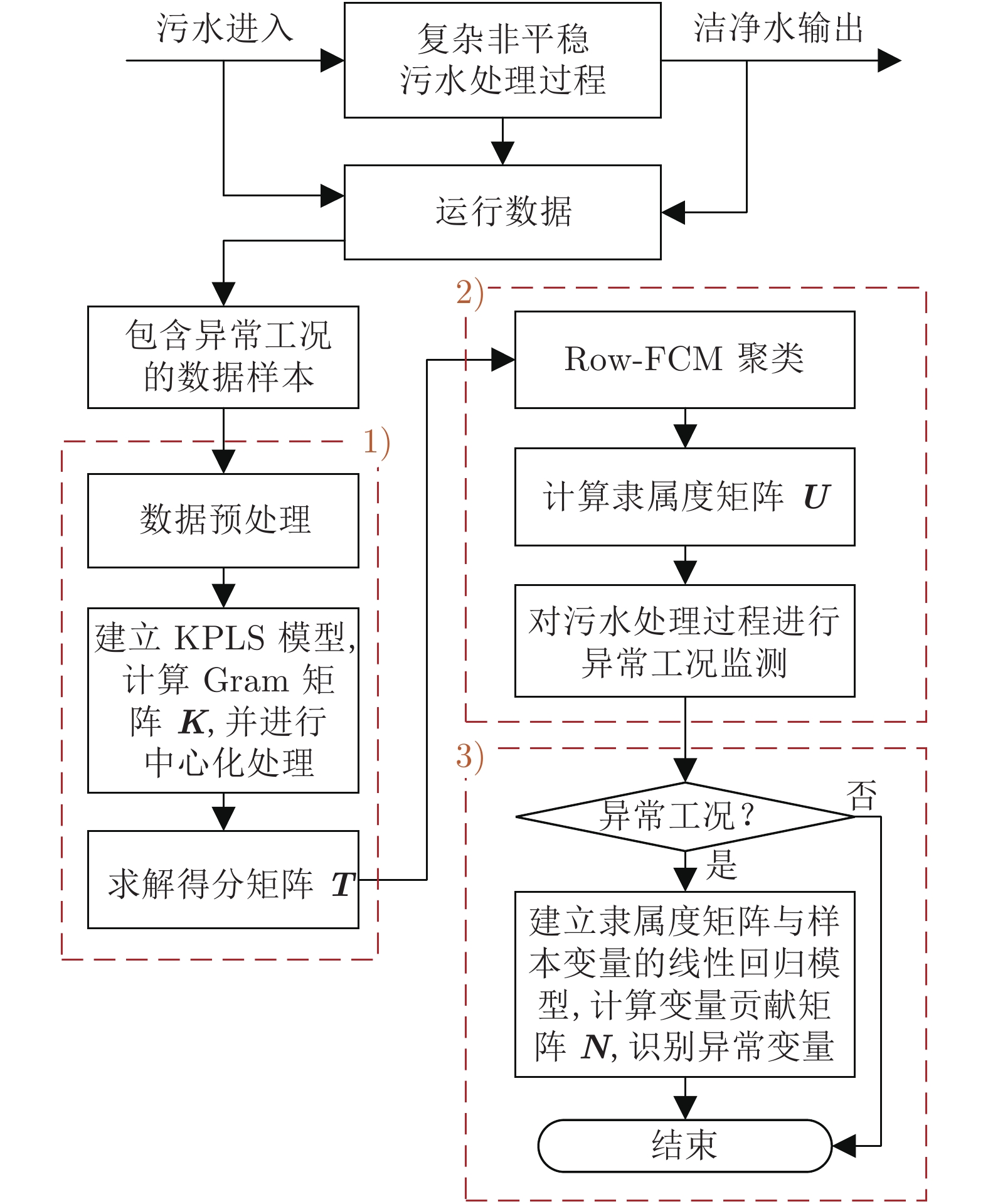
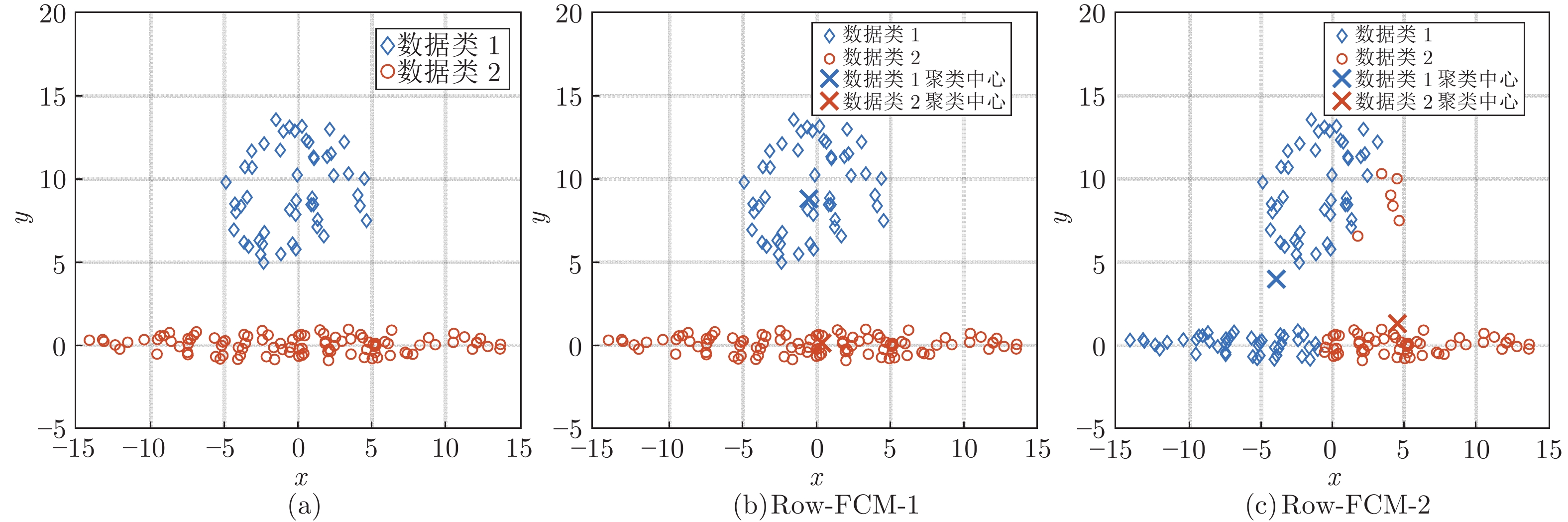
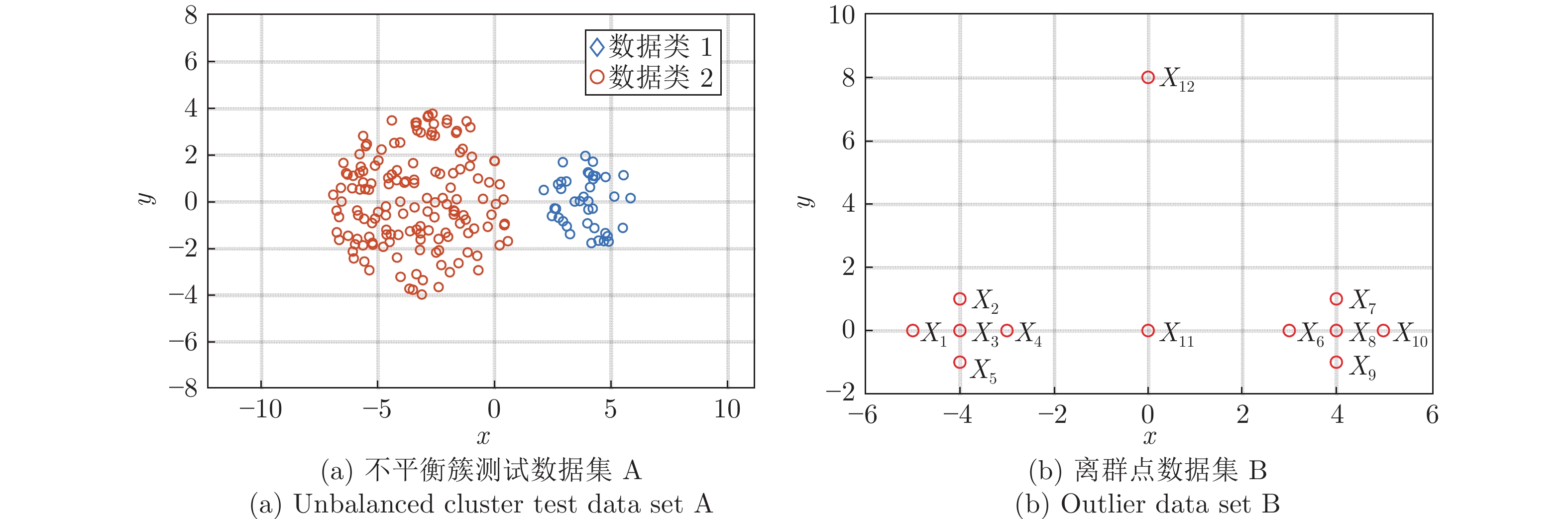
摘要: 针对非线性强、先验故障知识少、异常工况识别难的污水处理过程监测问题, 提出一种基于鲁棒加权模糊c均值(Robust weighted fuzzy c-means, RoW-FCM)聚类与核偏最小二乘(Kernel partial least squares, KPLS)的过程监测方法. 首先, 针对污水处理过程的高维非线性耦合特性, 采用核偏最小二乘对高维输入变量进行降维; 其次, 针对传统基于最近邻分配的模糊c均值算法对离群点敏感以及存在聚类不平衡簇的问题, 提出充分考虑样本间相互关系的基于鲁棒加权模糊c均值聚类算法. 通过引入可能性划分矩阵作为权值参数实现不同样本数据的区分加权, 提高了离群点数据聚类的鲁棒性, 同时引入聚类大小控制参数解决不平衡簇的问题. 进一步将基于鲁棒加权模糊c均值算法对核偏最小二乘降维后的得分矩阵进行聚类, 利用聚类得到的隶属度矩阵实现异常工况的检测; 最后, 建立隶属度矩阵与过程变量的回归模型, 并利用得到的变量贡献矩阵描述变量对各个簇的解释程度, 实现异常工况的识别. 数值仿真以及污水处理过程数据实验表明该方法具有更好的鲁棒性能, 在异常工况检测和识别上具有较好的效果.Abstract: Aiming at the problems of strong nonlinearity, little prior knowledge of faults, and difficulty in identifying abnormal working-conditions in the sewage treatment process, this paper proposes a novel process monitoring method based on robust weighted fuzzy c-means (RoW-FCM) clustering and kernel partial least squares (KPLS). First, the KPLS algorithm is presented to reduce the dimensionality of the high-dimensional input variables for the sewage treatment process with complicated nonlinear coupling characteristics. Second, the fact that in view of the traditional fuzzy c-means algorithm based on nearest neighbor assignment is sensitive to outliers and there are unbalanced clusters in clustering, an RoW-FCM clustering algorithm is proposed, which fully considers the relationship between samples. For this RoW-FCM, by introducing the possibility partition matrix as the weight parameter to distinguish and weight different samples, the robustness of outlier data clustering is improved, and the problem of unbalanced cluster is solved by introducing the cluster size control parameter. By clustering the score matrix after dimension reduction with KPLS, the membership matrix can be obtained, which will be used for detecting the abnormal working-conditions. On this basis, the regression model between the membership matrix and the process variables is established, and the resulted variable contribution matrix, which describes the explanatory degree of each cluster, will be used to identify the abnormal working-conditions. At last, both numerical simulation and data experiments of sewage treatment process show that the proposed method has better robust performance and better effect in detecting and identifying the abnormal working-conditions.
-
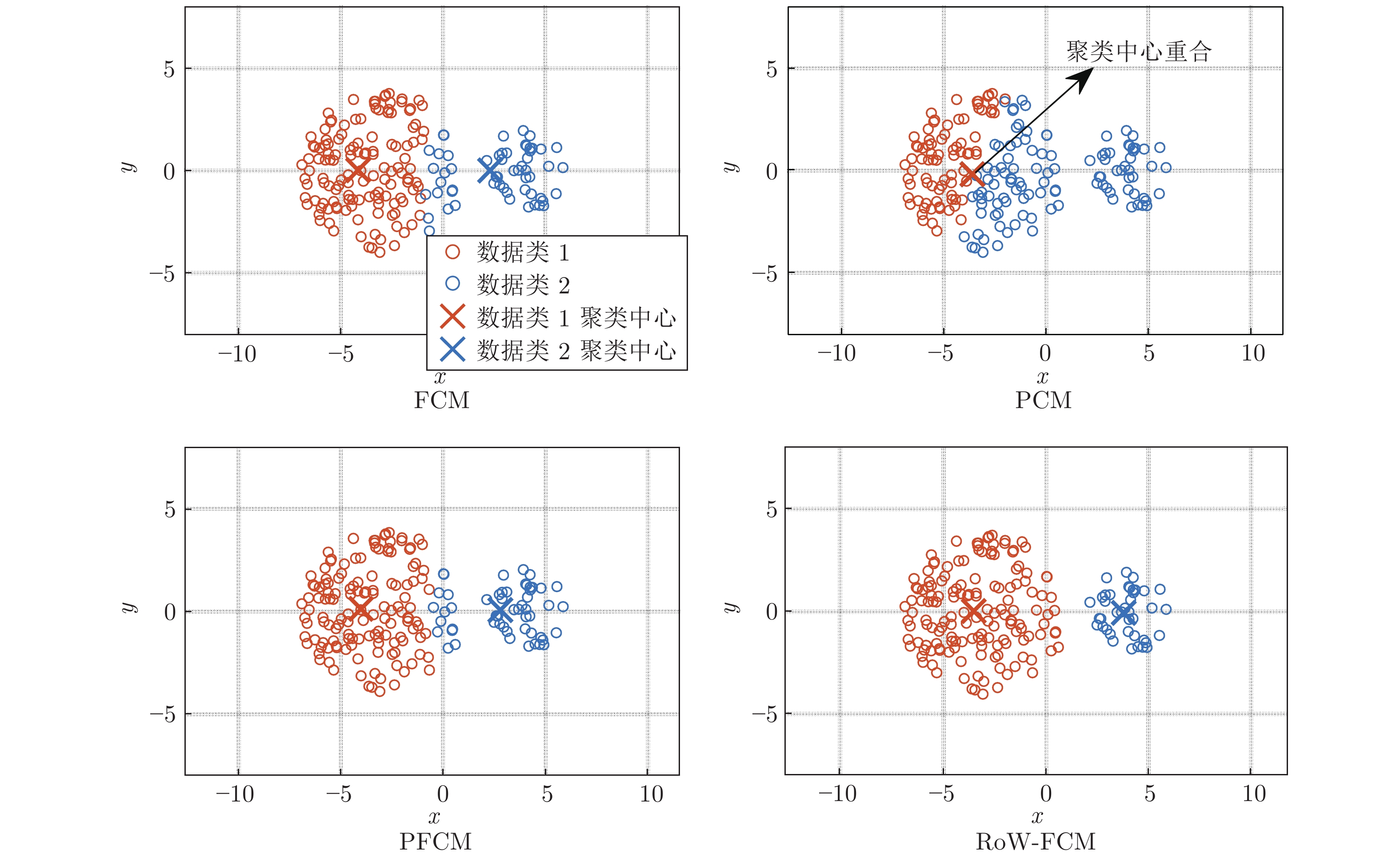
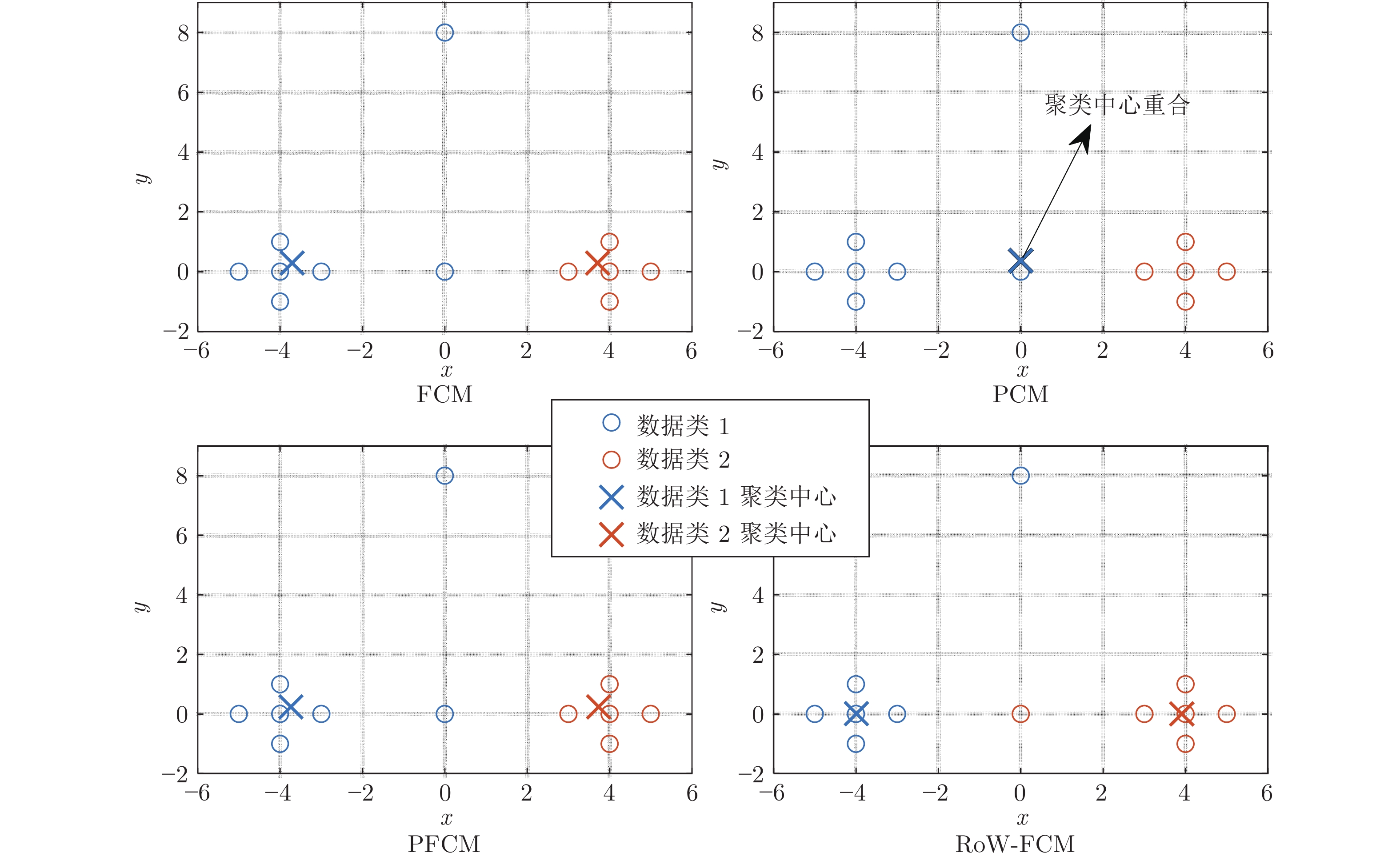
表 1 FCM、PCM、PFCM、RoW-FCM 聚类参数
Table 1 FCM, PCM, PFCM, RoW-FCM clustering parameters
编号 FCM PCM PFCM RoW-FCM ${ {{\boldsymbol{U}}} }_1^{\rm T}$ ${ {{\boldsymbol{U}}} }_2^{\rm T}$ ${ {{\boldsymbol{W}}} }_1^{\rm T}$ ${ {{\boldsymbol{W}}} }_2^{\rm T}$ ${ {{\boldsymbol{U}}} }_1^{\rm T}$ ${ {\boldsymbol{U}} }_2^{\rm T}$ ${ {{\boldsymbol{W}}} }_1^{\rm T}$ ${ {{\boldsymbol{W}}} }_2^{\rm T}$ ${ {{\boldsymbol{U}}} }_1^{\rm T}$ ${ {{\boldsymbol{U}}} }_2^{\rm T}$ ${ {{\boldsymbol{W}}} }_1^{\rm T}$ ${ {{\boldsymbol{W}}} }_2^{\rm T}$ 1 0.973 0.027 0.799 0.798 0.021 0.979 0.026 0.547 0.991 0.009 0.833 0.999 2 0.991 0.009 0.859 0.858 0.010 0.989 0.032 0.755 0.989 0.011 0.839 0.999 3 0.995 0.005 0.861 0.860 0.002 0.998 0.032 0.940 1.00 0.000 1.000 1.000 4 0.967 0.033 0.848 0.848 0.026 0.975 0.032 0.555 0.989 0.011 0.834 0.999 5 0.988 0.012 0.916 0.916 0.013 0.987 0.042 0.770 0.986 0.014 0.840 0.998 6 0.012 0.988 0.916 0.917 0.987 0.013 0.770 0.042 0.012 0.988 0.999 0.861 7 0.009 0.991 0.859 0.860 0.989 0.011 0.755 0.032 0.011 0.989 0.999 0.835 8 0.005 0.995 0.861 0.862 0.998 0.002 0.940 0.032 0.000 0.999 1.000 0.998 9 0.033 0.967 0.848 0.849 0.975 0.026 0.555 0.032 0.011 0.989 0.999 0.835 10 0.027 0.973 0.799 0.800 0.979 0.021 0.547 0.026 0.010 0.990 0.999 0.811 11 0.500 0.500 0.997 0.997 0.500 0.500 0.125 0.125 0.069 0.931 0.985 0.274 12 0.500 0.500 0.632 0.632 0.500 0.500 0.026 0.026 0.997 0.004 0.060 0.999 聚类中心 v1 = (−3.616, 0.383) v1 = (0.001, 0.369) v1 = (−3.736, 0.240) v1 = (−3.989, 0.010) v2 = (3.616, 0.384) v2 = (0.007, 0.369) v2 = (3.736, 0.240) v2 = (3.910, 0.000) 偏移距离 r1 = 0.543 r1 = 4.016 r1 = 0.357 r1 = 0.010 r2 = 0.543 r2 = 4.010 r2 = 0.357 r2 = 0.090 表 2 影响污水处理过程出水水质的主要过程变量
Table 2 The main process variables that affect the effluent quality of the sewage treatment process
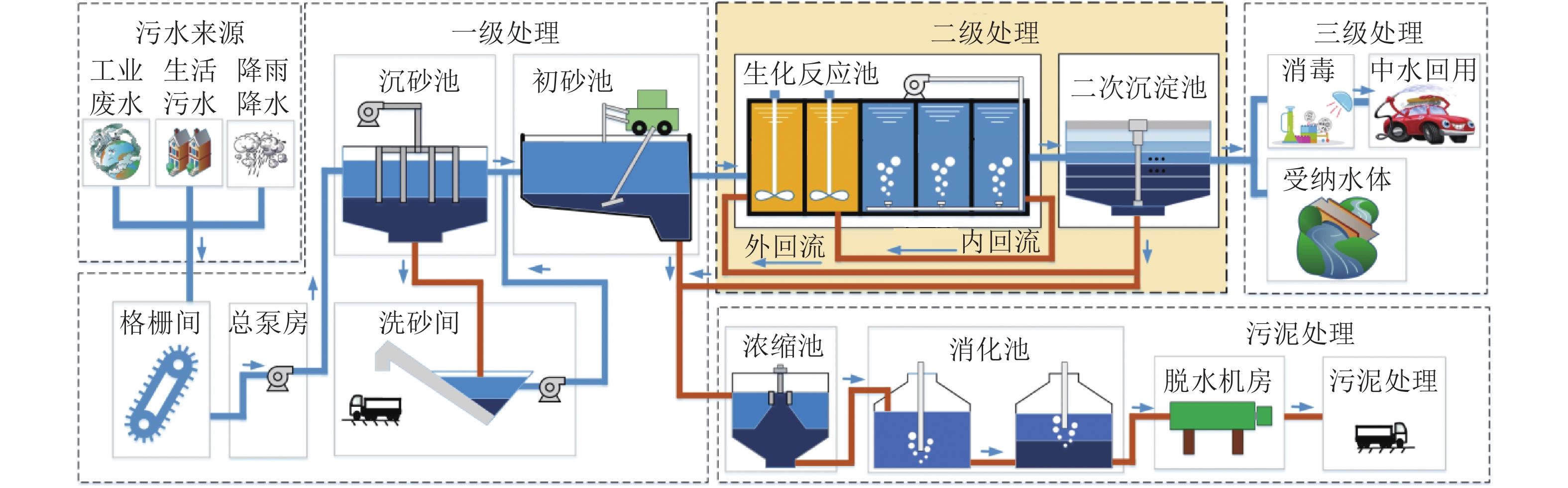
编号 符号 变量物理含义 编号 符号 变量物理含义 1 Qin 进水流量 15 SS,3 反应池 3易生物降解有机底物量 2 SNH,in 进水氨浓度 16 SALK,3 反应池 3 池碱度 3 XBH,1 反应池 1活性异养菌生物量 17 XBH,4 反应池 4 活性异养菌生物量 4 SNO,1 反应池 1 硝氮浓度 18 XBA,4 反应池 4 活性自养菌生物量 5 SS,1 反应池 1 易生物降解有机底物量 19 SO,4 反应池 4 溶解氧浓度 6 SALK,1 反应池 1 池碱度 20 SNH,4 反应池 4 氨氮浓度 7 XBH,2 反应池 2 活性异养菌生物量 21 SS,4 反应池 4 易生物降解有机底物量 8 SNO,2 反应池 2 硝氮浓度 22 SALK,4 反应池 4 池碱度 9 SS,2 反应池 2 易生物降解有机底物量 23 XBH,5 反应池 5 活性异养菌生物量 10 SALK,2 反应池 2 池碱度 24 XBA,5 反应池 5 活性自养菌生物量 11 XBH,3 反应池 3 活性异养菌生物量 25 SO,5 反应池 5 溶解氧浓度 12 XBA,3 反应池 3 活性自养菌生物量 26 SNH,5 反应池 5 氨氮浓度 13 SO,3 反应池 3 溶解氧浓度 27 SS,5 反应池 5 易生物降解有机底物量 14 SNH,3 反应池 3 氨氮浓度 28 SALK,5 反应池 5 池碱度 表 3 不同算法的聚类准确度与迭代次数
Table 3 Clustering accuracies and numbers of iterations of different algorithms
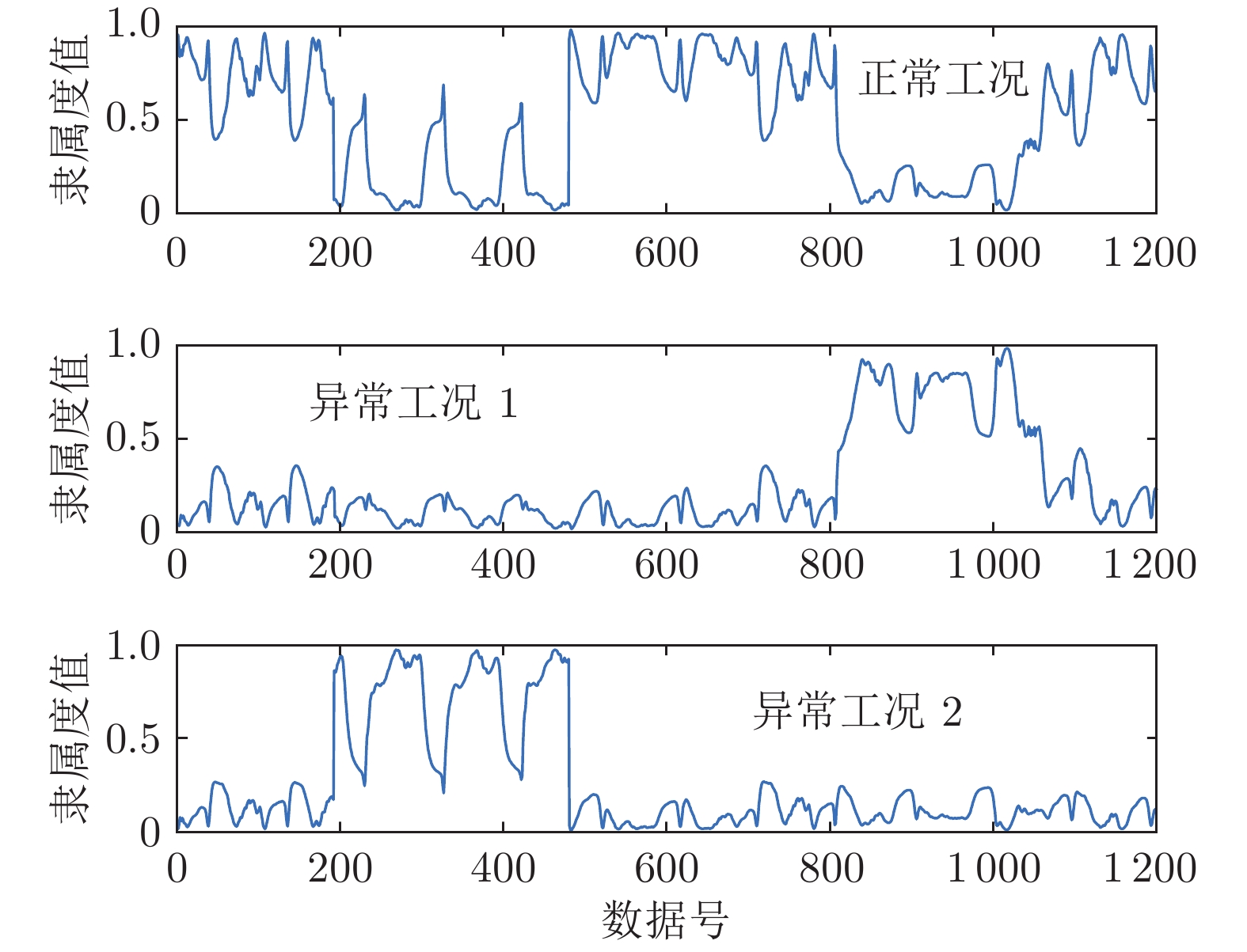
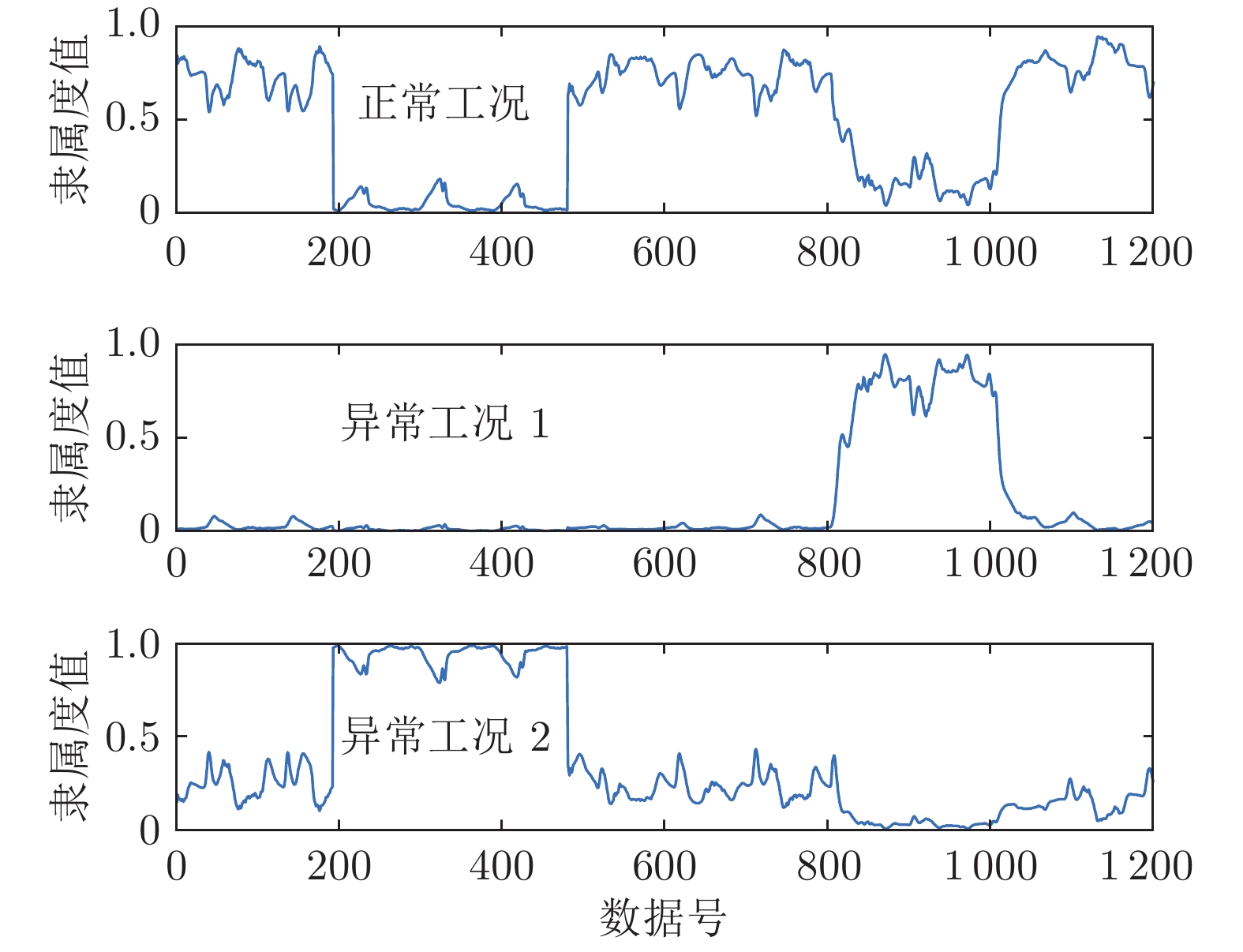
工况类型 聚类正确率 (%) 聚类收敛迭代次数
(收敛精度$10^{-5}, \;$30次仿真)FCM PCM PFCM RoW-FCM FCM PCM PFCM RoW-FCM 正常工况 92.3 80.8 93.9 97.5 — — — — 异常工况 1 75.0 6.3 76.3 96.0 45.1 14 29.1 23.6 异常工况 2 80.3 3.5 77.5 97.0 — — — — 表 4 异常工况识别结果表
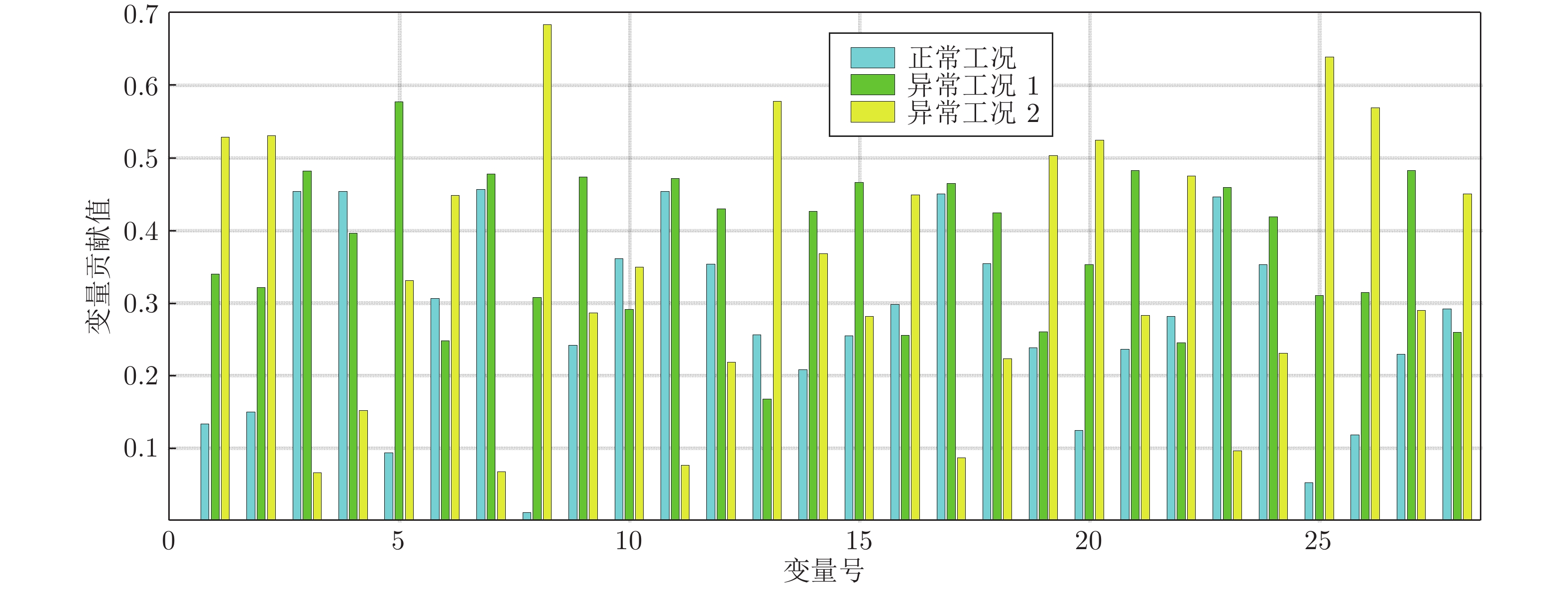
Table 4 Abnormal condition recognition result table
编号 正常工况 异常工况 1 异常工况 2 编号 正常工况 异常工况 1 异常工况 2 1 0.133 0.339 0.528 15 0.254 0.465 0.281 2 0.150 0.321 0.530 16 0.297 0.255 0.448 3 0.454 0.481 0.065 17 0.450 0.464 0.086 4 0.453 0.395 0.152 18 0.354 0.424 0.223 5 0.093 0.577 0.331 19 0.238 0.260 0.503 6 0.305 0.247 0.448 20 0.124 0.352 0.524 7 0.456 0.477 0.067 21 0.236 0.482 0.283 8 0.010 0.307 0.683 22 0.281 0.245 0.475 9 0.241 0.473 0.286 23 0.446 0.458 0.096 10 0.361 0.290 0.349 24 0.352 0.418 0.230 11 0.453 0.471 0.076 25 0.052 0.310 0.639 12 0.353 0.429 0.218 26 0.118 0.314 0.568 13 0.255 0.167 0.578 27 0.229 0.482 0.289 14 0.208 0.425 0.367 28 0.291 0.259 0.450 -
[1] 蒙西, 乔俊飞, 韩红桂. 基于类脑模块化神经网络的污水处理过程关键出水参数软测量. 自动化学报, 2019, 45(5): 906-919. doi: 10.16383/j.aas.2018.c170497.MENG Xi, QIAO Jun-Fei, HAN Hong-Gui. Soft Measurement of Key Effluent Parameters in Wastewater Treatment Process Using Brain-like Modular Neural Networks. ACTA AUTOMATICA SINICA, 2019, 45(5): 906-919. doi: 10.16383/j.aas.2018.c170497 [2] 乔俊飞, 韩改堂, 周红标. 基于知识的污水生化处理过程智能优化方法. 自动化学报, 2017, 43(6): 1038–1046Qiao Jun-Fei, Han Gai-Tang, Zhou Hong-Biao. Knowledge-based intelligent optimal control for wastewater biochemical treatment Process. Acta Automatica Sinica, 2017, 43(6): 1038–1046. [3] 张帅, 周平. 污水处理过程递推双线性子空间建模及无模型自适应控制. 自动化学报, 2022, 48(7): 1747−1759Zhang Shuai, Zhou Ping. Recursive bilinear subspace modeling and model-free adaptive control of wastewater treatment. Acta Automatica Sinica, 2022, 48(7): 1747−1759 [4] Cheng T, Dairi A, Harrou F, Sun Y and Leiknes T. Monitoring influent conditions of wastewater treatment plants by nonlinear data-based techniques, IEEE Access, 2019, 7: 108827–108837 doi: 10.1109/ACCESS.2019.2933616 [5] Han Hong-Gui, Qiao Jun-Fei, Hierarchical neural network modeling approach to predict sludge volume index of wastewater treatment process, IEEE Transactions on Control Systems Technology, 2013, 21(6): 2423–2431 doi: 10.1109/TCST.2012.2228861 [6] 韩红桂, 伍小龙, 张璐, 乔俊飞. 城市污水处理过程异常工况识别和抑制研究. 自动化学报, 2018, 44(11): 1971 –1984Han Hong-Gui, Wu Xiao-Long, Zhang Lu, Qiao Jun-Fei. Identification and suppression of abnormal conditions in municipal wastewater treatment process. Acta Automatica Sinica, 2018, 44(11): 1971–1984 [7] Liu Hong-Bin, Zhang Hao, Zhang Yu-Cheng, Zhang Feng-Shan and Huang Ming-Zhi, Modeling of wastewater treatment processes using dynamic Bayesian networks based on fuzzy PLS, IEEE Access, 2020, 8: 92129–92140 [8] Fuente M J, Vega P. Neural networks applied to fault detection of a biotechnological process. Engineering Applications of Artificial Intelligence, 1999, 12(5): 569–584 doi: 10.1016/S0952-1976(99)00028-7 [9] 范昕炜, 杜树新, 吴铁军. 粗SVM分类方法及其在污水处理过程中的应用. 控制与决策, 2004, (05): 573–576 doi: 10.3321/j.issn:1001-0920.2004.05.022Fan Xin-Wei, Du Shu-Xin, Wu Tie-Jun. Rough support vector machine and its application to wastewater treatment processes. Control and Decision, 2004, (05): 573–576 doi: 10.3321/j.issn:1001-0920.2004.05.022 [10] 刘乙奇, 李艳, 孙宗海, 黄道平. 面向污水处理过程因子分析故障诊断方法的研究. 控制工程, 2015, 22(3): 447–451Liu Yi-Qi, Li Yan, Sun Zong-Hai, Huang Dao-Ping. Research on fault diagnosis of wastewater treatment process based on factor analysis. Control Engineering of China, 2015, 22(3): 447–451 [11] 慈嘉伟, 罗健旭. 基于加权模糊聚类的污水处理过程故障检测. 华东理工大学学报(自然科学版), 2018, 44(04): 504–510Ci Jia-Wei, Luo Jian-Xu. Fault detection in sewage treatment process based on weighted fuzzy clustering algorithm. Journal of East China University of Science and Technology(Natural Science Edition), 2018, 44(04): 504–510 [12] 康韦晓. 基于马氏距离的PFCM算法的非线性系统故障诊断方法 [硕士论文], 哈尔滨工业大学, 中国, 2016Kang Wei-Xiao. Fault Diagnosis Method for Nonlinear System Based on PFCM Algorithm With Mahalanobis Distance[Master thesis], Harbin Institute of Technology, China, 2016 [13] Teppola P, Minkkinen P. Possibilistic and fuzzy c-means clustering for process monitoring in an activated sludge waste-water treatment plant. Journal of Chemometrics, 1999, 13(3–4): 445–459 doi: 10.1002/(SICI)1099-128X(199905/08)13:3/4<445::AID-CEM557>3.0.CO;2-W [14] Qin S J. Statistical process monitoring: basics and beyond. Journal of Chemometrics, 2003, 17(8–9): 480–502 doi: 10.1002/cem.800 [15] Zhou P, Zhang R Y, Xie J, Liu J P, Wang H, Chai T Y. Data-driven monitoring and diagnosing of abnormal furnace conditions in blast furnace ironmaking: an integrated PCA-ICA method. IEEE Transactions on Industrial Electronics, 2020, Doi: 10.1109/TIE.2020.2967708. [16] Dunia R, Qin S J, Edgar T F, McAvoy T J. Identification of faulty sensors using principal component analysis. AICHE Journal, 2010, 42(10): 2797–2812 [17] Choi S W, Lee C, Lee J M, Park J H, Lee I B. Fault detection and identification of nonlinear processes based on kernel PCA. Chemometrics & Intelligent Laboratory Systems, 2005, 75(1): 55–67 [18] Xu H B, Chen G H, Wang X H. Fault identification of bearings based on bispectrum distribution of ARMA model and FCM method. Journal of South China University of Technology, 2012, 40(7): 78–82+89 [19] Khormali, A O, Shoorehdeli, M A. Gas turbine fault detection and identification by using fuzzy clustering methods. In: Proce-edings of the 2014 Second RSI/ISM International Conference on Robotics and Mechatronics. Tehran, Iran: 2014. 70−75 [20] Bezdek J C, Ehrlich R, Full W. FCM: The fuzzy c-means clustering algorithm. Computers & Geosciences, 1984, 10(2): 191–203 [21] Krishnapuram R, Keller J M. A possibilistic approach to clustering. IEEE Transactions on Fuzzy Systems, 1993, 1(2): 98–110 doi: 10.1109/91.227387 [22] Zhang X, Pan W, Wu Z, Chen J, Mao Y, Wu R, Robust Image Segmentation Using Fuzzy C-Means Clustering With Spatial Information Based on Total Generalized Variation. IEEE Access, 2020, 8: 95681-95697 doi: 10.1109/ACCESS.2020.2995660 [23] Krinidis S, Chatzis V. A robust fuzzy local information c-means clustering algorithm. IEEE Transactions on Image Processing, 2010, 19(5): 1328–1337 doi: 10.1109/TIP.2010.2040763 [24] Barni M, Capellini V, Mecocci A. Comments on a possibilistic approach to clustering. IEEE Transactions on Fuzzy Systems, 1996, 4(3): 393–396 doi: 10.1109/91.531780 [25] Timm H, Borgelt C, Döring C, Kruse R. An extension to possibilistic fuzzy cluster analysis. Fuzzy Sets and Systems, 2004, 147(1): 3–16 doi: 10.1016/j.fss.2003.11.009 [26] Pal N R, Pal K, Keller J M, Bezdek J C. A possibilistic fuzzy c-means clustering algorithm. IEEE Transactions on Fuzzy Systems, 2005, 13(4): 517–530 doi: 10.1109/TFUZZ.2004.840099 [27] Miyamoto S, Ichihashi H, Honda K. Algorithms for Fuzzy Clustering-methods in c-means Clustering With Applications. Berlin: Springer-Verlag, 2008. [28] Komazaki Y, Miyamoto S. Variables for controlling cluster sizes on fuzzy c-means. In: Proceedings of the Modeling Decisions for Artificial Intelligence. Berlin, Heidelberg: Springer, 2013. 192− 203 [29] Qiao Junfei, Zhang Wei, Han Honggui. Self-organizing fuzzy control for dissolved oxygen concentration using fuzzy neural network1. Journal of Intelligent & Fuzzy Systems, 2016, 30(6): 3411–3 [30] Garcia-Alvarez D, Fuente M J, Vega P, Sainz G. Fault detection and diagnosis using multivariate statistical techniques in a wastewater treatment plant. IFAC Proceedings Volumes, 2009, 42(11): 952–957 doi: 10.3182/20090712-4-TR-2008.00156 -




 下载:
下载: