Customized Interior-point Method for Cooperative Trajectory Planning of Multiple Unmanned Aerial Vehicles
-
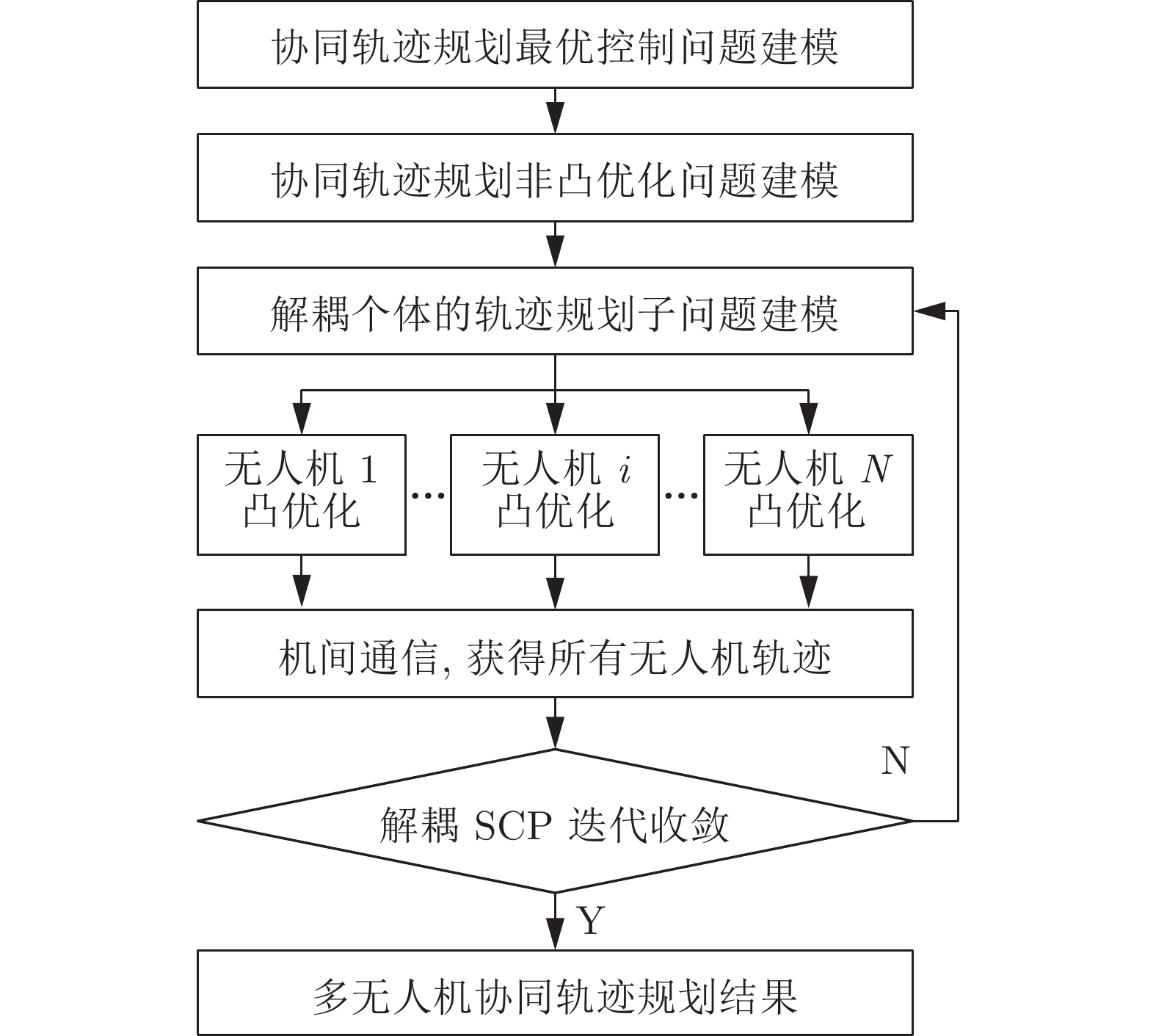
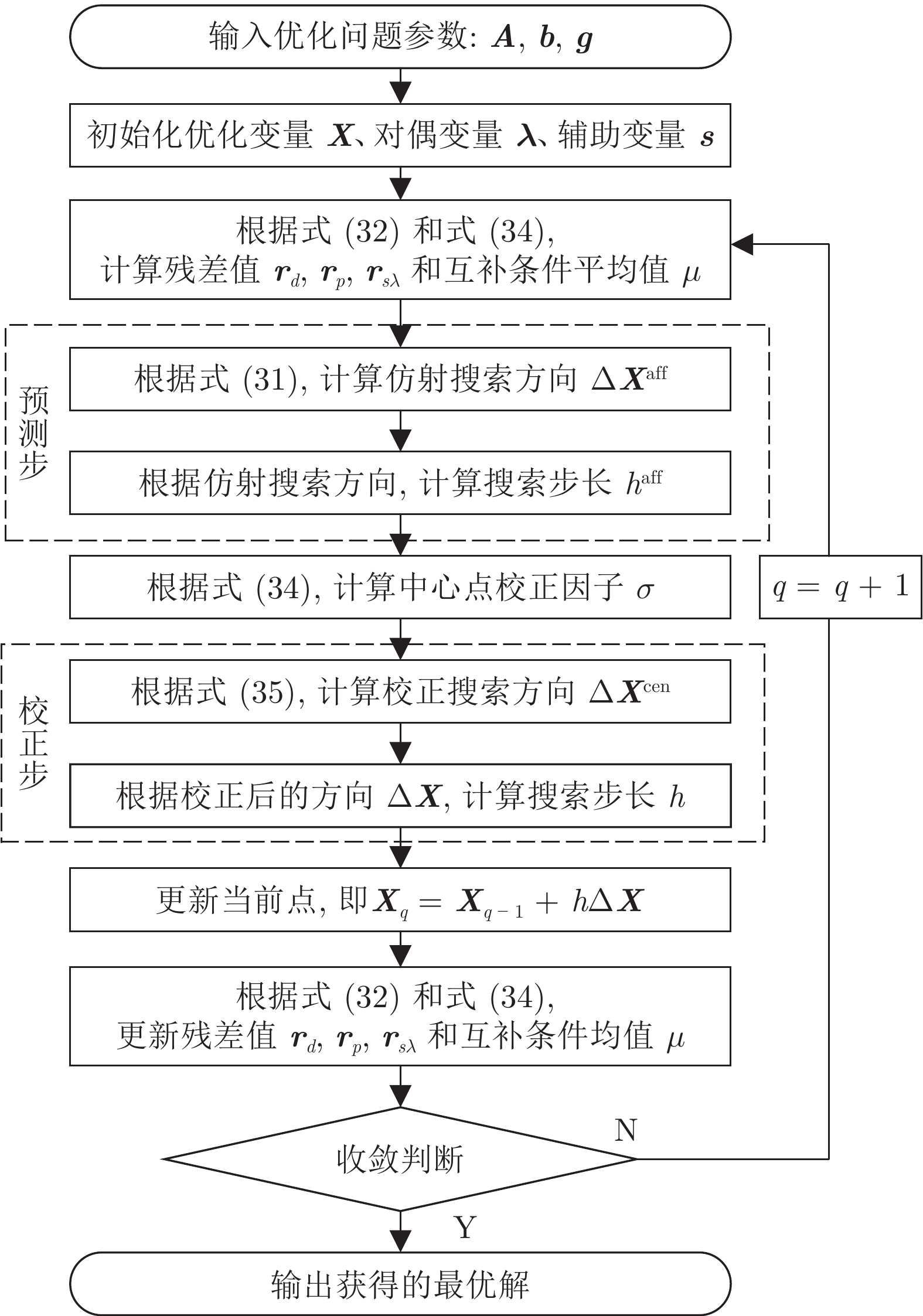
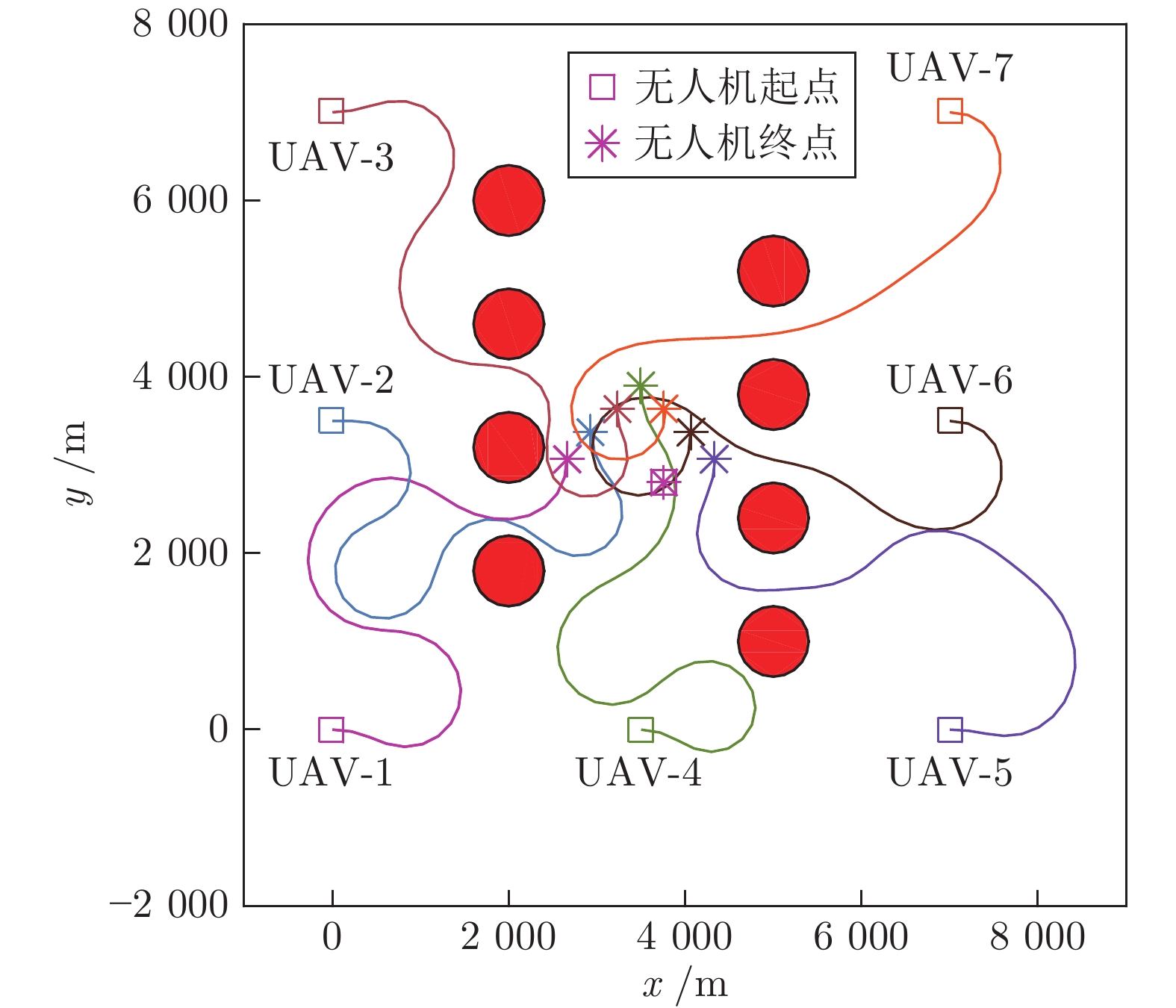
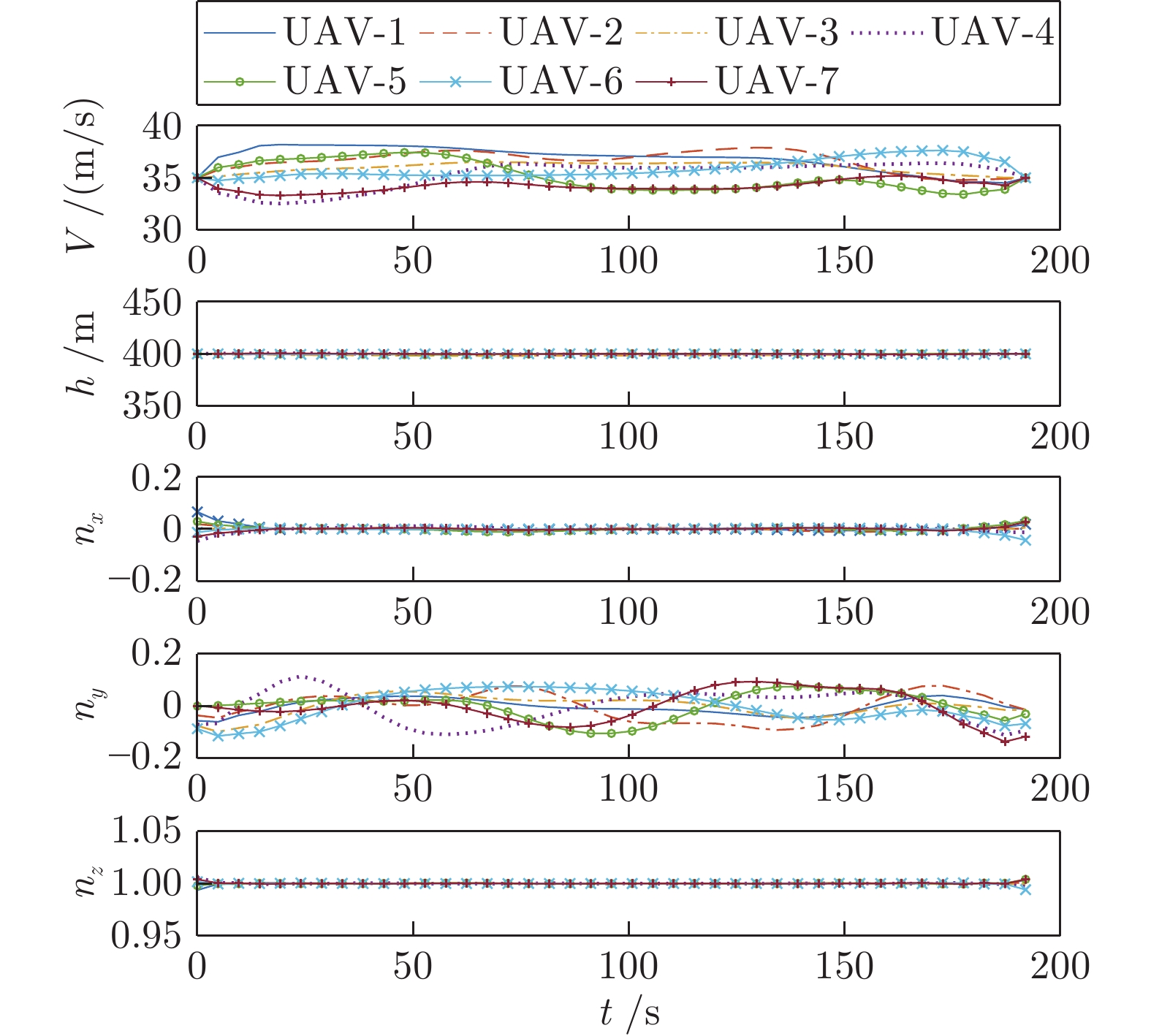
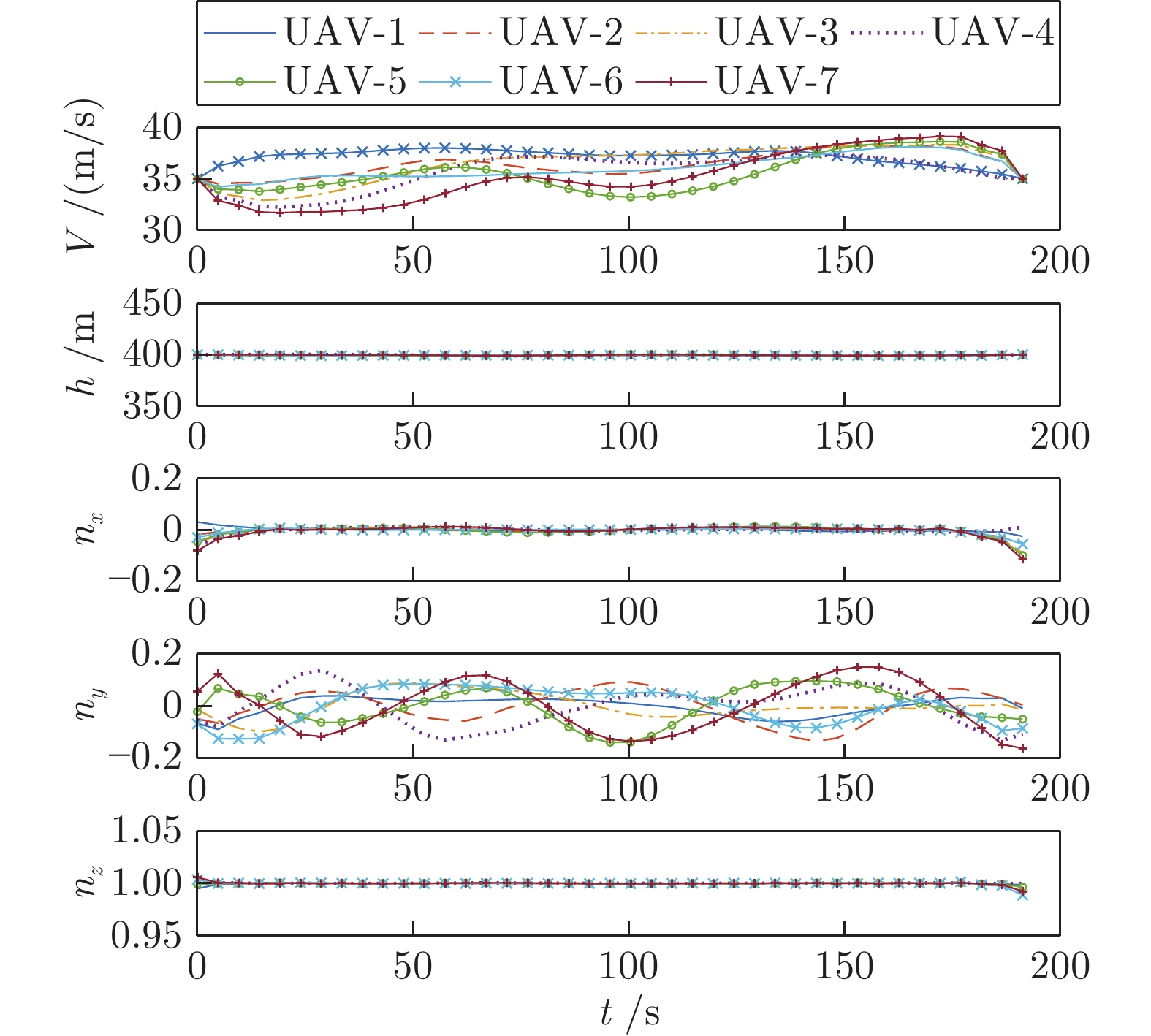
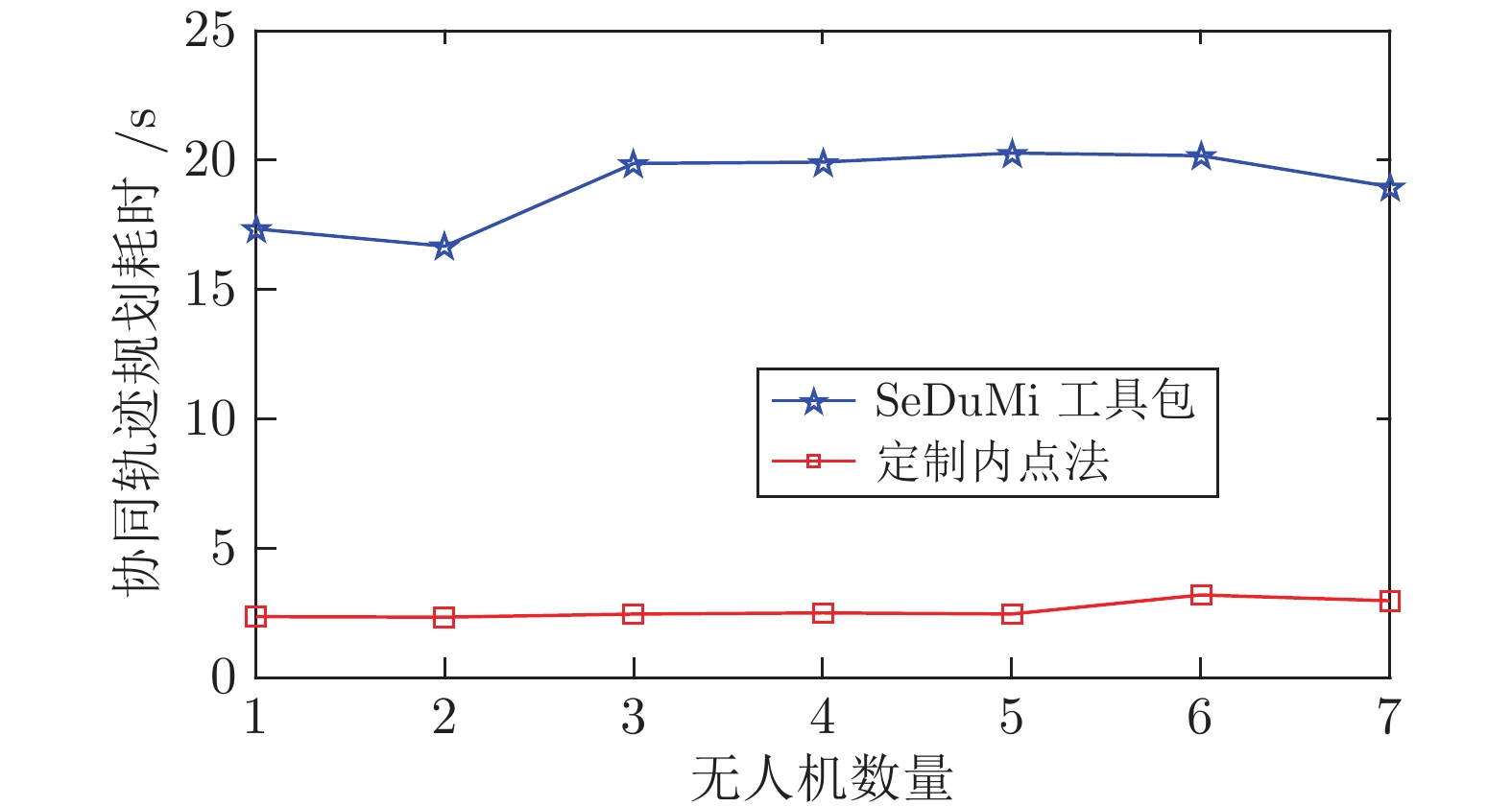
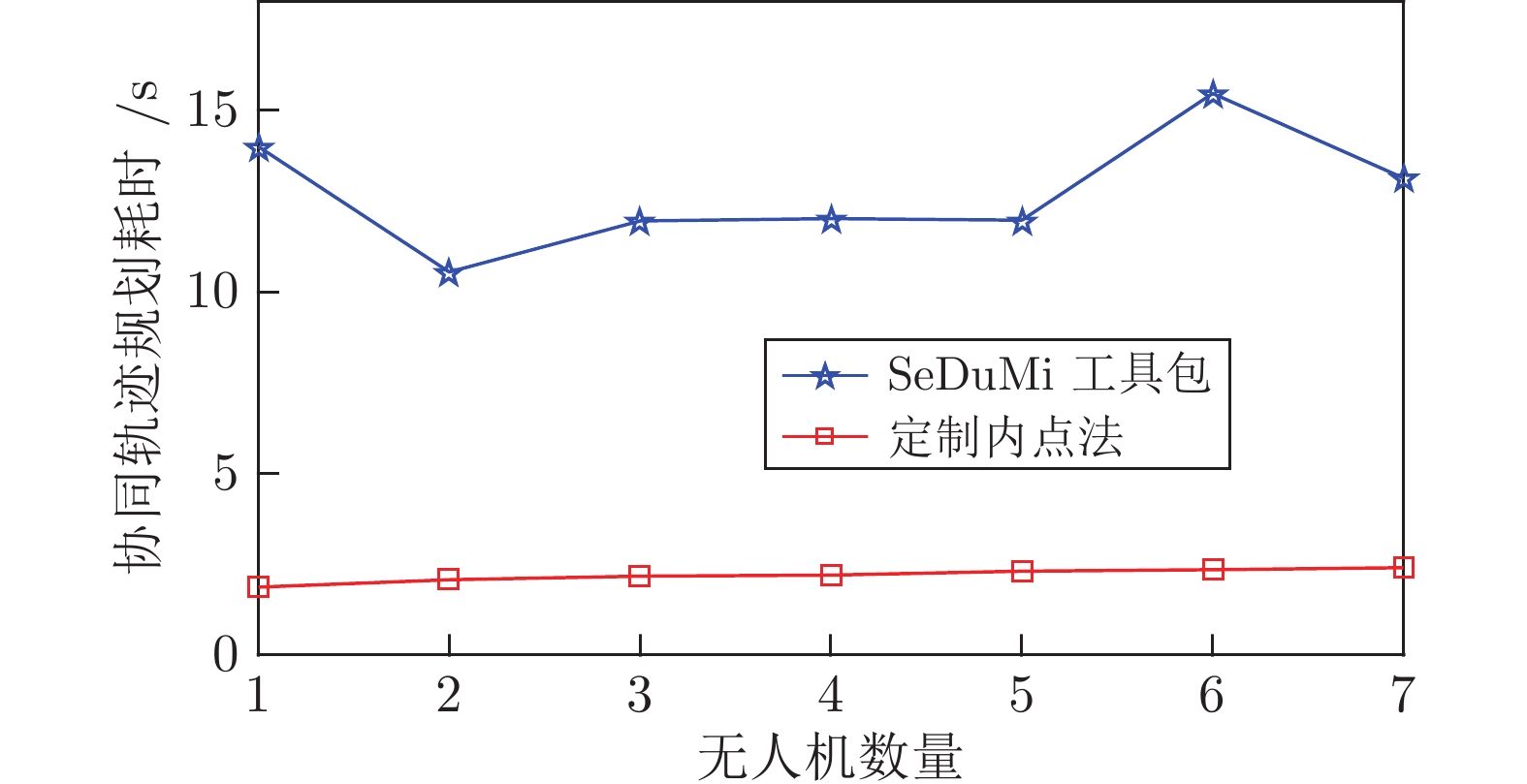
摘要: 为提高多无人机(Unmanned aerial vehicles, UAV)协同轨迹规划(Cooperative trajectory planning, CTP)效率, 在解耦序列凸优化(Sequential convex programming, SCP)方法基础上, 提出一种高效求解凸优化子问题的定制内点法. 首先引入松弛变量, 构建子问题的等价描述形式, 并推导该形式下的子问题最优性条件. 然后在预测−校正原对偶内点法的框架下, 构建一套高效求解最优性条件方程组的计算流程以降低子问题计算复杂度, 并利用约束矩阵特征提出一种快速计算原对偶搜索方向的方法以提高规划效率. 仿真结果表明, 在解耦序列凸优化框架下, 定制内点法可将协同轨迹规划耗时降低一个数量级, 达到秒级.Abstract: To improve the efficiency of cooperative trajectory planning (CTP) for multiple unmanned aerial vehicles (UAVs), a customized interior-point method is proposed for efficiently solving convex subproblems within the decoupled sequential convex programming (SCP) method. Firstly, slack variables are introduced to construct an equivalent form of the subproblem, and the optimality conditions of the subproblem in this equivalent form are derived. Then, under the frame of the predictor-corrector primal-dual interior-point method, an efficient computation procedure for solving the equations of optimality conditions is developed. And through exploring the matrix characteristics of constraints to reduce the complexity of solving subproblems, a fast generation method for primal-dual search direction is proposed to improve the planning efficiency. Simulation results demonstrate that the customized interior-point method can decrease the computation times of CTP by one order of magnitude to several seconds.
-
图 1 多无人机协同轨迹规划问题示意图
Fig. 1 Illustration of multi-UAV cooperative trajectory planning problems
图 4 原对偶搜索方向计算复杂度变化图
Fig. 4 Variations of computation complexity for primal-dual search direction
图 7 编队重构协同轨迹规划二维结果图
Fig. 7 Cooperative trajectories in 2D for formation reconfiguration
图 8 编队重构协同轨迹规划三维结果图
Fig. 8 Cooperative trajectories in 3D for formation reconfiguration
图 9 编队集结任务无人机间最短距离变化曲线
Fig. 9 Variation curve of minimum distance between UAVs for formation rendezvous
图 10 编队重构任务无人机间最短距离变化曲线
Fig. 10 Variation curve of minimum distance between UAVs for formation reconfiguration
图 13 基于SeDuMi的编队集结轨迹规划结果
Fig. 13 Trajectory planning results using SeDuMi for formation rendezvous
图 14 基于定制内点法的编队集结轨迹规划结果
Fig. 14 Trajectory planning results using customized interior-point method for formation rendezvous
图 15 基于SeDuMi的编队重构轨迹规划结果
Fig. 15 Trajectory planning results using SeDuMi for formation reconfiguration
图 16 基于定制内点法的编队重构轨迹规划结果
Fig. 16 Trajectory planning results using customized interior-point method for formation reconfiguration
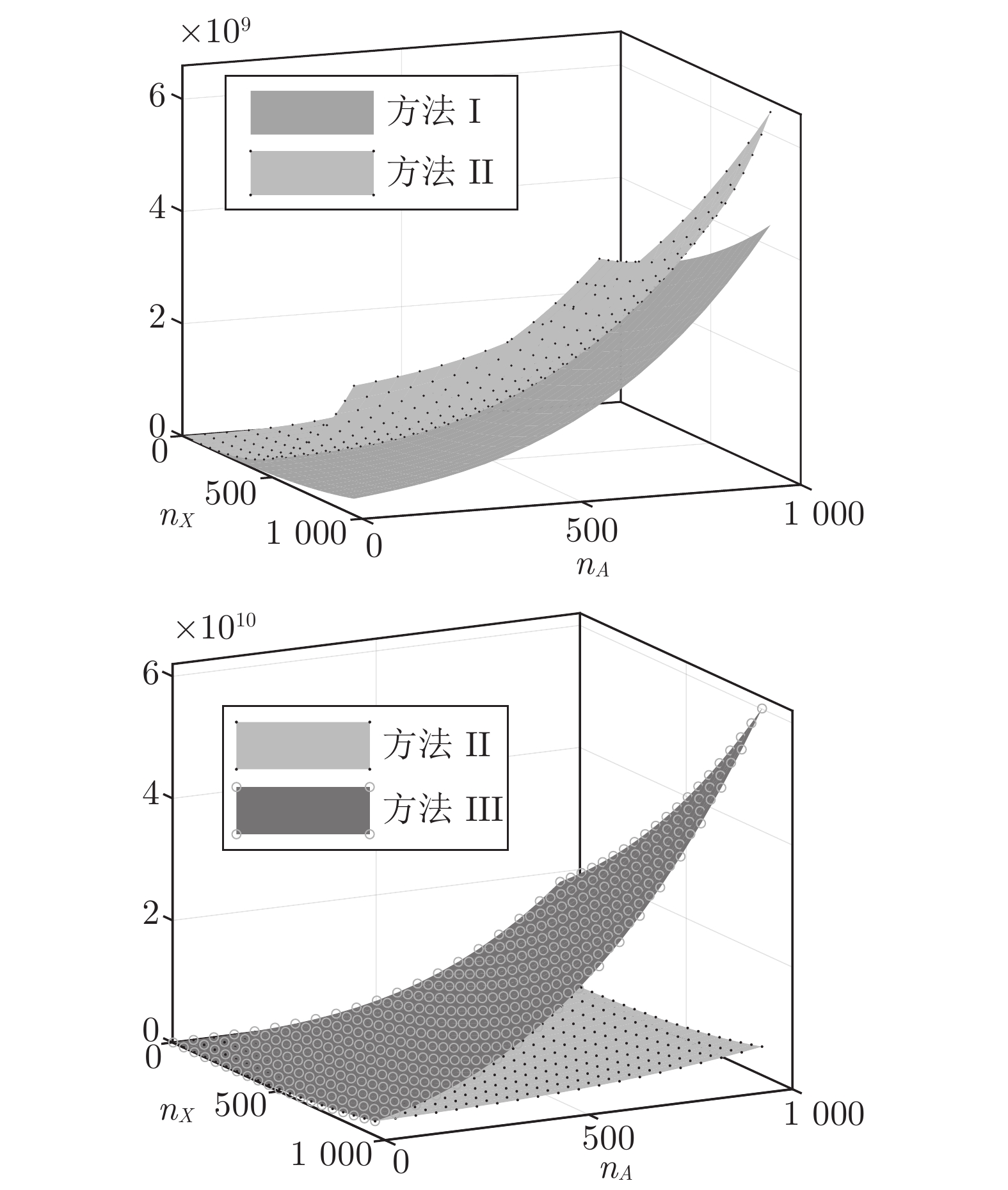
表 1 原对偶搜索方向计算复杂度
Table 1 Computation complexity for primal-dual search direction
计算方法 计算成本 方法 I 0.33$n_{{X}}^3$+ 3$n_A^3$+$n_{{X}}^2{n_A}$+${n_{{X}}}n_A^2$ 方法 II 2.67$n_{{X}}^3$+ 3$n_A^3$+$n_{{X}}^2{n_A}$+${n_{{X}}}n_A^2$ 方法III 2.67 (${n_{{X}}}$+2${n_A}$)3 
下载: 导出CSV
-
[1] 沈林成, 牛轶峰, 朱华勇. 多无人机自主协同控制理论与方法. 北京: 国防工业出版社, 2013. 1−9Shen Lin-Cheng, Niu Yi-Feng, Zhu Hua-Yong. Theories and Methods of Autonomous Cooperative Control for Multiple UAVs. Beijing: National Defense Industry Press, 2013. 1−9 [2] Liu X F, Lu P, Pan B F. Survey of convex optimization for aerospace applications. Astrodynamics, 2017, 1(1): 23-40 doi: 10.1007/s42064-017-0003-8 [3] Boyd S, Vandenberghe L. Convex Optimization. Cambridge: Cambridge University Press, 2004. 1−15 [4] Liu X F, Lu P. Solving nonconvex optimal control problems by convex optimization. Journal of Guidance, Control, and Dynamics 2014, 37(3): 750-765 doi: 10.2514/1.62110 [5] Schulman J, Duan Y, Ho J, Lee A, Awwal I, Bradlow H, et al. Motion planning with sequential convex optimization and convex collision checking. The International Journal of Robotics Research, 2014, 33(9): 1251-1270 doi: 10.1177/0278364914528132 [6] Misra G, Bai X L. Optimal path planning for free-flying space manipulators via sequential convex programming. Journal of Guidance, Control, and Dynamics, 2017, 40(11): 3019-3026 doi: 10.2514/1.G002487 [7] 刘延杰, 朱圣英, 崔平远. 序列凸优化的小天体附着轨迹优化. 宇航学报, 2018, 39(2): 177-183 doi: 10.3873/j.issn.1000-1328.2018.02.008Liu Yan-Jie, Zhu Sheng-Ying, Cui Ping-Yuan. Soft landing trajectory optimization on asteroids by convex programming. Journal of Astronautics, 2018, 39(2): 177-183 doi: 10.3873/j.issn.1000-1328.2018.02.008 [8] 王劲博, 崔乃刚, 郭继峰, 徐大富. 火箭返回着陆问题高精度快速轨迹优化算法. 控制理论与应用, 2018, 35(3): 389-398 doi: 10.7641/CTA.2017.70730Wang Jin-Bo, Cui Nai-Gang, Guo Ji-Feng, Xu Da-Fu. High precision rapid trajectory optimization algorithm for launch vehicle landing. Control Theory & Applications, 2018, 35(3): 389-398 doi: 10.7641/CTA.2017.70730 [9] Zhang Z, Li J X, Wang J. Sequential convex programming for nonlinear optimal control problems in UAV path planning. Aerospace Science and Technology, 2018, 76: 280-290 doi: 10.1016/j.ast.2018.01.040 [10] Zhou D, Zhang Y Q, Li S L. Receding horizon guidance and control using sequential convex programming for spacecraft 6-DOF close proximity. Aerospace Science and Technology, 2019, 87: 459-477 doi: 10.1016/j.ast.2019.02.041 [11] Augugliaro F, Schoellig A P, D＇Andrea R. Generation of collision-free trajectories for a quadrocopter fleet: A sequential convex programming approach. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura-Algarve, Portugal: IEEE, 2012. 1917−1922 [12] Chen Y F, Cutler M, How J P. Decoupled multiagent path planning via incremental sequential convex programming. In: Proceedings of the IEEE International Conference on Robotics and Automation (ICRA). Seattle, USA: IEEE, 2015. 5954−5961 [13] Morgan D, Subramanian G P, Chung S J, Hadaegh F. Swarm assignment and trajectory optimization using variable-swarm, distributed auction assignment and sequential convex programming. The International Journal of Robotics Research, 2016, 35(10): 1261-1285 doi: 10.1177/0278364916632065 [14] 王祝, 刘莉, 龙腾, 温永禄. 基于罚函数序列凸规划的多无人机轨迹规划. 航空学报, 2016, 37(10): 3149-3158Wang Zhu, Liu Li, Long Teng, Wen Yong-Lu. Trajectory planning for multi-UAVs using penalty sequential convex programming. Acta Aeronautica et Astronautica Sinica 2016, 37(10): 3149-3158 [15] Wang Z, Liu L, Long T. Minimum-time trajectory planning for multi-unmanned-aerial-vehicle cooperation using sequential convex programming. Journal of Guidance, Control, and Dynamics, 2017, 40(11): 2976-2982 doi: 10.2514/1.G002349 [16] Wang Z, Liu L, Long L, Xu G T. Efficient unmanned aerial vehicle formation rendezvous trajectory planning using Dubins path and sequential convex programming. Engineering Optimization, 2019, 51(8): 1412-1429 doi: 10.1080/0305215X.2018.1524461 [17] Sturm J F. Using SeDuMi 1.02, a matlab toolbox for optimization over symmetric cones. Optimization Methods and Software, 1999, 11(1-4): 625-653 doi: 10.1080/10556789908805766 [18] Andersen E D, Roos C, Terlaky T. On implementing a primal-dual interior-point method for conic quadratic optimization. Mathematical Programming, 2003, 95(2): 249-277 doi: 10.1007/s10107-002-0349-3 [19] Dueri D, Açıkmeşe B, Scharf D P, Harris M W. Customized real-time interior-point methods for onboard powered-descent guidance. Journal of Guidance, Control, and Dynamics, 2017, 40(2): 197-212 doi: 10.2514/1.G001480 [20] Xu G T, Long T, Wang Z, Cao Y. Matrix structure driven interior point method for quadrotor real-time trajectory planning. IEEE Access, 2019, 7: 90941-90953 doi: 10.1109/ACCESS.2019.2926782 [21] Mehrotra S. On the implementation of a primal-dual interior point method. SIAM Journal on Optimization, 1992, 2(4): 575-601 doi: 10.1137/0802028 [22] Duff I S. MA57-A code for the solution of sparse symmetric definite and indefinite systems. ACM Transactions on Mathematical Software, 2004, 30(2): 118-144 doi: 10.1145/992200.992202 [23] Mehrotra S. Asymptotic convergence in a generalized predictor-corrector method. Mathematical Programming, 1996, 74(1): 11-28. doi: 10.1007/BF02592143 [24] Mao Y Q, Szmuk M, Açıkmeşe B. Successive convexification of non-convex optimal control problems and its convergence properties. In: Proceedings of the 55th IEEE Conference on Decision and Control (CDC). Las Vegas, USA: IEEE, 2016. 3636−3641 -
计量
- 文章访问数: 1709
- HTML全文浏览量: 708
- PDF下载量: 278
- 被引次数: 0
