Multi-strategy Adaptive Multi-objective Particle Swarm Optimization Algorithm Based on Swarm Partition
-
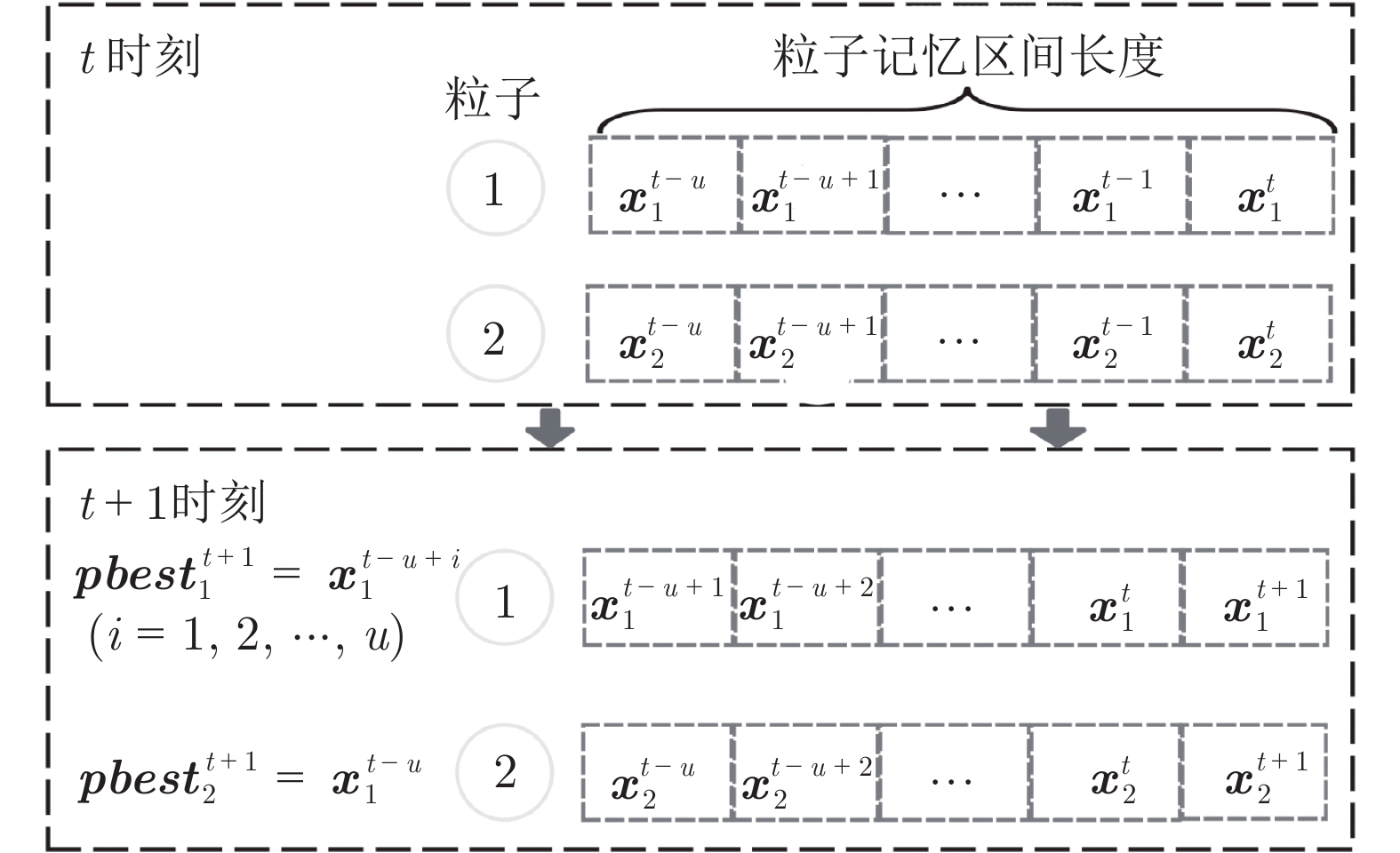
摘要: 在多目标粒子群优化算法中, 平衡算法收敛性和多样性是获得良好分布和高精度Pareto前沿的关键, 多数已提出的方法仅依靠一种策略引导粒子搜索, 在解决复杂问题时算法收敛性和多样性不足. 为解决这一问题, 提出一种基于种群分区的多策略自适应多目标粒子群优化算法. 采用粒子收敛性贡献对算法环境进行检测, 自适应调整粒子的探索和开发过程; 为准确制定不同性能的粒子的搜索策略, 提出一种多策略的全局最优粒子选取方法和多策略的变异方法, 根据粒子的收敛性评价指标, 将种群划分为3个区域, 将粒子性能与算法寻优过程结合, 提升种群中各个粒子的搜索效率; 为解决因选取的个体最优粒子不能有效指导粒子飞行方向, 使算法停滞, 陷入局部最优的问题, 提出一种带有记忆区间的个体最优粒子选取方法, 提升个体最优粒子选取的可靠性并加快粒子收敛过程; 采用包含双性能测度的融合指标维护外部存档, 避免仅根据粒子密度对外部存档维护时, 删除收敛性较好的粒子, 导致种群产生退化, 影响粒子开发能力. 仿真实验结果表明, 与其他几种多目标优化算法相比, 该算法具有良好的收敛性和多样性.Abstract: In the multi-objective particle swarm optimization algorithm, balancing the convergence and diversity of the algorithm is the key to obtain the Pareto front with good distribution and accuracy. Most of the proposed methods rely on only one strategy to guide the particle search, and the algorithm may lack convergence and diversity when solving complex problems. To solve this problem, a multi-strategy adaptive multi-objective particle swarm optimization based on swarm partition is proposed. Firstly, the algorithm detects environment by the convergence contribution of particles and adjusts the process of particle exploration and exploitation adaptively. Secondly, in order to accurately formulate the search strategy of particles with different performances, a multi-strategy global optimal particle selection method and a mutation method are proposed. According to the evaluation index of the convergence of the particles, the population is divided into three regions. Combining particle performance with the algorithm optimization process can improve the search efficiency of each particle. Thirdly, an individual optimal particle selection scheme with memory interval is proposed to solve the problem that the algorithm falls into local optimization because the selected individual optimal particles cannot guide the flight direction of particles effectively. That can improve the reliability of individual optimal particle selection, and accelerate the process of particle convergence. Finally, the fusion metric including particle convergence and diversity is used to maintain the external archive. It can avoid deleting the particles with good convergence and resulting in population degradation and affecting particle development capabilities, when external archive maintenance is just based on the particle density. Experimental results show that the proposed algorithm has good performance compared with some other multi-objective optimization algorithms.
-
图 4
$\eta_{1}$ 和$\eta_{2}$ 的不同取值方案下IGD指标变化Fig. 4 IGD metric changes of different
$\eta_{1}$ and$\eta_{2}$ value schemes
图 5 不同分区参数取值方案下IGD指标变化
Fig. 5 IGD metric changes of different partition parameter value schemes
图 6 不同多目标优化算法对ZDT3函数的Pareto前沿
Fig. 6 Pareto front of ZDT3 function of different multi-objective optimization algorithms
图 7 不同多目标优化算法对DTLZ2函数的Pareto前沿
Fig. 7 Pareto front of DTLZ2 function of different multi-objective optimization algorithms
图 8 不同多目标优化算法对DTLZ7函数的Pareto前沿
Fig. 8 Pareto front of DTLZ7 function of different multi-objective optimization algorithms
图 9 7种多目标优化算法在测试ZDT3、DTLZ2和DTLZ7问题时IGD、SP以及ER指标的箱形图
Fig. 9 Box plots of IGD, SP and ER metric on ZDT3, DTLZ2 and DTLZ7 problems of multi-objective optimization algorithms
表 1 本文算法与其他多目标粒子群算法的IGD评价指标对比
Table 1 Results of IGD metric of the proposed algorithm and MOPSOs
测试函数 spmsAMOPSO clusterMOPSO[23] cdMOPSO[8] pccsAMOPSO[13] CMOPSO[27] 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 ZDT1 ${\bf{2.34\times 10^{-3}}}$ ${\bf{5.46\times 10^{-6}}}$ $1.25\times 10^{-2}$ $1.78\times 10^{-3}$ $4.24\times 10^{-3}$ $2.58\times 10^{-4}$ $3.83\times 10^{-3}$ $2.67\times 10^{-4}$ $3.82\times 10^{-3}$ $2.15\times 10^{-5}$ ZDT2 ${\bf{1.98\times 10^{-3}}}$ ${\bf{6.18\times 10^{-6}}}$ $1.78\times10^{-2}$ $5.09\times 10^{-3}$ $4.28\times 10^{-3}$ $1.14\times 10^{-4}$ $3.81\times 10^{-3}$ $5.81\times 10^{-5}$ $3.86\times 10^{-3}$ $2.83\times 10^{-5}$ ZDT3 ${\bf{8.83\times 10^{-4}}}$ ${\bf{1.02\times 10^{-5}}}$ $1.05\times 10^{-1}$ $7.05\times 10^{-2}$ $3.06\times 10^{-3}$ $7.13\times 10^{-5}$ $4.91\times 10^{-3}$ $6.56\times 10^{-4}$ $4.50\times 10^{-3}$ $2.83\times 10^{-5}$ ZDT4 ${\bf{2.32\times 10^{-3}}}$ ${\bf{3.96\times 10^{-6}}}$ $3.99\times 10^{0} $ $2.61\times 10^{0} $ $5.91\times 10^{-1}$ $4.52\times 10^{-1}$ $5.79\times 10^{-3}$ $2.98\times 10^{-4}$ $3.70\times 10^{-2}$ $4.59\times 10^{-2}$ ZDT6 ${\bf{1.60\times 10^{-3}}}$ ${\bf{5.20\times 10^{-7}}}$ $4.39\times 10^{-1}$ $2.37\times 10^{-2}$ $2.99\times 10^{-3}$ $1.54\times 10^{-4}$ $4.68\times 10^{-3}$ $7.67\times 10^{-4}$ $3.09\times 10^{-3}$ $2.61\times 10^{-5}$ DTLZ1 ${\bf{1.23\times 10^{-2}}}$ $1.23\times 10^{-3}$ $4.15\times 10^{1} $ $2.29\times 10^{1} $ $2.75\times 10^{1}$ $9.34\times 10^{0}$ $1.36\times 10^{-1}$ $1.12\times 10^{-1}$ $4.44\times 10^{-2}$ $7.83\times 10^{-2}$ DTLZ2 ${\bf{3.62\times 10^{-3}}}$ $8.56\times 10^{-5}$ $1.26\times 10^{-1}$ $1.68\times 10^{-2}$ $1.02\times 10^{-1}$ $1.34\times 10^{-2}$ $6.14\times 10^{-2}$ $1.89\times 10^{-3}$ $4.40\times 10^{-3}$ ${\bf{3.61\times 10^{-5}}}$ DTLZ3 ${\bf{3.28\times 10^{-3}}}$ ${\bf{9.62\times 10^{-5}}}$ $4.76\times 10^{1}$ $2.87\times 10^{1}$ $4.46\times 10^{1}$ $1.02\times 10^{1}$ $2.19\times 10^{-1}$ $1.85\times 10^{-1}$ $4.24\times 10^{-3}$ $1.71\times 10^{-4}$ DTLZ4 $7.58\times 10^{-3}$ $3.45\times 10^{-3}$ $2.28\times 10^{-1}$ $8.45\times 10^{-2}$ $1.02\times 10^{-1}$ $3.66\times 10^{-2}$ $ {\bf{4.21\times 10^{-3} }} $ $3.37\times 10^{-3}$ $4.41\times 10^{-3}$ $7.58\times 10^{-5}$ DTLZ5 $9.76\times 10^{-3}$ $6.42\times 10^{-4}$ $1.62\times 10^{-4}$ $2.48\times 10^{-3}$ $6.05\times 10^{-3}$ $7.29\times 10^{-4}$ $1.18\times 10^{-2}$ $2.48\times 10^{-3}$ ${\bf{4.40\times 10^{-3}}}$ $5.66\times 10^{-5}$ DTLZ6 ${\bf{3.62\times 10^{-3}}}$ $3.47\times 10^{-5}$ $7.38\times 10^{-2}$ $1.55\times 10^{-1}$ $5.23\times 10^{-3}$ $3.90\times 10^{-4}$ $5.04\times 10^{-3}$ $2.27\times 10^{-4}$ $4.09\times 10^{-3}$ ${\bf{1.83\times 10^{-5}}}$ DTLZ7 ${\bf{4.23\times 10^{-3}}}$ $1.37\times 10^{-4}$ $4.02\times 10^{-2}$ $2.06\times 10^{-3}$ $5.78\times 10^{-2}$ $8.49\times 10^{-3}$ $4.27\times 10^{-2}$ $9.51\times 10^{-4}$ $4.43\times 10^{-3}$ ${\bf{4.01\times 10^{-5}}}$ 
下载: 导出CSV
表 2 本文算法与其他多目标进化算法的IGD评价指标对比
Table 2 Results of IGD metric of the proposed algorithm and multi-objective genetic algorithms
测试函数 spmsAMOPSO NSGA-II[24] SPEA2[25] MOEA/D[26] SPEA2 + DAA[28] 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 ZDT1 ${\bf{2.34\times 10^{-3}}}$ ${\bf{5.46\times 10^{-6}}}$ $5.74\times 10^{-3}$ $3.39\times 10^{-4}$ $4.15\times 10^{-3}$ $1.77\times 10^{-4}$ $4.03\times 10^{-3}$ $5.59\times 10^{-5}$ $3.92\times 10^{-3}$ $5.05\times 10^{-5}$ ZDT2 ${\bf{1.98\times 10^{-3}}}$ ${\bf{6.18\times 10^{-6}}}$ $5.36\times 10^{-3}$ $2.02\times 10^{-4}$ $4.17\times 10^{-3}$ $2.56\times 10^{-4}$ $3.85\times 10^{-3}$ $4.34\times 10^{-5}$ $4.02\times 10^{-3}$ $1.07\times 10^{-4}$ ZDT3 ${\bf{8.83\times 10^{-4}}}$ ${\bf{1.02\times 10^{-5}}}$ $5.83\times 10^{-3}$ $2.02\times 10^{-4}$ $3.16\times 10^{-3}$ $5.96\times 10^{-3}$ $8.42\times 10^{-2}$ $7.02\times 10^{-3}$ $8.46\times 10^{-3}$ $9.45\times 10^{-3}$ ZDT4 ${\bf{2.32\times 10^{-3}}}$ ${\bf{3.96\times 10^{-6}}}$ $2.53\times 10^{1}$ $7.21\times 10^{0}$ $2.49\times 10^{1}$ $7.25\times 10^{-5}$ $4.86\times 10^{-3}$ $8.41\times 10^{-4}$ — — ZDT6 ${\bf{1.60\times 10^{-3}}}$ ${\bf{5.20\times 10^{-7}}}$ $1.65\times 10^{0}$ $9.80\times 10^{-1}$ $5.32\times 10^{-3}$ $2.65\times 10^{-8}$ $3.99\times 10^{-3}$ $6.02\times 10^{-5}$ — — DTLZ1 ${\bf{1.23\times 10^{-2}}}$ $1.23\times 10^{-3}$ $1.41\times 10^{1}$ $6.65\times 10^{0}$ $3.77\times 10^{1}$ ${\bf{1.45\times 10^{-4}}}$ $6.04\times 10^{-1}$ $2.89\times 10^{-1}$ $1.51\times 10^{-2}$ $1.48\times 10^{-3}$ DTLZ2 ${\bf{3.62\times 10^{-3}}}$ $8.56\times 10^{-5}$ $1.06\times 10^{-1}$ $8.38\times 10^{-3}$ $8.22\times 10^{-2}$ $2.83\times 10^{-7}$ $6.24\times 10^{-1}$ $6.44\times 10^{-5}$ $3.81\times 10^{-2}$ $3.03\times 10^{-4}$ DTLZ3 ${\bf{3.28\times 10^{-3}}}$ ${\bf{9.62\times 10^{-5}}}$ $1.64\times 10^{1}$ $7.56\times 10^{0}$ $4.87\times 10^{1}$ $0.00\times 10^{0}$ $6.52\times 10^{-1}$ $2.59\times 10^{-1}$ — — DTLZ4 $7.58\times 10^{-3}$ $3.45\times 10^{-3}$ $7.30\times 10^{-2}$ $5.09\times 10^{-2}$ $7.29\times 10^{-2}$ $1.42\times 10^{-7}$ $2.70\times 10^{-1}$ $6.83\times 10^{-3}$ — — DTLZ5 $9.76\times 10^{-3}$ $6.42\times 10^{-4}$ $8.05\times 10^{-3}$ $1.63\times 10^{-3}$ $1.41\times 10^{-2}$ $3.54\times 10^{-5}$ $5.94\times 10^{-1}$ ${\bf{8.43\times 10^{-8}}}$ — — DTLZ6 ${\bf{3.62\times 10^{-3}}}$ $3.47\times 10^{-5}$ $1.47\times 10^{0}$ $6.09\times 10^{-1}$ $2.49\times 10^{-1}$ $5.67\times 10^{-5}$ $6.17\times 10^{-1}$ $1.01\times 10^{-4}$ — — DTLZ7 ${\bf{4.23\times 10^{-3}}}$ $1.37\times 10^{-4}$ $6.14\times 10^{-1}$ $1.29\times 10^{-3}$ $6.24\times 10^{-2}$ $9.50\times 10^{-3}$ $6.57\times 10^{-1}$ $9.87\times 10^{-4}$ $3.69\times 10^{-2}$ $5.02\times 10^{-4}$
下载: 导出CSV
表 3 本文算法与其他多目标粒子群算法的SP评价指标对比
Table 3 Results of SP metric of the proposed algorithm and MOPSOs
测试函数 spmsAMOPSO clusterMOPSO[23] cdMOPSO[8] pccsAMOPSO[13] 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 ZDT1 ${\bf{4.09\times 10^{-3}}}$ ${\bf{5.57\times 10^{-5}}}$ $7.25\times 10^{-2}$ $6.17\times 10^{-4}$ $8.56\times 10^{-2}$ $1.43\times 10^{-2}$ $1.33\times 10^{-2}$ $5.42\times 10^{-3}$ ZDT2 ${\bf{3.19\times 10^{-3}}}$ ${\bf{5.58\times 10^{-5}}}$ $1.77\times 10^{-2}$ $1.95\times 10^{-3}$ $1.91\times 10^{-2}$ $6.42\times 10^{-4}$ $1.06\times 10^{-2}$ $4.63\times 10^{-3}$ ZDT3 ${\bf{4.35\times 10^{-3}}}$ ${\bf{4.54\times 10^{-5}}}$ $7.78\times 10^{-2}$ $4.36\times 10^{-2}$ $5.97\times 10^{-1}$ $2.25\times 10^{-1}$ $1.25\times 10^{-1}$ $6.48\times 10^{-2}$ ZDT4 ${\bf{3.84\times 10^{-3}}}$ ${\bf{9.84\times 10^{-5}}}$ $9.19\times 10^{-3}$ $1.32\times 10^{-3}$ $8.49\times 10^{-3}$ $5.85\times 10^{-4}$ $1.09\times 10^{-2}$ $2.78\times 10^{-3}$ ZDT6 ${\bf{3.11\times 10^{-3}}}$ ${\bf{3.91\times 10^{-5}}}$ $2.69\times 10^{-2}$ $1.67\times 10^{-2}$ $9.83\times 10^{-3}$ $4.65\times 10^{-4}$ $1.10\times 10^{-2}$ $5.89\times 10^{-3}$ DTLZ1 ${\bf{2.24\times 10^{-2}}}$ ${\bf{3.36\times 10^{-4}}}$ $9.32\times 10^{-2}$ $1.74\times 10^{-2}$ $4.12\times 10^{-2}$ $5.64\times 10^{-3}$ $5.79\times 10^{0}$ $4.83\times 10^{-1}$ DTLZ2 ${\bf{3.60\times 10^{-2}}}$ ${\bf{1.74\times 10^{-4}}}$ $7.06\times 10^{-2}$ $3.42\times 10^{-3}$ $6.91\times 10^{-2}$ $4.03\times 10^{-3}$ $6.08\times 10^{-2}$ $2.54\times 10^{-3}$ DTLZ3 ${\bf{4.12\times 10^{-2}}}$ $2.33\times 10^{-3}$ $7.93\times 10^{-1}$ $2.06\times 10^{-2}$ $5.88\times 10^{-2}$ $3.96\times 10^{-3}$ $6.09\times 10^{-1}$ ${\bf{7.45\times 10^{-4}}}$ DTLZ4 ${\bf{3.80\times 10^{-2}}}$ ${\bf{8.63\times 10^{-4}}}$ $6.81\times 10^{-1}$ $9.94\times 10^{-3}$ $4.76\times 10^{-2}$ $2.84\times 10^{-3}$ $5.97\times 10^{-1}$ $6.33\times 10^{-2}$ DTLZ5 $7.52\times 10^{-2}$ $5.83\times 10^{-3}$ $8.93\times 10^{-2}$ $7.52\times 10^{-3}$ ${\bf{2.42\times 10^{-2}}}$ $6.22\times 10^{-3}$ $1.02\times 10^{-1}$ $3.74\times 10^{-2}$ DTLZ6 ${\bf{3.47\times 10^{-2}}}$ $2.14\times 10^{-3}$ $6.80\times 10^{-2}$ $1.83\times 10^{-2}$ $4.65\times 10^{-2}$ $2.73\times 10^{-3}$ $5.86\times 10^{-2}$ ${\bf{1.26\times 10^{-4}}}$ DTLZ7 ${\bf{9.47\times 10^{-2}}}$ $4.81\times 10^{-2}$ $3.90\times 10^{-1}$ $1.29\times 10^{-2}$ $5.97\times 10^{-1}$ $2.13\times 10^{-1}$ $1.08\times 10^{-1}$ $3.14\times 10^{-2}$
下载: 导出CSV
表 4 本文算法与其他多目标进化算法的SP评价指标对比
Table 4 Results of SP metric of the proposed algorithm and multi-objective genetic algorithms
测试函数 spmsAMOPSO NSGA-II[24] SPEA2[25] MOEA/D[26] 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 ZDT1 ${\bf{4.09\times 10^{-3}}}$ ${\bf{5.57\times 10^{-5}}}$ $5.83\times 10^{-2}$ $9.39\times 10^{-3}$ $3.73\times 10^{-2}$ $2.67\times 10^{-3}$ $4.85\times 10^{-3}$ $7.19\times 10^{-4}$ ZDT2 ${\bf{3.19\times 10^{-3}}}$ ${\bf{5.58\times 10^{-5}}}$ $7.24\times 10^{-3}$ $7.41\times 10^{-3}$ $1.09\times 10^{-2}$ $1.04\times 10^{-3}$ $4.36\times 10^{-3}$ $7.41\times 10^{-4}$ ZDT3 ${\bf{4.35\times 10^{-3}}}$ ${\bf{4.54\times 10^{-5}}}$ $9.22\times 10^{-2}$ $8.42\times 10^{-3}$ $6.07\times 10^{-1}$ $1.03\times 10^{0}$ $1.02\times 10^{-1}$ $9.33\times 10^{-3}$ ZDT4 ${\bf{3.84\times 10^{-3}}}$ ${\bf{9.84\times 10^{-5}}}$ $2.83\times 10^{-2}$ $6.13\times 10^{-3}$ $4.06\times 10^{-2}$ $1.59\times 10^{-2}$ $7.52\times 10^{-3}$ $6.93\times 10^{-4}$ ZDT6 ${\bf{3.11\times 10^{-3}}}$ ${\bf{3.91\times 10^{-5}}}$ $3.43\times 10^{-2}$ $4.33\times 10^{-3}$ $4.72\times 10^{-2}$ $7.74\times 10^{-3}$ $1.88\times 10^{-2}$ $5.52\times 10^{-3}$ DTLZ1 ${\bf{2.24\times 10^{-2}}}$ ${\bf{3.36\times 10^{-4}}}$ $7.21\times 10^{-1}$ $6.34\times 10^{-2}$ $2.92\times 10^{-1}$ $3.62\times 10^{-2}$ $9.83\times 10^{-1}$ $2.33\times 10^{-1}$ DTLZ2 ${\bf{3.60\times 10^{-2}}}$ ${\bf{1.74\times 10^{-4}}}$ $4.67\times 10^{-2}$ $7.71\times 10^{-3}$ $5.38\times 10^{-2}$ $3.42\times 10^{-3}$ $8.14\times 10^{-2}$ $8.49\times 10^{-3}$ DTLZ3 ${\bf{4.12\times 10^{-2}}}$ $2.33\times 10^{-3}$ $8.26\times 10^{-2}$ $2.09\times 10^{-3}$ $6.34\times 10^{-2}$ $5.12\times 10^{-3}$ $1.79\times 10^{-1}$ $3.36\times 10^{-2}$ DTLZ4 ${\bf{3.80\times 10^{-2}}}$ ${\bf{8.63\times 10^{-4}}}$ $7.14\times 10^{-2}$ $1.97\times 10^{-3}$ $4.38\times 10^{-2}$ $6.54\times 10^{-3}$ $9.25\times 10^{-2}$ $5.61\times 10^{-3}$ DTLZ5 $7.52\times 10^{-2}$ $5.83\times 10^{-3}$ $6.37\times 10^{-2}$ ${\bf{1.74\times 10^{-3}}}$ $3.15\times 10^{-2}$ $5.31\times 10^{-3}$ $8.02\times 10^{-2}$ $4.39\times 10^{-3}$ DTLZ6 ${\bf{3.47\times 10^{-2}}}$ $2.14\times 10^{-3}$ $7.03\times 10^{-2}$ $1.56\times 10^{-3}$ $5.11\times 10^{-2}$ $4.89\times 10^{-3}$ $3.93\times 10^{-2}$ $3.31\times 10^{-3}$ DTLZ7 ${\bf{9.47\times 10^{-2}}}$ $4.81\times 10^{-2}$ $4.19\times 10^{-1}$ $7.96\times 10^{-3}$ $2.96\times 10^{-1}$ ${\bf{5.29\times 10^{-3}}}$ $1.85\times 10^{-1}$ $7.93\times 10^{-2}$
下载: 导出CSV
表 5 本文算法与其他多目标粒子群算法的ER评价指标对比
Table 5 Results of ER metric of the proposed algorithm and MOPSOs
测试函数 spmsAMOPSO clusterMOPSO[23] cdMOPSO[8] pccsAMOPSO[13] 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 ZDT1 ${\bf{6.73\times 10^{-4}}}$ ${\bf{1.34\times 10^{-4}}}$ $1.06\times 10^{-2}$ $1.00\times 10^{-2}$ $9.90\times 10^{-2}$ $1.25\times 10^{-3}$ $8.12\times 10^{-3}$ $1.43\times 10^{-2}$ ZDT2 ${\bf{3.75\times 10^{-3}}}$ ${\bf{1.17\times 10^{-5}}}$ $4.92\times 10^{-1}$ $8.72\times 10^{-2}$ $1.30\times 10^{0}$ $1.21\times 10^{-1}$ $9.00\times 10^{-3}$ $2.36\times 10^{-3}$ ZDT3 ${\bf{8.95\times 10^{-3}}}$ ${\bf{1.37\times 10^{-3}}}$ $2.66\times 10^{-1}$ $9.30\times 10^{-2}$ $2.89\times 10^{-1}$ $7.24\times 10^{-2}$ $2.60\times 10^{-2}$ $8.32\times 10^{-3}$ ZDT4 $2.70\times 10^{-2}$ $8.35\times 10^{-3}$ $4.42\times 10^{-1}$ $1.02\times 10^{-1}$ $9.34\times 10^{-2}$ $6.83\times 10^{-2}$ ${\bf{2.37\times 10^{-2}}}$ ${\bf{4.74\times 10^{-3}}}$ ZDT6 ${\bf{1.60\times 10^{-3}}}$ $1.24\times 10^{-2}$ $2.98\times 10^{-2}$ $7.43\times 10^{-3}$ $6.77\times 10^{-3}$ $3.43\times 10^{-3}$ $1.10\times 10^{-2}$ ${\bf{4.64\times 10^{-4}}}$ DTLZ1 $6.81\times 10^{-2}$ ${\bf{4.24\times 10^{-3}}}$ ${\bf{4.83\times 10^{-2}}}$ $6.52\times 10^{-3}$ $6.22\times 10^{-1}$ $3.81\times 10^{-2}$ $9.90\times 10^{0}$ $7.13\times 10^{-1}$ DTLZ2 ${\bf{4.74\times 10^{-1}}}$ ${\bf{3.52\times 10^{-3}}}$ $1.19\times 10^{0}$ $7.62\times 10^{-1}$ $8.32\times 10^{-1}$ $3.53\times 10^{-2}$ $9.10\times 10^{-1}$ $5.31\times 10^{-2}$ DTLZ3 ${\bf{8.15\times 10^{-2}}}$ $2.47\times 10^{-2}$ $4.07\times 10^{-1}$ $5.26\times 10^{-2}$ $7.21\times 10^{-1}$ $2.12\times 10^{-2}$ $9.53\times 10^{-2}$ $3.64\times 10^{-2}$ DTLZ4 $8.02\times 10^{-2}$ ${\bf{1.14\times 10^{-3}}}$ $8.24\times 10^{-2}$ $3.01\times 10^{-3}$ $2.42\times 10^{-1}$ $9.71\times 10^{-2}$ $6.33\times 10^{-1}$ $3.60\times 10^{-2}$ DTLZ5 ${\bf{1.43\times 10^{-2}}}$ $3.90\times 10^{-3}$ $4.81\times 10^{-1}$ $5.32\times 10^{-2}$ $1.99\times 10^{-1}$ $9.73\times 10^{-2}$ $2.72\times 10^{-2}$ $4.74\times 10^{-3}$ DTLZ6 $1.73\times 10^{-1}$ $5.69\times 10^{-2}$ ${\bf{4.62\times 10^{-2}}}$ ${\bf{6.39\times 10^{-3}}}$ $3.48\times 10^{-1}$ $2.15\times 10^{-3}$ $1.92\times 10^{-1}$ $8.13\times 10^{-2}$ DTLZ7 ${\bf{2.18\times 10^{-1}}}$ ${\bf{7.64\times 10^{-2}}}$ $4.77\times 10^{-1}$ $5.07\times 10^{-1}$ $5.89\times 10^{-1}$ $4.33\times 10^{-1}$ $3.16\times 10^{-1}$ $9.57\times 10^{-2}$
下载: 导出CSV
表 6 本文算法与其他多目标进化算法的ER评价指标对比
Table 6 Results of ER metric of the proposed algorithm and multi-objective genetic algorithms
测试函数 spmsAMOPSO NSGA-II[24] SPEA2[25] MOEA/D[26] 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 ZDT1 ${\bf{6.73\times 10^{-4}}}$ ${\bf{1.34\times 10^{-4}}}$ $8.06\times 10^{-3}$ $5.82\times 10^{-3}$ $3.00\times 10^{-3}$ $6.75\times 10^{-3}$ $7.65\times 10^{-2}$ $2.44\times 10^{-3}$ ZDT2 ${\bf{3.75\times 10^{-3}}}$ ${\bf{1.17\times 10^{-5}}}$ $5.74\times 10^{-1}$ $3.41\times 10^{-2}$ $9.11\times 10^{-1}$ $4.68\times 10^{-2}$ $6.53\times 10^{-1}$ $2.78\times 10^{-2}$ ZDT3 ${\bf{8.95\times 10^{-3}}}$ ${\bf{1.37\times 10^{-3}}}$ $2.09\times 10^{-2}$ $4.12\times 10^{-2}$ $1.49\times 10^{-1}$ $6.92\times 10^{-2}$ $4.87\times 10^{-2}$ $6.47\times 10^{-3}$ ZDT4 $2.70\times 10^{-2}$ $8.35\times 10^{-3}$ $3.49\times 10^{-2}$ $7.66\times 10^{-3}$ $8.45\times 10^{-2}$ $2.93\times 10^{-2}$ $7.60\times 10^{-1}$ $5.36\times 10^{-2}$ ZDT6 ${\bf{1.60\times 10^{-3}}}$ $1.24\times 10^{-2}$ $9.93\times 10^{-3}$ $7.64\times 10^{-4}$ $8.02\times 10^{-3}$ $3.24\times 10^{-3}$ $1.73\times 10^{-2}$ $2.12\times 10^{-3}$ DTLZ1 $6.81\times 10^{-2}$ ${\bf{4.24\times 10^{-3}}}$ $2.80\times 10^{-1}$ $1.55\times 10^{-2}$ $8.31\times 10^{-2}$ $4.85\times 10^{-3}$ $4.64\times 10^{-1}$ $3.06\times 10^{-2}$ DTLZ2 ${\bf{4.74\times 10^{-1}}}$ ${\bf{3.52\times 10^{-3}}}$ $7.06\times 10^{-1}$ $5.44\times 10^{-2}$ $9.47\times 10^{-1}$ $2.13\times 10^{-1}$ $2.59\times 10^{0}$ $7.42\times 10^{-1}$ DTLZ3 ${\bf{8.15\times 10^{-2}}}$ $2.47\times 10^{-2}$ $8.60\times 10^{-1}$ $3.75\times 10^{-2}$ $9.83\times 10^{-1}$ $3.41\times 10^{-2}$ $2.17\times 10^{-1}$ ${\bf{4.54\times 10^{-3}}}$ DTLZ4 $8.02\times 10^{-2}$ ${\bf{1.14\times 10^{-3}}}$ $4.85\times 10^{-1}$ $4.21\times 10^{-2}$ ${\bf{6.13\times 10^{-2}}}$ $1.90\times 10^{-3}$ $1.36\times 10^{-1}$ $6.29\times 10^{-2}$ DTLZ5 ${\bf{1.43\times 10^{-2}}}$ $3.90\times 10^{-3}$ $9.43\times 10^{-2}$ $4.16\times 10^{-3}$ $8.32\times 10^{-2}$ ${\bf{2.73\times 10^{-3}}}$ $v1.03\times 10^{-1}$ $6.51\times 10^{-2}$ DTLZ6 $1.73\times 10^{-1}$ $5.69\times 10^{-2}$ $5.84\times 10^{-2}$ $7.91\times 10^{-3}$ $4.36\times 10^{-1}$ $2.26\times 10^{-2}$ $2.53\times 10^{-1}$ $9.06\times 10^{-2}$ DTLZ7 ${\bf{2.18\times 10^{-1}}}$ ${\bf{7.64\times 10^{-2}}}$ $4.34\times 10^{-1}$ $2.64\times 10^{-1}$ $3.92\times 10^{-1}$ $8.70\times 10^{-2}$ $3.76\times 10^{-1}$ $2.92\times 10^{-1}$
下载: 导出CSV
表 7 不同算法对多目标测试问题的运行时间 (s)
Table 7 Computational time of different algorithms for multi-objective test problems (s)
函数 spmsAMOPSO clusterMOPSO[23] cdMOPSO[8] pccsAMOPSO[13] NSGA-II[24] SPEA2[25] MOEA/D[26] ZDT1 105.26 108.87 ${\bf{101.72}}$ 121.95 129.17 135.23 152.45 ZDT2 ${\bf{104.72}}$ 114.95 112.74 108.34 133.15 126.65 139.13 ZDT3 ${\bf{111.23}}$ 136.38 135.81 124.57 132.40 137.98 135.02 ZDT4 ${\bf{115.17}}$ 132.09 129.69 122.19 125.67 130.61 147.61 ZDT6 ${\bf{122.48}}$ 131.62 124.23 126.62 133.52 128.74 149.55 DTLZ1 ${\bf{210.77}}$ 230.82 226.47 219.83 248.13 232.47 280.73 DTLZ2 218.93 233.49 ${\bf{212.73}}$ 215.63 250.26 238.69 289.36 DTLZ3 ${\bf{212.61}}$ 228.34 217.51 218.26 250.98 242.81 281.75 DTLZ4 218.34 230.25 220.98 ${\bf{216.44}}$ 247.37 241.33 276.84 DTLZ5 ${\bf{219.15}}$ 234.16 228.21 221.92 255.91 250.62 286.17 DTLZ6 ${\bf{216.37}}$ 236.59 225.40 225.73 245.69 247.97 288.33 DTLZ7 ${\bf{215.42}}$ 243.52 224.64 232.41 246.38 238.11 295.42
下载: 导出CSV
-
[1] 乔俊飞, 李霏, 杨翠丽. 一种基于均匀分布策略的NSGAⅡ算法. 自动化学报, 2019, 45(7): 1325-1334.Qiao Jun-Fei, Li-Fei, Yang Cui-Li. An NSGAⅡ algorithm based on uniform distribution strategy. Acta Automatica Sinica, 2019, 45(7): 1325-1334. [2] Cheng S, Zhao L L, Jiang X Y. Many-objective particle swarm optimization based on adaptive fuzzy dominance. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017, 14(1): 56-63. [3] Feng Q, Li Q, Chen P, Hen W, Xue Z E, Yin L, Ge C. Multiobjective particle swarm optimization algorithm based on adaptive angle division. IEEE Access, 2019, 7: 87916-87930. [4] Liu X F, Zhan Z H, Gao Y, Zhang J, Kwong S, Zhang J. Coevolutionary particle swarm optimization with bottleneck objective learning strategy for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2019, 23(4): 587-602. [5] 余伟伟, 谢承旺, 闭应洲, 夏学文, 李雄, 任柯燕, 赵怀瑞, 王少锋. 一种基于自适应模糊支配的高维多目标粒子群算法. 自动化学报, 2018, 44(12): 2278-2289Yu Wei-Wei, Xie Cheng-Wang, Bi Ying-Zhou, Xia Xue-Wen, Li Xiong, Ren Ke-Yan, Zhao Huai-Rui, Wang Shao-Feng. Many-objective particle swarm optimization based on adaptive fuzzy dominance. Acta Automatica Sinica, 2018, 44(12): 2278-2289. [6] Li L, Wang W L, Li W K, Xu X L, Zhao Y W. A novel ranking-based optimal guides selection strategy in MOPSO. Procedia Computer Science, 2016, 91: 1001-1010. [7] Coello C A C, Pulido G T, Lechuga M S. Handling multiple objectives with particle swarm optimization. IEEE Trans on Evolutionary Computation, 2004, 8(3): 256-279. [8] Raquel C R, Naval P C. An effective use of crowding distance in multiobjective particle swarm optimization. In: Proceedings of the 2005 Conference on Genetic and Evolutionary Computation. New York, USA: 2005. 257−264 [9] Yen G G, Wen F. Leong. Dynamic multiple swarms in multiobjective particle swarm optimization. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2009, 39(4): 890−911 [10] Peng W, Zhang Q F. A decomposition-based multi-objective particle swarm optimization algorithm for continuous optimization problems. In: Proceedings of the 2008 IEEE International Conference on Granular Computing. Hangzhou, China: 2008. 534−537 [11] Martínez S Z, Coello C A C. A multi-objective particle swarm optimizer based on decomposition. In: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation. Dublin, Ireland: 2011. 69−76 [12] Dai C, Wang Y, Ye M. A new multi-objective particle swarm optimization algorithm based on decomposition. Information Sciences, 2015, 325: 541-557. [13] Hu W, Yen G G. Adaptive multiobjective particle swarm optimization based on parallel cell coordinate system. IEEE Transactions on Evolutionary Computation, 2015, 19(1): 1-18. [14] Kumar R S, Kondapaneni K, Dixit V, Goswami A, Thakur L S, Tiwari M K. Multi-objective modeling of production and pollution routing problem with time window: a self-learning particle swarm optimization approach. Computers and Industrial Engineering, 2016, 99: 29-40. [15] Kennedy J, Eberhart R C. Particle swarm optimization. In: Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, USA: 1995. 1942−1948 [16] 韩敏, 何泳. 基于高斯混沌变异和精英学习的自适应多目标粒子群算法. 控制与决策, 2016, 31(8): 1372-1378.Han Ming, He Yong. Adaptive multi-objective particle swarm optimization with Gaussian chaotic mutation and elite learning. Control and Decision, 2016, 31(8): 1372-1378. [17] Rajani, Kumar D, Kumar V. Impact of controlling parameters on the performance of MOPSO algorithm. Procedia Computer Science, 2020, 167: 2132–2139. [18] Luo J P, Huang X W, Yang Y, Li X, Wang Z K, Feng J Q. A many-objective particle swarm optimizer based on indicator and direction vectors for many-objective optimization. Information Sciences, 2020, 514: 166–202. [19] Lin Q Z, Liu S B, Zhu Q L, Tang C Y, Song R Z, Chen J Y, et al. Particle swarm optimization with a balanceable fitness estimation for many-objective optimization problems. IEEE Trans on Evolutionary Computation, 2018, 22(1): 32-46. [20] El-Shorbagy M A, Elhoseny M, Hassanien A E, Ahmed S H. A novel PSO algorithm for dynamic wireless sensor network multiobjective optimization problem. Transactions on Emerging Telecommunications Technologies, 2018, 30(11):1-14. [21] Mohamed A M, Enrico Z. An adaptive particle swarm optimization method for multi-objective system reliability optimization. Journal of Risk and Reliability, 2019, 233: 990-1001. [22] Helwig S, Branke J, Mostaghim S. Experimental analysis of bound handling techniques in particle swarm optimization. IEEE Transactions on Evolutionary Computation, 2013, 17(2): 259–271. [23] Chakraborty P, Das S, Roy G G, Abraham A. On convergence of the multi-objective particle swarm optimizers. Information Sciences, 2011, 181: 1411-1425. [24] Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. [25] Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm. TIK-Report 103, Swiss Federal Institute of Technology, Switzerland, 2001 [26] Zhang Q F, Li H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. [27] Zhang X Y, Zheng X T, Cheng R, Qiu J F, Jin Y C. A competitive mechanism based multi-objective particle swarm optimizer with fast convergence. Information Sciences, 2018, 427: 63-76. [28] Zhang Y, Gong D W, Sun J Y, Qu B Y. A decomposition-based archiving approach for multi-objective evolutionary optimization. Information Sciences, 2018, 430: 397-413. -
图(9) / 表(7)
计量
- 文章访问数: 985
- HTML全文浏览量: 379
- PDF下载量: 364
- 被引次数: 0
