Design of Asynchronous Correlation Discriminant Single Object Tracker Based on Siamese Network
-
摘要: 现有基于孪生网络的单目标跟踪算法能够实现很高的跟踪精度, 但是这些跟踪器不具备在线更新的能力, 而且其在跟踪时很依赖目标的语义信息, 这导致基于孪生网络的单目标跟踪算法在面对具有相似语义信息的干扰物时会跟踪失败. 为了解决这个问题, 提出了一种异步相关响应的计算模型, 并提出一种高效利用不同帧间目标语义信息的方法. 在此基础上, 提出了一种新的具有判别性的跟踪算法. 同时为了解决判别模型使用一阶优化算法收敛慢的问题, 使用近似二阶优化的方法更新判别模型. 为验证所提算法的有效性, 分别在Got-10k、TC128、OTB和VOT2018 数据集上做了对比实验, 实验结果表明, 该方法可以明显地改进基准算法的性能.Abstract: The existing single target object tracking algorithms based on the siamese network can achieve very high tracking performance, but these trackers can not update online, and they heavily rely on the semantic information of the target in tracking. It caused the trackers, which based on the siamese network, fail when facing the disruptor who has similar semantic information. To address this issue, this paper proposes an asynchronous correlation response calculation model and an efficient method of using the target＇s semantic information in different frames. Based on this, a new discriminative siamese network-based tracker is proposed. To address the convergence speed issue in the traditional first-order optimization algorithm, an approximate second-order optimization method is introduced to update the discriminant model online. To evaluate the effectiveness of the proposed method, comparison experiments on Got-10k, TC128, OTB, and VOT2018 between the proposed tracker and other lastest state-of-the-art trackers are adopted. The experimental results demonstrate that the proposed method can significantly improve the performance of the baseline.
-
Key words:
- Siamese network /
- semantic information /
- asynchronous correlation /
- discriminative /
- update online
-
图 2 本文算法与其他先进跟踪器在Got-10k上的对比情况
Fig. 2 Comparison between the proposed method with other advanced trackers on Got-10k
图 4 本文算法在TC128 上的精度−成功率对比实验结果
Fig. 4 The accuracy-success rate comparison experiment results of the proposed algorithm on TC128
图 5 本文算法在OTB2015上的精度−成功率对比实验结果
Fig. 5 The accuracy-success rate comparison experiment results of the proposed algorithm on OTB2015
图 6 OTB50中6个序列的响应对比结果
Fig. 6 The response comparisons of 6 different sequences on OTB50
图 8 在VOT2018序列的不同情景下精度−鲁棒性对比情况
Fig. 8 Comparison of accuracy robustness performance under different attributes on VOT2018
图 9 跟踪器在VOT2018基准模式下的期望重叠率性能对比
Fig. 9 Trackers＇expected overlap performance comparisons on VOT2018
图 10 在VOT2018的非监督模式下的EOA对比曲线
Fig. 10 EOA comparison curve of unsupervisized training on VOT2018
图 12 在VOT2018的实时性能对比下不同跟踪器的期望重叠率性能排名情况对比
Fig. 12 Ranking of different trackers＇expected overlap ratio in realtime on VOT2018
表 1 本文方法与基准算法的消融实验
Table 1 Ablation studies between the proposedalgorithm and baseline
算法 AO $ {\rm SR}_{0.5} $ $ {\rm SR}_{0.75} $ FPS Baseline 0.445 0.539 0.208 21.95 Baseline + AC 0.445 0.539 0.211 20.03 Baseline + AC + S 0.447 0.542 0.211 19.63 Baseline + AC + S + $D^{m\;=\;3}_{ {KL} }$ 0.442 0.537 0.209 18.72 Baseline + AC + S + $D^{m \;=\; 6}_{ KL }$ 0.457 0.553 0.215 18.60 Baseline + AC + S + $D^{m\;=\;9}_{ KL }$ 0.440 0.532 0.211 18.49 
下载: 导出CSV
表 2 OTB2013上的背景干扰、形变等情景下的跟踪性能对比
Table 2 Tracking performance comparisons among trackers on OTB2013 in terms of background clustersand deformation
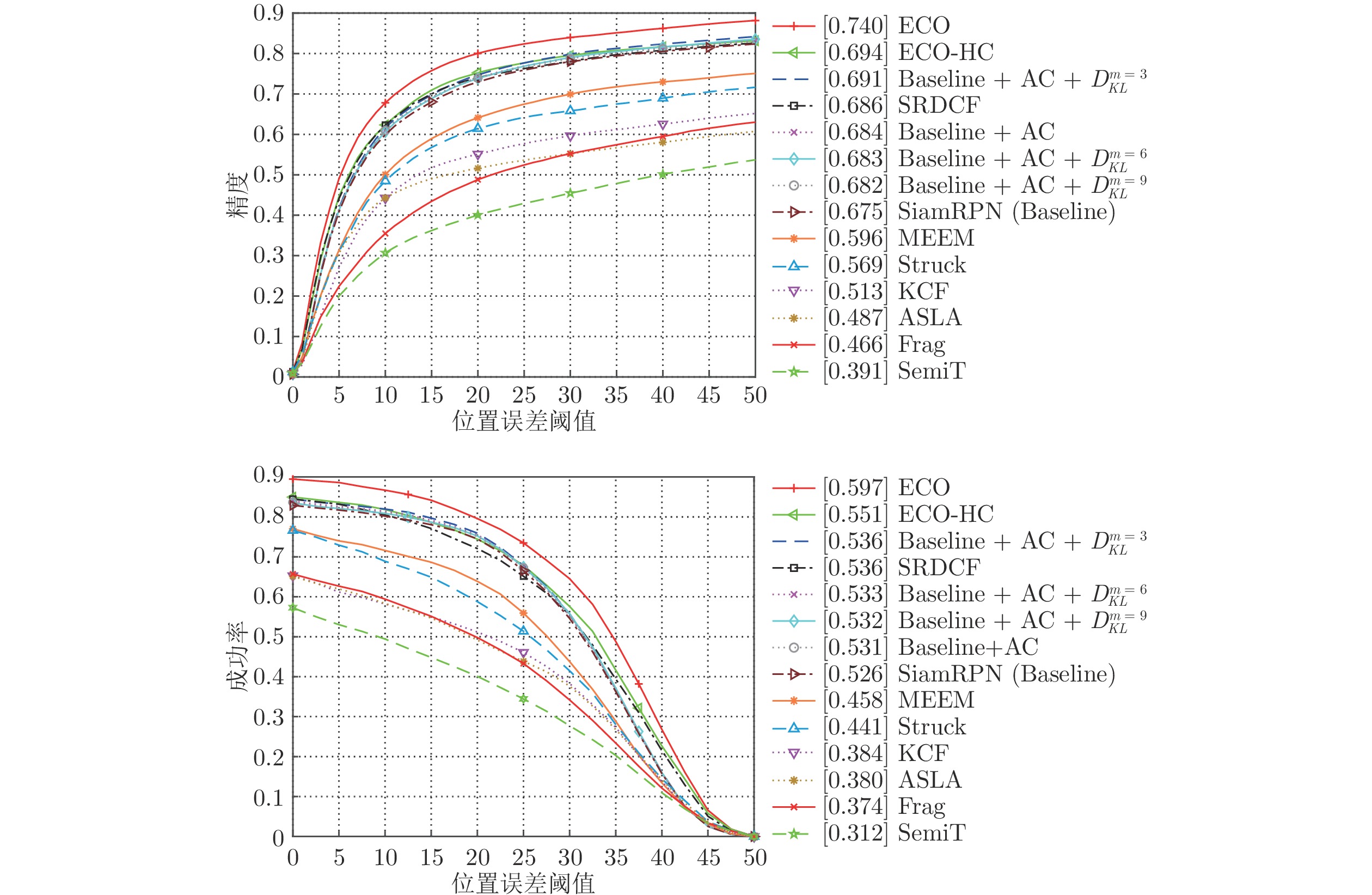
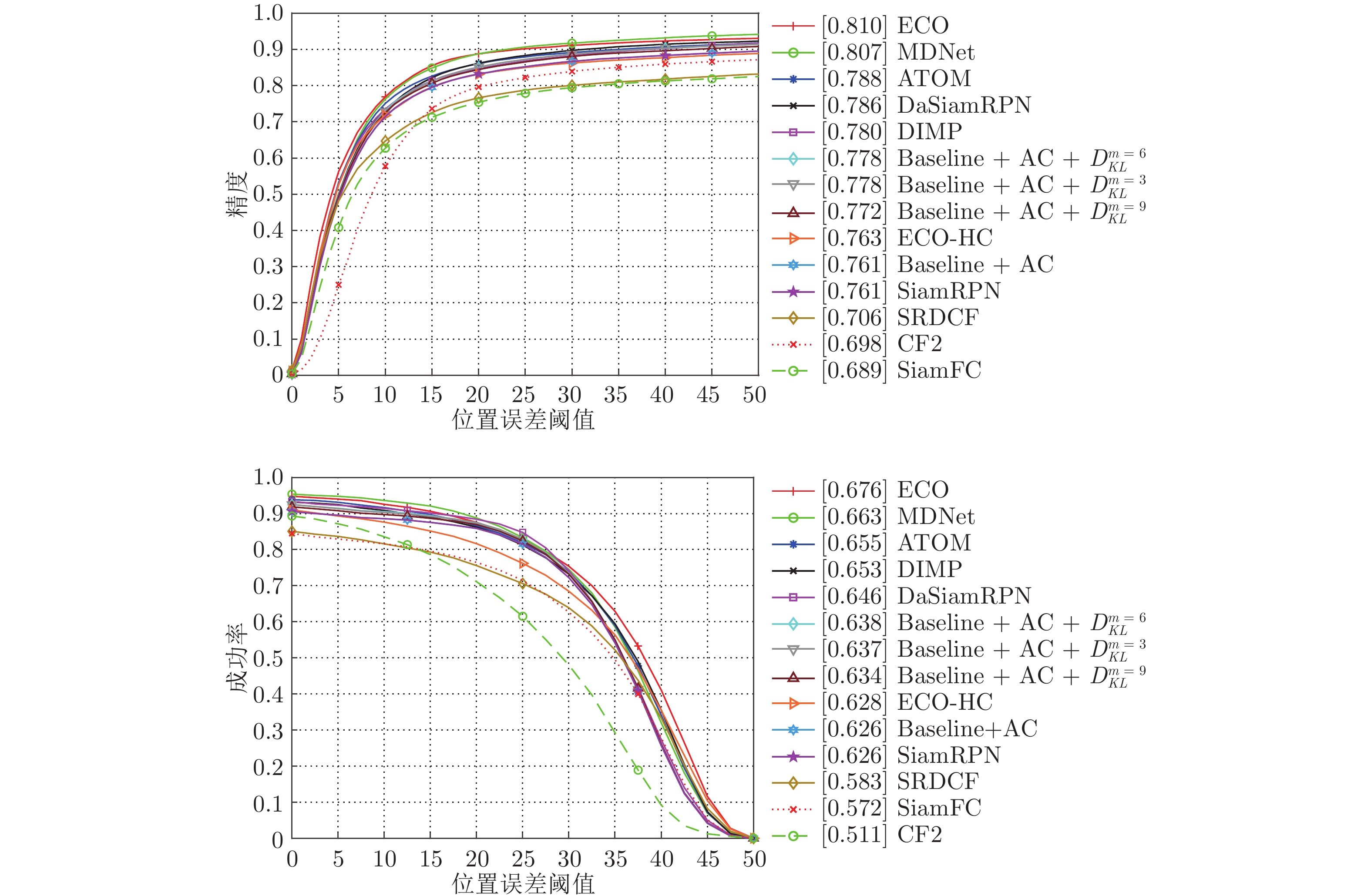
算法 背景干扰 形变 快速运动 平面内转动 成功率 精度 成功率 精度 成功率 精度 成功 精度 ECO-HC 0.700 0.559 0.567 0.719 0.570 0.697 0.517 0.648 ECO 0.776 0.619 0.613 0.772 0.655 0.783 0.630 0.764 ATOM 0.733 0.598 0.623 0.771 0.595 0.709 0.579 0.714 DIMP 0.749 0.607 0.602 0.740 0.618 0.739 0.561 0.685 MDNet 0.777 0.621 0.620 0.780 0.652 0.796 0.658 0.822 SiamFC 0.605 0.494 0.487 0.608 0.509 0.618 0.483 0.583 DaSiamRPN 0.728 0.592 0.609 0.761 0.565 0.702 0.625 0.780 SiamRPN (Baseline) 0.605 0.745 0.591 0.724 0.589 0.724 0.627 0.770 Baseline + AC 0.605 0.745 0.591 0.724 0.589 0.724 0.627 0.770 Baseline + AC + ${ D}_{ { {KL} } }^{ { {m} } \;=\; 3}$ 0.599 0.741 0.603 0.749 0.645 0.797 0.651 0.808 Baseline + AC + ${ D}_{ { {KL} } }^{ { {m} } \;=\; 6}$ 0.592 0.733 0.597 0.742 0.636 0.787 0.650 0.807 Baseline + AC + ${ D}_{ { {KL} } }^{ { {m} } \;=\; 9}$ 0.598 0.736 0.586 0.725 0.587 0.723 0.654 0.809
下载: 导出CSV
表 3 OTB2013上的光照变化、低分辨率等情景下的跟踪性能对比
Table 3 Tracking performance comparisons among trackers on OTB2013 in terms of illumination changeand low resolution
算法 光照变化 低分辨率 运动模糊 遮挡 成功率 精度 成功率 精度 成功率 精度 成功率 精度 ECO-HC 0.556 0.690 0.536 0.619 0.566 0.685 0.586 0.749 ECO 0.616 0.766 0.569 0.677 0.659 0.786 0.636 0.800 ATOM 0.604 0.749 0.554 0.654 0.529 0.665 0.617 0.762 DIMP 0.606 0.749 0.485 0.571 0.564 0.695 0.610 0.750 MDNet 0.619 0.780 0.644 0.804 0.662 0.813 0.623 0.777 SiamFC 0.479 0.593 0.499 0.600 0.485 0.617 0.512 0.635 DaSiamRPN 0.589 0.736 0.490 0.618 0.533 0.688 0.583 0.726 SiamRPN (Baseline) 0.585 0.723 0.519 0.653 0.532 0.684 0.586 0.726 Baseline + AC 0.585 0.723 0.519 0.653 0.532 0.684 0.586 0.726 Baseline + AC + ${ D}_{ {{KL} } }^{ {{m} } = 3}$ 0.600 0.749 0.554 0.697 0.610 0.785 0.593 0.740 Baseline + AC + ${ D}_{ {{KL} } }^{ {{m} } = 6}$ 0.592 0.741 0.546 0.688 0.596 0.770 0.586 0.732 Baseline + AC + ${ D}_{ {{KL} } }^{ {{m} } = 9}$ 0.581 0.724 0.549 0.689 0.533 0.687 0.576 0.716
下载: 导出CSV
表 4 OTB2013上的平面外旋转、视野外等情景下的跟踪性能对比
Table 4 Tracking performance comparisons among trackers on OTB2013 in terms of out-of-plane rotationand out of view
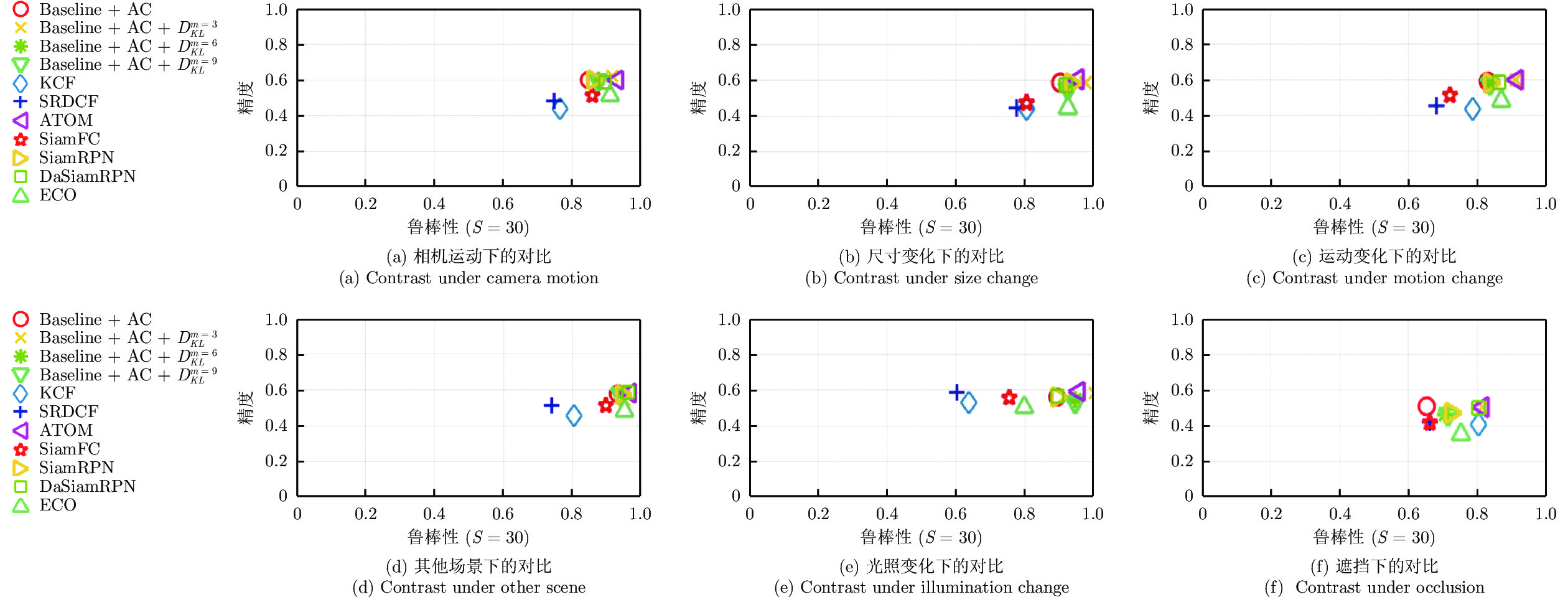
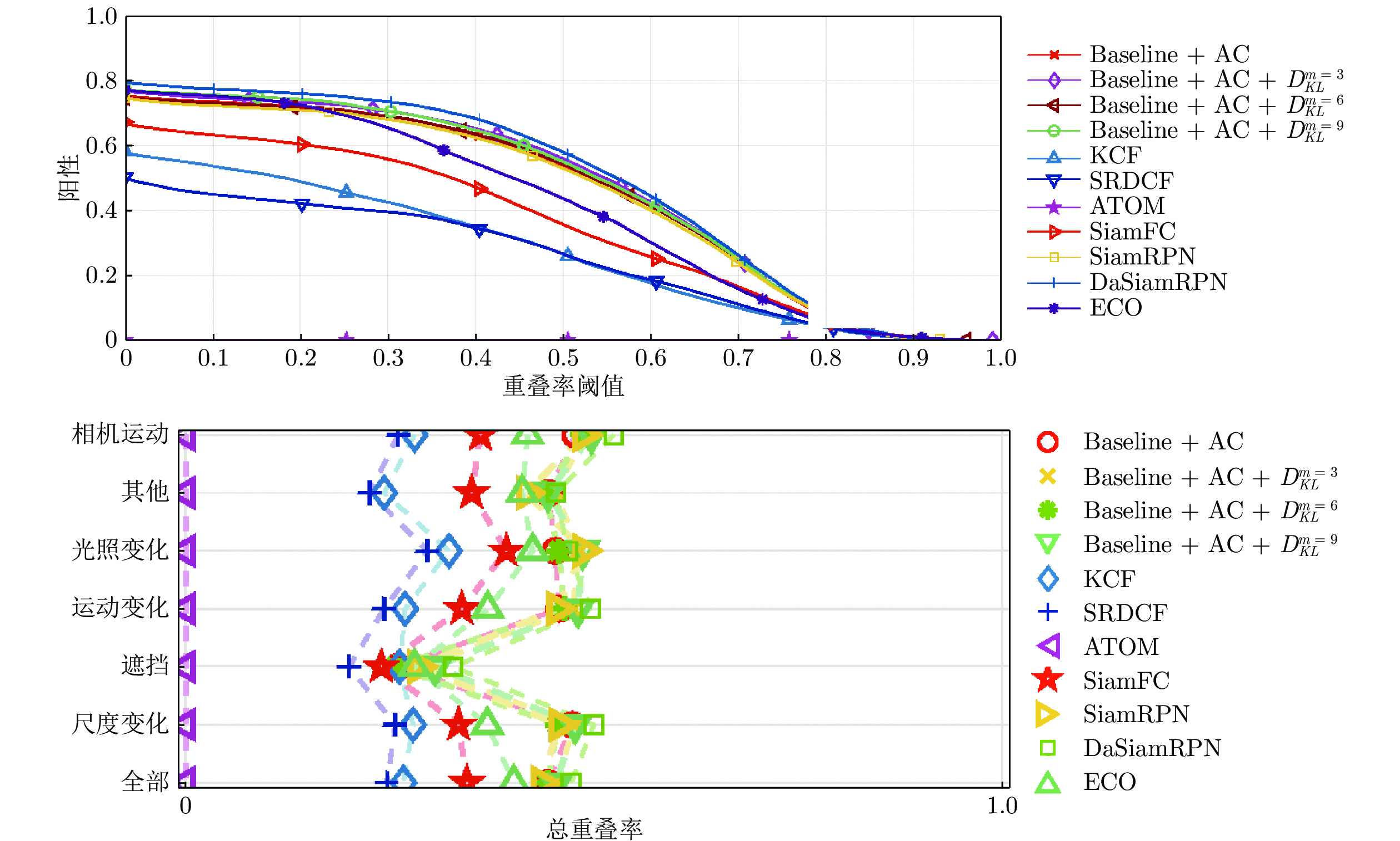
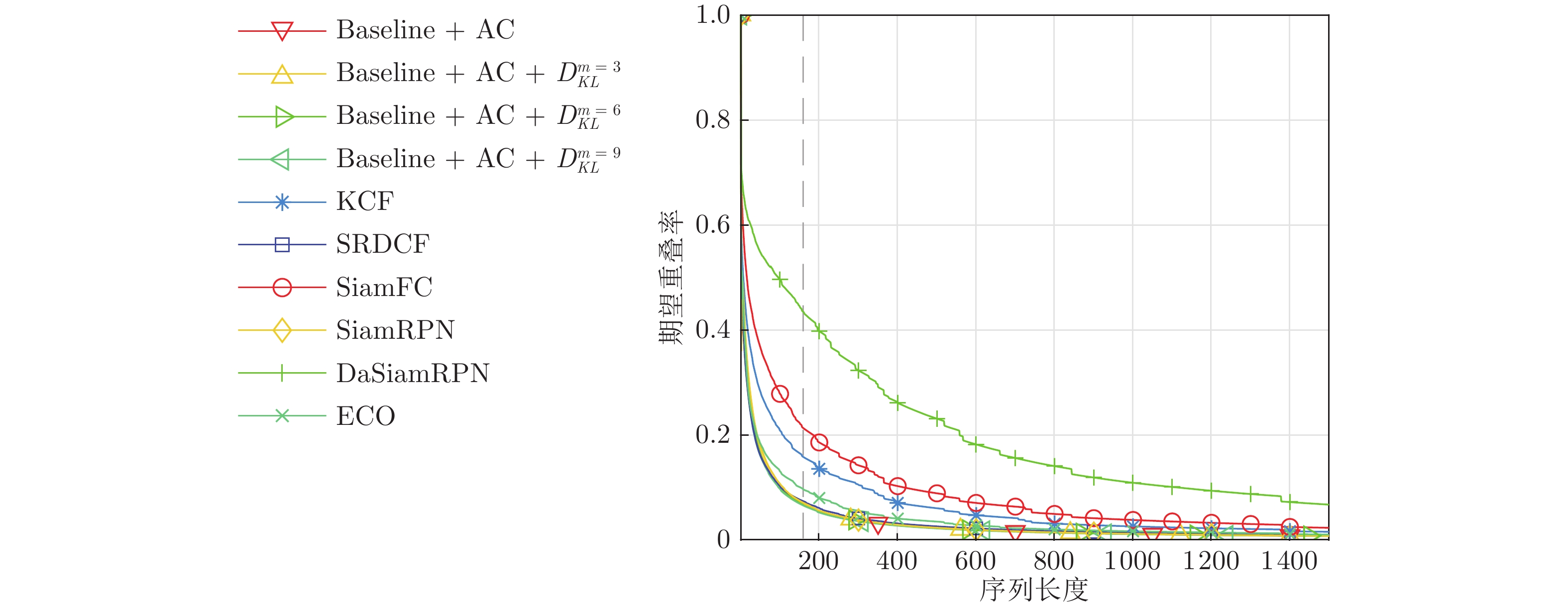
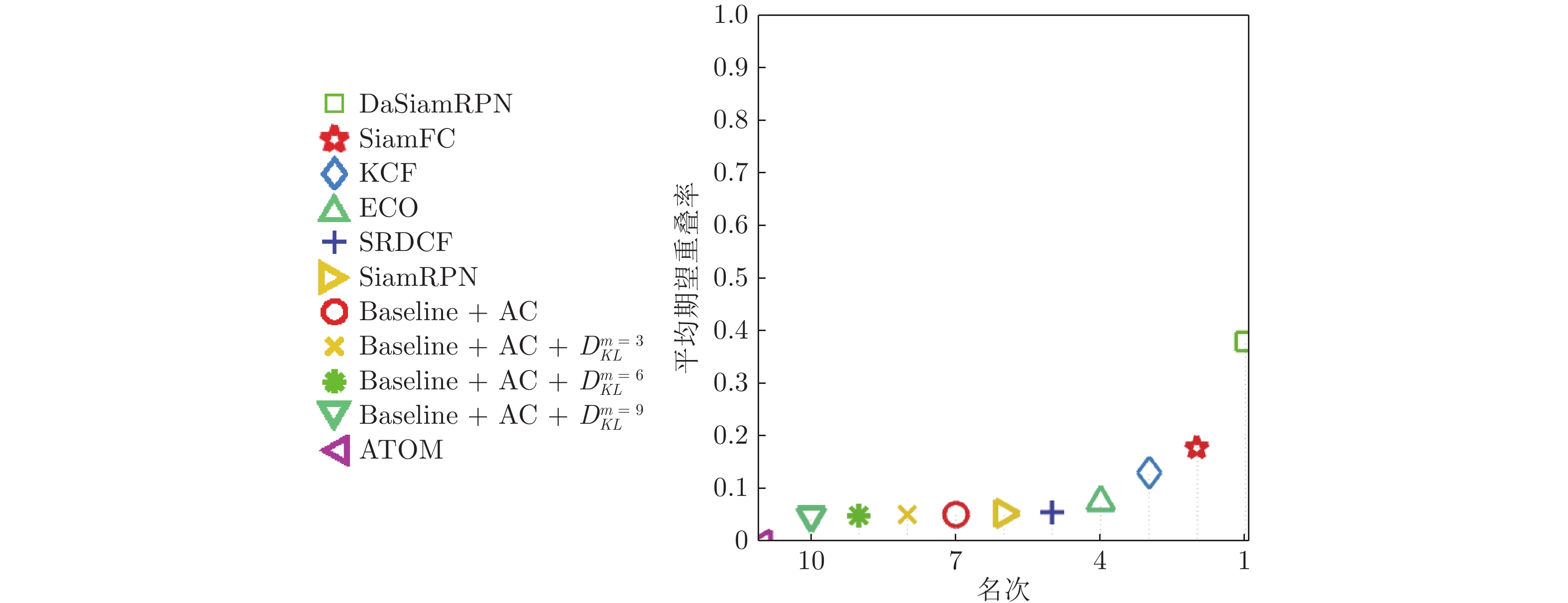
算法 平面外旋转 视野外 尺度变化 成功率 精度 成功率 精度 成功率 精度 ECO-HC 0.563 0.718 0.549 0.763 0.587 0.740 ECO 0.628 0.787 0.733 0.827 0.651 0.793 ATOM 0.607 0.751 0.522 0.563 0.654 0.792 DIMP 0.596 0.737 0.549 0.593 0.636 0.767 MDNet 0.628 0.787 0.698 0.769 0.675 0.842 SiamFC 0.500 0.620 0.574 0.642 0.542 0.665 DaSiamRPN 0.599 0.750 0.570 0.633 0.587 0.740 SiamRPN (Baseline) 0.598 0.736 0.658 0.725 0.608 0.751 Baseline + AC 0.598 0.736 0.658 0.725 0.608 0.751 Baseline + AC + ${ D}_{ { {KL} } }^{ { {m} } \;=\; 3}$ 0.611 0.760 0.702 0.778 0.656 0.819 Baseline + AC + ${ D}_{ {{KL} } }^{ {{m} } = 6}$ 0.604 0.752 0.659 0.733 0.631 0.791 Baseline + AC + ${ D}_{ {{KL} } }^{ {{m} } = 9}$ 0.597 0.740 0.660 0.735 0.603 0.755
下载: 导出CSV
表 5 VOT2018 上的实验结果
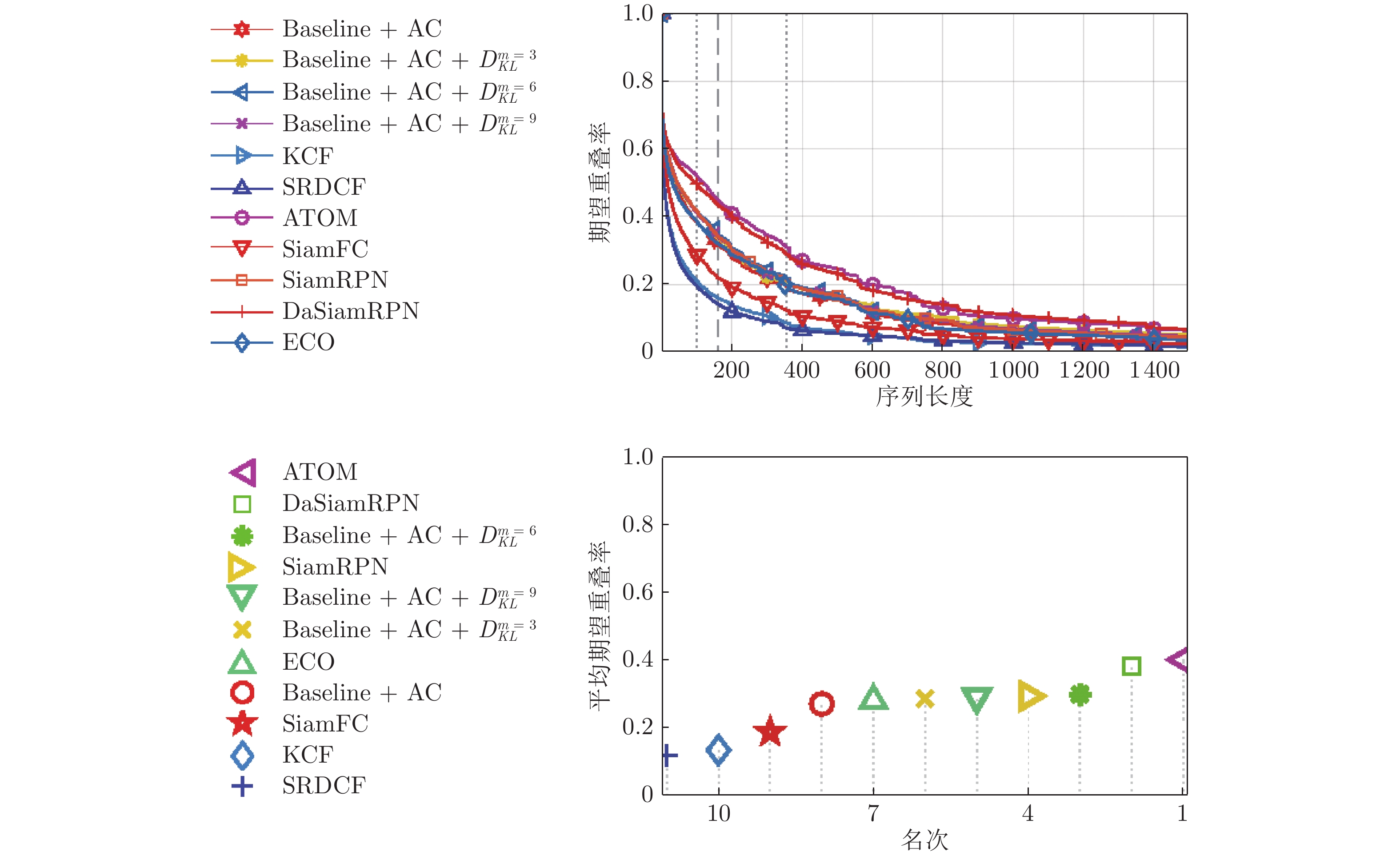
Table 5 Experimental results on VOT2018
算法 Baseline 非监督 实时性能 精度−鲁棒性 失败率 EAO FPS AO FPS EAO KCF 0.4441 50.0994 0.1349 60.0053 0.2667 63.9847 0.1336 SRDCF 0.4801 64.1136 0.1189 2.4624 0.2465 2.7379 0.0583 ECO 0.4757 17.6628 0.2804 3.7056 0.4020 4.5321 0.0775 ATOM 0.5853 12.3591 0.4011 5.2061 0 0 0 SiamFC 0.5002 34.0259 0.188 31.889 0.3445 35.2402 0.182 DaSiamRPN 0.5779 17.6608 0.3826 58.854 0.4722 64.4143 0.3826 SiamRPN (Baseline) 0.5746 23.5694 0.2941 14.3760 0.4355 14.4187 0.0559 Baseline + AC 0.5825 27.0794 0.2710 13.7907 0.4431 13.8772 0.0539 Baseline + AC + ${ D}_{ { {KL} } }^{ { {m} } \;=\; 3}$ 0.5789 14.8312 0.2865 13.6035 0.4537 13.4039 0.0536 Baseline + AC + ${ D}_{ { {KL} } }^{ { {m} } \;=\; 6}$ 0.5722 22.6765 0.2992 13.5359 0.4430 12.4383 0.0531 Baseline + AC + ${ D}_{ { {KL} } }^{ { {m} } \;=\; 9}$ 0.5699 22.9148 0.2927 13.5046 0.4539 12.1159 0.0519
下载: 导出CSV
-
[1] 刘巧元, 王玉茹, 张金玲, 殷明浩. 基于相关滤波器的视频跟踪方法研究进展. 自动化学报, 2019, 45(2): 265-275Liu Qiao-Yuan, Wang Yu-Ru, Zhang Jin-Ling, Yin Ming-Hao. Research progress of visual tracking methods based on correlation filter. Acta Automatica Sinica, 2019, 45(2): 265-275 [2] 刘畅, 赵巍, 刘鹏, 唐降龙. 目标跟踪中辅助目标的选择、跟踪与更新. 自动化学报, 2018, 44(7): 1195-1211Liu Chang, Zhao Wei, Liu Peng, Tang Xiang-Long. Auxiliary objects selecting, tracking and updating in target tracking. Acta Automatica Sinica, 2018, 44(7): 1195-1211 [3] 蔺海峰, 马宇峰, 宋涛. 基于SIFT特征目标跟踪算法研究. 自动化学报, 2010, 36(8): 1204-1208 doi: 10.3724/SP.J.1004.2010.01204Lin Hai-Feng, Ma Yu-Feng, Song Tao. Research on object tracking algorithm based on SIFT. Acta Automatica Sinica, 2010, 36(8): 1204-1208 doi: 10.3724/SP.J.1004.2010.01204 [4] Held D, Thrun S, Savarese S. Learning to track at 100 FPS with deep regression networks. In: Proceedings of the European Conference on Computer Vision. Amsterdam, Netherlands: 2016. 749−765 [5] Bertinetto L, Valmadre J, Henriques J F, Vedaldi A, Torr P H S. Fully-convolutional siamese networks for object tracking. In: Proceedings of the European Conference on Computer Vision. Amsterdam, Netherlands: 2016. 850−865 [6] Li B, Yan J J, Wu W, Zhu Z, Hu X L. High performance visual tracking with Siamese region proposal network. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 8971−8980 [7] Zhu Z, Wang Q, Li B, Wu W, Yan J J, Hu W M. Distractor-aware Siamese networks for visual object tracking. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: 2018. 103−119 [8] Li B, Wu W, Wang Q, Zhang F Y, Xing J L, Yan J J. SiamRPN++: Evolution of Siamese visual tracking with very deep networks. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA: IEEE, 2019. 4277−4286 [9] Nam H, Han B. Learning multi-domain convolutional neural networks for visual tracking. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Veg-as, USA: IEEE, 2016. 4293−4302 [10] Henriques J F, Caseiro R, Martins P, Batista J. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596 doi: 10.1109/TPAMI.2014.2345390 [11] Danelljan M, Hager G, Khan F S, Felsberg M. Learning spatially regularized correlation filters for visual tracking. In: Proceedings of the IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015. 4310−4318 [12] Ma C, Huang J B, Yang X K, Yang M H. Hierarchical convolutional features for visual tracking. In: Proceedings of the IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015. 3074−3082 [13] Wang N Y, Yeung D Y. Learning a deep compact image representation for visual tracking. In: Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, USA: 2013. 809−817 [14] Danelljan M, Robinson A, Khan F S, Felsberg M. Beyond correlation filters: Learning continuous convolution operators for visual tracking. In: Proceedings of the 14th European Conference on Computer Vision. Amsterdam, Netherlands: 2016. 472− 488 [15] Danelljan M, Bhat G, Khan F S, Felsberg M. ECO: Efficient convolution operators for tracking. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolul, USA: IEEE, 2017. 6931−6939 [16] Bolme D S, Beveridge J R, Draper B A, Lui Y M. Visual object tracking using adaptive correlation filters. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, USA: 2010. 2544−2550 [17] Ren S Q, He K M, Girshick R, Sun J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149 doi: 10.1109/TPAMI.2016.2577031 [18] Danelljan M, Bhat G, Khan F S, Felsberg M. ATOM: Accurate tracking by overlap maximization. In: Proceedings of the IEEE/ CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA: IEEE, 2019. 4655−4664 [19] Jiang B R, Luo R X, Mao J Y, Xiao T T, Jiang Y N. Acquisition of localization confidence for accurate object detection. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: 2018. 816−832 [20] Wang Q, Zhang L, Bertinetto L, Hu W M, Torr P H S. Fast online object tracking and segmentation: A unifying approach. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA: IEEE, 2019. 1328− 1338 [21] Huang L H, Zhao X, Huang K Q. GOT-10k: A large high-diversity benchmark for generic object tracking in the wild. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(5): 1562-1577 doi: 10.1109/TPAMI.2019.2957464 [22] Liang P P, Blasch E, Ling H B. Encoding color information for visual tracking: Algorithms and benchmark. IEEE Transactions on Image Processing, 2015, 24(12): 5630-5644 doi: 10.1109/TIP.2015.2482905 [23] Wu Y, Lim J, Yang M H. Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848 doi: 10.1109/TPAMI.2014.2388226 [24] Kristan M, Matas J, Leonardis A, Vojir T, Pflugfelder R, Fernandez G, et al. A novel performance evaluation methodology for single-target trackers. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(11): 2137-2155 doi: 10.1109/TPAMI.2016.2516982 [25] Ramasubramanian K, Singh A. Machine Learning Using R: With Time Series and Industry-Based Use Cases in R. Berkeley: Springer, 2017. 219−424 [26] Pearlmutter B A. Fast exact multiplication by the Hessian. Neural Computation, 1994, 6(1): 147-160 doi: 10.1162/neco.1994.6.1.147 [27] Zhang J M, Ma S G, Sclaroff S. MEEM: Robust tracking via multiple experts using entropy minimization. In: Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland: 2014. 188−203 [28] Hare S, Golodetz S, Saffari A, Vineet V, Cheng M M, Hicks S L, et al. Struck: Structured output tracking with kernels. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(10): 2096-2109 doi: 10.1109/TPAMI.2015.2509974 [29] Jia X, Lu H C, Yang M H. Visual tracking via adaptive structural local sparse appearance model. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Pro-vidence, USA: IEEE, 2012. 1822−1829 [30] Adam A, Rivlin E, Shimshoni I. Robust fragments-based tracking using the integral histogram. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York, USA: IEEE, 2006. 798−805 [31] Bhat G, Danelljan M, Van Gool L, Timofte R. Learning discriminative model prediction for tracking. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. Seo-ul, South Korea: IEEE, 2019. 6181−6190 -
计量
- 文章访问数: 1713
- HTML全文浏览量: 259
- PDF下载量: 221
- 被引次数: 0
