深度神经模糊系统算法及其回归应用

赵文迪; 陈德旺; 卓永强; 黄允浒

doi:10.16383/j.aas.c200100

深度神经模糊系统算法及其回归应用

doi: 10.16383/j.aas.c200100

赵文迪^{1, 2,},
陈德旺^{1, 2,},
卓永强^3,,
黄允浒^{1, 2,}

1.
福州大学数学与计算机科学学院福州 350108
2.
福州大学智慧地铁福建省高校重点实验室福州 350108
3.
广州航海学院海运学院广州 510725

基金项目: 国家自然科学基金面上项目(61976055), 智慧地铁福建省高校重点实验室(53001703, 50013203)资助

详细信息

作者简介:
赵文迪：福州大学数学与计算机科学学院, 智慧地铁福建省高校重点实验室科研助理. 主要研究方向为深度学习, 模糊系统.E-mail: wdzhao@aliyun.com

陈德旺：福建省“闽江学者”特聘教授, 福州大学数学与计算机学院教授. 主要研究方向为深度学习, 模糊系统和智能交通系统. 本文通信作者.E-mail: dwchen@fzu.edu.cn

卓永强：广州海航学院海运学院教授. 主要研究方向为船舶运动智能控制, 海上交通系统工程和模糊系统.E-mail: zhuoyq@aliyun.com

黄允浒：福州大学数学与计算机科学学院博士研究生. 主要研究方向为机器学习, 模糊系统与智能交通系统.E-mail: N190310001@fzu.edu.cn

计量
- 文章访问数: 2005
- HTML全文浏览量: 359
- PDF下载量: 450
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-02
- 录用日期: 2020-06-28
- 刊出日期: 2020-11-24

Deep Neural Fuzzy System Algorithm and Its Regression Application

ZHAO Wen-Di^{1, 2
,},
CHEN De-Wang^{1, 2
,},
ZHUO Yong-Qiang^3
,,
HUANG Yun-Hu^{1, 2
,}

1.
College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350108
2.
Key laboratory of Intelligent Metro of Universities in Fujian Province, Fuzhou University, Fuzhou 350108
3.
College of Maritime, Guangzhou Maritime University, Guangzhou 510725

Funds: Supported by General Program of National Natural Science Foundation of China (61976055), Key laboratory of Intelligent Metro of Universities in Fujian Province (53001703, 50013203)

摘要

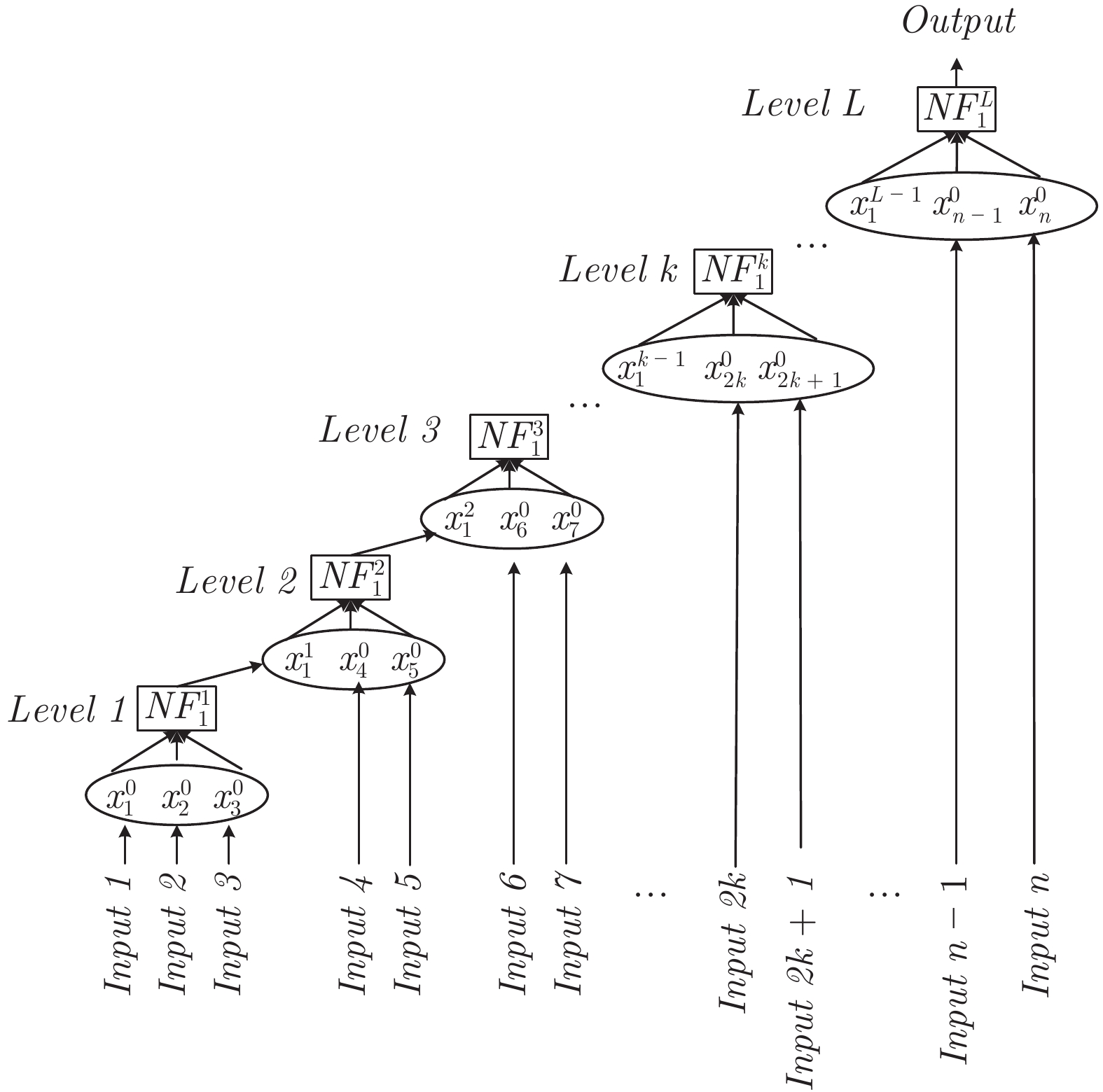
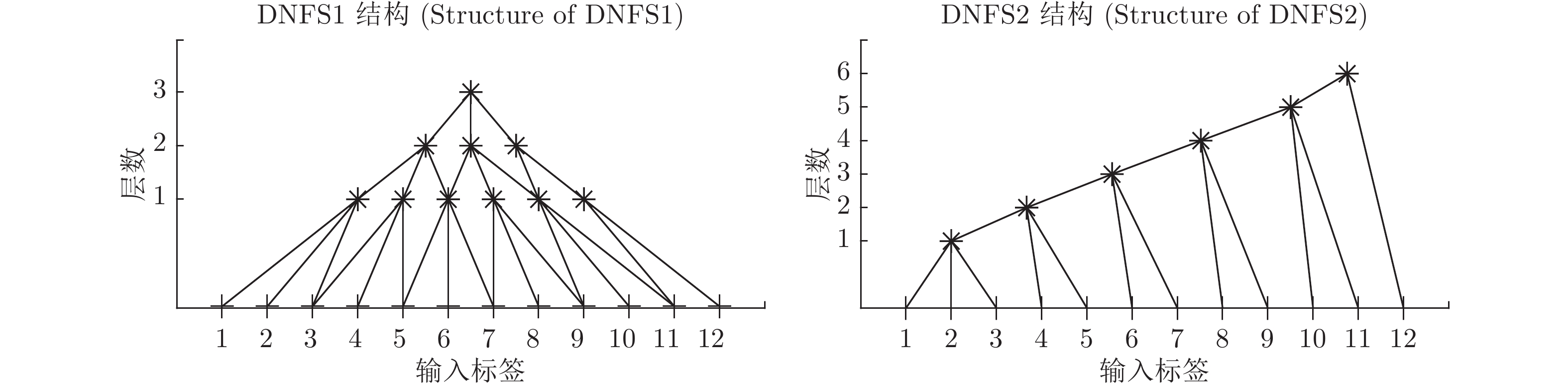
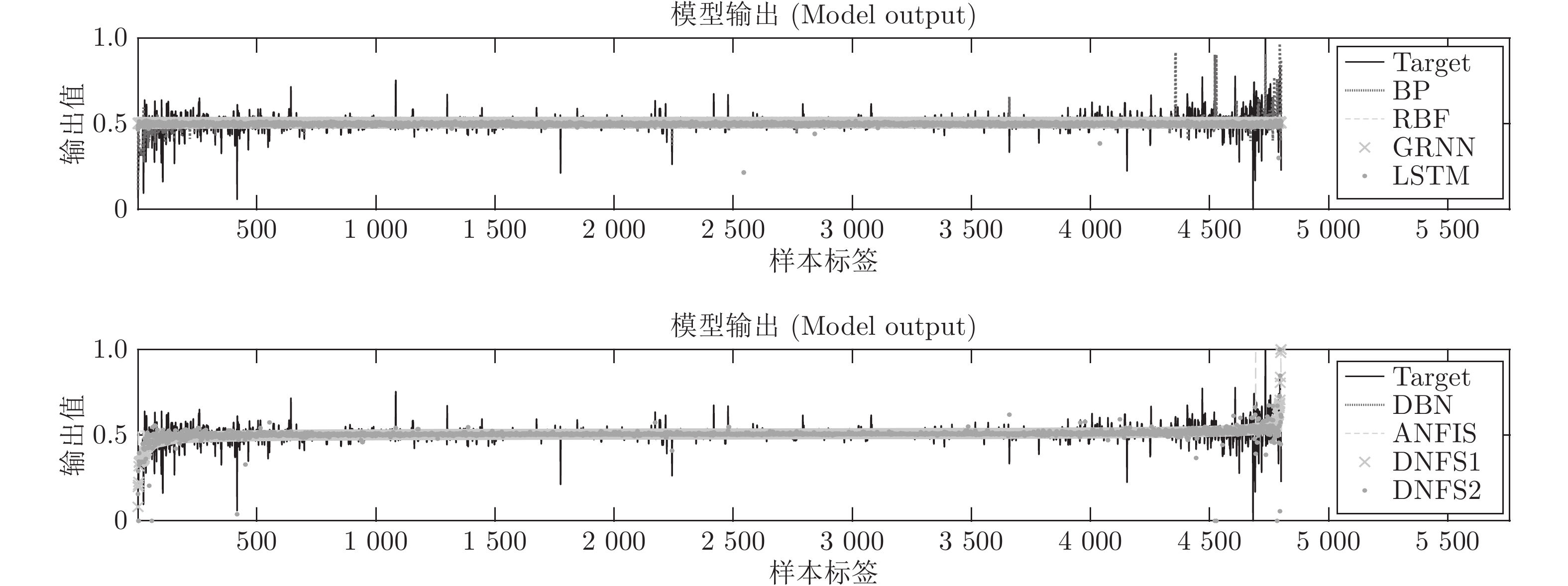
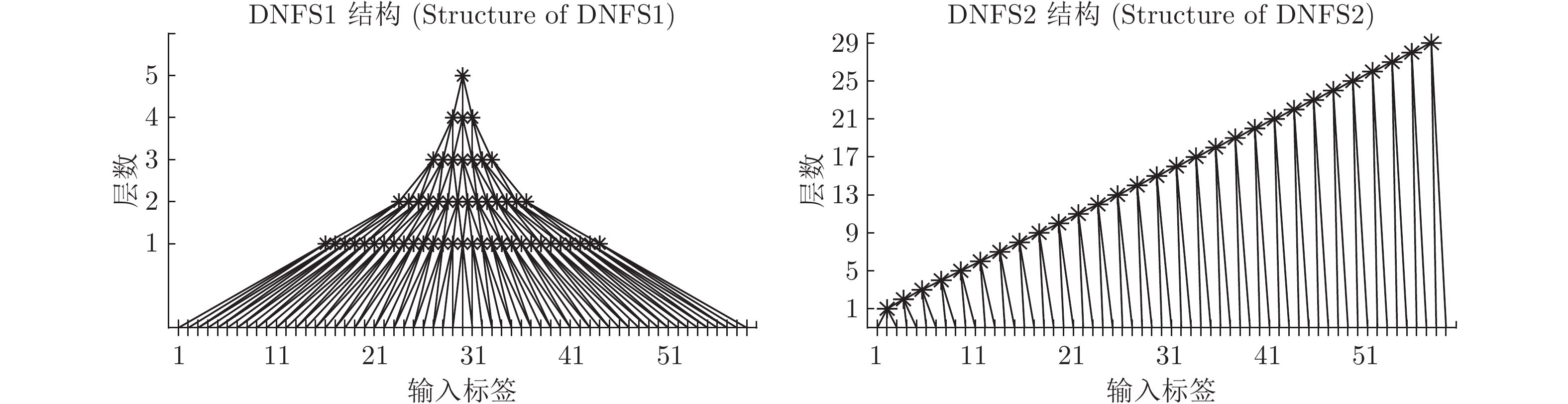
摘要: 深度神经网络是人工智能的热点, 可以很好处理高维大数据, 却有可解释性差的不足. 通过IF-THEN规则构建的模糊系统, 具有可解释性强的优点, 但在处理高维大数据时会遇到“维数灾难”问题. 本文提出一种基于ANFIS (Adaptive network based fuzzy inference system)的深度神经模糊系统(Deep neural fuzzy system, DNFS)及两种基于分块和分层的启发式实现算法: DNFS1和DNFS2. 通过四个面向回归应用的数据集的测试, 我们发现: 1)采用分块、分层学习的DNFS在准确度与可解释性上优于BP、RBF、GRNN等传统浅层神经网络算法, 也优于LSTM和DBN等深度神经网络算法; 2)在低维问题中, DNFS1具有一定优势; 3)在面对高维问题时, DNFS2表现更为突出. 本文的研究结果表明DNFS是一种新型深度学习方法, 不仅可解释性好, 而且能有效解决处理高维数据时模糊规则数目爆炸的问题, 具有很好的发展前景.
- 高维大数据 /
- 深度神经模糊系统 /
- 自适应神经模糊系统 /
- 分层结构 /
- 可解释性
Abstract: Deep neural network is a hot spot of artificial intelligence, which can deal with high-dimensional big data well, but has the disadvantage of poor interpretability. The fuzzy system constructed by if-then rules has the advantage of strong interpretability, but it will encounter the problem of “the curse of dimension” when dealing with high dimension big data. This paper presents a DNFS (Deep neural fuzzy system) based on ANFIS (Adaptive network based fuzzy inference system) and two heuristic algorithms based on block and layer: DNFS1 and DNFS2. Through the testing of four regression-oriented data sets, we found: 1) DNFS with block and layer learning is superior to BP, RBF, GRNN and other traditional shallow neural network algorithms in accuracy and interpretability, as well as LSTM, DBN and other deep neural network algorithms; 2) In low dimensional problems, DNFS1 has certain advantages; 3) In the face of high dimensional problems, DNFS2 is more prominent. The results of this paper show that DNFS is a new deep learning method, which not only has good interpretability, but also can effectively solve the problem that the number of fuzzy rules explodes when dealing with high-dimensional data, and has a good development prospect.
- High-dimensional big data /
- deep neural fuzzy system /
- adptive network based fuzzy inference system /
- hierarchical structure /
- interpretability

HTML全文

图 1 DNFS1基本结构

Fig. 1 Basic structure of DNFS1

下载: 全尺寸图片幻灯片

图 2 DNFS2基本结构

Fig. 2 Basic structure of DNFS2

下载: 全尺寸图片幻灯片

图 3 DNFS算法流程

Fig. 3 DNFS algorithm flow

下载: 全尺寸图片幻灯片

图 4 SMW数据集深度结构

Fig. 4 The deep structure of SMW data set

下载: 全尺寸图片幻灯片

图 5 SMW测试集预测效果

Fig. 5 Prediction effect of SMW test set

下载: 全尺寸图片幻灯片

图 6 ONP数据集深度结构

Fig. 6 The deep structure of ONP data set

下载: 全尺寸图片幻灯片

图 7 ONP测试集预测效果

Fig. 7 Prediction effect of ONP test set

下载: 全尺寸图片幻灯片

图 8 SUP数据集深度结构

Fig. 8 The deep structure of SUP data set

下载: 全尺寸图片幻灯片

图 9 SUP测试集预测效果

Fig. 9 Prediction effect of SUP test set

下载: 全尺寸图片幻灯片

图 10 BF测试集预测效果

Fig. 10 Prediction effect of BF test set

下载: 全尺寸图片幻灯片

表 1 实验数据集

Table 1 Experimental data set

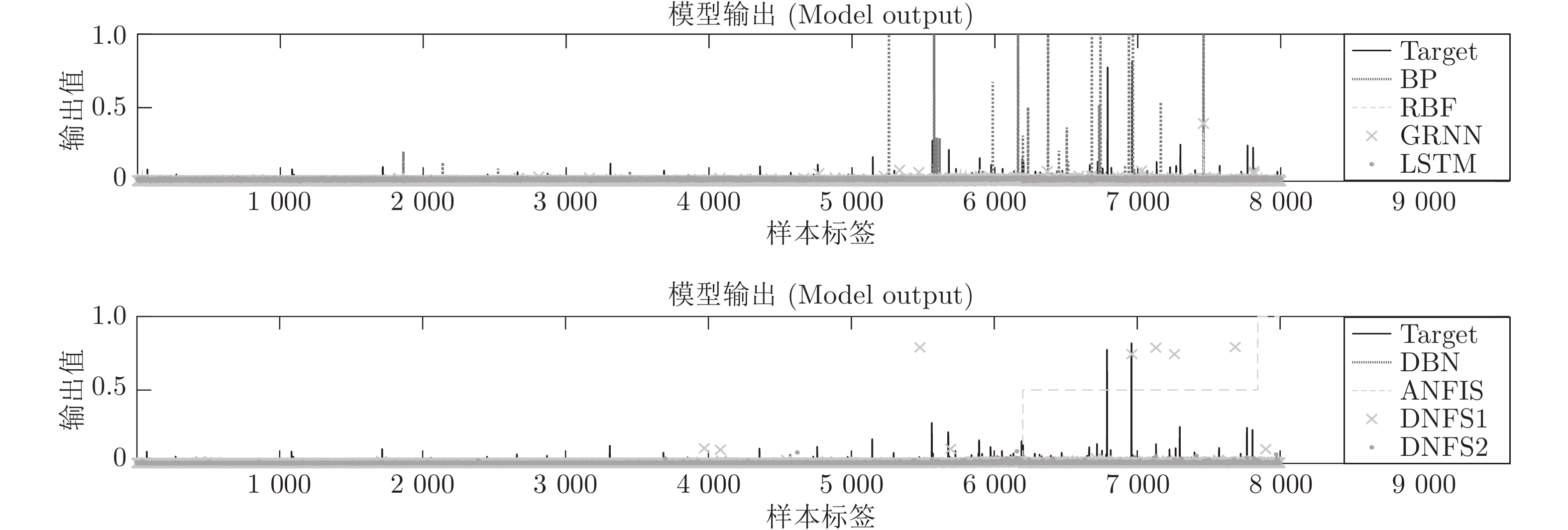
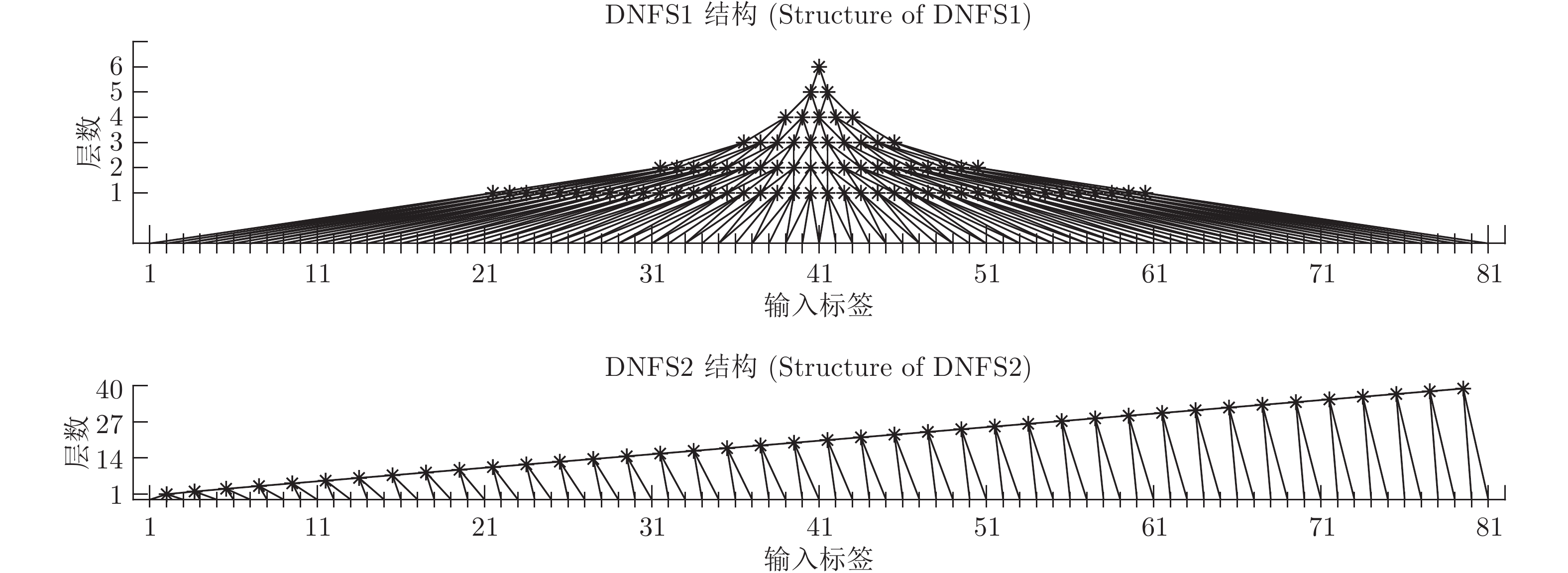
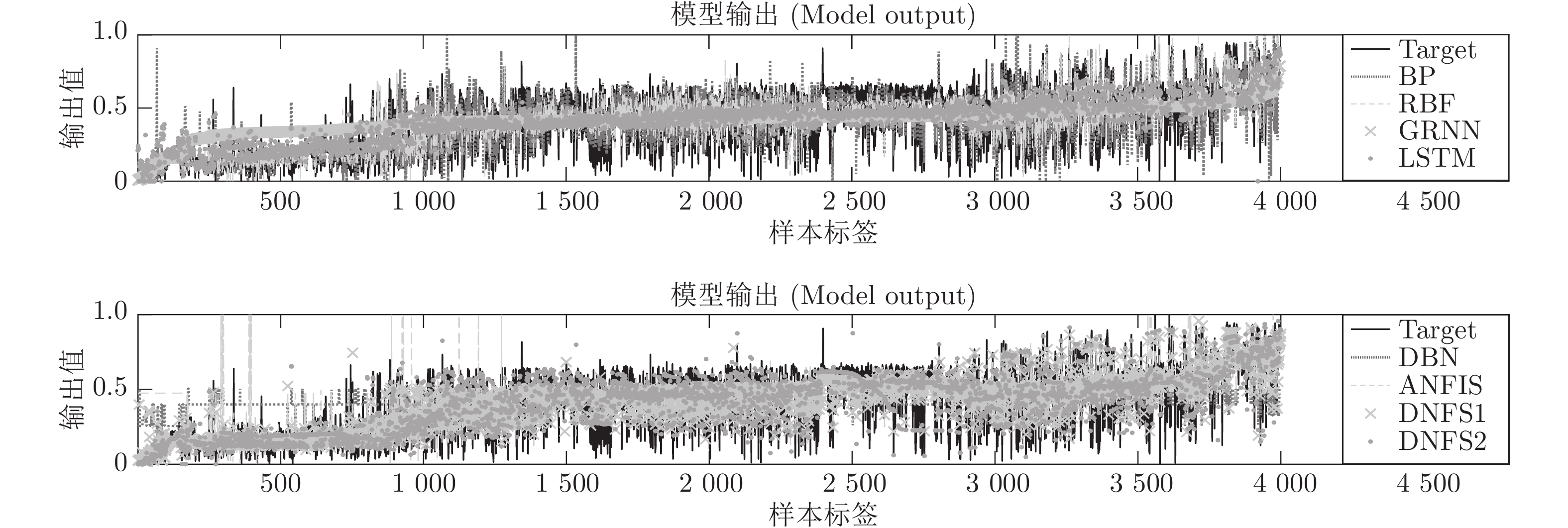
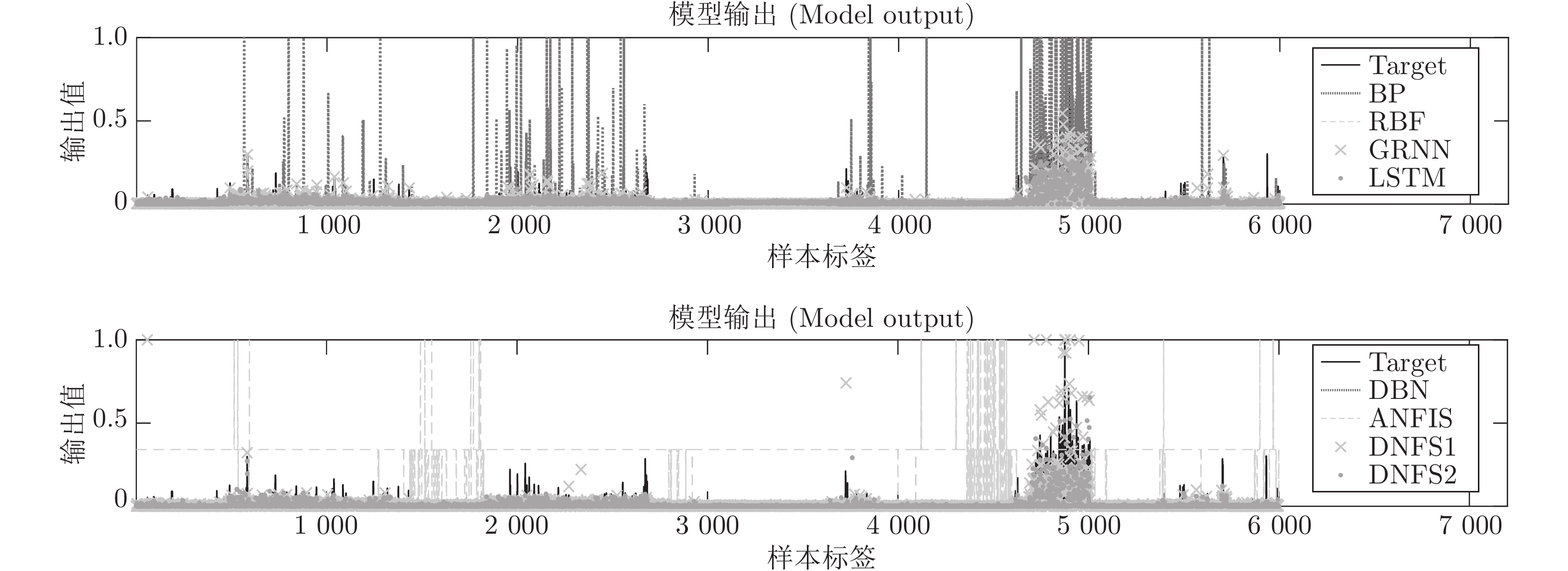
项目编号	数据集	输入维度	输出维度	样本数	DNFS1总层数	DNFS2总层数
1	Smartwatch_sens (SMW)	12	1	12000	15	30
2	Online News Popularity (ONP)	59	1	20000	25	145
3	Superconductivty (SUP)	81	1	10000	30	200
4	BlogFeedback (BF)	271	1	15000	40	675

下载: 导出CSV

表 2 SMW测试集评价指标

Table 2 Evaluation index of SMW test set

	BP	RBF	GRNN	LSTM	DBN	ANFIS	DNFS1	DNFS2
STD	0.038869	0.038510	0.038441	0.039385	0.038596	0.039398	0.037643	0.040971
RMSE	0.038865	0.038506	0.038437	0.040219	0.038592	0.039397	0.037640	0.040970
MAE	0.017789	0.018355	0.017081	0.020928	0.017088	0.017965	0.016639	0.016834
SMAPE	3.5849 %	3.7368 %	3.4864 %	4.2653 %	3.4872 %	3.6510 %	3.3553 %	3.5535 %
Score	16	16	27	7	21	11	32	14

下载: 导出CSV

表 3 ONP测试集评价指标

Table 3 Evaluation index of ONP test set

	BP	RBF	GRNN	LSTM	DBN	ANFIS	DNFS1	DNFS2
STD	0.040148	0.017565	0.016941	0.016321	0.016217	0.234585	0.025012	0.016195
RMSE	0.040173	0.017567	0.016941	0.018827	0.016216	0.263966	0.025011	0.016195
MAE	0.005824	0.005347	0.004060	0.011639	0.004153	0.123609	0.004400	0.003975
SMAPE	83.1325 %	110.4412 %	77.8989 %	136.6059 %	88.0204 %	106.8444 %	78.3964 %	79.4094 %
Score	12	15	26	13	24	6	18	30

下载: 导出CSV

表 4 SUP测试集评价指标

Table 4 Evaluation index of SUP test set

	BP	RBF	GRNN	LSTM	DBN	ANFIS	DNFS1	DNFS2
STD	0.12385	0.13038	0.17493	0.15997	0.21074	0.16866	0.13415	0.12293
RMSE	0.12384	0.13038	0.17527	0.16004	0.21076	0.16972	0.13418	0.12293
MAE	0.08786	0.10038	0.14956	0.12958	0.18245	0.12657	0.10165	0.08735
SMAPE	30.1760 %	32.4668 %	43.0296 %	38.5752 %	51.2832 %	37.7120 %	31.2728 %	28.7900 %
Score	28	23	8	14	4	14	21	32

下载: 导出CSV

表 5 BF测试集评价指标

Table 5 Evaluation index of BF test set

	BP	RBF	GRNN	LSTM	DBN	ANFIS	DNFS1	DNFS2
STD	0.10900	0.04217	0.04322	0.03355	0.04457	0.09683	0.04465	0.03155
RMSE	0.10973	0.04259	0.04324	0.03398	0.04457	0.33922	0.04466	0.03156
MAE	0.02304	0.01112	0.01120	0.01409	0.01607	0.32630	0.01028	0.00859
SMAPE	54.675 %	76.842 %	81.804 %	96.684 %	102.462 %	142.341 %	64.263 %	54.162 %
Score	12	23	19	21	13	5	19	32

下载: 导出CSV

参考文献(22)

[1]	Mcclloch W S, Pitts W. A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biology, 1943, 10(5): 115−133
[2]	Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 1958, 65: 386−408 doi: 10.1037/h0042519
[3]	Minsky M L, Papert S A. Perceptrons. American Journal of Psychology, 1969, 84(3): 449−452
[4]	Hopfield J J. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences of the United States of America, 1982, 79(8): 2554−2558 doi: 10.1073/pnas.79.8.2554
[5]	Lv Y S, Chen Y Y, Zhang X Q, Duan Y J, Li N Q. Social media based transportation research: The state of the work and the networking. IEEE/CAA Journal of Automatica Sinica, 2017, 4(1): 19−26 doi: 10.1109/JAS.2017.7510316
[6]	Rumelhart, David E, Hinton, Geoffrey E, Williams, Ronald J. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533−536 doi: 10.1038/323533a0
[7]	Cortes C, Vapnik V. Support-vector networks. Machine Learning, 1995, 20(3): 273−297
[8]	Hinton, G. E. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504−507 doi: 10.1126/science.1127647
[9]	Lecun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436−444 doi: 10.1038/nature14539
[10]	Sabour S, Frosst N, Hinton G E. Dynamic routing between capsules. In: Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA. 2017. 1−11
[11]	Guha A, Ghosh S, Roy A, Chatterjee S. Epileptic seizure recognition using deep neural network. Emerging Technology in Modelling and Graphics. Springer, Singapore, 2020. 21−28
[12]	Kantz E D, Tiwari S, Watrous J D, Cheng S. Deep neural networks for classification of lc-ms spectral peaks. Analytical Chemistry, 2019, 91(19): 12407−12413. DOI: 10.1021/acs.analchem.9b02983
[13]	Liu B S, Chen X M, Han Y H, Li J J, Xu H B, Li X W. Accelerating DNN-based 3D point cloud processing for mobile computing. Science China. Information Sciences, 2019, 32(11): 36−46
[14]	Mercedes E. Paoletti. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(2): 740−754 doi: 10.1109/TGRS.2018.2860125
[15]	Yang H, Luo L, Chueng L P, Ling D, Chin F. Deep learning and its applications to natural language processing. Deep Learning: Fundamentals, Theory and Applications. Springer, Cham, 2019. 89−109
[16]	Zadeh, L.A. Fuzzy sets. Information & Control, 1965, 8(3): 338−353
[17]	Mamdani E H, Baaklini N. Prescriptive method for deriving control policy in a fuzzy-logic controller. Electronics Letters, 1975, 11(25): 625−626
[18]	Wang L X. Fuzzy systems are universal approximators. In: Proceedings of the 1992 IEEE International Conference on Fuzzy Systems. San Diego, CA, USA: IEEE, 1992.1163−1170
[19]	Wang L X, Mendel J M. Generating fuzzy rules by learning from examples. IEEE Transactions on Systems, Man and Cybernetics, 1992, 22(6): 1414−1427 doi: 10.1109/21.199466
[20]	Jang J S R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Transactions on Systems Man and Cybernetics, 1993, 23(3): 665−685
[21]	Sun B X, Gao K, Jiang J C, Luo M, He T T, Zheng F D, Guo H Y. Research on discharge peak power prediction of battery based on ANFIS and subtraction clustering. Transactions of China Electrotechnical Society, 2015, 30(4): 272−280
[22]	陈伟宏, 安吉尧, 李仁发, 李万里. 深度学习认知计算综述. 自动化学报, 2017, 43(11): 1886−1897 Chen Wei-Hong, An Ji-Yao, Li Ren-Fa, Li Wan-Li. Review on deep-learning-based cognitive computing. Acta Automatica Sinica, 2017, 43(11): 1886−1897