A Contour Detection Method Based on Hierarchical Structure Response Model in Primary Visual Pathway
-
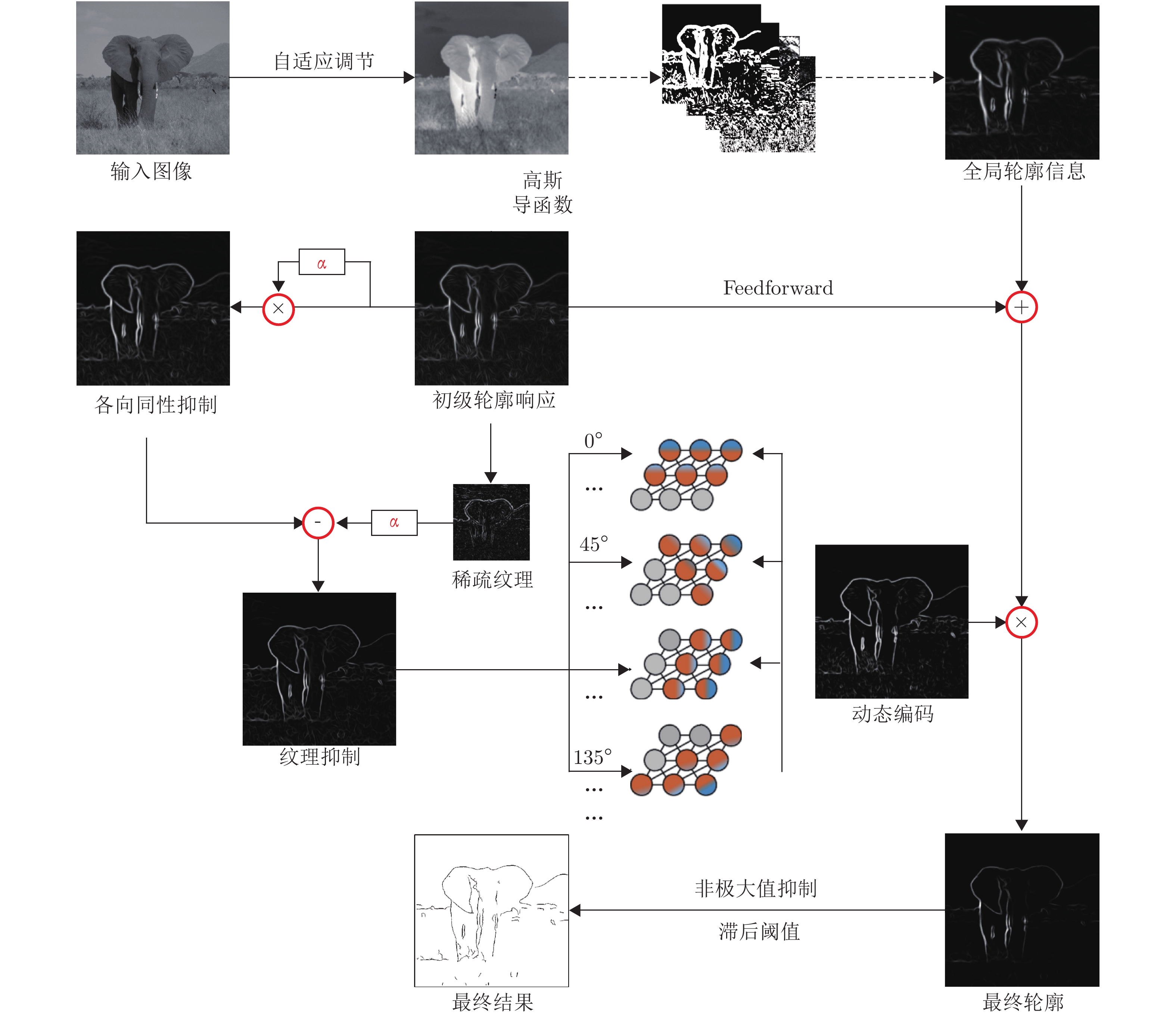
摘要: 基于视通路结构分级响应与动态传递的方式, 本文提出了一种图像轮廓检测的新方法. 针对视网膜感光细胞的暗视觉特性, 建立亮度自适应的暗视野调节模型, 利用多尺度经典感受野的方位选择性, 构建高级轮廓与全局轮廓的检测路径; 模拟外侧膝状体(Lateral geniculate nucleus, LGN)细胞特性对信息进行纹理稀疏编码, 并结合非经典感受野的侧抑制作用抑制背景强纹理; 另外在LGN区提出微动整合机制, 减少纹理冗余信息, 再经适应性突触实现信息关联传递; 最后将初级轮廓响应跨视区前馈至V1区并经全局轮廓修正后, 与高级轮廓响应实现快速融合. 分别以RuG40、BSDS500图像库中的自然图像作为实验数据, 检测结果与基准轮廓图的平均最优P指标分别为0.50、0.32, 结果表明本方法能更有效地区分轮廓与纹理边缘, 凸显主体轮廓. 本文利用视神经细胞的内在机制以及神经信息的动态传递过程实现图像轮廓信息的编码与检测, 也为研究后续高级视皮层的视觉感知提供了新思路.Abstract: Based on the hierarchical response and dynamic transmission of the visual path structure, this paper proposes a new method of image contour detection. Aiming at the dark vision characteristics of retinal photoreceptor cells, a brightness-adaptive dark field adjustment model was established, and the orientation selectivity of multiscale classical receptive fields was used to construct the detection path of advanced contours and global contours; the characteristics of lateral geniculate nucleus (LGN) cells were simulated to sparse the information, combined with the side inhibition of non-classical receptive fields to suppress strong background textures; in addition, a micro-motion integration mechanism is proposed in the LGN region to reduce redundant texture information, and then the information is transmitted through adaptive synapses; finally, the primary contour response is transmitted across the view area is fed forward to the V1 area and global contour correction is performed, it quickly integrates with the advanced contour response. The natural images in the RuG40 and BSDS500 image libraries are used as experimental data. The average optimal P indicators of the detection results and the reference contour map are 0.50 and 0.32, respectively. The results show that this method can more effectively distinguish contours from textured edges and highlight the contours of the subject. This paper uses the inner mechanism of optic nerve cells and the dynamic transmission process of neural information to realize the encoding and detection of image contour information. It also provides new ideas for studying the subsequent visual perception of advanced visual cortex.
-
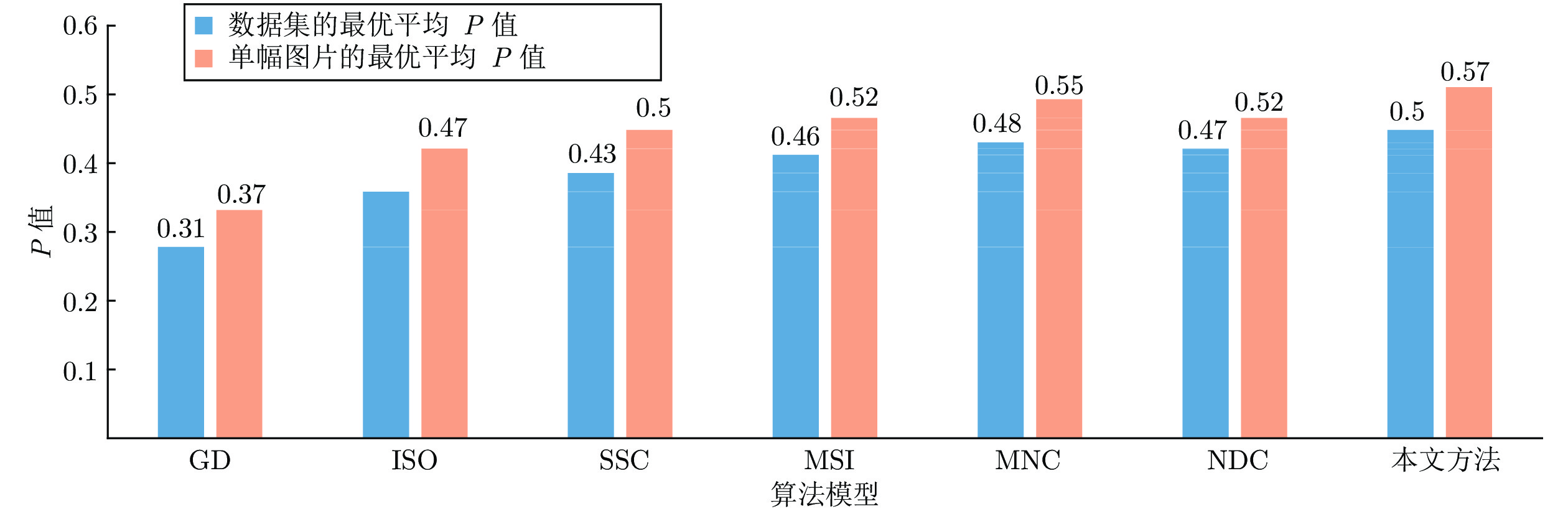
图 4 RuG40自然图像库的轮廓检测结果 (第1行为自然图像测试集; 第2行为真实轮廓图; 第3行为GD方法检测结果;第4行为ISO方法检测结果; 第5行为SSC方法检测结果; 第6行为MNC方法检测结果; 第7行为MCI方法检测结果;第8行为NDC方法检测结果; 第9行为本文方法检测结果)
Fig. 4 Contour detection results of RuG40 natural image library (the first line is the natural image test sets; the second line is the true contour maps; the third line is the results of GD; the fourth line is the results of ISO; the fifth line is the results of SSC; The sixth line is the results of the MNC; the seventh line is the results of the MCI; the eighth line is the results of NDC; the ninth line is the results of ours method)
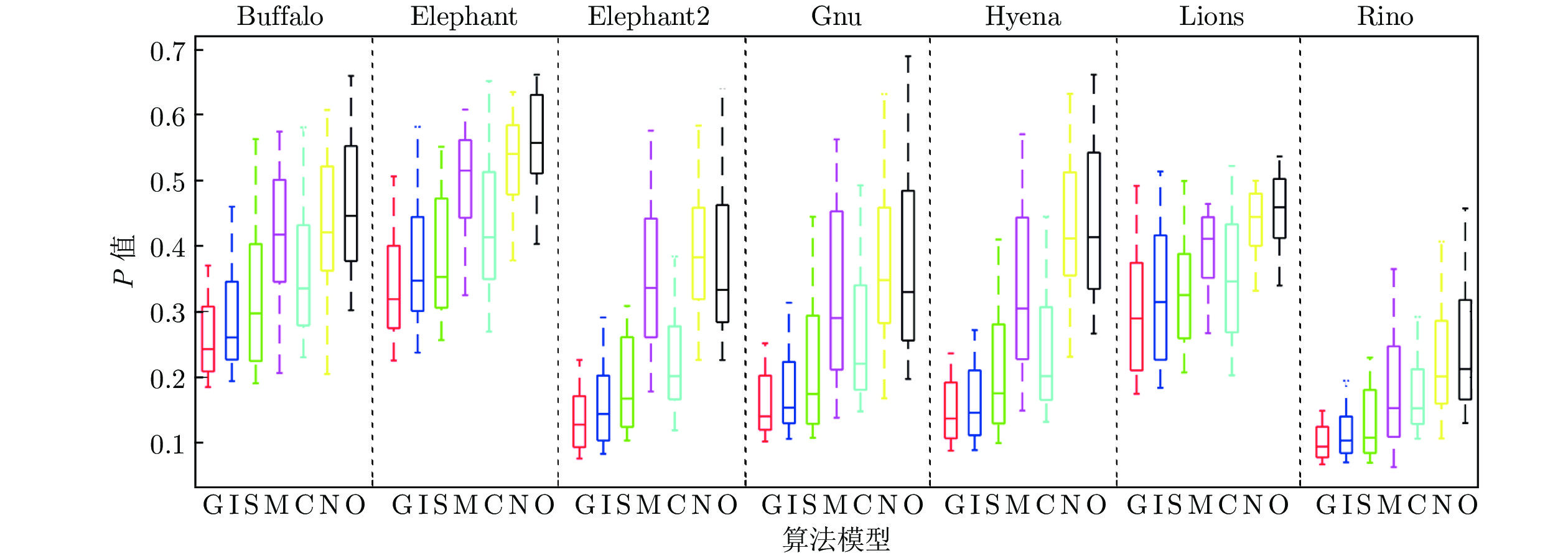
图 6 部分图像在多组参数下检测结果的P值箱线图(G表示GD算法, I表示ISO算法, S表示SSC算法, M表示MNC算法, C表示MCI算法, N表示NDC算法, O表示本文算法)
Fig. 6 P-value box plot of the detection results of some images under multiple sets of parameters (G represents the GD, I represents the ISO, S represents the SSC, M represents the MNC, C represents the MCI, N represents the NDC, and O represents the algorithm in this paper)
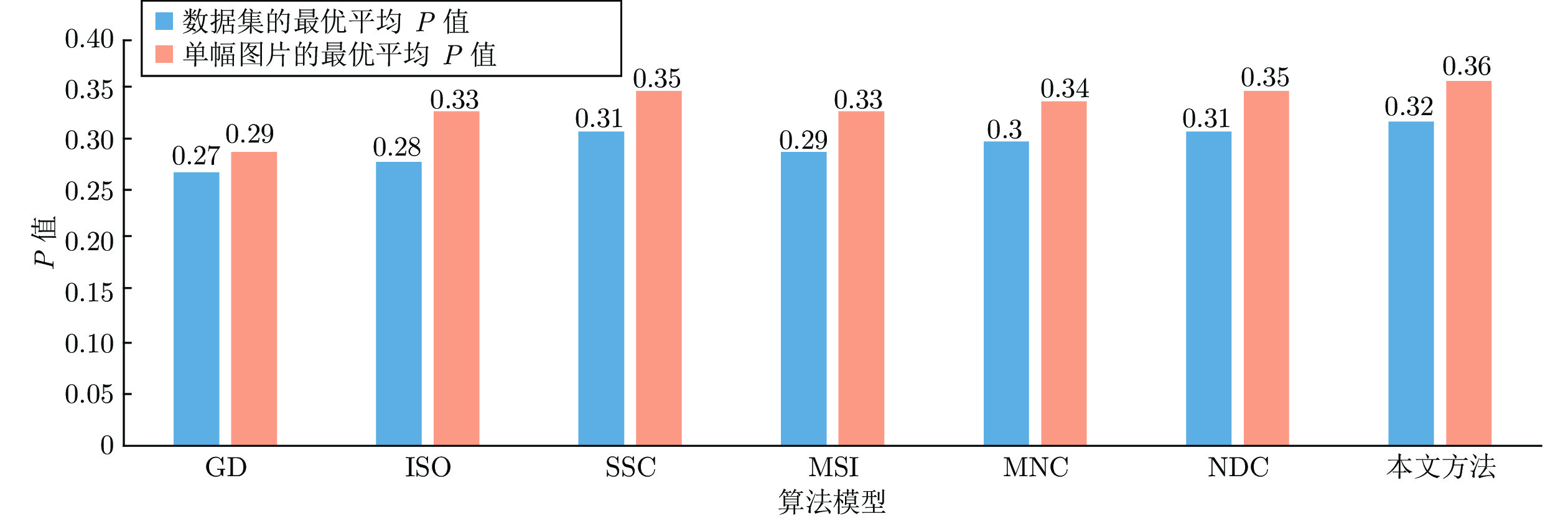
图 7 BSDS500图像数据集的轮廓检测结果(第1行为自然图像测试集; 第2行为图像真实轮廓; 第3行为GD方法检测结果; 第4行为ISO方法检测结果; 第5行为SSC方法检测结果; 第6行为MCI方法检测结果; 第7行为MNC方法检测结果; 第8行为NDC方法检测结果; 第9行为本文方法检测结果)
Fig. 7 Contour detection results of BSDS500 image library (the first line is the natural image test sets; the second line is the true contour maps; the third line is the results of GD; the fourth line is the results of ISO; the fifth line is the results of SSC; The sixth line is the results of the MNC; the seventh line is the results of the MCI; the eighth line is the results of NDC; the ninth line is the results of ours method)
图 8 BSDS500部分图像在多组参数下检测结果的P值箱线图(G表示GD算法, I表示ISO算法, S表示SSC算法, C表示MCI算法, M表示MNC算法, N表示NDC算法, O表示本文算法)
Fig. 8 P-value box plot of the detection results of some BSDS500 images under multiple sets of parameters (G represents the GD, I represents the ISO, S represents the SSC, C represents the MCI, M represents the MNC, N represents the NDC, and O represents the algorithm in this paper)
图像 算法 参数 性能 $\alpha $ $t$ ${e_{{\rm{FP}}} }$ ${e_{{\rm{FN}}} }$ $P$ FPS Buffalo GD — 0.10 0.35 0.23 0.58 4 ISO 0.60 0.10 0.25 0.28 0.59 3 SSC — 0.10 0.27 0.31 0.56 1/8 MCI 0.80 0.15 0.23 0.27 0.60 1/22 MNC 0.50 0.30 0.23 0.28 0.63 1/2 NDC 0.20 0.20 0.25 0.24 0.61 1/19 本文方法 0.20 0.30 0.16 0.27 0.66 1/27 Elephant2 GD — 0.05 0.74 0.20 0.50 ISO 0.10 0.05 0.33 0.25 0.59 SSC — 0.05 0.14 0.32 0.60 MCI 0.30 0.05 0.31 0.28 0.58 MNC 0.70 0.20 0.16 0.34 0.62 NDC 0.60 0.20 0.28 0.27 0.59 本文方法 0.10 0.35 0.22 0.28 0.64 Gnu GD — 0.05 0.24 0.21 0.63 ISO 0.10 0.05 0.24 0.29 0.59 SSC — 0.05 0.14 0.30 0.62 MCI 0.70 0.10 0.35 0.14 0.65 MNC 0.50 0.20 0.40 0.21 0.61 NDC 0.10 0.10 0.24 0.17 0.67 本文方法 0.10 0.20 0.22 0.20 0.69 Rino GD — 0.05 1.04 0.13 0.45 ISO 1.00 0.05 0.68 0.18 0.52 SSC — 0.05 0.38 0.22 0.60 MCI 0.50 0.05 0.28 0.22 0.62 MNC 0.60 0.10 0.31 0.31 0.60 NDC 0.80 0.10 0.31 0.24 0.60 本文方法 0.90 0.15 0.26 0.29 0.63 Lions GD — 0.05 0.25 0.44 0.49 ISO 0.20 0.10 0.56 0.28 0.51 SSC — 0.15 0.70 0.24 0.50 MCI 0.80 0.15 0.51 0.29 0.51 MNC 0.90 0.50 0.53 0.31 0.51 NDC 0.50 0.30 0.54 0.29 0.50 本文方法 0.10 0.30 0.44 0.33 0.54 图像 算法 参数 性能 $\alpha $ $t$ ${e_{{\rm{FP}}} }$ ${e_{{\rm{FN}}} }$ $P$ 197 017 GD — 0.05 0.40 0.28 0.54 ISO 0.10 0.05 0.38 0.27 0.58 SSC — 0.10 0.48 0.29 0.53 MCI 0.30 0.10 0.48 0.19 0.58 MNC 0.30 0.20 0.54 0.26 0.55 NDC 0.70 0.15 0.30 0.35 0.59 本文方法 0.50 0.20 0.28 0.34 0.60 3096 GD — 0.05 0.48 0.03 0.66 ISO 0.90 0.05 0.13 0.15 0.78 SSC — 0.05 0.12 0.16 0.78 MCI 1.00 0.05 0.08 0.27 0.72 MNC 0.80 0.20 0.17 0.17 0.75 NDC 1.00 0.50 0.18 0.15 0.77 本文方法 0.60 0.50 0.10 0.19 0.78 38092 GD — 0.10 0.67 0.16 0.54 ISO 0.90 0.10 0.31 0.31 0.58 SSC — 0.10 0.31 0.37 0.53 MCI 0.10 0.10 0.54 0.28 0.53 MNC 0.50 0.20 0.60 0.31 0.52 NDC 0.50 0.15 0.38 0.30 0.59 本文方法 0.10 0.20 0.38 0.29 0.60 42049 GD — 0.10 0.16 0.05 0.83 ISO 0.10 0.10 0.09 0.07 0.86 SSC — 0.30 0.15 0.12 0.78 MCI 0.20 0.15 0.11 0.11 0.82 MNC 0.20 0.60 0.15 0.14 0.80 NDC 0.20 0.55 0.10 0.10 0.85 本文方法 0.20 0.60 0.09 0.10 0.86 69020 GD — 0.05 0.49 0.20 0.59 ISO 0.90 0.05 0.14 0.32 0.64 SSC — 0.05 0.25 0.43 0.52 MCI 0.60 0.05 0.11 0.21 0.75 MNC 0.10 0.05 0.07 0.32 0.73 NDC 0.30 0.10 0.06 0.23 0.79 本文方法 0.10 0.10 0.05 0.25 0.79 -
[1] Gupta S, Mazumdar S G. Sobel edge detection algorithm. International Journal of Computer Science and Management Research, 2013, 2(2): 1578-1583 [2] McIlhagga W. The canny edge detector revisited. International Journal of Computer Vision, 2011, 91(3): 251-261 doi: 10.1007/s11263-010-0392-0 [3] Wei H, Lang B, Zuo Q S. Contour detection model with multi-scale integration based on non-classical receptive field. Neurocomputing, 2013, 103: 247-262 doi: 10.1016/j.neucom.2012.09.027 [4] Lin C, Xu G L, Cao Y J. Contour detection model using linear and non-linear modulation based on non-CRF suppression. IET Image Processing, 2018, 12(6): 993-1003 doi: 10.1049/iet-ipr.2017.0679 [5] 张明琦, 范影乐, 武薇. 基于初级视通路视觉感知机制的轮廓检测方法. 自动化学报, 2020, 46(2): 264-273Zhang Ming-Qi, Fan Ying-Le, Wu Wei. A contour detection method based on visual perception mechanism in primary visual pathway. Acta Automatica Sinica, 2020, 46(2): 264-273 [6] Yedjour H, Meftah B, Léoray O, Benyettou A. Edge detection based on Hodgkin-Huxley neuron model simulation. Cognitive Processing, 2017, 18(3): 315-323 doi: 10.1007/s10339-017-0803-z [7] Kang X M, Kong Q Q, Zeng Y, Xu B. A fast contour detection model inspired by biological mechanisms in primary vision system. Frontiers in Computational Neuroscience, 2018, 12: Article No. 28 doi: 10.3389/fncom.2018.00028 [8] Fang T, Fan Y L, Wu W. Salient contour detection on the basis of the mechanism of bilateral asymmetric receptive fields. Signal, Image and Video Processing, 2020, 14(7): 1461-1469 doi: 10.1007/s11760-020-01689-1 [9] Wassle H, Boycott B B. Functional architecture of the mammalian retina. Physiological Reviews, 1991, 71(2): 447-480 doi: 10.1152/physrev.1991.71.2.447 [10] Lamb T D. Why rods and cones?. Eye, 2016, 30(2): 179-185 doi: 10.1038/eye.2015.236 [11] Fried S I, Münch T A, Werblin F S. Mechanisms and circuitry underlying directional selectivity in the retina. Nature, 2002, 420(6914): 411-414 doi: 10.1038/nature01179 [12] De Valois R L, Cottaris N P, Mahon L E, Elfar S D, Wilson J A. Spatial and temporal receptive fields of geniculate and cortical cells and directional selectivity. Vision Research, 2000, 40(27): 3685-3702 doi: 10.1016/S0042-6989(00)00210-8 [13] Liu J Q, Jia Y D. A lateral inhibitory spiking neural network for sparse representation in visual cortex. In: Proceedings of the 5th International Conference on Brain Inspired Cognitive Systems. Shenyang, China: Springer-Verlag, 2012. 259–267 [14] Li Z T, Zhang J, Zhang K H, Li Z Y. Visual tracking with weighted adaptive local sparse appearance model via spatio-temporal context learning. IEEE Transactions on Image Processing, 2018, 27(9): 4478-4489 doi: 10.1109/TIP.2018.2839916 [15] Alpert S, Galun M, Brandt A, Basri R. Image segmentation by probabilistic bottom-up aggregation and cue integration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(2): 315-327 doi: 10.1109/TPAMI.2011.130 [16] Anderson A G, Olshausen B A, Ratnam K, Roorda A. A neural model of high-acuity vision in the presence of fixational eye movements. In: Proceedings of the 50th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, USA: IEEE, 2016. 588–592 [17] Abbott L F, Regehr W G. Synaptic computation. Nature, 2004, 431(7010): 796-803 doi: 10.1038/nature03010 [18] Poltoratski S, Maier A, Newton A T, Tong F. Figure-ground modulation in the human lateral geniculate nucleus is distinguishable from top-down attention. Current Biology, 2019, 29(12): 2051-2057.e3 doi: 10.1016/j.cub.2019.04.068 [19] Angelucci A, Sainsbury K. Contribution of feedforward thalamic afferents and corticogeniculate feedback to the spatial summation area of macaque V1 and LGN. Journal of Comparative Neurology, 2006, 498(3): 330-351 doi: 10.1002/cne.21060 [20] Theeuwes J. Top–down and bottom-up control of visual selection. Acta Psychologica, 2010, 135(2): 77-99 doi: 10.1016/j.actpsy.2010.02.006 [21] Grigorescu C, Petkov N, Westenberg M A. Contour detection based on nonclassical receptive field inhibition. IEEE Transactions on Image Processing, 2003, 12(7): 729-739 doi: 10.1109/TIP.2003.814250 [22] Yang K F, Gao S B, Guo C F, Li C Y, Li Y J. Boundary detection using double-opponency and spatial sparseness constraint. IEEE Transactions on Image Processing, 2015, 24(8): 2565-2578 doi: 10.1109/TIP.2015.2425538 [23] Yang K F, Li C Y, Li Y J. Multifeature-based surround inhibition improves contour detection in natural images. IEEE Transactions on Image Processing, 2014, 23(12): 5020-5032 doi: 10.1109/TIP.2014.2361210 -





 下载:
下载: