结合聚类分解的增强蚁群算法求解复杂绿色车辆路径问题

胡蓉; 李洋; 钱斌; 金怀平; 向凤红

doi:10.16383/j.aas.c190872

结合聚类分解的增强蚁群算法求解复杂绿色车辆路径问题

doi: 10.16383/j.aas.c190872

胡蓉^{1, 2,},
李洋^{1, 3,},
钱斌^{1, 2,},
金怀平^1,,
向凤红^1,

1.
昆明理工大学信息工程与自动化学院昆明 650500
2.
昆明理工大学云南省人工智能重点实验室昆明 650500
3.
云南电力技术有限责任公司昆明 650051

基金项目: 国家自然科学基金(61963022, 51665025), 云南省应用基础研究计划重点项目(202201AS070030)资助

详细信息

作者简介:
胡蓉：昆明理工大学信息工程与自动化学院副教授. 2004年获得清华大学自动化系硕士学位. 主要研究方向为调度理论与方法, 智能计算, 决策支持系统. E-mail: ronghu@vip.163.com

李洋：昆明理工大学信息工程与自动化学院硕士研究生. 2009年获得昆明理工大学电力工程学院学士学位. 主要研究方向为调度理论与智能优化算法. E-mail: yang.l.liam@hotmail.com

钱斌：昆明理工大学信息工程与自动化学院教授. 2009年获得清华大学自动化系博士学位. 主要研究方向为调度理论与方法, 智能优化. 本文通信作者.E-mail: bin.qian@vip.163.com

金怀平：昆明理工大学信息工程与自动化学院副教授. 2016年获得北京理工大学博士学位. 主要研究方向为智能计算和软测量方法.E-mail: jinhuaiping@gmail.com

向凤红：昆明理工大学信息工程与自动化学院教授. 2002年获得昆明理工大学博士学位. 主要研究方向为智能优化与控制. E-mail: xiangfh5447@sina .com.cn

中图分类号: TP399
计量
- 文章访问数: 2376
- HTML全文浏览量: 267
- PDF下载量: 233
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-22
- 录用日期: 2020-05-03
- 网络出版日期: 2022-10-24
- 刊出日期: 2022-12-23

An Enhanced Ant Colony Optimization Combined With Clustering Decomposition for Solving Complex Green Vehicle Routing Problem

HU Rong^{1, 2
,},
LI Yang^{1, 3
,},
QIAN Bin^{1, 2
,},
JIN Huai-Ping^1
,,
XIANG Feng-Hong^1
,

1.
School of Information Engineering and Automation, Kun-ming University of Science and Technology, Kunming 650500
2.
Yunnan Key Laboratory of Artificial Intelligence, Kunming University of Science and Technology, Kunming 650500
3.
Yunnan Electric Power Technology Co., Ltd., Kunming 650051

Funds: Supported by National Natural Science Foundation of China (61963022, 51665025) and Applied Basic Research Key Project of Yunnan Province (202201AS070030)

More Information

Author Bio:
HU Rong　Associate professor at the School of Information Engineering and Automation, Kunming University of Science and Technology. She received her master degree from Tsinghua University in 2004. Her research interest covers scheduling theory and method, intelligent computation, and decision support system

LI Yang　Master student at the School of Information Engineering and Automation, Kunming University of Science and Technology. He received his bachelor degree from Kunming University of Science and Technology in 2009. His research interest covers scheduling methods and intelligent optimization algorithms

QIAN Bin　Professor at the School of Information Engineering and Automation, Kunming University of Science and Technology. He received his Ph.D. degree from Tsinghua University in 2009. His research interest covers scheduling theory and method, and intelligent optimization. Corresponding author of this paper

JIN Huai-Ping　Associate professor at the School of Information Engineering and Automation, Kunming University of Science and Technology. He received his Ph.D. degree from Beijing Institute of Technology in 2016. His research interest covers intelligent computation and soft sensor methods

XIANG Feng-Huang　Professor at the School of Information Engineering and Automation, Kunming University of Science and Technology. He received his Ph.D. degree from Kunming University of Science and Technology in 2002. His research interest covers intelligent optimization and control

摘要

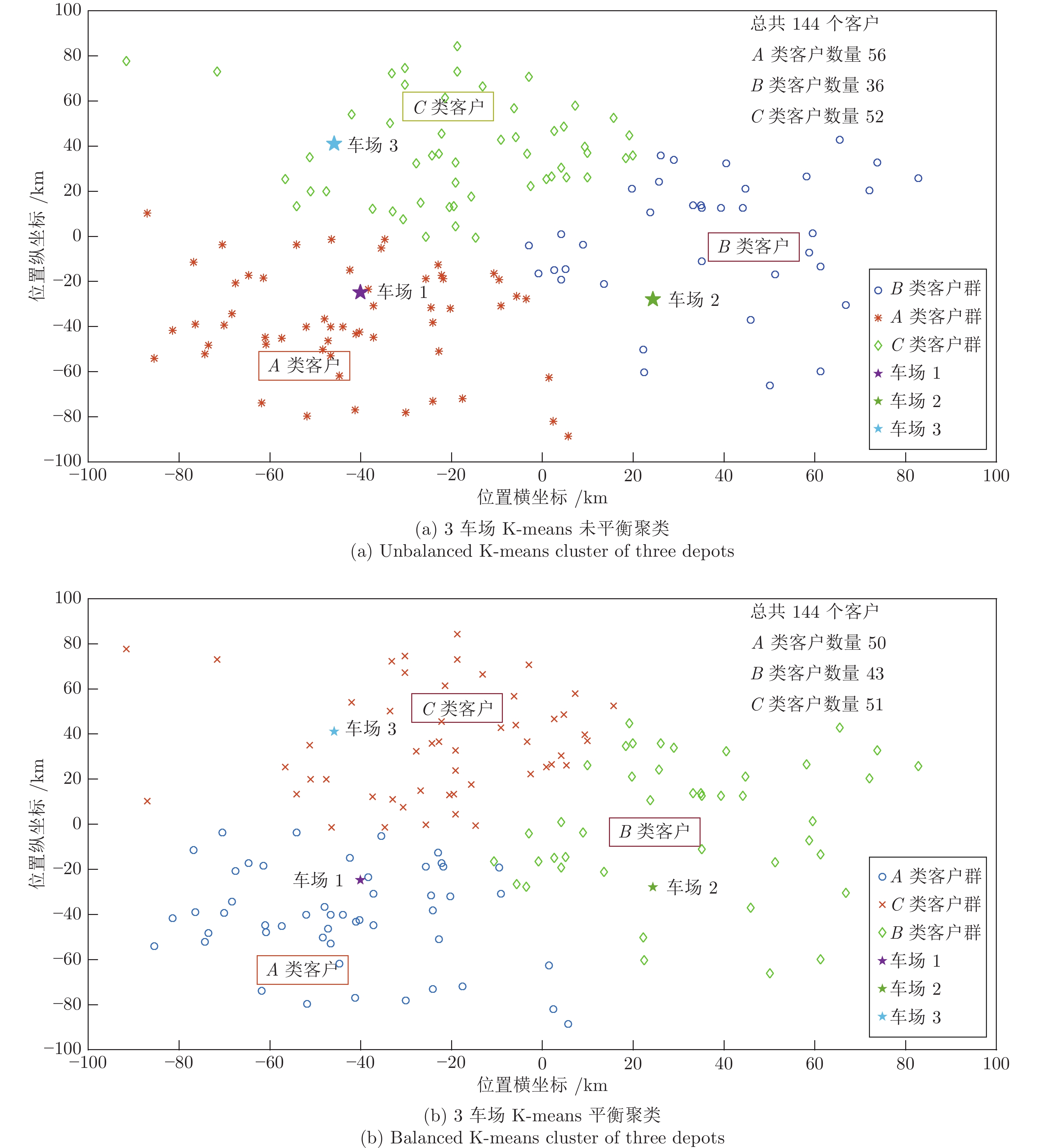
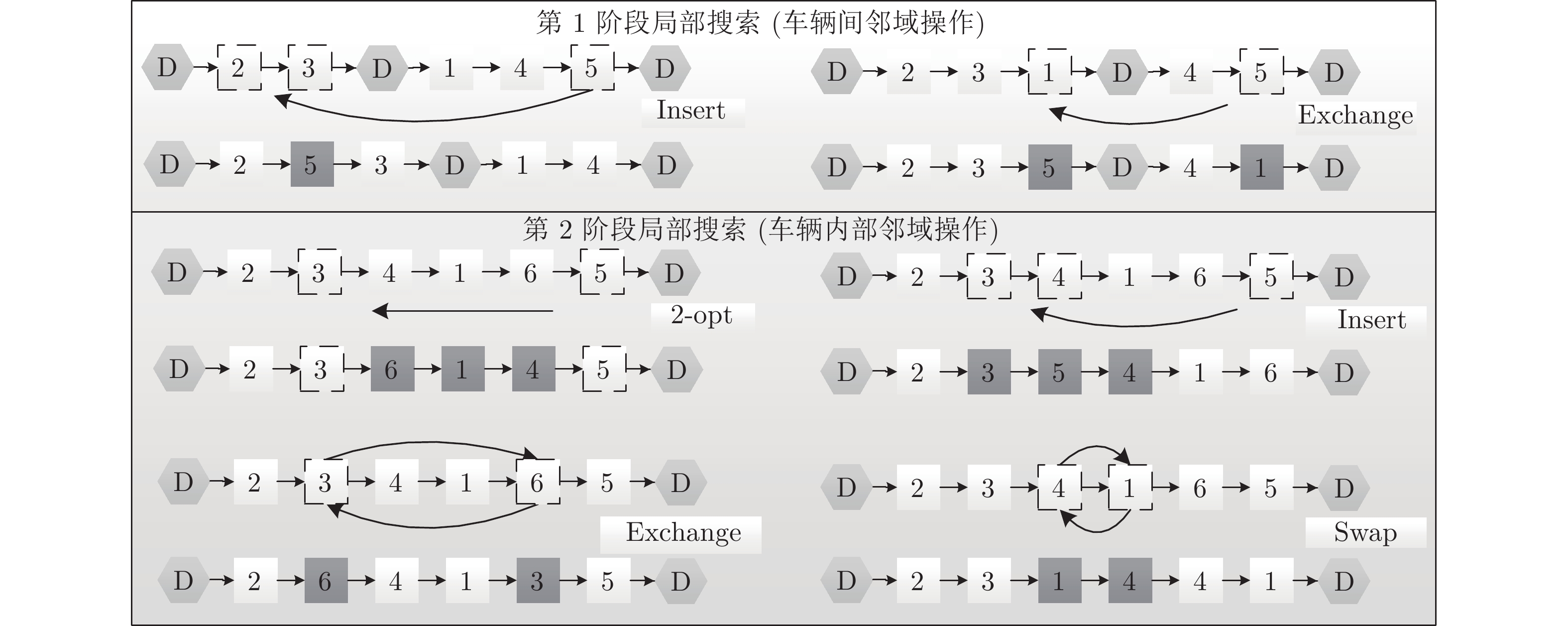
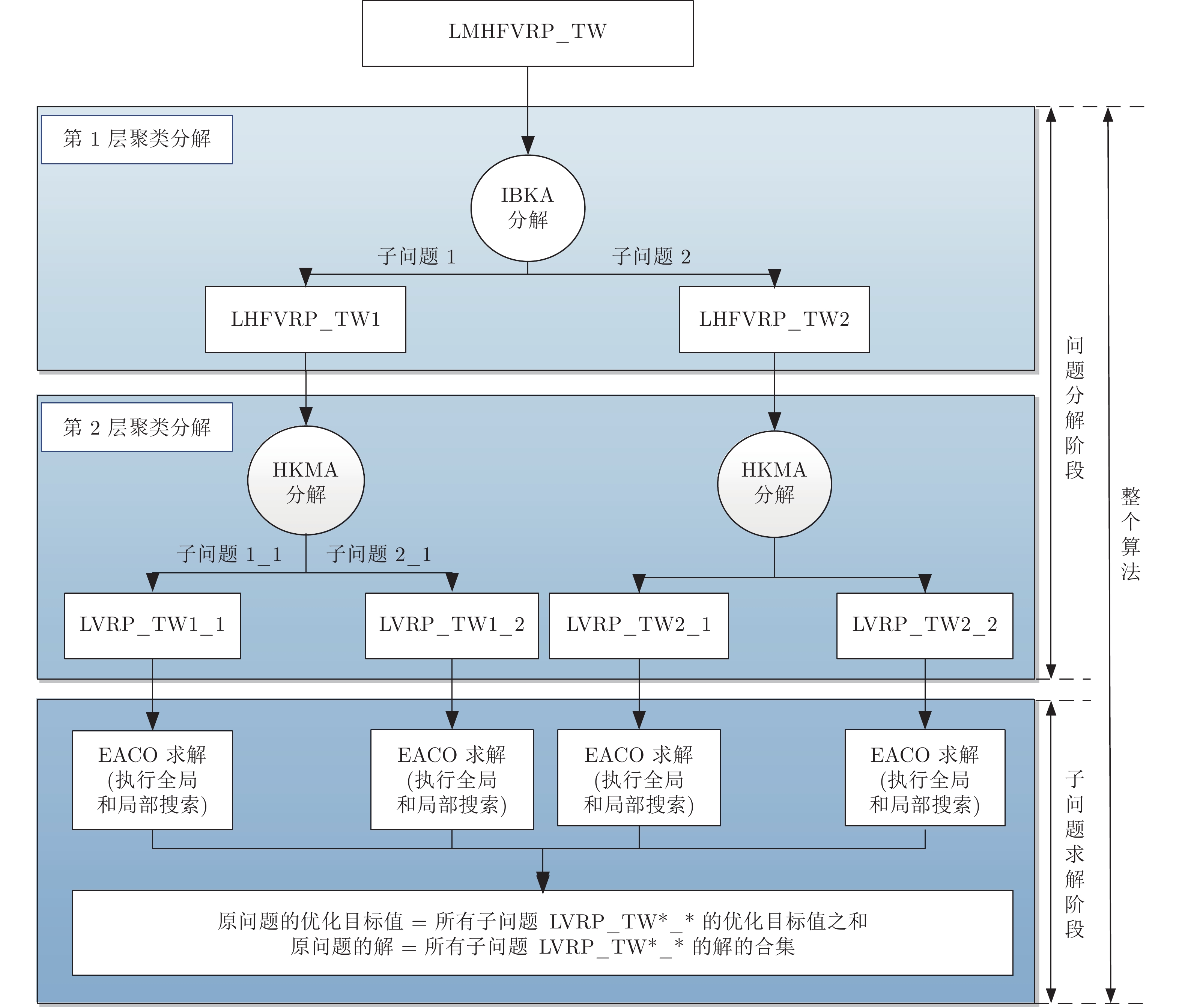
摘要: 针对带时间窗的低能耗多车场多车型车辆路径问题(Low-energy-consumption multi-depots heterogeneous-fleet vehicle routing problem with time windows, LMHFVPR_TW), 提出一种结合聚类分解策略的增强蚁群算法(Enhanced ant colony optimization based on clustering decomposition, EACO_CD)进行求解. 首先, 由于该问题具有强约束、大规模和NP-Hard等复杂性, 为有效控制问题的求解规模并合理引导算法在优质解区域搜索, 根据问题特点设计两种基于K-means的聚类策略, 将LMHFVPR_TW合理分解为一系列带时间窗的低能耗单车场单车型车辆路径子问题(Low-energy-consumption vehicle routing problem with time windows, LVRP_TW); 其次, 本文提出一种增强蚁群算法(Enhanced ant colony optimization, EACO)求解分解后的各子问题(LVRP_TW), 进而获得原问题的解. EACO不仅引入信息素挥发系数控制因子进一步动态调节信息素挥发系数, 从而有效控制信息素的挥发以提高算法的全局搜索能力, 而且设计基于4种变邻域操作的两阶段变邻域局部搜索(Two-stage variable neighborhood search, TVNS)来增强算法的局部搜索能力. 最后, 在不同规模问题上的仿真和对比实验验证了所提EACO_CD的有效性.
- 低能耗车辆路径问题 /
- 多车场多车型 /
- 时间窗 /
- 聚类分解 /
- 增强蚁群算法
Abstract: In this paper, an enhanced ant colony optimization combined with clustering decomposition strategy (EACO_CD) is proposed for solving the low-energy-consumption multi-depots heterogeneous-fleet vehicle routing problem with time windows (LMHFVPR_TW). Firstly, since the considered problem is a complex one with strong constraints, large scale and NP-hardness, In order to control the scale of problem and reasonably guide the algorithm to search in the high-quality solution region, two kinds of clustering methods based on K-means strategies are designed to reasonably decompose it into a series of subproblems (i.e., the low-energy-consumption vehicle routing problems with time windows (LVRP_TW) by utilizing the problem characteristics. Secondly, an enhanced ant colony optimization (EACO) to solve the decomposed subproblems (LVRP_TW) for obtaining the solution of the original problem is proposed. Not only a control factor of pheromone decay parameter in EACO is added to adjust the pheromone decay parameter dynamically so as to control the volatilization of pheromone effectively and improve the global search ability of ACO, but also a two-stage variable neighborhood search (TVNS) is designed based on four variable neighborhood operations to enhance its the local search ability. Finally, simulation experiments and comparisons on instances with different scales demonstrate the effectiveness of proposed EACO_CD.
- Low-energy-consumption vehicle routing problem (LVRP) /
- multiple depots and heterogeneous fleet /
- time windows /
- cluster of decomposition /
- enhanced ant colony optimization (EACO)
注释:

1) ¹ 表7 ~ 表9的完整测试结果可在: https://pan.baidu.com/s/19sqBboZHLCgFqtiZS7Id-Q 提取码3cv6下载.

HTML全文

图 1 EACO_CD (EACO_IBKA_HKMA)结构

Fig. 1 Framework of EACO_CD (EACO_IBKA_HKMA)

下载: 全尺寸图片幻灯片

图 2 4类客户平衡移动示意图

Fig. 2 Diagram of balanced movement for four customer groups

下载: 全尺寸图片幻灯片

图 3 3车场K-means未平衡聚类与平衡聚类比较

Fig. 3 Comparison of unbalanced K-means cluster and balanced K-means cluster of three depots

下载: 全尺寸图片幻灯片

图 4 HKMA工作机制

Fig. 4 Running mechanism of HKMA

下载: 全尺寸图片幻灯片

图 5 HKMA三维聚类效果

Fig. 5 The 3D clustering results of HKMA

下载: 全尺寸图片幻灯片

图 6 HKMA二维结果

Fig. 6 The 2D results of HKMA

下载: 全尺寸图片幻灯片

图 7 局部搜索策略

Fig. 7 Local search strategy

下载: 全尺寸图片幻灯片

表 1 符号及定义

Table 1 Symbols and definitions

符号	释义	符号	释义
$F_1$	运输距离费用	$H_{PM}$	车场P 中有$H_{PM}$辆$M$类型的车辆
$F_2$	车辆固定成本	$r(A)$	完成客户子集$A$中所有客户的配送需要的最少车辆数
$F_3$	燃油消耗费用	$N$	总共有$N$个客户
$F_4$	时间窗惩罚费用	$V$	客户编号集合$\{1,2,\cdots,\ N\} $ (0 表示车场)
$C_{M1}$	第$M$种类型车辆的距离费用系数	$M_t$	共有$M_t$种类型的车辆
$C_{M2}$	第$M$种类型车辆的固定发车费用系数	$k$	车辆编号
$C_{M3}$	第$M$种类型车辆的燃油费用系数	$x_{PMijk}$	车场$P$车型$M$的第$k$辆车从客户$i$到客户$j$的决策变量
$C_1$	配送车辆提前到达的单位惩罚费用	$d_{ij}$	客户$i$到客户$j$的距离
$C_2$	配送车辆迟到的单位惩罚费用	${ET}_i$	客户$i$要求的最早到达时间
$i$	客户点$i$	${LT}_i$	客户$i$要求的最晚到达时间
$j$	客户点$j$	$S_i$	客户$i$要求的卸货时间
$P$	$\{1,2,\cdots,\ P_t\} $	车场编号$q_i$	客户i 要求的货物需求量
$P_s$	全部车场集合	$t_i$	车辆到达客户$i$的时间
$P_t$	总共有$P_t$个车场$P$	$M$	车型编号
$M_s$	全部车型集合$\{1,2,\cdots,\ M_t\}$	$Q_M$	第$M$种车型的最大载重量
$H_{PMS}$	车场$P$中车型$M$的全部车辆集合$\{1,2,\cdots,\ H_{PM}\}$	${FU}_{Mij}$	车型为$M$的车辆从客户$i$到客户$j$之间的耗油量
注: 综合燃油消耗模型中的其他相关参数设定参考文献 [25].

下载: 导出CSV

表 2 目标函数中的相关系数

Table 2 Coefficients in the object function

符号	数值
$C_{M1}$	1.5 (元/km)
$C_{M2}$	300 ~ 800 (元/辆)
$C_{M3}$	7.6 (元/l)
$C_{1}$	15 (元/h)
$C_{2}$	20 (元/h)

下载: 导出CSV

表 3 主要参数与水平

Table 3 Main parameters and level

主要参数	水平设置
主要参数	1	2	3	4
$\alpha$	1.25	1.5	1.75	2.0
$\beta$	10	1.5	2.0	2.5
$P_m$	1.1	1.2	1.3	1.4
$W$	500	1000	1500	2000

下载: 导出CSV

表 4 参数设置的正交表

Table 4 Orthogonal table of parameter settings

组合编号	水平设置				AVR (元)
组合编号	$\alpha$	$\beta$	$P_m$	$W$	AVR (元)
1	1	1	1	1	9677
2	1	2	2	2	9625
3	1	3	3	3	9613
4	1	4	4	4	9541
5	2	1	2	3	9745
6	2	2	1	4	9624
7	2	3	4	1	9602
8	2	4	3	2	9593
9	3	1	3	4	9836
10	3	2	4	3	9703
11	3	3	1	2	9654
12	3	4	2	1	9612
13	4	1	4	2	9865
14	4	2	3	1	9689
15	4	3	2	4	9656
16	4	4	1	3	9672

下载: 导出CSV

表 5 各参数不同水平下的平均响应值和影响力

Table 5 Average response values and influences table at different levels of each parameter

水平	水平设置
水平	$\alpha$	$\beta$	$P_m$	$W$
1	9614	9780	9656	9645
2	9641	9660	9659	9684
3	9701	9631	9683	9683
4	9720	9604	9677	9664
极差	106	176	27	39
影响力排名	2	1	4	3

下载: 导出CSV

表 6 4种不同车型相关参数设置

Table 6 Related parameter settings for four different vehicle types

车型列表	车型参数
车型列表	载重量 (kg)	空车重量(kg)	平均速度(km/h)	固定费用(元)	最大承载货物数 (件)
Type 1	200	1600	60 ~ 80	300 ~ 400	20
Type 2	500	2700	50 ~ 70	400 ~ 500	30
Type 3	600	3500	40 ~ 60	500 ~ 600	40
Type 4	800	5000	30 ~ 50	600 ~ 800	50

下载: 导出CSV

表 7 EACO_IBKA与其他算法对比结果

Table 7 Comparison results of EACO_IBKA with other algorithms

N_P_t	EACO_IBKA				EACO_KM				EACO_NNA				EACO1				DHACO				${ {T} }({{\rm{s}}} )$
N_P_t	最优	平均	最差	标准差	最优	平均	最差	标准差	最优	平均	最差	标准差	最优	平均	最差	标准差	最优	平均	最差	标准差	${ {T} }({{\rm{s}}} )$
48_2	11118	11800	12163	95	10745	11181	11579	97	11558	12080	12539	99	9650	10390	11026	87	10255	11068	11663	90	10
96_2	17483	18155	18549	183	18037	18379	19146	187	16768	17675	18229	190	15371	17009	17771	169	16011	17559	18161	174	19
144_2	24628	25435	26983	308	24880	25369	27201	314	25435	26710	27702	320	24366	25969	27419	318	24475	26884	28356	328	29
192_2	27522	28546	29649	411	28457	29482	30261	419	28758	29560	31019	428	28379	29838	30618	432	28524	30863	31665	445	38
240_2	31505	32699	34166	508	32517	33677	35235	518	32676	33723	35179	529	32722	34769	35906	534	33643	36475	37487	550	48
288_2	39217	41028	43326	592	40412	42363	44162	604	41179	42142	44696	616	41283	43164	44325	622	42606	43930	45137	641	58
360_2	53748	56268	58544	847	54672	57402	60199	864	55251	57847	59619	881	56276	58653	61938	890	56965	59409	62929	916	72
48_3	10767	11035	11572	83	10221	10827	11115	84	10995	11492	11929	93	9178	9883	10489	81	9754	10529	11095	83	14
96_3	16638	17278	17654	174	17066	17491	18222	182	15957	16821	17349	180	14627	16582	17912	191	15236	17186	18141	184	29
144_3	23443	24211	25685	293	23659	24149	25893	290	24211	25426	26371	302	23194	24720	26101	296	23297	25592	26993	305	43
192_3	26199	27175	28225	392	27090	28066	28826	399	27376	28140	29529	403	27016	28405	29147	407	27153	29381	30145	420	58
240_3	29992	31130	32527	484	30956	32061	33545	494	31108	32105	33491	499	31151	33101	34184	504	32029	34726	35690	519	72
288_3	37337	39062	41251	564	38476	40333	42047	575	39205	41123	42555	581	39305	41096	42202	587	40565	41826	42975	604	86
360_3	51176	53576	55744	806	52056	54656	57320	823	52608	55080	56768	831	53584	55848	58976	839	54240	56568	59920	864	108
48_4	10239	10617	11313	82	9943	10418	10886	84	10807	11144	11671	86	8939	9615	9883	78	9545	10051	10539	80	19
96_4	16062	16943	17257	166	16810	17146	17481	175	15871	16425	17434	160	16012	16907	17336	179	16391	16991	17496	177	38
144_4	22700	23723	25488	279	23650	24242	25187	291	23765	24990	25945	296	22747	24273	25602	288	22841	25114	26506	294	58
192_4	25690	26612	27737	373	26528	27235	27938	383	26846	27620	28988	391	26443	27896	28628	403	26623	28850	29614	411	77
240_4	29375	30447	31877	461	30317	31401	32874	473	30447	31411	32863	483	30545	32484	33502	511	31411	34401	34997	521	96
288_4	36519	38266	40433	537	37624	39493	41240	549	38365	39338	41737	560	38442	40278	41339	583	39692	40974	42135	595	115
360_4	50480	52904	55056	768	51344	53960	56608	786	51904	54392	56088	802	52088	55184	58312	833	53584	55904	59216	850	144
平均值	28183	29377	30724	400	28831	29968	31284	409	29100	30250	31510	416	28634	30289	31553	421	29278	31156	32422	431	—

下载: 导出CSV

表 8 HKMA与其他划分算法的对比结果

Table 8 Comparison results of HKMA and the other dividing algorithms

$ {{N}}\_ {{M}}_{{t}}$	EACO_HKMA			EACO_RDA			EACO_RAA			EACO_KEW			EACO2			TSA_RDA			$ {T}({{{\rm{s}}}})$
$ {{N}}\_ {{M}}_{{t}}$	最优	平均	最差	最优	平均	最差	最优	平均	最差	最优	平均	最差	最优	平均	最差	最优	平均	最差	$ {T}({{{\rm{s}}}})$
48_2	12801	13612	13901	13220	14646	15128	12467	13293	13998	12607	13317	13922	12218	13798	14202	13352	14792	15279	15
96_2	16299	16759	17342	17570	19461	20106	16238	17661	18591	16754	17704	18101	16543	17838	18777	17746	19656	20307	29
144_2	22061	23265	24089	23361	25860	26717	22390	23665	24721	22266	23533	24590	22838	23934	25215	23595	26119	26984	44
192_2	24847	25998	26933	25983	26905	28228	26000	27201	28372	26039	26918	28238	26520	27745	28939	26243	27174	28510	57
240_2	25958	27124	28797	26951	28002	29726	29253	30130	30753	29409	30076	30878	30131	31034	31976	27221	28282	30023	72
288_2	32225	33356	33838	33783	34713	36290	32740	35242	37189	32540	35156	37175	34050	36652	38677	34121	35060	36653	87
360_2	48344	50050	51763	50695	52088	54440	49129	52874	55793	48828	52743	53780	51094	54989	58025	51202	52609	54984	108
48_3	11896	12400	13111	12574	13919	14386	11755	11999	13312	11995	12658	13236	11520	12240	13999	12700	14058	14530	21
96_3	15777	15929	16997	16704	18494	19122	16011	16792	17680	15932	16839	17594	16171	16960	17857	16871	18679	19313	44
144_3	20965	21171	22661	22207	24587	25394	21291	22312	23490	21170	22366	23380	21717	22758	23960	22429	24833	25648	65
192_3	23624	24718	25597	24704	25570	26823	24714	25850	26974	24748	25588	26836	25455	26626	27783	24951	25826	27091	87
240_3	24680	25776	27367	25620	26616	28248	27804	28634	29235	27948	28582	29351	28916	29779	30404	25876	26882	28530	108
288_3	30621	31700	32158	32106	32984	34483	31111	33493	35335	30929	33414	35335	32667	35168	37102	32427	33314	34828	129
360_3	45933	47554	48245	48172	49502	51726	46691	50237	53019	47401	50118	51004	49026	52749	55670	48654	49997	52243	162
48_4	10755	10998	12257	11330	12533	12956	10700	11393	11985	10800	11402	11927	10999	11766	11999	11443	12658	13086	29
96_4	14214	14349	14672	15047	16655	17221	14422	15118	15927	14346	15171	15843	14566	15269	16086	15197	16822	17393	57
144_4	18878	19057	20506	19998	22039	22865	19165	20085	21148	19057	20140	21048	19548	20487	21571	20198	22360	23094	87
192_4	21273	22251	23043	22237	23018	24145	22257	23268	24281	22282	23034	24158	22925	23966	25009	22459	23248	24386	116
240_4	22215	23209	24642	23073	23966	25438	25035	25778	26316	25161	25735	26431	26036	26809	27369	23304	24206	25692	144
288_4	27563	28542	29950	28902	29689	31040	28012	30149	31812	27842	30088	31815	29413	31656	33403	29191	29986	31350	173
360_4	41350	42809	44034	43360	44558	46561	42028	45218	47722	41776	43111	45711	44129	47479	50108	43794	45004	47027	216
平均值	24407	25197	25970	25600	26948	28145	25201	26659	27983	25230	26652	27636	26023	27605	28944	25856	27217	28426	—

下载: 导出CSV

表 9 EACO_CD性能验证

Table 9 Performance verification of EACO_CD

$ {{N}}\_{{ P}}_{{t}}\_{{M}}_{{t}}$	EACO_CD (EACO_IBKA_HKMA)				IACO_CD (IACO_NNA_SWA)				IHGA				${ {T} }({ {{\rm{s}}} })$
$ {{N}}\_{{ P}}_{{t}}\_{{M}}_{{t}}$	最优值	平均值	最差值	标准差	最优值	平均值	最差值	标准差	最优值	平均值	最差值	标准差	${ {T} }({ {{\rm{s}}} })$
48_2_2	12145	12478	12859	232	12880	13212	13509	241	11632	11967	12227	220	15
96_2_2	16370	16526	16904	295	17800	18071	18381	272	15852	16011	16376	285	31
144_2_2	21010	21305	21704	324	24589	24825	25406	336	21049	21640	22154	348	51
192_2_2	23664	24760	25650	556	26040	27250	28218	576	24863	26010	26948	590	71
240_2_2	24722	25832	27426	588	26707	27903	29640	641	27444	28720	29947	692	96
288_2_2	30690	31768	32227	724	33772	34962	35457	803	35311	36550	37076	824	123
360_2_2	39903	41303	41906	951	43907	45448	46111	1059	45507	46098	47781	1197	162
48_3_2	12999	14064	14425	293	13656	14787	15372	336	12742	13802	14337	304	21
96_3_2	16883	17869	18993	358	18568	20115	20999	343	16800	18283	19011	363	48
144_3_2	21916	23728	24668	456	25647	27774	28874	539	23029	24921	25906	491	76
192_3_2	24257	25492	26408	668	26692	28059	29065	671	26688	28052	29053	746	109
240_3_2	24672	26558	28026	792	27884	30021	31675	740	28382	30554	32236	787	144
288_3_2	30258	31572	32860	907	34814	36319	37797	1017	35414	36956	38450	1092	183
360_3_2	39347	41061	42734	1141	43291	45187	47020	1263	47228	49291	51297	1389	243
48_3_3	12284	13225	13755	280	12830	13906	14446	322	12123	13253	13797	287	29
96_3_3	15867	17082	17860	388	17470	18911	19664	368	16514	17874	18584	478	62
144_3_3	20620	22321	23193	438	22488	24336	25294	490	24128	26136	27154	522	102
192_3_3	22816	23977	24832	631	25108	26383	27320	708	26242	27588	28567	743	145
240_3_3	24209	25982	27348	655	26693	28731	30318	770	27859	29995	31632	803	192
288_3_3	28458	29693	30892	828	32742	34157	35530	957	35582	37120	38622	1048	245
360_3_3	37006	38610	40166	1079	40722	42474	44186	1198	47081	49427	51523	1399	288
平均值	23814	25010	25945	599	26395	27754	28775	650	26737	28107	29175	696	—

下载: 导出CSV

参考文献(43)

[1]	Dantzig G B, Ramser J H. The truck dispatching problem. Management Science, 1959, 6(1): 80−91 doi: 10.1287/mnsc.6.1.80
[2]	Anbuudayasankar S P, Ganesh K, Mohapatra S. Models for Practical Routing Problems in Logistics. Cham: Springer, 2014.
[3]	Li H Q, Yuan J L, Lv T, Chang X Y. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems considering carbon dioxide emissions. Transportation Research Part D: Transport and Environment, 2016, 49: 231−245 doi: 10.1016/j.trd.2016.10.002
[4]	赵燕伟, 张景玲, 王万良. 物流配送的车辆路径优化方法. 北京: 科学出版社, 2014. Zhao Yan-Wei, Zhang Jing-Ling, Wang Wan-Liang. Vehicle Routing Optimization Methods for Logistics Distribution. Beijing: Science Press, 2014.
[5]	Sbihi A, Eglese R W. Combinatorial optimization and green logistics. 4OR, 2007, 5(2): 99−116 doi: 10.1007/s10288-007-0047-3
[6]	Chen D S, Batson R G, Dang Y. Applied Integer Programming. Hoboken: John Wiley & Sons, 2010.
[7]	Jabir E, Panicker V V, Sridharan R. Design and development of a hybrid ant colony-variable neighbourhood search algorithm for a multi-depot green vehicle routing problem. Transportation Research Part D: Transport and Environment, 2017, 57: 422−457 doi: 10.1016/j.trd.2017.09.003
[8]	Kaabachi I, Jriji D, Krichen S. An improved ant colony optimization for green multi-depot vehicle routing problem with time windows. In: Proceedings of the 18th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD). Kanazawa, Japan: IEEE, 2017.
[9]	Xiao Y Y, Konak A. The heterogeneous green vehicle routing and scheduling problem with time-varying traffic congestion. Transportation Research Part E: Logistics and Transportation Review, 2016, 88: 146−166 doi: 10.1016/j.tre.2016.01.011
[10]	Kwon Y J, Choi Y J, Lee D H. Heterogeneous fixed fleet vehicle routing considering carbon emission. Transportation Research Part D: Transport and Environment, 2013, 23: 81−89 doi: 10.1016/j.trd.2013.04.001
[11]	Geetha S, Vanathi P T, Poonthalir G. Metaheuristic approach for the multi-depot vehicle routing problem. Applied Artificial Intelligence, 2012, 26(9): 878−901 doi: 10.1080/08839514.2012.727344
[12]	Geetha S, Poonthalir G, Vanathi P T. Nested particle swarm optimisation for multi-depot vehicle routing problem. International Journal of Operational Research, 2013, 16(3): 329−348 doi: 10.1504/IJOR.2013.052336
[13]	Ho W, Ho G T S, Ji P, Lau H C W. A hybrid genetic algorithm for the multi-depot vehicle routing problem. Engineering Applications of Artificial Intelligence, 2008, 21(4): 548−557 doi: 10.1016/j.engappai.2007.06.001
[14]	Wang Y, Assogba K, Liu Y, Ma X L, Xu M Z, Wang Y H. Two-echelon location-routing optimization with time windows based on customer clustering. Expert Systems With Applications, 2018, 104: 244−260 doi: 10.1016/j.eswa.2018.03.018
[15]	Dondo R, Cerdá J. A cluster-based optimization approach for the multi-depot heterogeneous fleet vehicle routing problem with time windows. European Journal of Operational Research, 2007, 176(3): 1478−1507 doi: 10.1016/j.ejor.2004.07.077
[16]	Tang Y L, Cai Y G, Yang Q J. Improved ant colony optimization for multi-depot heterogeneous vehicle routing problem with soft time windows. Journal of Southeast University (English Edition), 2015, 31(1): 94−99
[17]	Dorigo M, Maniezzo V, Colorni A. Ant system: Optimization by a colony of cooperating agents. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 1996, 26(1): 29−41 doi: 10.1109/3477.484436
[18]	王素欣, 高利, 崔小光, 曹宏美. 多需求点车辆调度模型及其群体智能混合求解. 自动化学报, 2008, 34(1): 102−104 Wang Su-Xin, Gao Li, Cui Xiao-Guang, Cao Hong-Mei. Study on multi-requirement points vehicle scheduling model and its swarm mix algorithm. Acta Automatica Sinica, 2008, 34(1): 102−104
[19]	Lee C Y, Lee Z J, Lin S W, Ying K C. An enhanced ant colony optimization (EACO) applied to capacitated vehicle routing problem. Applied Intelligence, 2010, 32(1): 88−95 doi: 10.1007/s10489-008-0136-9
[20]	Yu B, Yang Z Z. An ant colony optimization model: The period vehicle routing problem with time windows. Transportation Research Part E: Logistics and Transportation Review, 2011, 47(2): 166−181 doi: 10.1016/j.tre.2010.09.010
[21]	Ding Q L, Hu X P, Sun L J, Wang Y Z. An improved ant colony optimization and its application to vehicle routing problem with time windows. Neurocomputing, 2012, 98: 101−107 doi: 10.1016/j.neucom.2011.09.040
[22]	Yan F L. Autonomous vehicle routing problem solution based on artificial potential field with parallel ant colony optimization (ACO) algorithm. Pattern Recognition Letters, 2018, 116: 195−199 doi: 10.1016/j.patrec.2018.10.015
[23]	陈希琼, 胡大伟, 杨倩倩, 胡卉, 高扬. 多目标同时取送货车辆路径问题的改进蚁群算法. 控制理论与应用, 2018, 35(9): 1347−1356 doi: 10.7641/CTA.2018.80085 Chen Xi-Qiong, Hu Da-Wei, Yang Qian-Qian, Hu Hui, Gao Yang. An improved ant colony algorithm for multi-objective vehicle routing problem with simultaneous pickup and delivery. Control Theory & Applications, 2018, 35(9): 1347−1356 doi: 10.7641/CTA.2018.80085
[24]	Xu H T, Pu P, Duan F. Dynamic vehicle routing problems with enhanced ant colony optimization. Discrete Dynamics in Nature and Society, 2018, 2018: Article No. 1295485
[25]	Demir E, Bektaš T, Laporte G. An adaptive large neighborhood search heuristic for the pollution-routing problem. European Journal of Operational Research, 2012, 223(2): 346−359 doi: 10.1016/j.ejor.2012.06.044
[26]	Bektaš T, Gouveia L. Requiem for the Miller-Tucker-Zemlin subtour elimination constraints. European Journal of Operational Research, 2014, 236(3): 820−832 doi: 10.1016/j.ejor.2013.07.038
[27]	Toth P, Vigo D. 车辆路径问题. 北京: 清华大学出版社, 2011. Toth P, Vigo D. The Vehicle Routing Problem. Beijing: Tsinghua University Press, 2011.
[28]	Wolsey L A. Integer Programming. New York: Wiley, 1998.
[29]	Schneider M, Stenger A, Goeke D. The electric vehicle-routing problem with time windows and recharging stations. Transportation Science, 2014, 48(4): 500−520 doi: 10.1287/trsc.2013.0490
[30]	Gu S S. A polynomial time solvable algorithm to linearly constrained binary quadratic programming problems with Q being a tri-diagonal matrix. In: Proceedings of the 5th International Conference on Intelligent Control and Information Processing (ICCIP). Dalian, China: IEEE, 2011.
[31]	Meng X H, Li J, Zhou M C, Dai X Z, Dou J P. Population-based incremental learning algorithm for a serial colored traveling salesman problem. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(2): 277−288 doi: 10.1109/TSMC.2016.2591267
[32]	Wang Y, Ma X L, Lao Y T, Wang Y H. A fuzzy-based customer clustering approach with hierarchical structure for logistics network optimization. Expert Systems With Applications, 2014, 41(2): 521−534 doi: 10.1016/j.eswa.2013.07.078
[33]	Wang Y, Zhang J, Assogba K, Liu Y, Xu M Z, Wang Y H. Collaboration and transportation resource sharing in multiple centers vehicle routing optimization with delivery and pickup. Knowledge-Based Systems, 2018, 160: 296−310 doi: 10.1016/j.knosys.2018.07.024
[34]	Wang B D, Miao Y W, Zhao H Y, Jin J, Chen Y Z. A biclustering-based method for market segmentation using customer pain points. Engineering Applications of Artificial Intelligence, 2016, 47: 101−109 doi: 10.1016/j.engappai.2015.06.005
[35]	Ji J C, Pang W, Zhou C G, Han X, Wang Z. A fuzzy k-prototype clustering algorithm for mixed numeric and categorical data. Knowledge-Based Systems, 2012, 30: 129−135 doi: 10.1016/j.knosys.2012.01.006
[36]	Wang Y, Ma X L, Liu M W, Gong K, Liu Y, Xu M Z, et al. Cooperation and profit allocation in two-echelon logistics joint distribution network optimization. Applied Soft Computing, 2017, 56: 143−157 doi: 10.1016/j.asoc.2017.02.025
[37]	He R H, Xu W B, Sun J X, Zu B Q. Balanced k-means algorithm for partitioning areas in large-scale vehicle routing problem. In: Proceedings of the 3rd International Symposium on Intelligent Information Technology Application. Nanchang, China: IEEE, 2009.
[38]	王东风, 孟丽. 粒子群优化算法的性能分析和参数选择. 自动化学报, 2016, 42(10): 1552−1561 doi: 10.16383/j.aas.2016.c150774 Wang Dong-Feng, Meng Li. Performance analysis and parameter selection of PSO algorithms. Acta Automatica Sinica, 2016, 42(10): 1552−1561 doi: 10.16383/j.aas.2016.c150774
[39]	Beasley J E. Route first―Cluster second methods for vehicle routing. Omega, 1983, 11(4): 403−408 doi: 10.1016/0305-0483(83)90033-6
[40]	Gillett B E, Miller L R. A heuristic algorithm for the vehicle-dispatch problem. Operations Research, 1974, 22(2): 340−349 doi: 10.1287/opre.22.2.340
[41]	Yu B, Yang Z Z, Yao B Z. An improved ant colony optimization for vehicle routing problem. European Journal of Operational Research, 2009, 196(1): 171−176 doi: 10.1016/j.ejor.2008.02.028
[42]	Mladenović N, Hansen P. Variable neighborhood search. Computers & Operations Research, 1997, 24(11): 1097−1100
[43]	李进, 傅培华. 具有固定车辆数的多车型低碳路径问题及算法. 计算机集成制造系统, 2013, 19(6): 1351−1362 doi: 10.13196/j.cims.2013.06.189.lij.007 Li Jin, Fu Pei-Hua. Heterogeneous fixed fleet low-carbon routing problem and algorithm. Computer Integrated Manufacturing Systems, 2013, 19(6): 1351−1362 doi: 10.13196/j.cims.2013.06.189.lij.007