-
摘要:
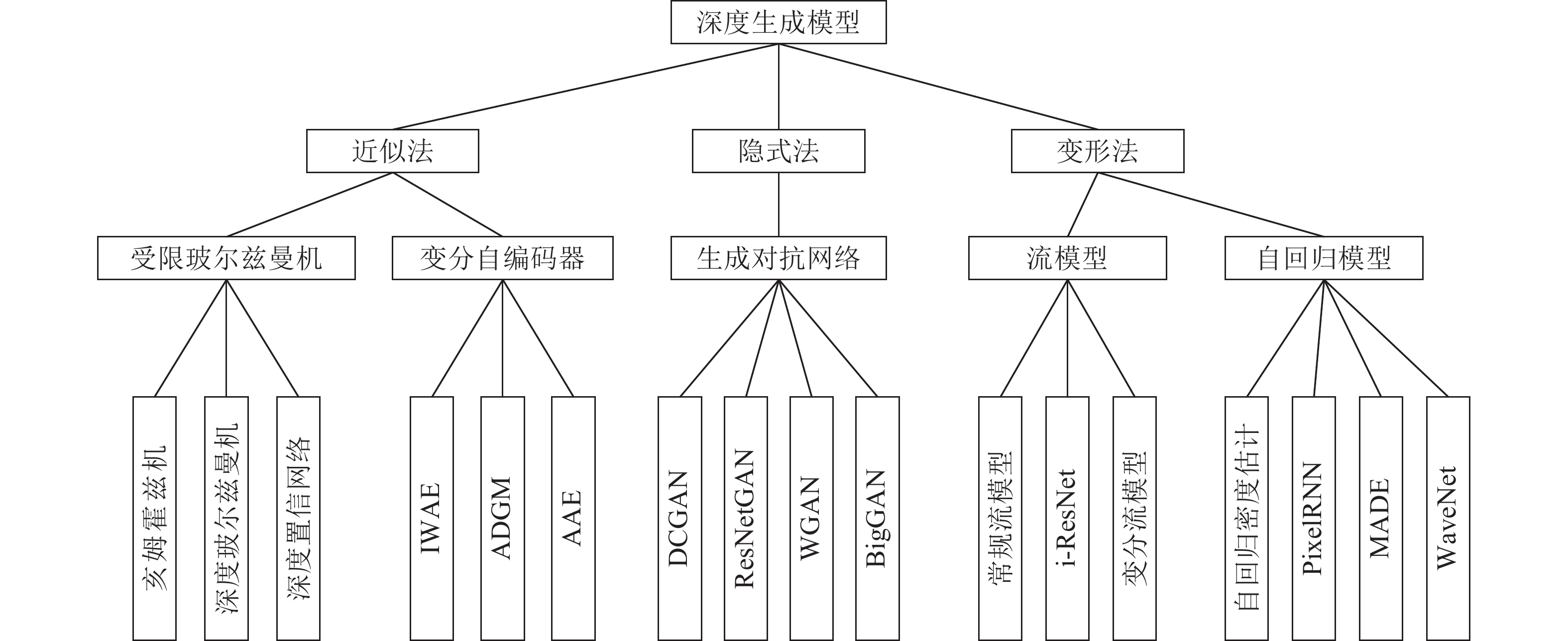
通过学习可观测数据的概率密度而随机生成样本的生成模型在近年来受到人们的广泛关注, 网络结构中包含多个隐藏层的深度生成式模型以更出色的生成能力成为研究热点, 深度生成模型在计算机视觉、密度估计、自然语言和语音识别、半监督学习等领域得到成功应用, 并给无监督学习提供了良好的范式. 本文根据深度生成模型处理似然函数的不同方法将模型分为三类: 第一类方法是近似方法, 包括采用抽样方法近似计算似然函数的受限玻尔兹曼机(Restricted Boltzmann machine, RBM)和以受限玻尔兹曼机为基础模块的深度置信网络(Deep belief network, DBN)、深度玻尔兹曼机(Deep Boltzmann machines, DBM)和亥姆霍兹机, 与之对应的另一种模型是直接优化似然函数变分下界的变分自编码器以及其重要的改进模型, 包括重要性加权自编码和可用于半监督学习的深度辅助深度模型; 第二类方法是避开求极大似然过程的隐式方法, 其代表模型是通过生成器和判别器之间的对抗行为来优化模型参数从而巧妙避开求解似然函数的生成对抗网络以及重要的改进模型, 包括WGAN、深度卷积生成对抗网络和当前最顶级的深度生成模型BigGAN; 第三类方法是对似然函数进行适当变形的流模型和自回归模型, 流模型利用可逆函数构造似然函数后直接优化模型参数, 包括以NICE为基础的常规流模型、变分流模型和可逆残差网络(i-ResNet), 自回归模型(NADE)将目标函数分解为条件概率乘积的形式, 包括神经自回归密度估计(NADE)、像素循环神经网络(PixelRNN)、掩码自编码器(MADE)以及WaveNet等. 详细描述上述模型的原理和结构以及模型变形后, 阐述各个模型的研究进展和应用, 最后对深度生成式模型进行展望和总结.
Abstract:The generative model, which can generate samples randomly by learning the probability density of observable data, has been widely concerned for the past few years. It has been successfully applied in a wide range of fields, such as image generation, image restoration, density estimation, natural language and speech recognition, style transfer and super resolution, and so on. Deep generative model with multiple hidden layers in the network structure becomes a research hotspot because of its better generation ability. Depending on the different methods of calculating the maximum likelihood function, we divide the models into three types: the first kind of method is the approximate method, which use the sampling method to calculate approximately the likelihood function, such as Restricted Boltzmann machines (RBM) and Deep belief network (DBN), Deep Boltzmann machines (DBM), helmholtz machine based on RBM. The alternatives are to optimize directly the variational lower bound of likelihood function, it is named as variational autoencoder. The important improvements to these variants include importance weighted autoencoders and auxiliary deep generative models; the second kind is implicit methods, the representative model is generative adversarial nets (GAN), GAN's model parameters is optimized by the adversaring behavior between the generator and the discriminator. The principal instantiations of GAN include Wasserstein GAN, deep convolutional generative adversarial networks and BigGAN. The third kind involve flow and neural autoregressive net, the main variations of the flow paradigm include normalizing flow based on nonlinear independent components estimation, invertible residual networks and variational inference with flow. The successful improvements to the neural autoregressive net include neural autoregressive distribution estimation, pixel recurrent neural network, masked autoencoder for distribution estimation and WaveNet. We outline the principle and structure of these deep generative models, and look forward to the future work.
1) 收稿日期 2019-12-19 录用日期 2020-07-27 Manuscript received December 19, 2019; accepted July 27, 2020 中国石油大学(北京)科研基金(2462020YXZZ023)资助 Supported by the Science Foundation of China University of Petroleum, Beijing (2462020YXZZ023)2) 本文责任编委 朱军 Recommended by Associate Editor ZHU Jun 1. 中国石油大学(北京)自动化系 北京 102249 1. Department of Automation, China University of Petroleum, Beijing 102249 -
表 1 基于RBM的模型
Table 1 RBM based models
方法名称 改进方式 改进目的 核心方法 rtRBM 训练算法 提高模型性能 改进回火 RBM, 加入循环机制 ReLU-RBM 激活函数 改善训练效果 将线性修正单元引入到 RBM 中 3-Order RBM 模型结构 提高模型性能 将可见单元和隐单元分解成三元交互隐单元控制可见单元协方差和阈值 PGBM 模型结构 结构扩展 在 RBM 中使用门控单元用于特征选择 RBM-SVM 模型结构 提高模型性能 上层 RBM 用于特征提取下层 SVM 进行回归 RNN-RBM 模型结构 结构扩展 RBM 与循环网络结合 apRBM 模型结构 结构扩展 构造层权重之间的确定性函数 cRBM 模型结构 实现监督学习 将自回归结构和标签信息应用到 RBM Factored- cRBM 模型结构 提高模型性能 将三元交互方法用在条件 RBM 中 Gaussian-Bernoulli RBM 数据类型 将 RBM 推广到实值 可见单元为参数化高斯分布, 隐藏单元为参数化伯努利分布 mcRBM 模型结构 捕获同层神经元之间的关系 在隐藏层中添加协方差单元对条件协方差结构建模 ssRBM 模型结构 捕获同层神经元之间的关系 使用辅助实值变量编码条件协方差 mPoT 模型结构 捕获同层神经元之间的关系 添加非零高斯均值的隐变量条件分布为条件独立的 Gamma 分布 fBMMI-DBN 训练算法 改进预训练算法 用梅尔频率倒谱系数训练 DBN 产生特征以预测 HMM 状态上的后验分布 CDBN 模型结构 结构扩展 DBN 与卷积结构结合 3-Order DBN 模型结构 提高模型性能 将三元交互方法用在 DBN 中 fsDBN 训练算法 提高模型性能 用连续判别训练准则优化权值、状态变换参数和语言模型分数 DBN-HMM 模型结构 提高模型性能 DBN 与隐马尔科夫模型结合 CAST 训练算法 改进训练算法 将自适应算法和 MCMC 结合训练 DBN Trans-SAP 训练算法 改进训练算法 将回火算法和 MCMC 结合训练 DBN aiDBM 训练算法 改进训练算法 提出一种近似推断算法, 用单独的识别模型加速 DBN 训练速度 Centered DBM 训练算法 改进训练算法 通过重参数化模型使开始学习时代价函数的 Hessian 具有更好的条件数 MP-DBM 训练算法 改进训练算法 允许反向传播算法, 避免 MCMC 估计梯度带来的训练问题 CDBM 模型结构 结构扩展 DBM 与卷积结构结合 表 2 重要的VAE模型
Table 2 Important VAE models
方法名称 主要贡献 核心方法 CVAE 使 VAE 实现监督学习 在输入数据中加入 one-hot 向量用于表示标签信息 ADGM 提高 CVAE 处理标签信息的能力 在 VAE 中同时引入标签信息和辅助变量用 5 个神经网络构造各变量之间的关系 kg-CVAE 提高生成样本的多样性 在 ADGM 上引入额外损失(Bag-of-words loss)使隐变量包含单词出现概率的信息 hybrid-CVAE 用 CVAE 建立鲁棒的结构化预测算法 输入中加入噪声、使用随机前馈推断构造带有随机高斯网络的混合变分下界: $L(x) = \alpha {L_{{\rm{CVAE}}}} + (1 - \alpha ){L_{{\rm{GSNN}}}}$ SSVAE 使 VAE 实现半监督学习 构造两个模型: M2 为半监督模型 M1 模型为 VAE 用于提升 M2 的能力 IMVAE 提高 SSVAE 处理混合信息的能力 用非参数贝叶斯方法构造无限混合模型混合系数由 Dirichlet 过程获得 AAE 使模型可以学习出后验分布 构造聚合的伪先验分布匹配真实分布在隐变量处附加一个对抗网络学习伪先验分布 ARAE 使 AAE 能够处理离散结构 编码器和解码器采用循环神经网络里变分下界中添加额外的正则项 IWAE 使后验分布的假设更符合真实后验分布 构造比 VAE 更紧的变分下界形式, 通过弱化变分下界中编码器的作用提升变分推断的能力 DC-IGN 保留图片样本中的局部相关性 用卷积层和池化层替代原来的全连接网络 infoVAE 提高隐变量和可观测变量之间的互信息,
使近似后验更逼近真实后验分布在变分下界中引入互信息: $\alpha {I_q}(x)$ β-VAE 从原始数据中获取解开纠缠的可解释隐表示 在变分下界中添加正则系数:
$L(x) = { {\rm{E} }_{Q(z| x )} }(\log P(x|z)) - \beta {D_{ {\rm{KL} } } }(Q(z| x )||P(z))$β-TCVAE 解释 β-VAE 能够解开纠缠的原因并提升模型性能 在 β-VAE 变分下界中引入互信息和额外正则项: $ - {I_q}(z)$和$ - {D_{{\rm{KL}}}}(Q(x)||P(x))$ HFVAE 使 VAE 对离散变量解开纠缠总结主流 VAE 的变分下界 对变分下界分解成 4 项并逐一解释作用:
$\begin{aligned} L(x) =& { {\rm{E} }_{Q(z| x )} }[\log { {(P(x|z)} / {P(x)} }) - \log { {(Q(z|x)} / {Q(z)} })] -\\& {D_{ {\rm{KL} } } }(Q(z)||P(z)) - {D_{ {\rm{KL} } } }(Q(x)||P(z)) \end{aligned}$DRAM 处理时间序列样本 在 VAE 框架中引入注意力机制和长短时记忆网络结构 MMD-VAE 用最大平均差异替换KL散度 将变分下界中的KL散度项替换成: ${D_{{\rm{MMD}}}}(Q(x)||P(x))$ HVI 使用精度更高的抽样法替代重参数方法 用 Hamiltonian Monte Carlo 抽样替换重参数化方法直接对后验分布抽样以获得更精确的后验近似 VFAE 学习敏感或异常数据时使隐变量保留更多的信息 在变分下界中附加基于最大平均差异的惩罚项:
$\sqrt {2/D} \cos (\sqrt {2/r} xW + b)$LVAE 逐层、递归的修正隐变量的分布, 使变分下界更紧 利用多层的隐变量逐层构造更复杂的分布在变分下界中使用预热法 wd-VAE 解决输入缺失词情况下的语言生成 将输入文本转换成 UNK 格式并进行 dropout 操作使解码器的 RNN 更依赖隐变量表示 VLAE 用流模型学习出更准确的后验分布 用流模型学习的后验分布替代高斯分布, 根据循环网络学到的全局表示抛弃无关信息 PixelVAE 捕获样本元素间的关系以生成更清晰锐利的图片样本 将隐变量转成卷积结构, 解码器使用PixelCNNCNN只需要很少几层, 压缩了计算量 DCVAE 通过调整卷积核的宽度改善解码器理解编码器信息的能力 在解码器中使用扩张卷积加大感受野对上下文容量与有效的编码信息进行权衡 MSVAE 用双层解码器提高模型生成高清图像的能力 第一层解码器生成粗略的样本第二层解码器使用残差方法和跳跃连接的超分模型将模糊样本作为输入生成高清样本 表 3 重要的GAN模型
Table 3 Important GANs
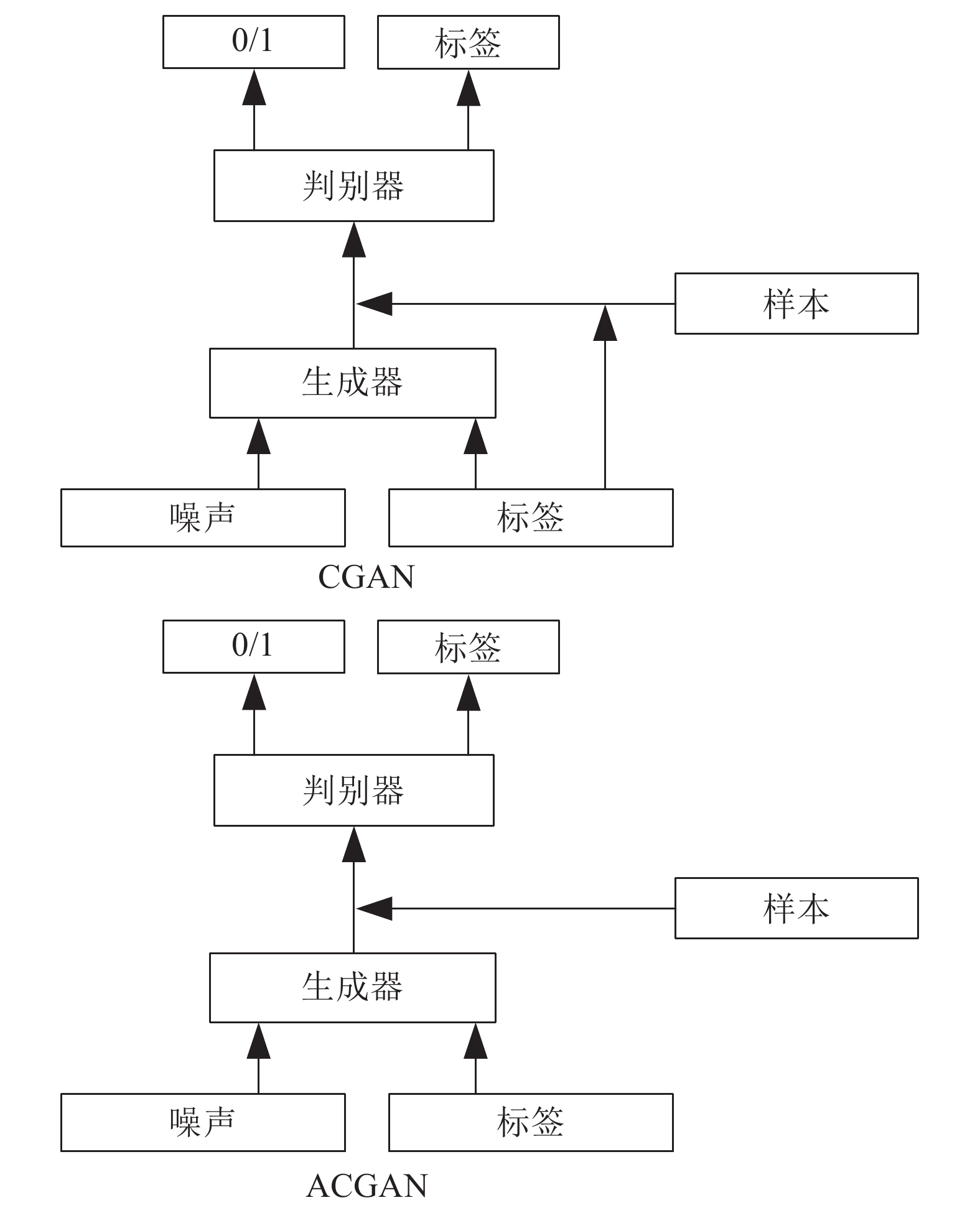
模型名称 核心方法 生成图片类型 生成最高分辨率 CGAN 将标签信息作为附加信息输入到生成器中再与生成样本一起输入到判别器中 MNIST $28 \times 28$ DCGAN 在多种结构中筛选出最优的一组生成器和判别器生成器和判别器均使用深度卷积网络 LSUN
FACES
ImageNet-1k$32 \times 32$ VAE-GAN 在VAE结构外嵌套GAN的框架, 用GAN中的判别器学习VAE的两个分布间的相似程度 CelebA
LFW$64 \times 64$ BiGAN 生成器是输入输出不相关的编码器和解码器判别器同时输入样本和隐变量判断两者来自编码器还是解码器 MNIST
ImageNet$64 \times 64$ CoGAN 在实现风格转换学习时, 为了让两个编码器的输出尽量接近, 共享两者的最后几层参数 MNIST
CelebA$64 \times 64$ Info-GAN 将噪声$z$拆分成子向量$c$和$z'$子向量$c$用于调节输出的类别和形状等条件信息用额外的判别器判定生成样本的子向量$c$ MNIST
SVHN$64 \times 64$ LSGAN 使用最小二乘损失函数最小二乘可以将图像的分布尽可能接近决策边界 LSUN
HWDB$64 \times 64$ WGAN 从理论上分析GAN训练不稳定的原因通过使用Wasserstein距离等方法提高了训练稳定性 LSUN $64 \times 64$ f-GAN 证明了任意散度都适用于GAN框架 MNIST
LSUN$96 \times 96$ LAPGAN 基于拉普拉斯金字塔结构逐层增加样本分辨率上层高分图像的生成以下层低分图像为条件 CIFAR10
LSUN
STL$96 \times 96$ WGAN-GP 将判别器的梯度作为正则项加入到判别器的损失函数中 ImageNet
CIFAR10
LSUN$128 \times 128$ SNGAN 使用谱归一化代替梯度惩罚 CIFAR10
STL10
ImageNet$128 \times 128$ Improved-DCGAN 使用多种方法对DCGAN的稳定性和生成效果进一步加强 MNIST
CIFAR10
SVHN
ImageNet$128 \times 128$ EBGAN 将判别器的功能改为鉴别输入图像重构性的高低, 生成器可以在刚开始训练时获得较大的能力驱动(Energy based)并在短期内获得效果不错的生成器 MNIST
LSUN
CelebA
ImageNet$128 \times 128$ BEGAN 判别器为自编码结构, 用于估计分布之间的误差分布提出使用权衡样本多样性和质量的超参数 CelebA $128 \times 128$ ACGAN 每个样本都有类标签类标签同时输入到生成器和判别器中 ImageNet
CIFAR10$128 \times 128$ SAGAN 用自注意力机制代替卷积层进行特征提取 ImageNet $128 \times 128$ SRGAN 生成器用低分图像生成高分图像判别器判断图像是生成器生成的还是真实图像 StackGAN 第一阶段使用CGAN生成$64 \times 64$的低分图像第二阶段以低分图像和文本为输入, 用另一个GAN生成高分图像 CUB
Oxford-102
COCO$256 \times 256$ StackGAN++ 在StackGAN的基础上用多个生成器生成不同尺度的图像, 每个尺度有相应的判别器引入非条件损失和色彩正则化项 CUB
Oxford-102
COCO$256 \times 256$ Cycle-GAN 由两个对称的GAN构成的环形网络两个GAN共享两个生成器, 各自使用单独的判别器 Cityscapes label $256 \times 256$ Star-GAN 为了实现多个领域的转换引入域的控制信息判别器需要额外判断真实样本来自哪个域 CelebA
RaFD$256 \times 256$ BigGAN 训练时增加批次数量和通道数让权重矩阵为正交矩阵, 降低权重系数的相互干扰 ImageNet
JFT-300M$512 \times 512$ PGGAN 网络结构可以随着训练进行逐渐加深使用浅层网络训练好低分图像后加深网络深度训练分辨率更高的图像 CelebA
LSUN$1024 \times 1024$ Style-GAN 在PGGAN的基础上增加映射网络、样式模块增加随机变换、样式混合等功能块使用新的权重截断技巧 FHHQ $1024 \times 1024$ -
[1] Smolensky P. Information processing in dynamical systems: Foundations of harmony theory. In: Proceedings of the 1986 Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations. Cambridge, United States: MIT Press, 1986. 194−281 [2] Kingma D P, Welling M. Auto-encoding variational bayes. arXiv: 1312.6114, 2013 [3] Goodfellow I J, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. In: Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2014. 2672−2680 [4] Bengio Y, Thibodeau-Laufer E, Alain G, Yosinski J. Deep generative stochastic networks trainable by backprop. In: Proceedings of the 31st International Conference on Machine Learning. Beijing, China: JMLR.org, 2014. II-226−II-234 [5] Dinh L, Krueger D, Bengio Y. NICE: Non-linear independent components estimation. arXiv: 1410.8516, 2014 [6] Larochelle H, Murray I. The neural autoregressive distribution estimator. In: Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, USA: JMLR, 2011. 29−37 [7] Salakhutdinov R. Learning deep generative models. Annual Review of Statistics and Its Application, 2015, 2(1): 361-385 doi: 10.1146/annurev-statistics-010814-020120 [8] 刘建伟, 刘媛, 罗雄麟. 玻尔兹曼机研究进展. 计算机研究与发展, 2014, 51(1): 1-16 doi: 10.7544/issn1000-1239.2014.20121044Liu Jian-Wei, Liu Yuan, Luo Xiong-Lin. Research and development on Boltzmann machine. Journal of Computer Research and Development, 2014, 51(1): 1-16 doi: 10.7544/issn1000-1239.2014.20121044 [9] Salakhutdinov R, Hinton G E. Replicated softmax: An undirected topic model. In: Proceedings of the 22nd International Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates Inc., 2009. 1607−1614 [10] Hyvarinen A. Some extensions of score matching. Computational Statistics & Data Analysis, 2007, 51(5): 2499-2512 [11] Gutmann M, Hyvarinen A. Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS). Cagliari, Italy: JMLR, 2010. 297−304 [12] Hyvarinen A. Estimation of non-normalized statistical models by score matching. Journal of Machine Learning Research, 2005, 6(4): 695-709 [13] Hinton G E. Training products of experts by minimizing contrastive divergence. Neural Computation, 2002, 14(8): 1771-1800 doi: 10.1162/089976602760128018 [14] Cho K H, Raiko T, Ilin A. Parallel tempering is efficient for learning restricted Boltzmann machines. In: Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN). Barcelona, Spain: IEEE, 2012. 1−8 [15] Tieleman T, Hinton G E. Using fast weights to improve persistent contrastive divergence. In: Proceedings of the 26th Annual International Conference on Machine Learning. Montreal, Canada: ACM, 2009. 1033−1044 [16] Carreira-Perpiñan M A, Hinton G E. On contrastive divergence learning. In: Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics. Bridgetown, Barbados: Society for Artificial Intelligence and Statistics, 2005. 33−40 [17] Bengio Y, Delalleau O. Justifying and generalizing contrastive divergence. Neural Computation, 2009, 21(6): 1601-1621 doi: 10.1162/neco.2008.11-07-647 [18] Jarzynski C. Nonequilibrium equality for free energy differences. Physical Review Letters, 1997, 78(14): 2690-2693 doi: 10.1103/PhysRevLett.78.2690 [19] Montufar G, Rauh J, Ay N. Expressive power and approximation errors of restricted Boltzmann machines. In: Proceedings of the 24th International Conference on Neural Information Processing Systems. Granada, Spain: Curran Associates Inc., 2011. 415−423 [20] Sutskever I, Hinton G, Taylor G. The recurrent temporal restricted Boltzmann machine. In: Proceedings of the 21st International Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates Inc., 2008. 1601−1608 [21] Nair V, Hinton G E. Rectified linear units improve restricted Boltzmann machines. In: Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel: Omnipress, 2010. 807−814 [22] Ranzato M A, Krizhevsky A, Hinton G E. Factored 3-way restricted Boltzmann machines for modeling natural images. In: Proceedings of the 13th International Conference on Artificial Intelligence and Statistics. Cagliari, Italy: JMLR, 2010. 621−628 [23] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527-1554 doi: 10.1162/neco.2006.18.7.1527 [24] Taylor G W, Hinton G E, Roweis S. Modeling human motion using binary latent variables. In: Proceedings of the 19th International Conference on Neural Information Processing Systems. Vancouver, Canada: MIT Press, 2006. 1345−1352 [25] Dayan P, Hinton G E, Neal R M, Zemel R S. The Helmholtz machine. Neural Computation, 1995, 7(5): 889-904 doi: 10.1162/neco.1995.7.5.889 [26] Hinton G E, Dayan P, Frey B J, Neal R M. The “wake-sleep” algorithm for unsupervised neural networks. Science, 1995, 268(5214): 1158-1161 doi: 10.1126/science.7761831 [27] Mohamed A R, Yu D, Deng L. Investigation of full-sequence training of deep belief networks for speech recognition. In: Proceedings of the 11th Annual Conference of the International Speech Communication Association. Makuhari, Japan: ISCA, 2010. 2846−2849 [28] Dahl G E, Yu D, Deng L, Acero A. Large vocabulary continuous speech recognition with context-dependent DBN-HMMS. In: Proceedings of the 2011 International Conference on Acoustics, Speech and Signal Processing (ICASSP). Prague, Czech Republic: IEEE, 2011. 4688−4691 [29] Salakhutdinov R, Hinton G E. Using deep belief nets to learn covariance kernels for Gaussian processes. In: Proceedings of the 20th International Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates Inc., 2007. 1249−1256 [30] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507 doi: 10.1126/science.1127647 [31] Lee H, Grosse R, Ranganath R, Ng A Y. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In: Proceedings of the 26th Annual International Conference on Machine Learning. Montreal, Canada: ACM, 2009. 609−616 [32] Salakhutdinov R, Hinton G E. Deep Boltzmann machines. In: Proceedings of the 12th International Conference on Artificial Intelligence and Statistics. Clearwater Beach, USA: JMLR, 2009. 448−455 [33] Montavon G, Muller K R. Deep Boltzmann machines and the centering trick. Neural Networks: Tricks of the Trade. Berlin, Heidelberg: Springer, 2012. 621−637 [34] Melchior J, Fischer A, Wiskott L. How to center deep Boltzmann machines. The Journal of Machine Learning Research, 2016, 17(1): 3387-3447 [35] Goodfellow I J, Mirza M, Courville A, Bengio Y. Multi-prediction deep Boltzmann machines. In: Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc., 2013. 548−556 [36] Salakhutdinov R. Learning in Markov random fields using tempered transitions. In: Proceedings of the 22nd International Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates Inc., 2009. 1598−1606 [37] Hinton G E. To recognize shapes, first learn to generate images. Progress in Brain Research, 2007, 165: 535-547 [38] Mohamed A, Sainath T N, Dahl G, Ramabhadran B, Hinton G H, Picheny M A. Deep belief networks using discriminative features for phone recognition. In: Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Prague, Czech Republic: IEEE, 2011. 5060−5063 [39] Ghahabi O, Hernando J. Deep belief networks for i-vector based speaker recognition. In: Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Florence, Italy: IEEE, 2014. 1700−1704 [40] Deselaers T, Hasan S, Bender O, Ney H. A deep learning approach to machine transliteration. In: Proceedings of the 4th Workshop on Statistical Machine Translation. Athens, Greece: Association for Computational Linguistics, 2009. 233−241 [41] Abdollahi B, Nasraoui O. Explainable restricted Boltzmann machines for collaborative filtering. In: Proceedings of the 2016 ICML Workshop on Human Interpretability in Machine Learning (WHI 2016). New York, USA: ACM, 2016. 31−35 [42] Xing L N, Demertzis K, Yang J H. Identifying data streams anomalies by evolving spiking restricted Boltzmann machines. Neural Computing and Applications, 2020, 32(11): 6699-6713 doi: 10.1007/s00521-019-04288-5 [43] Zheng J, Fu X, Zhang G J. Research on exchange rate forecasting based on deep belief network. Neural Computing and Applications, 2019, 31(1): 573-582 [44] Mnih V, Larochelle H, Hinton G E. Conditional restricted Boltzmann machines for structured output prediction. arXiv: 1202.3748, 2012 [45] Paisley J, Blei D, Jordan M. Variational Bayesian inference with stochastic search. arXiv: 1206.6430, 2012 [46] Theis L, van den Oord A, Bethge M. A note on the evaluation of generative models. arXiv: 1511.01844, 2015 [47] Burda Y, Grosse R, Salakhutdinov R. Importance weighted autoencoders. arXiv: 1509.00519, 2015 [48] Sohn K, Yan X C, Lee H. Learning structured output representation using deep conditional generative models. In: Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2015. 3483−3491 [49] Walker J, Doersch C, Gupta A, Hebert M. An uncertain future: Forecasting from static images using variational autoencoders. In: Proceedings of the 14th European Conference on Computer Vision. Amsterdam, The Netherlands: Springer, 2016. 835−851 [50] Abbasnejad M E, Dick A, van den Hengel A. Infinite variational autoencoder for semi-supervised learning. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recpgnition (CVPR). Honolulu, USA: IEEE, 2017. 781−790 [51] Xu W D, Tan Y. Semisupervised text classification by variational autoencoder. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(1): 295-308 doi: 10.1109/TNNLS.2019.2900734 [52] Maal\oe L, S\onderby C K, S\onderby S K, Winther O. Auxiliary deep generative models. arXiv: 1602.05473, 2016 [53] Kingma D P, Rezende D J, Mohamed S, Welling M. Semi-supervised learning with deep generative models. In: Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2014. 3581−3589 [54] Kulkarni T D, Whitney W F, Kohli P, Tenenbaum J B. Deep convolutional inverse graphics network. In: Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2015. 2539−2547 [55] Makhzani A, Shlens J, Jaitly N, Goodfellow I, Frey B. Adversarial autoencoders. arXiv: 1511.05644, 2015 [56] Zhao S J, Song J M, Ermon S. InfoVAE: Information maximizing variational autoencoders. arXiv: 1706.02262, 2017 [57] Higgins I, Matthey L, Pal A, Burgess C, Glorot X, Botvinick M, et al. β-VAE: Learning basic visual concepts with a constrained variational framework. In: Proceedings of the 5th International Conference on Learning Representations. Toulon, France: OpenReview.net, 2017. [58] S\onderby C K, Raiko T, Maal\oe L, S\onderby S K, Winther O. Ladder variational autoencoders. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016. 3745−3753 [59] Cai L, Gao H Y, Ji S W. Multi-stage variational auto-encoders for coarse-to-fine image generation. arXiv: 1705.07202, 2017 [60] van den Oord A, Vinyals O, Kavukcuoglu K. Neural discrete representation learning. In: Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 6306−6315 [61] Razavi A, van den Oord A, Vinyals O. Generating diverse high-fidelity images with VQ-VAE-2. In: Proceedings of the 33rd Conference on Neural Information Processing Systems. Vancouver, Canada, 2019. 14866−14876 [62] Salimans T, Kingma D, Welling M. Markov chain Monte Carlo and variational inference: Bridging the gap. In: Proceedings of the 32nd International Conference on Machine Learning. Lille, France: JMLR, 2015. 1218−1226 [63] Gregor K, Danihelka I, Graves A, Rezende D J, Wierstra D. DRAW: A recurrent neural network for image generation. arXiv: 1502.04623, 2015 [64] Chen R T Q, Li X C, Grosse R, Duvenaud D. Isolating sources of disentanglement in variational autoencoders. In: Proceedings of the 32nd Conference on Neural Information Processing Systems. Montreal, Canada: Curran Associates Inc., 2018. 2610−2620 [65] Gregor K, Besse F, Rezende D J, Danihelka I, Wierstra D. Towards conceptual compression. In: Proceedings of the 30th Conference on Neural Information Processing Systems. Barcelona, Spain: MIT Press, 2016. 3549−3557 [66] Bowman S R, Vilnis L, Vinyals O, Dai A M, Jozefowicz R, Bengio S. Generating sentences from a continuous space. arXiv: 1511.06349, 2015 [67] Kusner M J, Paige B, Hernandez-Lobato J M. Grammar variational autoencoder. In: Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia: JMLR.org, 2017. 1945−1954 [68] Jang M, Seo S, Kang P. Recurrent neural network-based semantic variational autoencoder for sequence-to-sequence learning. Information Sciences, 2019, 490: 59-73 doi: 10.1016/j.ins.2019.03.066 [69] Ravanbakhsh S, Lanusse F, Mandelbaum R, Schneider J, Poczos B. Enabling dark energy science with deep generative models of galaxy images. In: Proceedings of 31st AAAI Conference on Artificial Intelligence. San Francisco, California, USA: AAAI, 2017. 1488−1494 [70] Li X P, She J. Collaborative variational autoencoder for recommender systems. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax, NS, Canada: ACM, 2017. 305−314 [71] White T. Sampling generative networks. arXiv: 1609.04468, 2016 [72] Gomez-Bombarelli R, Wei J N, Duvenaud D, Hernandez-Lobato J M, Sanchez-Lengeling B, Sheberla D, et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Science, 2018, 4(2): 268-276 doi: 10.1021/acscentsci.7b00572 [73] Arjovsky M, Bottou L. Towards principled methods for training generative adversarial networks. arXiv: 1701.04862, 2017 [74] Huszar F. How (not) to train your generative model: Scheduled sampling, likelihood, adversary? arXiv: 1511.05101, 2015 [75] Arjovsky M, Chintala S, Bottou L. Wasserstein GAN. arXiv: 1701.07875, 2017 [76] Nowozin S, Cseke B, Tomioka R. f-GAN: Training generative neural samplers using variational divergence minimization. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016. 271−279 [77] Gulrajani I, Ahmed F, Arjovsky M, Dumonlin V, Courville A C. Improved training of wasserstein GANs. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 5769−5779 [78] Miyato T, Kataoka T, Koyama M, Yoshida Y. Spectral normalization for generative adversarial networks. In: Proceedings of the 6th International Conference on Learning Representations. Vancouver, Canada: OpenReview.net, 2018. [79] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. In: Proceedings of the 4th International Conference on Learning Representations. San Juan, Puerto Rico: JMLR, 2016. [80] Shaham T R, Dekel T, Michaeli T. SinGAN: Learning a generative model from a single natural image. In: Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV). Seoul, Korea (South): IEEE, 2019. 4569−4579 [81] Karras T, Aila T, Laine S, Lehtinen J. Progressive growing of GANs for improved quality, Stability, and Variation. In: Proceedings of the 5th International Conference on Learning Representations. Toulon, France: OpenReview.net, 2017. [82] Brock A, Donahue J, Simonyan K. Large scale GAN training for high fidelity natural image synthesis. In: Proceedings of 7th International Conference on Learning Representations. New Orleans, USA: OpenReview.net, 2019. [83] Mirza M, Osindero S. Conditional generative adversarial nets. arXiv: 1411.1784, 2014 [84] Odena A, Olah C, Shlens J. Conditional image synthesis with auxiliary classifier GANs. In: Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia: JMLR.org, 2017. 2642−2651 [85] Sricharan K, Bala R, Shreve M, Ding H, Saketh K, Sun J. Semi-supervised conditional GANs. arXiv: 1708.05789, 2017 [86] Zhang H, Xu T, Li H S, Zhang S T, Wang X G, Huang X L, et al. StackGAN: Text to photo-realistic image synthesis with stacked generative adversarial networks. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy: IEEE, 2017. 5908−5916 [87] Zhang H, Xu T, Li H S, Zhang S T, Wang X G, Huang X L, et al. StackGAN++: Realistic image synthesis with stacked generative adversarial networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(8): 1947-1962 doi: 10.1109/TPAMI.2018.2856256 [88] Tran L, Yin X, Liu X M. Disentangled representation learning GAN for pose-invariant face recognition. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, USA: IEEE, 2017. 1283−1292 [89] Huang R, Zhang S, Li T Y, He R. Beyond face rotation: Global and local perception GAN for photorealistic and identity preserving frontal view synthesis. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy: IEEE, 2017. 2458−2467 [90] Ma L Q, Jia X, Sun Q R, Schiele B, Tuytelaars T, van Gool L. Pose guided person image generation. In: Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 406−416 [91] Siarohin A, Sangineto E, Lathuiliere S, Sebe N. Deformable GANs for pose-based human image generation. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 3408−3416 [92] Chang H W, Lu J W, Yu F, Finkelstein A. PairedCycleGAN: Asymmetric style transfer for applying and removing makeup. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 40−48 [93] Pumarola A, Agudo A, Martinez A M, Sanfeliu A, Moreno-Noguer F. Ganimation: Anatomically-aware facial animation from a single image. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 835−851 [94] Donahue C, Lipton Z C, Balsubramani A, McAuley J. Semantically decomposing the latent spaces of generative adversarial networks. arXiv: 1705.07904, 2017 [95] Shu Z X, Sahasrabudhe M, Guler R A, Samaras D, Paragios N, Kokkinos I. Deforming autoencoders: Unsupervised disentangling of shape and appearance. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 664−680 [96] Lu Y Y, Tai Y W, Tang C K. Attribute-guided face generation using conditional CycleGAN. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 293−308 [97] Ledig C, Theis L, Huszar F, Caballero J, Cunningham A, Acosta A, et al. Photo-realistic single image super-resolution using a generative adversarial network. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, USA: IEEE, 2017. 105−114 [98] Wang X T, Yu K, Wu S X, Gu J J, Liu Y H, Dong C, et al. EsrGAN: Enhanced super-resolution generative adversarial networks. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 63−79 [99] Zhu J Y, Park T, Isola P, Efros A A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy: IEEE, 2017. 2242−2251 [100] Bansal A, Ma S G, Ramanan D, Sheikh Y. Recycle-GAN: Unsupervised video retargeting. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 122−138 [101] Yuan Y, Liu S Y, Zhang J W, Zhang Y B, Dong C, Lin L. Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW). Salt Lake City, USA: IEEE, 2018. 701−710 [102] Li J, Liang X D, Wei Y C, Xu T F, Feng J S, Yan S C. Perceptual generative adversarial networks for small object detection. In: Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE, 2017. 1951−1959 [103] Bai Y C, Zhang Y Q, Ding M L, Ghanem B. SOD-MTGAN: Small object detection via multi-task generative adversarial network. In: Proceedings of the 15th European Conference on Computer Vision. Munich, Germany: Springer, 2018. 210−226 [104] Ehsani K, Mottaghi R, Farhadi A. SeGAN: Segmenting and generating the invisible. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE, 2018. 6144−6153 [105] Vondrick C, Pirsiavash H, Torralba A. Generating videos with scene dynamics. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016. 613−621 [106] Villegas R, Yang J M, Hong S, Lin X Y, Lee H. Decomposing motion and content for natural video sequence prediction. arXiv: 1706.08033, 2018 [107] Chan C, Ginosar S, Zhou T H, Efros A. Everybody dance now. In: Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV). Seoul, Korea (South): IEEE, 2019. 5932−5941 [108] Mathieu M, Couprie C, LeCun Y. Deep multi-scale video prediction beyond mean square error. arXiv: 1511.05440, 2015 [109] Yu L T, Zhang W N, Wang J, Yu Y. SeqGAN: Sequence generative adversarial nets with policy gradient. In: Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco, California, USA: AAAI, 2017. 2852−2858 [110] Saito Y, Takamichi S, Saruwatari H. Statistical parametric speech synthesis incorporating generative adversarial networks. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(1): 84-96 doi: 10.1109/TASLP.2017.2761547 [111] Pascual S, Bonafonte A, Serra J. SEGAN: Speech enhancement generative adversarial network. arXiv: 1703.09452, 2017 [112] Wang J, Yu L T, Zhang W N, Gong Y, Xu Y H, Wang B Y, et al. IRGAN: A minimax game for unifying generative and discriminative information retrieval models. In: Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2017. 515−524 [113] Lin K, Li D Q, He X D, Zhang Z Y, Sun M T. Adversarial ranking for language generation. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 3158−3168 [114] Qiao T T, Zhang J, Xu D Q, Tao D C. MirrorGAN: Learning text-to-image generation by redescription. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, USA: IEEE, 2019. 1505−1514 [115] Schlegl T, Seebock P, Waldstein S M, Schmidt-Erfurth U, Langs G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In: Proceedings of the 25th International Conference on Information Processing in Medical Imaging. Boone, USA: Springer, 2017. 146−157 [116] Xue Y, Xu T, Zhang H, Long L R, Huang X L. SegAN: Adversarial network with multi-scale L_1 loss for medical image segmentation. Neuroinformatics, 2018, 16(3-4): 383-392 doi: 10.1007/s12021-018-9377-x [117] Yang Q S, Yan P K, Zhang Y B, Yu H Y, Shi Y Y, Mou X Q, et al. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE Transactions on Medical Imaging, 2018, 37(6): 1348-1357 doi: 10.1109/TMI.2018.2827462 [118] Zheng Z D, Zheng L, Yang Y. Unlabeled samples generated by GAN improve the person re-identification baseline in vitro. In: Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy: IEEE, 2017. 3774−3782 [119] Gupta A, Johnson J, Li F F, Savarese S, Alahi A. Social GAN: Socially acceptable trajectories with generative adversarial networks. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA: IEEE, 2018. 2255−2264 [120] Barratt S, Sharma R. A note on the inception score. arXiv: 1801.01973, 2018 [121] Chen X, Duan Y, Houthooft R, Schulman J, Sutskever I, Abbeel P. InfoGAN: Interpretable representation learning by information maximizing generative adversarial nets. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016. 2180−2188 [122] Zhang H, Goodfellow I J, Metaxas D N, et al. Self-attention generative adversarial networks. In: Proceedings of the 36th International Conference on Machine Learning. New York, USA: JMLR.org, 2019. 7354−7363 [123] Dinh L, Sohl-Dickstein J, Bengio S. Density estimation using Real NVP. In: Proceedings of the 5th International Conference on Learning Representations. Toulon, France: OpenReview.net, 2017. [124] Kingma D P, Dhariwal P. Glow: Generative flow with invertible 1\times1 convolutions. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montreal, Canada: Curran Associates Inc., 2018. 10236−10245 [125] Behrmann J, Grathwohl W, Chen R T Q, Duvenaud D, Jacobsen J H. Invertible residual networks. In: Proceedings of the 36th International Conference on Machine Learning. Long Beach, California: PMLR, 2019. 573−582 [126] Rezende D J, Mohamed S. Variational inference with normalizing flows. In: Proceedings of the 32nd International Conference on Machine Learning. Lile, France: JMLR, 2015. 1530−1538 [127] Kingma D P, Salimans T, Jozefowicz R, Chen X, Sutskever I, Welling M. Improved variational inference with inverse autoregressive flow. In: Proceedings of the 30th Conference on Neural Information Processing Systems. Barcelona, Spain: MIT Press, 2016. 4743−4751 [128] Papamakarios G, Pavlakou T, Murray I. Masked autoregressive flow for density estimation. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, California, USA: Curran Associates Inc., 2017. 2335−2344 [129] Frey B J. Graphical Models for Machine Learning and Digital Communication. Cambridge: MIT Press, 1998. [130] Bengio S, Bengio Y. Taking on the curse of dimensionality in joint distributions using neural networks. IEEE Transactions on Neural Networks, 2000, 11(3): 550-557 doi: 10.1109/72.846725 [131] Neal R M. Connectionist learning of belief networks. Artificial Intelligence, 1992, 56(1): 71-113 doi: 10.1016/0004-3702(92)90065-6 [132] Bengio Y. Discussion of “the neural autoregressive distribution estimator”. In: Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, USA: JMLR, 2011. 38−39 [133] Raiko T, Li Y, Cho K, Bengio Y. Iterative neural autoregressive distribution estimator (NADE-k). In: Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2014. 325−333 [134] Reed S, van den Oord A, Kalchbrenner N, Colmenarejo S G, Wang Z Y, Belov D, et al. Parallel multiscale autoregressive density estimation. arXiv: 1703.03664, 2017 [135] Uria B, Murray I, Larochelle H. A deep and tractable density estimator. In: Proceedings of the 31st International Conference on Machine Learning. Beijing, China: JMLR.org, 2014. I-467−I-475 [136] Uria B, Cote M A, Gregor K, Murray I, Larochelle H. Neural autoregressive distribution estimation. The Journal of Machine Learning Research, 2016, 17(1): 7184-7220 [137] van den Oord A, Kalchbrenner N, Kavukcuoglu K. Pixel recurrent neural networks. arXiv: 1601.06759, 2016 [138] Germain M, Gregor K, Murray I, Larochelle H. MADE: Masked autoencoder for distribution estimation. In: Proceedings of the 32nd International Conference on Machine Learning. Lille, France: JMLR, 2015. 881−889 [139] Socher R, Huang E H, Pennington J, Ng A Y, Manning C D. Dynamic pooling and unfolding recursive autoencoders for paraphrase detection. In: Proceedings of the 24th International Conference on Neural Information Processing Systems. Granada, Spain: Curran Associates Inc., 2011. 801−809 [140] Socher R, Pennington J, Huang E H, Ng A T, Manning C D. Semi-supervised recursive autoencoders for predicting sentiment distributions. In: Proceedings of the 2011 Conference on Empirical Methods in Natural Language Processing. Edinburgh, United Kingdom: Association for Computational Linguistics, 2011. 151−161 [141] Gretton A, Borgwardt K M, Rasch M J, Scholkopf B, Smola A. A kernel two-sample test. Journal of Machine Learning Research, 2012, 13(5): 723-773 [142] Dziugaite G K, Roy D M, Ghahramani Z. Training generative neural networks via maximum mean discrepancy optimization. arXiv: 1505.03906, 2015 [143] Li C L, Chang W C, Cheng Y, Yang Y M, Poczos B. MMD GAN: Towards deeper understanding of moment matching network. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 2200−2210 [144] Ren Y, Li J L, Luo Y C, Zhu J. Conditional generative moment-matching networks. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016. 2936−2944 [145] Bengio Y, Yao L, Alain G, Vincent P. Generalized denoising auto-encoders as generative models. In: Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc., 2013. 899−907 [146] Rezende D J, Mohamed S, Wierstra D. Stochastic backpropagation and approximate inference in deep generative models. In: Proceedings of the 31st International Conference on Machine Learning. Beijing, China: JMLR.org, 2014. II-1278−II-1286 [147] Zohrer M, Pernkopf F. General stochastic networks for classification. In: Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2014. 2015−2023 [148] Jang E, Gu S X, Poole B. Categorical reparameterization with gumbel-softmax. arXiv: 1611.01144, 2016 [149] Song J K, He T, Gao L L, Xu X, Hanjalic A, Shen H T. Binary generative adversarial networks for image retrieval. In: Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans, USA: AAAI, 2018. 394−401 -




 下载:
下载: