深度<b>EM</b>胶囊网络全重叠手写数字识别与分离

姚红革; 董泽浩; 喻钧; 白小军

doi:10.16383/j.aas.c190849

深度EM胶囊网络全重叠手写数字识别与分离

doi: 10.16383/j.aas.c190849

姚红革^1,,
董泽浩^1,,
喻钧^1,,
白小军^{1, 2,}

1.
西安工业大学计算机科学与工程学院西安 710021
2.
电子信息现场勘验应用技术公安部重点实验室西安 710121

详细信息

作者简介:
姚红革：博士, 西安工业大学计算机科学与工程学院副教授. 主要研究方向为机器学习, 计算机视觉.E-mail: yaohongge@xatu.edu.cn

董泽浩：西安工业大学计算机科学与工程学院硕士研究生.主要研究方向为深度学习, 胶囊网络.E-mail: axxddzh@gmail.com

喻钧：西安工业大学计算机科学与工程学院教授. 主要研究方向为图像处理, 模式识别.E-mail: yujun@xatu.edu.cn

白小军：西安工业大学计算机科学与工程学院副教授, 电子信息现场勘验应用技术公安部重点实验室研究员. 主要研究方向为数字图像处理, 人工智能与机器学习. 本文通信作者.E-mail: baixiaojun@xatu.edu.cn

计量
- 文章访问数: 877
- HTML全文浏览量: 426
- PDF下载量: 121
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-18
- 修回日期: 2020-04-16
- 网络出版日期: 2022-10-24
- 刊出日期: 2022-12-23

Fully Overlapped Handwritten Number Recognition and Separation Based on Deep EM Capsule Network

YAO Hong-Ge^1
,,
DONG Ze-Hao^1
,,
YU Jun^1
,,
BAI Xiao-Jun^{1, 2
,}

1.
College of Computer Science and Engineering, Xi＇an Technological University, Xi＇an 710021
2.
Key Laboratory of Electronic Information Processing with Applications in Crime Scene Investigation, Ministry of Public Security, Xi＇an 710121

More Information

Author Bio:
YAO Hong-Ge　Ph.D., associate professor at the School of Computer Science and Engineering, Xi＇an Technological University. His research interest covers machine learning and computer vision

DONG Ze-Hao　Master student at the School of Computer Science and Engineering, Xi＇an Technological University. His research interest covers deep learning and capsule network

YU Jun　Professor at the School of Computer Science and Engineering, Xi＇an Technology University. Her research interest covers image processing and pattern recognition

BAI Xiao-Jun　Associate professor at the School of Computer Science and Engineering, Xi＇an Technological University, and also a researcher of the Key Laboratory of Electronic Information Processing with Applications in Crime Scene Investigation, Ministry of Public Security. His research interest covers digital image processing, artificial intelligence, and machine learning. Corresponding author of this paper

摘要

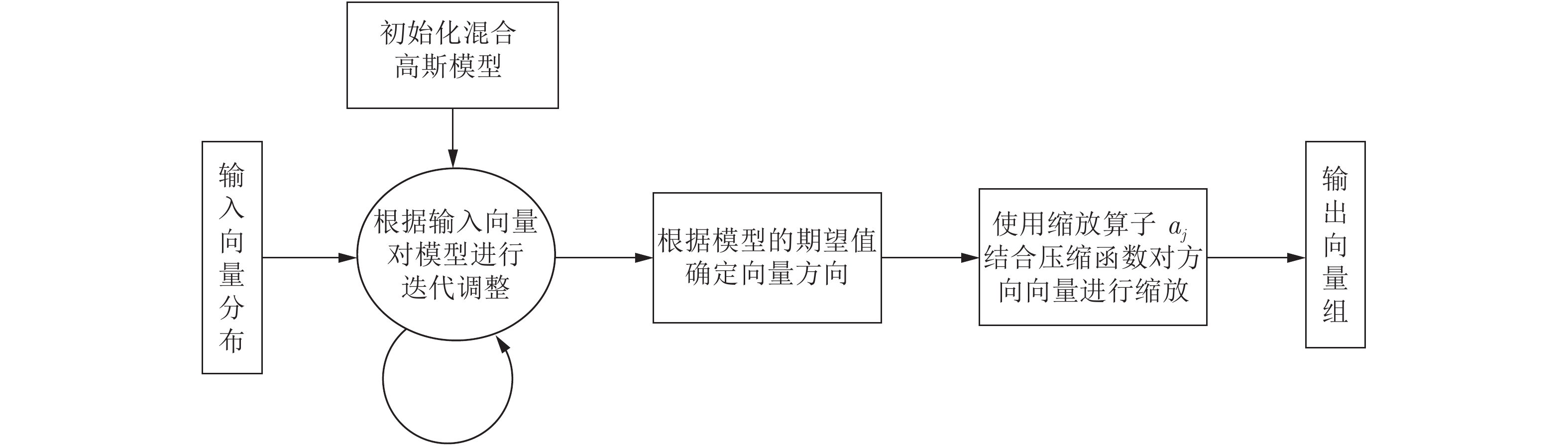
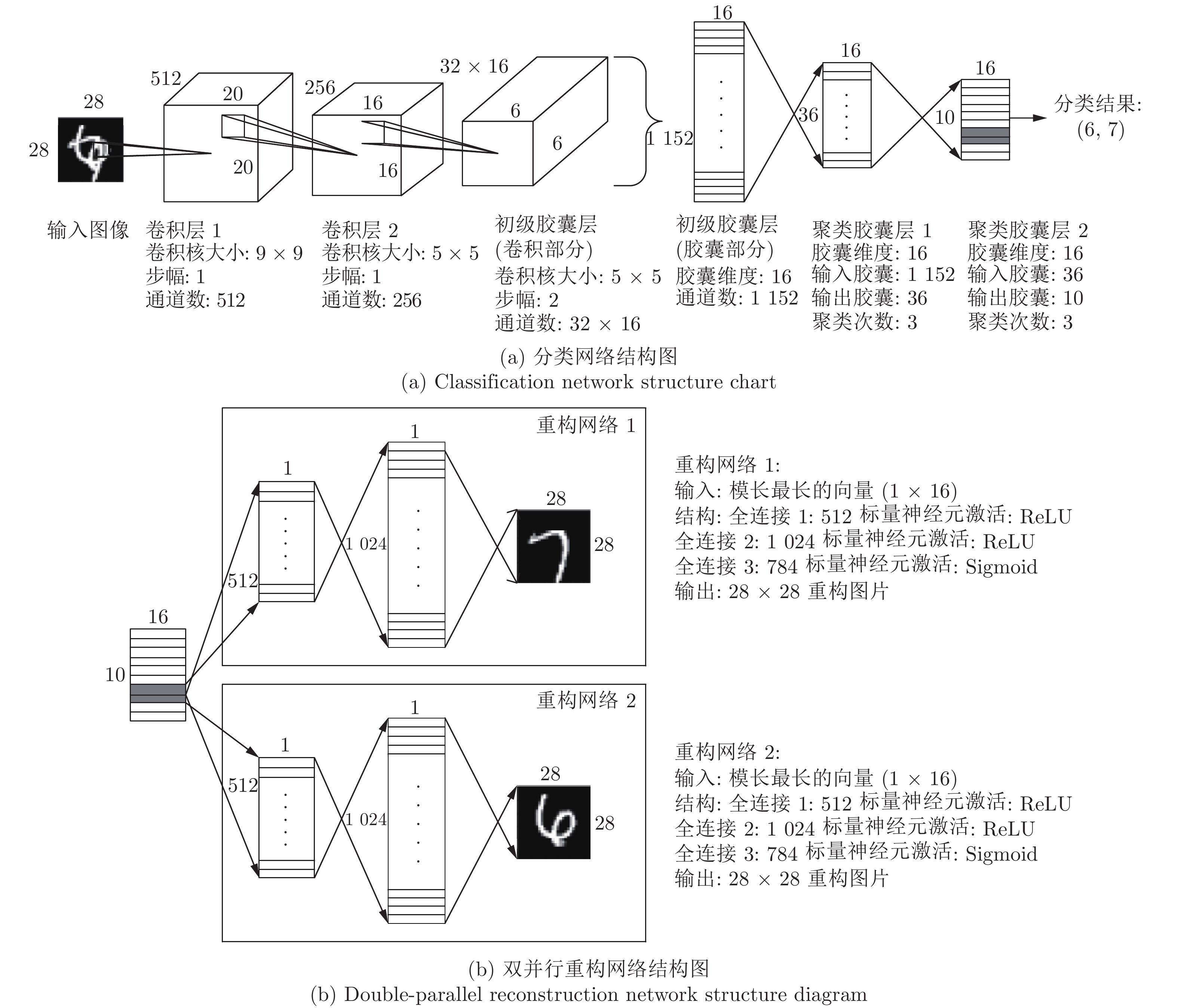
摘要: 基于胶囊网络的向量神经元思想和期望最大算法(Expectation-maximization, EM), 设计了一种以EM为向量聚类算法的深度胶囊网络(Deep capsule network, DCN), 实现了重叠手写数字的识别与分离. 该网络由两部分组成, 第 1 部分是“识别网络”, 将 EM 算法改为 EM 向量聚类算法, 以替换原胶囊网络CapsNet 中的迭代路由部分, 这一改动优化了网络的运算过程, 实现了重叠数字识别. 第 2 部分是“重构网络”, 由结构完全相同的两个并行网络组成, 对双向量进行并行重构, 实现了重叠数字的分离. 实验结果显示, 对于 100% 全重叠手写数字图片本网络识别率达到了 96%, 对比CapsNet 在 80% 的重叠率下 95% 的识别率, 本文网络在难度提升的情况下, 识别率有明显提高, 能够将完全重叠的两张手写数字进行图片进行准确地分离.
- 深度胶囊网络 /
- 重叠数字识别 /
- 重叠数字分离 /
- EM向量聚类
Abstract: Based on the idea of vector neuron of capsule network and expectation maximization algorithm (EM), a deep capsule network (DCN) with EM as the vector clustering algorithm is designed to recognize and separate overlapping handwritten digits The network consists of two parts. The first part is “identification network”. The EM algorithm is changed to EM vector clustering algorithm to replace the iterative routing part of the original capsule network CapsNet. This change optimizes the network operation process and realizes overlapping number recognition. The second part is the “reconstruction network”, which is composed of two parallel networks with identical structure. The bi-vector are reconstructed in parallel to realize the separation of overlapping digits. The experimental results show that for 100% full overlap handwritten digit, the recognition rate of the network reaches 96%. Compared with the 95% recognition rate of CapsNet at 80% overlap rate, the recognition rate of the network in this paper is significantly improved in the case of increased difficulty, and can accurately separate two completely overlapping handwritten digits.
- Deep capsule network (DCN) /
- overlapping number recognition /
- overlapping number separation /
- EM vector clustering

HTML全文

图 1 深度胶囊网络结构图

Fig. 1 Deep capsule network structure diagram

下载: 全尺寸图片幻灯片

图 2 EM向量聚类算法流程图

Fig. 2 Flow chart of EM vector clustering algorithm

下载: 全尺寸图片幻灯片

图 3 全重叠数据集

Fig. 3 Full-overlapping dataset

下载: 全尺寸图片幻灯片

图 4 不同聚类次数下输出向量的模长

Fig. 4 Module length of output vector under different clustering times

下载: 全尺寸图片幻灯片

图 5 DCN对全重叠手写数字的识别率与损失函数值曲线

Fig. 5 Recognition rate and loss value curve of DCN for fully overlapped handwritten digits

下载: 全尺寸图片幻灯片

图 6 重构loss函数占比收敛对比

Fig. 6 Comparison of proportion convergence of reconstructed loss function

下载: 全尺寸图片幻灯片

图 7 重构结果

Fig. 7 Reconstructing results

下载: 全尺寸图片幻灯片

图 8 训练识别率

Fig. 8 Training recognition rate

下载: 全尺寸图片幻灯片

表 1 数据集标签

Table 1 Dataset label

输入图像	标签	说明
	(0, 0, 0, 0, 0, 0, 0, 1, 0, 0)	无叠加
	(0, 0, 0, 0, 0, 0, 0, 0, 0, 2)	两个相同数字叠加
	(0, 0, 0, 1, 0, 0, 0, 1, 0, 0)	两个不同数字叠加

下载: 导出CSV

表 2 在不同聚类次数下的激活向量模长

Table 2 Active vector module length under different clustering times

网络结构及聚类形式	所用训练集	R = 1	R = 2	R = 3
DCN EM 聚类/CapsNet 路由聚类	MNIST数据集	0.0413/0.0536	0.5241/0.4122	0.9800/0.8792
	全重叠数据集	0.0332/0.0423	0.4342/0.5865	0.9943/0.8653
	混合数据集	0.0323/0.0354	0.4543/0.3252	0.9923/0.9173

下载: 导出CSV

表 3 参数量与不同聚类次数下的单Epoch消耗时间(s)

Table 3 Parameter quantity and single epoch consumption time under different clustering times (s)

网络结构	参数量	聚类算法	R = 1	R = 2	R = 3
CapsNet	8 215568	迭代路由	150±2	210±2	240±2
DCN	20128032	EM	240±2	300±2	340±2

下载: 导出CSV

表 4 DCN不同聚类算法单Epoch消耗时间(s)

Table 4 Single epoch consumption time of different DCN clustering algorithms (s)

聚类算法	R = 1	R = 2	R = 3
迭代路由	350±2	410±2	440±2
EM	240±2	300±2	340±2

下载: 导出CSV

表 5 DCN识别手写数字效果对比 (%)

Table 5 Effect comparison of handwritten digits recognized by DCN (%)

所用训练集	无重叠手写数字识别率	全重叠手写数字识别率
MNIST 数据集	99.6	55.2
全重叠手写数字数据集	80.7	96.75
混合数据集	95.7	96.55

下载: 导出CSV

表 6 重叠手写数字识别率对比(R = 3) (%)

Table 6 Comparison of recognition rate of overlapping handwritten digits (R = 3) (%)

网络模型	训练集	重叠率	正确率
CapsNet	MutiMNIST	80	95
CapsNet	全重叠数据集	100	88
DCN	全重叠数据集	100	96.75

下载: 导出CSV

表 7 全重叠手写数字分类与重构的部分结果

Table 7 Partial results of classification and reconstruction of fully overlapped handwritten digits

分类标签	(3, 7)	(9, 1)	(0, 8)	(0, 4)	(9, 7)*	(7, 9)*	(7, 9)*	(5, 9)•
分类结果	(3, 7)	(9, 1)	(8, 0)	(0, 4)	(7, 9)*	(7, 9)*	(7, 9)*	(8, 9)•
输入图片
重构图片 1
重构图片 2

下载: 导出CSV

表 8 部分识别和分离结果

Table 8 Partial identification and separation results

分类标签	(不, 专)	(下, 不)	(丑, 下)	(不, 丑)	(下, 世)	(下, 专)	(王, 丑)	(也, 卫)
分类结果	(不, 专)	(下, 不)	(丑, 下)	(不, 丑)	(下, 世)	(下, 专)	(丑, 不能确定)	(不能确定, 不能确定)
输入图片
重构图片 1
重构图片 2

下载: 导出CSV

参考文献(16)

[1]	Hinton G E, Ghahramani Z, Teh Y W. Learning to parse images. In: Proceedings of the 12th International Conference on Neural Information Processing Systems. Denver, USA: MIT Press, 1999. 463−469
[2]	Goodfellow I J, Bulatov Y, Ibarz J, Arnoud S, Shet V B. Multi-digit number recognition from street view imagery using deep convolutional neural networks. In: Proceedings of the 2nd International Conference on Learning Representations. Banff, Canada: ICLR, 2014.
[3]	Ba J, Mnih V, Kavukcuoglu K. Multiple object recognition with visual attention. In: Proceedings of the 3rd International Conference on Learning Representations. San Diego, USA: ICLR, 2015.
[4]	Greff K, Rasmus A, Berglund M, Hao T H, Schmidhuber J, Valpola H. Tagger: Deep unsupervised perceptual grouping. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016. 4491−4499
[5]	Sabour S, Frosst N, Hinton G E. Dynamic routing between capsules. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates Inc., 2017. 3859−3869
[6]	Gupta M R, Chen Y H. Theory and use of the EM algorithm. Foundations and Trends in Signal Processing, 2011, 4(3): 223−296
[7]	Xuan G R, Zhang W, Chai P Q. EM algorithms of Gaussian mixture model and hidden Markov model. In: Proceedings of the 2001 International Conference on Image Processing (Cat. No.01CH37205). Thessaloniki, Greece: IEEE, 2001. 145−148
[8]	Jain A K, Dubes R C. Algorithms for Clustering Data. Prentice-Hall Inc., 1988.
[9]	Wang D L, Liu Q. An optimization view on dynamic routing between capsules. In: Proceedings of the 6th International Conference on Learning Representations. Vancouver, Canada: ICLR, 2018.
[10]	Jaiswal A, AbdAlmageed W, Wu Y, Natarajan P. CapsuleGAN: Generative adversarial capsule network. In: Proceedings of the 2018 European Conference on Computer Vision. Munich, Germany: Springer, 2018. 526−535
[11]	LaLonde R, Bagci U. Capsules for object segmentation. arXiv Preprint arXiv:1804.04241, 2018.
[12]	Rajasegaran J, Jayasundara V, Jayasekara S, Jayasekara H, Seneviratne S, Rodrigo R. DeepCaps: Going deeper with capsule networks. In: Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA: IEEE, 2019. 10717−10725
[13]	Hinton G E, Sabour S, Frosst N. Matrix capsules with EM routing. In: Proceedings of the 6th International Conference on Learning Representations. Vancouver, Canada: ICLR, 2018.
[14]	Zhang H Y, Cissé M, Dauphin Y N, Lopez-Paz D. mixup: Beyond empirical risk minimization. In: Proceedings of the 6th International Conference on Learning Representations. Vancouver, Canada: ICLR, 2018.
[15]	Tokozume Y, Ushiku Y, Harada T. Between-class learning for image classification. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA: IEEE, 2018. 5486−5494
[16]	朱周华. 期望最大(EM)算法及其在混合高斯模型中的应用. 现代电子技术, 2003, 26(24): 88−90 doi: 10.3969/j.issn.1004-373X.2003.24.032 Zhu Zhou-Hua. EM algorithm and its application in mixture of Gaussian. Modern Electronics Technique, 2003, 26(24): 88−90 doi: 10.3969/j.issn.1004-373X.2003.24.032