-
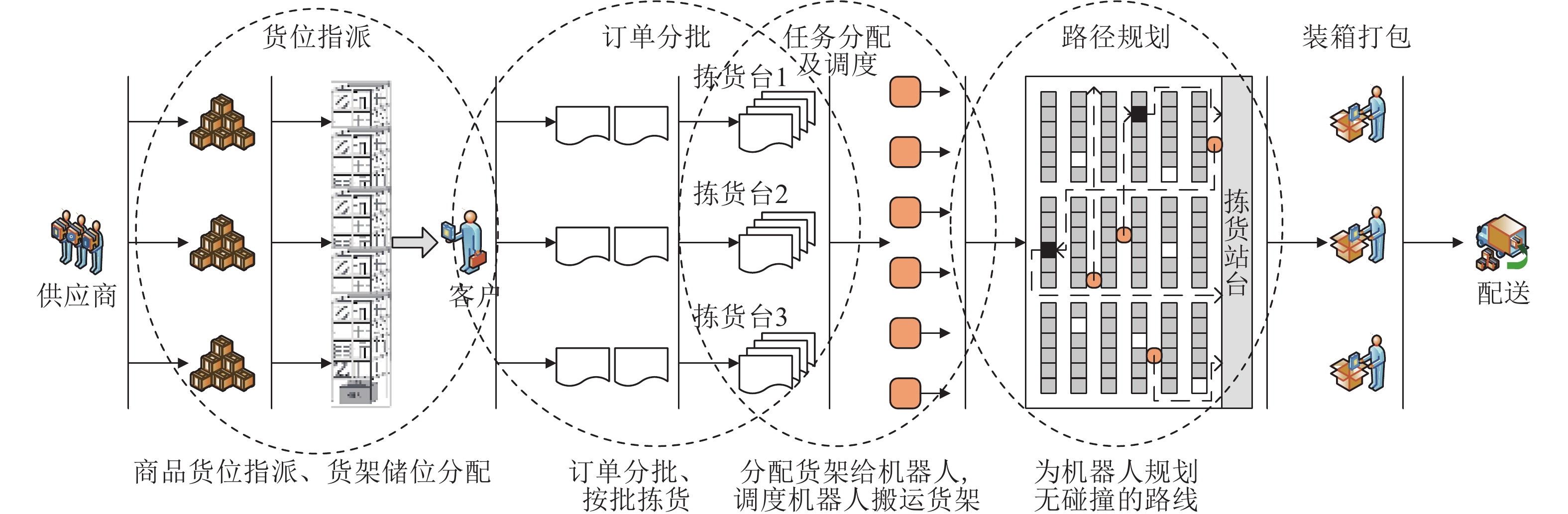
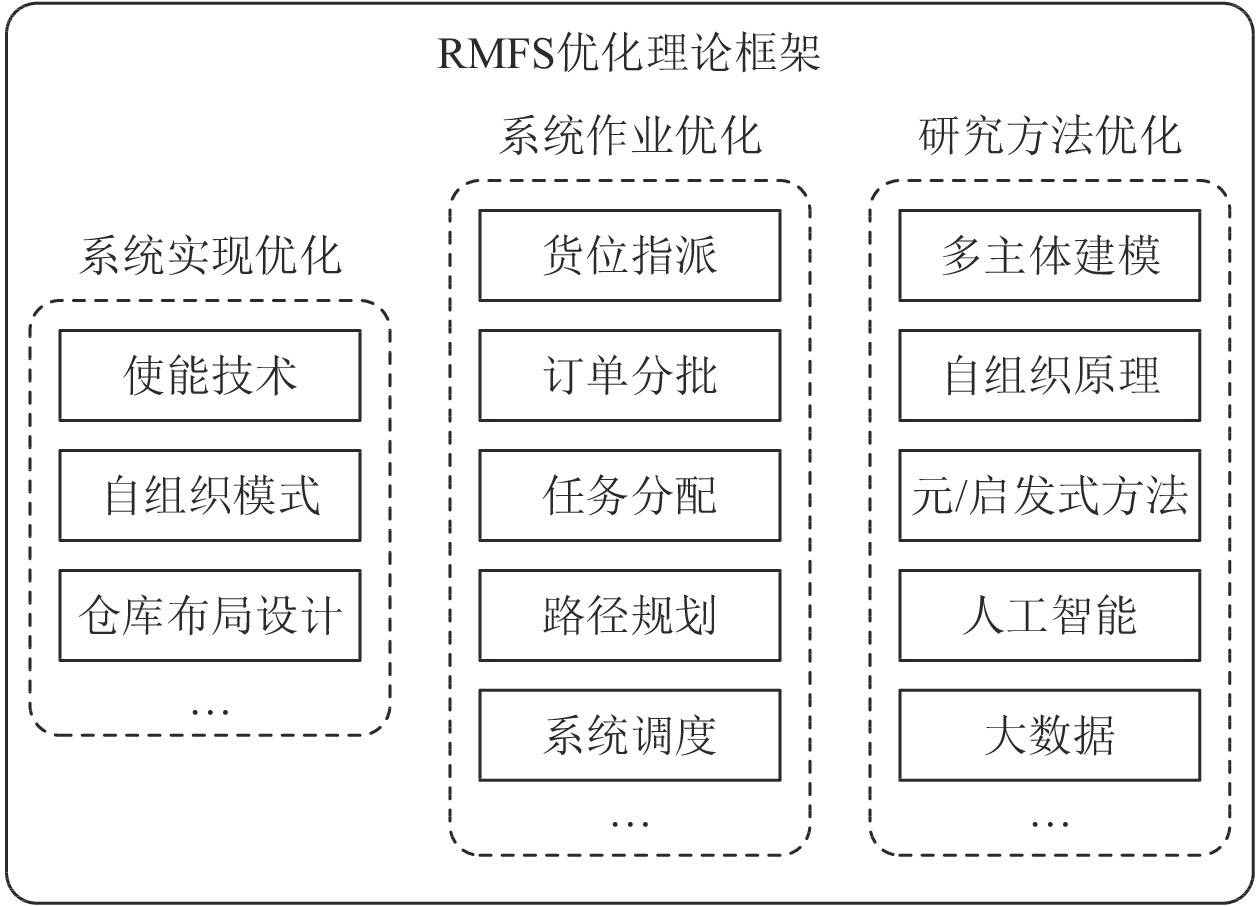
摘要: 基于移动机器人的拣货系统(Robotic mobile fulfillment systems, RMFS)作为一种新型物至人的拣货系统, 相比人工拣货系统和AS/RS拣货系统(下文统称传统拣货系统)具有更高的拣货效率、更好的系统可扩展性和柔性. 为全面了解RMFS的运行模式及其优化方向, 本文首先回顾了RMFS的工作流程及优化理论框架, 然后对RMFS的货位指派、订单分批、任务分配、路径规划以及建模方法等问题进行了文献回顾和总结, 并指出了RMFS与传统拣货系统在拣货过程方面的异同及当前研究的不足. 最后, 讨论了RMFS的几个重要研究方向, 为RMFS的理论研究和应用实践提供参考.Abstract: As a new kind of parts-to-pickers order picking systems, robotic mobile fulfillment systems (RMFS) have higher picking efficiency, better system scalability and flexibility compared with manual picking systems and AS/RS picking systems (hereinafter referred to as traditional picking systems). In order to fully understand the operation mode and optimization direction of RMFS, this paper first reviews the workflow and optimization theoretical framework of RMFS, then reviews and summarizes the problems of storage location assignment, order batching, task assignment, path planning and modeling methods of RMFS, as well as points out the similarities and differences between RMFS and traditional picking systems in the picking process and the shortcomings of current research. Finally, several important research directions of RMFS are discussed, which provides reference for the theoretical research and application practice of RMFS.
-
表 1 RMFS研究文献汇总
Table 1 Summary of literature on RMFS
问题分类 作者 研究问题 解决方法 货位指派 Nigam 等[4] (2014) 货架储位指派问题 多类封闭排队网络 Lamballais 等[3] (2017) 仓库布局、商品储位指派、补货作业优化问题 半开放排队网络 Onal 等[15] (2017) 商品储位指派问题 爆炸存储策略、仿真方法 Krenzler 等[16] (2018) 货架储位再指派问题 确定性模型、组合优化算法 Yuan 等[17] (2019) 货架储位指派问题 流体模型、基于策略的存储方法 Weidinger 等[18] (2018) 货架储位动态指派 混合整数规划模型、自适应规划方法 Yuan 等[19] (2018) 货位指派问题 分区存储策略、仿真方法 Xiang 等[20] (2018) 商品储位指派问题与订单分批协同优化 混合整数规划模型、可变邻域搜索方法、自适应算法 蔺一帅等[21] (2020) 商品储位指派与路径规划协同优化 改进的协同优化遗传算法 徐翔斌等[22] (2021) 货架储位动态指派 改进的模拟退火算法 订单分批 吴颖颖等[23] (2016) 订单排序问题 订单排序优化模型、k-means聚类算法 Boysen 等[24] (2017) 订单分批与订单排序以及货架在拣货
站台排序的综合优化混合整数规划模型、Cplex以及仿真方法 Xiang 等[20] (2018) 商品储位指派问题与订单分批协同优化 混合整数规划模型、可变邻域搜索方法、自适应算法 任务分配及调度 Zhou 等[11] (2020) 多机器人任务分配问题 平衡启发式机制与仿真 Dou 等[25] (2020) 任务调度和路径规划协同优化 遗传算法、强化学习 徐贤浩等[26] (2016) 搬运机器人待命泊位策略问题 统计建模方法、基于策略的方法 Yuan 等[27] (2017) 搬运机器人共享分配问题 共享协议策略、排队网络 Zou 等[28] (2017) RMFS分配规则问题 半开放排队网络、基于规则的方法、
邻域搜索方法Merschformann 等[12] (2018) RMFS作业调度决策问题 基于行走策略的研究方法 Merschformann 等[29] (2018) RMFS作业调度决策问题 基于策略的存储和仿真方法 Ghassemi 等[30] (2018) 多机器人任务分配问题 基于二部图匹配和模糊聚类的分散多主体任务分配算法、仿真 Zou 等[31] (2018) 评估机器人充电与更换电池策略的优劣 半开放排队网络、Arena仿真 袁瑞萍等[32] (2018) 拣货过程任务调度 共同进化遗传算法 Roy 等[33] (2019) RMFS系统绩效评估、机器人分配策略 封闭排队网络、两阶段随机模型、Arena仿真 Yoshitake 等[34] (2019) 机器人调度 实时全息调度方法 Zhang 等[35] (2020) RMFS多机器人分配问题 改进的遗传算法 路径规划 沈博闻等[8] (2014) 多机器人路径规划问题 改进的A*算法 Dou 等[25] (2020) 任务调度和路径规划协同优化 遗传算法、强化学习 Kumar 等[36] (2018) RMFS路径规划问题 无冲突路径规划算法 Zhang 等[37] (2018) 多机器人无冲突路径规划 改进的Dijkstra算法、避碰规则 张丹露等[38] (2018) 多机器人协同路径规划 改进的A*算法、动态加权图 夏清松等[39] (2019) 路径规划与作业避障协同研究 蚁群算法、避障规则设计 Lee 等[40] (2019) 多机器人无冲突路径规划 网络物理系统模型、改进的A*算法以及避碰规则 于赫年等[41] (2020) 多机器人路径规划问题 自调优A*算法、主动避障规则 蔺一帅等[21] (2020) 商品储位指派与路径规划协同优化 改进的协同优化遗传算法 RMFS系统设计、评估及其他问题研究 Gue 等[42] (2014) RMFS机器人系统控制与评估 面向对象建模与仿真 Yuan 等[43] (2016) 评估RMFS的性能, 主要关注机器人
数量、速度优化开放排队网络模型 Lee 等[44] (2019) 变形RMFS的拣货流程优化 混合整数规划模型、Gurobi Bozer 等[45] (2018) RMFS系统与miniload系统对比 仿真方法 Wang 等[46] (2020) 机器人搬运货架的运行周期问题 旅行时间模型 Zhang 等[47] (2019) RMFS快递分拣仓库布局自动化设计 机器学习与进化计算组合的方法 Petković 等[48] (2019) RMFS工作人员的意图评估 隐马尔科夫模型和心理理论 Wang 等[49] (2020) RMFS系统设计框架研究 基于瓶颈的模型和开放排队网络模型 -
[1] De Koster R, Le-Duc T, Roodbergen K J. Design and control of warehouse order picking: A literature review. European Journal of Operational Research, 2007, 182(2): 481-501 doi: 10.1016/j.ejor.2006.07.009 [2] Guizzo E. Three engineers, hundreds of robots, one warehouse. IEEE Spectrum, 2008, 45(7): 26-34 doi: 10.1109/MSPEC.2008.4547508 [3] Lamballais T, Roy D, De Koster M B M. Estimating performance in a robotic mobile fulfillment system. European Journal of Operational Research, 2017, 256(3): 976-990 doi: 10.1016/j.ejor.2016.06.063 [4] Nigam S, Roy D, de Koster R, Adan I. Analysis of class-based storage strategies for the mobile shelf-based order pick system. In: 13th IMHRC Proceedings. Cincinnati, Ohio, USA, 2014 [5] D'Andrea R. Guest editorial: A revolution in the warehouse: A retrospective on Kiva systems and the grand challenges ahead. IEEE Transactions on Automation Science & Engineering, 2012, 9(4): 638-639 [6] Wurman P R, D'Andrea R, Mountz M. Coordinating hundreds of cooperative, autonomous vehicles in warehouses. AI Magazine, 2008, 29(1): 9-19 [7] D′Andrea R, Wurman P. Future challenges of coordinating hundreds of autonomous vehicles in distribution facilities. In: Proceedings of the 2008 IEEE International Conference on Technologies for Practical Robot Applications. Woburn, MA, USA: IEEE, 2008. 80−83 [8] 沈博闻, 于宁波, 刘景泰. 仓储物流机器人集群的智能调度和路径规划. 智能系统学报, 2014, 9(6): 659-664Shen Bo-Wen, Yu Ning-Bo, Liu Jing-Tai. Intelligent scheduling and path planning of warehouse mobile robots. CAAI Transactions on Intelligent Systems, 2014, 9(6): 659-664 [9] Flipse M. Altering and Improving Kiva Some Suggestions for Improvement of the Current Kiva System, Marcel Flipse 1473379, Vrije Universiteit, Articial Intelligence Department, Amsterdam, Netherland, 2011. [10] Zhang J, Wang X P, Chan F T S, Ruan J H. On-line order batching and sequencing problem with multiple pickers: A hybrid rule-based algorithm. Applied Mathematical Modelling, 2017, 45: 271-284 doi: 10.1016/j.apm.2016.12.012 [11] Zhou L W, Shi Y Y, Wang J L, Yang P. A balanced heuristic mechanism for multirobot task allocation of intelligent warehouses [Online], available: http://downloads.hindawi.com/journals/mpe/2014/380480.pdf, August 31, 2020 [12] Merschformann M, Lin X, Erdmann D. Path planning for Robotic Mobile Fulfillment Systems [Online], available: https://arxiv.org/abs/1706.09347.pdf, November 19, 2018 [13] 徐翔斌, 李秀. 自组织物流研究综述及前景展望. 包装工程, 2017, 38(11): 111-116Xu Xiang-Bin, Li Xiu. Research overview and prospects of self-organizing logistics. Packaging Engineering, 2017, 38(11): 111-116 [14] Roodbergen K J, Vis I F A. A survey of literature on automated storage and retrieval systems. European Journal of Operational Research, 2009, 194(2): 343-362 doi: 10.1016/j.ejor.2008.01.038 [15] Onal S, Zhang J R, Das S. Modelling and performance evaluation of explosive storage policies in internet fulfilment warehouses. International Journal of Production Research, 2017, 55(20): 5902-5915 doi: 10.1080/00207543.2017.1304663 [16] Krenzler R, Xie L, Li H Y. Deterministic pod repositioning problem in robotic mobile fulfillment systems [Online], available: https://arxiv.org/pdf/1810.05514.pdf, October 9, 2018 [17] Yuan R, Graves S C, Cezik T. Velocity-based storage assignment in semi-automated storage systems. Production and Operations Management, 2019, 28(2): 354-373 doi: 10.1111/poms.12925 [18] Weidinger F, Boysen N, Briskorn D. Storage assignment with rack-moving mobile robots in KIVA warehouses. Transportation Science, 2018, 52(6): 1479-1495 doi: 10.1287/trsc.2018.0826 [19] Yuan R, Cezik T, Graves S C. Stowage decisions in multi-zone storage systems. International Journal of Production Research, 2018, 56(1-2): 333-343 doi: 10.1080/00207543.2017.1398428 [20] Xiang X, Liu C C, Miao L X. Storage assignment and order batching problem in Kiva mobile fulfilment system. Engineering Optimization, 2018, 50(11): 1941-1962 doi: 10.1080/0305215X.2017.1419346 [21] 蔺一帅, 李青山, 陆鹏浩, 孙雨楠, 王亮, 王颖芝. 智能仓储货位规划与AGV路径规划协同优化算法. 软件学报, 2020, 31(9): 2770-2784Lin Yi-Shuai, Li Qing-Shan, Lu Peng-Hao, Sun Yu-Nan, Wang Liang, Wang Ying-Zhi. Shelf and AGV path coopeartive optimization algorithm used in intelligent warehousing. Journal of Software, 2020, 31(9): 2770-2784 [22] 徐翔斌, 马中强. RMFS订单拣选系统动态货位再指派研究. 计算机集成制造系统, 2021, 27(4): 1146-1154Xu Xiang-Bin, Ma Zhong-Qiang. Dynamic location reassignment of RMFS order picking system. Computer Integrated Manufacturing Systems, 27(4): 1146-1154 [23] 吴颖颖, 孟祥旭, 王艳艳, 胡金昌. “货到人”拣选系统订单排序优化. 机械工程学报, 2016, 52(4): 206-212 doi: 10.3901/JME.2016.04.206Wu Ying-Ying, Meng Xiang-Xu, Wang Yan-Yan, Hu Jin-Chang. Order sequence optimization for “part-to-picker” order picking system. Journal of Mechanical Engineering, 2016, 52(4): 206-212 doi: 10.3901/JME.2016.04.206 [24] Boysen N, Briskorn D, Emde S. Parts-to-picker based order processing in a rack-moving mobile robots environment. European Journal of Operational Research, 2017, 262(2): 550-562 doi: 10.1016/j.ejor.2017.03.053 [25] Dou J J, Chen C L, Yang P. Genetic scheduling and reinforcement learning in multirobot systems for intelligent warehouses [Online], available: http://downloads.hindawi.com/journals/mpe/2015/597956.pdf, August 31, 2020 [26] 徐贤浩, 郭依, 邹碧攀. 基于最短取货时间的仓储机器人待命位策略研究. 工业工程与管理, 2016, 21(4): 35-42, 49 doi: 10.3969/j.issn.1007-5429.2016.04.006Xu Xian-Hao, Guo Yi, Zou Bi-Pan. Research on the dwell point policy for the warehouse robot based on minimum expected travel time. Industrial Engineering and Management, 2016, 21(4): 35-42, 49 doi: 10.3969/j.issn.1007-5429.2016.04.006 [27] Yuan Z, Gong Y Y. Bot-in-time delivery for robotic mobile fulfillment systems. IEEE Transactions on Engineering Management, 2017, 64(1): 83-93 doi: 10.1109/TEM.2016.2634540 [28] Zou B P, Gong Y M, Xu X H, Zhe Y. Assignment rules in robotic mobile fulfilment systems for online retailers. International Journal of Production Research, 2017, 55(20): 6175-6192 doi: 10.1080/00207543.2017.1331050 [29] Merschformann M, Lamballais T, De Koster R, Suhl L. Decision rules for robotic mobile fulfillment systems [Online], available: https://arxiv.org/abs/1801.06703.pdf, January 20, 2018 [30] Ghassemi P, Chowdhury S. Decentralized task allocation in multi-robot systems via bipartite graph matching augmented with fuzzy clustering. In: Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Quebec City, Quebec, Canada: American Society of Mechanical Engineers Digital Collection, 2018. [31] Zou B P, Xu X H, Gong Y M, De Koster R. Evaluating battery charging and swapping strategies in a robotic mobile fulfillment system. European Journal of Operational Research, 2018, 267(2): 733-753 doi: 10.1016/j.ejor.2017.12.008 [32] 袁瑞萍, 王慧玲, 孙利瑞, 李俊韬. 基于物流AGV的“货到人”订单拣选系统任务调度研究. 运筹与管理, 2018, 27(10): 133-138Yuan Rui-Ping, Wang Hui-Ling, Sun Li-Rui, Li Jun-Tao. Research on the task scheduling of “goods to picker”order picking system based on logistics AGV. Operations Research and Management Science, 2018, 27(10): 133-138 [33] Roy D, Nigam S, De Koster R, Adan I, Resing J. Robot-storage zone assignment strategies in mobile fulfillment systems. Transportation Research Part E: Logistics and Transportation Review, 2019, 122: 119-142 doi: 10.1016/j.tre.2018.11.005 [34] Yoshitake H, Kamoshida R, Nagashima Y. New automated guided vehicle system using real-time holonic scheduling for warehouse picking. IEEE Robotics and Automation Letters, 2019, 4(2): 1045-1052 doi: 10.1109/LRA.2019.2894001 [35] Zhang J T, Yang F X, Weng X. A building-block-based genetic algorithm for solving the robots allocation problem in a robotic mobile fulfilment system [Online], available: http://downloads.hindawi.com/journals/mpe/2019/6153848.pdf, August 31, 2020 [36] Kumar N V, Kumar C S. Development of collision free path planning algorithm for warehouse mobile robot. Procedia Computer Science, 2018, 133: 456-463 doi: 10.1016/j.procs.2018.07.056 [37] Zhang Z, Guo Q, Chen J, Yuan P J. Collision-free route planning for multiple AGVs in an automated warehouse based on collision classification. IEEE Access, 2018, 6: 26022-26035 doi: 10.1109/ACCESS.2018.2819199 [38] 张丹露, 孙小勇, 傅顺, 郑彬. 智能仓库中的多机器人协同路径规划方法. 计算机集成制造系统, 2018, 24(2): 410-418Zhang Dan-Lu, Sun Xiao-Yong, Fu Shun, Zheng Bin. Cooperative path planning in multi-robots for intelligent warehouse. Computer Integrated Manufacturing Systems, 2018, 24(2): 410-418 [39] 夏清松, 唐秋华, 张利平. 多仓储机器人协同路径规划与作业避碰. 信息与控制, 2019, 48(1): 22-28, 34Xia Qing-Song, Tang Qiu-Hua, Zhang Li-Ping. Cooperative path planning and operation collision avoidance for multiple storage robots. Information and control, 2019, 48(1): 22-28, 34 [40] Lee C K M, Lin B B, Ng K K H, Lv Y Q, Tai W C. Smart robotic mobile fulfillment system with dynamic conflict-free strategies considering cyber-physical integration. Advanced Engineering Informatics, 2019, 42: 100998 doi: 10.1016/j.aei.2019.100998 [41] 于赫年, 白桦, 李超. 仓储式多AGV系统的路径规划研究及仿真. 计算机工程与应用, 2020, 56(2): 233-241 doi: 10.3778/j.issn.1002-8331.1904-0178Yu He-Nian, Bai Hua, Li Chao. Research and simulation on path planning of warehouse multi-AGV system. Computer Engineering and Applications, 2020, 56(2): 233-241 doi: 10.3778/j.issn.1002-8331.1904-0178 [42] Gue K R, Furmans K, Seibold Z, Uludağ O. GridStore: A puzzle-based storage system with decentralized control. IEEE Transactions on Automation Science and Engineering, 2014, 11(2): 429-438 doi: 10.1109/TASE.2013.2278252 [43] Yuan Z, Gong Y M. Improving the speed delivery for robotic warehouses. IFAC-PapersOnLine, 2016, 49(12): 1164-1168 doi: 10.1016/j.ifacol.2016.07.661 [44] Lee H Y, Murray C C. Robotics in order picking: Evaluating warehouse layouts for pick, place, and transport vehicle routing systems. International Journal of Production Research, 2019, 57(18): 5821-5841 doi: 10.1080/00207543.2018.1552031 [45] Bozer Y A, Aldarondo F J. A simulation-based comparison of two goods-to-person order picking systems in an online retail setting. International Journal of Production Research, 2018, 56(11): 3838-3858 doi: 10.1080/00207543.2018.1424364 [46] Wang K, Yang Y M, Li R X. Travel time models for the rack-moving mobile robot system. International Journal of Production Research, 2020, 58(14): 4367-4385 doi: 10.1080/00207543.2019.1652778 [47] Zhang H F, Guo Z L, Zhang W N, Cai H, Wang C, Yu Y, et al. Layout design for intelligent warehouse by evolution with fitness approximation. IEEE Access, 2019, 7: 166310-166317 doi: 10.1109/ACCESS.2019.2953486 [48] Petković T, Puljiz D, Marković I, Hein B. Human intention estimation based on hidden markov model motion validation for safe flexible robotized warehouses. Robotics and Computer-Integrated Manufacturing, 2019, 57: 182-196 doi: 10.1016/j.rcim.2018.11.004 [49] Wang W, Wu Y H, Zheng J, Chi C. A comprehensive framework for the design of modular robotic mobile fulfillment systems. IEEE Access, 2020, 8: 13259-13269 doi: 10.1109/ACCESS.2020.2966403 [50] Öncan T. A survey of the generalized assignment problem and its applications. INFOR: Information Systems and Operational Research, 2007, 45(3): 123-141 doi: 10.3138/infor.45.3.123 [51] 徐翔斌, 李秀. 固定路径下多阶段货位调整研究. 工业工程与管理, 2017, 22(5): 24-31Xu Xiang-Bin, Li Xiu. Research on route-based multi-staged storage location adjustment. Industrial Engineering and Management, 2017, 22(5): 24-31 [52] Roodbergen K J, De Koster R. Routing order pickers in a warehouse with a middle aisle. European Journal of Operational Research, 2001, 133(1): 32-43 doi: 10.1016/S0377-2217(00)00177-6 [53] Hausman W H, Schwarz L B, Graves S C. Optimal storage assignment in automatic warehousing systems. Management Science, 1976, 22(6): 629-638 doi: 10.1287/mnsc.22.6.629 [54] Manzini R. Correlated storage assignment in an order picking system. International Journal of Industrial Engineering: Theory Applications & Practice, 2006, 13(4): 384-394 [55] 李英德. 波次分区拣货时装箱与货位指派问题协同优化的模型与算法. 系统工程理论与实践, 2013, 33(5): 1269-1276 doi: 10.3969/j.issn.1000-6788.2013.05.023Li Ying-De. Model and algorithm for cartonization and slotting optimization simultaneously in wave-picking zone-based system. Systems Engineering - Theory & Practice, 2013, 33(5): 1269-1276 doi: 10.3969/j.issn.1000-6788.2013.05.023 [56] Petersen C G, Schmenner R W. An evaluation of routing and volume-based storage policies in an order picking operation. Decision Sciences, 1999, 30(2): 481-501 doi: 10.1111/j.1540-5915.1999.tb01619.x [57] Caron F, Marchet G, Perego A. Routing policies and COI-based storage policies in picker-to-part systems. International Journal of Production Research, 1998, 36(3): 713-732 doi: 10.1080/002075498193651 [58] 李建斌, 杨光耀, 陈峰. 零售业电子商务仓储中心货位指派问题研究. 工业工程与管理, 2013, 18(4): 102-108 doi: 10.3969/j.issn.1007-5429.2013.04.016Li Jian-Bin, Yang Guang-Yao, Chen Feng. Retail warehouse center storage location assignment research for E-commerce. Industrial Engineering and Management, 2013, 18(4): 102-108 doi: 10.3969/j.issn.1007-5429.2013.04.016 [59] Wutthisirisart P, Noble J S, Chang C A. A two-phased heuristic for relation-based item location. Computers & Industrial Engineering, 2015, 82: 94-102 [60] Li J X, Moghaddam M, Nof S Y. Dynamic storage assignment with product affinity and ABC classification--a case study. The International Journal of Advanced Manufacturing Technology, 2016, 84(9-12): 2179-2194 doi: 10.1007/s00170-015-7806-7 [61] 李英德, 鲁建厦, 潘国强. 穿越策略下考虑相关性的货位优化方法. 浙江大学学报(工学版), 2012, 46(8): 1424-1430 doi: 10.3785/j.issn.1008-973X.2012.08.011Li Ying-De, Lu Jian-Sha, Pan Guo-Qiang. Slotting optimization based on SKUs correlations with serpentine routing policy. Journal of Zhejiang University (Engineering Science), 2012, 46(8): 1424-1430 doi: 10.3785/j.issn.1008-973X.2012.08.011 [62] Ho S. Intentional Fragmentation for Material Storage [Ph. D. dissertation], Massachusetts Institute of Technology, USA, 2004 [63] Grosse E H, Glock C H, Neumann W P. Human factors in order picking: A content analysis of the literature. International Journal of Production Research, 2017, 55(5): 1260-1276 doi: 10.1080/00207543.2016.1186296 [64] Cai J W, Kuang X A, Song S H, Zhao Q L. Automated warehouse storage assignment policy based on storage frequency and workload balance. In: Proceedings of the 2016 International Conference on Logistics, Informatics and Service Sciences (LISS). Sydney, NSW, Australia: IEEE, 2016. 1−6 [65] Matusiak M, De Koster R, Saarinen J. Utilizing individual picker skills to improve order batching in a warehouse. European Journal of Operational Research, 2017, 263(3): 888-899 doi: 10.1016/j.ejor.2017.05.002 [66] Pan J C H, Shih P H, Wu M H. Storage assignment problem with travel distance and blocking considerations for a picker-to-part order picking system. Computers & Industrial Engineering, 2012, 62(2): 527-535 [67] Bodnar P, Lysgaard J. A dynamic programming algorithm for the space allocation and aisle positioning problem. Journal of the Operational Research Society, 2014, 65(9): 1315-1324 doi: 10.1057/jors.2013.64 [68] Yang P, Miao L X, Xue Z J, Ye B. Variable neighborhood search heuristic for storage location assignment and storage/retrieval scheduling under shared storage in multi-shuttle automated storage/retrieval systems. Transportation Research Part E: Logistics and Transportation Review, 2015, 79: 164-177 doi: 10.1016/j.tre.2015.04.009 [69] Pang K W, Chan H L. Data mining-based algorithm for storage location assignment in a randomised warehouse. International Journal of Production Research, 2017, 55(14): 4035-4052 doi: 10.1080/00207543.2016.1244615 [70] 冯乾, 乐美龙, 赵毅. 物料聚类分析下的仓库货位指派优化. 辽宁工程技术大学学报(自然科学版), 2015, 34(10): 1207-1212 doi: 10.11956/j.issn.1008-0562.2015.10.020Feng Qian, Le Mei-Long, Zhao Yi. Optimization of storage location assignment based on materials clustering analysis. Journal of Liaoning Technical University (Natural Science Edition), 2015, 34(10): 1207-1212 doi: 10.11956/j.issn.1008-0562.2015.10.020 [71] Weidinger F, Boysen N. Scattered storage: How to distribute stock keeping units all around a mixed-shelves warehouse. Transportation Science, 2018, 52(6): 1412-1427 doi: 10.1287/trsc.2017.0779 [72] Gademann N, Velde S. Order batching to minimize total travel time in a parallel-aisle warehouse. IIE Transactions, 2005, 37(1): 63-75 doi: 10.1080/07408170590516917 [73] Ackerman K B. Practical Handbook of Warehousing. US: Springer, 1990. [74] 王旭坪, 张珺, 马骏. 考虑完成期限的电子商务在线订单分批模型及算法. 管理科学, 2014, 27(6): 103-113 doi: 10.3969/j.issn.1672-0334.2014.06.009Wang Xu-Ping, Zhang Jun, Ma Jun. E-commerce on-line order batching model and algorithm: Considering due time. Journal of Management Science, 2014, 27(6): 103-113 doi: 10.3969/j.issn.1672-0334.2014.06.009 [75] Rouwenhorst B, Reuter B, Stockrahm V, Houtum G, Mantel R J, Zijm W. Warehouse design and control: Framework and literature review. European Journal of Operational Research, 2000, 122(3): 515-533 [76] Menéndez B, Pardo E G, Alonso-Ayuso A, Molina E, Duarte A. Variable neighborhood search strategies for the order batching problem. Computers & Operations Research, 2017, 78: 500-512 [77] Scholz A, Wäscher G. Order batching and picker routing in manual order picking systems: The benefits of integrated routing. Central European Journal of Operations Research, 2017, 25(2): 491-520 doi: 10.1007/s10100-017-0467-x [78] Chen M C, Wu H P. An association-based clustering approach to order batching considering customer demand patterns. Omega, 2005, 33(4): 333-343 doi: 10.1016/j.omega.2004.05.003 [79] 李诗珍, 杜文宏. 基于聚类分析的订单分批拣货模型及启发式算法. 统计与决策, 2008(12): 53-56Li Shi-Zhen, Du Wen-Hong. Order batch picking model and heuristic algorithm based on cluster analysis. Statistics & Decision, 2008(12): 53-56 (查阅所有网上资料, 未找到对应的英文翻译, 请联系作者确认) [80] Henn S, Wäscher G. Tabu search heuristics for the order batching problem in manual order picking systems. European Journal of Operational Research, 2012, 222(3): 484-494 doi: 10.1016/j.ejor.2012.05.049 [81] 马士华, 文坚. 基于时间延迟的订单分批策略研究. 工业工程与管理, 2004, 9(6): 1-4 doi: 10.3969/j.issn.1007-5429.2004.06.001Ma Shi-Hua, Wen Jian. The order batching strategies based on time postponement. Industrial Engineering and Management, 2004, 9(6): 1-4 doi: 10.3969/j.issn.1007-5429.2004.06.001 [82] Zhang J, Wang X P, Huang K. Integrated on-line scheduling of order batching and delivery under B2C e-commerce. Computers & Industrial Engineering, 2016, 94: 280-289 [83] Hong S, Johnson A L, Peters B A. Batch picking in narrow-aisle order picking systems with consideration for picker blocking. European Journal of Operational Research, 2012, 221(3): 557-570 doi: 10.1016/j.ejor.2012.03.045 [84] Tsai C Y, Liou J J H, Huang T M. Using a multiple-GA method to solve the batch picking problem: Considering travel distance and order due time. International Journal of Production Research, 2008, 46(22): 6533-6555 doi: 10.1080/00207540701441947 [85] Scholz A, Schubert D, Wäscher G. Order picking with multiple pickers and due dates-simultaneous solution of order batching, batch assignment and sequencing, and picker routing problems. European Journal of Operational Research, 2017, 263(2): 461-478 doi: 10.1016/j.ejor.2017.04.038 [86] Yu M F, De Koster R B M. The impact of order batching and picking area zoning on order picking system performance. European Journal of Operational Research, 2009, 198(2): 480-490 doi: 10.1016/j.ejor.2008.09.011 [87] Hur S, Lee Y H, Lim S Y, Lee M H. A performance estimation model for AS/RS by M/G/1 queuing system. Computers & Industrial Engineering, 2004, 46(2): 233-241 [88] 王艳艳, 周以齐, 沈长鹏, 吴耀华. 一种两类“货到人”订单拣选系统的适用性选择方法. 机械工程学报, 2015, 51(4): 206-212 doi: 10.3901/JME.2015.04.206Wang Yan-Yan, Zhou Yi-Qi, Shen Chang-Peng, Wu Yao-Hua. Applicability selection method of two parts-to-picker order picking systems. Journal of Mechanical Engineering, 2015, 51(4): 206-212 doi: 10.3901/JME.2015.04.206 [89] Al-Araidah O, Dalalah D, Al-Abdel Azeez M E, Khasawneh M T. A heuristic for clustering and picking small items considering safe reach of the order picker. European Journal of Industrial Engineering, 2017, 11(2): 256-269 doi: 10.1504/EJIE.2017.083256 [90] Khamis A, Hussein A, Elmogy A. Multi-robot task allocation: A review of the state-of-the-art. Cooperative Robots and Sensor Networks 2015. Switzerland: Springer-Verlag, 2015. 31−51 [91] 张嵛, 刘淑华. 多机器人任务分配的研究与进展. 智能系统学报, 2008, 3(2): 115-120Zhang Yu, Liu Shu-Hua. Survey of multi-robot task allocation. CAAI Transactions on Intelligent Systems, 2008, 3(2): 115-120 [92] Ross G T, Zoltners A A. Weighted assignment models and their application. Management Science, 1979, 25(7): 683-696 doi: 10.1287/mnsc.25.7.683 [93] 施展, 陈庆伟. 基于改进的多目标量子行为粒子群优化算法的多无人机协同任务分配. 南京理工大学学报, 2012, 36(6): 945-951Shi Zhan, Chen Qing-Wei. Cooperative task allocation for multiple UAVs based on improved multi-objective quantum-behaved particle swarm optimization algorithm. Journal of Nanjing University of Science and Technology, 2012, 36(6): 945-951 [94] 孙博寒, 王浩, 方宝富, 凌兆龙, 林杰华. 基于自组织算法的情感机器人追捕任务分配. 机器人, 2017, 39(5): 680-687Sun Bo-Han, Wang Hao, Fang Bao-Fu, Ling Zhao-Long, Lin Jie-Hua. Task allocation in emotional robot pursuit based on self-organizing algorithm. Robot, 2017, 39(5): 680-687 [95] Fang B F, Chen L, Wang H, Dai S L, Zhong Q B. Research on multirobot pursuit task allocation algorithm based on emotional cooperation factor. The Scientific World Journal, 2014, 2014: 864180 [96] 柳林, 季秀才, 郑志强. 基于市场法及能力分类的多机器人任务分配方法. 机器人, 2006, 28(3): 337-343 doi: 10.3321/j.issn:1002-0446.2006.03.019Liu Lin, Ji Xiu-Cai, Zheng Zhi-Qiang. Multi-robot task allocation based on market and capability classification. Robot, 2006, 28(3): 337-343 doi: 10.3321/j.issn:1002-0446.2006.03.019 [97] Irfan M, Farooq A. Auction-based task allocation scheme for dynamic coalition formations in limited robotic swarms with heterogeneous capabilities. In: Proceedings of the 2016 International Conference on Intelligent Systems Engineering (ICISE). Islamabad, Pakistan: IEEE, 2016. 210−215 [98] 刘淑华, 张嵛, 吴洪岩, 刘杰. 基于群体智能的多机器人任务分配. 吉林大学学报(工学版), 2010, 40(1): 123-129Liu Shu-Hua, Zhang Yu, Wu Hong-Yan, Liu Jie. Multi-robot task allocation based on swarm intelligence. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(1): 123-129 [99] Gong J W, Qi J Y, Xiong G M, Chen H Y, Huang W N. A GA based combinatorial auction algorithm for multi-robot cooperative hunting. In: Proceedings of the 2007 International Conference on Computational Intelligence and Security (CIS 2007). Harbin, China: IEEE, 2007. 137−141 [100] Janati F, Abdollahi F, Ghidary S S, Jannatifar M, Baltes J, Sadeghnejad S. Multi-robot task allocation using clustering method. Robot Intelligence Technology and Applications 4. Switzerland: Springer, 2017. 233−247 [101] Farinelli A, Iocchi L, Nardi D. Distributed on-line dynamic task assignment for multi-robot patrolling. Autonomous Robots, 2017, 41(6): 1321-1345 doi: 10.1007/s10514-016-9579-8 [102] 陈培友, 汪定伟. 组合拍卖竞胜标确定问题的混沌搜索算法. 管理科学学报, 2003, 6(5): 24-28 doi: 10.3321/j.issn:1007-9807.2003.05.005Chen Pei-You, Wang Ding-Wei. Chaotic search algorithm for winner determination in combinatorial auctions. Journal of Management Sciences in China, 2003, 6(5): 24-28 doi: 10.3321/j.issn:1007-9807.2003.05.005 [103] Cavalcante R C, Noronha T F, Chaimowicz L. Improving combinatorial auctions for multi-robot exploration. In: Proceedings of the 16th International Conference on Advanced Robotics (ICAR). Montevideo, Uruguay: IEEE, 2013. 1−6 [104] 马磊, 张文旭, 戴朝华. 多机器人系统强化学习研究综述. 西南交通大学学报, 2014, 49(6): 1032-1044 doi: 10.3969/j.issn.0258-2724.2014.06.015Ma Lei, Zhang Wen-Xu, Dai Chao-Hua. A review of developments in reinforcement learning for multi-robot systems. Journal of Southwest JiaoTong University, 2014, 49(6): 1032-1044 doi: 10.3969/j.issn.0258-2724.2014.06.015 [105] Bektas T. The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega, 2006, 34(3): 209-219 doi: 10.1016/j.omega.2004.10.004 [106] Pandey A. Mobile robot navigation and obstacle avoidance techniques: A review. International Robotics & Automation Journal, 2017, 2(3): 00023 [107] 成伟明, 唐振民, 赵春霞, 刘华军. 移动机器人路径规划中的图方法应用综述. 工程图学学报, 2008, 29(4): 6-14Cheng Wei-Ming, Tang Zhen-Min, Zhao Chun-Xia, Liu Hua-Jun. A survey of mobile robots path planning using geometric methods. Journal of Engineering Graphics, 2008, 29(4): 6-14 [108] 王慧, 王光宇, 潘德文. 基于改进粒子群算法的移动机器人路径规划. 传感器与微系统, 2017, 36(5): 77-79Wang Hui, Wang Guang-Yu, Pan De-Wen. Mobile robot path planning based on modified particle swarm optimization algorithm. Transducer and Microsystem Technologies, 2017, 36(5): 77-79 [109] Shen C E, He J. A hybrid path planning algorithm for indoor mobile robot using hierarchy reinforcement learning. International Journal of Control and Automation, 2016, 9(5): 351-362 doi: 10.14257/ijca.2016.9.5.34 [110] 高翔, 苏青. 基于双层模糊逻辑的多机器人路径规划与避碰. 计算机技术与发展, 2014, 24(11): 79-82Gao Xiang, Su Qing. Multi-robot path planning and collision avoidance based on double fuzzy logic. Computer Technology and Development, 2014, 24(11): 79-82 [111] 胡世亮, 席裕庚. 一种通用的移动机器人路径规划仿真系统. 系统仿真学报, 2004, 16(8): 1714-1716, 1720 doi: 10.3969/j.issn.1004-731X.2004.08.029Hu Shi-Liang, Xi Yu-Geng. A general-purpose moving robot path-planning simulation system. Journal of System Simulation, 2004, 16(8): 1714-1716, 1720 doi: 10.3969/j.issn.1004-731X.2004.08.029 [112] Lu W R, McFarlane D, Giannikas V, Zhang Q. An algorithm for dynamic order-picking in warehouse operations. European Journal of Operational Research, 2016, 248(1): 107-122 doi: 10.1016/j.ejor.2015.06.074 [113] 高志伟, 代学武, 郑志达. 基于运动控制和频域分析的移动机器人能耗最优轨迹规划. 自动化学报, 2020, 46(5): 934-945Gao Zhi-Wei, Dai Xue-Wu, Zheng Zhi-Da. Optimal energy consumption trajectory planning for mobile robot based on motion control and frequency domain analysis. Acta Automatica Sinica, 2020, 46(5): 934-945 [114] 宋勇, 李贻斌, 栗春, 李彩虹. 基于神经网络的移动机器人路径规划方法. 系统工程与电子技术, 2008, 30(2): 316-319 doi: 10.3321/j.issn:1001-506X.2008.02.030Song Yong, Li Yi-Bin, Li Chun, Li Cai-Hong. Path planning methods of mobile robot based on neural network. Systems Engineering and Electronics, 2008, 30(2): 316-319 doi: 10.3321/j.issn:1001-506X.2008.02.030 [115] 孙志军, 薛磊, 许阳明, 王正. 深度学习研究综述. 计算机应用研究, 2012, 29(8): 2806-2810 doi: 10.3969/j.issn.1001-3695.2012.08.002Sun Zhi-Jun, Xue Lei, Xu Yang-Ming, Wang Zheng. Overview of deep learning. Application Research of Computers, 2012, 29(8): 2806-2810 doi: 10.3969/j.issn.1001-3695.2012.08.002 [116] Li H, Yang S X, Seto M L. Neural-network-based path planning for a multirobot system with moving obstacles. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2009, 39(4): 410-419 doi: 10.1109/TSMCC.2009.2020789 [117] Zhu A, Yang S X. A neural network approach to dynamic task assignment of multirobots. IEEE Transactions on Neural Networks, 2006, 17(5): 1278-1287 doi: 10.1109/TNN.2006.875994 [118] Heo Y J, Kim D, Lee W, Kim H, Park J, Chung W K. Collision detection for industrial collaborative robots: A deep learning approach. IEEE Robotics and Automation Letters, 2019, 4(2): 740-746 doi: 10.1109/LRA.2019.2893400 [119] 徐翔斌, 李志鹏. 强化学习在运筹学的应用: 研究进展与展望. 运筹与管理, 2020, 29(5): 227-239Xu Xiang-Bin, Li Zhi-Peng. Research progress and prospects for application of reinforcement learning in operations research. Operations Research and Management Science, 2020, 29(5): 227-239 [120] 刘丹, 曹建彤, 陈建名. 基于Agent建模的应用: 研究综述. 技术经济, 2014, 33(11): 96-102 doi: 10.3969/j.issn.1002-980X.2014.11.014Liu Dan, Cao Jian-Tong, Chen Jian-Ming. Application of agent-based modeling: Literature review. Technology Economics, 2014, 33(11): 96-102 doi: 10.3969/j.issn.1002-980X.2014.11.014 [121] Green D G. Hierarchy, complexity and agent based models. Our Fragile World: Challenges and Opportunities for Sustainable Development. Pairs: UNESCO, 2010. 1273−1292 [122] 陈仁际, 吴镇炜, 王韬, 董昌. 基于Agent的分布式多机器人系统建模及分析. 中国机械工程, 2001, 12(6): 667-671 doi: 10.3321/j.issn:1004-132X.2001.06.017Chen Ren-Ji, Wu Zhen-Wei, Wang Tao, Dong Chang. Modeling and analysis for agent-based distributed multiple robot system. China Mechanical Engineering, 2001, 12(6): 667-671 doi: 10.3321/j.issn:1004-132X.2001.06.017 [123] 柏继云, 李士勇. 基于agent的蚁群觅食行为建模及在机器人路径规划问题中的应用. 计算机应用研究, 2014, 31(1): 47-50, 54 doi: 10.3969/j.issn.1001-3695.2014.01.010Bai Ji-Yun, Li Shi-Yong. Modeling of ant colony foraging behavior based on agent and application of model in robotic path planning. Application Research of Computers, 2014, 31(1): 47-50, 54 doi: 10.3969/j.issn.1001-3695.2014.01.010 [124] Hazard C J, Wurman P R, D’Andrea R. Alphabet soup: A testbed for studying resource allocation in multi-vehicle systems. In: Proceedings of the 2006 AAAI Workshop on Auction Mechanisms for Robot Coordination. Boston, Massachusetts, USA: AAAI, 2006. 23−30 [125] Merschformann M, Xie L, Li H Y. RAWSim-O: A simulation framework for robotic mobile fulfillment systems [Online], available: https://arxiv.org/pdf/1710.04726.pdf, October 12, 2017 [126] Keung K L, Lee C K M, Ji P, Ng K K H. Cloud-based cyber-physical robotic mobile fulfillment systems: A case study of collision avoidance. IEEE Access, 2020, 8: 89318-89336 doi: 10.1109/ACCESS.2020.2992475 [127] Azadeh K, De Koster R, Roy D. Robotized and automated warehouse systems: review and recent developments. Transportation Science, 2019, 53(4): 917-945 doi: 10.1287/trsc.2018.0873 [128] 孙长银, 穆朝絮. 多智能体深度强化学习的若干关键科学问题. 自动化学报, 2020, 46(7): 1301-1312Sun Chang-Yin, Mu Chao-Xu. Important scientific problems of multi-agent deep reinforcement learning. Acta Automatica Sinica, 2020, 46(7): 1301-1312 [129] 秦方博, 徐德. 机器人操作技能模型综述. 自动化学报, 2019, 45(8): 1401-1418Qin Fang-Bo, Xu De. Review of robot manipulation skill models. Acta Automatica Sinica, 2019, 45(8): 1401-1418 [130] 曹风魁, 庄严, 闫飞, 杨奇峰, 王伟. 移动机器人长期自主环境适应研究进展和展望. 自动化学报, 2020, 46(2): 205-221Cao Feng-Kui, Zhuang Yan, Yan Fei, Yang Qi-Feng, Wang Wei. Long-term autonomous environment adaptation of mobile robots: State-of-the-art methods and prospects. Acta Automatica Sinica, 2020, 46(2): 205-221 -




 下载:
下载: