多中心联合配送模式下集货需求随机的<b>VRPSDP</b>问题

范厚明; 刘鹏程; 刘浩; 侯登凯

doi:10.16383/j.aas.c190519

多中心联合配送模式下集货需求随机的VRPSDP问题

doi: 10.16383/j.aas.c190519

1.
大连海事大学交通运输工程学院大连 116026

基金项目: 国家自然科学基金(61473053), 辽宁省社会科学规划基金(L19BGL006), 辽宁省重点研发计划指导计划(2018401002)资助

详细信息

作者简介:
范厚明：大连海事大学交通运输工程学院教授. 主要研究方向为交通运输系统规划与设计, 战略管理与系统规划. 本文通信作者. E-mail: fhm468@163.com

刘鹏程：大连海事大学交通运输工程学院硕士研究生. 主要研究方向为交通运输规划与管理. E-mail: lpc0369@163.com

刘浩：大连海事大学交通运输工程学院硕士研究生. 主要研究方向为物流工程与管理. E-mail: lhao66@126.com

侯登凯：大连海事大学交通运输工程学院博士研究生. 主要研究方向为交通运输规划与管理. E-mail: houdk@dlmusp.com

计量
- 文章访问数: 1055
- HTML全文浏览量: 384
- PDF下载量: 129
- 被引次数: 0
出版历程
- 收稿日期: 2019-07-08
- 录用日期: 2019-11-16
- 刊出日期: 2021-07-27

The Multi-depot Vehicle Routing Problem With Simultaneous Deterministic Delivery and Stochastic Pickup Based on Joint Distribution

1.
College of Transportation Engineering, Dalian Maritime University, Dalian 116026

Funds: National Natural Science Foundation of China (61473053), Liaoning Social Science Planning Fund (L19BGL006), the Key Research Plan Guidance Plan of Liaoning Province (2018401002)

More Information

Author Bio:
FAN Hou-Ming　Professor at the College of Transportation Engineering, Dalian Maritime University. His research interest covers transportation system planning and design, strategic management and system planning. Corresponding author of this paper

LIU Peng-Cheng　Master student at the College of Transportation Engineering, Dalian Maritime University. His main research interest is transportation planning and management

LIU Hao　Master student at the College of Transportation Engineering, Dalian Maritime University. His main research interest is logistics engineering and management

HOU Deng-Kai　Ph. D. candidate at the College of Transportation Engineering, Dalian Maritime University. His main research interest is transportation planning and management

摘要

摘要:
针对多中心联合配送模式下集货需求随机的同时配集货车辆路径问题(MDVRPSDDSPJD), 构建了两阶段MDVRPSDDSPJD模型. 预优化阶段基于随机机会约束机制以及车载量约束为客户分配车辆, 生成预优化方案; 重优化阶段采用失败点重优化策略对服务失败点重新规划路径. 根据问题特征, 设计了自适应变邻域文化基因算法(Adaptive memetic algorithm and variable neighborhood search, AMAVNS), 针对文化基因算法易早熟、局部搜索能力弱等缺陷, 将变邻域搜索算法的深度搜索能力运用到文化基因算法的局部搜索策略中, 增强算法的局部搜索能力; 提出自适应邻域搜索次数策略和自适应劣解接受机制平衡种群进化所需的广度和深度. 通过多组算例验证了提出模型及算法的有效性. 研究成果不仅深化和拓展了VRP (Vehicle routing problem)相关理论研究, 也为物流企业制定车辆调度计划提供一种科学合理的方法.
- 车辆路径问题 /
- 多中心 /
- 同时配集货 /
- 随机需求 /
- 文化基因算法 /
- 变邻域搜索算法
Abstract:
A two-stage model is constructed to solve the multi-depot vehicle routing problem with simultaneous deterministic delivery and stochastic pickup based on joint distribution (MDVRPSDDSPJD). In pre-optimization stage, the pre-optimization scheme is generated, and the vehicles is assigned to the customers based on the stochastic chance constrained and vehicle capacity constraints. In re-optimization stage, the failure points rescheduling strategy is used to re-plan the path of the service failure points. According to the characteristics of the problem, a metaheuristic combined adaptive memetic algorithm and variable neighborhood search (AMAVNS) is designed to solve the problem. In this metaheuristic, aiming at the shortcomings of memetic algorithm such as fast convergence speed and weak local search capability, the deep search ability of the variable neighborhood search algorithm is applied to the local search strategy of the memetic algorithm to enhance the local search ability of the algorithm. The strategies include self-adaptive number of neighborhood iterations and adaptive mechanism of selective acceptance of inferior solutions are used to balance the diversification and exploitation in the algorithm iteration process. Numerical results show that the model and metaheuristic we proposed are rather effective. The research results not only deepen and expand the vehicle routing problem (VRP) theory research, but also provide a scientific and reasonable method for logistics enterprises to draw up the vehicle scheduling plan.
- Vehicle routing problem /
- multi-depot /
- simultaneous delivery and pickup /
- stochastic demand /
- memetic algorithm /
- variable neighborhood search

HTML全文

图 1 MDVRPSDDSPJD的衍生进程

Fig. 1 Derivation of MDVRPSDDSPJD

下载: 全尺寸图片幻灯片

图 2 不同失败点重优化策略对比图

Fig. 2 Different failure points re-optimized strategies

下载: 全尺寸图片幻灯片

图 3 自适应变邻域文化基因算法框架图

Fig. 3 The basic flow of adaptive memetic algorithm and variable neighborhood search

下载: 全尺寸图片幻灯片

图 4 编码方式示意图

Fig. 4 Encoding mode diagram

下载: 全尺寸图片幻灯片

图 5 解码路径图

Fig. 5 Decoding routing diagram

下载: 全尺寸图片幻灯片

图 6 顺序交叉算子示意图

Fig. 6 The diagram of ordered crossover operator

下载: 全尺寸图片幻灯片

图 7 邻域结构示意图

Fig. 7 Neighborhood structures

下载: 全尺寸图片幻灯片

图 8 最短路径变化趋势图

Fig. 8 The iterative trend of optimal solution

下载: 全尺寸图片幻灯片

图 9 实验3部分算例的求解路径图

Fig. 9 The specific path diagrams of some cases of experiment 3

下载: 全尺寸图片幻灯片

表 1 算法性能比较

Table 1 Performance comparison of different types of metaheuristics

算法	$BKS$	$Best$	${\text{%}}Dev$(%)	$Worst$	${\text{%}}Dev$(%)	$Avg$	${\text{%}}Dev$(%)	$CPU\,({\rm{s} })$
聚类分层法^[22]	116.01	123.33	6.31
狼群算法^[23]		122.42	5.53
禁忌搜索算法^[24]		116.01	0.00	343.31	195.93	187.34	61.49	243.00
量子遗传算法^[24]		116.01	0.00	326.48	181.42	176.37	52.03	216.00
云量子遗传算法^[24]		116.01	0.00	162.38	39.97	156.32	34.75	168.00
自适应变邻域文化基因算法		113.62	−2.06	115.39	−0.53	114.33	−1.45	4.78

下载: 导出CSV

表 2 本文算法求解路径

Table 2 The algorithm solution path of this paper

算法	车辆行驶路径	总路程
本文	A-22-30-14-10-7-4-A	113.62
	B-11-29-28-13-8-15-1-B
	C-16-25-5-12-26-18-3-6-C
	C-17-21-19-20-23-24-2-9-27-C

下载: 导出CSV

表 3 MDVRP算例结果比较

Table 3 The results comparison of MDVRP instances

算例	客户规模	$BKS$	GRASP/VND^[25]		GA^[26]		ILS^[27]		AMAVNS
算例	客户规模	$BKS$	$Best$	${\text{%}}Dev$(%)	$Best$	${\text{%}}Dev$(%)	$Best$	${\text{%}}Dev$(%)	$Best$	${\text{%} }Dev\ ({\text{%} })$	$CPU\, ({\rm{s} })$
p01	50	576.87	592.21	2.66	598.45	3.74	606.11	5.07	576.87	0.00	32.60
p02	50	473.53	529.64	11.85	478.65	1.08	496.45	4.84	473.53	0.00	39.22
p03	75	641.19	648.68	1.17	699.23	9.05	675.32	5.32	646.33	0.80	84.06
p04	100	1 001.59	1 055.26	5.36	1 011.36	0.98	1 062.60	6.09	1 039.69	3.80	155.23
p05	100	750.03	769.37	2.58	—	—	782.34	4.31	765.98	2.13	143.73
p06	100	876.50	924.68	5.50	882.88	0.72	910.13	3.84	902.27	2.94	164.82
p07	100	885.80	925.80	4.52	—	—	904.44	2.10	909.22	2.64	159.01

下载: 导出CSV

表 4 VRPSDP算例结果比较

Table 4 The results comparison of VRPSDP instances

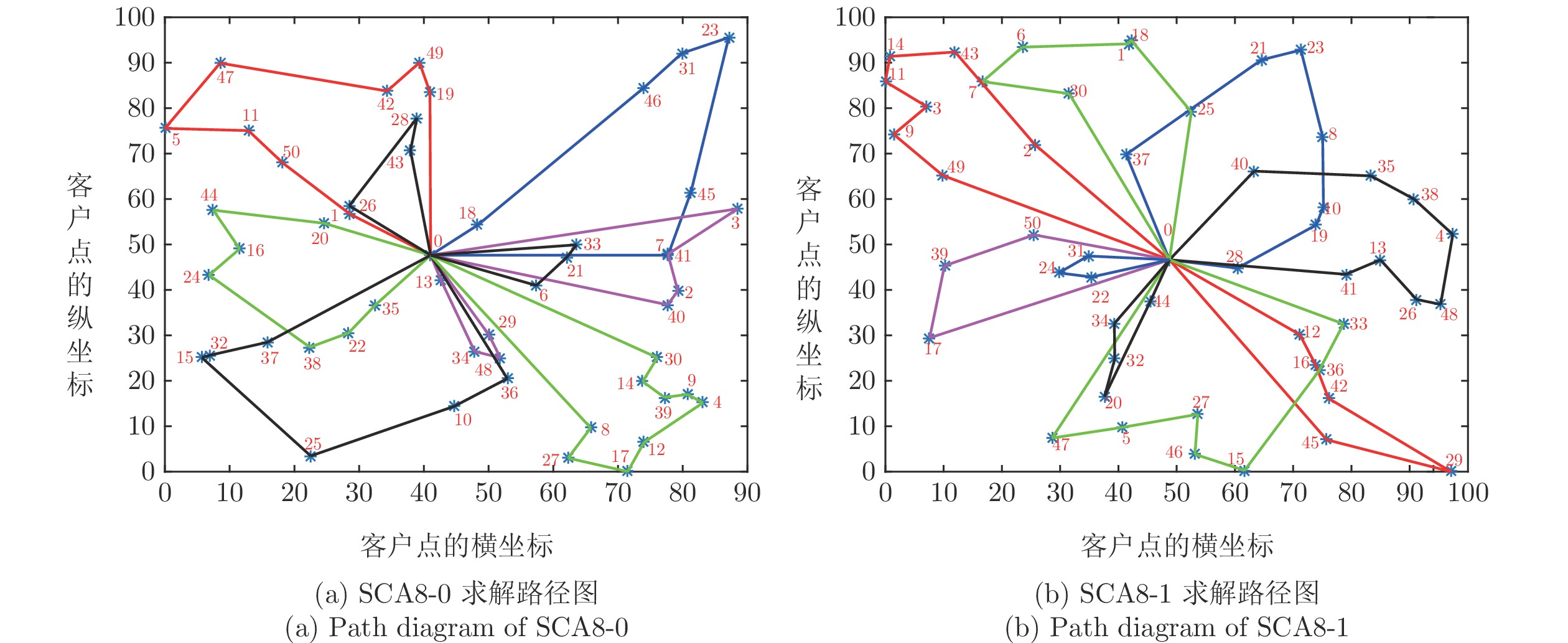
算例	TS^[29]			EPSA3^[30]			SavAnt^[31]			SS^[32]		AMAVNS
算例	$Best$	${\text{%}}Dev$(%)	$CPU\,({\rm{s} })$	$Best$	${\text{%}}Dev$(%)	$CPU \,({\rm{s} })$	$Best$	${\text{%}}Dev$(%)	$CPU\,({\rm{s} })$	$Best$	${\text{%}}Dev$(%)	$Best$	${\text{%}}Dev$(%)	$CPU\,({\rm{s} })$
SCA8-0	981.47	2.07	4.14	1 015.06	5.57	—	961.6	0.01	—	981.17	2.05	961.50	0.00	35.31
SCA8-1	1 077.44	2.65	4.27	1 098.91	4.69	—	1 063.0	1.27	—	1 077.44	2.65	1 049.65	0.00	42.05
SCA8-2	1 050.98	1.00	4.20	1 064.54	2.30	—	1 040.6	0.00	—	1 050.98	1.00	1 049.22	0.83	36.63
SCA8-3	983.34	0.00	4.17	1 021.61	3.89	—	985.9	0.26	—	983.34	0.00	983.34	0.00	31.59
SCA8-4	1 073.46	0.55	4.13	1 114.50	4.40	—	1 071.0	0.32	—	1 073.46	0.55	1 065.49	0.00	42.87
SCA8-5	1 047.24	1.68	4.02	1 060.43	2.96	—	1 054.3	2.36	—	1 047.24	1.68	1 029.95	0.00	38.19
SCA8-6	995.59	2.37	3.85	1 004.66	3.31	—	972.5	0.00	—	995.59	2.37	973.27	0.08	34.88
SCA8-7	1 068.56	0.84	4.22	1 080.17	1.93	—	1 059.7	0.00	—	1 068.56	0.84	1 063.22	0.33	29.01
SCA8-8	1 080.58	0.88	3.85	1 098.02	2.51	—	1 082.7	1.08	—	1 080.58	0.88	1 071.18	0.00	33.54
SCA8-9	1 084.80	1.32	4.20	1 123.55	4.94	—	1 081.4	1.00	—	1 084.80	1.32	1 070.71	0.00	46.03
CON8-0	860.48	0.39	4.19	857.17	0.00	—	858.9	0.20	—	860.48	0.39	857.40	0.03	37.86
CON8-1	740.85	0.00	3.89	742.41	0.21	—	740.9	0.01	—	740.85	0.00	740.85	0.00	40.75
CON8-2	723.32	1.38	3.76	715.17	0.24	—	714.3	0.12	—	723.32	1.38	713.44	0.00	35.99
CON8-3	811.23	0.00	4.12	815.59	0.54	—	812.3	0.13	—	811.23	0.00	811.23	0.00	39.37
CON8-4	772.25	0.28	3.75	789.13	2.47	—	770.1	0.00	—	772.25	0.28	772.25	0.28	41.22
CON8-5	756.91	0.23	3.99	759.09	0.52	—	766.6	1.51	—	756.91	0.23	755.16	0.00	40.84
CON8-6	678.92	0.00	4.04	707.83	4.26	—	697.2	2.69	—	678.92	0.00	684.11	0.76	53.95
CON8-7	814.50	0.00	4.00	834.64	2.47	—	814.8	0.04	—	814.50	0.00	814.77	0.03	49.99
CON8-8	775.59	1.05	3.74	787.43	2.59		−771.3	0.49	—	775.59	1.05	767.53	0.00	33.40
CON8-9	809.00	0.00	4.13	813.84	0.60	—	815.1	0.75	—	809.00	0.00	809.00	0.00	34.21
平均值	909.33	0.83	4.03	925.19	2.52	2.98	906.71	0.61	441	909.31	0.83	902.27	0.12	39.38

下载: 导出CSV

表 5 MDVRPSDDSPJD算例结果比较

Table 5 The results comparison of MDVRPSDDSPJD

$\alpha$	规则1			规则2
$\alpha$	$Best$	$Avg$	$CPU\,({\rm{s} })$	$Best$	${\text{%}}Dev$(%)	$Avg$	${\text{%}}Dev$(%)	$CPU\;({\rm{s} })$
0.1	558.98	732.61	98.85	548.86	−1.81	674.40	−7.95	101.57
0.2	565.26	726.67	92.75	549.51	−2.79	673.54	−7.31	110.48
0.3	545.30	713.16	97.43	542.30	−0.55	676.67	−5.12	108.43
0.4	568.42	713.75	108.26	550.14	−3.22	678.61	−4.92	102.49
0.5	549.96	709.65	105.43	543.59	−1.16	650.79	−8.29	109.47
0.6	548.04	651.97	105.67	537.83	−1.86	640.07	−1.83	114.64
0.7	533.85	624.97	102.20	499.96	−6.35	610.54	−2.31	101.35
0.8	545.30	668.99	110.46	537.83	−1.37	641.70	−4.08	148.57
0.9	546.83	657.50	90.26	537.44	−1.72	653.35	−0.63	96.84
1.0	564.64	655.98	95.33	563.24	−0.25	650.85	−0.78	110.28
平均值	552.66	685.53	100.66	541.07	−2.10	655.05	−4.45	110.41

下载: 导出CSV

表 6 MDVRPSDDSPJD算例求解最优解

Table 6 The best solutions of MDVRPSDDSPJD

	车辆行驶路径	车辆数	总路程
规则 1	51-4-18-13-41-40-19-42-51	8	533.85
	53-38-5-37-17-44-15-45-33-39-10-49-53
	53-30-34-21-16-50-9-53
	54-20-3-36-35-54
	52-11-32-27-48-23-7-43-24-52
	54-29-2-1-8-26-31-28-22-54
	52-47-12-46-52
	52-6-14-25-52
规则 2	54-20-2-16-21-29-54	7	499.96
	54-35-36-3-28-31-26-8-22-54
	53-38-5-37-17-44-15-45-33-39-10-49-53
	52-46-11-32-1-27-48-23-7-43-24-6-52
	51-42-19-40-41-13-25-14-52
	52-12-47-18-4-51
	53-30-34-50-9-53

下载: 导出CSV

参考文献(33)

[1]	Dantzig G B, Ramser J H. The truck dispatching problem. Management Science, 1959, 6(1): 80−91 doi: 10.1287/mnsc.6.1.80
[2]	葛显龙, 王旭, 邓蕾. 基于联合配送的开放式动态车辆路径问题及算法研究. 管理工程学报, 2013, 27(3): 60−68 doi: 10.3969/j.issn.1004-6062.2013.03.008 Ge Xian-Long, Wang Xu, Deng Lei. Research on open and dynamic vehicle routing problems based on joint distribution. Journal of Industrial Engineering and Engineering Management, 2013, 27(3): 60−68 doi: 10.3969/j.issn.1004-6062.2013.03.008
[3]	杨翔, 范厚明, 张晓楠, 李阳. 基于模糊时间窗的多中心开放式车辆路径问题. 计算机集成制造系统, 2016, 22(7): 1768−1778 Yang Xiang, Fan Hou-Ming, Zhang Xiao-Nan, Li Yang. Optimization of multi-deport open vehicle routing problem with fuzzy time window. Computer Integrated Manufacturing Systems, 2016, 22(7): 1768−1778
[4]	Gruler A, Fikar C, Juan A A, Hirsch P, Contreras-Bolton C. Supporting multi-depot and stochastic waste collection management in clustered urban areas via simulation-optimization. Journal of Simulation, 2017, 11(1): 11−19 doi: 10.1057/s41273-016-0002-4
[5]	Alinaghian M, Shokouhi N. Multi-depot multi-compartment vehicle routing problem, solved by a hybrid adaptive large neighborhood search. Omega, 2018, 76(3): 85−99
[6]	葛显龙, 邹登波. 供应链环境下带越库配送的多配送中心车辆路径问题. 控制与决策, 2018, 33(12): 2169−2176 Ge Xian-Long, Zou Deng-Bo. Vehicle routing problem of multi-distribution centers with cross-docking in the supply chain. Control and Decision, 2018, 33(12): 2169−2176
[7]	陈呈频, 韩胜军, 鲁建厦, 陈青丰, 王成. 多车场与多车型车辆路径问题的多染色体遗传算法. 中国机械工程, 2018, 29(2): 218−223 doi: 10.3969/j.issn.1004-132X.2018.02.014 Chen Cheng-Pin, Han Sheng-Jun, Lu Jian-Sha, Chen Qing-Feng, Wang Cheng. A multi-chromosome genetic algorithm for multi-depot and multi-type vehicle routing problems. China Mechanical Engineering, 2018, 29(2): 218−223 doi: 10.3969/j.issn.1004-132X.2018.02.014
[8]	Wang Y, Assogba K, Xu M Z, Liu Y, Wang H Z. Multi-depot green vehicle routing problem with shared transportation resource: Integration of time-dependent speed and piecewise penalty cost. Journal of Cleaner Production, 2019, 232(27): 12−29
[9]	Li Y B, Soleimani H, Zohal M. An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives. Journal of Cleaner Production, 2019, 227(22): 1161−1172
[10]	Li J, Pardalos P M, Sun H, Pei J, Zhang Y. Iterated local search embedded adaptive neighborhood selection approach for the multi-depot vehicle routing problem with simultaneous deliveries and pickups. Expert Systems With Applications an International Journal, 2015, 42(7): 3551−3561 doi: 10.1016/j.eswa.2014.12.004
[11]	Kachitvichyanukul V, Sombuntham P, Kunnapapdeelert S. Two solution representations for solving multi-depot vehicle routing problem with multiple delivery and pickup requests via PSO. Computers & Industrial Engineering, 2015, 89(11): 125−136
[12]	Soriano A, Gansterer M, Hartl R F. The two-region multi-depot delivery and pickupproblem. Or Spectrum, 2018, 40(4): 1077−1108 doi: 10.1007/s00291-018-0534-2
[13]	Ben Alaia E, Harbaoui I, Borne P, Bouchriha H. A comparative study of the PSO and GA for the m-MDPDPTW. International Journal of Computers Communications & Control, 2018, 13(1): 8−23
[14]	Bouanane K, Benadada Y, Bencheikh G. Multi-depots vehicle routing problem with simultaneous delivery and pickup and inventory restrictions: Formulation and resolution. International Journal of Advanced Computer Science and Applications, 2019, 10(2): 110−120
[15]	Gauvin C, Desaulniers G, Gendreau M. A branch-cut-and-price algorithm for the vehicle routing problem with stochastic demands. Computers & Operations Research, 2014, 50(10): 141−153
[16]	Yang W H, Mathur K, Ballou R H. Stochastic vehicle routing problem with restocking. Transportation Science, 2000, 34(1): 99−112 doi: 10.1287/trsc.34.1.99.12278
[17]	谢秉磊, 安实, 郭耀煌. 随机车辆路径问题的多回路优化策略. 系统工程理论与实践, 2007, 27(2): 167−171 doi: 10.3321/j.issn:1000-6788.2007.02.024 Xie Bing-Lei, An Shi, Guo Yao-Huang. Multi-tour optimization policy for stochastic vehicle routing problem. Systems Engineering-theory & Practice, 2007, 27(2): 167−171 doi: 10.3321/j.issn:1000-6788.2007.02.024
[18]	赵燕伟, 李川, 张景玲, 陆游, 王万良. 一种新的求解多目标随机需求车辆路径问题的算法. 计算机集成制造系统, 2012, 18(3): 523−530 Zhao Yan-Wei, Li Chuan, Zhang Jing-Ling, Lu You, Wang Wan-Liang. Novel algorithm for multi-objective vehicle routing problem with stochastic demand. Computer Integrated Manufacturing Systems, 2012, 18(3): 523−530
[19]	Hu Z H, Sheu J B, Zhao L, Lu C C. A dynamic closed-loop vehicle routing problem with uncertainty and incompatible goods. Transportation Research Part C, 2015, 55(6): 273−297
[20]	李阳, 范厚明, 张晓楠, 杨翔. 随机需求车辆路径问题及混合变邻域分散搜索算法求解. 控制理论与应用, 2017, 34(12): 1594−1604 doi: 10.7641/CTA.2017.60888 Li Yang, Fan Hou-Ming, Zhang Xiao-Nan, Yang Xiang. Two-phase variable neighborhood scatter search for the capacitated vehicle routing problem with stochastic demand. Control Theory & Applications, 2017, 34(12): 1594−1604 doi: 10.7641/CTA.2017.60888
[21]	郎茂祥. 多配送中心车辆调度问题的模型与算法研究. 交通运输系统工程与信息, 2006, 6(5): 65−69 doi: 10.3969/j.issn.1009-6744.2006.05.011 Lang Mao-Xiang. Study on the model and algorithm for multi-depot vehicle scheduling problem. Journal of Transportation Systems Engineering and Information Technology, 2006, 6(5): 65−69 doi: 10.3969/j.issn.1009-6744.2006.05.011
[22]	殷脂, 叶春明. 多配送中心物流配送车辆调度问题的分层算法模型. 系统管理学报, 2014, 6(4): 602−606 Yin Zhi, Ye Chun-Ming. Study on the hierarchical model for multi-depot logistic vehicle scheduling problem. Journal of Systems & Management, 2014, 6(4): 602−606
[23]	叶勇, 张惠珍. 多配送中心车辆路径问题的狼群算法. 计算机应用研究, 2017, 34(9): 36−39 Ye Yong, Zhang Hui-Zhen. Wolf pack algorithm for multi-depot vehicle routing problem. Application Research of Computers, 2017, 34(9): 36−39
[24]	葛显龙, 许茂增, 王伟鑫. 基于联合配送的城市物流配送路径优化. 控制与决策, 2016, 31(3): 503−512 Ge Xian-Long, Xu Mao-Zeng, Wang Wei-Xin. Route optimization of urban logistics in joint distribution. Control and Decision, 2016, 31(3): 503−512
[25]	Villegas J G, Prins C, Prodhon C, Medaglia A. GRASP/VND and multi-start evolutionary local search for the single truck and trailer routing problem with satellite depots. Engineering Applications of Artificial Intelligence, 2010, 623(5): 780−794
[26]	Karakatic S, Podgorelec V. A survey of genetic algorithms for solving multi depot vehicle routing problem. Applied Soft Computing Journal, 2015, 27(C): 519−532
[27]	Tlili T, Krichen S, Drira G, Faiz S. On solving the multi-depot vehicle routing problem. In: Proceedings of the 3rd International Conference on Advanced Computing, Networking and Informatics. New Delhi: Springer, 2016. 103-108
[28]	Dethloff J. Vehicle routing and reverse logistics: The vehicle routing problem with simultaneous delivery and pick-up. OR-Spektrum, 2001, 23(1): 79−96 doi: 10.1007/PL00013346
[29]	Montané F A T, Galvao R D. A tabu search algorithm for the vehicle routing problem with simultaneous pick-up and delivery service. Science Technology & Engineering, 2006, 33(3): 595−619
[30]	Gajpal Y, Abad P. Saving-based algorithms for vehicle routing problem with simultaneous pickup and delivery. Journal of the Operational Research Society, 2010, 61(10): 1498−1509 doi: 10.1057/jors.2009.83
[31]	Catay B. A new saving-based ant algorithm for the vehicle routing problem with simultaneous delivery and pickup. Expert Systems With Applications, 2010, 37(10): 6809−6817 doi: 10.1016/j.eswa.2010.03.045
[32]	Maquera G, Laguna M, Dan A G, Sant' Anna A P. Scatter search applied to the vehicle routing problem with simultaneous delivery and pickup. International Journal of Applied Metaheuristic Computing, 2011, 2(2): 1−20 doi: 10.4018/jamc.2011040101
[33]	Salhi S, Nagy G. A cluster insertion heuristic for single and multiple depot vehicle routing problems with backhauling. Journal of the Operational Research Society, 1999, 50(10): 1034−1042 doi: 10.1057/palgrave.jors.2600808