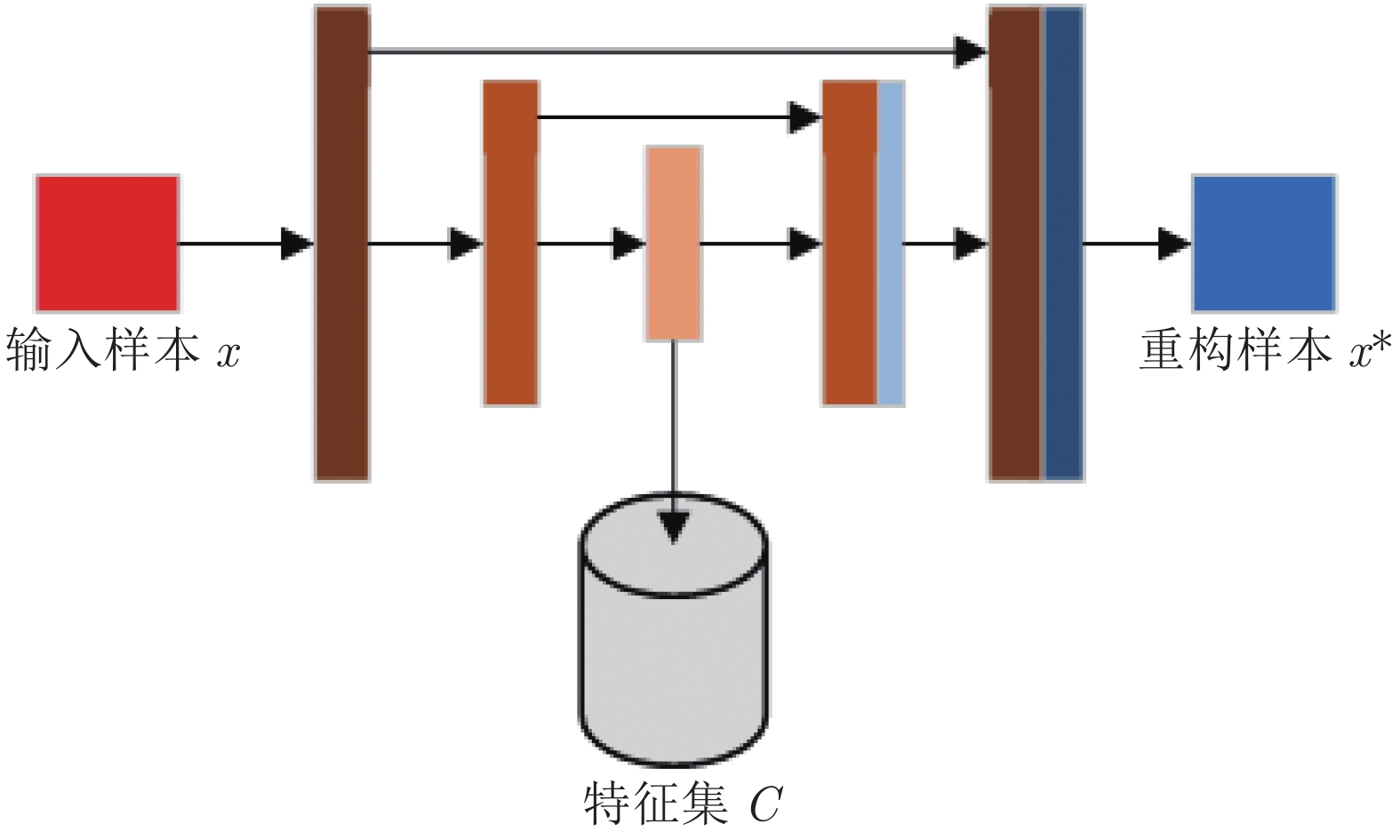
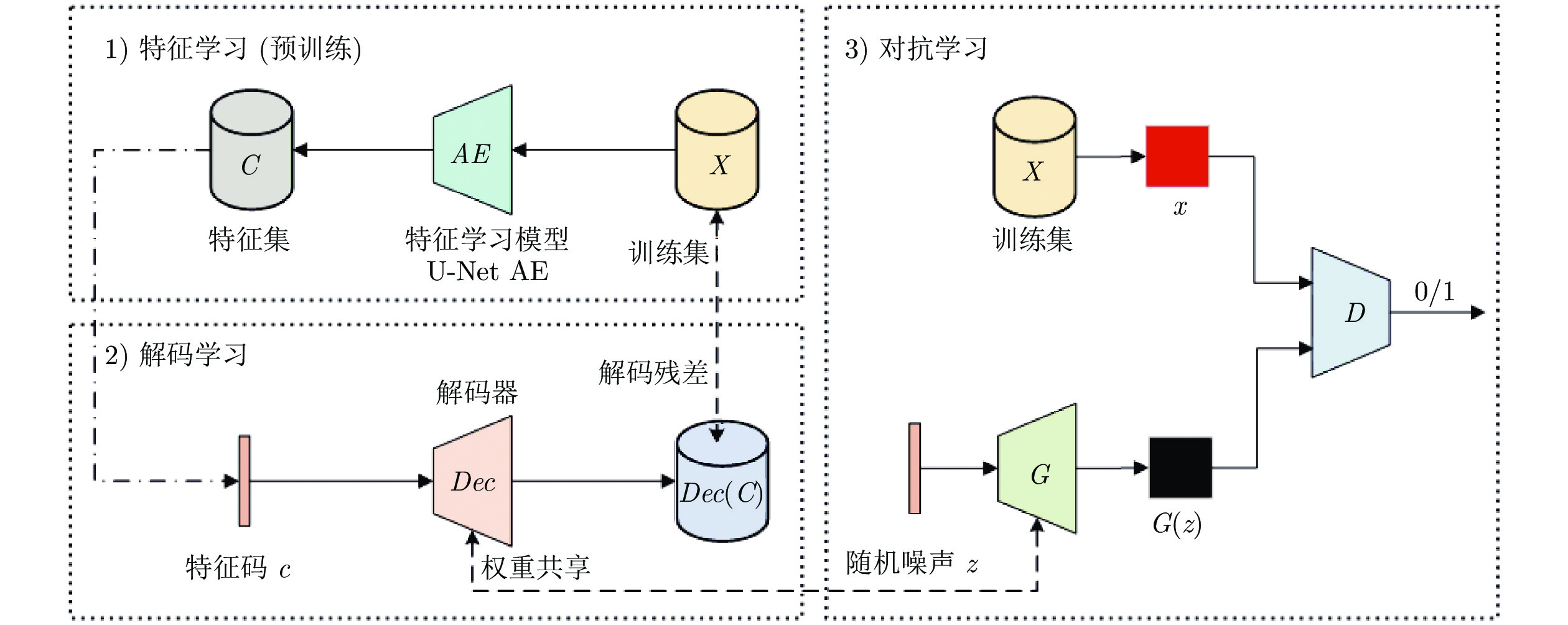
-
摘要: 生成式对抗网络(Generative adversarial networks, GANs)是一种有效模拟训练数据分布的生成方法, 其训练的常见问题之一是优化Jensen-Shannon (JS)散度时可能产生梯度消失问题. 针对该问题, 提出了一种解码约束条件下的GANs, 以尽量避免JS散度近似为常数而引发梯度消失现象, 从而提高生成图像的质量. 首先利用U-Net结构的自动编码机(Auto-encoder, AE)学习出与用于激发生成器的随机噪声同维度的训练样本网络中间层特征. 然后在每次对抗训练前使用设计的解码约束条件训练解码器. 其中, 解码器与生成器结构相同, 权重共享. 为证明模型的可行性, 推导给出了引入解码约束条件有利于JS散度不为常数的结论以及解码损失函数的类型选择依据. 为验证模型的性能, 利用Celeba和Cifar10数据集, 对比分析了其他6种模型的生成效果. 通过实验对比Inception score (IS)、弗雷歇距离和清晰度等指标发现, 基于样本特征解码约束的GANs能有效提高图像生成质量, 综合性能接近自注意力生成式对抗网络.Abstract: Generative adversarial networks (GANs) model is a generative approach for effectively simulating the distribution of training data. One of the common problems in training GANs is the possible vanishing gradient problem while optimizing Jensen-Shannon (JS) divergence. Aiming at the problem, a GANs model under decoding constraint is proposed to avoid JS divergence approximating a constant, thus improving the quality of generated images. Firstly, an auto-encoder (AE) structured under U-Net is utilized to learn the training sample network middle layer feature. It has the same dimension as the random noise used for triggering generative network. Then, the decoding constraint is designed, which shares the same structure and weights as that of the generative network, is used to train decoder before each adversarial training. To prove the feasibility of model, the conclusion is deduced that introducing decoding constraint is beneficial to avoiding JS divergence approximating a constant and the type selection basis of decoding loss function is given. To verify the performance of the model, Celeba and Cifar10 datasets are used to compare and analyze the generated results of other 6 models. By comparing Inception score, Frechet inception distance, clarity and other index via experiment, it is discovered that the novel GANs can improve the quality of generated images, comprehensive performance close to self-attention generation adversarial networks.
-
Key words:
- Generative adversarial networks /
- vanishing gradient /
- feature learning /
- auto-encoder /
- deep learning
-
图 7 Celeba中L2解码不限制权重实验样本
Fig. 7 L2 decoding with not restrict weight experimental samples in Celeba
图 10 Cifar10中L2解码不限制权重实验样本
Fig. 10 L2 decoding with not restrict weight experimental samples in Cifar10
表 1 原图像与重构图像的PSNR和SSIM值统计
Table 1 PSNR & SSIM between original and reconstructed images
数据集 指标 均值 标准差 极小值 极大值 Celeba PSNR 40.588 5.558 22.990 61.158 SSIM 0.9984 0.0023 0.9218 1.0000 Cifar10 PSNR 46.219 6.117 28.189 66.779 SSIM 0.9993 0.0019 0.8180 1.0000 
下载: 导出CSV
表 2 Celeba中不同解码实验结果
Table 2 Results of different decoding experiments in Celeba
对比项 IS ($ \sigma \times 0.01 $) FID 清晰度均值 清晰度均值差值 训练集 2.71 ± 2.48 0.00 107.88 0.00 正态特征 1.88 ± 1.25 42.54 121.40 13.52 均匀特征 1.82 ± 1.48 43.04 123.02 15.14 L1 1.99 ± 1.53 32.95 120.16 12.28 L2* 1.69 ± 0.97 46.08 96.88 11.00 L2 (本文) 2.05 ± 1.84 25.62 114.95 7.07
下载: 导出CSV
表 3 Cifar10中不同解码实验结果
Table 3 Results of different decoding experiments in Cifar10
对比项 IS ($ \sigma \times 0.1 $) FID 清晰度均值 清晰度均值差值 训练集 10.70 ± 1.47 0.00 120.56 0.00 正态特征 5.63 ± 0.64 48.21 139.88 19.32 均匀特征 5.51 ± 0.79 46.57 137.13 16.57 L1 5.63 ± 0.79 44.53 138.04 17.48 L2* 4.69 ± 0.55 79.10 119.62 0.94 L2 (本文) 5.83 ± 0.70 42.70 134.97 14.41
下载: 导出CSV
表 5 Celeba中不同GANs对比
Table 5 Comparsion of different GANs in Celeba
GANs 模型 epoch 数 优化项 参数量 ($ \times 10^6 $) IS ($ \sigma \times 0.01 $) FID 清晰度均值 清晰度均值差值 训练集 — — — 2.71 ± 2.48 0.00 107.88 0.00 BEGANs[16] 35 沃瑟斯坦距离 4.47 1.74 ± 1.29 46.24 77.58 30.30 DCGANs[9] 20 JS 散度 9.45 1.87 ± 1.58 50.11 124.82 16.94 LSGANs[15] 35 Pearson 散度 9.45 2.02 ± 1.63 39.11 122.19 14.31 WGANs[14] 35 沃瑟斯坦距离 9.45 2.03 ± 1.75 40.31 117.15 9.27 WGANsGP[17] 35 沃瑟斯坦距离 9.45 1.98 ± 1.82 37.01 121.16 13.28 SAGANs1[23] 30 沃瑟斯坦距离 10.98 2.06 ± 1.79 21.94 109.94 2.06 SAGANs2[23] 30 JS 散度 10.98 1.99 ± 1.79 31.04 99.57 8.31 本文方法 15 JS + $ \lambda \cdot $KL 散度 9.45 + 0.84 2.05 ± 1.84 25.62 114.95 7.07
下载: 导出CSV
表 6 Cifar10中不同GANs对比
Table 6 Comparsion of different GANs in Cifar10
GANs 模型 epoch 数 优化项 参数量 ($ \times 10^6 $) IS ($ \sigma \times 0.1 $) FID 清晰度均值 清晰度均值差值 训练集 — — — 10.70 ± 1.47 0.00 120.56 0.00 BEGANs[16] 35 沃瑟斯坦距离 3.67 5.36 ± 0.65 107.64 80.89 39.67 DCGANs[9] 20 JS 散度 8.83 5.04 ± 0.27 54.27 139.12 18.56 LSGANs[15] 35 Pearson 散度 8.83 5.70 ± 0.36 43.35 135.80 15.24 WGANs[14] 35 沃瑟斯坦距离 8.83 5.25 ± 0.33 53.88 136.74 16.18 WGANsGP[17] 35 沃瑟斯坦距离 8.83 5.39 ± 0.30 50.60 139.17 18.61 SAGANs1[23] 30 沃瑟斯坦距离 8.57 6.09 ± 0.47 42.90 126.28 5.72 SAGANs2[23] 30 JS 散度 8.57 5.37 ± 0.46 53.49 133.54 12.98 本文方法 15 JS + $ \lambda \cdot $KL 散度 8.83 + 0.23 5.83 ± 0.70 42.70 134.97 14.41
下载: 导出CSV
-
[1] Goodfellow I J, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. In: Proceedings of the International Conference on Neural Information Processing Systems. Montreal, Canada: 2014. 2672−2680 [2] Creswell A, White T, Dumoulin V, Arulkumaran K, Sengupta B, Bharath A A. Generative adversarial networks:an overview[J]. IEEE Signal Processing Magazine, 2018, 35(1): 53-65 doi: 10.1109/MSP.2017.2765202 [3] Hong Y J, Hwang U, Yoo J, Yoon S. How generative adversarial networks and their variants work: an overview. ACM Computing Surveys, 2019, 52(1): Article 10, 1-43 [4] Mirza M, Osindero S. Conditional generative adversarial nets. arXiv preprint, 2014, arXiv: 1411.1784v1 [5] Odena A. Semi-supervised learning with generative adversarial networks. arXiv preprint, 2016, arXiv: 1606.01583v2 [6] Odena A, Olah C, Shlens J. Conditional image synthesis with auxiliary classifier GANs. In: Proceedings of the International Conference on Machine Learning. Sydney, Australia: 2017. [7] Chen X, Duan Y, Houthooft R, Schulman J, Sutskever I, Abbeel P. InfoGAN: Interpretable representation learning by information maximizing generative adversarial nets. In: Proceedings of the International Conference on Neural Information Processing Systems. Barcelona, Spain: 2016. 2180−2188 [8] Donahue J, Krahenbuhl K, Darrell T. Adversarial feature learning. In: Proceedings of the International Conference on Learning Representations. Toulon, France: 2017. [9] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. In: Proceedings of the International Conference on Learning Representations. San Juan, Puerto Rico: 2016. [10] Denton E, Chintala S, Szlam A, Fergus R. Deep generative image using a laplacian pyramid of adversarial networks. In: Proceedings of the International Conference on Neural Information Processing Systems. Montreal, Canada: 2015. 1486−14944 [11] Brock A, Donahue J, Simonyan K. Large scale GAN training for high fidelity natural image synthesis. In: Proceedings of the International Conference on Learning Representations. New Orleans, USA: 2019. [12] Nguyen T D, Le T, Vu H, Phung D. Dual discriminator generative adversarial nets. In: Proceedings of the Proceedings of International Conference on Neural Information Processing Systems. Long Beach, USA: 2017. [13] 张龙, 赵杰煜, 叶绪伦, 董伟. 协作式生成对抗网络[J]. 自动化学报, 2018, 44(5): 804-810Zhang Long, Zhao Jie-Yu, Ye Xu-Lun, Dong Wei. Cooperative generative adversarial nets[J]. Acta Automatica Sinica, 2018, 44(5): 804-810 [14] Arjovsky M, Chintala S, Bottou L. Wasserstein generative adversarial networks. In: Proceedings of the International Conference on Machine Learning. Sydney, Australia: 2017. 214−223 [15] Mao X D, Li Q, Xie H R, Lau R Y K, Wang Z, Smolley S P. Least squares generative adversarial networks. In: Proceedings of the IEEE International Conference on Computer Vision. Venice, Italy: 2017. 2813−2821 [16] Berthelot D, Schumm T, Metz L. BEGAN: Boundary equilibrium generative adversarial networks. arXiv preprint, 2017, arXiv: 1703.10717v4 [17] Gulrajani I, Ahmed G, Arjovsky M, Dumoulin V, Courville A. Improved training of Wasserstein GANs. In: Proceedings of the International Conference on Neural Information Processing Systems. Long beach, USA: 2017. [18] Wu J Q, Huang Z W, Thoma J, Acharya D, Gool L V. Wasserstein divergence for GANs. In: Proceedings of the European Conference on Computer Vision. Munich, Germany: 2018. 673− 688 [19] Su J L. GAN-QP: A novel GAN framework without gradient vanishing and Lipschitz constraint. arXiv preprint, 2018, arXiv: 1811.07296v2 [20] Zhao J B, Mathieu M, LeCun Y. Energy-based generative adversarial networks. In: Proceedings of the International Conference on Learning Representations. Toulon, France: 2017 [21] 王功明, 乔俊飞, 乔磊. 一种能量函数意义下的生成式对抗网络. 自动化学报, 2018, 44(5): 793-803Wang Gong-Ming, Qiao Jun-Fei, Qiao Lei. A generative adversarial network in terms of energy function. Acta Automatica Sinica, 2018, 44(5): 793-803 [22] Qi G J. Loss-sensitive generative adversarial networks on Lipschitz densities. arXiv preprint, 2017, arXiv: 1701.06264v5 [23] Zhang H, Goodfellow I, Metaxas D, Odena A. Self-attention generative adversarial networks. In: Proceedings of the International Conference on Machine Learning. Long Beach, USA: 2019 [24] Cover T M, Thomas J A. Elements of Information Theory. New York: John Wiley & Sons Inc., 2006. 12−49 [25] Nielsen F. A family of statistical symmetric divergences based on Jensen＇s inequality. arXiv preprint, 2011, arXiv: 1009.4004v2 [26] Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge: MIT Press, 2017. 502−525 [27] Alain G, Bengio Y. What regularized autoencoders learn from the data generating distribution. The Journal of Machine Learning Research, 2014, 15(1): 3563-3593 [28] Vincent P, Larochelle H, Bengio Y, Manzagol P A. Extracting and composing robust features with denoising autoencoders. In: proceedings of the International Conference on Machine Learning. Rhineland, Germany: 2008. [29] Rifai S, Vincent P, Muller X, Glorot X, Bengio Y. Contractive auto-encoders: Explicit invariance during feature extraction. In: proceedings of the International Conference on Machine Learning. Washington, USA: 2011. [30] Kavukcuoglu K, Ranzato M, LeCun Y. Fast inference in sparse coding algorithms with applications to object recognition. arXiv preprint, 2010, arXiv: 1010.3467v1 [31] Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. In: Proceedings of the International Conference on Medical Image Computing and Computer-assisted Intervention. Munich, Germany: 2015. 234− 241 [32] Salimans T, Goodfellow I J, Zaremaba W, Cheung V, Radford A, Chen X. Improved techniques for training GANs. In: Proceedings of the International Conference on Neural Information Processing Systems. Barcelona, Spain: 2016. 2234−2242 [33] Xu Q T, Huang G, Yuan Y, Huo C, Sun Y, Wu F, et al. An empirical study on evaluation metrics of generative adversarial networks. arXiv preprint, 2018, arXiv: 1806.07755v2 [34] Shmelkov K, Schmid C, Alahari K. How good is my GAN? In: Proceedings of the European Conference on Computer Vision. Munich, Germany: 2018. 218−234 -
图(19) / 表(6)
计量
- 文章访问数: 1017
- HTML全文浏览量: 455
- PDF下载量: 223
- 被引次数: 0
