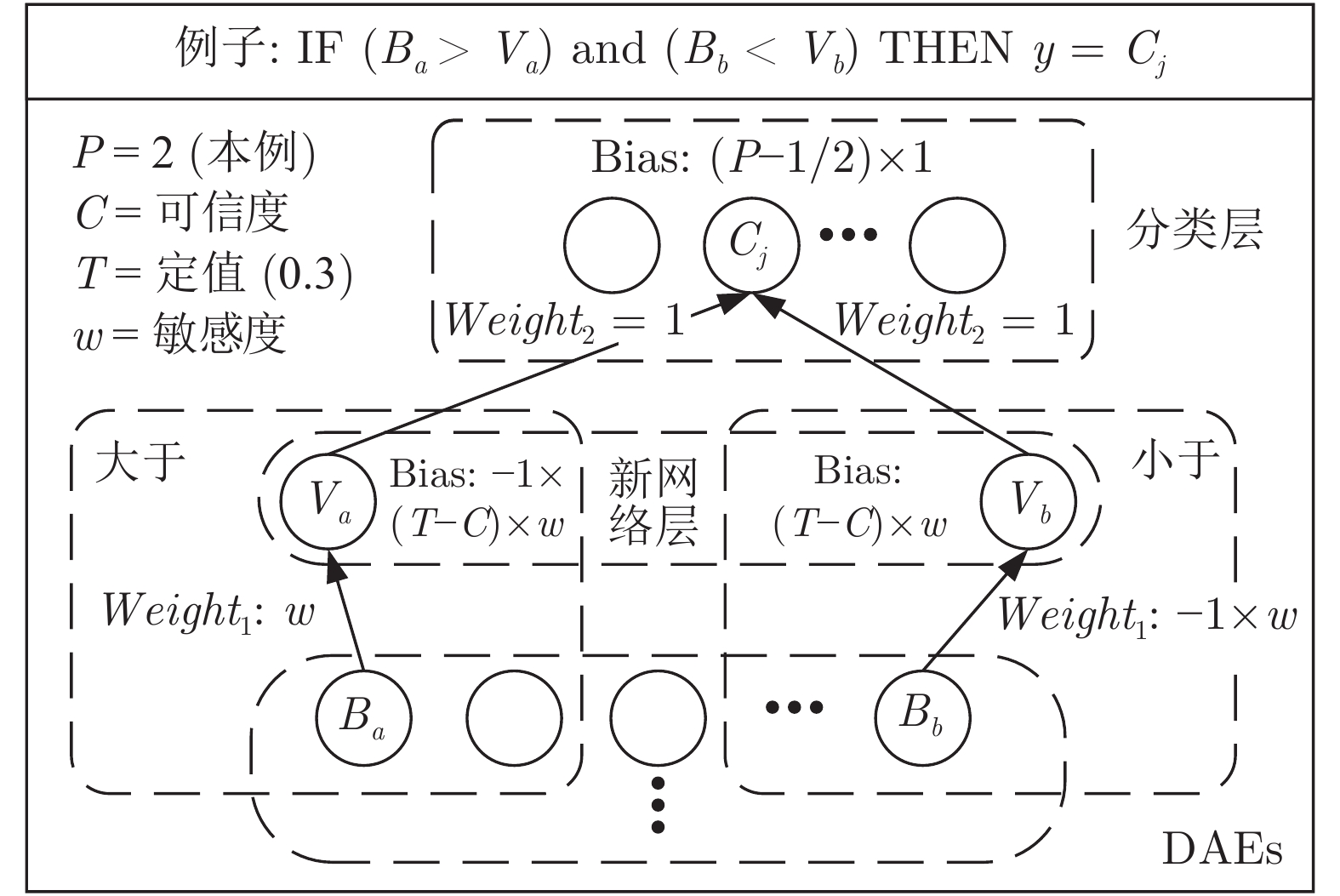
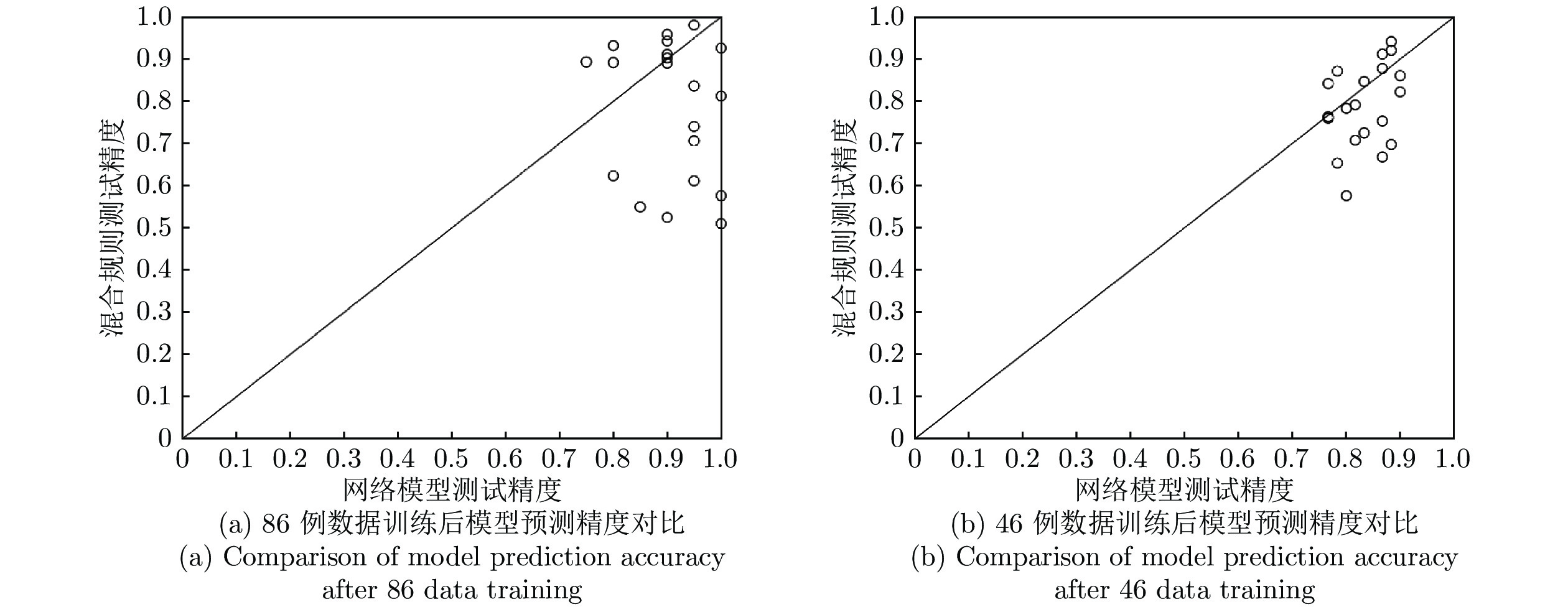
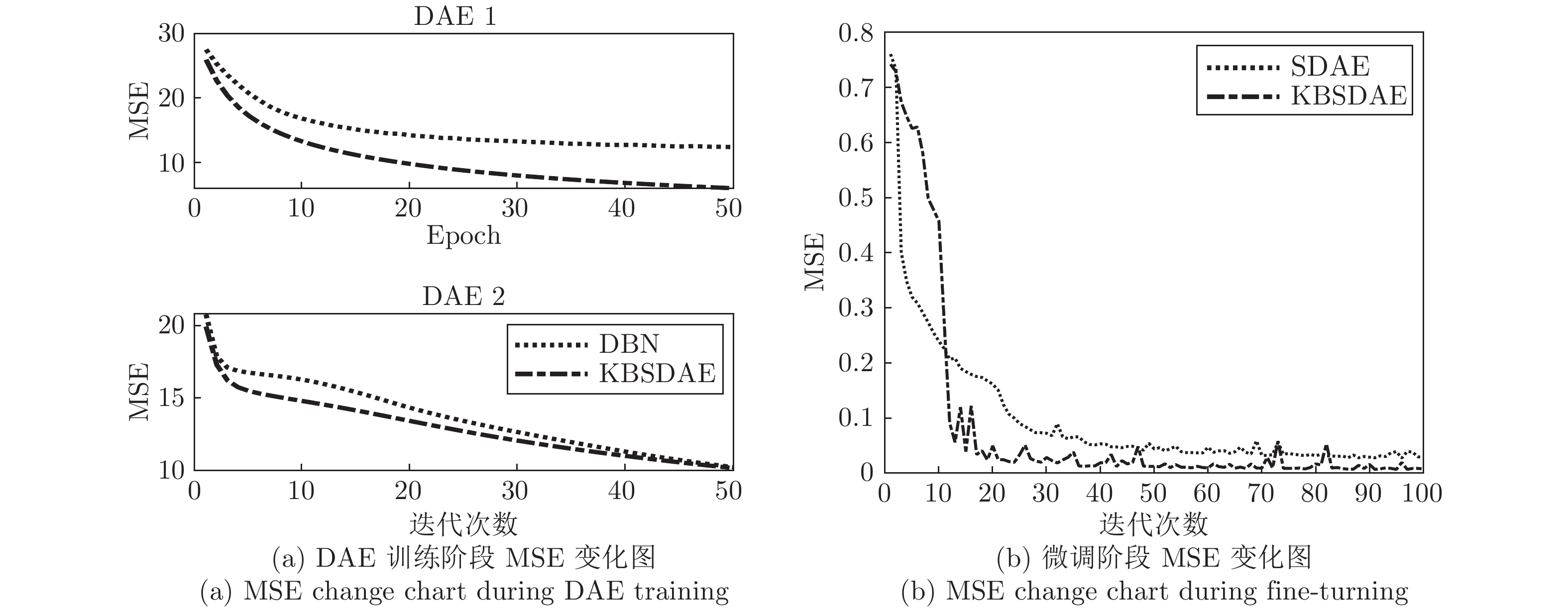
-
摘要: 深度神经网络是具有复杂结构和多个非线性处理单元的模型, 广泛应用于计算机视觉、自然语言处理等领域. 但是, 深度神经网络存在不可解释这一致命缺陷, 即“黑箱问题”, 这使得深度学习在各个领域的应用仍然存在巨大的障碍. 本文提出了一种新的深度神经网络模型 —— 知识堆叠降噪自编码器(Knowledge-based stacked denoising autoencoder, KBSDAE). 尝试以一种逻辑语言的方式有效解释网络结构及内在运作机理, 同时确保逻辑规则可以进行深度推导. 进一步通过插入提取的规则到深度网络, 使KBSDAE不仅能自适应地构建深度网络模型并具有可解释和可视化特性, 而且有效地提高了模式识别性能. 大量的实验结果表明, 提取的规则不仅能够有效地表示深度网络, 还能够初始化网络结构以提高KBSDAE的特征学习性能、模型可解释性与可视化, 可应用性更强.Abstract: Deep neural network is a complex structure and multiple nonlinear processing units models. It has achieved great success in computer vision, natural language processing and speech recognition. However, deep neural networks have unexplained fatal flaws, namely the “black box” problem, which makes the application of deep neural networks (DNNs) in various fields have huge obstacles. This paper proposes a new deep network system, knowledge-based stacked denoising autoencoder (KBSDAE). Try to extract and insert knowledge from the stacked denoising autoencoder (SDAE) with a simple logic language, and ensure that logic rules can perform deep reasoning. The system not only accurately represents the SDAE, but also adaptively builds the network model and improves network performance. Experiments show that this modular learning system can effectively explain SDAE and improve network performance.
-
图 5 SDAE和对应混合规则DNA promoter的识别率对比(%)
Fig. 5 Comparison of DNA promoter recognition rate between SDAE and corresponding blending rules (%)
图 6 KBSDAE和SDAE在HAR数据集上训练过程的均方误差变化对比
Fig. 6 Comparison of mean square error of KBSDAE and SDAE training process on HAR dataset
图 7 不同DNA promoter数据量训练的SDAE与KBSDAE分类性能对比
Fig. 7 Comparison of classification performance between SDAE and KBSDAE trained by different DNA promoter data
图 8 不同Fine-tuning训练步数的SDAE与KBSDAE分类性能对比
Fig. 8 Comparison of SDAE and KBSDAE classification performance of different fine-tuning training steps
表 1 遗传算法基因编码示意表
Table 1 Genetic algorithm gene coding schematic
Gene 1 Gene 2 ··· Gene N Act1 DS1 V1 Act2 DS2 V2 ··· ActN DSN VN 
下载: 导出CSV
表 2 部分DAE符号规则抽取结果
Table 2 DAE symbol rule extraction result
隐藏单元 DAE 的置信度符号规则束 3 $2.2874: {h_2} \leftrightarrow \neg x \wedge y \wedge z $
$2.9129: {h_3} \leftrightarrow \neg x \wedge \neg y \wedge \neg z$10 $1.4163: {h_1} \leftrightarrow \neg x \wedge \neg y \wedge \neg z $
$2.4803: {h_2} \leftrightarrow \neg x \wedge \neg y \wedge \neg z $
$1.9159: {h_3} \leftrightarrow x \wedge \neg y \wedge z $
$1.0435: {h_4} \leftrightarrow \neg x \wedge \neg y \wedge \neg z $
$0.6770: {h_5} \leftrightarrow \neg x \wedge y \wedge \neg z $
$1.9298: {h_6} \leftrightarrow x \wedge \neg y \wedge z $
$1.9785: {h_7} \leftrightarrow x \wedge \neg y \wedge z $
$1.9448: {h_8} \leftrightarrow \neg x \wedge y \wedge z $
$2.4405: {h_9} \leftrightarrow x \wedge y \wedge \neg z $
$ 2.0322: {h_{10}} \leftrightarrow \neg x \wedge y \wedge z $
下载: 导出CSV
表 3 复杂数据集降维后SVM 10折交叉分类结果(%)
Table 3 Ten-fold cross-classification results of dimensionally reduced complex data on SVM (%)
MNIST HAR One DAE (J = 500) 98.00 97.27 Symbolic rule 94.43 96.73 Two DAEs (top J = 100) 98.74 98.07 Symbolic rule 96.03 96.84 Two DAEs (top J = 200) 98.90 97.74 Symbolic rule 95.42 97.33 SVM (linear) 92.35 96.55
下载: 导出CSV
表 4 基于DNA promoter 的分类规则明细表(%)
Table 4 Classification rule schedule based on DNA promoter (%)
分类规则 可信度 覆盖率 ${\rm IF}\; (h_2^1 > 0.771 \wedge h_3^1 > 0.867) $
${\rm THEN}\;promoter $98.62 50.00 $ {\rm IF} \;(h_1^1 < 0.92 \wedge h_2^1 < 0.634 \wedge h_3^1 < 0.643) $
$ {\rm THEN}\; \neg promoter $84.42 50.00
下载: 导出CSV
表 5 基于DNA promote 数据集的部分符号规则明细
Table 5 Partial symbol rule details based on DNA promote
节点 置信度 规则片段 1 起始位 终止位 规则片段 2 起始位 终止位 规则片段 3 起始位 终止位 @-36 @-32 @-12 @-7 @-45 @-41 ${{h} }_1^1$ 0.76 A C [ ] G T G G T C (T) G C G C T A T (A) ${{h} }_2^1$ 1.29 T T G T (A) C T (A) A A A G C A A T A A ${{h} }_3^1$ 1.47 G (A) T G T (A) C T (A) T (A) G (A) T C (T) G (A) A A T C A 基本规则 L1 minus-35: T T G A C minus-10: T A [ ] [ ] [ ] T Conformation: A A [ ] [ ] A L2 contact←minus-35∧minus-10 L3 promoter←contact∧conformation
下载: 导出CSV
表 6 UCI数据集信息
Table 6 UCI dataset information
数据集 特征数量 类别数 数据量 Credit card 14 2 690 Diabetes 8 2 768 Pima 8 2 759 Wine 13 3 178 Cancer 9 2 689 Vehicle 8 4 846 Heart 13 2 270 German 24 2 1 000 Iris 4 3 150
下载: 导出CSV
表 7 UCI数据集信息 (%)
Table 7 UCI dataset information (%)
数据集 DBN SDAE INSS-KBANN BPNN Sym-DBN KBSDAE Credit card 84.29 84.14 81.17 85.00 85.57 87.18 Diabetes 73.20 73.47 74.00 72.40 76.53 78.27 Pima 72.57 70.00 73.73 73.73 74.00 76.40 Wine 96.67 96.00 97.67 96.00 98.00 97.00 Cancer 96.92 97.38 97.21 96.31 97.69 97.12 Vehicle 75.29 73.97 71.82 68.69 74.67 75.85 Heart 81.60 76.80 78.80 78.40 82.40 84.00 German 70.90 71.30 71.60 69.40 71.30 79.10 Iris 84.00 82.00 93.00 92.33 92.33 94.33
下载: 导出CSV
表 8 复杂数据集分类结果对比(%)
Table 8 Classification results of comparison on complex datasets (%)
数据集及网络参数 数据标签 SDAE KBSDAE USPS: 0 98.97 98.38 SDAE: 256-100-20-10/learning rate: 0.01/noising rate: 0.1
KBSDAE: 256-100-25-18-10/learning rate: 0.01/noising rate: 0.11 99.13 99.06 2 96.46 97.28 3 96.37 95.20 4 96.33 96.74 5 94.19 94.53 6 97.62 97.97 7 97.49 97.44 8 94.46 96.61 9 98.25 97.88 Mean 97.24 97.33 HAR SDAE: 561-300-20-6/learning rate: 0.01/noising rate: 0.1
KBSDAE: 561-300-25-11-6/learning rate: 0.01/noising rate: 0.1Walking 98.84 100.00 Walking upstairse 88.17 98.77 Walking downstairse 92.31 98.49 Sitting 97.05 98.85 Standing 89.36 94.99 Laying 100 100.00 Mean 94.10 98.50
下载: 导出CSV
表 9 复杂数据集5折交叉分类结果对比(%)
Table 9 Comparison of five-fold cross-classification results on complex datasets (%)
数据集 KBSDAE Sym-DBN DBN SDAE BPNN SVM USPS 97.43 97.47 96.72 97.24 97.22 93.37 HAR 98.40 97.09 96.89 95.32 95.84 96.55
下载: 导出CSV
-
[1] Towell G G. Extracting Refined Rules from Knowledge-Based Neural Networks. Machine Learning, 1993, 13(1): 71-101 [2] Lecun Y, Bengio Y, Hinton G E. Deep learning. Nature, 2015, 521(7553): 436-444 doi: 10.1038/nature14539 [3] Hinton G E, Osindero S, Teh Y W. A Fast Learning Algorithm for Deep Belief Nets. Neural Computation, 2006, 18(7): 1527-1554 doi: 10.1162/neco.2006.18.7.1527 [4] Bengio Y, Lamblin P, Popovici D, Larochelle H. Greedy layer-wise training of deep networks. In: Proceedings of the 2006 Advances in Neural Information Processing Systems 19, Proceedings of the 20th Annual Conference on Neural Information Processing Systems, Vancouver, British Columbia, Canada, December 4−7, 2006. DBLP, 2007. [5] Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324 doi: 10.1109/5.726791 [6] Vincent P, Larochelle H, Bengio Y, Manzagol P A. Extract-ing and composing robust features with denoising autoen-coders. In: Proceedings of the 25th International Conferenceon Machine Learning. Helsinki, Finland: ACM, 2008. 1096−1103 [7] Towell G G, Shavlik J W. Knowledge-based artificial neural networks. Artificial Intelligence, 1994, 70(1-2): 119-165 doi: 10.1016/0004-3702(94)90105-8 [8] Gallant S I. Connectionist expert systems. Comm Acm, 1988, 31(2): 152-169 doi: 10.1145/42372.42377 [9] Garcez A D A, Zaverucha G. The Connectionist Inductive Learning and Logic Programming System. Applied Intelligence: The International Journal of Artificial, Intelligence, Neural Networks, and Complex Problem-Solving Technologies, 1999, 11(1): 59-77 [10] Fernando S. Osório, Amy B. INSS: A hybrid system for constructive machine learning. Neurocomputing, 1999, 28(1-3): 191-205 doi: 10.1016/S0925-2312(98)00124-6 [11] Setiono R. Extracting rules from neural networks by pruning and hidden-unit splitting. Neural Computation, 2014, 9(1): 205-225 [12] 杨莉, 袁静, 胡守仁. 神经网络问题求解机制. 计算机学报, 1993, (11): 814-822Yang Li, Yuan Jing, Hu Shou-Ren. The problem solving mechanism of neural networks. Chinese J. Compuers, 1993, (11): 814-822 [13] 黎明, 张化光. 基于粗糙集的神经网络建模方法研究. 自动化学报, 1994, 20(3): 349-351Qian Da-Qun, Sun Zheng-Fei. Knowledge Acquisition and Behavioral Explanation on Neural Network. Acta Automatica Sinica, 2002, 28(1): 27-33 [14] 钱大群, 孙振飞. 神经网络的知识获取与行为解释. 自动化学报, 2002, 28(1): 27-33Li Ming, Zhang Hua-Guang. Research on the method of neural network modeling based on rough sets theory. Acta Automatica Sinica, 1994, 20(3): 349-351 [15] Penning L D, Garcez A S D, Lamb L C, Meyer J J C. A neural-symbolic cognitive agent for online learning and reasoning. In: Proceedings of the 22nd International Joint Conference on Artificial Intelligence, Barcelona, Catalonia, Spain, 2011. 1653−1658 [16] Odense S, Garcez A S D. Extracting M of N rules from restricted Boltzmann machines. In: Proceedings of the 2017 International Conference on Artificial Neural Networks. Springer, Cham, 2017. 120−127 [17] Tran S N, Garcez A S D. Deep Logic Networks: Inserting and Extracting Knowledge from Deep Belief Networks. IEEE Transactions on Neural Networks & Learning Systems, 2018, 29(2): 246-258 [18] Li S, Xu H R, Lu Z D. Generalize symbolic knowledge with neural rule engine. arXiv preprint arXiv: 1808.10326v1, 2018. [19] Garcez A D A, Gori M, Lamb L C, Serafini L. Neural-symbolic computing: An effective methodology for principled integration of machine learning and reasoning. arXiv preprint arXiv: 1905.06088, 2019. [20] Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors. Nature, 1986, 323: 533−536 [21] Pinkas G. Reasoning, nonmonotonicity and learning in connectionist networks that capture propositional knowledge. Artificial Intelligence, 1995, 77(2): 203-247 doi: 10.1016/0004-3702(94)00032-V [22] Mitchell T M. Machine Learning. McGraw-Hill, 2014. [23] Yu J B, Xi L, Zhou X. Deep Logic Networks: Intelligent monitoring and diagnosis of manufacturing processes using an integrated approach of KBANN and GA. Computers in Industry, 2008, 59(5): 489-501 doi: 10.1016/j.compind.2007.12.005 [24] Tran S N, Garcez A S D. Knowledge extraction from deep belief networks for images. In: Proceedings of the 2013 IJCAI-Workshop Neural-Symbolic Learning and Reasoning, 2013. 1−6 [25] Towell G G, Shavlik J W. The extraction of refined rules from knowledge-based neural networks. Mach. Learn, 2018, 13(1): 71-101 [26] Murphy P M, Aha D W. UCI repository of machine learning databases. Depth Information Compute Science, University California, Irvine, CA, 1994. [27] Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In: Proceedings of the 14th International Joint Conference on Artificial Intelligence. San Francisco, CA, USA: Morgan Kaufmann, 1995. 1137−1143 [28] Anguita D, Ghio A, Oneto L, Parra X, Reyes-Ortiz J L. Human activity recognition on smartphones using a multiclass hardware-friendly support vector machine. In: Proceedings of the 4th International Workshop of Ambient Assited Living, IWAAL 2012, Vitoria-Gasteiz, Spain, 2012. 216−223 -
计量
- 文章访问数: 579
- HTML全文浏览量: 604
- PDF下载量: 178
- 被引次数: 0
