Online Reinforcement Learning Control Algorithm for Concentration of Thickener Underflow
Author Bio:
YUAN Zhao-Lin Ph.D. candidate at the School of Computer and Communication Engineering, University of Science and Technology Beijing. He received his bachelor degree in computer science from University of Science and Technology Beijing in 2017. His research interest covers adaptive dynamic programming and reinforcement learning
HE Run-Zi Master student at the School of Computer and Communication Engineering, University of Science and Technology in Beijing. She received her bachelor degree from Beijing Science and Technology University in 2017. Her research interest covers fluid simulation and reinforcement learning
YAO Chao Assistant professor at University of Science Technology, Beijing (USTB), China. He received his bachelor degree in computer science from Beijing Jiaotong University (BJTU), Beijing, China in 2009 and the Ph.D. degree from the Institute of Information Science, BJTU in 2016. From 2014 to 2015, he served as a visiting Ph.D. student at the Ecole Polytechnique Federale de Lausanne, Switzerland. From 2016 to 2018, he served as a post-doctoral at the Institute of Sensing Technology and Business, Beijing University of Posts and Telecommunications, Beijing. His research interest covers image and video processing and computer vision
LI Jia Master student at the School of Computer and Communication Engineering, University of Science and Technology in Beijing. His research interest covers adaptive dynamic programming, adaptive control, and reinforcement learning
BAN Xiao-Juan Professor at University of Science and Technology Beijing and she is an executive council member in Chinese Association for Artificial Intelligence (CAAI). Her research interest covers artificial intelligence, natural human-computer interaction, and 3D visualization. Corresponding author of this paper
-
摘要:
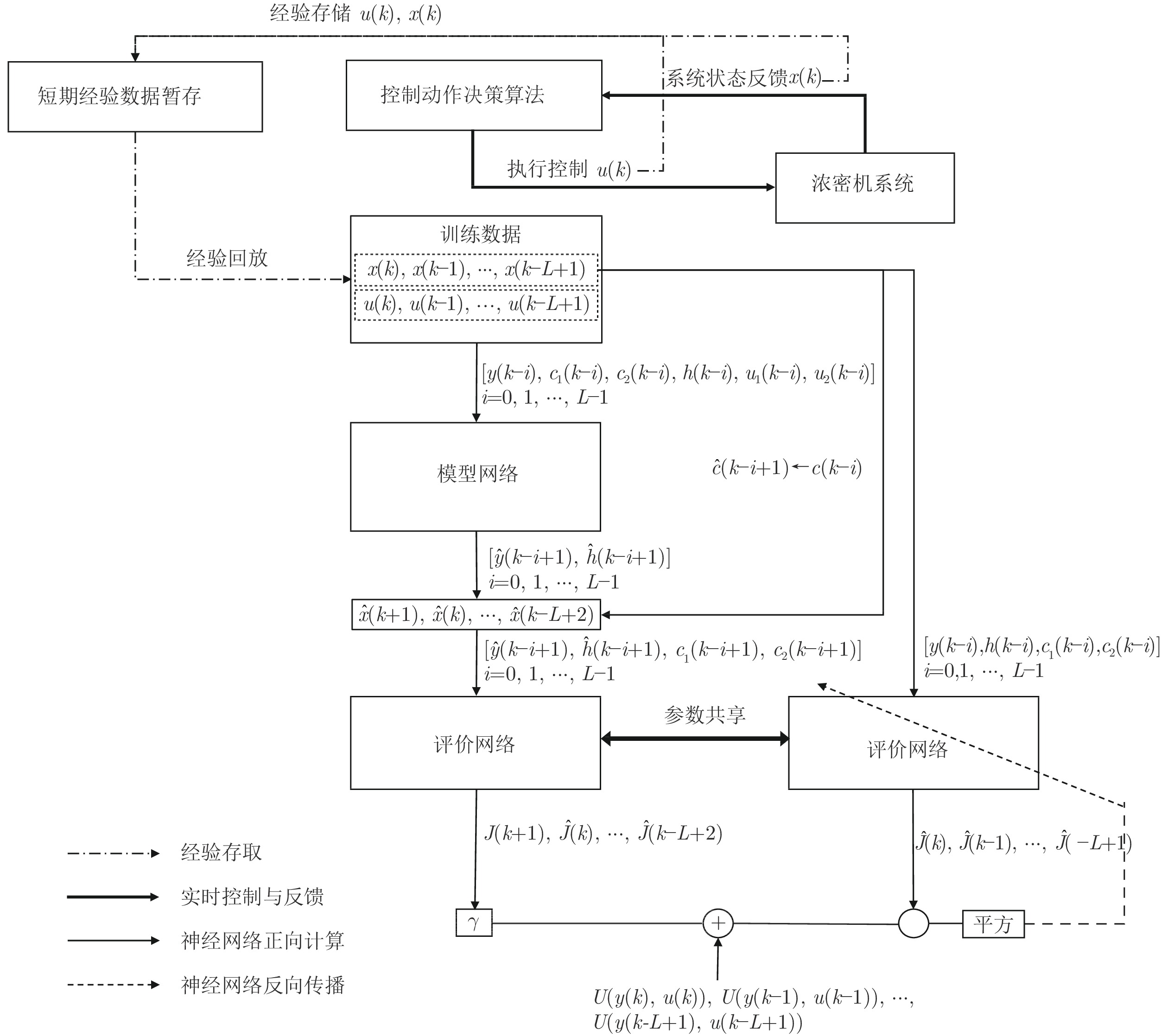
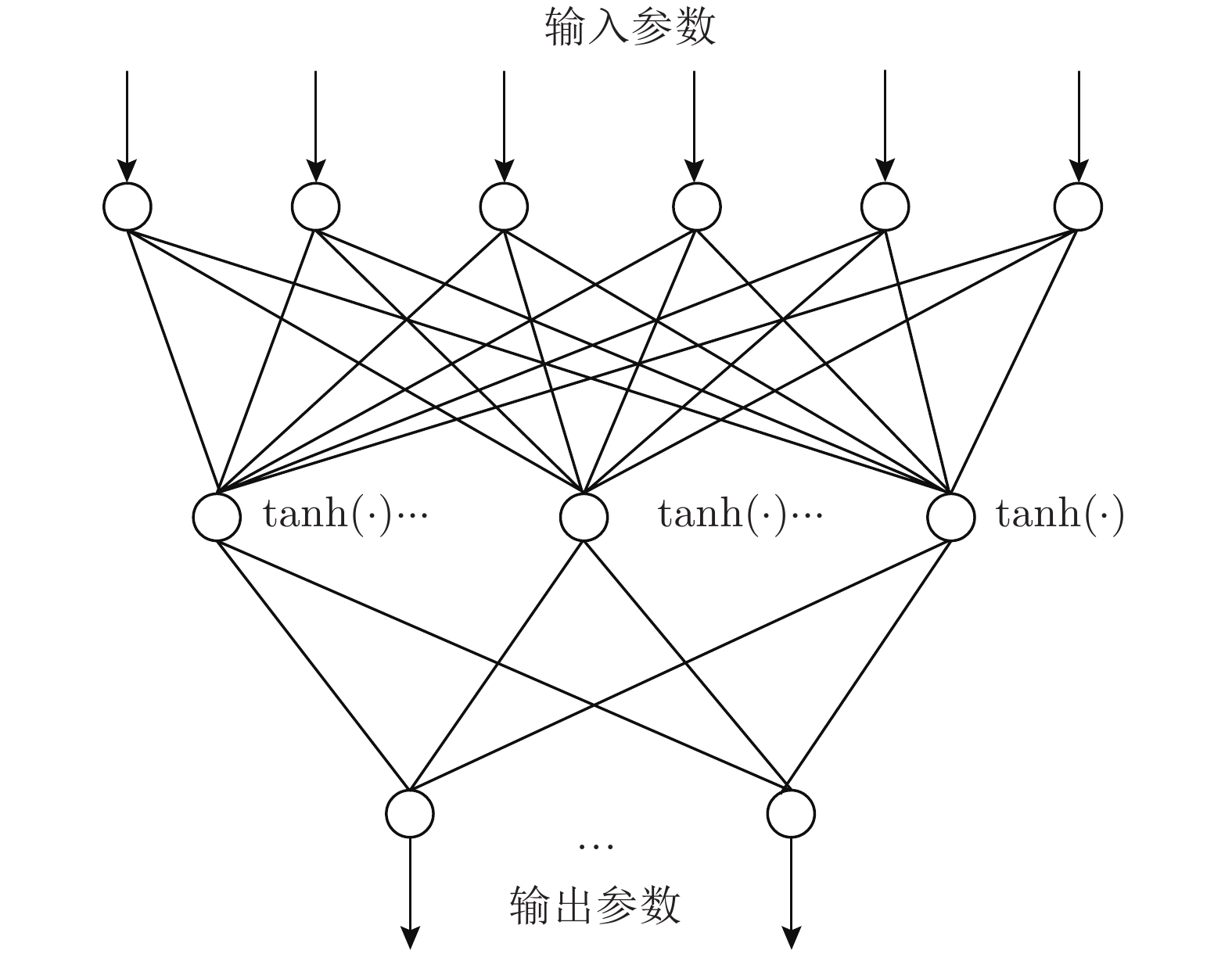
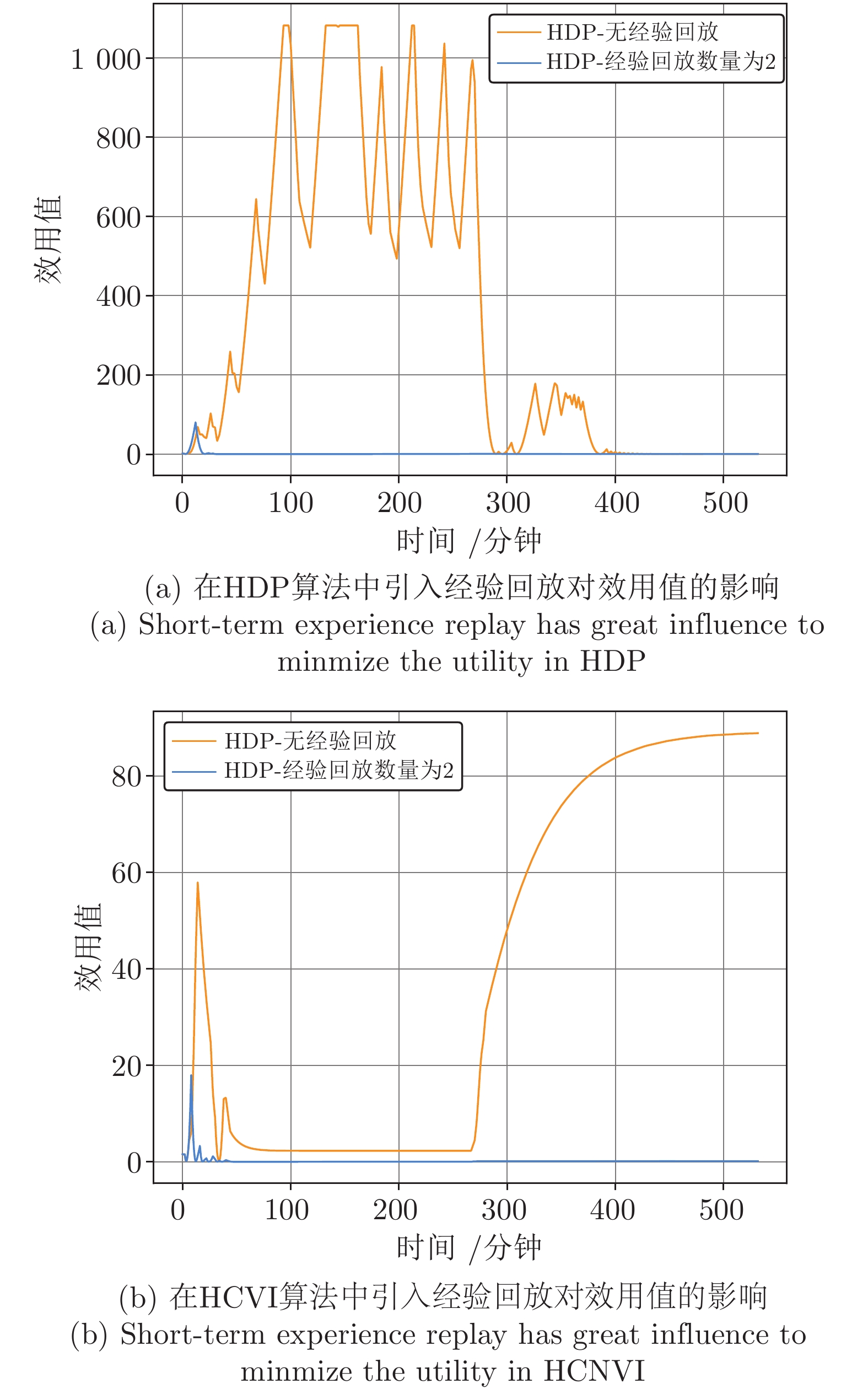
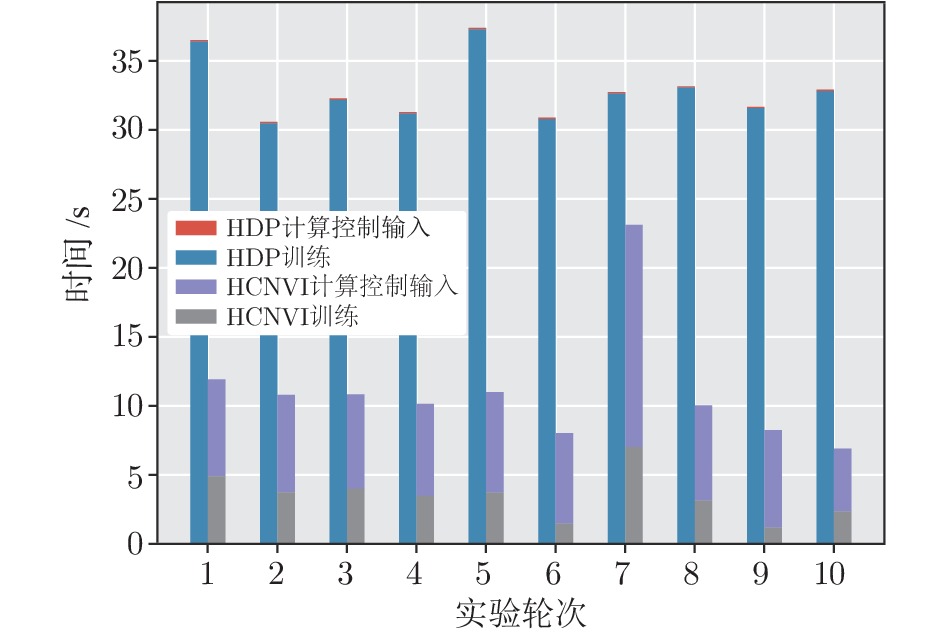
复杂过程工业控制一直是控制应用领域研究的前沿问题. 浓密机作为一种复杂大型工业设备广泛用于冶金、采矿等领域. 由于其在运行过程中具有多变量、非线性、高时滞等特点, 浓密机的底流浓度控制技术一直是学界、工业界的研究难点与热点. 本文提出了一种基于强化学习技术的浓密机在线控制算法. 该算法在传统启发式动态规划 (Heuristic dynamic programming, HDP)算法的基础上, 设计融合了评价网络与模型网络的双网结构, 并提出了基于短期经验回放的方法用于增强评价网络的训练准确性, 实现了对浓密机底流浓度的稳定控制, 并保持控制输入稳定在设定范围之内. 最后, 通过浓密机仿真实验的方式验证了算法的有效性, 实验结果表明本文提出的方法在时间消耗、控制精度上优于其他算法.
Abstract:Complex process industrial control is a widely concerned problem in the field of control application. As a kind of complex huge industrial equipment, thickener has been widely used in metallurgy, mining and other applications. Due to its characteristics of complicated variables, nonlinear and long delay in the operational process, the control strategy of underflow concentration for thickener has always been a hot and difficult issue in the academia and industry. This paper proposes a novel online control algorithm for thickener which is based on reinforcement learning. Inspired by the traditional heuristic dynamic programming (Heuristic dynamic programming, HDP) algorithm. The proposed method designs a double net framework which is composed of the critic network and the model network. To achieve the stabilization of underflow concentration, an optimal method which is based on reviewing the history data in a short term is proposed in the training phase of critic network. Simulation experiments verify efficiency of the proposed method. The results show that the proposed method can maintain the concentration of underflow in a stable horizon and performs better than other algorithms in accuracy and time consuming.
1) 1(Mean Square Error, MSE)=$\frac{1}{T} \sum_{k=1}^{T}\left|(y(k)-y^*(k))\right|^{2}$ 2(Max Absolute Error, MAE)=$\max _{1 \leq k \leq T}\{|y(k)-y^*(k)|\}$ 3(Integral Absolute Error, IAE)=$\frac{1}{T} \sum_{k=1}^{T}\left|(y(k)-y^*(k))\right|$ -
图 5 短期经验回放对评价网络的输出值的影响
Fig. 5 The effect of short-term experience replay on critic network
图 7 HCNVI与其他ADP算法在恒定噪音输入下的对比
Fig. 7 HCNVI versu other ADP algorithms under stable noisy input
图 8 短期经验回放对HDP与HCNVI的影响
Fig. 8 The influence of short-term experience replay on HDP and HCNVI
图 9 实验一中HDP与HCNVI在时间消耗上的对比
Fig. 9 Comparison of time consuming in HDP and HCNVI in Experiment 1
图 11 HCNVI与其他ADP算法在波动噪声输入下的对比
Fig. 11 HCNVI versu other ADP algorithms under fluctuate noisy input
图 12 噪音持续变化下短期经验回放对HCNVI的影响
Fig. 12 The influence of short-term experience replay on HCNVI
图 13 实验二中HCNVI算法与HDP算法在时间消耗上的对比
Fig. 13 Comparison of time consuming in HDP and HCNVI in Experiment 2
表 1 参量定义
Table 1 Variables definition
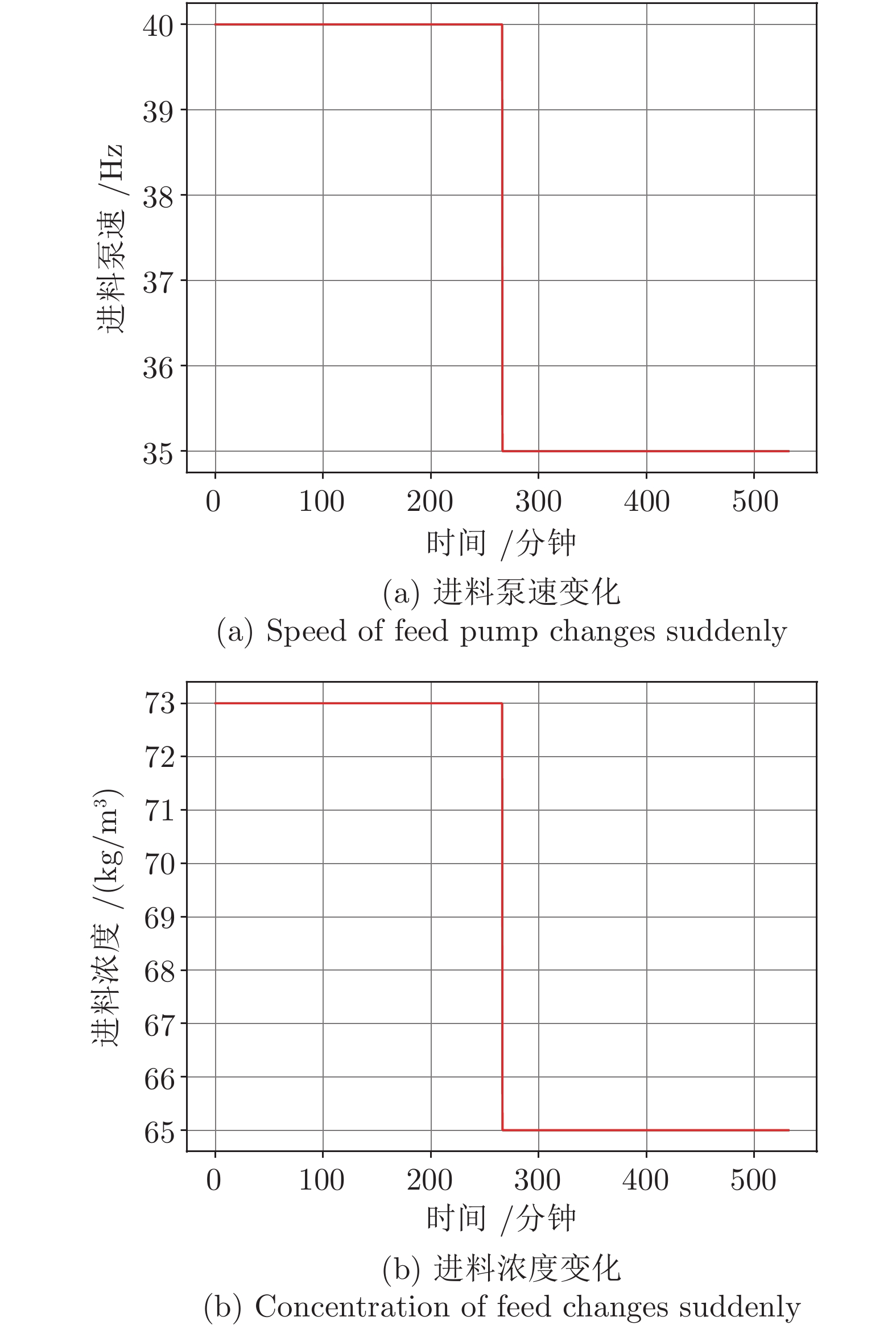
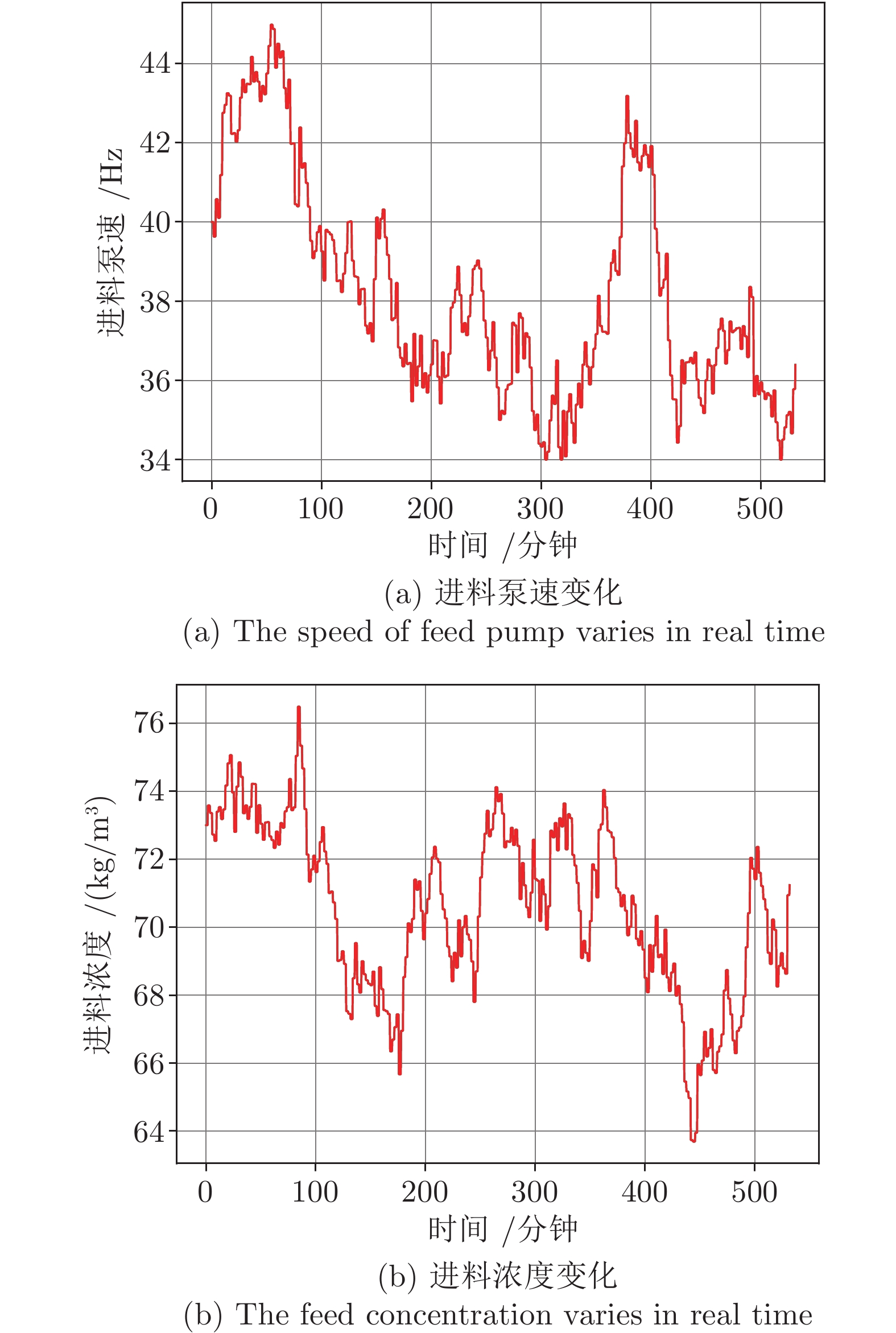
变量 含义 量纲 初始值 补充说明 $f_{i}(t)$ 进料泵频 ${\rm Hz}$ 40 扰动量 $f_{u}(t)$ 底流泵频 ${\rm Hz}$ 85 控制量 $f_{f}(t)$ 絮凝剂泵频 ${\rm Hz}$ 40 控制量 $c _ { i } ( t )$ 进料浓度 ${\rm kg/m^3}$ 73 扰动量 $h(t)$ 泥层高度 ${\rm m}$ 1.48 状态量 $c_u(t)$ 底流浓度 ${\rm kg/m^3}$ 680 目标量 
下载: 导出CSV
表 2 仿真模型常量
Table 2 Definitions for constant variables
变量 含义 量纲 参考值 $\rho _s$ 干砂密度 ${\rm kg/m^3}$ 4150 $\rho _e$ 介质表观密度 ${\rm kg/m^3}$ 1803 $\mu _ { e }$ 悬浮体系的表观粘度 ${\rm Pa \cdot s}$ 1 $d_0$ 进料颗粒直径 ${\rm m}$ 0.00008 $p$ 平均浓度系数 无 0.5 $A$ 浓密机横截面积 ${\rm m^2}$ 300.5 $k_s$ 絮凝剂作用系数 ${\rm s/m^2}$ 0.157 $k_i$ 压缩层浓度系数 ${\rm m^3/s}$ 0.0005×3600 $K_i$ 进料流量与进料泵频的系数 ${\rm m^3/r}$ 50/3600 $K_u$ 底流流量与底流泵频的系数 ${\rm m^3/r}$ 2/3600 $K_f$ 絮凝剂流量与絮凝剂泵频的系数 ${\rm m^3/r}$ 0.75/3600 $\theta$ 压缩时间 ${\rm s}$ 2300
下载: 导出CSV
表 3 部分变量计算方法
Table 3 Definitions for part intermediate variables
变量 含义 公式 $q_i(t)$ 进料流量 $q _ { i } ( t ) = K _ { i } f _ { i } ( t )$ $q_u(t)$ 底流流量 $q _ { u } ( t ) = K _ { u } f _ { u } ( t )$ $q_f(t)$ 絮凝剂添加量 $q _ { f } ( t ) = K _ { f } f _ { f } ( t )$ $d(t)$ 絮凝作用后的颗粒直径 $d ( t ) = k _ { s } q _ { f } ( t ) + d _ { 0 }$ $u_t(t)$ 颗粒的干涉沉降速度 $u _ { t} ( t ) = \dfrac { d ^ { 2 } ( t ) \left( \rho _ { s } - \rho _ { e } \right) g } { 18 \mu _ { e } }$ $u_r(t)$ 底流导致的颗粒下沉速度 $u _ { r } ( t ) = \dfrac { q _ { u } ( t ) } { A }$ $c_l(t)$ 泥层高度处单位体积含固量 $c _ { l } ( t ) = k _ { i } q _ { i } ( t ) c _ { i } ( t )$ $c_a(t)$ 泥层界面内单位体积含固量 $c _ { a } ( t ) = p \left[ c _ { l } ( t ) + c _ { u } ( t ) \right]$ $r(t)$ 泥层内液固质量比 $r(t)=\rho_{l}\left(\dfrac{1}{c_ a(t)}-\frac{1}{\rho_s}\right)$ $W ( t )$ 单位时间进入浓密机内的固体质量 $W ( t ) = c _ { i } (t ) q _ { i } ( t )$
下载: 导出CSV
表 4 不同控制算法之间性能分析
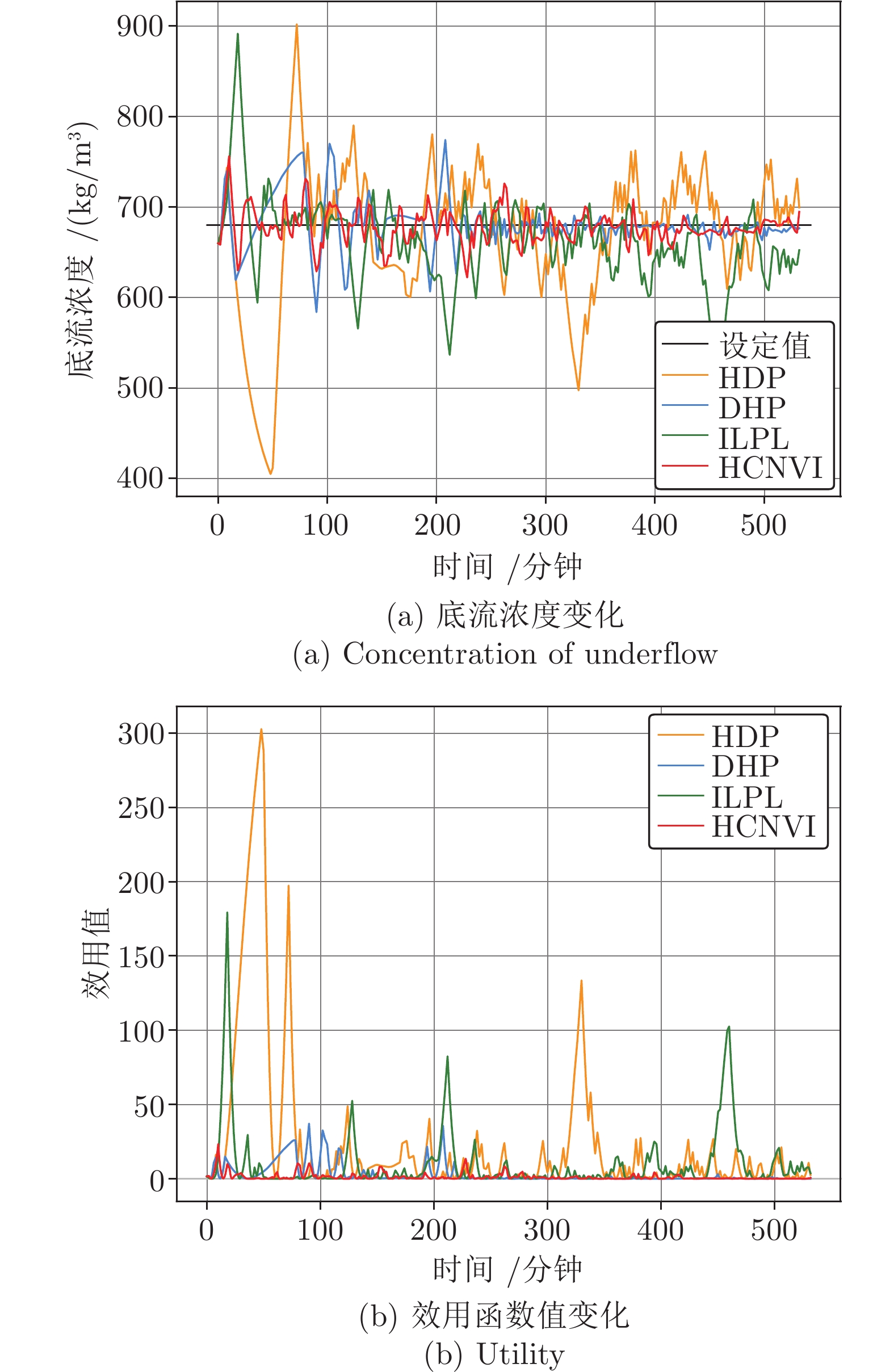
Table 4 Performances analysis of different algorithms
实验组 实验1 实验2 对比指标 MSE1 MAE2 IAE3 MSE MAE IAE HDP 414.182 141.854 7.246 6 105.619 275.075 54.952 DHP 290.886 109.312 5.392 732.814 96.145 16.560 ILPL 364.397 135.474 8.289 2 473.661 211.615 35.222 HCNVI 44.445 66.604 3.867 307.618 76.176 12.998
下载: 导出CSV
-
[1] Shen Y, Hao L, Ding S X. Real-time implementation of fault tolerant control systems with performance optimization. IEEE Trans. Ind. Electron, 2014, 61(5): 2402−2411 doi: 10.1109/TIE.2013.2273477 [2] Kouro S, Cortes P, Vargas R, Ammann U, Rodriguez J. Model predictive control — A simple and powerful method to control power converters. IEEE Trans. Ind. Electron, 2009, 56(6): 1826−1838 doi: 10.1109/TIE.2008.2008349 [3] Dai W, Chai T, Yang S X. Data-driven optimization control for safety operation of hematite grinding process. IEEE Trans. Ind. Electron, 2015, 62(5): 2930−2941 doi: 10.1109/TIE.2014.2362093 [4] Wang D, Liu D, Zhang Q, Zhao D. Data-based adaptive critic designs for nonlinear robust optimal control with uncertain dynamics. IEEE Trans. Syst., Man, Cybern., Syst., 2016, 46(11): 1544−1555 doi: 10.1109/TSMC.2015.2492941 [5] Sutton S R, Barto G A. Reinforcement Learning: An Introduction. Cambridge: MIT Press, 2nd edition, 2018. [6] Lewis F L, Vrabie D, Syrmos V L. Optimal Control. New York, USA: John Wiley & Sons, Hoboken, 3rd Edition, 2012. [7] Prokhorov V D, Wunsch C D. Adaptive critic design. IEEE Transactions on Neural Networks, 1997, 8(5): 997−1007 doi: 10.1109/72.623201 [8] Werbos P J. Foreword - ADP: the key direction for future research in intelligent control and understanding brain intelligence. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics)., 2008, 38(4): 898−900 doi: 10.1109/TSMCB.2008.924139 [9] 段艳杰, 吕宜生, 张杰, 赵学亮, 王飞跃. 深度学习在控制领域的研究现状与展望. 自动化学报, 2016, 42(5): 643−654Duan Yan-Jie, Lv Yi-Sheng, Zhang Jie, Zhao Xue-Liang, Wang Fei-Yue. Deep learning for control: the state of the art and prospects. Acta Automatica Sinica, 2016, 42(5): 643−654 [10] Liu Y-J, Tang L, Tong S-C, Chen C L P, Li D-J. Reinforcement learning design-based adaptive tracking control with less learning parameters for nonlinear discrete-time MIMO systems. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(1): 165−176 doi: 10.1109/TNNLS.2014.2360724 [11] Liu L, Wang Z, Zhang H. Adaptive fault-tolerant tracking control for MIMO discrete-time systems via reinforcement learning algorithm with less learning parameters. IEEE Transactions on Automation Science and Engineering, 2017, 14(1): 299−313 doi: 10.1109/TASE.2016.2517155 [12] Xu X, Yang H, Lian C, Liu J. Self-learning control using dual heuristic programming with global laplacian eigenmaps. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9517−9526 doi: 10.1109/TIE.2017.2708002 [13] Wei Q-L, Liu D-R. Adaptive dynamic programming for optimal tracking control of unknown nonlinear systems with application to coal gasification. IEEE Transactions on Automation Science and Engineering, 2014, 11(4): 1020−1036 doi: 10.1109/TASE.2013.2284545 [14] Jiang Y, Fan J-L, Chai T-Y, Li J-N, Lewis L F. Data-driven flotation industrial process operational optimal control based on reinforcement learning. IEEE Transactions on Industrial Informatics, 2017, 14(5): 1974−1989 [15] Jiang Y, Fan J-L, Chai T-Y, Lewis L F. Dual-rate operational optimal control for flotation industrial process with unknown operational model. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4587−4599 doi: 10.1109/TIE.2018.2856198 [16] Modares H, Lewis F L. Automatica integral reinforcement learning and experience replay for adaptive optimal control of partiallyunknownconstrained-input. Automatica, 2014, 50(1): 193−202 doi: 10.1016/j.automatica.2013.09.043 [17] Mnih V, Silver D, Riedmiller M. Playing atari with deep reinforcement learning. In: Procedings of the NIPS Deep Learning Workshop 2013, Lake Tahoe, USA: NIPS 2013, 1−9 [18] Wang D, Liu D R, Wei Q L, Zhao D B, Jin N. Automatica optimal control of unknown nonaffine nonlinear discrete-time systems basedon adaptive dynamic programming. Automatica, 2012, 48(8): 1825−1832 doi: 10.1016/j.automatica.2012.05.049 [19] Chai T Y, Jia Y, Li H B, Wang H. An intelligent switching control for a mixed separation thickener process. Control Engineering Practice, 2016, 57: 61−71 doi: 10.1016/j.conengprac.2016.07.007 [20] Kim B H, Klima M S. Development and application of a dynamic model for hindered-settling column separations. Minerals Engineering, 2004, 17(3): 403−410 doi: 10.1016/j.mineng.2003.11.013 [21] Wang L Y, Jia Y, Chai T Y, Xie W F. Dual rate adaptive control for mixed separationthickening process using compensation signal basedapproach. IEEE Transactions on Industrial Electronics, 2017, PP: 1−1 [22] 王猛. 矿浆中和沉降分离过程模型软件的研发. 东北大学, 2011Wang Meng. Design and development of model software of processes of slurry neutralization, sedimentation and separation. Northeastern University, 2011 [23] 唐谟堂. 湿法冶金设备. 中南大学出版社, 2009Tang Mo-Tang. Hydrometallurgical equipment. Central South University, 2009 [24] 王琳岩, 李健, 贾瑶, 柴天佑. 混合选别浓密过程双速率智能切换控制. 自动化学报, 2018, 44(2): 330−343Wang Lin-Yan, Li Jian, Jia Yao, Chai Tian-You. Dual-rate intelligent switching control for mixed separation thickening process. Acta Automatica Sinica, 2018, 44(2): 330−343 [25] Luo B, Liu D R, Huang T W, Wang D. Model-free optimal tracking control via critic-only Q-learning. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(10): 2134−2144 doi: 10.1109/TNNLS.2016.2585520 [26] Padhi R, Unnikrishnan N, Wang X H, Balakrishnan S N. A single network adaptive critic (SNAC) architecture for optimal controlsynthesis for a class of nonlinear systems. Neural Networks, 2006, 19(10): 1648−1660 doi: 10.1016/j.neunet.2006.08.010 -
计量
- 文章访问数: 6404
- HTML全文浏览量: 1542
- PDF下载量: 456
- 被引次数: 0
