基于参数优化 <b>VMD</b> 和样本熵的滚动轴承故障诊断

刘建昌; 权贺; 于霞; 何侃; 李镇华

doi:10.16383/j.aas.c190345

基于参数优化 VMD 和样本熵的滚动轴承故障诊断

doi: 10.16383/j.aas.c190345

刘建昌^1,,
权贺^1,,
于霞^1,,
何侃^2,,
李镇华^1,

1.
东北大学信息科学与工程学院沈阳 110819
2.
华为技术有限公司杭州研究所杭州 310007

基金项目: 国家自然科学基金(61773106)资助

详细信息

作者简介:
刘建昌：东北大学信息科学与工程学院教授. 主要研究方向为控制理论与控制工程, 故障诊断. E-mail: liujianchang@ise.neu.edu.cn

权贺：东北大学信息科学与工程学院硕士研究生. 2017年获得哈尔滨理工大学自动化学院学士学位. 主要研究方向为电机的故障诊断. 本文通信作者. E-mail: quanhee@163.com

于霞：东北大学信息科学与工程学院讲师. 主要研究方向为复杂系统建模与控制, 传感器故障监测与诊断. E-mail: yuxia@ise.neu.edu.cn

何侃：华为技术有限公司软件开发工程师. 2019年获得东北大学硕士学位. 主要研究方向为电机的故障诊断. E-mail: hekan940112@gmail.com

李镇华：东北大学信息科学与工程学院硕士研究生. 2017年获得哈尔滨理工大学自动化学院学士学位. 主要研究方向为切换系统的控制设计, 时滞系统. E-mail: lizhenhuagd@163.com

计量
- 文章访问数: 1272
- HTML全文浏览量: 391
- PDF下载量: 403
- 被引次数: 0
出版历程
- 收稿日期: 2019-05-08
- 录用日期: 2019-07-30
- 网络出版日期: 2022-03-02
- 刊出日期: 2022-03-25

Rolling Bearing Fault Diagnosis Based on Parameter Optimization VMD and Sample Entropy

LIU Jian-Chang^1
,,
QUAN He^1
,,
YU Xia^1
,,
HE Kan^2
,,
LI Zhen-Hua^1
,

1.
College of Information Science and Engineering, Northeastern University, Shenyang 110819
2.
Hangzhou Research Institute, Huawei Technology Co., Ltd., Hangzhou 310007

Funds: Supported by National Natural Science Foundation of China (61773106)

More Information

Author Bio:
LIU Jian-Chang　Professor at the College of Information Science and Engineering, Northeastern University. His research interest covers control theory and control engineering, and fault diagnosis

QUAN He　Master student at the College of Information Science and Engineering, Northeastern University. He received his bachelor degree from Harbin University of Science and Technology in 2017. His main research interest is motor fault diagnosis. Corresponding author of this paper

YU Xia　Lecturer at the School of Information Science and Engineering, Northeastern University. Her research interest covers complex system modeling and control, sensor fault monitoring and diagnosis

HE Kan　Software development engineer at Huawei Technology Co., Ltd.. He received his master degree from Northeastern University in 2019. His main research interest is motor fault diagnosis

LI Zhen-Hua　Master student at the College of Information Science and Engineering, Northeastern University. He received his bachelor degree from Harbin University of Science and Technology in 2017. His research interest covers control design of switched systems and time-delay systems

摘要

摘要: 针对滚动轴承故障特征提取不丰富而导致的诊断识别率低的情况, 提出了基于参数优化变分模态分解(Variational mode decomposition, VMD)和样本熵的特征提取方法, 采用支持向量机(Support vector machine, SVM)进行故障识别. VMD方法的分解效果受限于分解个数和惩罚因子的选取, 本文分析了这两个影响参数选取的不规律性, 采用遗传变异粒子群算法进行参数优化, 利用参数优化的VMD方法处理故障信号. 样本熵在衡量滚动轴承振动信号的复杂度时, 得到的熵值并不总是和信号的复杂度相关, 故结合滚动轴承的故障机理, 提出基于滚动轴承故障机理的样本熵, 此样本熵衡量振动信号的复杂度与机理分析的结果一致. 仿真实验表明, 利用本文提出的特征提取方法, 滚动轴承的故障诊断准确率有明显的提高.
- 变分模态分解 /
- 参数优化 /
- 遗传变异粒子群 /
- 样本熵 /
- 故障诊断
Abstract: In this paper, aiming at the low diagnostic recognition rate caused by insufficient fault feature extraction of rolling bearings, a feature extraction method based on parameter optimization variational mode decomposition (VMD) and sample entropy is proposed. Support vector machine (SVM) is used for fault identification. The decomposition effect of VMD method is limited by the number of decomposition and the selection of penalty factor. This paper analyses the irregularity of the two influencing parameters, uses genetic mutation particle swarm optimization to optimize the parameters, and uses parameter optimization VMD method to process fault signals. Sample entropy is not always related to the complexity of the signal when it is used to measure the complexity of the vibration signal of rolling bearings. Therefore, according to the fault mechanism of rolling bearings, a sample entropy based on the fault mechanism of rolling bearings is proposed, which is consistent with the result of mechanism analysis. The simulation results show that the fault diagnosis accuracy of rolling bearings is obviously improved by using the feature extraction method proposed in this paper.
- Varational mode decomposition (VMD) /
- parameter optimization /
- particle swarm algorithm based on genetic variation /
- sample entropy /
- fault diagnosis

HTML全文

图 1 仿真信号的频谱

Fig. 1 The frequency spectrum of simulated signal

下载: 全尺寸图片幻灯片

图 2 中心频率随分解个数 $ K $ 的变化

Fig. 2 Evolution of central frequency with the number of decomposition $ K $

下载: 全尺寸图片幻灯片

图 3 中心频率随惩罚因子 $ \alpha $ 的变化

Fig. 3 Evolution of central frequency with punishment factor $ \alpha $

下载: 全尺寸图片幻灯片

图 4 基于遗传变异粒子群算法的参数优化流程

Fig. 4 Parameter optimization process based on genetic mulation particle swarm optimization

下载: 全尺寸图片幻灯片

图 5 4种状态的振动信号

Fig. 5 Vibration signal in four conditions

下载: 全尺寸图片幻灯片

图 6 样本熵的变化曲线

Fig. 6 Evolution of sample entropy

下载: 全尺寸图片幻灯片

图 7 测试样本的分类结果

Fig. 7 Classification of test samples

下载: 全尺寸图片幻灯片

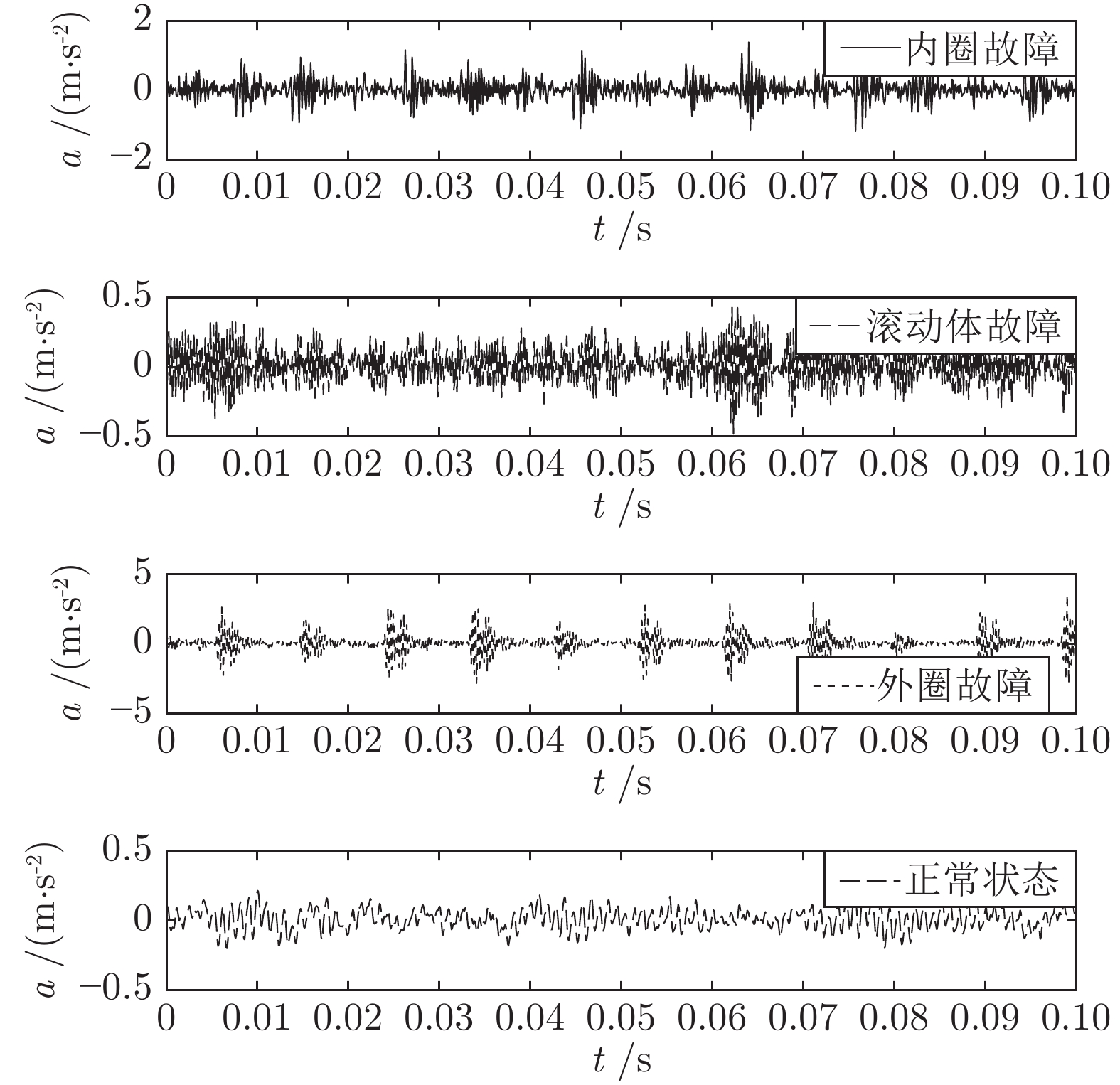
表 1 样本熵值

Table 1 Sample entropy

工况类型	熵值 1	熵值 2
正常状态	0.9717	0.9696
内圈故障	1.5976	1.7200
滚动体故障	1.6937	1.6883
外圈故障	0.7099	0.8600

下载: 导出CSV

表 2 遗传变异粒子群算法的参数值

Table 2 The values of parameters in the particle swarm algorithm based on the genetic variation

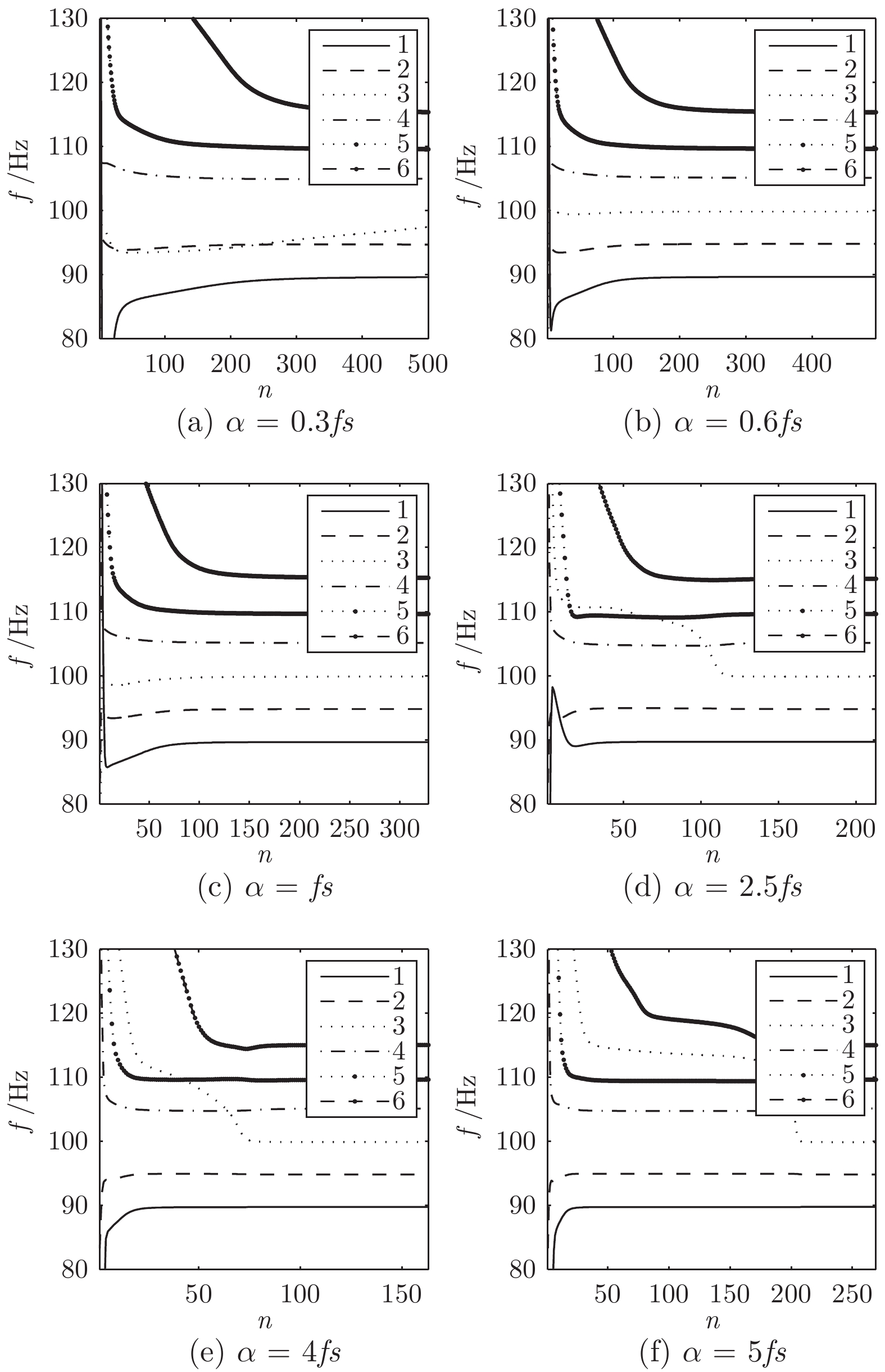
D	m'	c₁	c₂	n_max	maxAge	$\omega_{\max}$	$\omega_{\min}$	q
2	20	2	2	40	2	0.9	0.4	0.5

下载: 导出CSV

表 3 最佳参数组合$\left[ {{K_0},{\alpha_0}} \right]$

Table 3 Optimum combination of parameters

轴承状态	$\left[ {{K_0},{\alpha _0}} \right]$
正常状态	$\left[ {7,2\,082} \right]$
内圈故障	$\left[ {8,277} \right]$
滚动体故障	$\left[ {3,2\,400} \right]$
外圈故障	$\left[ {5,1\,957} \right]$

下载: 导出CSV

表 4 其他处理方法的正确率 (%)

Table 4 Correctness of other processing methods (%)

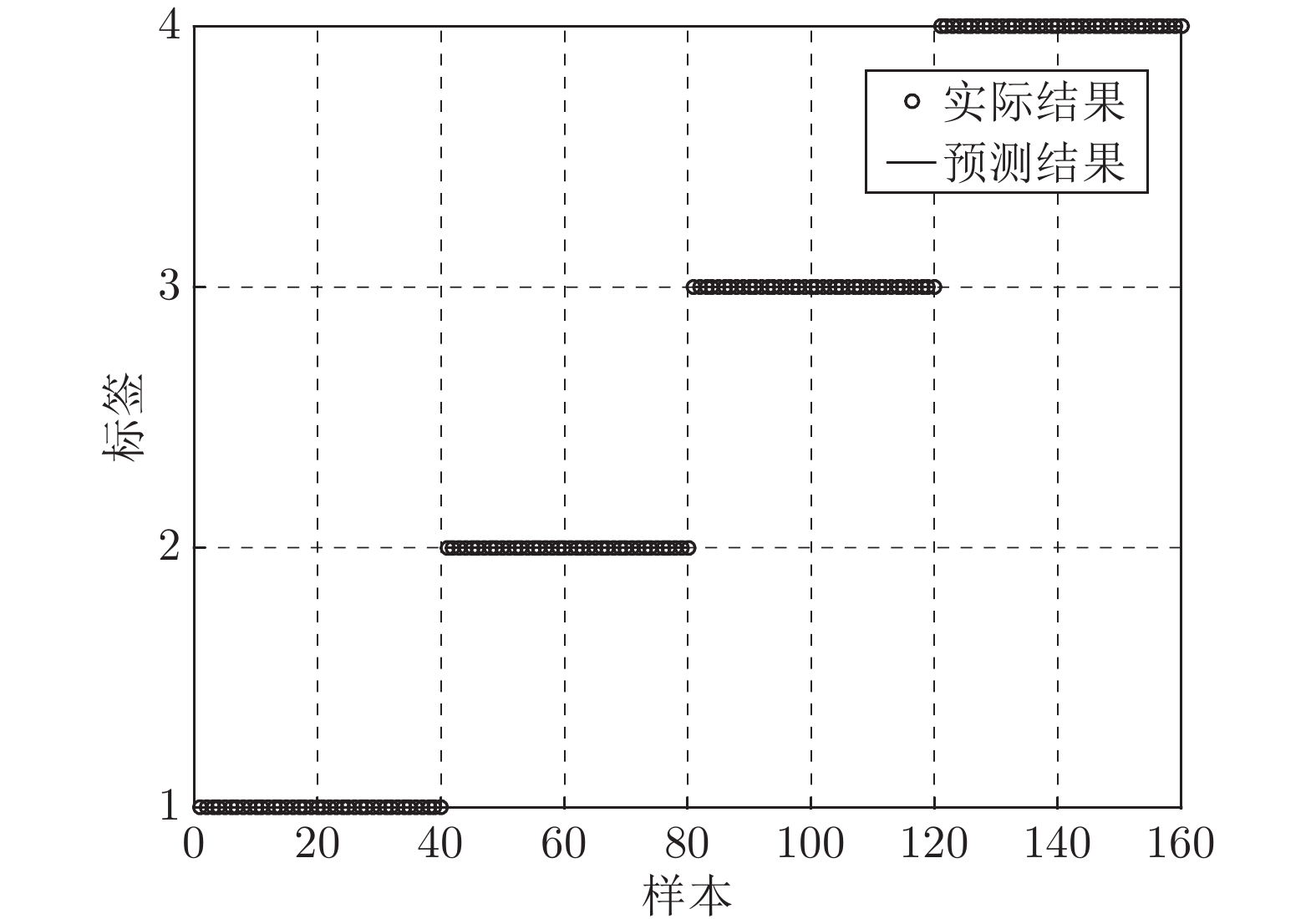
处理方法	内圈	滚动体	外圈	正常	平均
EMD + SampEn	82.5	82.5	100	100	91.25
LMD + SampEn	90	90	100	100	95
DTCWT + SampEn	97.5	100	97.5	100	98.75
VMD + SampEn	100	90	100	100	97.5

下载: 导出CSV

表 5 测试样本的分类正确率 (%)

Table 5 Classification accuracy of test samples (%)

NO	负载 (kW)	样本类型	VMD + SampEn	本文方法
1	0	${F_0}$	85	97.5
2	0.75	${F_1}$	70	95
3	1.5	${F_2}$	95	97.5
4	2.25	${F_3}$	95	100
5	0	${F_0}$	82.5	97.5
6	0.75	${F_1}$	72.5	92.5
7	1.5	${F_2}$	95	97.5
8	2.25	${F_3}$	95	100
平均正确率	—	—	86.5	97.1875

下载: 导出CSV

表 6 IMF 分量样本熵的均值

Table 6 The mean of IMF sample entropy

负载大小 (kW)	IMF 1	IMF 2	IMF 3	IMF 4
0	0.651	0.668	0.307	0.275
0.75	0.707	0.312	0.208	0.189
1.5	0.546	0.286	0.164	0.168
2.25	0.542	0.229	0.197	0.193

下载: 导出CSV

表 7 IMF 分量传统样本熵的均值

Table 7 The mean of IMF traditional sample entropy

负载大小 (kW)	IMF 1	IMF 2	IMF 3	IMF 4
0	0.633	0.572	0.448	0.325
0.75	0.631	0.588	0.417	0.309
1.5	0.633	0.566	0.376	0.251
2.25	0.627	0.556	0.341	0.332

下载: 导出CSV

参考文献(33)

[1]	Liu B, Riemenschneider S, Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum. Mechanical Systems And Signal Processing, 2006, 20(3):718-734 doi: 10.1016/j.ymssp.2005.02.003
[2]	程军圣, 于德介, 杨宇. 基于内禀模态奇异值分解和支持向量机的故障诊断方法. 自动化学报, 2006, 32(3): 476-480 Cheng Jun-Sheng, Yu De-Jie, Yang Yu. Fault diagnosis method based on intrinsic modal singular value decomposition and support vector machine. Acta Automatica Sinica, 2006, 32(3): 476-480
[3]	Smith J S. The local mean decomposition and its application to EEG perception data. Journal of the Royal Society Interface, 2005, 2(5): 443-454 doi: 10.1098/rsif.2005.0058
[4]	Li Y, Xu M, Wang R, Huang W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. Journal of Sound and Vibration, 2016, 360: 277-299 doi: 10.1016/j.jsv.2015.09.016
[5]	Wu Z. Ensemble empirical mode decomposition: a noiseassisted data analysis method. Advances in Adaptive Data Analysis, 2009, 1(01): 41-45
[6]	Lei Y, He Z, Zi Y. EEMD method and WNN for fault diagnosis of locomotive roller bearings. Expert Systems with Applications, 2011, 38(6): 7334-7341 doi: 10.1016/j.eswa.2010.12.095
[7]	任达千, 杨世锡, 吴昭同. 基于LMD的信号瞬时频率求取方法及实验. 浙江大学学报(工学版), 2009, 43(3): 523-528 doi: 10.3785/j.issn.1008-973X.2009.03.024 Ren Da-Qian, Yang Shi-Xi, Wu Zhao-Tong. Method and experiment of obtaining instantaneous frequency of signal based on LMD. Journal of Zhejiang University, 2009, 43(3):523-528 doi: 10.3785/j.issn.1008-973X.2009.03.024
[8]	Dragomiretskiy K, Zosso D. Variational mode decomposition. IEEE Transactions on Signal Processing, 2014, 62(3):531-544 doi: 10.1109/TSP.2013.2288675
[9]	Richman J S, Randall M J. Physiological time-series analysis, using approximate entropy and sample entropy. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049 doi: 10.1152/ajpheart.2000.278.6.H2039
[10]	赵志宏, 杨绍普. 一种基于样本熵的轴承故障诊断方法. 振动与冲击, 2012, 31(6): 136-140 Zhao Zhi-Hong, Yang Shao-Pu. A method of bearing fault diagnosis based on sample entropy. Vibration and Shock, 2012, 31(6): 136-140
[11]	Marwaha P, Sunkaria R K. Complexity quantiflcation of cardiac variability time series using improved sample entropy (I-SampEn). Australasian Physical and Engineering Sciences in Medicine, 2016, 39: 755-763 doi: 10.1007/s13246-016-0457-7
[12]	苏文胜, 王奉涛, 张志新, 郭正刚, 李宏坤. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用. 振动与冲击, 2010, 29(3):18-21 doi: 10.3969/j.issn.1000-3835.2010.03.005 Su Wen-Sheng, Wang Feng-Tao, Zhang Zhi-Xin, Guo Zheng-Gang, Li Hong-Kun. Application of EMD noise reduction and spectral kurtosis method in early fault diagnosis of rolling bearing. Vibration and Shock, 2010, 29(3):18-21 doi: 10.3969/j.issn.1000-3835.2010.03.005
[13]	郭小萍, 刘诗洋, 李元. 基于稀疏残差距离的多工况过程故障检测方法研究. 自动化学报, 2019, 45(3): 618-625 Guo Xiao-Ping, Liu Shi-Yang, Li Yuan. Research on fault detection method for multi-condition process based on sparse residual gap distance. Acta Automatica Sinica, 2019, 45(3): 618-625
[14]	杨宇, 于德介, 程军圣. 基于EMD与神经网络的滚动轴承故障诊断方法. 振动与冲击, 2005, 24(1): 85-88 doi: 10.3969/j.issn.1000-3835.2005.01.023 Yang Yu, Yu De-Jie, Cheng Jun-Sheng. Fault diagnosis method of rolling bearing based on EMD and neural network. Vibration and Shock, 2005, 24(1): 85-88 doi: 10.3969/j.issn.1000-3835.2005.01.023
[15]	B.A. Paya, Esat I I, Badi M N M. Artiflcial neural network based fault diagnostics of rotating machinery using wavelet transforms as a preprocessor. Mechanical Systems and Signal Processing, 1997, 11(5): 751-765 doi: 10.1006/mssp.1997.0090
[16]	Vapnik V. The Nature of Statistical Learning Theory. Berlin: Springer, 1995.
[17]	Ni J, Zhang C, Yang S X. An adaptive approach based on KPCA and SVM for real-time fault diagnosis of HVCBs. IEEE Transactions on Power Delivery, 2011, 26(3):1960-1971 doi: 10.1109/TPWRD.2011.2136441
[18]	Zidi S, Moulahi T, Alaya B. Fault detection in wireless sensor networks through SVM classifler. IEEE Sensors Journal, 2018, 18(1): 211-244
[19]	Sapankevych N, Sankar R. Time series prediction using support vector machines: a survey. IEEE Computational Intelligence Magazine, 2009, 4(2): 211-244
[20]	Yang H, Hassan S G, Liang W, Li D. Fault diagnosis method for water quality monitoring and control equipment in aquaculture based on multiple SVM combined with D-S evidence theory. Computers and Electronics in Agriculture, 2017, 141: 96-108 doi: 10.1016/j.compag.2017.05.016
[21]	Zhou S, Qian S, Chang W, Xiao Y, Cheng Y. A novel bearing multi-fault diagnosis approach based on weighted permutation entropy and an improved SVM ensemble classifler. Sensors, 2018, 18(6): 1934-1957 doi: 10.3390/s18061934
[22]	吕中亮. 基于变分模态分解与优化多核支持向量机的旋转机械早期故障诊断方法研究 [博士学位论文], 重庆大学, 中国, 2016. Lv Zhong-Liang. Research on Early Fault Diagnosis of Rotating Machinery Based on Variational Model Decomposition and Optimized Multi-Core Support Vector Machine [Ph.D. dissertation], Chongqing University, China, 2016.
[23]	Tipping M E. Sparse bayesian learning and the relevance vector machine. Journal of Machine Learning Research, 2001, 1(3): 755-763
[24]	高明哲, 许爱强, 唐小峰. 基于多核多分类相关向量机的模拟电路故障诊断方法. 自动化学报, 2019, 45(02): 203-213 Gao Ming-Zhe, Xu Ai-Qiang, Tang Xiao-Feng. Analog circuit fault diagnosis method based on multi-core and multiclassiflcation relevant vector machine. Acta Automatica Sinica, 2019, 45(02): 203-213
[25]	Breiman L. Random forests. Machine Learning, 2001, 45(1):5-32 doi: 10.1023/A:1010933404324
[26]	Waljee A K, Lipson R, Wiitala W L. Predicting hospitalization and outpatient corticosteroid use in inflammatory bowel disease patients using machine learning. Inflammatory Bowel Diseases, 2017, 24(1): 45-53
[27]	Waljee A K, Sauder K, Patel A. Machine learning algorithms for objective remission and clinical outcomes with thiopurines. Journal of Crohnn＇s and Colitis, 2017, 11(7): 801−810
[28]	张西宁, 张雯雯, 周融通, 余迪. 基于多维缩放和随机森林的轴承故障诊断方法. 西安交通大学学报, 2019, 53(8): 1−7 Zhang Xi-Ning, Zhang Wen-Wen, Zhou Rong-Tong, Yu-Di. Bearing fault diagnosis method based on multiple dimensional scaling and random forest. Journal of Xi＇an Jiaotong University, 2019, 53(8): 1−7
[29]	Carson, J R. Notes on the theory of modulation. Proceedings of the IEEE, 1963, 51(6): 893-896 doi: 10.1109/PROC.1963.2322
[30]	杨志鹏. 粒子群优化算法分析及研究进展. 计算机工程与应用, 2006, 43(5): 24-27 Yang Zhi-Peng. Analysis and research progress of particle swarm optimization. Computer Engineering and Application, 2006, 43(5): 24-27
[31]	刘衍民. 粒子群算法的研究与应用 [博士学位论文], 山东师范大学, 中国, 2011. Liu Yan-Min. Research and Application of Particle Swarm Optimization [Ph.D. dissertation], Shandong Normal University, China, 2011.
[32]	唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用. 西安交通大学学报, 2015, 49(5): 73−81 Tang Gui-Ji, Wang Xiao-Long. Application of variational modal decomposition method for optimizing parameters in early fault diagnosis of rolling bearings. Journal of Xi＇an Jiaotong University, 2015, 49(5): 73−81
[33]	Pincus S M. Approximate entropy as a measure of system complexity. Proceedings of the National Academy of Sciences, 1991, 88(6): 2297-2301 doi: 10.1073/pnas.88.6.2297