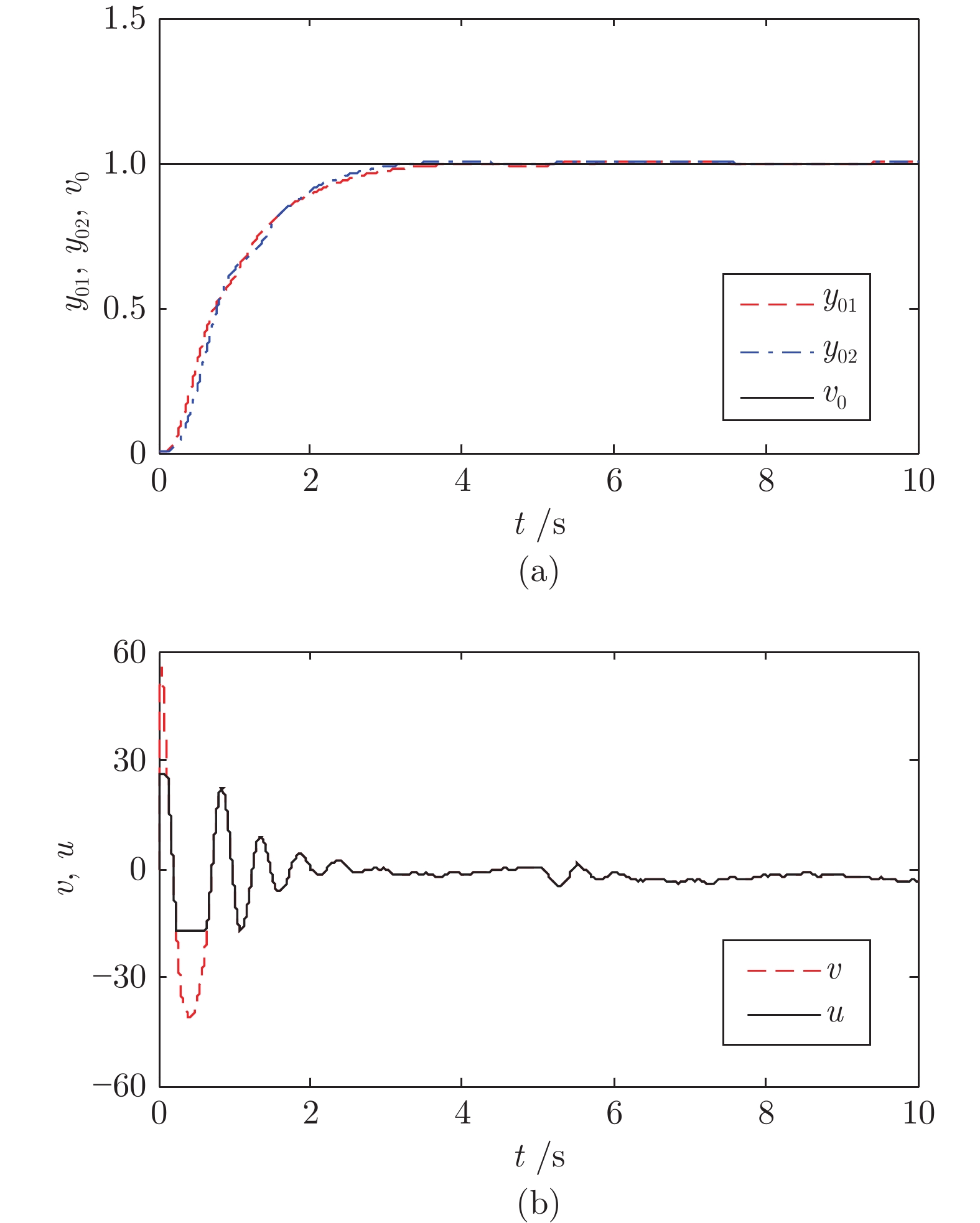
|
[1]
|
Gao Z Q. On the centrality of disturbance rejection in automatic control. ISA Transactions, 2014, 53(4): 850-857 doi: 10.1016/j.isatra.2013.09.012
|
|
[2]
|
郭宝珠. 非线性系统的自抗扰控制引论. 数学建模及其应用, 2017, 6(1): 13-22 doi: 10.3969/j.issn.2095-3070.2017.01.003Guo Bao-Zhu. An introduction to active disturbance rejection control for nonlinear systems. Mathematical Modeling and Its Applications, 2017, 6(1): 13-22 doi: 10.3969/j.issn.2095-3070.2017.01.003
|
|
[3]
|
Han J Q. From PID to active disturbance rejection control. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906 doi: 10.1109/TIE.2008.2011621
|
|
[4]
|
韩京清. 自抗扰控制器及其应用. 控制与决策, 1998, 13(1): 19-23 doi: 10.3321/j.issn:1001-0920.1998.01.005Han Jing-Qing. Active disturbance rejection controller and applications. Control and Decision, 1998, 13(1): 19-23 doi: 10.3321/j.issn:1001-0920.1998.01.005
|
|
[5]
|
Guo B Z, Zhao Z L. On convergence of nonlinear active disturbance rejection for SISO systems. In: Proceedings of the 24th Chinese Control and Decision Conference. Taiyuan, China: IEEE, 2012. 3507−3512
|
|
[6]
|
Qi X H, Li J, Xia Y Q, Gao Z Q. On the robust stability of active disturbance rejection control for SISO systems. Circuits, Systems, and Signal Processing, 2017, 36(1): 65-81 doi: 10.1007/s00034-016-0302-y
|
|
[7]
|
Xue W C, Huang Y. Performance analysis of 2-DOF tracking control for a class of nonlinear uncertain systems with discontinuous disturbances. International Journal of Robust Nonlinear Control, 2018, 28(4): 1456-1473 doi: 10.1002/rnc.3972
|
|
[8]
|
Li Z Y, Li X M, Zhou Z Y. Active disturbance rejection controller for loitering unit with parameter uncertainty. In: Proceedings of the 16th International Conference on Control, Automation and Systems. Gyeongju, Korea (South): IEEE, 2016. 140−144
|
|
[9]
|
Long Y, Du Z J, Cong L, Wang W D, Zhang Z M, Dong W. Active disturbance rejection control based human gait tracking for lower extremity rehabilitation exoskeleton. ISA Transactions, 2017, 67: 389-397 doi: 10.1016/j.isatra.2017.01.006
|
|
[10]
|
陈增强, 孙明玮, 杨瑞光. 线性自抗扰控制器的稳定性研究. 自动化学报, 2013, 39(5): 574-580Chen Zeng-Qiang, Sun Ming-Wei, Yang Rui-Guang. On the stability of linear active disturbance rejection control. Acta Automatica Sinica, 2013, 39(5): 574-580
|
|
[11]
|
Xue W C, Huang Y. Performance analysis of active disturbance rejection tracking control for a class of uncertain LTI systems. ISA Transactions, 2015, 58: 133-154 doi: 10.1016/j.isatra.2015.05.001
|
|
[12]
|
Xue W C, Huang Y. On performance analysis of ADRC for a class of MIMO lower-triangular nonlinear uncertain systems. ISA Transactions, 2014, 53(4): 955-962 doi: 10.1016/j.isatra.2014.02.002
|
|
[13]
|
高阳, 吴文海, 高丽. 高阶不确定非线性系统的线性自抗扰控制. 控制与决策, 2020, 35(2): 483−491Gao Yang, Wu Wen-Hai, Gao Li. Linear active disturbance rejection control for high-order nonlinear systems with uncertainty. Control and Decision, 2020, 35(2): 483−491
|
|
[14]
|
Li Y M, Tong S C, Li T S. Direct adaptive fuzzy backstepping control of uncertain nonlinear systems in the presence of input saturation. Neural Computing & Applications, 2013, 23(5): 1207-1216
|
|
[15]
|
Molavi A, Jalali A, Naraghi M G. Adaptive fuzzy control of a class of nonaffine nonlinear system with input saturation based on passivity theorem. ISA Transactions, 2017, 69: 202-213 doi: 10.1016/j.isatra.2017.03.020
|
|
[16]
|
Xu B, Huang X Y, Wang D W, Sun F C. Dynamic surface control of constrained hypersonic flight models with parameter estimation and actuator compensation. Asian Journal of Control, 2014, 16(1): 162-174 doi: 10.1002/asjc.679
|
|
[17]
|
彭秀艳, 贾书丽, 张彪. 一类具有执行器饱和的非线性系统抗饱和方法研究. 自动化学报, 2016, 42(5): 798-804Peng Xiu-Yan, Jia Shu-Li, Zhang Biao. An anti-saturation method for a class of nonlinear systems with actuator saturation. Acta Automatica Sinica, 2016, 42(5): 798-804
|
|
[18]
|
林安辉, 蒋德松, 曾建平. 具有输入饱和的欠驱动船舶编队控制. 自动化学报, 2018, 44(8): 1496-1504Lin An-Hui, Jiang De-Song, Zeng Jian-Ping. Underactuated Ship Formation Control With Input Saturation. Acta Automatica Sinica, 2018, 44(8): 1496-1504
|
|
[19]
|
Prasov A A, Khalil H K. A nonlinear high-gain observer for systems with measurement noise in a feedback control framework. IEEE Transactions on Automatic Control, 2013, 58(3): 569-580 doi: 10.1109/TAC.2012.2218063
|
|
[20]
|
Lee J, Choi J, Khalil H K. New implementation of high-gain observers in the presence of measurement noise using stochastic approximation. In: Proceedings of the 2016 European Control Conference. Aalborg, Denmark: IEEE, 2016. 1740−1745
|
|
[21]
|
Teel A R. Further variants of the Astolfi/Marconi high-gain observer. In: Proceedings of the 2016 American Control Conference. Boston, USA: IEEE, 2016. 993−998
|
|
[22]
|
Battilotti S. Robust observer design under measurement noise with gain adaptation and saturated estimates. Automatica, 2017, 81: 75-86 doi: 10.1016/j.automatica.2017.02.008
|
|
[23]
|
Nair R R, Behera L. Robust adaptive gain higher order sliding mode observer based control-constrained nonlinear model predictive control for spacecraft formation flying. IEEE/CAA Journal of Automatica Sinica, 2018, 5(1): 367-381 doi: 10.1109/JAS.2016.7510253
|




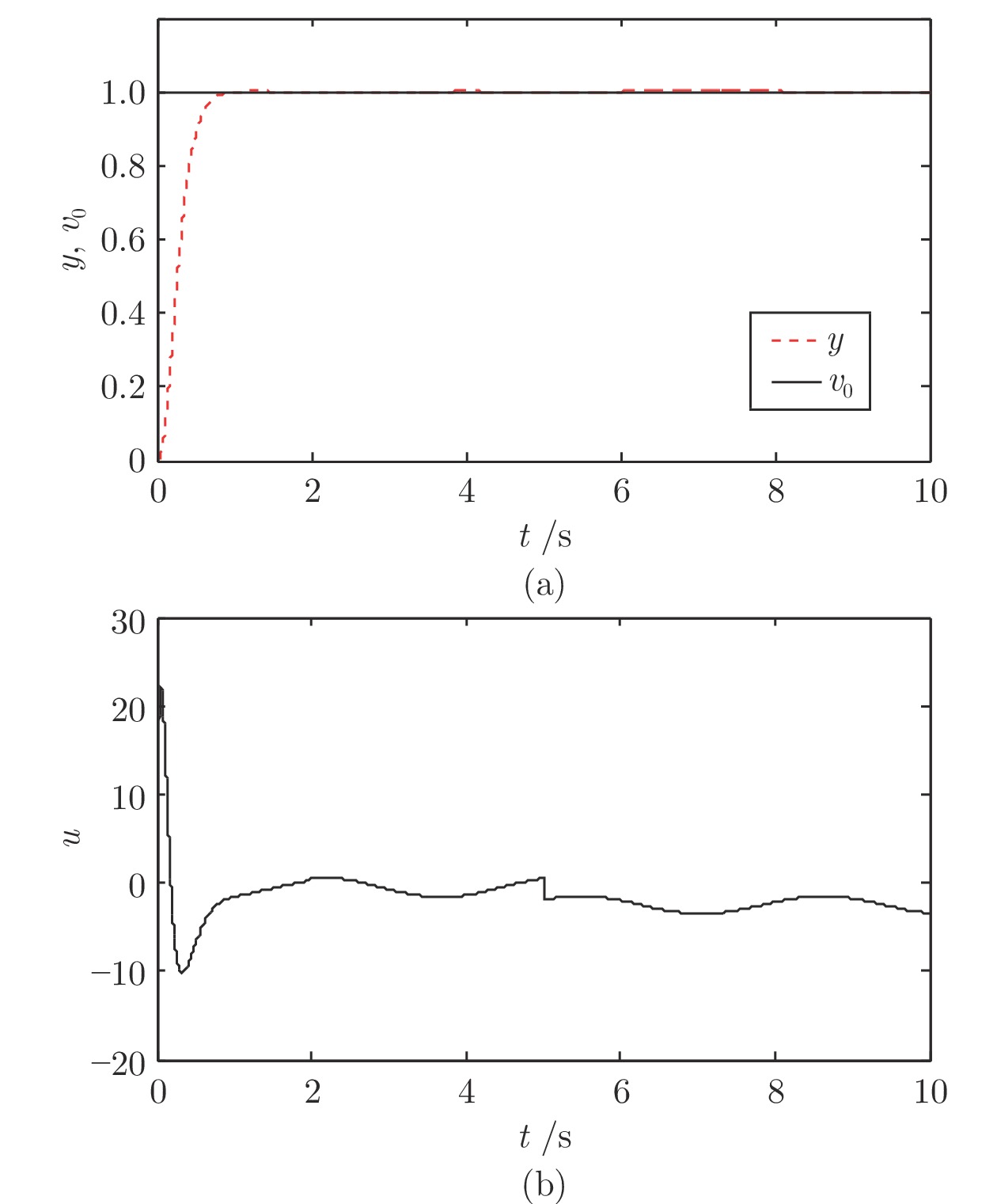
 下载:
下载: