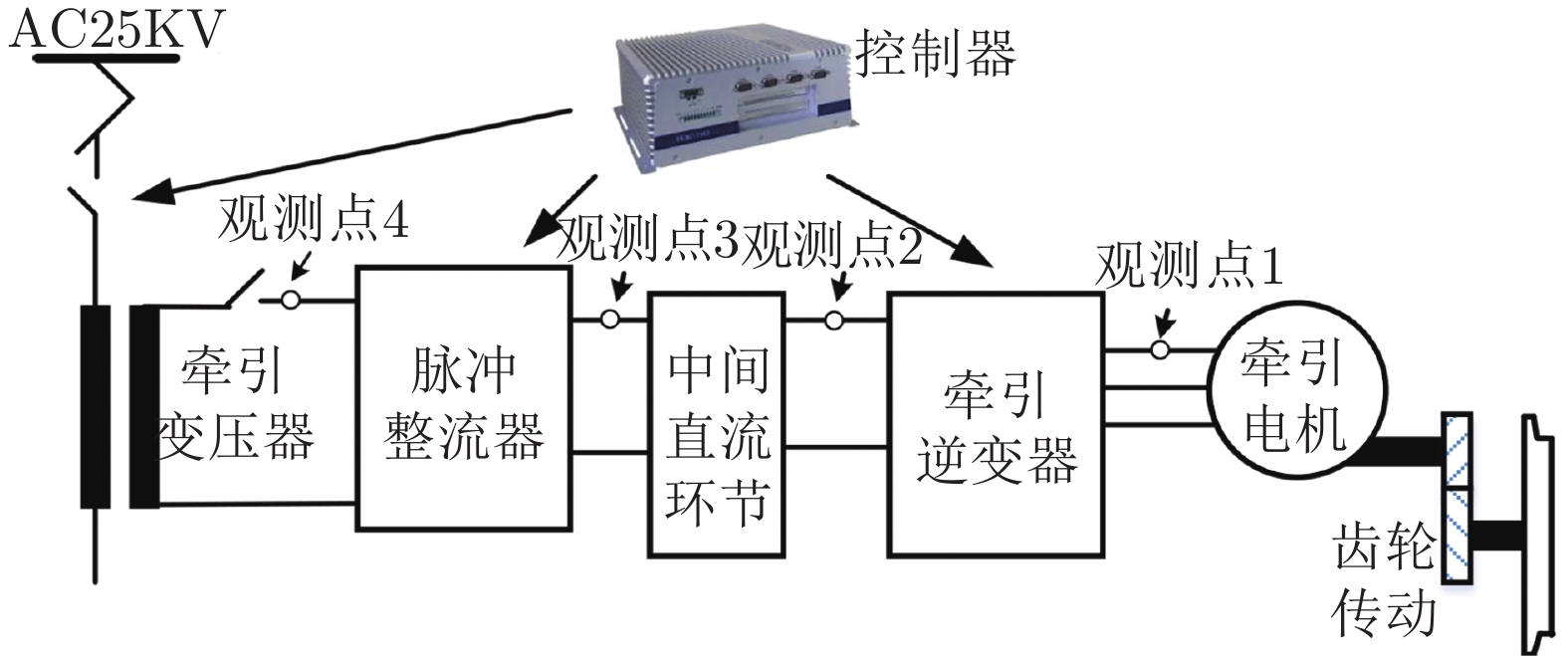
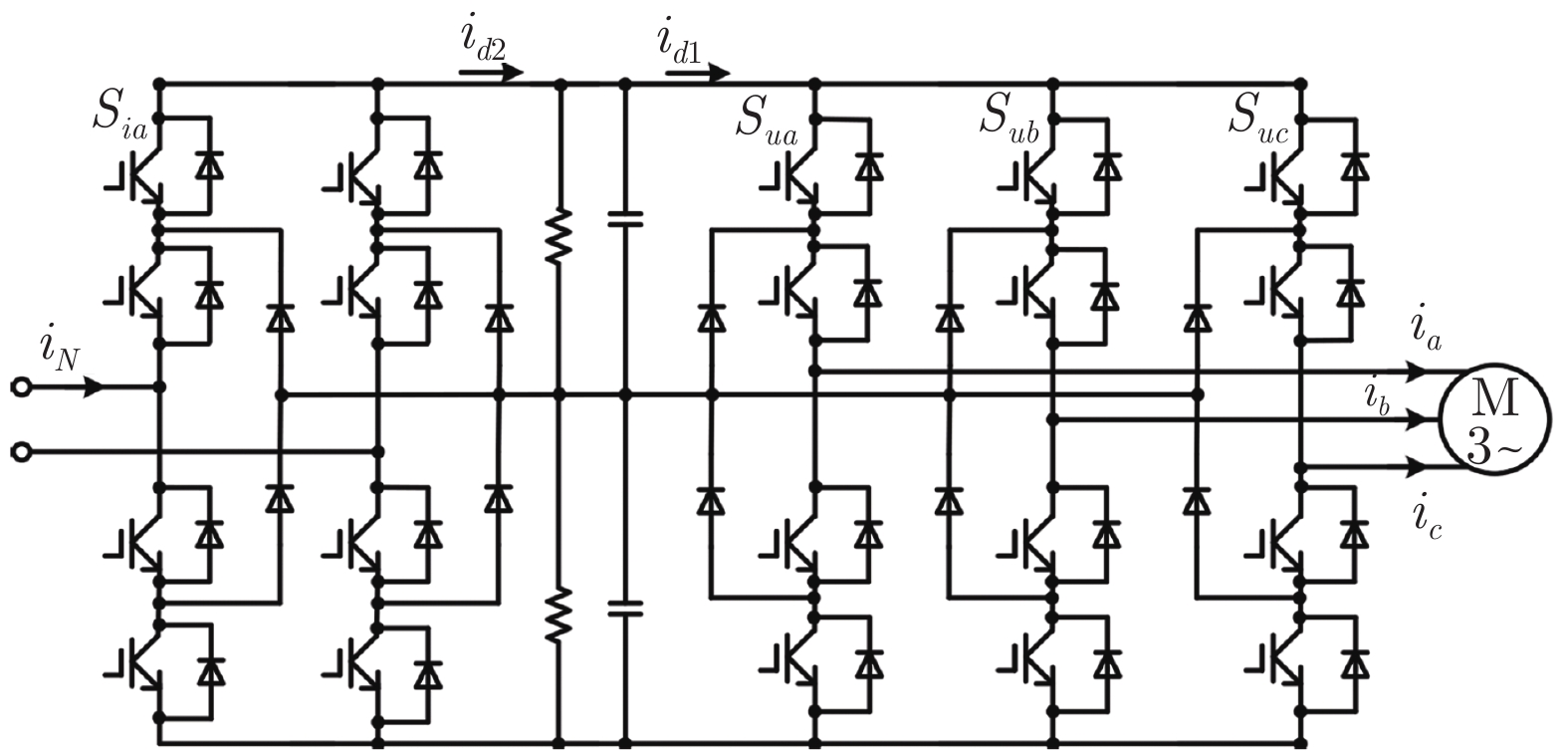
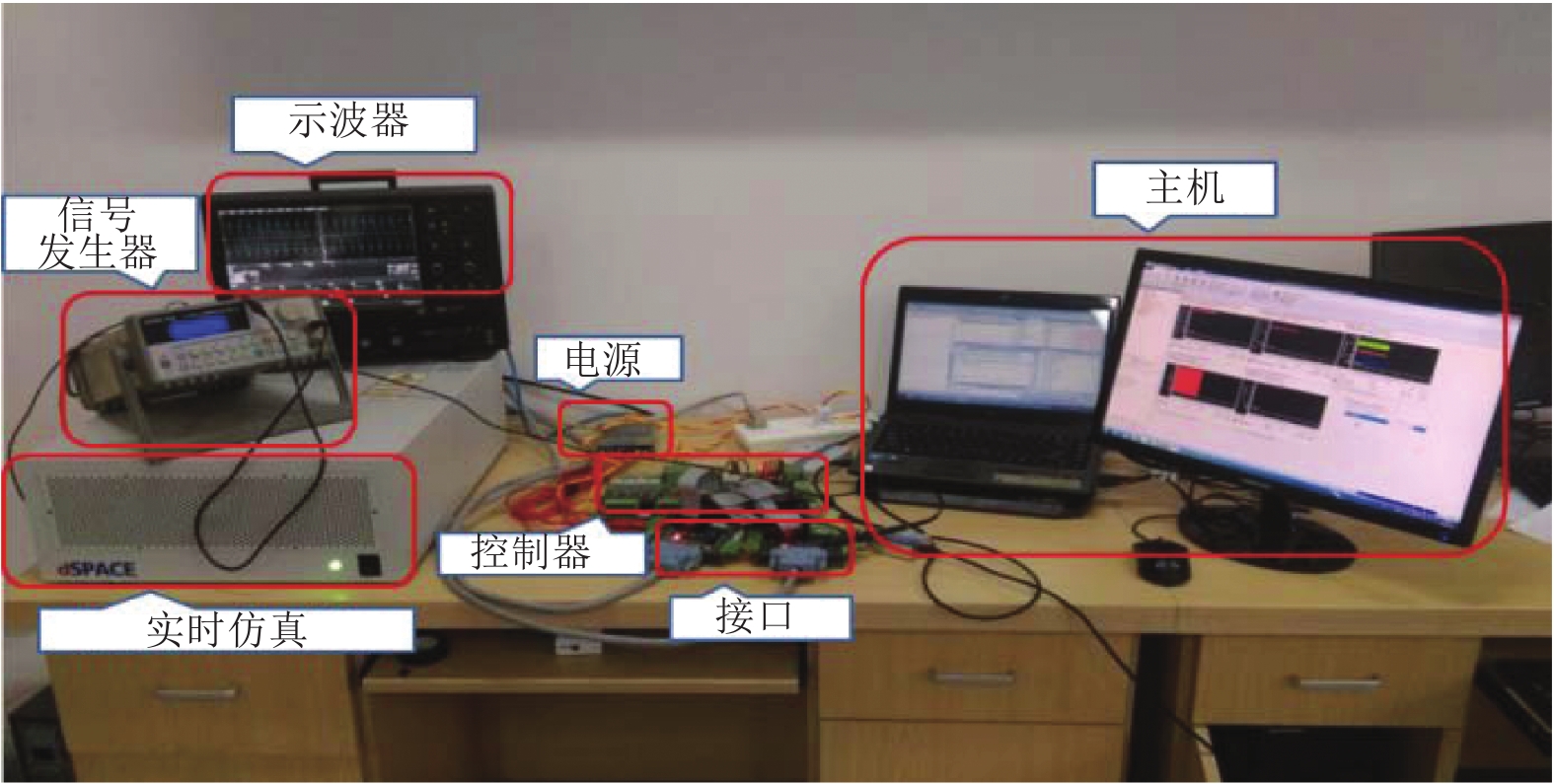
Fault Tracing Method Based on Fault Propagation and Causality With Its Application to the Traction Drive Control System
-
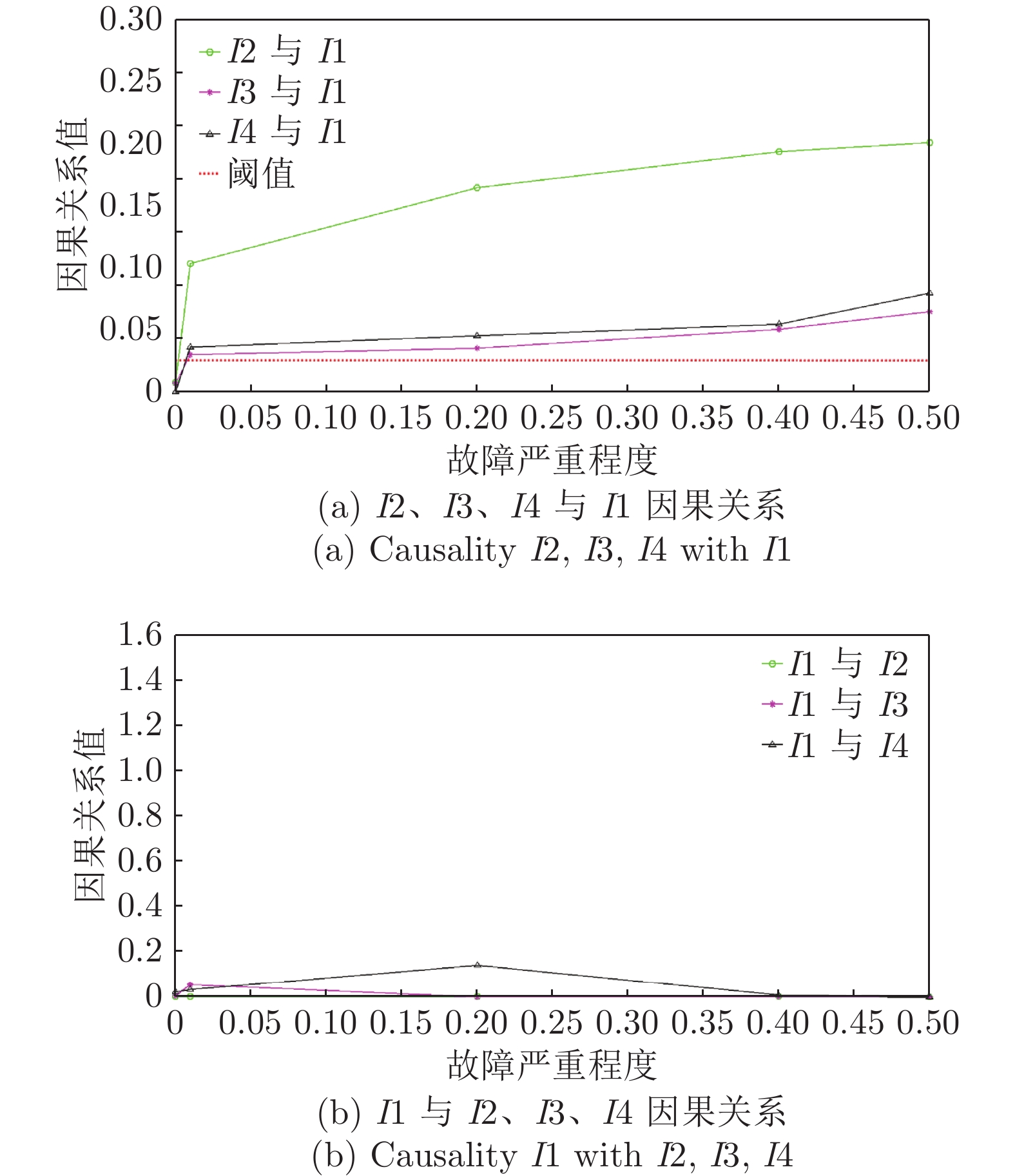
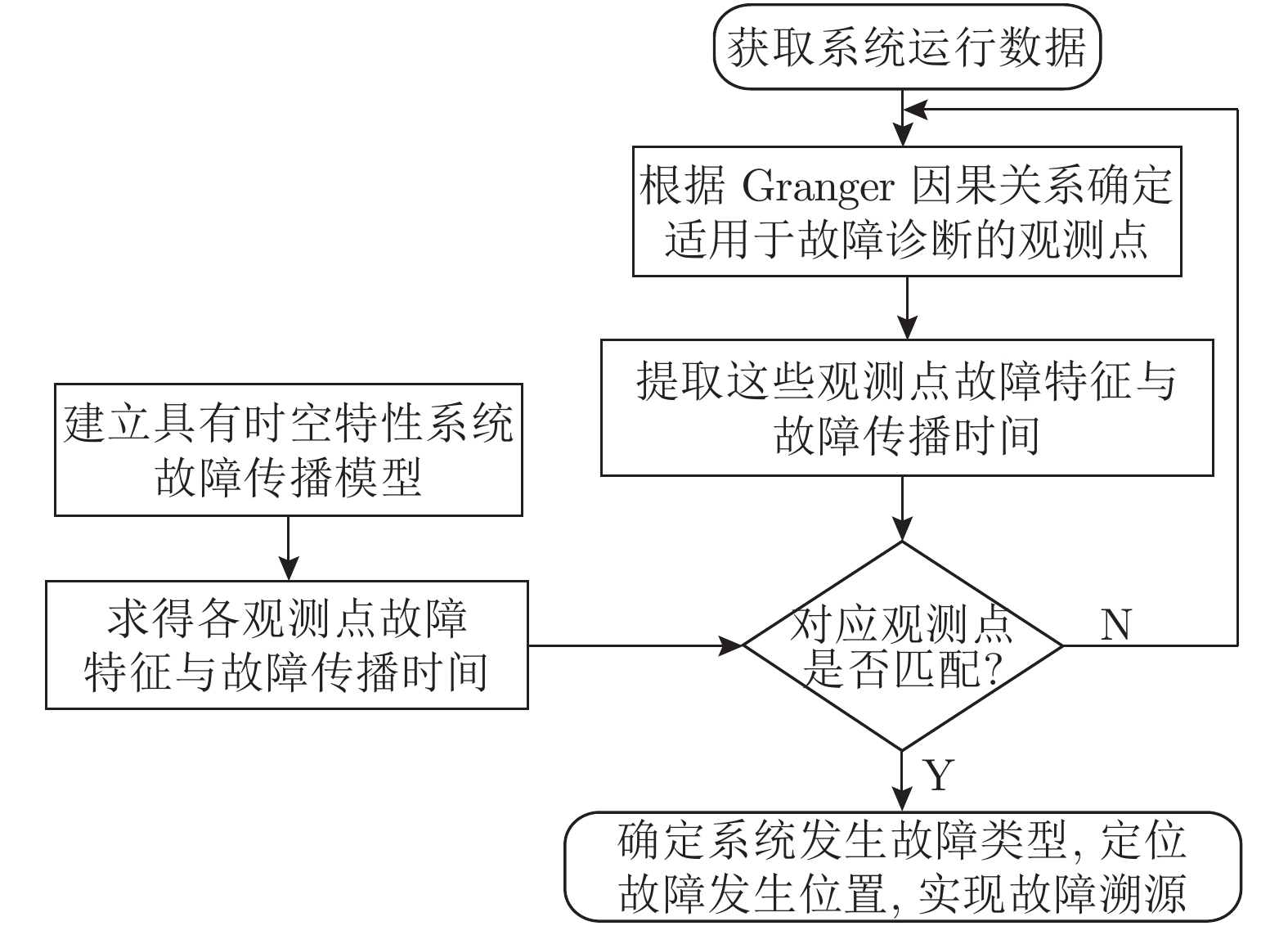
摘要: 针对故障溯源问题, 提出一种基于故障传播与因果关系的故障溯源方法. 该方法首先建立体现时空特性的系统故障传播模型; 其次利用Granger因果关系技术判定不同观测点信号间的因果关系, 确定适合提取信号故障特征用于故障诊断的观测点; 然后提取系统运行时这些观测点故障特征和故障传播时间; 最后同故障传播模型中对应观测点的时空特性相匹配, 从而确定故障类型与位置, 实现故障溯源. 所提方法在高速列车牵引传动控制系统半实物仿真平台上进行了实验验证, 结果表明该方法可行有效.
-
关键词:
- 牵引传动控制系统 /
- 故障传播模型 /
- 故障溯源 /
- 时空特性 /
- Granger因果关系
Abstract: To solve the problem of fault tracing, a fault tracing method based on fault propagation and causality is proposed in this paper. Firstly, the fault propagation model of the system, which reflects spatiotemporal characteristics, is established. Secondly, the Granger causality technique is used to determine the causality between signals of different observation points, and to determine the observation points suitable for extracting fault features for fault diagnosis. Thirdly, the fault features and fault propagation time of these observation points are extracted, and then compared with the spatiotemporal characteristics of the corresponding observation points in the fault propagation model to determine the fault type and location. The proposed method is verified by the semi-physical simulation platform of the traction drive control system of high-speed train, and the feasibility and efficacy of this method is verified.1) 收稿日期 2019-03-27 录用日期 2019-09-24 Manuscript received March 27, 2019; accepted September 24, 2019 国家自然科学基金 (61490702, 61773407, 61621062, 61803390, 61751312), 国家杰出青年科学基金 (61725306), 轨道交通节能控制与安全监测湖南省重点实验室 (2017TP1002), 湖南省科技厅科技计划项目 (2016TP1023), 装备预研教育部联合基金 (6141A02022110), 装备预研领域基金 (61400030501), 博士后基金 (2018M643000) 资助 Supported by National Natural Science Foundation of China (61490702, 61773407, 61621062, 61803390, 61751312), National Science Foundation for Distinguished Young Scholars of China (61725306), Key Laboratory of Energy Saving Control and Safety Monitoring for Rail Transportation (2017TP1002), Science and Technology Project of Hunan Science and Technology Agency (2016TP1023), Program of Joint Pre-research Foundation of the Chinese Ministry of Education (6141A02022110), General Program of Equipment Pre-research Field Foundation of China (61400030501), and Postdoctoral Foundation (2018M643000)2) 本文责任编委 董海荣 Recommended by Associate Editor DONG Hai-Rong 1. 中南大学自动化学院 长沙 410083 2. 邵阳学院多电源地区电网运行与控制湖南省重点实验室 邵阳 422000 1. School of Automation, Central South University, Changsha 410083 2. Hunan Provincial Key Laboratory of Grids Operation and Control on Multi-Power Sources Area, Shaoyang University, Shaoyang 422000 -
图 2 牵引传动控制系统观测点示意图
Fig. 2 Schematic diagram of observation point of traction drive control system
图 3 牵引传动控制系统主电路拓扑图
Fig. 3 Main circuit topology diagram of traction drive control system
图 5 观测点电流信号间Granger因果关系
Fig. 5 Granger causality between the current signals at different observation points
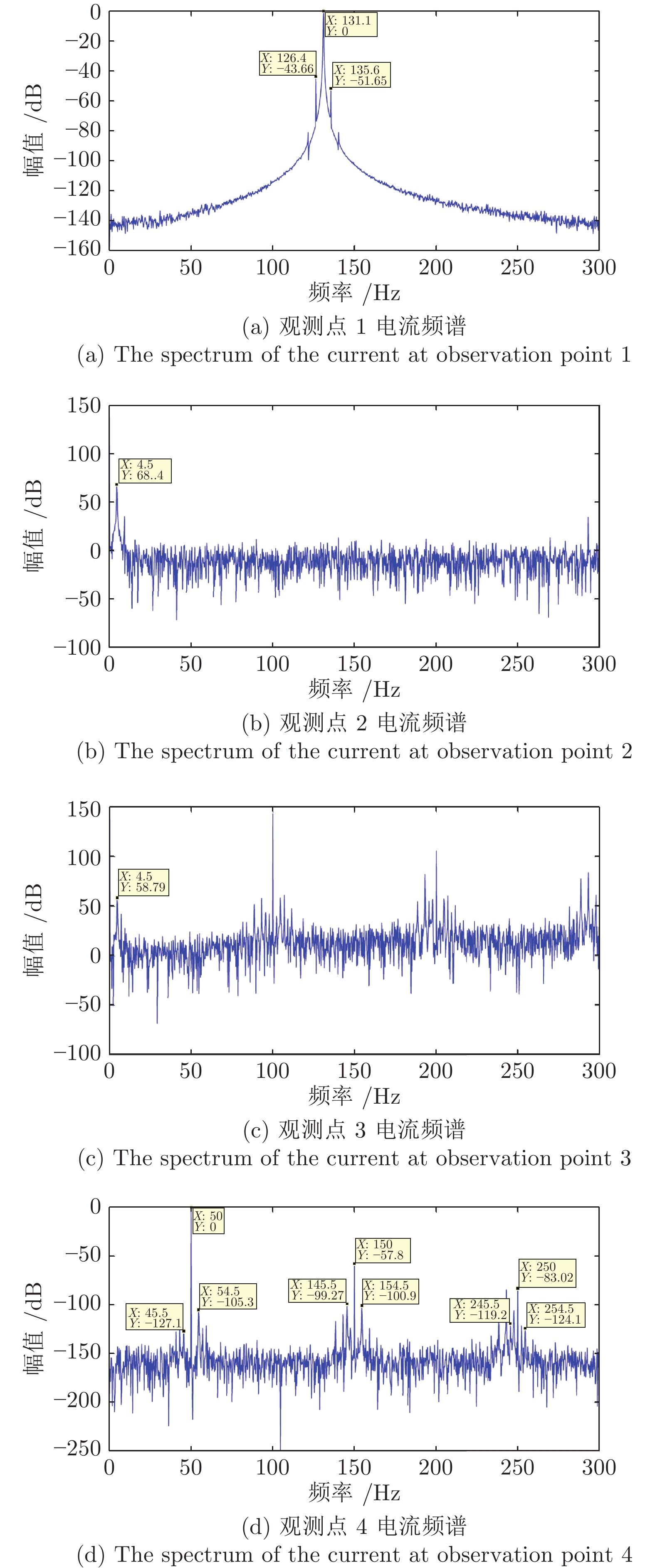
表 1 不同观测点故障特征频率值(Hz)
Table 1 Fault feature frequency value at different observation points (Hz)
电网
频率$ f $ 电机定子电流
频率$ f_1 $ 转差率 $ s $ 观测点1电流故障
特征频率$ (1\pm2s)f_1 $ 观测点2电流故障
特征频率$ 2sf_1 $ 观测点3电流故障
特征频率$ 2sf_1 $ 观测点4电流故障特征频率 $ (4n\pm1)f\pm2sf_1 $ 50 131.1 0.0172 126.4/135.6 4.5 4.5 45.5/54.5
145.5/154.5
245.5/254.5
下载: 导出CSV
-
[1] 周东华, 纪洪泉, 何潇. 高速列车信息控制系统的故障诊断技术. 自动化学报, 2018, 44(7): 1153−11641 Zhou Dong-Hua, Ji Hong-Quan, He Xiao. Fault diagnosis techniques for the information control system of high-speed trains. Acta Automatica Sinica, 2018, 44(7): 1153−1164 [2] 姜斌, 吴云凯, 陆宁云, 冒泽慧. 高速列车牵引系统故障诊断与预测技术综述. 控制与决策, 2018, 33(5): 841−8552 Jiang Bin, Wu Yun-Kai, Lu Ning-Yun, Mao Ze-Hui. Review of fault diagnosis and prognosis techniques for high-speed railway traction system. Control and Decision, 2018, 33(5): 841−855 [3] 3 Ning B, Dong H R, Gao S G, Tang T, Zheng W. Distributed cooperative control of multiple high-speed trains under a moving block system by nonlinear mapping-based feedback. Science China Information Sciences, 2018, 61(12): 1−12 [4] 4 Gou B, Ge X L, Wang S L, Feng X Y, James B. K, Thomas G. H. An open-switch fault diagnosis method for single phase PWM rectifier using a model-based approach in high-speed railway electrical traction drive system. IEEE Transactions on Power Electronics, 2016, 31(5): 3816−3826 doi: 10.1109/TPEL.2015.2465299 [5] 5 Chen Z W, Steven X D, Peng T, Yang C H, Gui W H. Fault detection for non-gaussian processes using generalized canonical correlation analysis and randomized algorithms. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1559−1567 doi: 10.1109/TIE.2017.2733501 [6] 6 Zhou C J, Huang X F, Xiong N X, Qin Y Q, Huang S. A class of general transient faults propagation analysis for networked control systems. IEEE Transactions on Systems, Man, Cybernetics-Systems, 2015, 45(4): 647−661 doi: 10.1109/TSMC.2014.2384480 [7] 7 Ying Y, Peter B L, Krishna R P. Fault diagnosis of HVAC air-handling systems considering fault propagation impacts among components. IEEE Transactions on Automation Science and Engineering, 2017, 14(2): 705−717 doi: 10.1109/TASE.2017.2669892 [8] Abhinav S, Goebel K, Simon D, Eklund N. Damage propagation modeling for aircraft engine run-to-failure simulation. In: Proceedings of the 2018 International Conference on Prognostics and Health Management. USA: IEEE, 2018. 1−9 [9] 9 Wang R X, Gao X, Gao J M, Gao Z Y, Kang J N. An information transfer based novel framework for fault root cause tracing of complex electromechanical systems in the processing industry. Mechanical Systems and Signal Processing, 2018, 101(15): 121−139 [10] 10 Wang P K, Conrad J M, Amir M G, Masahiro F. An ATPG method for double stuck-at faults by analyzing propagation paths of single faults. IEEE Transactions on Circuits and Systems I: Regular Papers, 2018, 65(3): 1063−1074 doi: 10.1109/TCSI.2017.2765721 [11] 11 Li J, Mark S, Jesus A P, Zhang H. Fault signal propagation through the PMSM motor drive systems. IEEE Transactions on Industry Applications, 2017, 53(3): 2915−2924 doi: 10.1109/TIA.2017.2677881 [12] 李辉, 贾晓风, 李利娟, 吴军, 马碧蔓. 基于元胞自动机的电网隐性故障传播模型关键线路识别方法. 电力系统保护与控制, 2018, 46(6): 16−2312 Li Hui, Jia Xiao-Feng, Li Li-Juan, Wu Jun, Ma Bi-Man. An approach for critical lines identification of power grid hidden fault propagation model based on cellular automata. Power System Protection and Control, 2018, 46(6): 16−23 [13] 13 Gregory L, Xing L D, Hanoch B H, Dai Y S. Reliability of series-parallel systems with random failure propagation time. IEEE Transactions on Reliability, 2013, 62(2): 637−647 [14] 14 Bhushan M, Rengaswamy R. Comprehensive design of a sensor network for chemical plants based on various diagnosability and reliability criteria, Part 1: framework. Industrial and Engineering Chemistry Research, 2002, 41(7): 1826−1839 [15] 15 Bhushan M, Rengaswamy R. Comprehensive design of a sensor network for chemical plants based on various diagnosability and reliability criteria, Part 2: applications. Industrial and Engineering Chemistry Research, 2002, 41(7): 1840−1860 doi: 10.1021/ie010437v [16] 薛婷, 钟麦英. 基于 SWT 与等价空间的 LDTV 系统故障检测. 自动化学报, 2017, 43(11): 1920−193016 Xue Ting, Zhong Mai-Ying. SWT and parity space based fault detection for linear discrete time-varying systems. Acta Automatica Sinica, 2017, 43(11): 1920−1930 [17] 17 Saleh M U, LaCombe J, Jayakumar N K T. Signal propagation through piecewise transmission lines for interpretation of reflectometry in photovoltaic systems. IEEE Journal of Photovoltaics, 2019, 9(2): 506−512 doi: 10.1109/JPHOTOV.2018.2884011 [18] 18 Maurya M R, Rengaswamy R, Venkatasubramanian V. Application of signed digraphs-based analysis for fault diagnosis of chemical process flowsheets. Engineering Applications of Artificial Intelligence, 2004, 17(5): 501−518 doi: 10.1016/j.engappai.2004.03.007 [19] 19 Li L, Su X N, Zhang Y, Lin Y T, Li Z H. Trend modeling for traffic time series analysis: an integrated study. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(6): 3430−3439 doi: 10.1109/TITS.2015.2457240 [20] 肖进胜, 朱力, 赵博强, 雷俊锋, 王莉. 基于主成分分析的分块视频噪声估计. 自动化学报, 2018, 44(9): 1618−162520 Xiao Jin-Sheng, Zhu Li, Zhao Bo-Qiang, Lei Jun-Feng, Wang Li. Block-based video noise estimation algorithm via principal component analysis. Acta Automatica Sinica, 2018, 44(9): 1618−1625 [21] 21 Granger C W J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 1969, 37(3): 424−438 doi: 10.2307/1912791 [22] 22 Hu S, Liang H. Causality analysis of neural connectivity: new tool and limitations of spectral granger causality. Neurocomputing, 2012, 76(1): 44−47 doi: 10.1016/j.neucom.2010.10.017 [23] 23 Yang C H, Yang C, Peng T, Yang X Y, Gui W H. A fault-injection strategy for traction drive control systems. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5719−5727 doi: 10.1109/TIE.2017.2674610 [24] 24 George G, Vicente C A, Jose A D, Ioannis P T, Chrysostomos D S, Antero A, George N. The use of a multilabel classification framework for the detection of broken bars and mixed eccentricity faults based on the start-up transient. IEEE Transactions on Industrial Informatics, 2017, 13(2): 625−634 doi: 10.1109/TII.2016.2637169 [25] 尹进田, 谢永芳, 阳春华. 基于 RVMD 的牵引电机转子初期断条故障监测. 控制与决策, 2018, 33(3): 497−50225 Yin Jin-Tian, Xie Yong-Fang, Yang Chun-Hua. Monitoring of incipient rotor bars broken fault in traction motors based on RVMD method. Control and Decision, 2018, 33(3): 497−502 [26] 26 Yang X Y, Yang C H, Peng T, Chen Z W, Liu B, Gui W H. Hardware-in-the-loop fault injection for traction control system. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(2): 696−706 doi: 10.1109/JESTPE.2018.2794339 [27] 27 Yin J T, Xie Y F, Peng T, Yang C H, Chen Z W. Current characteristics analysis and fault injection of an early weak fault in broken rotor bar of traction motor. Mathematical Problems in Engineering, 2018, 1(1): 1−8 [28] 28 Peng T, Tao H W, Yang C, Chen Z W, Yang C H, Gui W H, Karimi H R. A uniform modeling method based on open-circuit faults analysis for npc-three-level converter. IEEE Transactions on Circuits and Systems II—Express Briefs, 2019, 66(3): 457−461 doi: 10.1109/TCSII.2018.2856862 -
图(7) / 表(1)
计量
- 文章访问数: 3213
- HTML全文浏览量: 767
- PDF下载量: 449
- 被引次数: 0
