A Novel Method Based on Dynamic Model Correction on Train Integrated Navigation Positioning
-
摘要: 扩展卡尔曼滤波(Extended Kalman filter, EKF)的准确性依赖于观测的质量、观测对象的非线性程度及动态模型的准确性. 该方法通常假设其动态模型是不变的, 而且默认为非线性程度较弱, 这些在实际的车辆运动中都是不可靠的处理方式. 本文提出了一种利用最小二乘支持向量机(Least squares support vector machine, LSSVM)的技术增强扩展卡尔曼滤波的新算法. LSSVM改进后的EKF算法(LSSVM-EKF)一定程度上弥补了EKF处理强非线性问题的不足; 而且可以自适应地估计历史数据的动态建模偏差, 并使用估计偏差来补偿动态模型. 开发了一种引入Allan方差的K折交叉验证方法来确定LSSVM的训练参数; 将动态模型偏差通过有限数据集与LSSVM一起训练; 并引入无损变换将LSSVM与EKF进行了集成. 为了验证算法, 最后设计了车载试验, 并采用列车数据验证了文中所提的方法, 结果表明LSSVM-EKF可以较好地适应实际车辆运动环境, 可以提供一种可用的车辆定位方法.Abstract: The accuracy of extended Kalman filter (EKF) depends on the quality of the observation, the degree of nonlinearity of the observed object, and the accuracy of the dynamic model. The default is that the degree of nonlinearity is weak, and it is usually assumed that the dynamic model is constant, which is an unreliable treatment in actual vehicle motion. This paper proposes a new algorithm for enhancing the extended Kalman filtering using the technique of least squares support vector machine (LSSVM). The improved EKF algorithm (LSSVM-EKF) of LSSVM compensates for the insufficiency of the strong nonlinear problem of the EKF processing to some extent; and it can adaptively estimate the dynamic modeling deviation of historical data and use the estimated bias to compensate the dynamic model. A K-fold cross-validation method that introduces the Allan variance is developed to determine the training parameters of the LSSVM. The dynamic model deviation is trained with the LSSVM through the finite data set. The lossless transform is introduced to integrate the LSSVM with the EKF. In order to verify the algorithm, the paper finally designs the vehicle test, and uses the train data to verify the proposed method. The results show that LSSVM-EKF can adapt to the actual vehicle motion environment and provide a usable vehicle positioning method.1) 收稿日期 2019-03-18 录用日期 2019-09-12 Manuscript received March 18, 2019; accepted September 12, 2019 国家自然科学基金 (61863024, 71761023), 甘肃省高等学校科研项目 (2018C-11, 2018A-22), 甘肃省自然基金 (17JR5RA089, 18JR3RA130) 资助 Supported by National Natural Science Foundation of China (61863024, 71761023), Gansu Provincial Higher Education Research Project Funding (2018C-11, 2018A-22), and Natural Science Foundation of Gansu Provinaial of China (17JR5RA089, 18JR3RA130) 本文责任编委 阳春华2) Recommended by Associate Editor YANG Chun-Hua 1. 甘肃省高原交通信息工程及控制重点实验室, 兰州 7300702. 上海交通大学电子信息与电气工程学院, 上海 200240 3. 兰州交通大学交通运输学院, 兰州 730070 1. Gansu Provincial Key Laboratory of Traffic Information Engineering and Control, Lanzhou 730070 2. School of Electronic Information and Electrical Engineering, Shanghai Jiaotong University, Shanghai 200240 3. School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070
-
表 1 计算量对比结果
Table 1 Comparison of calculation results
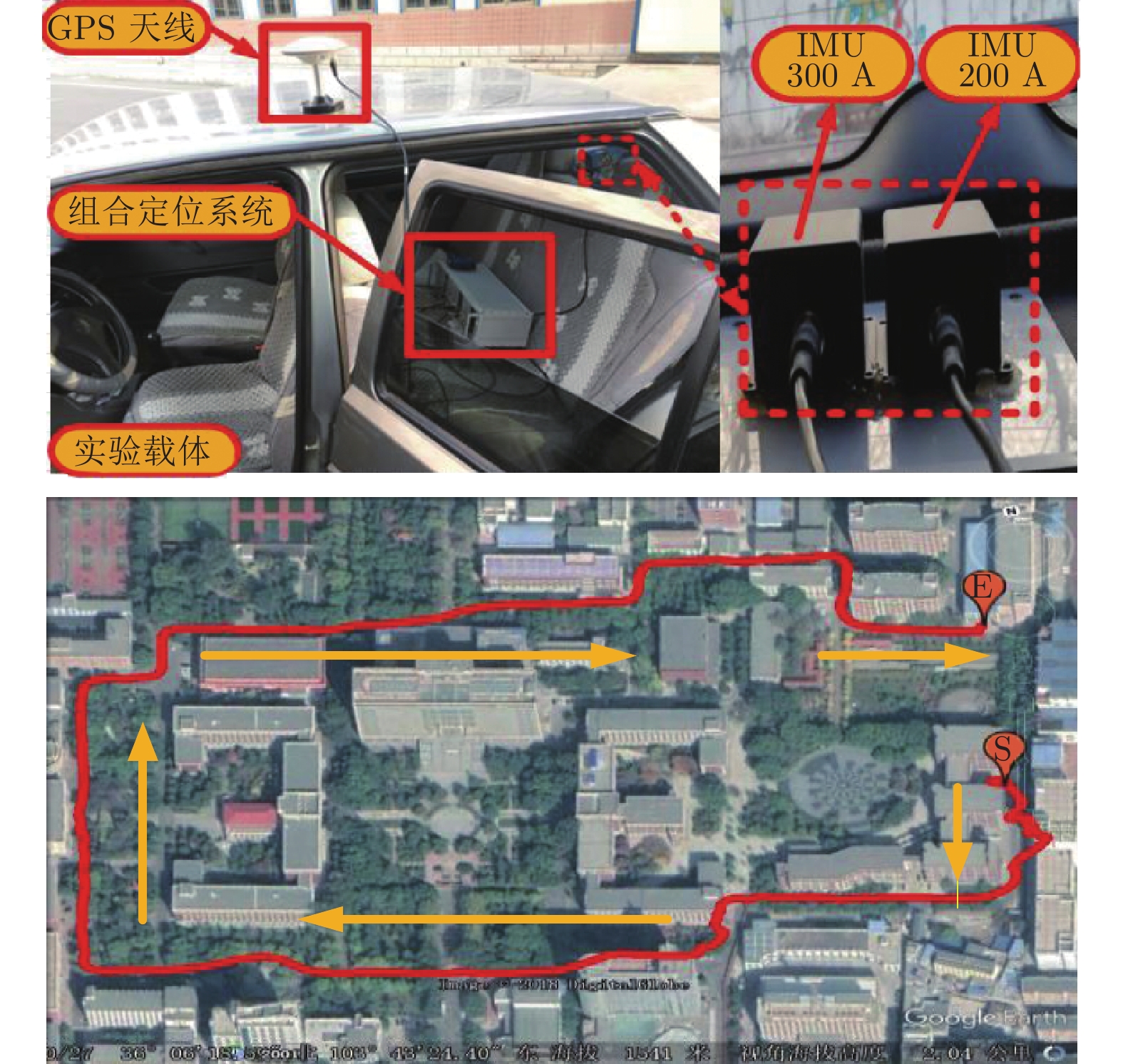
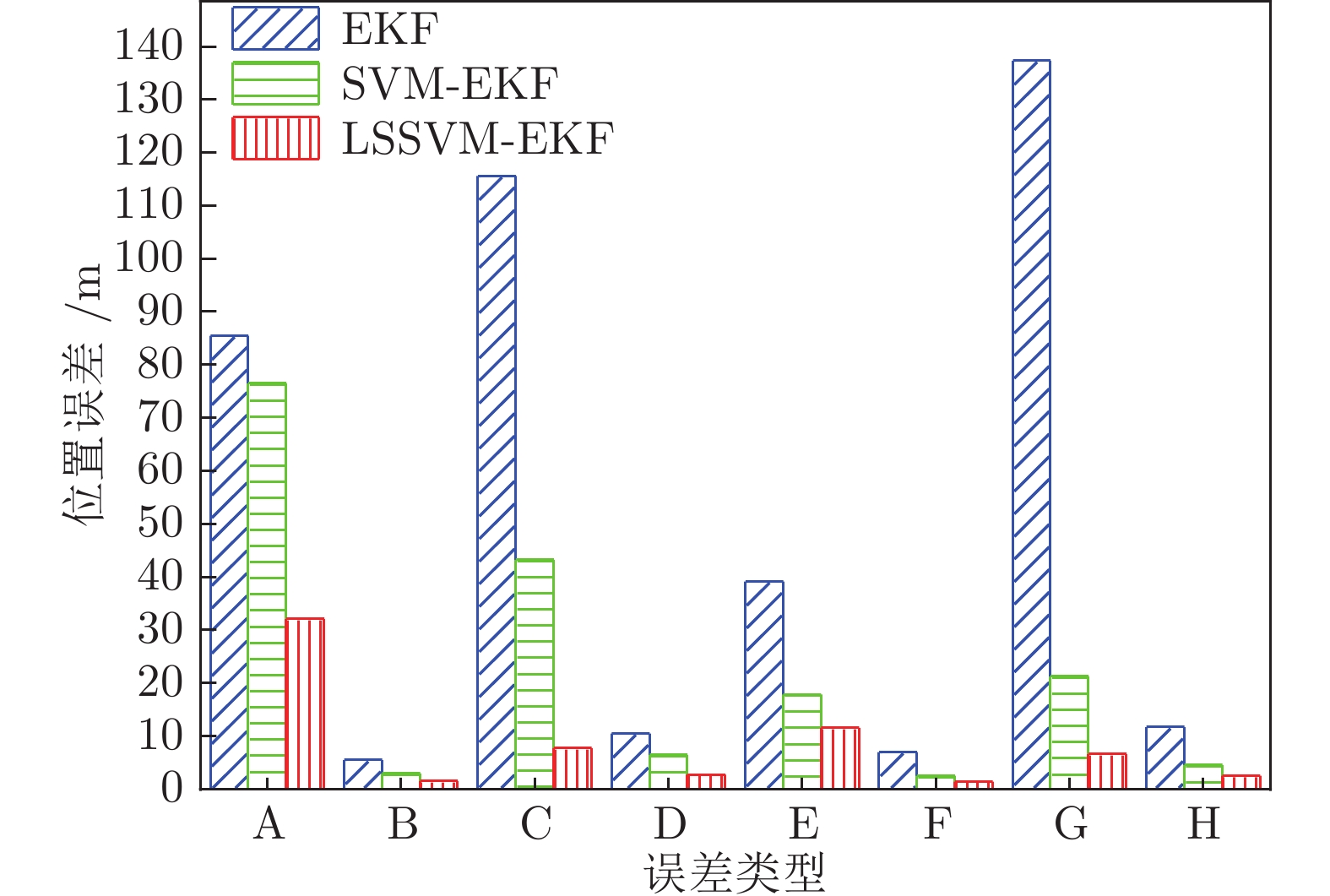
算法名称 绝对误差 (%) 具体运行时间 (s) NN 3.35 10.6 SVM 5.83 7.2 LSSVM 3.58 3.5 表 2 车载定位测量硬件主要参数
Table 2 Main parameters of vehicle positioning measurement hardware
性能指标 参数 IMU更新率 30 (Hz) 陀螺仪分辨率 0.007 (°/s) 陀螺仪零偏稳定性 0.007 (25 ℃, 1δ) (°/s) 陀螺仪随机游走 2.4 (25 ℃, 1δ) (°/ √Hz) 加速度计分辨率 0.33 (mg) 加速度计零偏稳定性 0.2 (25 ℃, 1δ) (mg) 加速度计随机游走 0.2 (25 ℃, 1δ) (m/s√Hz) 卫星板卡更新率 10 (Hz) 卫星单点定位精度 H: 3.0; V: 5.0 (m) 卫星测速精度 0.03 (m/s) 表 3 车载实验速度误差的分析
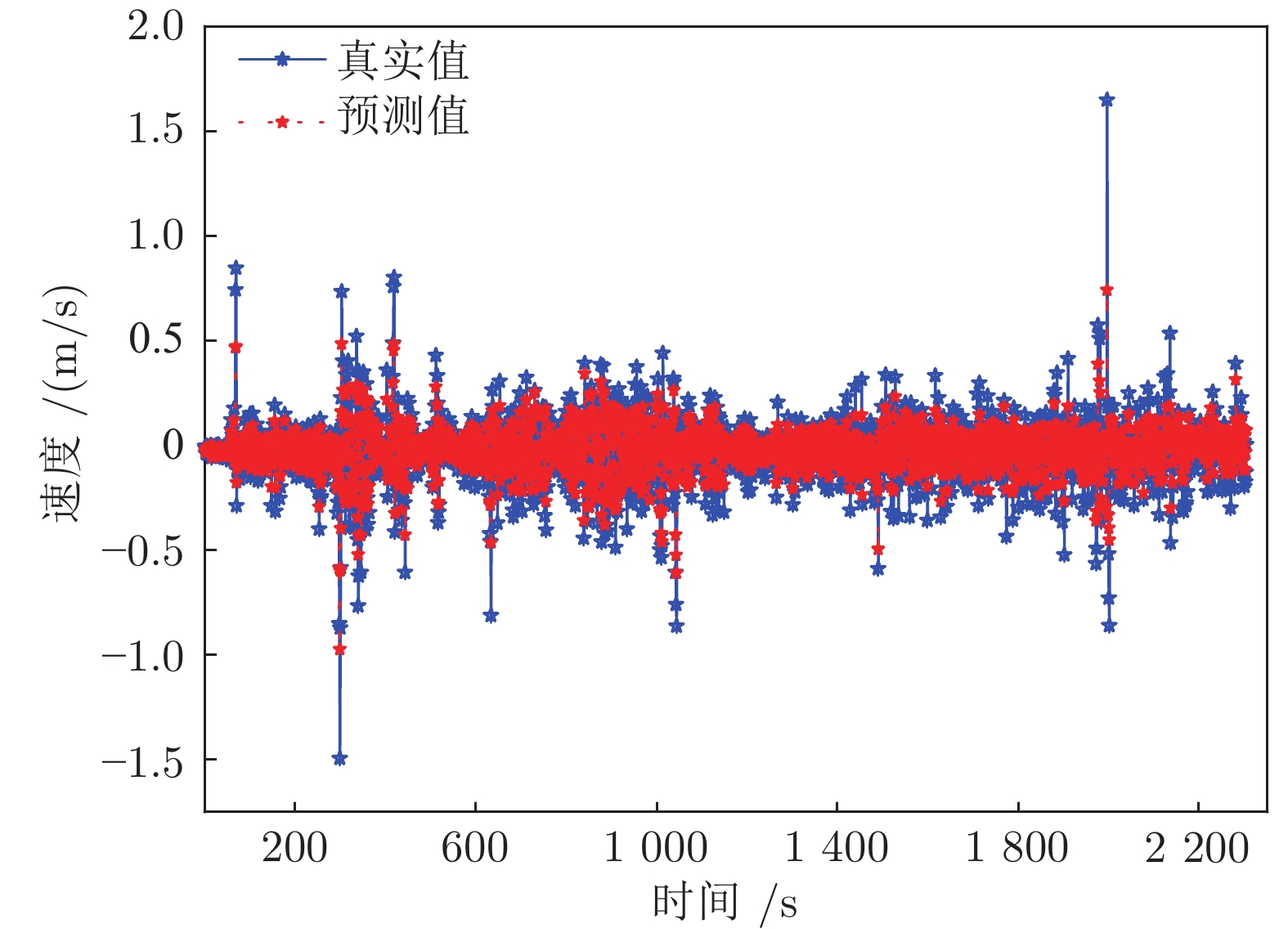
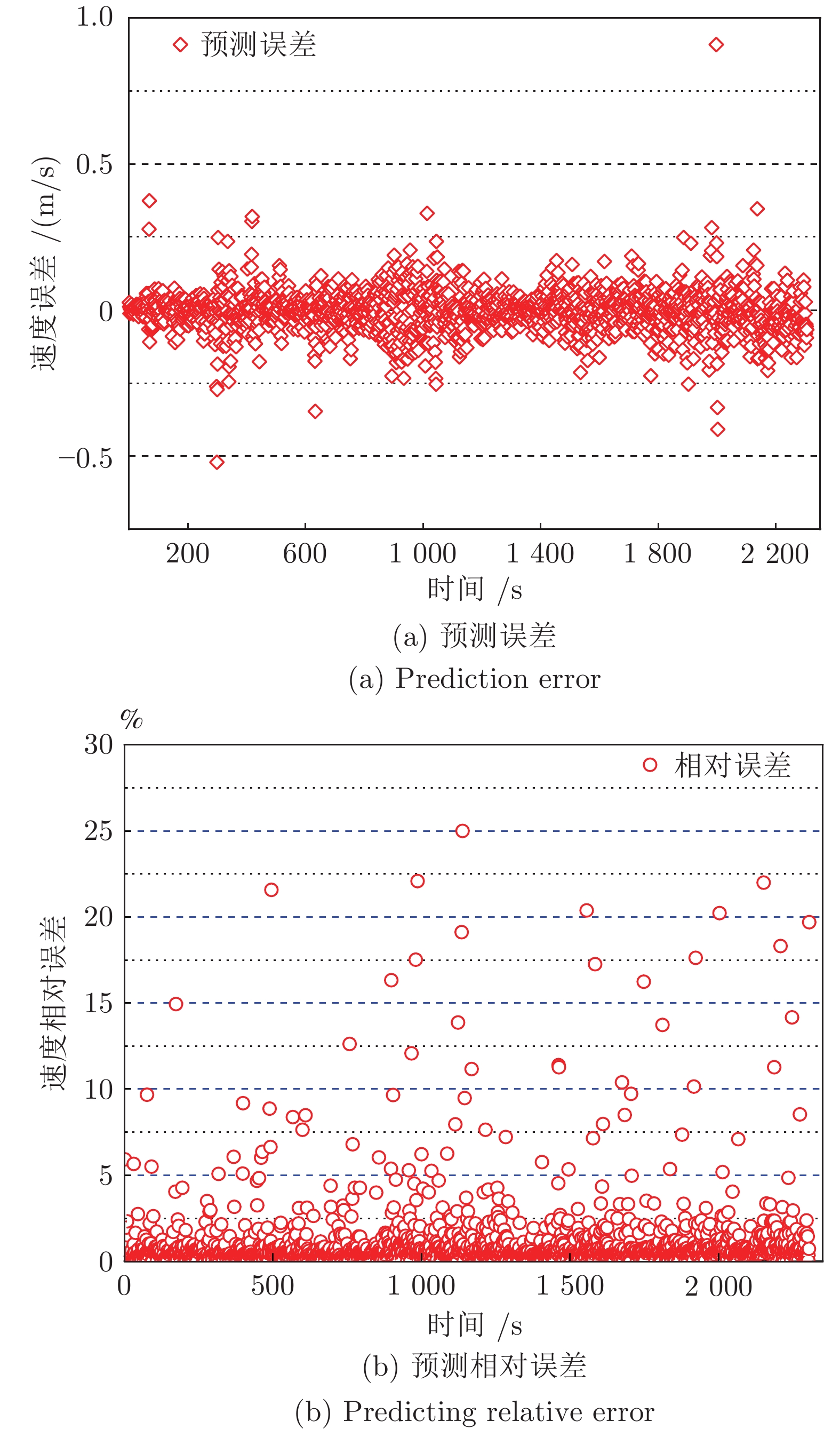
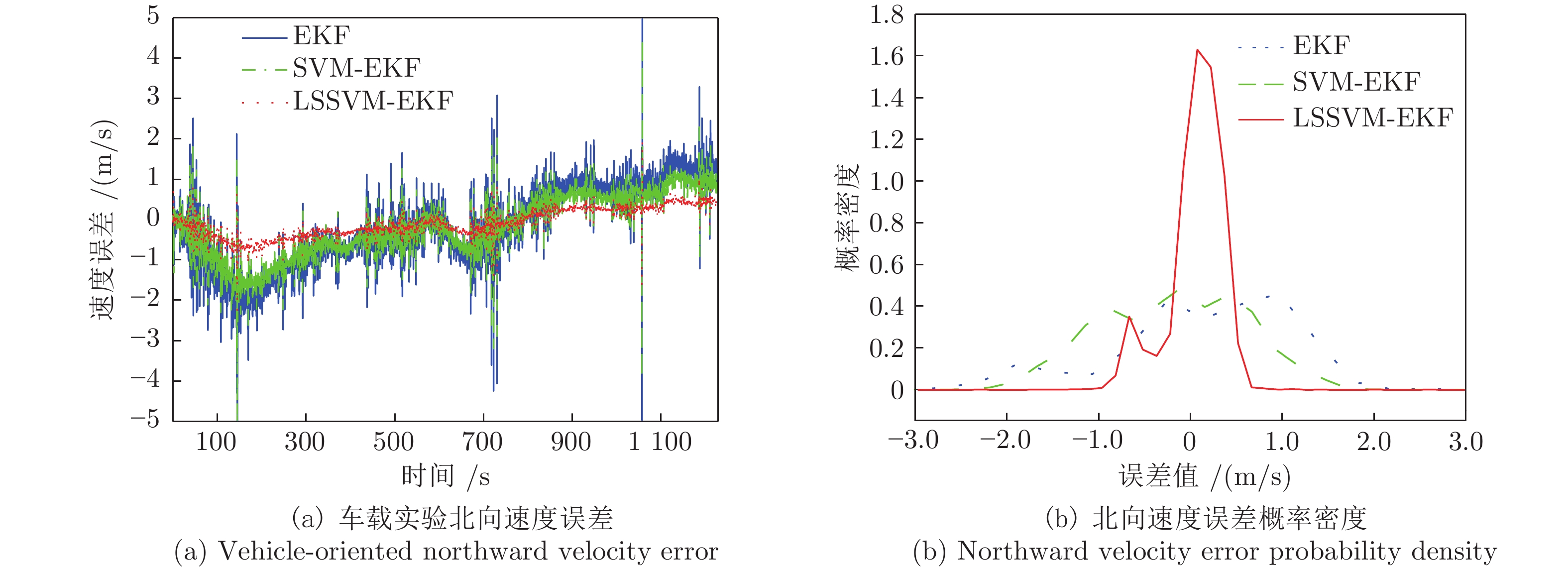
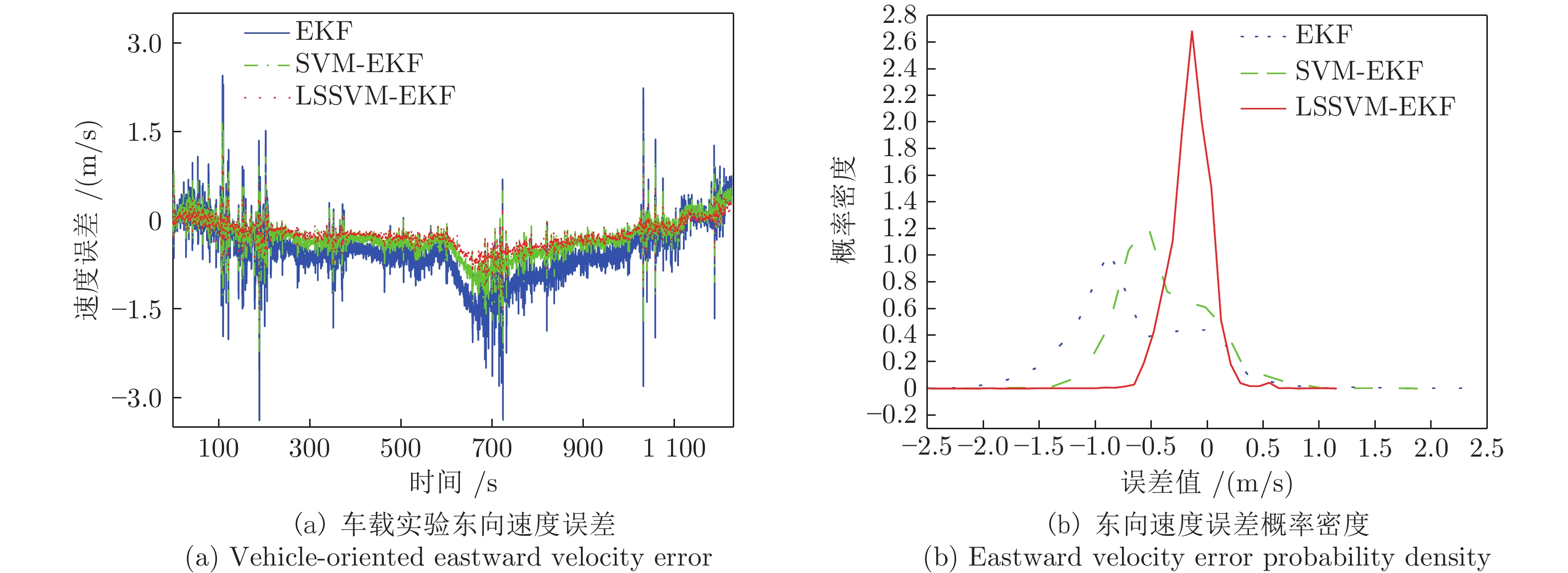
Table 3 Analysis of the speed error in vehicle test
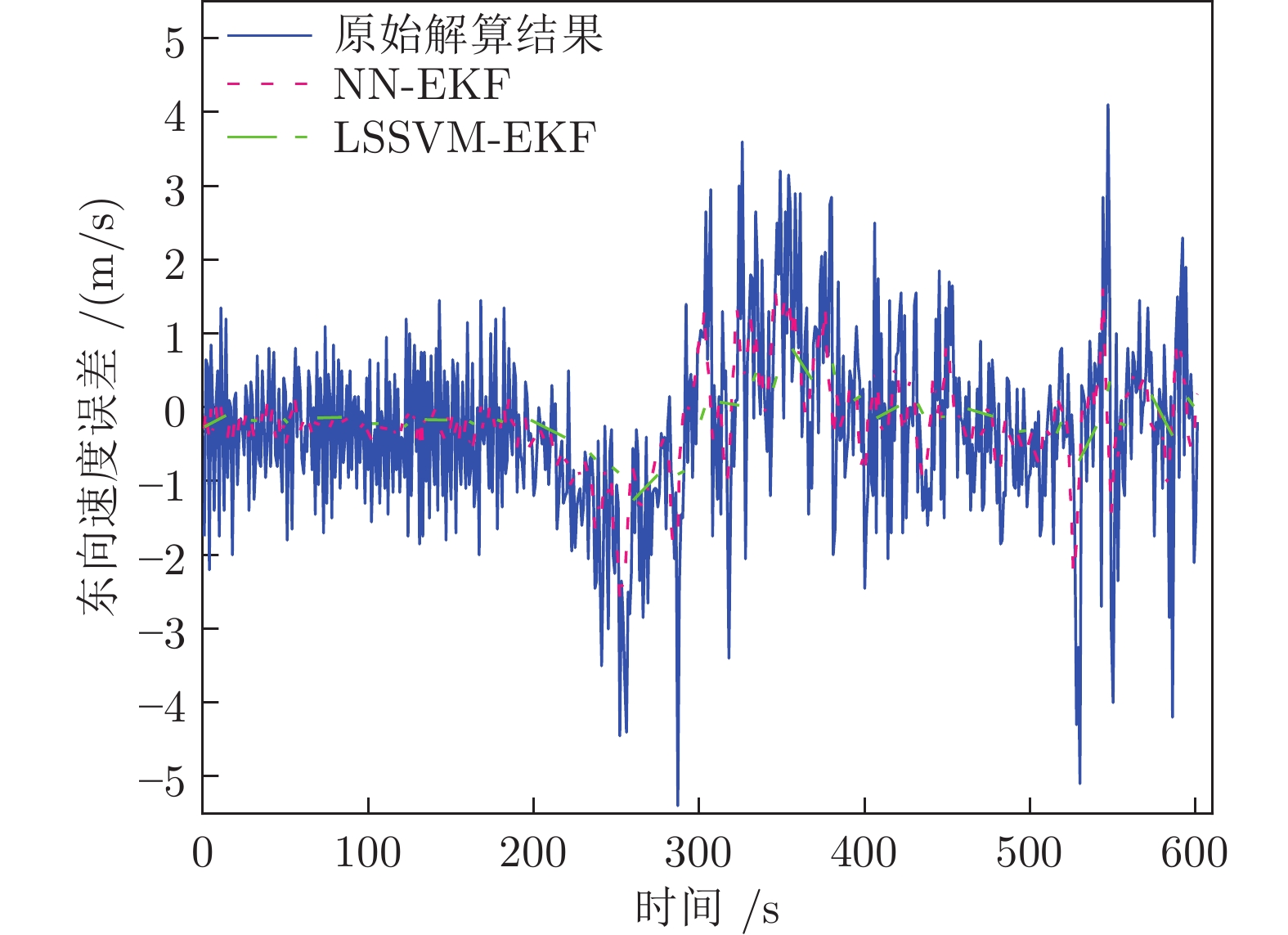
误差类型 算法 EKF SVM-EKF LSSVM-EKF 东向速度误差最大值) 2.44991596 1.64263965 1.08354018 东向速度误差均值 −0.51657986 −0.29959351 −0.21635647 东向速度平均绝对误差 0.57636153 0.35360989 0.23635647 东向速度误差均方差 0.46827009 0.17819068 0.10034921 北向速度误差最大值 5.95754509 4.48745292 1.98934116 北向速度误差均值 −0.17019196 −0.18793186 −0.08884883 北向速度平均绝对误差 0.81400385 0.65518412 0.30342385 北向速度误差均方差 0.92862895 0.59494707 0.12433562 表 4 车载实验位置误差的分析
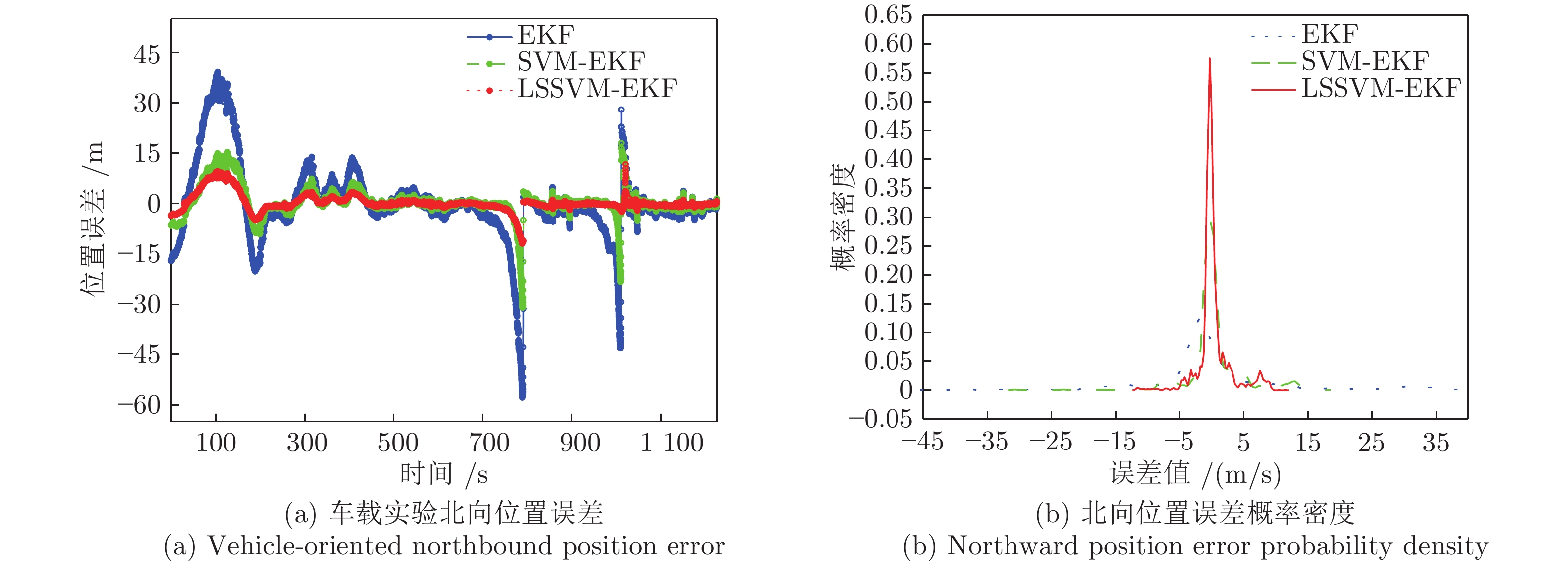
Table 4 Analysis of the position error in vehicle test
误差类型 算法 EKF SVM-EKF LSSVM-EKF 东向位置平均绝对误差 5.51618956 2.98874558 1.56598758 东向位置误差均方差 115.59446073 43.27129604 7.76993031 北向位置平均绝对误差 7.02954699 2.58372839 1.47242455 北向位置误差均方差 137.35228157 21.28974173 6.65581029 表 5 卫星失锁情况下位置误差的分析
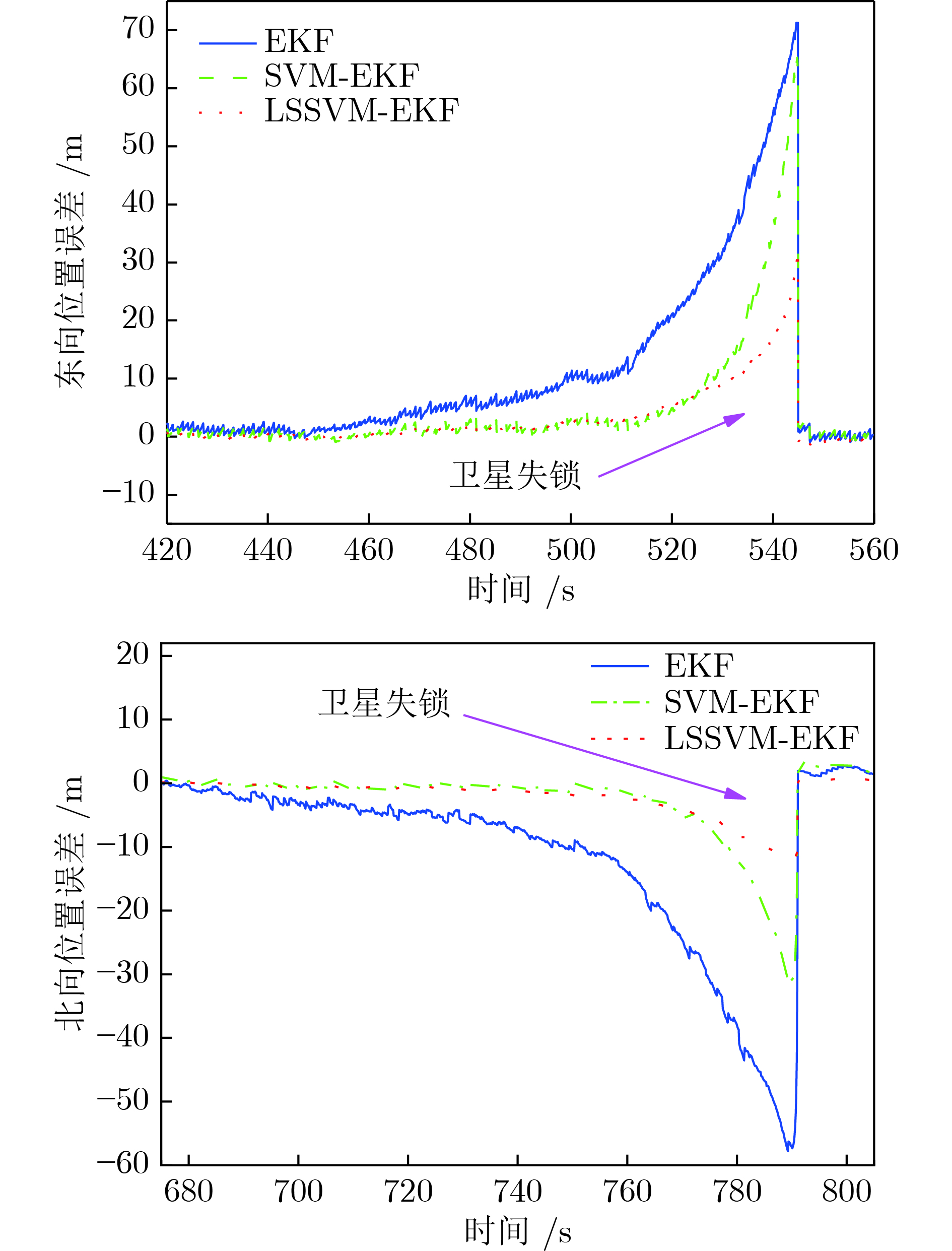
Table 5 Analysis of position error in case of satellite losing lock
误差类型 算法 EKF SVM-EKF LSSVM-EKF 东向速度误差最大值 71.277860 65.305870 32.099340 东向位置误差标准差 15.482577 10.476818 5.175138 北向位置误差最大值 57.812430 31.018930 15.966400 北向位置误差标准差 14.494762 6.471339 3.008621 表 6 列车北向位置误差对比
Table 6 Comparison of train northward position error
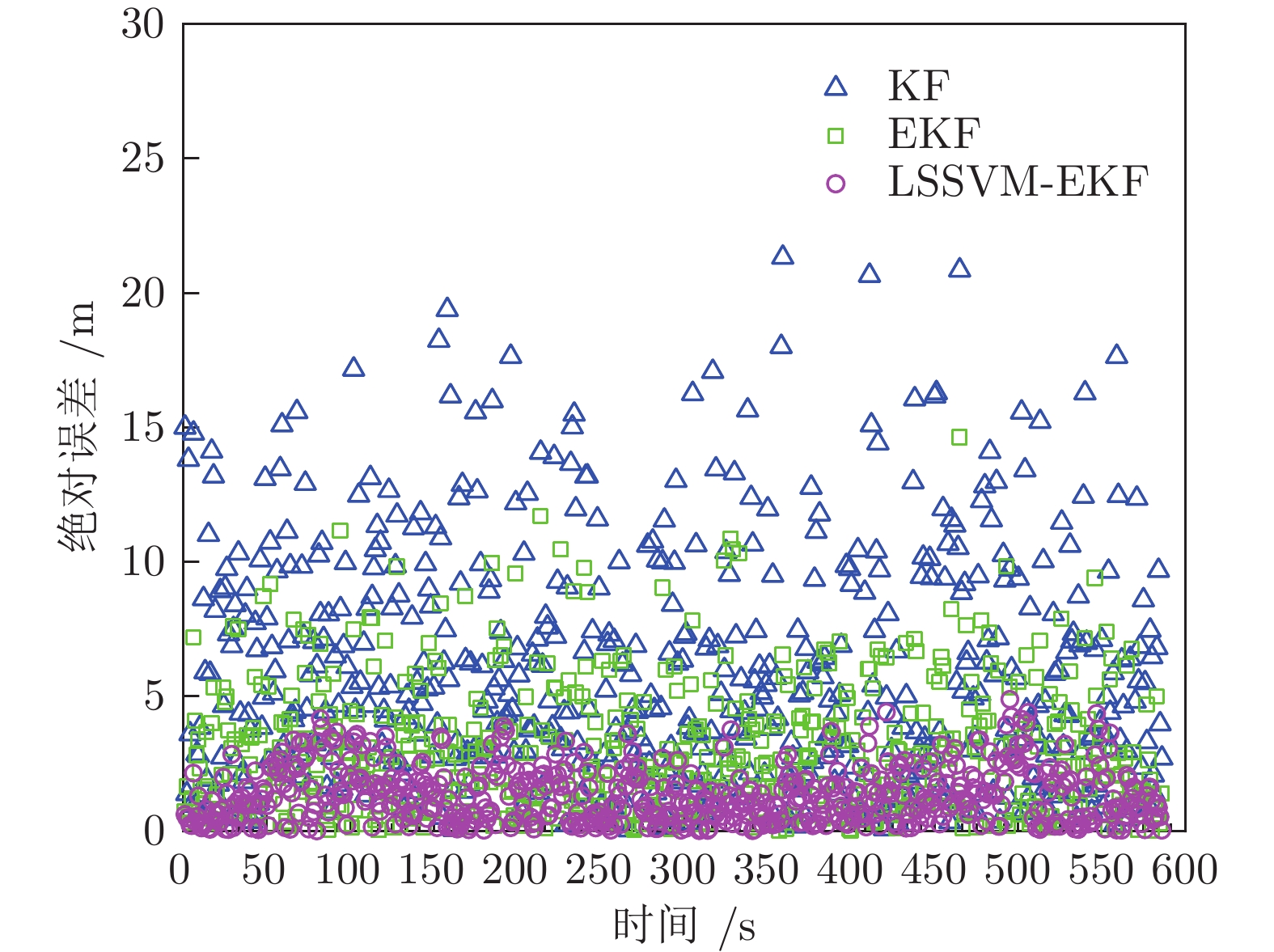
算法名称 北向位置误差标准差 KF 7.303605 EKF 3.888531 LSSVM-EKF 1.682587 -
[1] 王勋, 左启耀, 洪诗聘, 陈亮, 杨晓昆. 一种基于卡尔曼滤波的定位解算性能评估新方法. 导航定位与授时, 2018, 5(5): 73−821 Wang Xun, Zuo Qi-Yao, Hong Shi-Pin, Chen Liang, Yang Xiao-Kun. A noved evaluation method of positioning resolution performance based on Kalman filtering. Navigation and Timing, 2018, 5(5): 73−82 [2] 黄伟杰, 张国山. 基于快速不变卡尔曼滤波的视觉惯性里程计. 控制与决策, 2018. DOI: 10.13195/j. kzyjc. 2018. 0239Huang Wei-Jie, Zhang Guo-Shan. Visual-inertial odometer based on fast invariant Kalman filter. Control and Decision, 2018. DOI: 10.13195/j. kzyjc. 2018. 0239 [3] 燕必希, 朱立夫, 董明利, 孙鹏, 王君. 卡尔曼滤波单目相机运动目标定位研究. 仪器仪表学报, 2018, 39(8): 220−2293 Yan Bi-Xi, Zhu Li-Fu, Dong Ming-Li, Sun Peng, Wang Jun. Research on Kalman filtering in moving target loction with monocular camera. Chinese Journal of Scientific Instrument, 2018, 39(8): 220−229 [4] Kalman, R E, Bucy, R S. New results in linear filtering and prediction Theory. Journal of Basic Engineering ASME Transaction series D, 1960, 83. [5] 管庆林, 樊春明, 朱正平, 彭飞. 单点定位中一种载波相位平滑伪距方法. 测绘科学, 2019, 44(2): 116−1215 Guan Qing-Lin, Fan Chun-Ming, Zhu Zheng-Ping, Peng Fei. A carrier phase smoothing pseudorange method in single point positioning. Surveying Science, 2019, 44(2): 116−121 [6] 张悦, 袁莉芬, 何怡刚, 吕密. 基于量子粒子群优化容积卡尔曼滤波的LANDMARC室内定位算法. 电子测量与仪器学报, 2018, 32(2): 72−796 Zhang Yue, Yuan Li-Fen, He Yi-Gang, Lv Mi. LANDMARC indoor positioning algorithm based on quantum particle swarm optimization volume Kalman filter. Journal of Electronic Measurement and Instrument, 2018, 32(2): 72−79 [7] 王鼎杰, 孟德利, 李朝阳, 董毅, 吴杰. 抗野值自适应卫星/微惯性组合导航方法. 仪器仪表学报, 2017, 38(12): 2952−29587 Wang Ding-Jie, Meng De-Li, Li Chao-Yang, Dong Yi, Wu Jie. Adaptively outlier-restrained GNSS/MEMS-INS integrated navigation method. Chinese Journal of Scientific Instrument, 2017, 38(12): 2952−2958 [8] 刘射德, 陈光武, 王迪, 徐琛. 一种基于GPS/DR/MM组合的列车定位方法研究. 铁道科学与工程学报, 2018, 15(2): 474−482 doi: 10.3969/j.issn.1672-7029.2018.02.0278 Liu She-De, Chen Guang-Wu, Wang Di, Xu Chen. Train integrated positioning method based on GPS/DR/MM. Journal of Railway Science and Engineering, 2018, 15(2): 474−482 doi: 10.3969/j.issn.1672-7029.2018.02.027 [9] Liu J, Cai B G, Wang J. A GNSS/trackmap cooperative train positioning method for satellite-based train control. In: Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC). Qingdao, China: IEEE, 2014. 2718−2724 [10] 衷路生, 李兵, 龚锦红, 张永贤, 祝振敏. 高速列车非线性模型的极大似然辨识. 自动化学报, 2014, 40(12): 2950−299410 Zhong Lu-Sheng, Li Bing, Gong Jin-Hong, Zhang Yong-Xian, Zhu Zhen-Min. Maximum likelihood identification of multiple point model for high-speed electriced multiple units. Acta Automatica Sinica, 2014, 40(12): 2950−2994 [11] 刘江, 蔡伯根, 唐涛, 王剑. 基于GPS与惯性测量单元的列车组合定位系统. 中国铁道科学, 2010, 31(1): 123−12911 Liu Jiang, Cai Bogen, Tang Tao, Wang Jian. Train integrated positioning system based on GPS and inertial measurement unit. China Railway Science, 2010, 31(1): 123−129 [12] 刘昊, 陈光武, 魏宗寿, 程鉴皓. 改进的最小二乘自适应滤波陀螺仪去噪方法. 仪器仪表学报, 2018, 39(4): 107−11412 Liu Hao, Chen Guang-Wu, Wei Zong-Shou, Cheng Jian-Wei. An improved least squares adaptive filtering gyroscope denoising method. Chinese Journal of Scientific Instrument, 2018, 39(4): 107−114 [13] 王迪, 陈光武, 杨厅. 一种快速高精度GPS组合定位方法研究. 铁道学报, 2017, 39(2): 67−73 doi: 10.3969/j.issn.1001-8360.2017.02.01013 Wang Di, Chen Guang-Wu, Yang Ting. Study on a fast and precise GPS integrated positioning method. Journal of the China Railway Society, 2017, 39(2): 67−73 doi: 10.3969/j.issn.1001-8360.2017.02.010 [14] 王迪, 陈光武, 刘射德, 杨扬. 基于GNSS双差定姿的区间列车轨道占用判别方法研究. 铁道学报, 2018, 40(11): 81−87 doi: 10.3969/j.issn.1001-8360.2018.11.01114 Wang Di, Chen Guang-Wu, Liu She-De, Yang Yang. Study on GNSS double difference attitude determination based train track occupancy discrimination method. Journal of the China Railway Society, 2018, 40(11): 81−87 doi: 10.3969/j.issn.1001-8360.2018.11.011 [15] 张敬堂, 董艳婷, 翟燕. 基于SVM的GPS/DR组合定位算法研究. 信息工程大学学报, 2010, 11(4): 443−447 doi: 10.3969/j.issn.1671-0673.2010.04.01415 Zhang Jing-Tang, Dong Yan-Ting, Zhai Yan. Study on GPS/DR integratde location method based on SVM. Journal of Information Engineering University, 2010, 11(4): 443−447 doi: 10.3969/j.issn.1671-0673.2010.04.014 [16] Caron F, Duflos E, Vanheeghe P. Introduction of contextual information in a multisensor EKF for autonomous land vehicle positioning. In: Proceedings of the 2005 IEEE Networking, Sensing and Control. Villeneuve d'Ascq, France: IEEE, 2005. 592−597 [17] 17 Yang Y, Chen G W, Wang J W, Li C D. Study on train combination location method based on grey neural network. Journal of Measurement Science and Instrumentation, 2019, 10(2): 143−149 [18] 衷路生, 梁爽, 龚锦红, 张永贤. 基于LS-SVM的高速列车广义非线性模型子空间辨识. 中国科技论文, 2015, 10(19): 2225−2231, 2241 doi: 10.3969/j.issn.2095-2783.2015.19.00218 Zhong Lu-Sheng, Liang Shuang, Gong Jin-Hong, Zhang Yong-Xian. Subspace identification of generalized nonlinear model for high-speed, using least squares support vector machine. China Science Paper, 2015, 10(19): 2225−2231, 2241 doi: 10.3969/j.issn.2095-2783.2015.19.002 [19] 阎威武, 邵惠鹤. 支持向量机和最小二乘支持向量机的比较及应用研究. 控制与决策, 2003, 18(3): 358−360 doi: 10.3321/j.issn:1001-0920.2003.03.02519 Yan Wei-Wu, Shao Hui-He. Application of support rector machines and least squares support vector machines to heart disease diagnoses. Control and Decision, 2003, 18(3): 358−360 doi: 10.3321/j.issn:1001-0920.2003.03.025 [20] 徐爱功, 蔡赣飞, 潘峰, 隋心, 郝雨时, 刘韬. RBF神经网络辅助的UWB/INS组合导航算法. 导航定位学报, 2018, 6(3): 41−46 doi: 10.3969/j.issn.2095-4999.2018.03.00820 Xu Ai-Gong, Cai Gan-Fei, Pan Feng, Sui Xin, Hao Yu-Shi, Liu Wei. RBF neural network aided UWB/INS integrated navigation algorithm. Journal of Nautical Navigation, 2018, 6(3): 41−46 doi: 10.3969/j.issn.2095-4999.2018.03.008 [21] Jiang Z Q, Liu C H, Zhang G, Wang Y P, Huang C K, Liang J Y. GPS/INS integrated navigation based on ukf and simulated annealing optimized SVM. In: Proceedings of the 78th IEEE Vehicular Technology Conference (VTC Fall), Las Vegas, NV, USA: IEEE, 2013. 1−5 [22] 22 Rafael T M, Carlos C C, Javier T M. A multiple-model particle filter fusion algorithm for GNSS/DR slide error detection and compensation. Applied Sciences, 2018, 8(3): 445-1−445-9 [23] 23 Wang S S. A BLE-based pedestrian navigation system for car searching in indoor parking garages. Sensors (Basel, Switzerland), 2018, 18(5): 1442-1−1442-18 [24] 24 Song X, Li X, Tang W C, Zhang W G. RFID/In-vehicle sensors-integrated vehicle positioning strategy utilising LSSVM and federated UKF in a tunnel. Journal of Navigation, 2016, 69(4): 845−868 doi: 10.1017/S0373463315000946 [25] 25 Chen X Y, Xu Y, Li Q H, Tang J, Sheng C. Improving ultrasonic-based seamless navigation for indoor mobile robots utilizing EKF and LS-SVM. Measurement, 2016, 92: 243−251 doi: 10.1016/j.measurement.2016.06.025 [26] Shao Y H, Li C N, Huang L W, Wang Z, Deng N Y, Xu Y. Joint sample and feature selection via sparse primal and dual LSSVM. Knowledge-Based Systems, 2019. [27] 27 Xue X H, Xiao M. Deformation evaluation on surrounding rocks of underground caverns based on PSO-LSSVM. Tunnelling and Underground Space Technology, 2017, 69(Oct.): 171−181 -





 下载:
下载: