Learning-based Optimization of Active Distribution System Dispatch in Industrial Park Considering the Peak Operation Demand of Power Grid
-
摘要: 本文针对含光伏(Photovoltaic, PV)、全钒液流电池(Vanadium redox battery, VRB)储能装置与多类型柔性负荷的工业园区主动配电系统, 研究在考虑源荷随机性情况下该系统的动态经济调度问题. 首先, 将PV出力、多类型负荷需求和电网调峰需求的随机动态变化近似描述为连续马尔科夫过程, 并根据系统内VRB的充放电特性对储能系统进行建模; 然后, 以各决策时刻下PV出力、负荷需求、调峰需求以及储能荷电状态(State of charge, SOC)的离散等级为状态, 以储能充放电及多类型柔性负荷调整方案为行动, 在系统功率平衡等相关约束下, 以应对电网调峰需求和提高系统经济运行水平为目标, 将工业园区主动配电网系统动态经济调度优化问题建立成随机动态规划模型; 最后, 引入强化学习方法进行策略求解. 算例仿真结果表明所得策略可有效提高系统经济运行效益, 并在一定程度上满足电网调峰需求.Abstract: The dynamic economic dispatch problem of the active distribution system combined of photovoltaic (PV), vanadium redox battery (VRB) energy storage device and multiple types of flexible load in industrial parks with uncertain renewable sources and demands is focused in this paper. First, the random dynamic variations of photovoltaic, multiple loads demand and peak operation demand are described as continuous Markov processes, and the VRB energy storage system is modeled considering its charge-discharge characteristics. Then, decision epoch, outputs level of photovoltaic, multiple load demands level, peak operation demands level and state of charge (SOC) level of VRB are defined as states of the system, the adjustment level of VRB and multiple types of flexible load are set as the actions. Based on relevant restrictions including the power balance constraint, the dynamic optimal dispatch problem for the system was described as a stochastic dynamic programming model, which aims to meet the peak operation demand of power grid and realize economic operation of the system. Finally, a reinforcement learning method is adopted to obtain the optimal policy. Simulation results show that the operational efficiency is significantly enhanced and the peak operation demand of power grid is partly satisfied by the optimal policy.1) 收稿日期 2019-02-01 录用日期 2019-06-02 Manuscript received February 1, 2019; accepted June 2, 2019 国家重点研发计划项目 (2017YFB0902600), 国家电网公司科技项目(SGJS0000DKJS1700840) 资助 Supported by National Key Research and Development Program of China (2017YFB0902600) and the State Grid Corporation of China Project (SGJS0000DKJS1700840) 本文责任编委 诸兵 Recommended by Associate Editor ZHU Bing 1. 合肥工业大学 电气与自动化工程学院 合肥 230009 2. 国网江苏省电力公司电力科学研究院 南京 211103 3. 中国电力科学研究院 (南京) 南京 210003 4. 中国电力科学研究院(北京) 北京 100192 1. Electrical Engineering and Automation Hefei University of Technology, Hefei 230009 2. Electric Power Research Institute2) of State Grid Jiangsu Electric Power Company, Nanjing 211103 3. China Electric Power Research Institute (Nanjing), Nanjing 210003 4. Editorial China Electric Power Research Institute (Beijing), Beijing 100192
-
图 1 工业园区主动配电系统结构模型
Fig. 1 Structure model of active distribution system in industrial park
图 4 工业园区内PV出力与总负荷需求预测曲线
Fig. 4 Prediction curves of PV and loads demand in industrial parks
图 5 工业园区内各类柔性负荷典型日曲线
Fig. 5 Prediction curves of multi-type flexible loads in industrial parks
图 6 不同学习优化算法下的系统总学习优化过程曲线
Fig. 6 The optimal curve of the system under different learning optimization algorithm
图 7 系统学习优化过程的策略性能曲线
Fig. 7 The strategic performance curve of the system learning optimization process
图 11 不同初始荷电状态下各时段SOC变化情况
Fig. 11 Changing process of SOC under different initial values
图 12 学习优化前后系统负荷曲线
Fig. 12 The curves of load before and after learning optimization in the system
图 13 学习优化后各时段典型柔性负荷调整量
Fig. 13 Adjustment of multi-type flexible loads after optimization
图 14 不同调度模式下的调峰效果比较图
Fig. 14 Comparison effect of peak operation under different dispatching modes
图 15 不同调度模式下负荷优化结果比较图
Fig. 15 Comparison diagram of load optimal results under different dispatching modes
图 16 不同储能容量占比下的各项代价比较图
Fig. 16 Comparison of costs under different proportion of energy storage capacity
图 17 不同柔性负荷占比下的各项代价比较图
Fig. 17 Comparison of costs under different proportion of flexible load
图 18 不同方案下的调峰需求未完成量比较图
Fig. 18 Unfinished amount of peak operation demand under different projects
图 20 优化策略下不同模式的调峰需求未完成量比较图
Fig. 20 Unfinished amount of peak operation demand under different modes in optimal policy
表 1 部分变量符号
Table 1 Partial variable symbols
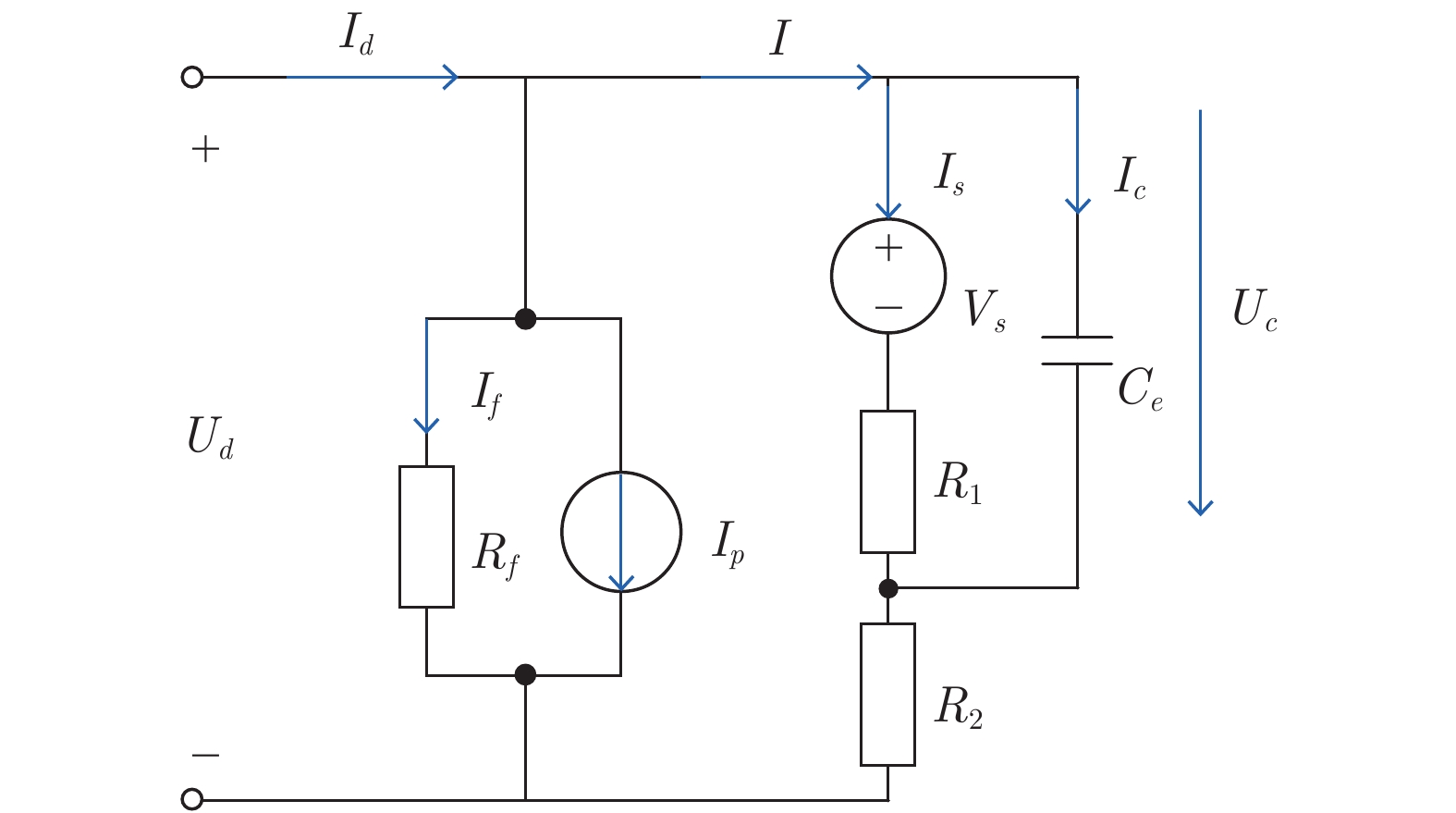
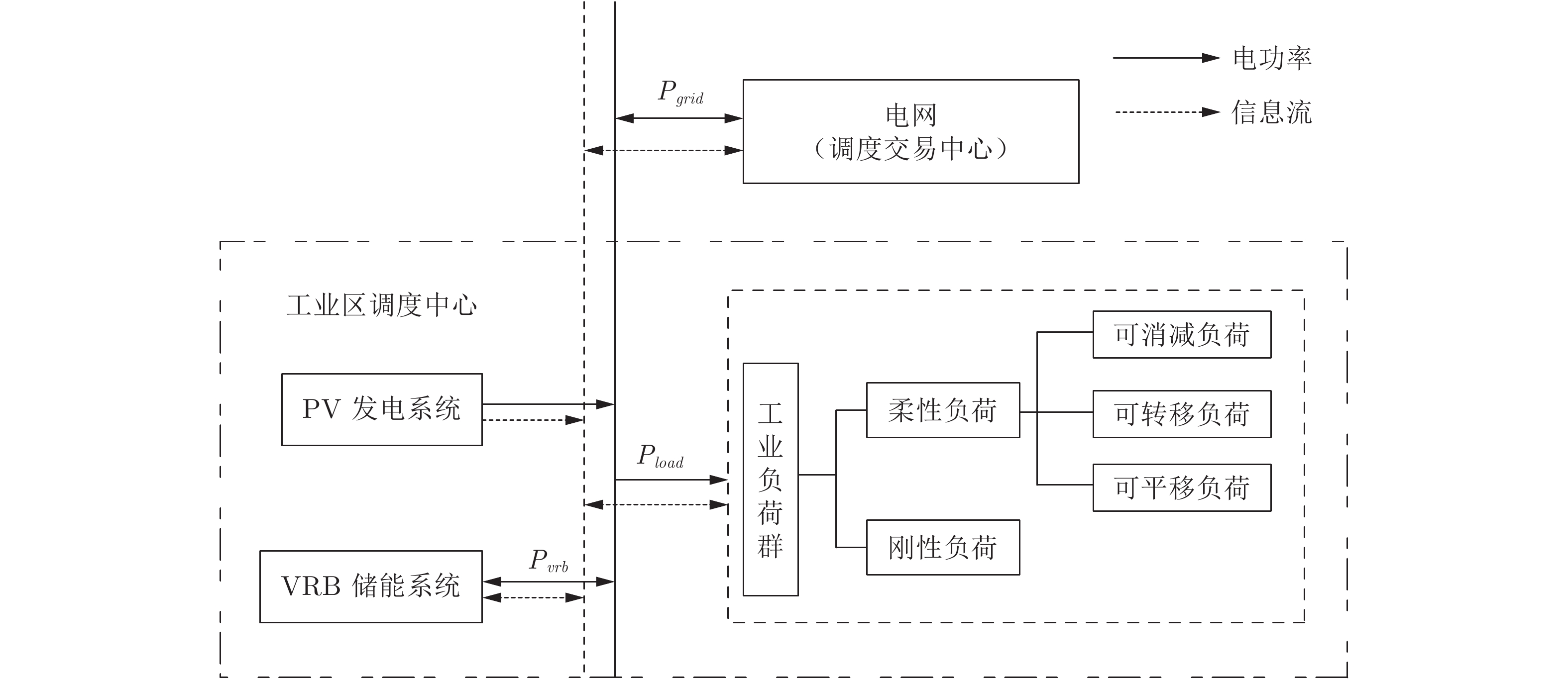
参数/变量 符号 $t$时刻与电网交互功率 $P_{grid}^t$ $t$时刻光伏出力 $P_{pv}^t$ $t$时刻刚性负荷功率 $P_{rl}^t$ $t$时刻可削减负荷功率 $P_{cu}^t$ $t$时刻可转移负荷功率 $P_{sh}^t$ $t$时刻电网调峰需求 $P_{peak}^t$ $t$时刻电网调峰需求未完成量 $P_{unf}^t$ $t$时刻储能装置充放电功率 $P_{vrb}^t$ $t$时刻储能装置功率上/下限 ${P_{vrbmax}^t/P_{vrbmin}^t}$ 调度周期始/末时刻 ${t_{beg}}/{t_{end}}$ 储能装置充/放电电流 ${I_d^{charge}/I_d^{discharge}}$ 储能装置充/放电电压 ${U_d^{charge}/U_d^{discharge}}$ 储能装置端电压上/下限 ${U_d^{max}U_d^{min}}$ 储能装置额定电流 ${I_d^{max}}$ 储能装置涓流充放电电流 ${I_d^{min}}$ 储能装置SOC上/下限 ${SOC_{vrb}^{max}/SOC_{vrb}^{min}}$ 始末时刻荷电状态期望值 ${{C_{con}}}$ 
下载: 导出CSV
表 2 VRB模型参数设置表
Table 2 Parameters of VRB
VRB本体参数名称 数值 VRB模型参数名称 数值 能量 30 kWh $R_1$ 0.045 Ω 容量 630 Ah $R_2$ 0.03 Ω 额定功率 5 kW $R_f$ 13.889 Ω 端电压 42 ~ 60 V $C_e$ 0.154 F 额定电流 105 A $I_p$ 5 A
下载: 导出CSV
表 3 学习优化前后系统总负荷特征
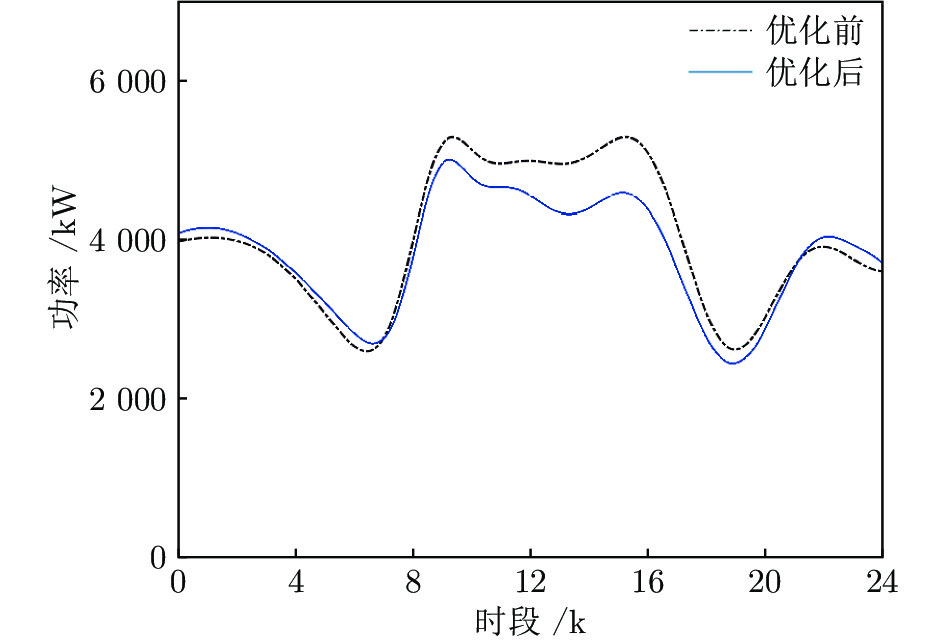
Table 3 The characteristic of load before and after learning optimization in the system
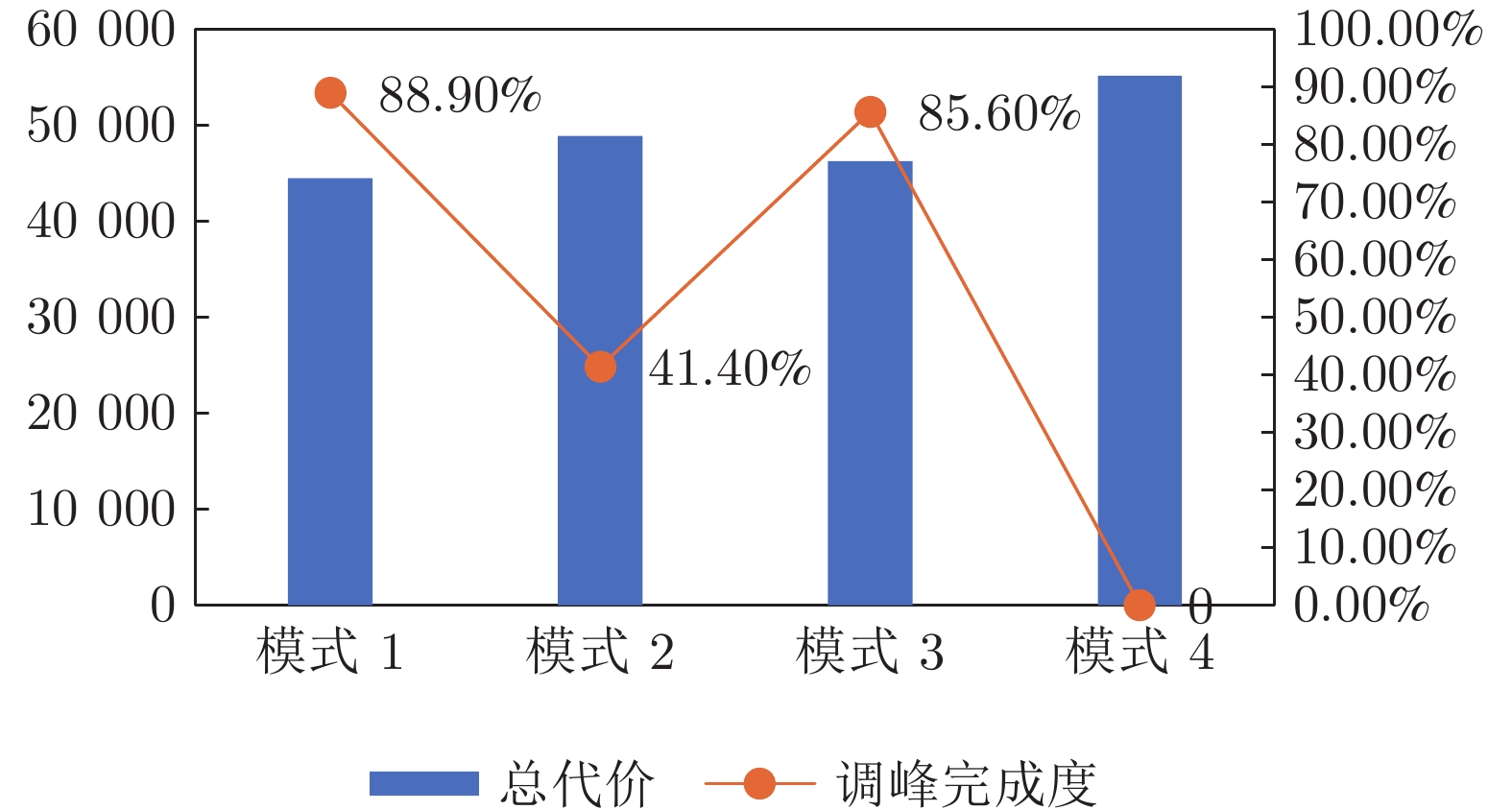
类型 峰值(kW) 谷值(kW) 峰谷差(kW) 优化前 5 289 2 600 2 689 优化后 4 995 2 460 2 535
下载: 导出CSV
表 4 不同调度模式下的相关指标
Table 4 Related indexes under different dispatching modes
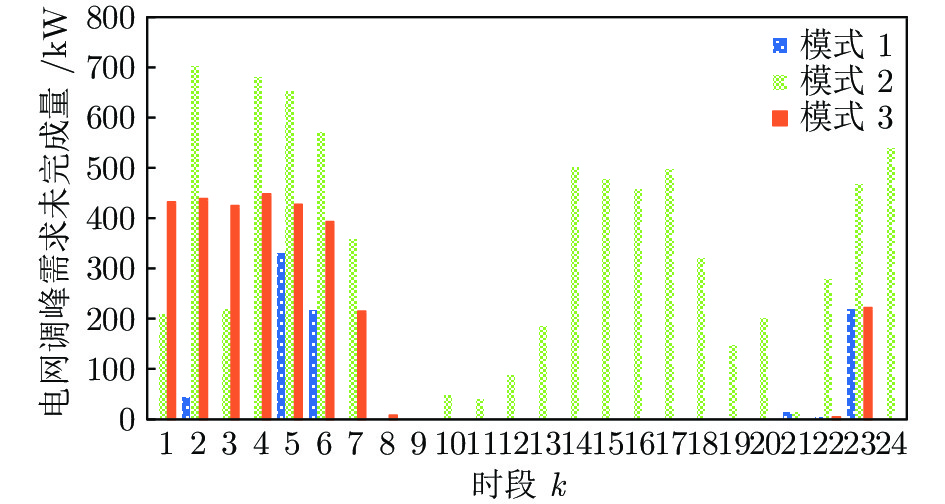
总体代价(元) 调峰代价(元) 购电代价(元) VRB充放代价(元) 柔性负荷补偿金额(元/d) 模式1 44 500 1 421 37 910 342 4 743 模式2 48 870 7 483 40 997 362 0 模式3 46 260 1 845 37 986 0 6 432 模式4 55 160 12 780 42 380 0 0
下载: 导出CSV
表 5 不同方案下的相关指标
Table 5 Related indexes under different projects
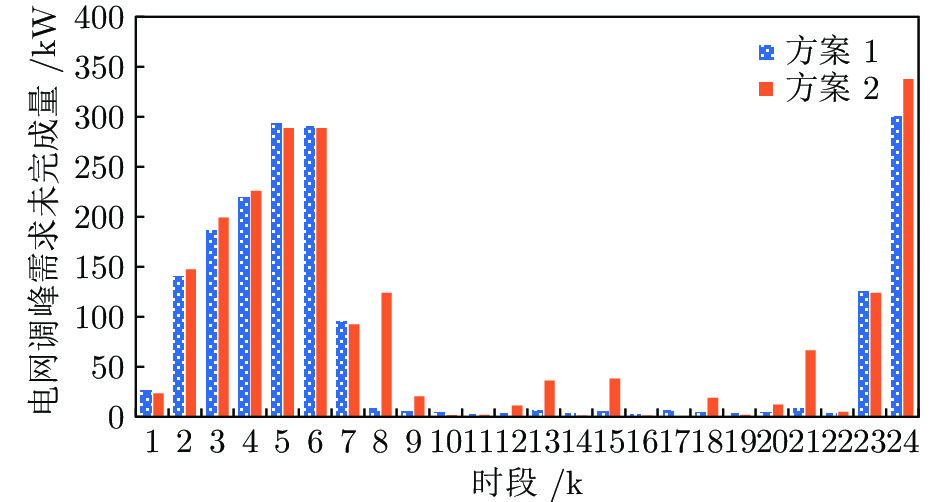
总体代价(元) 调峰代价(元) 调峰完成度 方案1 44 500 1421 88.9% 方案2 45 120 1772.9 86.1%
下载: 导出CSV
表 6 优化策略下部分状态行动
Table 6 Partial state-action pairs under optimal policy
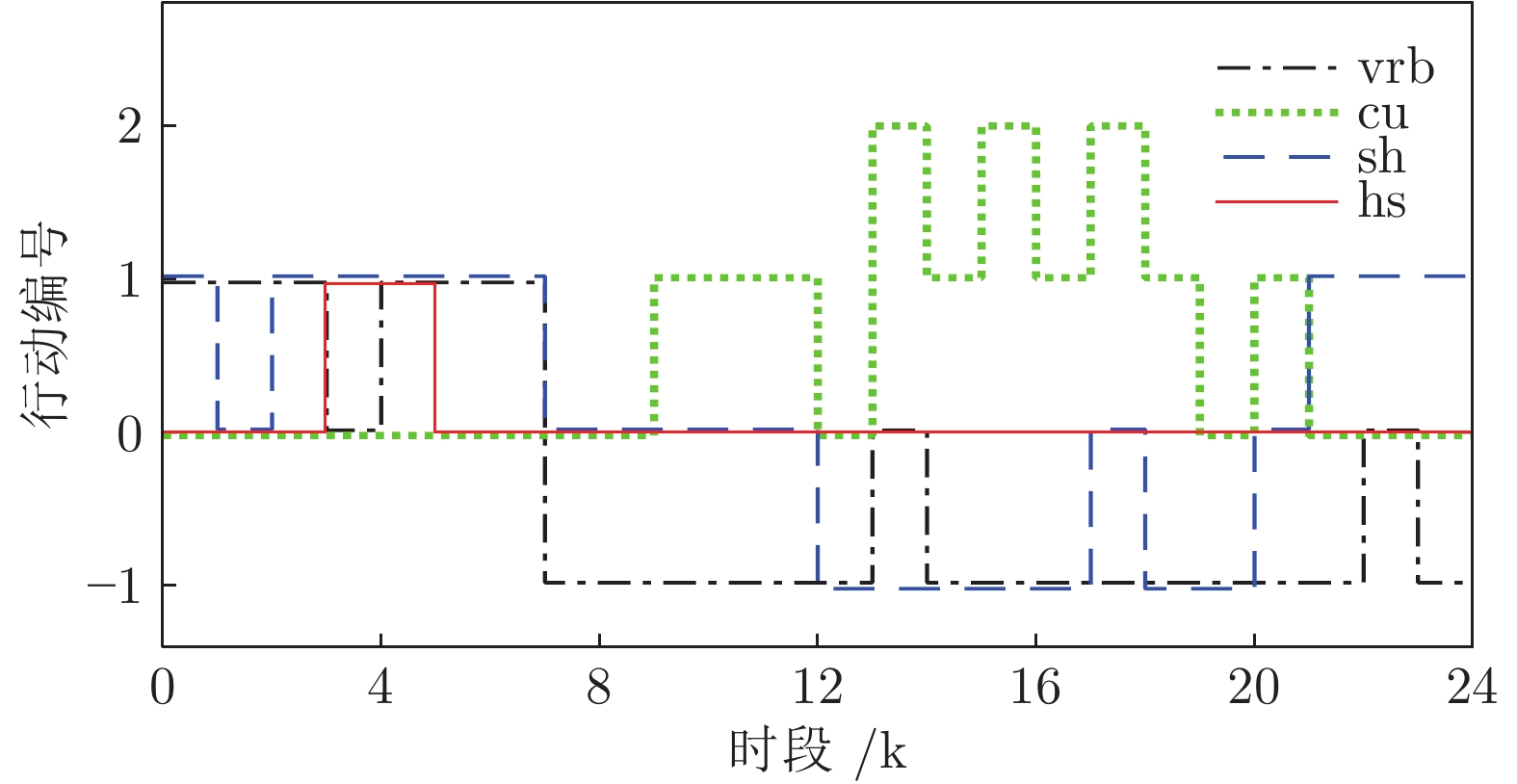
状态编号 407 8832 18549 24075 25533 33491 38955 42845 决策时刻 0时 4时 9时 12时 13时 17时 20时 22时 各类负荷状态 (1, 1, 0, 2) (1, 1, 2, 1) (1, 1, 1, 0) (2, 1, 1, 0) (2, 1, 1, 0) (0, 1, 2, 0) (1, 0, 1, 0) (1, 0, 2, 0) 储能装置动作 充电 充电 放电 放电 闲置 放电 放电 闲置 柔性负荷动作 (0, 1, 0) (0, 1, 1) (1, 0, 0) (0, −1, 0) (2, −1, 0) (2, 0, 0) (1, 0, 0) (0, 1, 0)
下载: 导出CSV
表 7 优化策略下不同模式的相关指标
Table 7 Related indexes under different modes in optimal policy
总体代价(元) 调峰代价(元) 购电代价(元) VRB充放代价(元) 柔性负荷补偿金额(元/d) 模式1 42 370 1 125 35 800 389 5 056 模式2 50 856 8 266 42 049 350 0 模式3 47 555 1 566 39 867 0 6 122 模式4 55 297 13 131 42 166 0 0
下载: 导出CSV
-
[1] 赵冬梅, 张楠, 刘燕华, 张旭. 基于储能的微网并网和孤岛运行模式平滑切换综合控制策略. 电网技术, 2013, 37(2): 301-306Zhao Dong-Mei, Zhang Nan, Liu Yan-Hua, Zhang Xu. Synthetical control strategy for smooth switching between grid-connected and islanded operation modes of microgrid based on energy storage system. Power System Technology, 2013, 37(2): 301-306 [2] 赵波, 王财胜, 周金辉, 赵俊晖, 杨野青, 余金龙. 主动配电网现状与未来发展. 电力系统自动化, 2014, 38(18): 125-135 doi: 10.7500/AEPS20131218007Zhao Bo, Wang Cai-Sheng, Zhou Jin-Hui, Zhao Jun-Hui, Yang Ye-Qing, Yu Jin-Long. Present and Future Development Trend of Active Distribution Network. Automation of Electric Power Systems, 2014, 38(18): 125-135 doi: 10.7500/AEPS20131218007 [3] 范明天. 主动配电系统定义与研究. 供用电, 2015, 32(2): 45-47 doi: 10.3969/j.issn.1006-6357.2015.02.011Fan Ming-Tian. The definition and research of the active power distribution. Distribution & Utilization, 2015, 32(2): 45-47 doi: 10.3969/j.issn.1006-6357.2015.02.011 [4] 马钊, 梁惠施, 苏剑. 主动配电系统规划和运行中的重要问题. 电网技术, 2015, 39(6): 1499-1503Ma Zhao, Liang Hui-Shi, Su Jian. Important issues in planning and operation of active distribution system. Power System Technology, 2015, 39(6): 1499-1503 [5] 朱泽锋, 赵晋泉, 魏文辉, et al. 主动配电网中电池储能系统最优充放电策略. 电力系统自动化, 2016, 40(20): 47-53 doi: 10.7500/AEPS20160417004Zhu Ze-Feng, Zhao Jin-Quan, Wei Wen-Hui, et al. Optimal charging and discharging scheme of battery energy storage system in active distribution network. Automation of Electric Power Systems, 2016, 40(20): 47-53 doi: 10.7500/AEPS20160417004 [6] Liu W, Niu S, Huiting X U. Optimal planning of battery energy storage considering reliability benefit and operation strategy in active distribution system. Journal of Modern Power Systems & Clean Energy, 2017, 5(2): 177-186 [7] 盛四清, 刘梦. 主动配电系统中分布式电源和储能系统协调规划. 电力系统及其自动化学报, 2017, 29(2): 71-76 doi: 10.3969/j.issn.1003-8930.2017.02.012Sheng Si-Qing, Liu Meng. Coordination planning of distributed generation and energy storage system in active distribution system. Proceedings of the CSU-EPSA, 2017, 29(2): 71-76 doi: 10.3969/j.issn.1003-8930.2017.02.012 [8] Shi J, Fei X, Li Y, et al. Active Distribution System Planning for Low-Carbon Objective Using Immune Binary Firefly Algorithm. Journal of Tianjin University, 2017, 50(5): 507-513 [9] Chen Q, Zhao X, Gan D. Active-reactive scheduling of active distribution system considering interactive load and battery storage. Protection & Control of Modern Power Systems, 2017, 2(1): 29 [10] 魏庆来, 宋睿卓, 孙秋野. 迭代自适应动态规划理论及应用. 科学出版社, 2015Wei Qing-Lai, Song Rui-Zhuo, Sun Qiu-Ye. Iterative Adaptive Dynamic Programming Theory and Application. Science Press, 2015 [11] 王澄, 刘德荣, 魏庆来, 赵冬斌, 夏振超. 带有储能设备的智能电网电能迭代自适应动态规划最优控制. 自动化学报, 2014, 40(9): 1984-1990Wang Cheng, Liu De-Rong, Wei Qing-Lai, Zhao Dong-Bin, Xia Zhen-Chao. Iterative adaptive dynamic programming approach to power optimal control for smart grid with energy storage devices. Acta Automatica Sinica, 2014, 40(9): 1984-1990 [12] 孙秋野, 杨凌霄, 张化光. 智慧能源—–人工智能技术在电力系统中的应用与展望. 控制与决策, 2018, v.33(05): 173-184Sun Qiu-Ye, Yang Ling-Xiao, Zhang Hua-Guang. Smart energy — Applications and prospects of artificial intelligence technology in power system. Control and Decision, 2018, v.33(05): 173-184 [13] 马韬韬, 郭创新, 曹一家, et al. 电网智能调度自动化系统研究现状及发展趋势. 电力系统自动化, 2010, 34(9): 7-11Ma Tao-Tao, Guo Chuang-Xin, Cao Yi-Jia, et al. Current status and development trend of intelligent dispatching automation system of power system. Automation of Electric Power Systems, 2010, 34(9): 7-11 [14] 刘爱华, 王双虎, 梁顺, 朱朝阳, 张楠. 工业园区主动配电网关键技术研究及应用. 供用电, 2017, 34(7): 21-27Liu Ai-Hua, Wang Shuang-Hu, Liang Shun, Zhu Chao-Yang, Zhang Nan. Research and Application of Key Technology of Active Distribution Network in Industrial Park. Distribution & Utilization, 2017, 34(7): 21-27 [15] 杨锡运, 董德华, 李相俊, et al. 商业园区储能系统削峰填谷的有功功率协调控制策略. 电网技术, 2018, 42(8)Yang Xi-Yun, Dong De-Hua, Li Xiang-Jun, et al. Active power coordinated control strategy of peak load shifting for energy storage system in business park. Power System Technology, 2018, 42(8) [16] 杨楠, 王波, 刘涤尘, et al. 考虑柔性负荷调峰的大规模风电随机优化调度方法. 电工技术学报, 2013, 28(11): 231-238 doi: 10.3969/j.issn.1000-6753.2013.11.032Yang Nan, Wang Bo, Liu Di-Chen, et al. Large-scale wind power scochastic optimation scheduling method considering flexible load peaking. Transaction of China Electrotechnical Society, 2013, 28(11): 231-238 doi: 10.3969/j.issn.1000-6753.2013.11.032 [17] 李东, 牟强, 申佃涛, 吕笃润, 李智. 智能化园区柔性负荷调控技术研究. 电子技术与软件工程, 2016(12): 230-230Li Dong, Mou Qiang, Shen Dian-Tao, Lv Du-Run, Li Zhi. Research on flexible load control technology in intelligent park. Electronic Technology & Software Engineering, 2016(12): 230-230 [18] 王珂, 姚建国, 姚良忠, 杨胜春, 雍太有. 电力柔性负荷调度研究综述. 电力系统自动化, 2014, 38(20): 127-135 doi: 10.7500/AEPS20140422005Wang Ke, Yao Jian-Guo, Yao Liang-Zhong, Yang Sheng-Chun, Yong Tai-You. Survey of research on flexible loads scheduling technologies. Automation of Electric Power Systems, 2014, 38(20): 127-135 doi: 10.7500/AEPS20140422005 [19] Lawrence D J. 2001 performance of New York ISO demand response programs. IEEE Power Engineering Society Winter Meeting, 2002: 995-998 [20] 王珂, 郭晓蕊, 周竞, 毛文博, 王勇, 杨胜春. 智能电网“源-荷”协同调度框架及实现. 电网技术, 2018, 42(8)Wang Ke, Guo Xiao-Rui, Zhou Jing, Mao Wen-Bo, Wang Yong, Yang Sheng-Chun. Framework and Realization for Smart Grid "Source - Load" Coordinated Scheduling. Power System Technology, 2018, 42(8) [21] 江琦, 路改香, 唐昊, 谭琦. 智能电网弹性响应时间业务需求的接入控制. 控制与决策, 2014(7): 1311-1315Jiang Qi, Lu Gai-Xiang, Tang Hao, Tan Qi. Access control of demand requests with response time flexibility in smart grids. Control and Decision, 2014(7): 1311-1315 [22] 李怡瑾, 唐昊, 吕凯, 郭晓蕊, 许丹. 源荷不确定冷热电联供微网能量调度的建模与学习优化. 控制理论与应用, 2018(1) doi: 10.7641/CTA.2017.60615Li Yi-Jin, Tang Hao, Lv Kai, Guo Xiao-Rui, Xu Dan. Modeling and learning-based optimization of the energy dispatch for a combined cooling, heat and power microgrid system with uncertain sources and loads. Control Theory & Applications, 2018(1) doi: 10.7641/CTA.2017.60615 [23] Li Y Z, Niu J C. Forecast of Power Generation for Grid-Connected Photovoltaic System Based on Markov Chain. IEEE Power and Energy Engineering Conference, 2009:1729-1733 [24] Liang H, Tamang A K, Zhuang W, et al. Stochastic Information Management in Smart Grid. IEEE Communications Surveys & Tutorials, 2014, 16(3):1746-1770 [25] Hong Y Y, Lian R C. Optimal Sizing of Hybrid Wind/PV/Diesel Generation in a Stand-Alone Power System Using Markov-Based Genetic Algorithm. IEEE Transactions on Power Delivery, 2014, 27(2):640-647 [26] Breipohl A M, Lee F N, Zhai D, et al. A Gauss-Markov load model for application in risk evaluation and production simulation. IEEE Transactions on Power Systems, 1992, 7(4):1493-1499 doi: 10.1109/59.207373 [27] Zhai D, Breipohl A M, Lee F N, et al. The effect of load uncertainty on unit commitment risk. IEEE Transactions on Power Systems, 1994, 9(1):510-517 doi: 10.1109/59.317572 [28] CHAHWAN J, ABBEY C, JOOS G. VRB modelling for the study of output terminal voltages, internal losses and performance. IEEE Electrical Power Conference, 2007: 387-392 [29] 邱亚, 李鑫, 魏达, 余玲. 全钒液流电池的柔性充放电控制. 储能科学与技术, 2017, 6(1):78-84 doi: 10.12028/j.issn.2095-4239.2016.0006Qiu Ya, Li Xin, Wei Da, Yu Ling. Flexible charge-discharge control of vanadium redox battery. Energy Storage Science and Technology, 2017, 6(1):78-84 doi: 10.12028/j.issn.2095-4239.2016.0006 [30] 沈玉明, 胡博, 谢开贵, 向彬, 万凌云. 计及储能寿命损耗的孤立微电网最优经济运行. 电网技术,2014, 38(9):2371-2378Shen Yu-Ming, Hu Bo, Xie Kai-Gui, Xiang Bin, Wan Ling-Yun. Optimal economic operation of isolated microgrid considering battery life loss. Power System Technology, 2014, 38(9):2371-2378 [31] 李衍杰. 扩展Markov决策过程的性能灵敏度分析与优化. 中国科学技术大学, 2006Li Yan-Jie. Performance sensitivity analysis and optimization of extended Markov decision [Ph. D. dissertation], University of Science and Technology of China, 2006 [32] 田兵, 喻磊, 雷金勇, et al. 工业型用户侧微电网储能运行方式与微电网的运营模式. 南方电网技术, 2016, 10(8): 48-55Tian Bing, Yu Lei, Lei Jin-Yong, et al. Energy storage operation mode and business mode of industrial type user-side microgrid. Southern Power System Technology, 2016, 10(8): 48-55 [33] 邱亚, 李鑫, 陈薇, 魏达, 段泽民. 基于RLS和EKF算法的全钒液流电池SOC估计. 控制与决策, 2018, 33(1): 37-44Qiu Ya, Li Xin, Chen Wei, Wei Da, Duan Ze-Min. Vanadium redox battery SOC estimation based on RLS and EKF algorithm. Control and Decision, 2018, 33(1): 37-44 [34] 赵娟, 谭忠富, 李强. 我国峰谷分时电价的状况分析. 现代电力, 2005, 22(2): 82-85 doi: 10.3969/j.issn.1007-2322.2005.02.019Zhao Juan, Tan Zhong-Fu, Li Qiang. Analysis of time-of-use power price in China. Modern Electric Power, 2005, 22(2): 82-85 doi: 10.3969/j.issn.1007-2322.2005.02.019 -
计量
- 文章访问数: 4213
- HTML全文浏览量: 4752
- PDF下载量: 268
- 被引次数: 0
