深度卷积记忆网络时空数据模型

秦超; 高晓光; 万开方

doi:10.16383/j.aas.c180788

深度卷积记忆网络时空数据模型

doi: 10.16383/j.aas.c180788

1.
西北工业大学电子信息学院西安 710100

基金项目: 国家自然科学基金(61573285)资助

详细信息

作者简介:
秦超：西北工业大学电子信息学院博士研究生. 主要研究方向为深度学习. E-mail: woshiqchi@gmail.com

高晓光：博士, 西北工业大学电子信息学院教授. 主要研究方向为深度学习, 贝叶斯网络. E-mail: cxg2012@nwpu.edu.cn

万开方：博士, 西北工业大学电子信息学院讲师. 主要研究方向为深度学习, 强化学习. 本文通信作者. E-mail: wankaifang@nwpu.edu.cn

计量
- 文章访问数: 2457
- HTML全文浏览量: 1587
- PDF下载量: 530
- 被引次数: 0
出版历程
- 收稿日期: 2018-11-27
- 录用日期: 2019-06-18
- 网络出版日期: 2020-03-30
- 刊出日期: 2020-03-30

Deep Spatio-temporal Convolutional Long-short Memory Network

1.
School of Electronics and Information Engineering, Northwestern Polytechnical University, Xi′ an 710100

Funds: Supported by National Natural Science Foundation of China (61573285)

摘要

摘要: 时空数据是包含时间和空间属性的数据类型. 研究时空数据需要设计时空数据模型, 用以处理数据与时间和空间的关系, 得到信息对象由于时间和空间改变而产生的行为状态变化的趋势. 交通信息数据是一类典型的时空数据. 由于交通网络的复杂性和多变性, 以及与时间和空间的强耦合性, 使得传统的系统仿真和数据分析方法不能有效地得到数据之间的关系. 本文通过对交通数据中临近空间属性信息的处理, 解决了由于传统时空数据模型只关注时间属性导致模型对短时间间隔数据预测能力不足的问题, 进而提高模型预测未来信息的能力. 本文提出一个全新的时空数据模型—深度卷积记忆网络. 深度卷积记忆网络是一个包含卷积神经网络和长短时间记忆网络的多元网络结构, 可以提取数据的时间和空间属性信息, 通过加入周期和镜像特征提取模块对网络进行修正. 通过对两类典型时空数据集的验证, 表明深度卷积记忆网络在预测短时间间隔的数据信息时, 相较于传统的时空数据模型, 不仅预测误差有了很大程度的降低, 而且模型的训练速度也得到提升.
- 时空数据模型 /
- 深度卷积记忆网络 /
- 时间特征 /
- 空间特征
Abstract: Spatio-temporal data is a data type that contains temporal and spatial attributes. Training spatio-temporal data needs spatio-temporal models to deal with the relationship between data and those two attributes, to get the trend as it changes with time and space. Traffic information data is a typical type of spatio-temporal data. Due to the complexity and variability of the traffic network, and the strong coupling with time and space, traditional system simulation and data analysis methods cannot effectively obtain the relationship between data. By dealing with the adjacent spatial attribute information in traffic data, this paper designs a new spatio-temporal model, DSTCL (deep spatio-temporal convolutional long-short memory network), to solve the problem that traditional spatio-temporal models only pay attention to the temporal attribute and these models have insufficient ability to predict short-term data, and then improve the ability to predict future information. DSTCL is a multi-network structure consisting of a convolutional neural network and a long short-term memory. It can extract the temporal and spatial attribute information of the data, and correct the network by adding the periodic feature extraction module and the mirror feature extraction module. By verifying the two types of typical spatio-temporal datasets, it is shown that when DSTCL predicts the short-term information, compared with the traditional spatio-temporal models, not only the prediction error is greatly reduced, but also the training speed has been improved.
- Spatio-temporal model /
- deep spatio-temporal convolutional long-short memory network (DSTCL) /
- temporal attribute feature /
- spatial attribute feature

HTML全文

图 1 按照时间顺序对不同位置的交通数据进行处理

Fig. 1 Processing traffic data at different locations in chronological order

下载: 全尺寸图片幻灯片

图 2 使用CNN训练空间特征

Fig. 2 Training spatial features with CNN

下载: 全尺寸图片幻灯片

图 3 循环神经网络的计算图模型

Fig. 3 Calculation graph model of RNN

下载: 全尺寸图片幻灯片

图 4 LSTM“细胞”结构框图

Fig. 4 Structure of LSTM cell

下载: 全尺寸图片幻灯片

图 5 使用LSTM训练时间特征

Fig. 5 Training temporal features with LSTM

下载: 全尺寸图片幻灯片

图 6 堆叠自动编码器训练周期特征

Fig. 6 Training periodic features with stacked auto-encoder

下载: 全尺寸图片幻灯片

图 7 建立训练模型

Fig. 7 Building the training model

下载: 全尺寸图片幻灯片

图 8 15:00$\sim $19:00各模型预测与真实值的对比

Fig. 8 Comparison of model predictions from real values from 15:00 to 19:00

下载: 全尺寸图片幻灯片

图 9 10个不同位置各模型预测与真实值的对比

Fig. 9 Comparison of model predictions from real values of each model in 10 different locations

下载: 全尺寸图片幻灯片

图 10 各个模型处理10 min间隔数据训练集RMSE变化

Fig. 10 Curve of RMSE of processing 10 min interval data in PeMSD7 training dataset

下载: 全尺寸图片幻灯片

图 12 各个模型处理100 min间隔数据训练集RMSE变化

Fig. 12 Curves of RMSE of processing 100 min interval data in PeMSD7 training dataset

下载: 全尺寸图片幻灯片

图 11 各个模型处理40 min间隔数据训练集RMSE变化

Fig. 11 Curves of RMSE of processing 40 min interval data in PeMSD7 training dataset

下载: 全尺寸图片幻灯片

图 13 各个模型处理FMD测试集RMSE变化

Fig. 13 Curves of RMSE of processing 100-minute interval data in FMD testing dataset

下载: 全尺寸图片幻灯片

表 1 预测PeMSD7时间间隔10 min各算法效果对比

Table 1 Prediction of the effect of each algorithm in the 10 min interval of PeMSD7

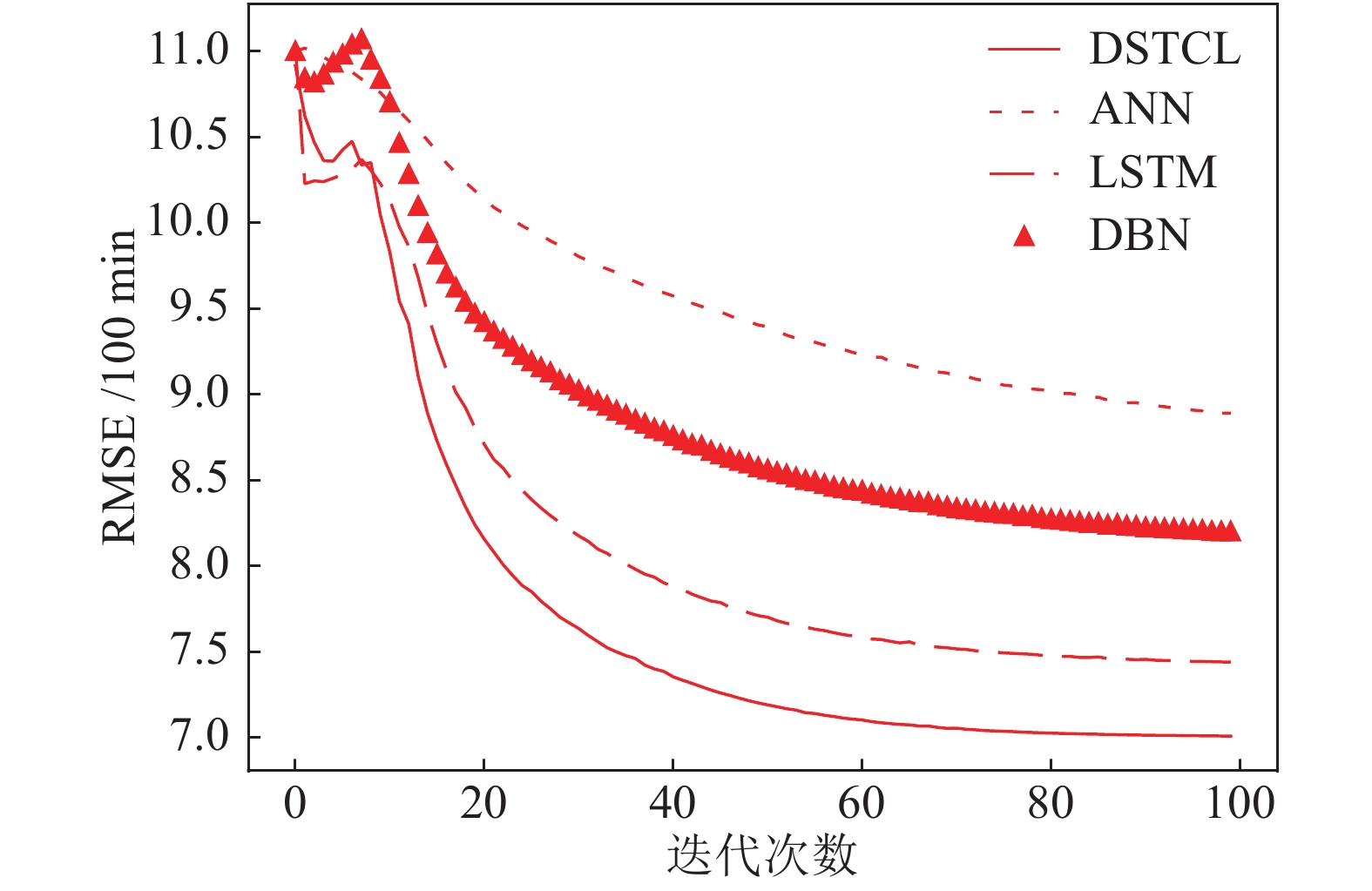
模型	MAE (10 min)	MAPE (10 min) (%)	RMSE (10 min)
DSTCL	2.61	6.0	4.32
LSTM	3.07	9.02	5.4
S-ARIMA	5.77	14.77	8.72
DBN	3.22	10.14	5.8
ANN	2.86	7.29	4.83

下载: 导出CSV

表 4 预测FMD时间间隔10 min各算法效果对比

Table 4 Prediction of the effect of each algorithm in the 10 min interval of FMD

模型	RMSE (10 min)
DSTCL	4.24
LSTM	4.62
S-ARIMA	8.44
DBN	5.21
ANN	5.37

下载: 导出CSV

表 2 预测PeMSD7时间间隔40 min各算法效果对比

Table 2 Prediction of the efiect of each algorithm in the 40 min interval of PeMSD7

模型	MAE (40 min)	MAPE (40 min) (%)	RMSE (40 min)
DSTCL	3.45	7.96	5.34
LSTM	3.81	9.46	5.92
S-ARIMA	4.8	14.47	8.6
DBN	4.11	10.66	6.5
ANN	3.63	9.98	5.77

下载: 导出CSV

表 3 预测PeMSD7时间间隔100 min各算法效果对比

Table 3 Prediction of the effect of each algorithm in the 100 min interval of PeMSD7

模型	MAE (100 min)	MAPE (100 min) (%)	RMSE (100 min)
DSTCL	4.15	9.94	7.05
LSTM	4.76	11.08	7.44
S-ARIMA	3.9	9.71	6.82
DBN	5.44	12.48	8.2
ANN	6.2	15.69	8.89

下载: 导出CSV

表 5 分别去掉三个模块RMSE结果对比

Table 5 Comparison of RMSE of removing three modules separately

	10 min	40 min	100 min
DSTCL1 (DSTCL去掉空间特征提取模块)	5.29	6.1	7.3
DSTCL2 (DSTCL去掉时间特征提取模块)	4.99	5.85	8.47
DSTCL3 (DSTCL去掉周期和镜像特征提取模块)	4.48	5.60	7.22

下载: 导出CSV

表 6 使用全连接神经网络替换三种结构的RMSE结果对比

Table 6 Comparison of RMSE of replacing three modules with fully ANN separately

	10 min	40 min	100 min
DSTCL4 (替换CNN)	5.16	5.98	7.21
DSTCL5 (替换LSTM)	4.85	5.52	8.1
DSTCL6 (替换堆叠自动编码器)	4.41	5.4	7.16

下载: 导出CSV

参考文献(33)

[1]	赵凡, 蒋同海, 周喜, 马博, 程力. 面向多维稀疏时空数据的可视化研究. 中国科学技术大学学报, 2017, 47(7): 556−568 doi: 10.3969/j.issn.0253-2778.2017.07.003 1 Zhao Fan, Jiang Tong-Hai, Zhou Xi, Ma Bo, Cheng Li. Visualization of multi-dimensional sparse spatial-temporal data. Journal of University of Science and Technology of China, 2017, 47(7): 556−568 doi: 10.3969/j.issn.0253-2778.2017.07.003
[2]	Cuturi M. Fast global alignment kernels. In: Proceedings of the 28th International Conference on Machine Learning (ICML-11). Bellevue, Washington, USA, 2011. 929−936
[3]	3 Goodchild M F. Citizens as sensors: the world of volunteered geography. GeoJournal, 2007, 69(4): 211−221 doi: 10.1007/s10708-007-9111-y
[4]	Ye M, Zhang Q, Wang L, Zhu J J, Yang R G, Gall J. A survey on human motion analysis from depth data. Time-of-flight and Depth Imaging. Sensors, Algorithms, and Applications. Springer, Berlin, Heidelberg, 2013: 149−187
[5]	5 Lagaros N, Papadrakakis M. Engineering and applied sciences optimization. Computational Methods in Applied Sciences, Springer, 2015, : 38
[6]	6 Vlahogianni E I. Computational intelligence and optimization for transportation big data: challenges and opportunities. Computational Methods in Applied Sciences, Springer, Cham, 2015, : 107−128
[7]	Ahmed M S, Cook A R. Analysis of Freeway Traffic Timeseries Data by Using Box-jenkins Techniques. 1979.
[8]	8 Williams B M, Hoel L A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results. Journal of Transportation Engineering, 2003, 129(6): 664−672 doi: 10.1061/(ASCE)0733-947X(2003)129:6(664)
[9]	9 Lippi M, Bertini M, Frasconi P. Short-term traffic flow forecasting: an experimental comparison of time-series analysis and supervised learning. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 871−882 doi: 10.1109/TITS.2013.2247040
[10]	10 Kumar S V, Vanajakshi L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. European Transport Research Review, 2015, 7(3): 21 doi: 10.1007/s12544-015-0170-8
[11]	11 Dougherty M. A review of neural networks applied to transport. Transportation Research Part C: Emerging Technologies, 1995, 3(4): 247−260 doi: 10.1016/0968-090X(95)00009-8
[12]	12 Hua J, Faghri A. AppHcations of artiflcial neural networks to intelligent vehicle-highway systems. Transportation Research Record, 1994, 1453: 83
[13]	Smith B L, Demetsky M J. Short-term traffic flow prediction models — a comparison of neural network and nonparametric regression approaches. In: Proceedings of the 1994 IEEE International Conference on Systems, Man, and Cybernetics. IEEE, 1994. 2: 1706−1709
[14]	14 Chan K Y, Dillon T S, Singh J, Chang E. Neural-network-based models for short-term traffic flow forecasting using a hybrid exponential smoothing and Levenberg-Marquardt algorithm. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 644−654 doi: 10.1109/TITS.2011.2174051
[15]	15 Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527−1554 doi: 10.1162/neco.2006.18.7.1527
[16]	16 LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436 doi: 10.1038/nature14539
[17]	17 Polson N G, Sokolov V O. Deep learning for short-term traffic flow prediction. Transportation Research Part C: Emerging Technologies, 2017, 79: 1−17 doi: 10.1016/j.trc.2017.02.024
[18]	Jia Y H, Wu J P, Du Y M. Traffic speed prediction using deep learning method. In: Proceedings of the 2016 IEEE International Conference on Intelligent Transportation Systems. IEEE, 2016. 1217−1222
[19]	19 Lv Y S, Duan Y J, Kang W W, Li Z X, Wang F Y. Traffic flow prediction with big data: a deep learning approach. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 865−873
[20]	20 Tan H C, Wu Y K, Shen B, Jin P J, Ran B. Short-term traffic prediction based on dynamic tensor completion. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(8): 2123−2133 doi: 10.1109/TITS.2015.2513411
[21]	Graves A. Generating sequences with recurrent neural networks. ArXiv Preprint, ArXiv: 1308.0850, 2013.
[22]	22 Ma X L, Tao Z M, Wang Y H, Yu H Y, Wang Y P. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transportation Research Part C: Emerging Technologies, 2015, 54: 187−197 doi: 10.1016/j.trc.2015.03.014
[23]	Krizhevsky A, Sutskever I, Hinton G E. Imagenet classiflcation with deep convolutional neural networks. In: Proceedings of the 2012 Advances in Neural Information Processing Systems, 2012. 1097−1105
[24]	Szegedy C, Liu W, Jia Y Q, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, 2015. 1−9
[25]	Springenberg J T, Dosovitskiy A, Brox T, Riedmiller M. Striving for simplicity: the all convolutional net. ArXiv Preprint, ArXiv: 1412.6806, 2014.
[26]	Qiu Z F, Yao T, Mei T. Learning spatio-temporal representation with pseudo-3d residual networks. In: Proceedings of the 2017 IEEE International Conference on Computer Vision. 2017. 5533−5541
[27]	27 Gers F A, Schmidhuber J, Cummins F. Learning to forget: continual prediction with LSTM. Neural Computation, 2000, 12(10): 2451−2471 doi: 10.1162/089976600300015015
[28]	28 Chen C, Petty K F, Skabardonis A, Varaiya P, Jia Z F. Freeway performance measurement system: mining loop detector data. Transportation Research Record: Journal of the Transportation Research Board, 2001, 1748(1): 96−102 doi: 10.3141/1748-12
[29]	Xiao T, Li H S, Ouyang W L, Wang X G. Learning deep feature representations with domain guided dropout for person re-identiflcation. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016. 1249−1258
[30]	Ozan I, Ethem A. Dropout Regularization in Hierarchical Mix-ture of Experts. ArXiv Preprint, ArXiv: 1812.10158, 2018.
[31]	Cai Y Q, Li Q X, Shen Z W. On the convergence and robust-ness of batch normalization. ArXiv Preprint, ArXiv: 1810.00122,2018.
[32]	Jung W, Jung D, Kim B, Lee S, Rhee W, Ahn J H. Restructur-ing batch normalization to accelerate CNN training. ArXiv Pre-print, ArXiv: 1807.01702, 2018.
[33]	Coates A, Lee H, Ng A. An analysis of single-layer networks in unsupervised feature learning. In: Proceedings of the 14th International Conference on Artiflcial Intelligence and Statistics, 2011. 215−223