Formulation and Solution Methodology for Repairman Allocation Problem in Serial Production Lines
-
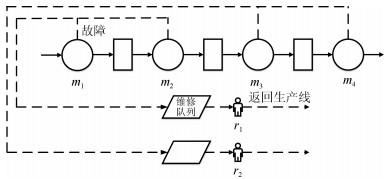
摘要: 在串行生产线中, 机器会发生故障而且故障间隔时间随机, 因此需要维修工人及时维修, 使得故障的机器恢复加工能力, 否则就可能导致系统吞吐率降低. 如何在满足系统吞吐率的前提下, 使用尽可能少的维修工人来完成机器的维修任务, 本文称这样一个全新的问题为串行生产线中机器维修工人的任务分配问题. 针对该问题, 本文首先建立了问题的优化模型, 并将该优化问题转换为多个判定问题进行求解; 然后, 通过合理地定义机器的维修工作量, 使得判定问题可以类比为并行机调度问题; 最后, 采用了一种基于最长处理时间优先算法(Longest processing time, LPT)和回溯策略的启发式算法, 搜索最优的维修工人任务分配方式. 实验结果表明, 该方法能有效求解维修工人的任务分配问题.Abstract: In serial production lines, machines are usually unreliable, i.e., they may break down randomly. In this situation, repairmen have to promptly repair the breakdown machines to recover their processing capability, or else the system throughput may drop. With the consideration of labor cost, how many repairmen should be employed in a production system to meet a desired throughput is called the repairman allocation problem. In this paper, the repairman allocation problem is formulated and solved. Specifically, first, it is transformed into a series of decision problems, each of which is a problem of assigning all machines to a fixed number of repairmen while guaranteeing the required throughput. Then, workloads of machines and of repairmen are defined and quantified by machine parameters. On the basis of the workloads, the decision problems are analogous to the parallel machine scheduling (PMS) problem, thus an algorithm, which is designed based on the longest processing time (LPT) algorithm for solving PMS and backtracking, is adopted to solve the decision problems. Extensive results show that this algorithm can effectively solve the decision problems, and thus, effectively solve the repairman allocation problem.
-
Key words:
- Production systems /
- machine maintenance /
- repairman allocation /
- LPT algorithm /
- backtracking
1) 本文责任编委 刘艳军 -
表 1 机器参数
Table 1 Machine parameters
机器编号 故障率(次/分钟) 维修率(次/分钟) 维修工作量(分钟) 1 0.2 5 0.04 2 0.2 5 0.04 3 0.6 5 0.12 4 0.6 5 0.12 5 0.4 5 0.08 6 0.4 5 0.08 7 0.2 5 0.04 8 0.2 5 0.04 表 2 实验结果
Table 2 Experimental results
回溯次数 吞吐率(个/分钟) 工人数(人) 0 0.8867 5 10 0.8428 4 50 0.8589 4 100 0.8589 4 表 3 维修工人任务分配
Table 3 Repairman task allocation
回溯次数 分配方案 0 $ D_1 = \{m_{3}\} $, $ D_2 = \{m_{4}\} $, $ D_3 = \{m_{5}, m_{7}\} $, $ D_4 = \{m_{6}, m_{8}\} $, $ D_5 = \{m_{1}, m_{2}\} $ 10 $ D_1 = \{m_{3}\} $, $ D_2 = \{m_{4}, m_{7}\} $, $ D_3 = \{m_{1}, m_{5}\} $, $ D_4 = \{m_{2}, m_{6}, m_{8}\} $ 50 $ D_1 = \{m_{2}, m_{3}\} $, $ D_2 = \{m_{4}\} $, $ D_3 = \{m_{1}, m_{5}\} $, $ D_4 = \{m_{6}, m_{7}, m_{8}\} $ 100 $ D_1 = \{m_{2}, m_{3}\} $, $ D_2 = \{m_{4}\} $, $ D_3 = \{m_{1}, m_{5}\} $, $ D_4 = \{m_{6}, m_{7}, m_{8}\} $ 表 4 50台机器实验结果
Table 4 Experimental results of 50 machines
回溯次数 吞吐率(个/分钟) 工人数(人) 0 0.6600 17 100 0.6586 15 -
[1] 张于贤, 李娜, 肖吉军. 基于排队论的生产线量化分析及优化. 制造业自动化, 2014, 7: 59-61 https://www.cnki.com.cn/Article/CJFDTOTAL-JXGY201407018.htmZhang Yu-Xian, Li Na, Xiao Ji-Jun. Quantitative analysisand optimizationofthe production line based on the queuing theory. Manufacturing Automation, 2014, 7: 59-61 https://www.cnki.com.cn/Article/CJFDTOTAL-JXGY201407018.htm [2] Yang F J, Gao K Z, Simon I W, Zhu Y T, Zhu R. Decomposition methods for manufacturing system scheduling: a survey. IEEE/CAA Journal of Automatica Sinica, 2018, 5(2): 389-400 doi: 10.1109/JAS.2017.7510805 [3] Zhao Y J, Yan C B, Zhao Q C, et al. Efficient simulation method for general assembly systems with material handling based on aggregated event-scheduling. IEEE Transactions on Automation Science and Engineering, 2010, 7(4): 762-775 doi: 10.1109/TASE.2009.2034135 [4] Li J S, Meerkov S M. Production Systems Engineering, New York: Springer, 2009. 17-37 [5] Xiao F L, Shao L P. Optimizing production line balance based on witness simulation. In: Proceedings of the 8th International Conference on Logistic, Informatics and Service Sciences. Toronto, ON, Canada: IEEE, 2018. 1-5 [6] Borba L, Ritt M, Miralles C. Exact and heuristic methods for solving the robotic assembly line balancing problem. European Journal of Operational Research, 2018, 270(1): 146-156 doi: 10.1016/j.ejor.2018.03.011 [7] Horng S L, Lin S S. Merging artificial immune system and ordinal optimization for solving the optimal buffer resource allocation of production line. In: Proceedings of the 9th International Conference on Knowledge and Smart Technology. Chonburi, Thailand: IEEE, 2017. 6-11 [8] Sophie W, Andrea M, Raik S. Optimization of buffer allocations in flow lines with limited supply. ⅡSE Transactions, 2018, 50(3): 191-202 doi: 10.1080/24725854.2017.1328751?src=recsys [9] Zou D X, Gao L Q, Li S. A novel global harmony search algorithm for task assignment problem. Journal of Systems and Software, 2010, 83(10): 1678-1688 doi: 10.1016/j.jss.2010.04.070 [10] Camacho G A, Cuellar D, Álvarez D. Heuristic approach for the multiple bin-size bin packing problem. IEEE Latin America Transactions, 2018, 16(2): 620-626 doi: 10.1109/TLA.2018.8327421 [11] 李孙寸, 施心陵, 张松海, 董易, 高莲, 基于多元优化的三维装箱问题的研究. 自动化学报, 2018, 44(1): 106-115 doi: 10.16383/j.aas.2018.c160381Li Sun-Cun, Shi Xin-Ling, Zhang Song-Hai, Dong Yi, Gao Lian. Multi-variant optimization algorithm for three dimensional container loading problem. Acta Automatica Sinica, 2018, 44(1): 106-115 doi: 10.16383/j.aas.2018.c160381 [12] Yan C B, Zhao Q C, Huang N J, Xiao G X, Li J S. Formulation and a simulation based algorithm for line-side buffer assignment problem in systems of general assembly line with material handling. IEEE Transactions on Automation Science and Engineering, 2010, 7(4): 902-920 doi: 10.1109/TASE.2010.2046892 [13] Sels V, Coelho J, Dias A M, Vanhoucke M. Hybrid tabu search and a truncated branch-and-bound for the unrelated parallel machine scheduling problem. Computers and Operations Research, 2015, 53: 107-117 doi: 10.1016/j.cor.2014.08.002 [14] Massabò I, Paletta G, Ruiz-Torres A J. A note on longest processing time algorithms for the two uniform parallel machine makespan minimization problem. Journal of Scheduling, 2016, 19(2): 207-211 doi: 10.1007/s10951-015-0453-x [15] Braun O, Chung F, Graham R. Worst-case analysis of the LPT algorithm for single processor scheduling with time restrictions. OR Spectrum, 2016, 38(2): 531-540 doi: 10.1007/s00291-016-0431-5 -





 下载:
下载: