An R2 Indicator and Reference Vector Based Many-objective Optimization Evolutionary Algorithm
-
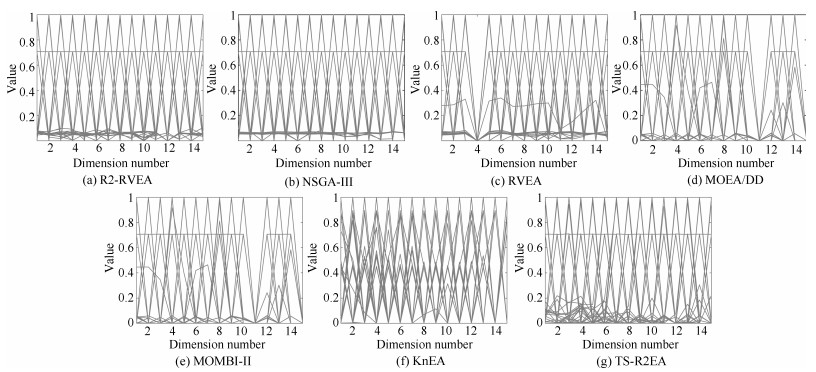
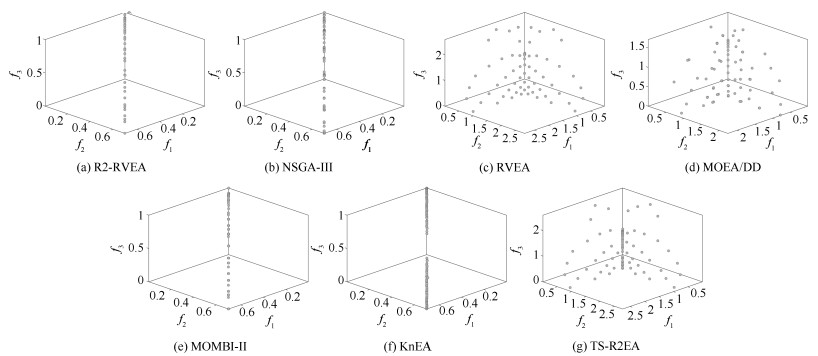
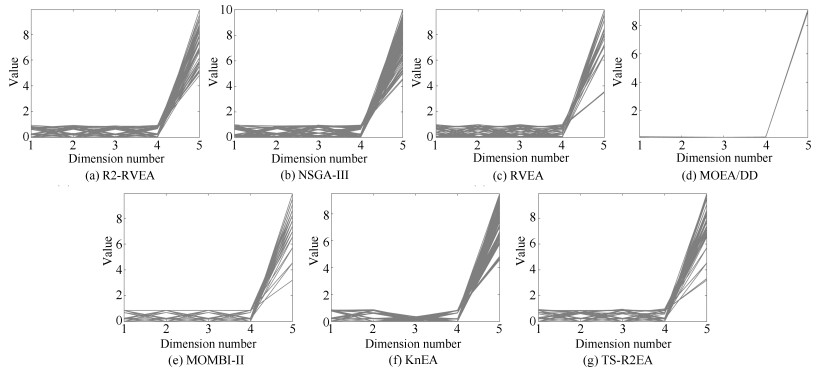
摘要: 在高维多目标优化中, 不同的优化问题存在不同形状的Pareto前沿(PF), 而研究表明大多数多目标进化算法(Multi-objective evolutionary algorithms, MOEAs) 在处理不同的优化问题时普适性较差. 为了解决这个问题, 本文提出了一个基于R2指标和参考向量的高维多目标进化算法(An R2 indicator and reference vector based many-objective optimization evolutionary algorithm, R2-RVEA). R2-RVEA基于Pareto支配选取非支配解来指导种群进化, 仅当非支配解的数量超过种群规模时, 算法进一步采用种群分解策略和R2指标选择策略进行多样性管理. 通过大量的实验证明, 本文提出的算法在处理不同形状的PF时具有良好的性能.Abstract: Some researches point out that the most of existing multi-objective optimization algorithms (MOEAs) shown poor versatility on different shapes of Pareto front (PF) in many-objective optimization. To address this issue, this paper proposes an R2 indicator and reference vector based evolutionary algorithm for many-objective optimization (R2-RVEA). R2-RVEA adopts pareto dominance to select the non-dominated solutions to guide the evolution of population, it will further introduce population partition strategy and R2 indicator selection strategy to manage the diversity when the number of non-dominated solutions is greater than population size. The experimental results demonstrate that the proposed algorithm has good performance in handling different shapes of Pareto front.
-
Key words:
- R2 indicator /
- reference vector /
- many-objective optimization /
- evolutionary algorithm
1) 本文责任编委 王鼎 -
表 1 种群规模设置
Table 1 Setting of population size
$M$ $(p_1, p_2)$ 种群规模 3 (12, 0) 105 5 (6, 0) 126 10 (3, 2) 275 15 (2, 1) 135 表 2 R2-RVEA、NSGA-Ⅲ、RVEA、MOEA/DD、MOMBI-Ⅱ、KnEA和TS-R2EA在DTLZ1$-$DTLZ7上获得的HV值的统计结果(均值和标准差). 最好的结果已突出
Table 2 The statistical results (mean and standard deviation) of the HV values obtained by R2-RVEA, NSGA-Ⅲ, RVEA, MOEA/DD, MOMBI-Ⅱ, KnEA and TS-R2EA on DTLZ1 to DTLZ7. The best results are highlighted
问题 $M$ R2-RVEA NSGA-Ⅲ RVEA MOEA/DD MOMBI-Ⅱ KnEA TS-R2EA DTLZ 1 3 $8.3819\times 10^{-1}$
$(1.31\times 10^{-2})$$8.4373\times 10^{-1}$
$(1.16\times 10^{-3}) +$$8.4431\times 10^{-1}$
$(1.41\times 10^{-4}) +$$8.4426\times 10^{-1}$
$(2.26\times 10^{-4}) +$$8.4357\times 10^{-1}$
$(9.08\times 10^{-4}) \approx$$7.8436\times 10^{-1}$
$(4.64\times 10^{-2}) -$$8.4419\times 10^{-1}$
$(3.44\times 10^{-4}) +$5 $9.6015\times 10^{-1}$
$(4.69\times 10^{-2})$$9.2764\times 10^{-1}$
$(1.43\times 10^{-1}) -$$9.7488\times 10^{-1}$
$(2.27\times 10^{-4}) +$$9.7484\times 10^{-1}$
$(2.75\times 10^{-4}) +$$9.3835\times 10^{-1}$
$(1.26\times 10^{-1}) -$$7.6616\times 10^{-1}$
$(9.09\times 10^{-2}) -$$9.7486\times 10^{-1}$
$(2.27\times 10^{-4}) +$10 $9.9892\times 10^{-1}$
$(5.94\times 10^{-4})$$9.9520\times 10^{-1}$
$(2.43\times 10^{-2}) -$$9.9968\times 10^{-1}$
$(1.88\times 10^{-5}) +$$9.9518\times 10^{-1}$
$(2.46\times 10^{-2}) -$$9.4328\times 10^{-1}$
$(4.34\times 10^{-2}) -$$4.0984\times 10^{-1}$
$(1.92\times 10^{-1}) -$$9.9970\times 10^{-1}$
$(2.11\times 10^{-5}) +$15 $8.7065\times 10^{-1}$
$(2.75\times 10^{-1})$$4.8134\times 10^{-1}$
$(4.84\times 10^{-1}) -$$9.4387\times 10^{-1}$
$(1.71\times 10^{-1}) +$$9.5591\times 10^{-1}$
$(1.36\times 10^{-1}) +$$7.4281\times 10^{-1}$
$(1.91\times 10^{-1}) -$$6.4831\times 10^{-2}$
$(1.30\times 10^{-1}) -$$6.1864\times 10^{-1}$
$(3.77\times 10^{-1}) -$DTLZ 2 3 $5.6302\times 10^{-1}$
$(5.99\times 10^{-6})$$5.6303\times 10^{-1}$
$(7.97\times 10^{-7}) \approx$$5.6302\times 10^{-1}$
$(6.53\times 10^{-7}) \approx$$5.6302\times 10^{-1}$
$(3.98\times 10^{-7}) \approx$$5.6299\times 10^{-1}$
$(2.19\times 10^{-5}) -$$5.2089\times 10^{-1}$
$(1.20\times 10^{-2}) -$$5.6302\times 10^{-1}$
$(2.36\times 10^{-6}) -$5 $7.9493\times 10^{-1}$
$(4.55\times 10^{-4})$$7.9498\times 10^{-1}$
$(3.66\times 10^{-4}) \approx$$7.9492\times 10^{-1}$
$(3.75\times 10^{-4}) \approx$$7.9484\times 10^{-1}$
$(3.71\times 10^{-4}) \approx$$7.9470\times 10^{-1}$
$(4.13\times 10^{-4}) -$$7.4725\times 10^{-1}$
$(1.23\times 10^{-2}) -$$7.9479\times 10^{-1}$
$(3.90\times 10^{-4}) \approx$10 $9.6978\times 10^{-1}$
$(1.74\times 10^{-4})$$9.4911\times 10^{-1}$
$(3.63\times 10^{-2}) \approx$$9.6983\times 10^{-1}$
$(1.64\times 10^{-4}) \approx$$9.6978\times 10^{-1}$
$(1.72\times 10^{-4}) \approx$$9.7090\times 10^{-1}$
$(1.49\times 10^{-3}) +$$9.2287\times 10^{-1}$
$(8.30\times 10^{-3}) -$$9.7057\times 10^{-1}$
$(1.66\times 10^{-4}) +$15 $9.9057\times 10^{-1}$
$(4.02\times 10^{-4})$$9.6345\times 10^{-1}$
$(1.75\times 10^{-2}) -$$9.7793\times 10^{-1}$
$(4.01\times 10^{-2}) -$$9.9063\times 10^{-1}$
$(2.44\times 10^{-4}) \approx$$8.1493\times 10^{-1}$
$(9.09\times 10^{-2}) -$$9.6726\times 10^{-1}$
$(9.69\times 10^{-3}) -$$9.8690\times 10^{-1}$
$(2.06\times 10^{-3}) \approx$DTLZ 3 3 $3.1493\times 10^{-1}$
$(2.64\times 10^{-1})$$3.3928\times 10^{-1}$
$(2.64\times 10^{-1}) \approx$$4.4454\times 10^{-1}$
$(2.26\times 10^{-1}) +$$3.8776\times 10^{-1}$
$(2.55\times 10^{-1}) +$$4.5790\times 10^{-1}$
$(2.08\times 10^{-1}) +$$3.8655\times 10^{-1}$
$(1.84\times 10^{-1}) \approx$$4.6543\times 10^{-1}$
$(2.12\times 10^{-1}) \approx$5 $3.7400\times 10^{-1}$
$(3.68\times 10^{-1})$$1.5350\times 10^{-1}$
$(2.96\times 10^{-1}) -$$2.8806\times 10^{-1}$
$(3.85\times 10^{-1}) -$$4.5110\times 10^{-1}$
$(3.88\times 10^{-1}) \approx$$3.9824\times 10^{-1}$
$(3.80\times 10^{-1}) \approx$$3.5245\times 10^{-1}$
$(3.42\times 10^{-1}) \approx$$7.9253\times 10^{-1}$
$(2.14\times 10^{-3}) +$10 $5.7253\times 10^{-1}$
$(2.29\times 10^{-1})$$1.2957\times 10^{-1}$
$(3.35\times 10^{-1}) -$$8.7219\times 10^{-1}$
$(2.96\times 10^{-1}) +$$7.7563\times 10^{-1}$
$(3.94\times 10^{-1}) +$$7.9552\times 10^{-1}$
$(2.33\times 10^{-1}) +$$9.4859\times 10^{-2}$
$(1.25\times 10^{-1}) -$$8.0885\times 10^{-1}$
$(3.68\times 10^{-1}) +$15 $1.8380\times 10^{-1}$
$(3.12\times 10^{-1})$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) -$$1.5858\times 10^{-1}$
$(3.61\times 10^{-1}) \approx$$6.5490\times 10^{-2}$
$(2.49\times 10^{-1}) -$$1.2904\times 10^{-1}$
$(1.89\times 10^{-1}) \approx$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) -$$1.2832\times 10^{-1}$
$(3.33\times 10^{-1}) \approx$DTLZ 4 3 $5.5571\times 10^{-1}$
$(4.00\times 10^{-2})$$4.9607\times 10^{-1}$
$(1.04\times 10^{-1}) -$$5.6302\times 10^{-1}$
$(1.76\times 10^{-6}) \approx$$5.6302\times 10^{-1}$
$(9.77\times 10^{-7}) \approx$$5.4835\times 10^{-1}$
$(5.57\times 10^{-2}) -$$5.2680\times 10^{-1}$
$(8.24\times 10^{-2}) -$$5.6302\times 10^{-1}$
$(3.79\times 10^{-6}) \approx$5 $7.9489\times 10^{-1}$
$(3.32\times 10^{-4})$$7.8461\times 10^{-1}$
$(3.14\times 10^{-2}) \approx$$7.9488\times 10^{-1}$
$(4.10\times 10^{-4}) \approx$$7.9488\times 10^{-1}$
$(3.94\times 10^{-4}) \approx$$7.5533\times 10^{-1}$
$(4.54\times 10^{-2}) -$$7.7479\times 10^{-1}$
$(4.58\times 10^{-3}) -$$7.9462\times 10^{-1}$
$(3.32\times 10^{-4}) -$10 $9.6980\times 10^{-1}$
$(1.43\times 10^{-4})$$9.5960\times 10^{-1}$
$(2.48\times 10^{-2}) \approx$$9.6983\times 10^{-1}$
$(1.87\times 10^{-4}) \approx$$9.6977\times 10^{-1}$
$(1.78\times 10^{-4}) \approx$$9.7012\times 10^{-1}$
$(4.66\times 10^{-3}) +$$9.5269\times 10^{-1}$
$(2.39\times 10^{-3}) -$$9.7122\times 10^{-1}$
$(1.77\times 10^{-4}) +$15 $9.9066\times 10^{-1}$
$(8.86\times 10^{-5})$$9.7301\times 10^{-1}$
$(1.36\times 10^{-2}) -$$9.8919\times 10^{-1}$
$(2.57\times 10^{-3}) \approx$$9.8905\times 10^{-1}$
$(3.03\times 10^{-3}) -$$9.7826\times 10^{-1}$
$(1.03\times 10^{-2}) -$$9.7895\times 10^{-1}$
$(2.52\times 10^{-3}) -$$9.8939\times 10^{-1}$
$(2.01\times 10^{-3}) -$DTLZ 5 3 $1.9397\times 10^{-1}$
$(1.20\times 10^{-4})$$1.9223\times 10^{-1}$
$(1.03\times 10^{-3}) -$$1.6284\times 10^{-1}$
$(3.84\times 10^{-3}) -$$1.8376\times 10^{-1}$
$(3.37\times 10^{-4}) -$$1.9214\times 10^{-1}$
$(3.58\times 10^{-7}) -$$1.7826\times 10^{-1}$
$(1.21\times 10^{-2}) -$$1.9283\times 10^{-1}$
$(7.92\times 10^{-4}) -$5 $9.2958\times 10^{-2}$
$(3.69\times 10^{-3})$$8.9794\times 10^{-2}$
$(2.82\times 10^{-2}) \approx$$1.0617\times 10^{-1}$
$(4.51\times 10^{-3}) +$$1.1298\times 10^{-1}$
$(4.15\times 10^{-4}) +$$9.0987\times 10^{-2}$
$(2.37\times 10^{-4}) -$$4.3747\times 10^{-2}$
$(4.20\times 10^{-2}) -$$1.0603\times 10^{-1}$
$(1.47\times 10^{-3}) +$10 $9.3278\times 10^{-2}$
$(1.61\times 10^{-3})$$6.7279\times 10^{-3}$
$(1.68\times 10^{-2}) -$$9.1255\times 10^{-2}$
$(4.75\times 10^{-4}) -$$9.4192\times 10^{-2}$
$(2.56\times 10^{-4}) +$$9.1736\times 10^{-2}$
$(1.49\times 10^{-3}) -$$8.5522\times 10^{-2}$
$(1.49\times 10^{-2}) -$$9.1402\times 10^{-2}$
$(5.49\times 10^{-4}) -$15 $9.2486\times 10^{-2}$
$(5.85\times 10^{-4})$$8.9842\times 10^{-2}$
$(2.02\times 10^{-3}) -$$9.1006\times 10^{-2}$
$(4.04\times 10^{-4}) -$$9.2026\times 10^{-2}$
$(4.99\times 10^{-4}) -$$9.1297\times 10^{-2}$
$(3.76\times 10^{-4}) -$$2.7606\times 10^{-2}$
$(3.86\times 10^{-2}) -$$9.1402\times 10^{-2}$
$(5.49\times 10^{-4}) -$DTLZ 6 3 $1.9395\times 10^{-1}$
$(1.70\times 10^{-4})$$1.9013\times 10^{-1}$
$(1.46\times 10^{-3}) -$$1.5924\times 10^{-1}$
$(5.93\times 10^{-3}) -$$1.8333\times 10^{-1}$
$(1.24\times 10^{-4}) -$$1.9214\times 10^{-1}$
$(4.32\times 10^{-7}) -$$1.7447\times 10^{-1}$
$(1.64\times 10^{-2}) -$$1.9123\times 10^{-1}$
$(1.38\times 10^{-3}) -$5 $9.5588\times 10^{-2}$
$(5.77\times 10^{-3})$$7.5292\times 10^{-2}$
$(3.47\times 10^{-2}) -$$1.0069\times 10^{-1}$
$(2.20\times 10^{-2}) +$$1.1288\times 10^{-1}$
$(2.53\times 10^{-4}) +$$9.0926\times 10^{-2}$
$(2.81\times 10^{-4}) -$$6.7599\times 10^{-2}$
$(3.79\times 10^{-2}) -$$1.0428\times 10^{-1}$
$(4.98\times 10^{-3}) +$10 $9.3189\times 10^{-2}$
$(1.68\times 10^{-3})$$1.5582\times 10^{-2}$
$(3.43\times 10^{-2}) -$$8.8629\times 10^{-2}$
$(1.68\times 10^{-2}) -$$9.4287\times 10^{-2}$
$(2.17\times 10^{-4}) \approx$$9.2894\times 10^{-2}$
$(9.94\times 10^{-4}) \approx$$9.1003\times 10^{-2}$
$(3.74\times 10^{-4}) -$$9.4393\times 10^{-2}$
$(9.71\times 10^{-4}) \approx$15 $9.1311\times 10^{-2}$
$(5.95\times 10^{-4})$$7.9684\times 10^{-3}$
$(2.45\times 10^{-2}) -$$9.0626\times 10^{-2}$
$(2.20\times 10^{-3}) \approx$$9.2156\times 10^{-2}$
$(2.50\times 10^{-4}) +$$9.1576\times 10^{-2}$
$(5.24\times 10^{-4}) +$$8.4945\times 10^{-2}$
$(2.31\times 10^{-2}) -$$8.7853\times 10^{-2}$
$(1.70\times 10^{-2}) -$DTLZ 7 3 $2.7062\times 10^{-1}$
$(1.53\times 10^{-2})$$2.7423\times 10^{-1}$
$(1.54\times 10^{-3}) +$$2.6741\times 10^{-1}$
$(1.06\times 10^{-3}) -$$2.1817\times 10^{-1}$
$(1.52\times 10^{-2}) -$$2.7096\times 10^{-1}$
$(1.47\times 10^{-2}) \approx$$2.6196\times 10^{-1}$
$(7.35\times 10^{-3}) -$$2.7791\times 10^{-1}$
$(4.93\times 10^{-4}) \approx$5 $2.5738\times 10^{-1}$
$(8.66\times 10^{-3})$$2.3857\times 10^{-1}$
$(7.76\times 10^{-3}) -$$2.0656\times 10^{-1}$
$(9.68\times 10^{-4}) -$$9.3745\times 10^{-2}$
$(1.55\times 10^{-2}) -$$2.4331\times 10^{-1}$
$(6.98\times 10^{-3}) -$$2.4015\times 10^{-1}$
$(2.17\times 10^{-2}) -$$2.5103\times 10^{-1}$
$(1.19\times 10^{-3}) -$10 $1.9133\times 10^{-1}$
$(2.17\times 10^{-3})$$1.9640\times 10^{-1}$
$(5.63\times 10^{-3}) +$$1.7601\times 10^{-1}$
$(1.34\times 10^{-2}) -$$5.6536\times 10^{-5}$
$(3.83\times 10^{-5}) -$$1.5718\times 10^{-1}$
$(9.13\times 10^{-3}) -$$7.5216\times 10^{-2}$
$(3.47\times 10^{-2}) -$$1.8524\times 10^{-1}$
$(4.94\times 10^{-3}) -$15 $1.4909\times 10^{-1}$
$(2.38\times 10^{-3})$$1.4039\times 10^{-1}$
$(1.21\times 10^{-2}) -$$1.0542\times 10^{-1}$
$(3.45\times 10^{-2}) -$$1.5473\times 10^{-7}$
$(5.89\times 10^{-8}) -$$9.7466\times 10^{-2}$
$(4.12\times 10^{-2}) -$$5.6787\times 10^{-4}$
$(1.49\times 10^{-3}) -$$1.0880\times 10^{-1}$
$(1.06\times 10^{-2}) -$$+$ / $\approx$ / $-$ 3 / 7 / 18 8 / 9 / 11 9 / 9 / 10 5 / 5 / 18 2 / 0 / 26 9 / 7 / 12 $+$, $\approx$和$-$分别表示获得的结果与R2-RVEA相比更好, 相似和更差. 表 3 R2-RVEA、NSGA-Ⅲ、RVEA、MOEA/DD、MOMBI-Ⅱ、KnEA和TS-R2EA在DTLZ1~DTLZ7上获得的IGD+值的统计结果(均值和标准差). 最好的结果已突出
Table 3 The statistical results (mean and standard deviation) of the IGD+ values obtained by R2-RVEA, NSGA-Ⅲ, RVEA, MOEA/DD, MOMBI-Ⅱ, KnEA and TS-R2EA on DTLZ1 to DTLZ7. The best results are highlighted
问题 $M$ R2-RVEA NSGA-Ⅲ RVEA MOEA/DD MOMBI-Ⅱ KnEA TS-R2EA DTLZ 1 3 $1.6235\times 10^{-2}$
$(7.90\times 10^{-3})$$1.3651\times 10^{-2}$
$(3.29\times 10^{-4}) +$$1.3492\times 10^{-2}$
$(1.25\times 10^{-4}) +$$1.3523\times 10^{-2}$
$(1.48\times 10^{-4}) +$$1.3709\times 10^{-2}$
$(2.71\times 10^{-4}) \approx$$2.6216\times 10^{-2}$
$(9.65\times 10^{-3}) -$$1.3571\times 10^{-2}$
$(3.33\times 10^{-4}) +$5 $5.0560\times 10^{-2}$
$(6.33\times 10^{-3})$$7.3388\times 10^{-2}$
$(7.15\times 10^{-2}) \approx$$4.6106\times 10^{-2}$
$(3.46\times 10^{-4}) +$$4.5988\times 10^{-2}$
$(1.35\times 10^{-4}) +$$4.8230\times 10^{-2}$
$(5.92\times 10^{-3}) \approx$$9.3292\times 10^{-2}$
$(4.42\times 10^{-2}) -$$5.3386\times 10^{-2}$
$(4.06\times 10^{-2}) -$10 $1.0287\times 10^{-1}$
$(8.43\times 10^{-3})$$9.0516\times 10^{-2}$
$(5.74\times 10^{-2}) +$$7.5684\times 10^{-2}$
$(3.45\times 10^{-2}) +$$6.9285\times 10^{-2}$
$(4.56\times 10^{-4}) +$$1.3489\times 10^{-1}$
$(3.62\times 10^{-2}) -$$2.7999\times 10^{-1}$
$(5.22\times 10^{-2}) -$$7.9575\times 10^{-2}$
$(3.48\times 10^{-2}) +$15 $2.8426\times 10^{-1}$
$(1.82\times 10^{-1})$$5.2357\times 10^{-1}$
$(3.38\times 10^{-1}) -$$2.0300\times 10^{-1}$
$(1.82\times 10^{-1}) +$$1.2789\times 10^{-1}$
$(8.21\times 10^{-2}) +$$2.8165\times 10^{-1}$
$(1.00\times 10^{-1}) \approx$$9.0915\times 10^{-1}$
$(7.61\times 10^{-1}) -$$2.7442\times 10^{-1}$
$(3.09\times 10^{-1}) \approx$DTLZ 2 3 $2.0861\times 10^{-2}$
$(5.70\times 10^{-6})$$2.0859\times 10^{-2}$
$(8.08\times 10^{-7}) \approx$$2.0859\times 10^{-2}$
$(5.36\times 10^{-7}) \approx$$2.0859\times 10^{-2}$
$(2.57\times 10^{-7}) \approx$$2.0870\times 10^{-2}$
$(8.77\times 10^{-6}) -$$3.6494\times 10^{-2}$
$(5.13\times 10^{-3}) -$$2.0861\times 10^{-2}$
$(1.10\times 10^{-6}) -$5 $7.1279\times 10^{-2}$
$(7.27\times 10^{-6})$$7.1282\times 10^{-2}$
$(1.80\times 10^{-6}) -$$7.1283\times 10^{-2}$
$(5.39\times 10^{-6}) -$$7.1283\times 10^{-2}$
$(6.73\times 10^{-7}) -$$7.1348\times 10^{-2}$
$(4.27\times 10^{-5}) -$$8.9581\times 10^{-2}$
$(4.33\times 10^{-3}) -$$7.1291\times 10^{-2}$
$(4.32\times 10^{-6}) -$10 $1.7493\times 10^{-1}$
$(2.35\times 10^{-5})$$1.9840\times 10^{-1}$
$(4.82\times 10^{-2}) -$$1.6809\times 10^{-1}$
$(2.66\times 10^{-5}) +$$1.7493\times 10^{-1}$
$(4.25\times 10^{-6}) \approx$$1.6874\times 10^{-1}$
$(1.06\times 10^{-3}) +$$1.8012\times 10^{-1}$
$(5.20\times 10^{-3}) -$$1.7207\times 10^{-1}$
$(3.32\times 10^{-4}) \approx$15 $2.3684\times 10^{-1}$
$(4.10\times 10^{-4})$$2.9249\times 10^{-1}$
$(1.82\times 10^{-2}) -$$2.6116\times 10^{-1}$
$(8.95\times 10^{-2}) -$$2.3623\times 10^{-1}$
$(2.02\times 10^{-4}) \approx$$4.0323\times 10^{-1}$
$(5.54\times 10^{-2}) -$$2.4998\times 10^{-1}$
$(1.79\times 10^{-2}) -$$2.3856\times 10^{-1}$
$(1.96\times 10^{-3}) -$DTLZ 3 3 $3.9763\times 10^{-1}$
$(5.49\times 10^{-1})$$4.5849\times 10^{-1}$
$(6.21\times 10^{-1}) \approx$$3.0314\times 10^{-1}$
$(5.74\times 10^{-1}) \approx$$1.8948\times 10^{-1}$
$(3.71\times 10^{-1}) +$$3.3114\times 10^{-1}$
$(6.46\times 10^{-1}) \approx$$4.0938\times 10^{-1}$
$(4.78\times 10^{-1}) -$$2.2115\times 10^{-1}$
$(4.00\times 10^{-1}) +$5 $3.9944\times 10^{-1}$
$(5.79\times 10^{-1})$$1.7578\times 10^{0}$
$(1.67\times 10^{0}) -$$7.4422\times 10^{-1}$
$(5.86\times 10^{-1}) \approx$$6.5811\times 10^{-1}$
$(5.59\times 10^{-1}) \approx$$3.7339\times 10^{-1}$
$(5.22\times 10^{-1}) +$$9.7538\times 10^{-1}$
$(1.31\times 10^{0}) -$$4.6878\times 10^{-1}$
$(5.40\times 10^{-1}) -$10 $3.7208\times 10^{-1}$
$(4.00\times 10^{-1})$$3.2503\times 10^{0}$
$(3.09\times 10^{0}) -$$4.5932\times 10^{-1}$
$(5.80\times 10^{-1}) -$$4.9410\times 10^{-1}$
$(5.27\times 10^{-1}) -$$3.9303\times 10^{-1}$
$(3.16\times 10^{-1}) \approx$$1.1755\times 10^{1}$
$(5.73\times 10^{1}) -$$3.9429\times 10^{-1}$
$(4.89\times 10^{-1}) -$15 $2.6642\times 10^{0}$
$(1.48\times 10^{0})$$9.7830\times 10^{0}$
$(5.23\times 10^{0}) -$$5.2490\times 10^{0}$
$(4.15\times 10^{0}) \approx$$2.7498\times 10^{0}$
$(2.09\times 10^{0}) -$$3.1399\times 10^{0}$
$(2.60\times 10^{0}) \approx$$1.3145\times 10^{1}$
$(8.69\times 10^{0}) -$$3.3117\times 10^{0}$
$(2.18\times 10^{0}) -$DTLZ 4 3 $2.0868\times 10^{-2}$
$(1.87\times 10^{-5})$$7.5928\times 10^{-2}$
$(9.29\times 10^{-2}) \approx$$2.0859\times 10^{-2}$
$(4.09\times 10^{-7}) \approx$$2.0859\times 10^{-2}$
$(2.72\times 10^{-7}) +$$4.1428\times 10^{-2}$
$(6.27\times 10^{-2}) -$$7.7586\times 10^{-2}$
$(1.50\times 10^{-1}) -$$2.0862\times 10^{-2}$
$(1.74\times 10^{-6}) \approx$5 $7.1276\times 10^{-2}$
$(1.24\times 10^{-5})$$9.3899\times 10^{-2}$
$(5.00\times 10^{-2}) -$$7.4060\times 10^{-2}$
$(1.52\times 10^{-2}) -$$7.4382\times 10^{-2}$
$(1.70\times 10^{-2}) -$$8.2438\times 10^{-2}$
$(2.87\times 10^{-2}) -$$8.0641\times 10^{-2}$
$(1.73\times 10^{-3}) -$$7.4077\times 10^{-2}$
$(1.52\times 10^{-3}) -$10 $1.7497\times 10^{-1}$
$(4.67\times 10^{-5})$$1.7695\times 10^{-1}$
$(2.02\times 10^{-2}) -$$1.6849\times 10^{-1}$
$(1.77\times 10^{-3}) \approx$$1.7081\times 10^{-1}$
$(3.43\times 10^{-3}) \approx$$1.6532\times 10^{-1}$
$(6.13\times 10^{-3}) +$$1.6217\times 10^{-1}$
$(2.21\times 10^{-3}) +$$1.6820\times 10^{-1}$
$(5.03\times 10^{-4}) \approx$15 $2.3729\times 10^{-1}$
$(3.58\times 10^{-4})$$2.6180\times 10^{-1}$
$(2.54\times 10^{-2}) \approx$$2.3958\times 10^{-1}$
$(4.59\times 10^{-3}) \approx$$2.4240\times 10^{-1}$
$(6.98\times 10^{-3}) -$$2.6824\times 10^{-1}$
$(2.33\times 10^{-2}) -$$2.3292\times 10^{-1}$
$(3.23\times 10^{-3}) +$$2.4469\times 10^{-1}$
$(8.10\times 10^{-3}) -$DTLZ 5 3 $6.4126\times 10^{-3}$
$(1.23\times 10^{-4})$$7.5607\times 10^{-3}$
$(8.01\times 10^{-4}) -$$3.3584\times 10^{-2}$
$(4.19\times 10^{-3}) -$$1.3345\times 10^{-2}$
$(3.02\times 10^{-4}) -$$7.6588\times 10^{-3}$
$(3.38\times 10^{-7}) -$$1.4326\times 10^{-2}$
$(7.18\times 10^{-3}) -$$7.1355\times 10^{-3}$
$(5.09\times 10^{-4}) -$5 $8.2311\times 10^{-2}$
$(1.90\times 10^{-2})$$2.3956\times 10^{-1}$
$(2.11\times 10^{-1}) -$$1.7521\times 10^{-1}$
$(5.25\times 10^{-2}) -$$7.2412\times 10^{-2}$
$(6.75\times 10^{-3}) \approx$$9.4200\times 10^{-2}$
$(3.23\times 10^{-5}) -$$2.4871\times 10^{-1}$
$(1.59\times 10^{-1}) -$$3.8136\times 10^{-2}$
$(4.16\times 10^{-3}) +$10 $1.2919\times 10^{-1}$
$(4.14\times 10^{-2})$$4.5326\times 10^{-1}$
$(1.29\times 10^{-1}) -$$1.7827\times 10^{-1}$
$(6.47\times 10^{-2}) -$$9.8182\times 10^{-2}$
$(1.79\times 10^{-2}) +$$3.5774\times 10^{-1}$
$(4.93\times 10^{-2}) -$$8.4408\times 10^{-2}$
$(9.10\times 10^{-3}) +$$1.0774\times 10^{-1}$
$(1.94\times 10^{-2}) \approx$15 $1.5729\times 10^{-1}$
$(9.70\times 10^{-2})$$1.5942\times 10^{-1}$
$(7.13\times 10^{-2}) \approx$$3.5936\times 10^{-1}$
$(5.81\times 10^{-2}) -$$5.1183\times 10^{-2}$
$(1.74\times 10^{-3}) +$$3.7512\times 10^{-1}$
$(2.29\times 10^{-3}) -$$3.3561\times 10^{-1}$
$(2.97\times 10^{-1}) -$$1.3229\times 10^{-1}$
$(6.34\times 10^{-2}) \approx$DTLZ 6 3 $6.4261\times 10^{-3}$
$(8.57\times 10^{-5}$$9.1282\times 10^{-3}$
$(1.10\times 10^{-3}) -$$3.3761\times 10^{-2}$
$(8.06\times 10^{-3}) -$$1.3955\times 10^{-2}$
$(5.10\times 10^{-4}) -$$7.6585\times 10^{-3}$
$(2.94\times 10^{-7}) -$$6.0051\times 10^{-2}$
$(1.07\times 10^{-2}) -$$7.4448\times 10^{-3}$
$(7.09\times 10^{-4}) -$5 $8.1474\times 10^{-2}$
$(1.79\times 10^{-2})$$2.3445\times 10^{-1}$
$(1.04\times 10^{-1}) -$$1.0892\times 10^{-1}$
$(1.71\times 10^{-2}) -$$7.1693\times 10^{-2}$
$(3.07\times 10^{-3}) +$$8.4850\times 10^{-2}$
$(3.26\times 10^{-4}) -$$2.0779\times 10^{-1}$
$(2.06\times 10^{-1}) -$$5.8034\times 10^{-2}$
$(6.23\times 10^{-3}) +$10 $7.1984\times 10^{-2}$
$(1.08\times 10^{-2})$$1.6206\times 10^{0}$
$(1.01\times 10^{0}) -$$2.3439\times 10^{-1}$
$(5.94\times 10^{-2}) -$$7.7284\times 10^{-2}$
$(2.48\times 10^{-2}) \approx$$3.5367\times 10^{-1}$
$(4.32\times 10^{-2}) -$$1.0960\times 10^{-1}$
$(7.24\times 10^{-2}) -$$6.0540\times 10^{-2}$
$(3.57\times 10^{-2}) +$15 $2.1340\times 10^{-1}$
$(9.95\times 10^{-2})$$1.8744\times 10^{0}$
$(1.17\times 10^{0}) -$$1.8445\times 10^{-1}$
$(1.19\times 10^{-1}) \approx$$5.1647\times 10^{-2}$
$(2.71\times 10^{-6}) +$$3.7468\times 10^{-1}$
$(4.84\times 10^{-3}) -$$2.9365\times 10^{-1}$
$(2.46\times 10^{-1}) \approx$$1.1096\times 10^{-1}$
$(1.49\times 10^{-1}) +$DTLZ 7 3 $9.8407\times 10^{-2}$
$(1.34\times 10^{-1})$$3.5754\times 10^{-2}$
$(2.15\times 10^{-3}) +$$4.3704\times 10^{-2}$
$(9.60\times 10^{-4}) +$$3.9831\times 10^{-1}$
$(1.74\times 10^{-1}) -$$4.6134\times 10^{-2}$
$(4.79\times 10^{-2}) \approx$$7.1748\times 10^{-2}$
$(6.52\times 10^{-2}) +$$3.4202\times 10^{-2}$
$(6.64\times 10^{-4}) +$5 $1.9604\times 10^{-1}$
$(5.86\times 10^{-2})$$1.8190\times 10^{-1}$
$(2.52\times 10^{-2}) \approx$$2.7929\times 10^{0}$
$(5.66\times 10^{-2}) -$$2.5348\times 10^{-1}$
$(1.65\times 10^{-1}) \approx$$1.1096\times 10^{-1}$
$(1.49\times 10^{-1}) +$$2.0713\times 10^{-1}$
$(1.30\times 10^{-1}) \approx$$1.4313\times 10^{-1}$
$(9.53\times 10^{-4}) +$10 $1.2600\times 10^{0}$
$(2.10\times 10^{-2})$$6.6488\times 10^{-1}$
$(4.91\times 10^{-2}) +$$1.0133\times 10^{0}$
$(5.93\times 10^{-2}) +$$1.2994\times 10^{0}$
$(6.05\times 10^{-2}) -$$4.5256\times 10^{0}$
$(8.62\times 10^{-1}) -$$6.6322\times 10^{-1}$
$(9.13\times 10^{-3}) +$$6.9956\times 10^{-1}$
$(1.88\times 10^{-1}) +$15 $8.3596\times 10^{0}$
$(3.76\times 10^{-2})$$7.3318\times 10^{0}$
$(1.12\times 10^{0}) +$$1.5286\times 10^{0}$
$(8.28\times 10^{-2}) +$$2.0686\times 10^{0}$
$(1.74\times 10^{-1}) +$$1.1458\times 10^{1}$
$(1.70\times 10^{0}) -$$4.7916\times 10^{0}$
$(9.31\times 10^{-1}) +$$2.0481\times 10^{0}$
$(6.97\times 10^{-1}) +$$+$ / $\approx$ / $-$ 5 / 7 / 16 8 / 8 / 12 11 / 7 / 10 3 / 8 / 17 6 / 2 / 20 11 / 6 / 11 $+$, $\approx$和$-$分别表示获得的结果与R2-RVEA相比更好, 相似和更差. 表 4 R2-RVEA、NSGA-Ⅲ、RVEA、MOEA/DD、MOMBI-Ⅱ、KnEA和TS-R2EA在WFG1-WFG9上获得的HV值的统计结果(均值和标准差). 最好的结果已突出
Table 4 The statistical results (mean and standard deviation) of the HV values obtained by R2-RVEA, NSGA-Ⅲ, RVEA, MOEA/DD, MOMBI-Ⅱ, KnEA and TS-R2EA on WFG1 to WFG9. The best results are highlighted
问题 $M$ R2-RVEA NSGA-Ⅲ RVEA MOEA/DD MOMBI-Ⅱ KnEA TS-R2EA WFG 1 3 $9.4097\times 10^{-1}$
$(1.32\times 10^{-2})$$9.3384\times 10^{-1}$
$(2.98\times 10^{-2}) -$$9.4502\times 10^{-1}$
$(1.09\times 10^{-3}) +$$9.1553\times 10^{-1}$
$(3.55\times 10^{-2}) -$$8.8329\times 10^{-1}$
$(5.34\times 10^{-2}) -$$9.2399\times 10^{-1}$
$(2.53\times 10^{-2}) -$$9.3418\times 10^{-1}$
$(3.48\times 10^{-2}) -$5 $9.9456\times 10^{-1}$
$(1.96\times 10^{-2})$$9.8643\times 10^{-1}$
$(3.60\times 10^{-2}) -$$9.8018\times 10^{-1}$
$(4.06\times 10^{-2}) -$$9.5451\times 10^{-1}$
$(3.40\times 10^{-2}) -$$8.4739\times 10^{-1}$
$(8.49\times 10^{-2}) -$$9.7995\times 10^{-1}$
$(1.87\times 10^{-2}) -$$9.9075\times 10^{-1}$
$(2.82\times 10^{-2}) -$10 $9.9957\times 10^{-1}$
$(2.10\times 10^{-4})$$9.9912\times 10^{-1}$
$(6.70\times 10^{-4}) -$$9.8000\times 10^{-1}$
$(3.93\times 10^{-2}) -$$9.8795\times 10^{-1}$
$(1.55\times 10^{-2}) -$$9.9607\times 10^{-1}$
$(1.91\times 10^{-2}) -$$9.9527\times 10^{-1}$
$(1.66\times 10^{-2}) -$$9.9888\times 10^{-1}$
$(3.64\times 10^{-2}) -$15 $9.9967\times 10^{-1}$
$(2.14\times 10^{-4})$$9.9949\times 10^{-1}$
$(3.42\times 10^{-4}) -$$8.9713\times 10^{-1}$
$(8.87\times 10^{-2}) -$$9.3763\times 10^{-1}$
$(7.46\times 10^{-2}) -$$6.5027\times 10^{-1}$
$(2.44\times 10^{-1}) -$$9.8089\times 10^{-1}$
$(3.34\times 10^{-2}) -$$9.4320\times 10^{-1}$
$(7.47\times 10^{-2}) -$WFG 2 3 $9.2138\times 10^{-1}$
$(8.02\times 10^{-3})$$9.2385\times 10^{-1}$
$(6.17\times 10^{-3}) \approx$$9.1683\times 10^{-1}$
$(1.11\times 10^{-2}) \approx$$9.1463\times 10^{-1}$
$(1.22\times 10^{-2}) -$$9.1075\times 10^{-1}$
$(1.81\times 10^{-2}) -$$9.0896\times 10^{-1}$
$(2.65\times 10^{-2}) -$$9.2318\times 10^{-1}$
$(1.17\times 10^{-2}) \approx$5 $9.8369\times 10^{-1}$
$(6.66\times 10^{-3})$$9.8358\times 10^{-1}$
$(7.88\times 10^{-3}) \approx$$9.5373\times 10^{-1}$
$(1.83\times 10^{-2}) -$$9.5536\times 10^{-1}$
$(1.32\times 10^{-2}) -$$9.6469\times 10^{-1}$
$(1.80\times 10^{-2}) -$$9.6900\times 10^{-1}$
$(1.21\times 10^{-2}) -$$9.7339\times 10^{-1}$
$(1.56\times 10^{-2}) -$10 $9.9168\times 10^{-1}$
$(4.71\times 10^{-3})$$9.8734\times 10^{-1}$
$(6.36\times 10^{-3}) -$$9.3682\times 10^{-1}$
$(2.27\times 10^{-2}) -$$9.3481\times 10^{-1}$
$(1.89\times 10^{-2}) -$$9.7730\times 10^{-1}$
$(1.08\times 10^{-2}) -$$9.8285\times 10^{-1}$
$(7.58\times 10^{-3}) -$$9.6436\times 10^{-1}$
$(2.13\times 10^{-2}) -$15 $9.5064\times 10^{-1}$
$(5.65\times 10^{-2})$$9.5605\times 10^{-1}$
$(1.68\times 10^{-2}) +$$8.3087\times 10^{-1}$
$(5.14\times 10^{-2}) -$$8.6774\times 10^{-1}$
$(3.16\times 10^{-2}) -$$6.0421\times 10^{-1}$
$(2.45\times 10^{-1}) -$$9.2373\times 10^{-1}$
$(3.23\times 10^{-2}) -$$8.9358\times 10^{-1}$
$(4.33\times 10^{-2}) -$WFG 3 3 $4.0241\times 10^{-1}$
$(3.81\times 10^{-3})$$3.9175\times 10^{-1}$
$(5.04\times 10^{-3}) -$$3.4039\times 10^{-1}$
$(7.94\times 10^{-3}) -$$3.0897\times 10^{-1}$
$(3.30\times 10^{-2}) -$$3.9392\times 10^{-1}$
$(6.40\times 10^{-3}) -$$3.7363\times 10^{-1}$
$(2.71\times 10^{-2}) -$$3.9530\times 10^{-1}$
$(4.16\times 10^{-3}) -$5 $1.9039\times 10^{-1}$
$(9.10\times 10^{-3})$$1.6387\times 10^{-1}$
$(2.03\times 10^{-2}) -$$9.9662\times 10^{-2}$
$(4.07\times 10^{-2}) -$$1.1461\times 10^{-1}$
$(2.06\times 10^{-2}) -$$8.9617\times 10^{-2}$
$(3.75\times 10^{-3}) -$$7.9870\times 10^{-2}$
$(2.78\times 10^{-2}) -$$1.5854\times 10^{-1}$
$(2.35\times 10^{-2}) -$10 $2.7662\times 10^{-2}$
$(3.29\times 10^{-2})$$2.3762\times 10^{-2}$
$(2.69\times 10^{-2}) \approx$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) -$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) -$$5.9165\times 10^{-4}$
$(2.45\times 10^{-3}) -$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) -$$2.6821\times 10^{-2}$
$(3.10e-2) \approx$15 $0.0000\times 10^{0}$
$(0.00\times 10^{0})$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) \approx$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) \approx$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) \approx$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) \approx$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) \approx$$0.0000\times 10^{0}$
$(0.00\times 10^{0}) \approx$WFG 4 3 $5.6274\times 10^{-1}$
$(1.26\times 10^{-4})$$5.6274\times 10^{-1}$
$(1.44\times 10^{-4}) \approx$$5.6096\times 10^{-1}$
$(5.24\times 10^{-4}) -$$5.5434\times 10^{-1}$
$(9.95\times 10^{-4}) -$$5.6138\times 10^{-1}$
$(3.92\times 10^{-3}) \approx$$5.4879\times 10^{-1}$
$(2.74\times 10^{-3}) -$$5.6251\times 10^{-1}$
$(3.63\times 10^{-4}) -$5 $7.9406\times 10^{-1}$
$(7.67\times 10^{-4})$$7.9388\times 10^{-1}$
$(6.34\times 10^{-4}) \approx$$7.9302\times 10^{-1}$
$(9.54\times 10^{-4}) -$$7.6900\times 10^{-1}$
$(8.68\times 10^{-4}) -$$7.8312\times 10^{-1}$
$(2.45\times 10^{-2}) -$$7.7583\times 10^{-1}$
$(4.18\times 10^{-3}) -$$7.9231\times 10^{-1}$
$(1.58\times 10^{-3}) -$10 $9.6852\times 10^{-1}$
$(7.59\times 10^{-4})$$9.6031\times 10^{-1}$
$(2.55\times 10^{-4}) -$$9.6066\times 10^{-1}$
$(4.21\times 10^{-3}) -$$7.6825\times 10^{-1}$
$(2.17\times 10^{-4}) -$$9.2141\times 10^{-1}$
$(6.09\times 10^{-4}) -$$9.5839\times 10^{-1}$
$(2.16\times 10^{-3}) -$$9.7052\times 10^{-1}$
$(7.92\times 10^{-4}) +$15 $9.8874\times 10^{-1}$
$(9.66\times 10^{-4})$$9.6088\times 10^{-1}$
$(2.38\times 10^{-2}) -$$9.5446\times 10^{-1}$
$(1.55\times 10^{-2}) -$$6.4744\times 10^{-1}$
$(1.70\times 10^{-1}) -$$3.9343\times 10^{-1}$
$(1.22\times 10^{-1}) -$$9.8038\times 10^{-1}$
$(4.46\times 10^{-3}) -$$9.8298\times 10^{-1}$
$(3.55\times 10^{-3}) -$WFG 5 3 $5.2186\times 10^{-1}$
$(1.51\times 10^{-5})$$5.2185\times 10^{-1}$
$(1.81\times 10^{-5}) -$$5.2114\times 10^{-1}$
$(2.33\times 10^{-4}) -$$5.1405\times 10^{-1}$
$(4.53\times 10^{-4}) -$$5.0698\times 10^{-1}$
$(2.74\times 10^{-3}) -$$5.0698\times 10^{-1}$
$(2.74\times 10^{-3}) -$$5.2191\times 10^{-1}$
$(2.07\times 10^{-4}) \approx$5 $7.4397\times 10^{-1}$
$(3.66\times 10^{-4})$$7.4384\times 10^{-1}$
$(3.37\times 10^{-4}) \approx$$7.4391\times 10^{-1}$
$(3.63\times 10^{-4}) \approx$$7.1885\times 10^{-1}$
$(5.68\times 10^{-4}) -$$7.2692\times 10^{-1}$
$(1.26\times 10^{-2}) -$$7.2414\times 10^{-1}$
$(3.96\times 10^{-3}) -$$7.4386\times 10^{-1}$
$(1.17\times 10^{-3}) \approx$10 $9.0487\times 10^{-1}$
$(1.77\times 10^{-4})$$9.0484\times 10^{-1}$
$(1.53\times 10^{-4}) \approx$$9.0455\times 10^{-1}$
$(2.23\times 10^{-4}) -$$7.8469\times 10^{-1}$
$(1.21\times 10^{-2}) -$$8.6080\times 10^{-1}$
$(1.05\times 10^{-2}) -$$8.9513\times 10^{-1}$
$(1.94\times 10^{-3}) -$$9.0589\times 10^{-1}$
$(2.49\times 10^{-4}) +$15 $9.1757\times 10^{-1}$
$(1.11\times 10^{-4})$$9.1595\times 10^{-1}$
$(6.23\times 10^{-3}) -$$9.1767\times 10^{-1}$
$(9.41\times 10^{-5}) +$$6.3350\times 10^{-1}$
$(2.39\times 10^{-2}) -$$1.6774\times 10^{-1}$
$(4.92\times 10^{-2}) -$$9.0854\times 10^{-1}$
$(4.69\times 10^{-3}) -$$9.1762\times 10^{-1}$
$(1.33\times 10^{-4}) \approx$WFG 6 3 $5.0818\times 10^{-1}$
$(1.36\times 10^{-2})$$5.1243\times 10^{-1}$
$(1.32\times 10^{-2}) \approx$$5.0823\times 10^{-1}$
$(1.24\times 10^{-2}) \approx$$5.0420\times 10^{-1}$
$(1.45\times 10^{-2}) \approx$$5.0752\times 10^{-1}$
$(1.29\times 10^{-2}) \approx$$4.8204\times 10^{-1}$
$(1.70\times 10^{-2}) -$$5.0745\times 10^{-1}$
$(1.42\times 10^{-2}) \approx$5 $7.2593\times 10^{-1}$
$(1.41\times 10^{-2})$$7.3070\times 10^{-1}$
$(1.66\times 10^{-2}) \approx$$7.3015\times 10^{-1}$
$(1.90\times 10^{-2}) \approx$$6.9856\times 10^{-1}$
$(2.16\times 10^{-2}) -$$7.1566\times 10^{-1}$
$(2.87\times 10^{-2}) \approx$$6.8244\times 10^{-1}$
$(2.81\times 10^{-2}) -$$7.3271\times 10^{-1}$
$(1.64\times 10^{-2}) \approx$10 $8.8346\times 10^{-1}$
$(1.26\times 10^{-2})$$8.8339\times 10^{-1}$
$(1.97\times 10^{-2}) \approx$$8.7673\times 10^{-1}$
$(2.06\times 10^{-2}) \approx$$7.2135\times 10^{-1}$
$(2.21\times 10^{-2}) -$$8.8534\times 10^{-1}$
$(3.14\times 10^{-2}) \approx$$8.5253\times 10^{-1}$
$(2.22\times 10^{-2}) -$$8.7590\times 10^{-1}$
$(1.91\times 10^{-2}) -$15 $8.9305\times 10^{-1}$
$(2.01\times 10^{-2})$$8.3062\times 10^{-1}$
$(3.59\times 10^{-2}) -$$7.0352\times 10^{-1}$
$(8.04\times 10^{-2}) -$$5.8993\times 10^{-1}$
$(4.37\times 10^{-2}) -$$4.7510\times 10^{-1}$
$(1.49\times 10^{-1}) -$$8.6942\times 10^{-1}$
$(3.32\times 10^{-2}) -$$8.8273\times 10^{-1}$
$(2.84\times 10^{-2}) -$WFG 7 3 $5.6255\times 10^{-1}$
$(1.73\times 10^{-4})$$5.6251\times 10^{-1}$
$(1.49\times 10^{-4}) \approx$$5.5223\times 10^{-1}$
$(1.21\times 10^{-3}) -$$8.8273\times 10^{-1}$
$(2.84\times 10^{-2}) -$$5.6238\times 10^{-1}$
$(2.13\times 10^{-3}) -$$5.4818\times 10^{-1}$
$(4.75\times 10^{-3}) -$$5.6293\times 10^{-1}$
$(4.19\times 10^{-5}) +$5 $7.9328\times 10^{-1}$
$(5.69\times 10^{-4})$$7.9299\times 10^{-1}$
$(5.80\times 10^{-4}) \approx$$7.9151\times 10^{-1}$
$(1.86\times 10^{-3}) -$$7.6426\times 10^{-1}$
$(5.52\times 10^{-3}) -$$7.8989\times 10^{-1}$
$(6.21\times 10^{-3}) \approx$$7.6829\times 10^{-1}$
$(8.45\times 10^{-3}) -$$7.9436\times 10^{-1}$
$(5.86\times 10^{-4}) +$10 $9.6815\times 10^{-1}$
$(4.10\times 10^{-4})$$9.6270\times 10^{-1}$
$(1.43\times 10^{-2}) -$$9.6055\times 10^{-1}$
$(3.10\times 10^{-3}) -$$8.3568\times 10^{-1}$
$(2.25\times 10^{-2}) -$$9.7072\times 10^{-1}$
$(1.25\times 10^{-3}) +$$9.5292\times 10^{-1}$
$(3.13\times 10^{-3}) -$$9.7156\times 10^{-1}$
$(8.72\times 10^{-4}) +$15 $9.9017\times 10^{-1}$
$(2.80\times 10^{-4})$$9.6427\times 10^{-1}$
$(1.91\times 10^{-2}) -$$5.4561\times 10^{-1}$
$(2.74\times 10^{-1}) -$$7.8897\times 10^{-1}$
$(1.15\times 10^{-1}) -$$5.8748\times 10^{-1}$
$(1.09\times 10^{-1}) -$$9.8220\times 10^{-1}$
$(7.12\times 10^{-3}) -$$9.8688\times 10^{-1}$
$(5.62\times 10^{-3}) -$WFG 8 3 $4.7920\times 10^{-1}$
$(1.78\times 10^{-3})$$4.8088\times 10^{-1}$
$(2.04\times 10^{-3}) +$$4.7329\times 10^{-1}$
$(3.40\times 10^{-3}) -$$4.6512\times 10^{-1}$
$(1.17\times 10^{-2}) -$$4.5390\times 10^{-1}$
$(3.39\times 10^{-3}) -$$4.5340\times 10^{-1}$
$(5.55\times 10^{-3}) -$$4.8156\times 10^{-1}$
$(2.27\times 10^{-3}) +$5 $6.8175\times 10^{-1}$
(1.97\times 10^{-3})$$6.8490\times 10^{-1}$
$(2.98\times 10^{-3}) +$$6.6856\times 10^{-1}$
$(1.16\times 10^{-2}) -$$6.5481\times 10^{-1}$
$(1.50\times 10^{-2}) -$$3.1317\times 10^{-1}$
$(8.51\times 10^{-3}) -$$6.3578\times 10^{-1}$
$(4.91\times 10^{-3}) -$$6.7843\times 10^{-1}$
$(2.33\times 10^{-3}) -$10 $8.8077\times 10^{-1}$
(8.46\times 10^{-3})$$8.4591\times 10^{-1}$
$(3.70\times 10^{-2}) -$$7.6098\times 10^{-1}$
$(7.42\times 10^{-2}) -$$6.1624\times 10^{-1}$
$(1.02\times 10^{-1}) -$$6.3967\times 10^{-1}$
$(2.31\times 10^{-2}) -$$7.9730\times 10^{-1}$
$(6.81\times 10^{-2}) -$$8.9025\times 10^{-1}$
$(1.77\times 10^{-2}) \approx$15 $9.1659\times 10^{-1}$
$(1.34\times 10^{-2})$$8.3508\times 10^{-1}$
$(4.47\times 10^{-2}) -$$4.6196\times 10^{-1}$
$(1.35\times 10^{-1}) -$$7.6426\times 10^{-1}$
$(1.77\times 10^{-1}) -$$3.3899\times 10^{-1}$
$(4.96\times 10^{-2}) -$$7.9415\times 10^{-1}$
$(1.18\times 10^{-1}) -$$7.6663\times 10^{-1}$
$(9.90\times 10^{-2}) -$WFG 9 3 $5.4672\times 10^{-1}$
$(4.01\times 10^{-3})$$5.4305\times 10^{-1}$
$(4.39\times 10^{-3}) -$$5.4556\times 10^{-1}$
$(4.15\times 10^{-3}) \approx$$5.3250\times 10^{-1}$
$(7.93\times 10^{-3}) -$$5.1727\times 10^{-1}$
$(6.14\times 10^{-3}) -$$5.3388\times 10^{-1}$
$(3.57\times 10^{-2}) -$$5.5169\times 10^{-1}$
$(2.77\times 10^{-3}) +$5 $7.4690\times 10^{-1}$
$(7.37\times 10^{-3})$$7.2964\times 10^{-1}$
$(3.46\times 10^{-2}) -$$7.4974\times 10^{-1}$
$(1.09\times 10^{-2}) \approx$$7.0129\times 10^{-1}$
$(2.16\times 10^{-2}) -$$5.6438\times 10^{-1}$
$(7.52\times 10^{-2}) -$$7.5745\times 10^{-1}$
$(8.38\times 10^{-3}) +$$7.6119\times 10^{-1}$
$(9.23\times 10^{-3}) +$10 $9.1417\times 10^{-1}$
(6.91\times 10^{-2})$$8.8646\times 10^{-1}$
$(5.24\times 10^{-2}) -$$8.6481\times 10^{-1}$
$(5.55\times 10^{-2}) -$$7.2445\times 10^{-1}$
$(3.42\times 10^{-2}) -$$7.8885\times 10^{-1}$
$(2.14\times 10^{-2}) -$$9.2002\times 10^{-1}$
$(3.54\times 10^{-2}) +$$9.0227\times 10^{-1}$
$(3.79\times 10^{-2}) -$15 $9.1357\times 10^{-1}$
$(2.00\times 10^{-2})$$8.8219\times 10^{-1}$
$(7.37\times 10^{-2}) -$$7.4786\times 10^{-1}$
$(6.55\times 10^{-2}) -$$6.3510\times 10^{-1}$
$(1.21\times 10^{-1}) -$$1.5569\times 10^{-1}$
$(5.20\times 10^{-2}) -$$8.5783\times 10^{-1}$
$(6.48\times 10^{-2}) -$$8.3130\times 10^{-1}$
$(6.30\times 10^{-2}) -$$+$ / $\approx$ / $-$ 3 / 13 / 20 2 / 8 / 26 0 / 2 / 34 1 / 6 / 29 2 / 1 / 33 8 / 9 / 19 $+$, $\approx$和$-$分别表示获得的结果与R2-RVEA相比更好, 相似和更差. 表 5 R2-RVEA、NSGA-Ⅲ、RVEA、MOEA/DD、MOMBI-Ⅱ、KnEA和TS-R2EA在WFG1-WFG9上获得的HV值的统计结果(均值和标准差). 最好的结果已突出
Table 5 The statistical results (mean and standard deviation) of the IGD + values obtained by R2-RVEA, NSGA-Ⅲ, RVEA, MOEA/DD, MOMBI-Ⅱ, KnEA and TS-R2EA on WFG1 to WFG9. The best results are highlighted
问题 $M$ R2-RVEA NSGA-Ⅲ RVEA MOEA/DD MOMBI-Ⅱ KnEA TS-R2EA WFG 1 3 $7.5115\times 10^{-2}$
$(4.52\times 10^{-2})$$8.7381\times 10^{-2}$
$(5.15\times 10^{-2}) -$$6.9562\times 10^{-2}$
$(6.53\times 10^{-3}) +$$1.0065\times 10^{-1}$
$(6.77\times 10^{-2}) -$$1.4254\times 10^{-1}$
$(8.81\times 10^{-2}) -$$5.6061\times 10^{-1}$
$(2.31\times 10^{-1}) -$$7.8279\times 10^{-2}$
$(5.68\times 10^{-2}) -$5 $1.8626\times 10^{-1}$
$(9.57\times 10^{-3})$$2.1152\times 10^{-1}$
$(4.66\times 10^{-2}) -$$2.0426\times 10^{-1}$
$(6.98\times 10^{-2}) -$$1.6063\times 10^{-1}$
$(5.98\times 10^{-2}) +$$5.4411\times 10^{-1}$
$(2.28\times 10^{-1}) -$$1.6029\times 10^{-1}$
$(3.40\times 10^{-2}) +$$2.0587\times 10^{-1}$
$(3.98\times 10^{-2}) -$10 $2.1900\times 10^{-1}$
$(9.07\times 10^{-3})$$2.1486\times 10^{-1}$
$(3.68\times 10^{-2}) +$$1.4214\times 10^{-1}$
$(6.67\times 10^{-2}) +$$1.4874\times 10^{-1}$
$(4.57\times 10^{-2}) +$$3.4832\times 10^{-1}$
$(2.62\times 10^{-2}) -$$2.7665\times 10^{-1}$
$(2.23\times 10^{-2}) -$$1.2162\times 10^{-1}$
$(2.67\times 10^{-2}) +$15 $2.8499\times 10^{-1}$
$(3.65\times 10^{-2})$$4.2663\times 10^{-1}$
$(1.78\times 10^{-1}) -$$3.6853\times 10^{-1}$
$(2.46\times 10^{-1}) \approx$$2.7065\times 10^{-1}$
$(1.77\times 10^{-1}) \approx$$4.1737\times 10^{0}$
$(5.59\times 10^{0}) -$$4.8136\times 10^{-1}$
$(1.63\times 10^{-1}) -$$2.5708\times 10^{-1}$
$(1.53\times 10^{-1}) \approx$WFG 2 3 $8.6719\times 10^{-2}$
$(3.01\times 10^{-2})$$7.6168\times 10^{-2}$
$(9.03\times 10^{-3}) +$$1.0187\times 10^{-1}$
$(2.00\times 10^{-2}) -$$8.9857\times 10^{-2}$
$(1.30\times 10^{-2}) -$$9.6736\times 10^{-2}$
$(1.76\times 10^{-2}) -$$1.0500\times 10^{-1}$
$(4.39\times 10^{-2}) -$$7.6067\times 10^{-2}$
$(1.80\times 10^{-2}) +$5 $1.8338\times 10^{-1}$
$(1.20\times 10^{-2})$$1.9276\times 10^{-1}$
$(1.34\times 10^{-2}) -$$1.8425\times 10^{-1}$
$(4.47\times 10^{-2}) \approx$$2.8035\times 10^{-1}$
$(2.30\times 10^{-2}) -$$2.7826\times 10^{-1}$
$(7.03\times 10^{-2}) -$$1.3904\times 10^{-1}$
$(2.72\times 10^{-2}) +$$2.0231\times 10^{-1}$
$(4.36\times 10^{-2}) -$10 $8.9305\times 10^{-2}$
$(1.58\times 10^{-2})$$4.1897\times 10^{-1}$
$(1.87\times 10^{-1}) -$$2.3948\times 10^{-1}$
$(6.82\times 10^{-2}) -$$3.1155\times 10^{-1}$
$(2.39\times 10^{-2}) -$$1.7810\times 10^{-1}$
$(2.42\times 10^{-1}) -$$1.7637\times 10^{-1}$
$(3.53\times 10^{-2}) -$$1.3011\times 10^{-1}$
$(5.09\times 10^{-2}) -$15 $2.1600\times 10^{-1}$
$(5.32\times 10^{-1})$$7.5861\times 10^{-1}$
$(1.48\times 10^{-1}) -$$5.0074\times 10^{-1}$
$(1.80\times 10^{-1}) -$$4.2257\times 10^{-1}$
$(1.08\times 10^{-1}) -$$4.3099\times 10^{0}$
$(4.12\times 10^{0}) -$$8.7000\times 10^{-1}$
$(3.55\times 10^{-1}) -$$2.8770\times 10^{-1}$
$(1.22\times 10^{-1}) -$WFG 3 3 $4.2032\times 10^{-2}$
$(5.04\times 10^{-3})$$6.1249\times 10^{-2}$
$(7.76\times 10^{-3}) -$$1.5612\times 10^{-1}$
$(1.82\times 10^{-2}) -$$1.6785\times 10^{-1}$
$(3.80\times 10^{-2}) -$$6.4076\times 10^{-2}$
$(1.72\times 10^{-2}) -$$2.7852\times 10^{-2}$
$(1.39\times 10^{-2}) +$$4.8933\times 10^{-2}$
$(8.39\times 10^{-3}) -$5 $2.8475\times 10^{-1}$
$(1.79\times 10^{-2})$$3.5253\times 10^{-1}$
$(3.53\times 10^{-2}) -$$4.6344\times 10^{-1}$
$(7.97\times 10^{-2}) -$$4.7518\times 10^{-1}$
$(5.46\times 10^{-2}) -$$9.7449\times 10^{-1}$
$(1.26\times 10^{-1}) -$$3.5587\times 10^{-1}$
$(8.30\times 10^{-2}) -$$3.6494\times 10^{-1}$
$(3.92\times 10^{-2}) -$10 $6.0947\times 10^{0}$
$(1.11\times 10^{0})$$1.3173\times 10^{0}$
$(3.71\times 10^{-1}) +$$2.7301\times 10^{0}$
$(1.39\times 10^{-1}) +$$2.1179\times 10^{0}$
$(5.86\times 10^{-2}) +$$9.6735\times 10^{0}$
$(4.62\times 10^{-2}) -$$1.2618\times 10^{0}$
$(1.71\times 10^{-1}) +$$1.3693\times 10^{0}$
$(2.64\times 10^{-1}) +$15 $9.9835\times 10^{0}$
$(3.20\times 10^{0})$$2.3745\times 10^{0}$
$(7.30\times 10^{-1}) +$$3.7988\times 10^{0}$
$(1.10\times 10^{-1}) +$$3.6219\times 10^{0}$
$(2.39\times 10^{-2}) +$$1.4650\times 10^{1}$
$(4.10\times 10^{-2}) -$$3.4151\times 10^{0}$
$(5.06\times 10^{-1}) +$$2.9664\times 10^{0}$
$(3.46\times 10^{-1}) +$WFG 4 3 $7.0960\times 10^{-1}$
$(2.95\times 10^{-4}) +$$7.1039\times 10^{-2}$
$(2.66\times 10^{-4}) \approx$$7.3769\times 10^{-2}$
$(9.55\times 10^{-4}) -$$8.7146\times 10^{-2}$
$(1.36\times 10^{-3}) -$$7.3561\times 10^{-2}$
$(6.52\times 10^{-3}) -$$9.2246\times 10^{-2}$
$(3.64\times 10^{-3}) -$$7.1212\times 10^{-2}$
$(5.81\times 10^{-4}) -$5 $3.2825\times 10^{-1}$
$(5.42\times 10^{-4})$$3.2857\times 10^{-1}$
$(9.93\times 10^{-4}) \approx$$3.3068\times 10^{-1}$
$(1.33\times 10^{-3}) -$$3.9675\times 10^{-1}$
$(9.57\times 10^{-4}) -$$3.3731\times 10^{-1}$
$(1.57\times 10^{-2}) -$$3.6449\times 10^{-1}$
$(6.75\times 10^{-3}) -$$3.2845\times 10^{-1}$
$(3.57\times 10^{-3}) \approx$10 $8.7337\times 10^{-1}$
$(2.69\times 10^{-3})$$1.0667\times 10^{0}$
$(5.15\times 10^{-1}) -$$8.9065\times 10^{-1}$
$(9.51\times 10^{-3}) -$$1.1221\times 10^{0}$
$(8.06\times 10^{-3}) -$$2.3431\times 10^{0}$
$(1.47\times 10^{0}) -$$1.0544\times 10^{0}$
$(8.22\times 10^{-3}) -$$8.7977\times 10^{-1}$
$(8.85\times 10^{-3}) -$15 $1.2733\times 10^{0}$
$(2.41\times 10^{-3})$$3.0661\times 10^{0}$
$(1.63\times 10^{0}) -$$1.3006\times 10^{0}$
$(1.64\times 10^{-1}) \approx$$1.6260\times 10^{0}$
$(6.21\times 10^{-1}) -$$1.7552\times 10^{1}$
$(2.32\times 10^{0}) -$$1.3759\times 10^{0}$
$(2.11\times 10^{-2}) -$$1.3775\times 10^{0}$
$(4.21\times 10^{-1}) -$WFG 5 3 $1.2755\times 10^{-1}$
$(4.48\times 10^{-6})$$1.2755\times 10^{-1}$
$(6.82\times 10^{-6}) \approx$$1.2881\times 10^{-1}$
$(4.47\times 10^{-4}) -$$1.4202\times 10^{-1}$
$(1.02\times 10^{-3}) -$$1.3745\times 10^{-1}$
$(1.38\times 10^{-3}) -$$1.9609\times 10^{-1}$
$(6.08\times 10^{-2}) -$$1.2741\times 10^{-1}$
$(3.43\times 10^{-4}) \approx$5 $3.8901\times 10^{-1}$
$(2.61\times 10^{-5})$$3.8902\times 10^{-1}$
$(4.13\times 10^{-5}) \approx$$3.8944\times 10^{-1}$
$(1.32\times 10^{-4}) -$$4.5522\times 10^{-1}$
$(4.11\times 10^{-4}) -$$4.0177\times 10^{-1}$
$(1.22\times 10^{-2}) -$$4.2985\times 10^{-1}$
$(8.65\times 10^{-3}) -$$3.8747\times 10^{-1}$
$(3.84\times 10^{-3}) \approx$10 $9.3301\times 10^{-1}$
$(9.11\times 10^{-4})$$9.3354\times 10^{-1}$
$(1.06\times 10^{-3}) \approx$$9.4055\times 10^{-1}$
$(4.40\times 10^{-3}) -$$1.1723\times 10^{0}$
$(3.55\times 10^{-3}) -$$1.2453\times 10^{0}$
$(2.17\times 10^{-2}) -$$1.0843\times 10^{0}$
$(2.67\times 10^{-2}) -$$9.5531\times 10^{-1}$
$(5.26\times 10^{-3}) -$15 $1.3309\times 10^{0}$
$(1.47\times 10^{-3})$$2.3724\times 10^{0}$
$(2.25\times 10^{0}) -$$1.3259\times 10^{0}$
$(7.86\times 10^{-3}) +$$1.5056\times 10^{0}$
$(9.76\times 10^{-3}) -$$2.3006\times 10^{1}$
$(2.02\times 10^{0}) -$$1.4335\times 10^{0}$
$(2.73\times 10^{-2}) -$$1.3346\times 10^{0}$
$(2.11\times 10^{-3}) -$WFG 6 3 $1.4696\times 10^{-1}$
$(1.96\times 10^{-2})$$1.3922\times 10^{-1}$
$(2.02\times 10^{-2}) \approx$$1.5111\times 10^{-1}$
$(1.85\times 10^{-2}) \approx$$1.6034\times 10^{-1}$
$(1.84\times 10^{-2}) -$$1.4684\times 10^{-1}$
$(2.31\times 10^{-2}) \approx$$1.9074\times 10^{-1}$
$(1.64\times 10^{-2}) -$$1.4918\times 10^{-1}$
$(2.14\times 10^{-2}) \approx$5 $4.1833\times 10^{-1}$
$(2.17\times 10^{-2})$$4.1223\times 10^{-1}$
$(2.09\times 10^{-2}) \approx$$4.1516\times 10^{-1}$
$(2.48\times 10^{-2}) \approx$$4.8181\times 10^{-1}$
$(2.89\times 10^{-2}) -$$4.2618\times 10^{-1}$
$(5.46\times 10^{-2}) \approx$$5.0750\times 10^{-1}$
$(2.91\times 10^{-2}) -$$4.0415\times 10^{-1}$
$(2.16\times 10^{-2}) \approx$10 $9.5617\times 10^{-1}$
$(1.65\times 10^{-2})$$9.6279\times 10^{-1}$
$(2.14\times 10^{-2}) \approx$$9.9145\times 10^{-1}$
$(3.18\times 10^{-2}) -$$1.2157\times 10^{0}$
$(2.50\times 10^{-2}) -$$9.5786\times 10^{-1}$
$(3.29\times 10^{-2}) \approx$$1.1230\times 10^{0}$
$(3.04\times 10^{-2}) -$$9.7574\times 10^{-1}$
$(2.37\times 10^{-2}) -$15 $1.3522\times 10^{0}$
$(1.58\times 10^{-2})$$1.6632\times 10^{0}$
$(1.10\times 10^{-1}) -$$1.4286\times 10^{0}$
$(4.27\times 10^{-2}) -$$1.5291\times 10^{0}$
$(2.96\times 10^{-2}) -$$1.5286\times 10^{1}$
$(3.49\times 10^{0}) -$$1.5321\times 10^{0}$
$(5.28\times 10^{-2}) -$$1.3721\times 10^{0}$
$(3.17\times 10^{-2}) -$WFG 7 3 $7.1361\times 10^{-2}$
$(3.23\times 10^{-4})$$7.1371\times 10^{-2}$
$(3.07\times 10^{-4}) \approx$$7.3630\times 10^{-2}$
$(5.88\times 10^{-4}) -$$8.9150\times 10^{-2}$
$(1.87\times 10^{-3}) -$$7.3845\times 10^{-2}$
$(8.23\times 10^{-3}) -$$3.2485\times 10^{-1}$
$(1.88\times 10^{-2}) -$$7.0651\times 10^{-2}$
$(7.82\times 10^{-5}) +$5 $3.3002\times 10^{-1}$
$(6.74\times 10^{-4})$$3.3105\times 10^{-1}$
$(1.15\times 10^{-3}) -$$3.3337\times 10^{-1}$
$(1.46\times 10^{-3}) -$$4.0782\times 10^{-1}$
$(9.79\times 10^{-3}) -$$3.2920\times 10^{-1}$
$(3.76\times 10^{-3}) +$$3.8174\times 10^{-1}$
$(1.44\times 10^{-2})$$3.2722\times 10^{-1}$
$(4.37\times 10^{-4}) +$10 $8.8858\times 10^{-1}$
$(4.99\times 10^{-3})$$9.3332\times 10^{-1}$
$(1.58\times 10^{-1}) \approx$$8.9287\times 10^{-1}$
$(4.96\times 10^{-3}) -$$1.1039\times 10^{0}$
$(1.27\times 10^{-2}) -$$9.8755\times 10^{-1}$
$(3.48\times 10^{-1}) -$$9.6895\times 10^{-1}$
$(1.47\times 10^{-2}) -$$8.9890\times 10^{-1}$
$(1.10\times 10^{-2}) -$15 $1.2798\times 10^{0}$
$(7.32\times 10^{-3})$$2.6475\times 10^{0}$
$(7.87\times 10^{-1}) -$$2.6579\times 10^{0}$
$(6.81\times 10^{-1}) -$$1.6730\times 10^{0}$
$(5.69\times 10^{-1}) -$$1.3576\times 10^{0}$
$(2.40\times 10^{0}) -$$1.5766\times 10^{0}$
$(5.83\times 10^{-1}) -$$1.6838\times 10^{0}$
$(6.24\times 10^{-1}) -$WFG 8 3 $2.0276\times 10^{-1}$
$(2.38\times 10^{-3})$$2.0043\times 10^{-1}$
$(5.27\times 10^{-3}) +$$2.1262\times 10^{-1}$
$(2.76\times 10^{-3}) -$$2.2068\times 10^{-1}$
$(8.51\times 10^{-3}) -$$2.2094\times 10^{-1}$
$(3.61\times 10^{-3}) -$$2.2380\times 10^{-1}$
$(4.90\times 10^{-3}) -$$1.9590\times 10^{-1}$
$(3.10\times 10^{-3}) +$5 $6.0819\times 10^{-1}$
$(1.75\times 10^{-3})$$6.0468\times 10^{-1}$
$(1.31\times 10^{-3}) +$$6.1524\times 10^{-1}$
$(9.59\times 10^{-3}) -$$6.4945\times 10^{-1}$
$(1.99\times 10^{-2}) -$$1.1632\times 10^{0}$
$(3.44\times 10^{-2}) -$$6.9589\times 10^{-1}$
$(2.50\times 10^{-2}) -$$6.1227\times 10^{-1}$
$(2.15\times 10^{-3}) -$10 $1.7814\times 10^{0}$
(2.24\times 10^{-1})$$3.1854\times 10^{0}$
$(1.15\times 10^{0}) -$$1.2981\times 10^{0}$
$(2.89\times 10^{-1}) +$$1.3753\times 10^{0}$
$(1.37\times 10^{-1}) +$$3.7183\times 10^{0}$
$(1.07\times 10^{0}) -$$1.4339\times 10^{0}$
$(2.03\times 10^{-1}) +$$1.5086\times 10^{0}$
$(3.02\times 10^{-1}) \approx$15 $4.1237\times 10^{0}$
$(1.62\times 10^{0})$$8.8664\times 10^{0}$
$(1.08\times 10^{0}) -$$2.7442\times 10^{0}$
$(1.99\times 10^{0}) +$$3.6008\times 10^{0}$
$(1.27\times 10^{0}) \approx$$1.6919\times 10^{1}$
$(2.15\times 10^{0}) -$$2.2133\times 10^{0}$
$(6.49\times 10^{-1}) +$$2.3419\times 10^{0}$
$(1.23\times 10^{0}) +$WFG 9 3 $9.1371\times 10^{-2}$
$(8.31\times 10^{-3})$$9.8060\times 10^{-2}$
$(7.55\times 10^{-3}) -$$9.4218\times 10^{-2}$
$(5.27\times 10^{-3}) -$$1.1083\times 10^{-1}$
$(7.33\times 10^{-3}) -$$1.2051\times 10^{-1}$
$(7.64\times 10^{-3}) -$$4.1313\times 10^{-1}$
$(5.50\times 10^{-2}) -$$8.5058\times 10^{-2}$
$(3.66\times 10^{-3}) +$5 $4.0014\times 10^{-1}$
$(3.90\times 10^{-2})$$4.1637\times 10^{-1}$
$(4.75\times 10^{-2}) -$$3.7828\times 10^{-1}$
$(1.29\times 10^{-2}) +$$4.8038\times 10^{-1}$
$(3.90\times 10^{-2}) -$$7.4087\times 10^{-1}$
$(1.12\times 10^{-1}) -$$3.8673\times 10^{-1}$
$(1.23\times 10^{-2}) \approx$$3.6848\times 10^{-1}$
$(1.24\times 10^{-2}) +$10 $1.0158\times 10^{0}$
(2.47\times 10^{-2})$$1.4614\times 10^{0}$
$(7.52\times 10^{-1}) -$$9.7817\times 10^{-1}$
$(3.09\times 10^{-2}) +$$1.2487\times 10^{0}$
$(6.41\times 10^{-2}) -$$1.8261\times 10^{0}$
$(4.88\times 10^{-1}) -$$1.0663\times 10^{0}$
$(2.44\times 10^{-2}) -$$1.0275\times 10^{0}$
$(6.41\times 10^{-2}) \approx$15 $1.6670\times 10^{0}$
(1.67\times 10^{-1})$$5.6055\times 10^{0}$
$(1.89\times 10^{0}) -$$1.5770\times 10^{0}$
$(3.10\times 10^{-1}) +$$2.0273\times 10^{0}$
$(6.11\times 10^{-1}) -$$2.4264\times 10^{1}$
$(1.08\times 10^{0}) -$$1.7242\times 10^{0}$
$(3.23\times 10^{-1}) \approx$$1.6462\times 10^{0}$
$(3.71\times 10^{-1}) \approx$$+$ / $\approx$ / $-$ 6 / 10 / 20 10 / 5 / 21 5 / 2 / 29 1 / 3 / 32 7 / 2 / 27 10 / 9 / 17 +, $\approx$和$-$分别表示获得的结果与R2-RVEA相比更好, 相似和更差. 表 6 R2-RVEA与其他算法的测试对比
Table 6 Comparison between R2-RVEA and other algorithms
对比算法 对比指标 HV IGD+ NSGA-Ⅲ 6 20 38 11 17 36 RVEA 10 17 37 18 13 33 MOEA/DD 9 11 44 16 9 39 MOMBI-Ⅱ 6 11 47 4 11 49 KnEA 4 1 59 13 4 47 TS-R2EA 17 16 31 21 15 28 + $\approx$ $-$ + $\approx$ $-$ -
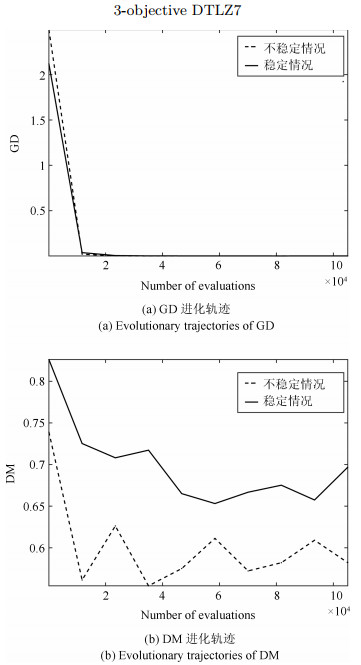
[1] Deb K. Multi-Objective Optimization using Evolutionary Algorithms. New York: John Wiley and Sons, 2001. 13-49 [2] Zhou A M, Qu B Y, Li H, Zhao S Z, Suganthan P N, Zhang Q F. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm and Evolutionary Computation, 2011, 1(1): 32-49 doi: 10.1016/j.swevo.2011.03.001 [3] Zhang J W, Xing L N. A survey of multiobjective evolutionary algorithms. In: Proceedings of the 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC). Guangzhou, China: IEEE, 2017. 93-100 [4] Fleming P J, Purshouse R C, Lygoe R J. Many-objective optimization: An engineering design perspective. In: Proceedings of the 3rd International Conference on Evolutionary Multi-Criterion Optimization. Guanajuato, Mexico: Springer, 2005. 14-32 [5] Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197 doi: 10.1109/4235.996017 [6] Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm, Technical Report 103, Computer Engineering and Communication Networks Lab (TIK), Swiss Federal Institute of Technology (ETH), Switzerland, 2001. [7] Batista L S, Campelo F, Guimarães F G, Ramírez J A. Pareto cone varepsilon-dominance: Improving convergence and diversity in multiobjective evolutionary algorithms. In: Proceedings of the 6th International Conference on Evolutionary Multi-Criterion Optimization. Ouro Preto, Brazil: Springer, 2011. 76-90 [8] Zou X F, Chen Y, Liu M Z, Kang L S. A new evolutionary algorithm for solving many-objective optimization problems. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2008, 38(5): 1402-1412 doi: 10.1109/TSMCB.2008.926329 [9] He Z N, Yen G G, Zhang J. Fuzzy-based Pareto optimality for many-objective evolutionary algorithms. IEEE Transactions on Evolutionary Computation, 2014, 18(2): 269-285 doi: 10.1109/TEVC.2013.2258025 [10] Di Pierro F, Khu S T, Savic D A. An investigation on preference order ranking scheme for multiobjective evolutionary optimization. IEEE Transactions on Evolutionary Computation, 2007, 11(1): 17-45 doi: 10.1109/TEVC.2006.876362 [11] Yang S X, Li M Q, Liu X H, Zheng J H. A grid-based evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2013, 17(5): 721-736 doi: 10.1109/TEVC.2012.2227145 [12] Zhang X Y, Tian Y, Jin Y C. A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2015, 19(6): 761-776 doi: 10.1109/TEVC.2014.2378512 [13] Zhang Q F, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731 doi: 10.1109/TEVC.2007.892759 [14] Liu H L, Gu F Q, Zhang Q F. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 450-455 doi: 10.1109/TEVC.2013.2281533 [15] Chen L, Liu H L, Lu C, Cheung Y M, Zhang J. A novel evolutionary multi-objective algorithm based on S metric selection and M2M population decomposition. In: Proceedings of the 18th Asia Pacific Symposium on Intelligent and Evolutionary Systems - Volume 2. Bangkok, Thailand: Springer, 2015. 441-452 [16] Cheng R, Jin Y C, Olhofer M, Sendhoff B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791 doi: 10.1109/TEVC.2016.2519378 [17] Jiang S Y, Yang S X. A strength Pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization. IEEE Transactions on Evolutionary Computation, 2017, 21(3): 329-346 doi: 10.1109/TEVC.2016.2592479 [18] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part Ⅰ: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601 doi: 10.1109/TEVC.2013.2281535 [19] Zitzler E, Künzli S. Indicator-based selection in multiobjective search. In: Proceedings of the 8th International Conference on Parallel Problem Solving from Nature. Birmingham, United Kingdom: Springer, 2004. 832-842 [20] Bader J, Zitzler E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary Computation, 2011, 19(1): 45-76 doi: 10.1162/EVCO_a_00009 [21] Beume N, Naujoks B, Emmerich M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. European Journal of Operational Research, 2007, 181(3): 1653-1669 doi: 10.1016/j.ejor.2006.08.008 [22] Li M Q, Yang S X, Liu X H. Pareto or non-Pareto: Bi-criterion evolution in multiobjective optimization. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 645-665 doi: 10.1109/TEVC.2015.2504730 [23] Van Veldhuizen D A, Lamont B G. Multiobjective evolutionary algorithms: Analyzing the state-of-the-art. Evolutionary Computation, 2000, 8(2): 125-147 doi: 10.1162/106365600568158 [24] Wang H D, Jin Y C, Yao X. Diversity assessment in many-objective optimization. IEEE Transactions on Cybernetics, 2017, 47(6): 1510-1522 doi: 10.1109/TCYB.2016.2550502 [25] Zhou A M, Jin Y C, Zhang Q F, Sendhoff B, Tsang E. Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion. In: Proceedings of the 2006 IEEE International Conference on Evolutionary Computation. Vancouver, BC, Canada: IEEE, 2006. 892-899 [26] While L, Hingston P, Barone L, Huband S. A faster algorithm for calculating hypervolume. IEEE Transactions on Evolutionary Computation, 2006, 10(1): 29-38 doi: 10.1109/TEVC.2005.851275 [27] Brockhoff D, Wagner T, Trautmann H. On the properties of the R2 indicator. In: Proceedings of the 14th Annual Conference on Genetic and Evolutionary Computation. Philadelphia, Pennsylvania, USA: ACM, 2012. 465-472 [28] Tian Y, Zhang X Y, Cheng R, Jin Y C. A multi-objective evolutionary algorithm based on an enhanced inverted generational distance metric. In: Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC). Vancouver, BC, Canada: IEEE, 2016. 5222-5229 [29] Tian Y, Cheng R, Zhang X Y, Cheng F, Jin Y C. An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility. IEEE Transactions on Evolutionary Computation, 2018, 22(4): 609-622 doi: 10.1109/TEVC.2017.2749619 [30] Sun Y N, Yen G G, Yi Z. IGD indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Transactions on Evolutionary Computation, 2019, 23(2): 173-187 doi: 10.1109/TEVC.2018.2791283 [31] Phan D H, Suzuki J. R2-IBEA: R2 indicator based evolutionary algorithm for multiobjective optimization. In: Proceedings of the 2013 IEEE Congress on Evolutionary Computation. Cancun, Mexico: IEEE, 2013. 1836-1845 [32] Trautmann H, Wagner T, Brockhoff D. R2-EMOA: Focused multiobjective search using R2-indicator-based selection. In: Proceedings of the 7th International Conference on Learning and Intelligent Optimization. Catania, Italy: Springer, 2013. 70-74 [33] Gómez R H, Coello C A C. Improved metaheuristic based on the R2 indicator for many-objective optimization. In: Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation. Madrid, Spain: ACM, 2015. 679-686 [34] Li F, Cheng R, Liu J C, Jin Y C. A two-stage R2 indicator based evolutionary algorithm for many-objective optimization. Applied Soft Computing, 2018, 67: 245-260 doi: 10.1016/j.asoc.2018.02.048 [35] Das I, Dennis J E. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM Journal on Optimization, 1998, 8(3): 631-657 doi: 10.1137/S1052623496307510 [36] Li K, Deb K, Zhang Q F, Kwong S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Transactions on Evolutionary Computation, 2015, 19(5): 694-716 doi: 10.1109/TEVC.2014.2373386 [37] Deb K, Thiele L, Laumanns M, Zitzler E. Scalable test problems for evolutionary multiobjective optimization. Evolutionary Multiobjective Optimization. London: Springer, 2005. 105-145 [38] Huband S, Barone L, While L, Hingston P. A scalable multi-objective test problem toolkit. In: Proceedings of the 3rd International Conference on Evolutionary Multi-Criterion Optimization. Guanajuato, Mexico: Springer, 2005. 280-295 [39] Tian Y, Cheng R, Zhang X Y, Jin Y C. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization[Educational Forum]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87 doi: 10.1109/MCI.2017.2742868 [40] Deb K, Agrawal R B. Simulated binary crossover for continuous search space. Complex Systems, 1995, 9(2): 115-148 http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=0A9E92AEA8531E5C5E5F48D5FA440D42?doi=10.1.1.26.8485&rep=rep1&type=pdf [41] Deb K, Goyal M. A combined genetic adaptive search (GeneAS) for engineering design. Computer Science and Informatics, 1996, 26(4): 30-45 http://www.researchgate.net/publication/2335418_A_Combined_Genetic_Adaptive_Search_GeneAS_for_Engineering [42] Ishibuchi H, Masuda H, Tanigaki Y, Nojima Y. Modified distance calculation in generational distance and inverted generational distance. In: Proceedings of the 8th International Conference on Evolutionary Multi-Criterion Optimization. Guimarães, Portugal: Springer, 2015. 110-125 -





 下载:
下载: