-
摘要: 在灰狼优化算法中, $ {{\pmb C}} $是一个重要的参数, 其功能是负责算法的勘探能力.目前, 针对参数$ {{\pmb C}} $的研究工作相对较少.另外, 在算法进化过程中, 群体中其他个体均向$\alpha$、$\beta$和$\delta$所在区域靠近以加快收敛速度.然而, 算法易陷入局部最优.为解决以上问题, 本文提出一种改进的灰狼优化算法(Lens imaging learning grey wolf optimizer algorithm, LIL-GWO).该算法首先分析了参数$ {{\pmb C}} $的作用, 提出一种新的参数$\pmb C$策略以平衡算法的勘探和开采能力; 同时, 分析了灰狼优化算法后期个体均向决策层区域聚集, 从而导致群体多样性较差, 提出一种基于光学透镜成像原理的反向学习策略以避免算法陷入局部最优.对LIL-GWO算法的收敛性进行了证明.选取12个通用的标准测试函数和30个CEC 2014测试函数进行实验, 在相同的适应度函数评价次数条件下, LIL-GWO算法在总体性能上优于基本GWO算法、改进GWO算法和其他比较算法.最后, 将LIL-GWO算法应用于辨识光伏模型的参数, 获得了满意的结果.Abstract: In the grey wolf optimizer algorithm, $\pmb C$ is an important parameter. The exploration capability of GWO mainly depends on the parameter $\pmb C$. At present, few of researchers are aiming at parameter $\pmb C$ in GWO algorithm. Many issues need to be settled. In addition, during the evolution process, the other individuals in the population move towards to the $\alpha$, $\beta$ and $\delta$ which are to accelerate convergence. However, the algorithm is easy to trap in the local optima. In this paper, an improved GWO algorithm called LIL-GWO is proposed to solve these problems. The proposed algorithm firstly analyzes the role of parameter $\pmb C$ and presents a new parameter $\pmb C$ strategy to balance between exploration and exploitation of GWO. Secondly, at the end of the GWO algorithm, all individuals assemble into the decision-making region which is resulted in poor population multiplicity. A new opposition-learning strategy based on optical lens imaging principle is proposed to help the population jump out of a local optimum. A theoretical proof of convergence for LIL-GWO algorithm is provided. Simulation experiments were conducted on the 12 widely used benchmark test functions and 30 benchmark test functions from the CEC 2014. The overall performance of LIL-GWO algorithm is much better than the basic GWO algorithm, several improved GWO algorithms, and other compared algorithms with the same number of fitness evaluations (FEs). Finally, LIL-GWO is applied to identify the parameters of PV model and the satisfied results are obtained.
-
Key words:
- Grey wolf optimizer (GWO) algorithm /
- lens imaging learning (LIL) /
- global optimization /
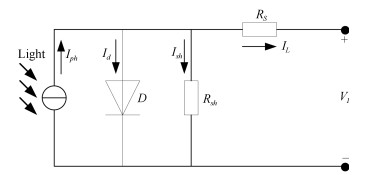
- photovoltaic model /
- parameter identification
1) 本文责任编委 王鼎 -
表 1 12个标准测试函数
Table 1 Twelve benchmark test functions
函数名 函数表达式 搜索空间 Sphere $ f_1 ({{\pmb X}}) =\sum\nolimits_{i = 1}^D {x_i^2 }$ $[-100, 100]$ Schwefel's 2.22 $ f_2 ({{\pmb X}}) =\sum\nolimits_{i = 1}^D {{\rm{|}}x_i {\rm{|}}}+\prod\nolimits_{i = 1}^D {|x_i |}$ $[-10, 10]$ Schwefel's 2.21 $ f_3 ({{\pmb X}}) = \max _i \{|x_i |, 1\le x_i\le D\}$ $[-100, 100]$ Rosenbrock $ f_4 ({{\pmb X}}) = \sum\nolimits_{i = 1}^D {[100{\kern 1pt} {\kern 1pt} (x_{i + 1} - x_i^2 )^2 + (x_i - 1)^2 ]}$ [-30, 30] Sum-Power $f_5 ({{\pmb X}}) = \sum\nolimits_{i=1}^D {|x_i |} ^{(i + 1)}$ [-1, 1] Elliptic $f_6 ({{\pmb X}}) =\sum\nolimits_{i =1}^D {(10^6)^{(i - 1)/(n - 1)} x_i^2 }$ [-100, 100] Rastrigin $f_7 ({{\pmb X}}) =\sum\nolimits_{i =1}^D {[x_i^2- 10\cos (2\pi x_i) + 10]}$ $[-5.12, 5.12]$ Ackley $ f_8 ({{\pmb X}}) =- 20\exp\left({ - 0.2\sqrt {{\textstyle{1 \over D}}\sum\nolimits_{i =1}^D {x_i^2 } } } \right) - \exp \left({{\frac{1}{D}}\sum\nolimits_{i =1}^D {\cos (2\pi x_i)} } \right) + 20 + e $ $[-32, 32]$ Griewank $ f_9 ({{\pmb X}}) = {\textstyle{1\over {4\, 000}}}\sum\nolimits_{i = 1}^D {x_i^2-\prod\nolimits_{i = 1}^D {\cos \left({{\textstyle{{x_i } \over{\sqrt i }}}} \right)} }+ 1$ $[-600, 600]$ Alpine $ f_{10} ({{\pmb X}}) =\sum\nolimits_{i= 1}^D {|x_i \sin (x_i) + 0.1x_i |} $ $[-10, 10]$ Levy $ f_{11} ({{\pmb X}}) =\sum\nolimits_{i = 1}^D {(x_i- 1)^2 [1 + \sin ^2 (3\pi x_{i + 1})] + \sin ^2 (3 \pi x_1) + |x_D- 1|} [1 + \sin ^2 (3\pi x_D)] $ $[-10, 10]$ Stretched V-sine $ f_{12} ({{\pmb X}}) =\sum\nolimits_{i = 1}^{D - 1} {(x_i^2+ 2x_{i + 1}^2)^{0.25}\cdot ((\sin 50(x_i^2+ x_{i + 1}^2)^{0.1})^2+ 1)} $ $[-10, 10]$ 表 2 LIL-GWO与其他5种算法对12个测试函数的结果比较
Table 2 Comparisons of LIL-GWO and other five algorithms for 12 test functions
函数 统计结果 GWO mGWO WAGWO AIGWO EEGWO LIL-GWO 平均值 $ 1.36 \times 10^{ - 29} $ $ 7.89 \times 10^{ - 44} $ $ 7.66 \times 10^{ - 35} $ $ 3.62 \times 10^{ - 42} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_1$ 标准差 $ 1.62 \times 10^{ - 29} $ $ 8.68 \times 10^{ - 44} $ $ 1.01 \times 10^{ - 34} $ $ 3.89 \times 10^{ - 42} $ 0 0 排名 6 3 5 4 1 1 平均值 $ 4.87 \times 10^{ - 18} $ $ 1.16\times 10^{ - 26} $ $ 6.83 \times 10^{ - 21} $ $ 1.38 \times 10^{ - 25} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_2$ 标准差 $ 2.58 \times 10^{ - 18} $ $ 6.14\times 10^{ - 27} $ $ 5.18 \times 10^{ - 21} $ $ 1.64 \times 10^{ - 25} $ 0 0 排名 6 3 5 4 1 1 平均值 $ 1.89 \times 10^{ - 7} $ $ 4.48\times 10^{ - 12} $ $ 6.97 \times 10^{ - 9} $ $ 3.17 \times 10^{ - 12} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_3$ 标准差 $ 8.81 \times 10^{ - 8} $ $ 6.38\times 10^{ - 12} $ $ 5.29 \times 10^{ - 9} $ $ 6.34 \times 10^{ - 12} $ 0 0 排名 6 4 5 3 1 1 平均值 $ 2.72 \times 10^{ 1} $ $ {\bf{2.71 \times 10}}^{\pmb{1}} $ $ 2.75 \times 10^{ 1} $ $ 2.78 \times 10^{ 1} $ $ 2.90 \times 10^{ 1} $ $ 2.89 \times 10^{ 1} $ $f_4$ 标准差 $ 9.99 \times 10^{ - 1} $ $ 6.53\times 10^{ - 1} $ $ 9.75 \times 10^{ - 1} $ $ 1.13 \times 10^{ 0} $ $ 5.58 \times 10^{ - 3} $ $ 7.43 \times 10^{ - 2} $ 排名 2 1 3 4 6 5 平均值 $ 1.44 \times 10^{ - 101} $ $ 4.69\times 10^{ - 152} $ $ 4.08 \times 10^{ - 121} $ $ 4.89 \times 10^{ - 154} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_5$ 标准差 $ 1.49 \times 10^{ - 101} $ $ 5.30\times 10^{ - 152} $ $ 5.77 \times 10^{ - 121} $ $ 2.80 \times 10^{ - 154} $ 0 0 排名 6 4 5 3 1 1 平均值 $ 9.01 \times 10^{ - 26} $ $ 3.12\times 10^{ - 40} $ $ 1.14 \times 10^{ - 31} $ $ 6.74 \times 10^{ - 40} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_6$ 标准差 $ 2.81 \times 10^{ - 25} $ $ 3.34\times 10^{ - 40} $ $ 9.06 \times 10^{ - 32} $ $ 1.24 \times 10^{ - 39} $ 0 0 排名 6 3 5 4 1 1 平均值 $ 2.08 \times 10^{ 0} $ $ {\pmb{0}} $ $ 4.54 \times 10^{ - 14} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_7$ 标准差 $ 4.64 \times 10^{ 0} $ 0 $ 2.54 \times 10^{ - 14} $ 0 0 0 排名 6 1 5 1 1 1 平均值 $ 6.84 \times 10^{ - 14} $ $ 1.23\times 10^{ - 14} $ $ 3.29 \times 10^{ - 14} $ $ 1.37 \times 10^{ - 14} $ $ {\pmb{8.88 \times 10}}^{ - {\pmb{16}}} $ $ {\pmb{8.88 \times 10}}^{ - {\pmb{16}}} $ $f_8$ 标准差 $ 1.08 \times 10^{ - 14} $ $ 3.89\times 10^{ - 15} $ $ 1.97 \times 10^{ - 15} $ $ 3.18 \times 10^{ - 15} $ 0 0 排名 6 3 5 4 1 1 平均值 $ 8.52 \times 10^{ - 13} $ $ 4.44\times 10^{ - 16} $ $ 4.17 \times 10^{ - 15} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_9$ 标准差 $ 3.03 \times 10^{ - 13} $ 0 $ 1.69 \times 10^{ - 15} $ 0 0 0 排名 6 4 5 1 1 1 平均值 $ 5.25 \times 10^{ - 4} $ $ 1.09\times 10^{ - 24} $ $ 1.05 \times 10^{ - 4} $ $ 9.70 \times 10^{ - 22} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_{10}$ 标准差 $ 5.34 \times 10^{ - 4} $ $ 2.18\times 10^{ - 24} $ $ 2.35 \times 10^{ - 4} $ $ 2.13 \times 10^{ - 21} $ 0 0 排名 6 3 5 4 1 1 平均值 $ 2.59 \times 10^{ - 31} $ $ 4.64\times 10^{ - 45} $ $ 6.40 \times 10^{ - 36} $ $ 2.32 \times 10^{ - 44} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_{11}$ 标准差 $ 1.34 \times 10^{ - 31} $ $ 7.73\times 10^{ - 45} $ $ 8.76 \times 10^{ - 36} $ $ 5.97 \times 10^{ - 44} $ 0 0 排名 6 3 5 4 1 1 平均值 $ 6.12 \times 10^{ - 8} $ $ 3.21\times 10^{ - 12} $ $ 3.82 \times 10^{ - 9} $ $ 1.75 \times 10^{ - 11} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_{12}$ 标准差 $ 1.74 \times 10^{ - 8} $ $ 2.24\times 10^{ - 12} $ $ 1.37 \times 10^{ - 9} $ $ 1.33 \times 10^{ - 11} $ 0 0 排名 6 3 5 4 1 1 平均排名 5.6667 2.9167 4.8333 3.3333 1.4167 1.3333 最终排名 6 3 5 4 2 1 表 3 LIL-GWOLIL-GWO与其他7种算法对12个函数的结果比较
Table 3 Comparisons of LIL-GWOLIL-GWO and other seven algorithms for 12 test functions
函数 统计结果 CMA-ES IPSO ODE GABC ETLBO IWOA ISCA LIL-GWO 平均值 $ 8.64 \times 10^{ - 11} $ $ 2.82\times 10^{ - 16} $ $ 2.68 \times 10^{ - 49} $ $ 4.00\times 10^{ - 16} $ $ 2.70 \times 10^{ - 119} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_1$ 标准差 $ 3.83 \times 10^{ - 11} $ $5.07 \times 10^{ - 16} $ $ 2.50 \times 10^{ - 49} $ $ 3.76\times 10^{ - 16} $ $ 4.29 \times 10^{ - 119} $ 0 0 0 排名 8 6 5 7 4 1 1 1 平均值 $ 2.03 \times 10^{ - 5} $ $4.03\times 10^{ - 3} $ $ 3.86 \times 10^{ - 31} $ $ 2.59\times 10^{ -7} $ $ 1.19 \times 10^{ - 60} $ $ 2.77 \times 10^{ - 267} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_2$ 标准差 $ 1.15 \times 10^{ - 5} $ $ 8.05\times10^{ - 3} $ $ 4.00 \times 10^{ - 31} $ $ 1.98 \times 10^{-8} $ $ 5.87 \times 10^{ - 61} $ 0 0 0 排名 7 8 5 6 4 3 1 1 平均值 $ 1.38 \times 10^{ - 4} $ $2.13\times 10^{ 0} $ $ 1.47 \times 10^{ - 2} $ $ 1.16\times 10^{ -1} $ $ 2.35 \times 10^{ - 36} $ $ 6.35 \times 10^{ - 95} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_3$ 标准差 $ 2.59 \times 10^{ - 5} $ $ 7.32\times10^{ - 1} $ $ 2.66 \times 10^{ - 3} $ $ 2.27 \times 10^{ -2} $ $ 1.82 \times 10^{ - 36} $ $ 1.26 \times 10^{ - 94} $ 0 0 排名 5 8 6 7 4 3 1 1 平均值 $ {\pmb{1.83 \times 10}}^{\pmb{1}}$ $ 7.98 \times 10^{ 1}$ $ 2.81 \times 10^{ 1} $ $ 2.86 \times 10^{ 1} $ $ 2.50 \times 10^{ 1} $ $ 2.87 \times 10^{ 1} $ $ 2.90 \times 10^{ 1} $ $ 2.89 \times 10^{ 1} $ $f_4$ 标准差 $ 3.56 \times 10^{ - 1} $ $ 5.57\times10^{ 1} $ $ 3.45 \times 10^{ - 1} $ $ 1.66\times 10^{ - 1} $ $ 2.65 \times 10^{ - 1} $ $ 5.87 \times 10^{ - 2} $ $ 4.55 \times 10^{ - 1} $ $ 7.43 \times 10^{ - 2} $ 排名 1 8 3 4 2 5 7 6 平均值 $ 3.91 \times 10^{ - 10} $ $2.17\times 10^{ - 34} $ $ 8.51 \times 10^{ - 149} $ $ 4.02\times 10^{ - 42} $ $ 3.26 \times 10^{ - 278} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_5$ 标准差 $ 4.00 \times 10^{ - 10} $ $ 4.21\times10^{ - 34} $ $ 8.47 \times 10^{ - 149} $ $ 6.81 \times10^{- 42} $ 0 0 0 0 排名 8 7 5 6 4 1 1 1 平均值 $ 2.89 \times 10^{ - 3} $ $5.28\times 10^{ - 8} $ $ 1.91 \times 10^{ - 44} $ $ 1.86\times 10^{ -12} $ $ 1.18 \times 10^{ - 115} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_6$ 标准差 $ 2.58 \times 10^{ - 3} $ $6.99\times 10^{ - 8} $ $ 2.23 \times 10^{ - 44} $ $ 1.02\times 10^{ -12} $ $ 1.30 \times 10^{ - 115} $ 0 0 0 排名 8 7 5 6 4 1 1 1 平均值 $ 1.26 \times 10^{ 2} $ $ 2.57 \times10^{ 1} $ $ 1.14 \times 10^{ - 14} $ $ 9.62 \times 10^{ -15} $ $ 8.96 \times 10^{ 0} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_7$ 标准差 $ 6.85 \times 10^{ 1} $ $ 1.54\times 10^{ 0} $ $ 2.54 \times 10^{ - 14} $ $1.88 \times 10^{ - 14} $ $ 6.17 \times 10^{ 0} $ 0 0 0 排名 8 7 5 4 6 1 1 1 平均值 $ 2.41 \times 10^{ - 6} $ $7.10\times 10^{ - 7} $ $ 1.07 \times 10^{ - 14} $ $ 3.81\times 10^{ - 14} $ $ 2.66 \times 10^{ - 15} $ $ {\pmb{8.88\times 10}}^{ - {\pmb{16}}} $ $ {\pmb{8.88 \times 10}}^{ -{\pmb{16}}} $ $ {\pmb{8.88 \times 10}}^{ - {\pmb{16}}}$ $f_8$ 标准差 $ 6.98 \times 10^{ - 7} $ $ 1.54\times10^{ - 6} $ $ 1.85 \times 10^{ - 15} $ $ 2.16 \times 10^{-15} $ $ 9.93 \times 10^{ - 16} $ 0 0 0 排名 8 7 5 6 4 1 1 1 平均值 $ 6.60 \times 10^{ - 11} $ $2.33\times10^{ - 1} $ $ 2.44 \times 10^{ - 16} $ $ 6.21 \times 10^{ - 16} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_9$ 标准差 $ 1.32 \times 10^{ - 11} $ $ 1.30\times10^{ - 1} $ $ 1.45 \times 10^{ - 16} $ $ 9.63\times 10^{ - 16} $ 0 0 0 0 排名 7 8 5 6 1 1 1 1 平均值 $ 9.71 \times 10^{ - 6} $ $6.32\times 10^{ - 5} $ $ 9.53 \times 10^{ 0} $ $ 1.35\times 10^{ - 6} $ $ 2.21 \times 10^{ - 61} $ $ 7.28 \times 10^{ - 262} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_{10}$ 标准差 $ 2.94 \times 10^{ - 6} $ $ 7.25\times10^{ - 5} $ $ 7.79 \times 10^{ 0} $ $ 2.42 \times 10^{ -6} $ $ 2.97 \times 10^{ - 61} $ 0 0 0 排名 6 7 8 5 4 3 1 1 平均值 $ 4.59 \times 10^{ - 5} $ $1.19\times 10^{ 1} $ $ 2.38 \times 10^{ - 49} $ $ 4.58\times 10^{ - 15} $ $ 2.62 \times 10^{ - 120} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_{11}$ 标准差 $ 4.27 \times 10^{ - 5} $ $ 8.43\times10^{ 0} $ $ 3.10 \times 10^{ - 49} $ $ 6.63 \times 10^{ -15} $ $ 3.04\times 10^{ - 120} $ 0 0 0 排名 7 8 5 6 4 1 1 1 平均值 $ 1.49 \times 10^{ - 1} $ $1.53\times 10^{ 1} $ $ 3.51 \times 10^{ - 15} $ $ 8.06\times 10^{ - 2} $ $ 2.08 \times 10^{ - 28} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $ {\pmb{0}} $ $f_{12}$ 标准差 $ 5.87 \times 10^{ - 3} $ $ 6.60\times10^{ 0} $ $ 2.45 \times 10^{ - 15} $ $ 1.85 \times 10^{ -2} $ $ 1.35 \times 10^{ - 28} $ 0 0 0 排名 7 8 5 6 4 1 1 1 平均排名 6.6667 7.4167 5.1667 5.7500 3.7500 1.9167 1.5000 1.4167 最终排名 7 8 5 6 4 3 2 1 表 4 LIL-GWO与其他7种算法的统计检验结果比较
Table 4 Statistical test results of LIL-GWO and other seven algorithms
算法 $ {\rm{R}}^ +$ $ {\rm{R}}^ -$ $p$-value $\alpha = 0.05$ $\alpha = 0.1$ LIL-GWO versus CMA-ES 67.0 11.0 $ 2.8848 \times 10^{ - 4} $ Yes Yes LIL-GWO versus IPSO 78.0 0.0 $ 4.5561 \times 10^{ - 4} $ Yes Yes LIL-GWO versus ODE 67.0 11.0 $ 1.3461 \times 10^{ - 3} $ Yes Yes LIL-GWO versus GABC 66.0 12.0 $ 7.0988 \times 10^{ - 4} $ Yes Yes LIL-GWO versus ETLBO 62.0 16.0 $ 5.7382 \times 10^{ - 3} $ Yes Yes LIL-GWO versus IWOA 40.0 38.0 $ 3.1412 \times 10^{ - 1} $ No No LIL-GWO versus ISCA 39.5 38.5 $ 9.8936 \times 10^{ - 1} $ No No 表 5 两种算法对12个函数的实验结果比较
Table 5 Experimental results of two algorithms for functions
函数 OBL-GWO LIBL-GWO 平均值 标准差 平均值 标准差 $f_{1}$ $ 2.37 \times 10^{ - 35} $ $ 3.66 \times 10^{ - 35} $ 0 0 $f_{2}$ $ 1.27 \times 10^{ - 18} $ $ 7.90 \times 10^{ - 19} $ 0 0 $f_{3}$ $ 2.50 \times 10^{ - 33} $ $ 4.36 \times 10^{ - 33} $ 0 0 $f_{4}$ $ {\bf{2.87 \times 10}}^{\pmb{1}}$ $ 1.55 \times 10^{ - 1} $ $ 2.89 \times 10^{ 1} $ $ 5.83 \times 10^{ - 2} $ $f_{5}$ $ 1.16 \times 10^{ - 145} $ $ 1.60 \times 10^{ - 145} $ 0 0 $f_{6}$ $ 1.46 \times 10^{ - 28} $ $ 2.05 \times 10^{ - 28} $ 0 0 $f_{7}$ 0 0 0 0 $f_{8}$ $ 4.44 \times 10^{ - 15} $ 0 $ {\pmb{8.88 \times10}}^{\bf{-16}} $ 0 $f_{9}$ 0 0 0 0 $f_{10}$ $ 5.91 \times 10^{ - 19} $ $ 8.32 \times 10^{ - 19} $ 0 0 $f_{11}$ $ 2.90 \times 10^{ - 34} $ $ 5.73 \times 10^{ - 34} $ 0 0 $f_{12}$ $ 1.68 \times 10^{ - 8} $ $ 1.46 \times 10^{ - 8} $ 0 0 表 6 8种算法对CEC2014测试集30个函数的实验结果比较
Table 6 Comparisons of eight algorithms for 30 test functions from CEC 2014
函数 统计结果 HS-SA PBA CoDE MoABC DGS-TLBO HSCA LM-BBO LIL-GWO 平均误差 $ 1.16 \times 10^{ 7} $ $3.50\times 10^{ 7} $ $ 1.21 \times 10^{ 7} $ $ 2.81 \times 10^{7} $ $ 1.04 \times 10^{ 7} $ $ 3.50 \times 10^{ 7} $ ${\bf{1.01 \times 10}}^{\bf{7}} $ $ 2.59 \times 10^{ 7} $ F1 标准差 $ 7.89 \times 10^{ 4} $ $2.16 \times 10^{ 7} $ $ 4.48 \times 10^{ 6} $ $ 1.01\times 10^{ 7} $ $ 8.61 \times 10^{ 6} $ $ 2.49 \times 10^{ 7} $ $ 3.81 \times 10^{ 6} $ $ 4.30 \times 10^{ 6} $ 排名 3 7 4 6 2 7 1 3 平均误差 $ {\bf{1.38 \times 10}}^{\bf{4}} $ $ 3.05\times 10^{ 8} $ $ 1.89 \times 10^{ 7} $ $ 2.88\times10^{ 4} $ $ 4.59 \times 10^{ 6} $ $ 1.95 \times 10^{ 7} $ $ 5.34 \times 10^{ 4} $ $ 1.02 \times 10^{ 7} $ F2 标准差 $ 1.34 \times 10^{ 4} $ $ 1.89\times10^{ 8} $ $ 9.45 \times 10^{ 6} $ $ 4.11 \times 10^{ 4} $ $ 1.11 \times 10^{ 7} $ $ 5.49 \times 10^{ 7} $ $ 2.14 \times 10^{4} $ $ 2.71 \times 10^{ 6} $ 排名 1 8 6 2 4 7 3 5 平均误差 $ 6.31 \times 10^{ 3} $ $ 6.97\times10^{ 3} $ $ 4.16 \times 10^{ 3} $ $ 1.06 \times 10^{ 4} $ $ {\bf{1.44 \times 10}}^{\bf{1}} $ $ 3.10 \times 10^{ 4} $ $ 1.64 \times 10^{ 4} $ $ 2.24 \times 10^{ 4} $ F3 标准差 $ 6.06 \times 10^{ 3} $ $ 3.96\times10^{3} $ $ 1.89 \times 10^{ 3} $ $ 3.66 \times 10^{ 3} $ $ 1.68 \times 10^{ 1} $ $ 1.36 \times 10^{ 4} $ $ 1.71 \times 10^{ 4} $ $ 2.72 \times 10^{ 4} $ 排名 3 4 2 5 1 8 6 7 平均误差 $ 1.11 \times 10^{ 2}$ $ 5.78 \times10^{ 2} $ $ 1.44 \times 10^{ 2} $ $ 1.59 \times 10^{ 2} $ $ 1.46 \times 10^{ 2} $ $ 2.03 \times 10^{ 2} $ $ {\bf{9.99 \times 10}}^{\bf{1}}$ $ 2.38 \times 10^{ 2} $ F4 标准差 $ 4.01 \times 10^{ 1} $ $ 3.62\times10^{ 1} $ $ 1.55 \times 10^{ 1} $ $ 2.76\times 10^{ 1} $ $ 3.78 \times 10^{ 1} $ $ 6.69 \times 10^{ 1} $ $ 2.85 \times 10^{ 1} $ $ 4.57 \times 10^{ 1} $ 排名 2 8 3 5 4 6 1 7 平均误差 $ 2.00 \times 10^{ 1} $ $ 5.21\times10^{ 2} $ $ 2.10 \times 10^{ 1} $ $ 2.04\times 10^{ 1} $ $ 2.10 \times 10^{ 1} $ $ 2.00 \times 10^{ 1} $ $ {\bf{3.06 \times 10}}^{\bf{0}}$ $ 2.04 \times 10^{ 1} $ F5 标准差 $ 3.01 \times 10^{ - 4} $ $ 5.26\times10^{ - 2} $ $ 6.56 \times 10^{ - 2} $ $ 3.53 \times 10^{- 2} $ $ 4.34 \times 10^{ - 2} $ $ 2.28 \times 10^{ - 3} $ $ 7.87 \times 10^{ - 1} $ $ 6.42 \times 10^{ - 2} $ 排名 2 8 6 4 6 2 1 4 平均误差 $ 1.31 \times 10^{ 1} $ $ 6.16\times10^{ 2} $ $ 5.57 \times 10^{ 1} $ $ 3.78 \times 10^{1} $ $ 1.67 \times 10^{ 1} $ $ 3.23 \times 10^{ 1} $ $ 1.69 \times 10^{ 1} $ $ {\bf{1.25 \times 10}}^{\bf{1}} $ F6 标准差 $ 2.12 \times 10^{ 0} $ $ 2.40\times10^{ 0} $ $ 2.67 \times 10^{ 0} $ $ 2.65 \times 10^{ 0} $ $ 3.45 \times 10^{0} $ $ 3.27 \times 10^{0} $ $ 3.12 \times 10^{0} $ $ 2.10 \times 10^{0} $ 排名 2 8 7 6 3 5 4 1 平均误差 $ {\bf{1.52 \times 10}}^{\bf{-2}} $ $ 7.04 \times10^{ 2} $ $ 1.20 \times 10^{ 0} $ $ 5.72 \times 10^{ -1} $ $ 1.01 \times 10^{ 0} $ $ 1.79 \times 10^{ 0} $ $ 1.76 \times 10^{ -1} $ $ 7.66 \times 10^{ 0} $ F7 标准差 $ 1.63 \times 10^{ -2} $ $ 1.72 \times 10^{ 0} $ $ 7.20 \times 10^{ - 2} $ $1.36 \times 10^{ - 1} $ $ 1.50 \times 10^{ 0} $ $ 2.19 \times 10^{ 0} $ $ 8.56 \times 10^{ -2} $ $ 4.50 \times 10^{ 0} $ 排名 1 8 5 3 4 6 2 7 平均误差 $ {\bf{4.10 \times 10}}^{\bf{-5}} $ $ 8.56\times 10^{ 2} $ $ 2.30 \times 10^{ 2} $ $ 1.26\times 10^{ 1} $ $ 7.67 \times 10^{ 1} $ $ 1.71 \times10^{2} $ $ 5.53 \times 10^{ 1} $ $ 3.49 \times 10^{ 1} $ F8 标准差 $ 8.13 \times 10^{ - 6} $ $ 1.48\times10^{ 1} $ $ 1.45 \times 10^{ 1} $ $ 1.74 \times 10^{ 0} $ $ 2.45 \times 10^{ 1} $ $ 3.46 \times 10^{ 1} $ $ 3.78 \times 10^{ 2} $ $ 1.20 \times 10^{ 1} $ 排名 1 8 7 2 5 6 4 3 平均误差 $ 6.71 \times 10^{ 1} $ $ 1.01\times10^{ 3} $ $ 3.80 \times 10^{ 2} $ $ 2.58 \times 10^{ 2} $ $ 9.84 \times 10^{ 1} $ $ 2.80 \times 10^{ 2} $ $ 7.66 \times 10^{ 1} $ $ {\bf{6.02 \times 10}}^{\bf{1}} $ F9 标准差 $ 1.52 \times 10^{ 1} $ $ 1.33\times10^{1} $ $ 1.89\times 10^{ 1} $ $ 2.83\times 10^{ 1} $ $ 3.08\times 10^{ 1} $ $ 5.16\times 10^{ 1} $ $ 1.61\times 10^{ 1} $ $ 8.59\times 10^{ 0} $ 排名 2 8 7 5 4 6 3 1 平均误差 $ {\bf{2.01 \times 10}}^{\bf{-1}} $ $ 1.89\times 10^{ 3} $ $ 7.26 \times 10^{ 3} $ $ 2.29\times 10^{ 2} $ $ 2.39 \times 10^{ 3} $ $ 2.66 \times 10^{ 3} $ $ 1.26 \times 10^{ 4} $ $ 1.72 \times 10^{ 3} $ F10 标准差 $ 4.66 \times 10^{ - 2} $ $ 3.68\times10^{ 2} $ $ 3.84 \times 10^{ 2} $ $ 1.07 \times 10^{ 2} $ $ 4.71 \times 10^{2} $ $ 5.34 \times 10^{2} $ $ 1.16 \times 10^{4} $ $ 1.81 \times 10^{2} $ 排名 1 4 7 2 5 6 8 3 平均误差 $ {\bf{1.99 \times 10}}^{\bf{3}} $ $ 4.49\times 10^{ 3} $ $ 1.21 \times 10^{ 4} $ $ 5.74\times 10^{ 3} $ $ 3.93 \times 10^{ 3} $ $ 4.13 \times 10^{ 3} $ $ 1.23 \times 10^{4} $ $ 2.64 \times 10^{ 3} $ F11 标准差 $ 4.34 \times 10^{ 2} $ $ 5.35\times10^{ 2} $ $ 4.27 \times 10^{ 2} $ $ 3.27 \times 10^{ 2} $ $ 5.45\times 10^{ 2} $ $ 5.35\times 10^{ 2} $ $ 3.42\times 10^{ 2} $ $ 3.12\times 10^{ 2} $ 排名 1 5 7 6 3 4 8 2 平均误差 $ 2.46 \times 10^{ - 2} $ $1.20\times 10^{ 3} $ $ 2.47 \times 10^{ 0} $ $ 4.71\times 10^{ - 1} $ $ 2.75 \times 10^{ 0} $ $ 5.11 \times 10^{ - 1} $ $ {\bf{1.11 \times 10}}^{\bf{-2}} $ $ 3.20 \times 10^{ - 1} $ F12 标准差 $ 1.26 \times 10^{ - 2} $ $ 1.43\times10^{ -1} $ $ 2.74 \times 10^{ - 1} $ $ 5.73 \times 10^{ -2} $ $ 2.62 \times 10^{ - 1} $ $ 2.56 \times 10^{ - 1} $ $ 1.75 \times 10^{ - 18} $ $ 3.19 \times 10^{ - 1} $ 排名 2 8 6 5 7 4 1 3 平均误差 $ 5.24 \times 10^{ - 1} $ $1.30\times 10^{ 3} $ $ 6.53 \times 10^{ -1} $ $ 4.51\times 10^{ - 1} $ $ 4.71 \times 10^{ -1} $ $ 4.81 \times 10^{ - 1} $ $ 6.55 \times 10^{ - 1} $ $ {\bf{3.40 \times 10}}^{\bf{-1}} $ F13 标准差 $ 1.04 \times 10^{ - 1} $ $ 9.49\times10^{ -2} $ $ 6.56 \times 10^{ - 2} $ $ 4.11 \times 10^{ -2} $ $ 1.31 \times 10^{ - 1} $ $ 1.17 \times 10^{ - 1} $ $ 1.56 \times 10^{ - 1} $ $ 5.48 \times 10^{ - 2} $ 排名 5 8 6 2 3 4 7 1 平均误差 $ 4.15 \times 10^{ - 1} $ $1.40\times 10^{ 3} $ $ 4.31 \times 10^{ -1} $ $ 2.98\times 10^{ - 1} $ $ {\bf{2.88 \times 10}}^{\bf{-1}} $ $ 3.08 \times 10^{ - 1} $ $ 6.20 \times 10^{ - 1} $ $ 4.10 \times 10^{ - 1} $ F14 标准差 $ 2.29 \times 10^{ - 1} $ $ 4.57\times10^{ -2} $ $ 8.50 \times 10^{ - 2} $ $ 2.50 \times 10^{ -2} $ $ 4.92 \times 10^{ - 2} $ $ 5.64 \times 10^{ - 2} $ $ 2.96 \times 10^{ - 1} $ $ 2.68 \times 10^{ - 2} $ 排名 5 8 6 2 1 3 7 4 平均误差 $ 1.64 \times 10^{ 1} $ $ 1.52\times10^{ 3} $ $ 3.78 \times 10^{ 1} $ $ 3.14\times 10^{ 1} $ $ 3.75 \times 10^{ 1} $ $ 9.80 \times 10^{ 1} $ $ 1.55 \times 10^{ 1} $ $ {\bf{1.68 \times 10}}^{\bf{0}} $ F15 标准差 $ 1.17 \times 10^{ 1} $ $ 3.36\times10^{ 0} $ $ 2.26 \times 10^{ 0} $ $ 6.02 \times 10^{ 0} $ $ 2.19 \times 10^{ 1} $ $ 3.02 \times 10^{ 1} $ $ 5.50 \times 10^{ 0} $ $ 4.92 \times 10^{ - 1} $ 排名 3 8 6 4 5 7 2 1 平均误差 $ 1.42 \times 10^{ 1} $ $ 1.63\times10^{ 3} $ $ 2.28 \times 10^{ 1} $ $ 1.97\times 10^{ 1} $ $ 1.11 \times 10^{ 1} $ $ 1.27 \times 10^{ 1} $ $ 1.08 \times 10^{ 1} $ $ {\bf{1.03 \times 10}}^{\bf{1}} $ F16 标准差 $ 7.83 \times 10^{ - 1} $ $ 3.78\times10^{ - 1} $ $ 3.26 \times 10^{ - 1} $ $ 4.02 \times 10^{ - 1} $ $ 6.62 \times 10^{ - 1} $ $ 5.01 \times 10^{ - 1} $ $ 5.84 \times 10^{ -1 } $ $ 9.04 \times 10^{ - 1} $ 排名 5 8 7 6 3 4 2 1 平均误差 $ 2.09 \times 10^{ 6} $ $ 3.40\times10^{ 6} $ $ 1.81 \times 10^{ 5} $ $ 1.01\times 10^{ 7} $ $ {\bf{1.67 \times 10}}^{\bf{5}} $ $ 1.48 \times 10^{ 6} $ $ 1.46 \times 10^{ 6} $ $ 1.29 \times 10^{ 6} $ F17 标准差 $ 1.31 \times 10^{ 6} $ $ 2.12\times10^{ 6} $ $ 1.24 \times 10^{ 5} $ $ 4.96 \times 10^{ 6} $ $ 2.13 \times 10^{ 5} $ $ 1.21 \times 10^{ 6} $ $ 9.34 \times 10^{ 5} $ $ 1.23 \times 10^{ 6} $ 排名 6 7 2 8 1 5 4 3 平均误差 $ 6.16 \times 10^{ 3} $ $ 1.70\times10^{ 6} $ $ 3.62 \times 10^{ 3} $ $ 9.92\times 10^{ 3} $ $ {\bf{8.71 \times 10}}^{\bf{2}} $ $ 7.67 \times 10^{ 3} $ $ 2.90 \times 10^{ 3} $ $ 4.07 \times 10^{ 5} $ F18 标准差 $ 6.22 \times 10^{ 3} $ $ 1.06\times10^{ 6} $ $ 2.31 \times 10^{ 3} $ $ 9.94 \times 10^{ 3} $ $ 1.02 \times 10^{ 3} $ $ 6.70 \times 10^{ 3} $ $ 4.27 \times 10^{ 3} $ $ 7.27 \times 10^{ 5} $ 排名 4 8 3 6 1 5 2 7 平均误差 $ 1.89 \times 10^{ 1} $ $ 1.91\times10^{ 3} $ $ 3.62 \times 10^{ 1} $ $ 3.33\times 10^{ 1} $ $ 2.71 \times 10^{ 1} $ $ 5.33 \times 10^{ 1} $ $ 5.19 \times 10^{ 3} $ $ {\bf{1.84 \times 10}}^{\bf{1}} $ F19 标准差 $ 2.46 \times 10^{ 1} $ $ 5.23\times10^{ 0} $ $ 1.08 \times 10^{ 1} $ $ 1.06 \times 10^{ 1} $ $ 2.86 \times 10^{ 1} $ $ 3.63 \times 10^{ 1} $ $ 5.67 \times 10^{ 3} $ $ 3.78 \times 10^{ 0} $ 排名 2 7 5 4 3 6 8 1 平均误差 $ 6.77 \times 10^{ 3} $ $8.77\times 10^{ 3} $ $ 5.04 \times 10^{ 2} $ $ 3.96\times 10^{ 4} $ $ {\bf{4.28 \times 10}}^{\bf{2}} $ $ 3.93 \times 10^{ 4} $ $ 2.61 \times 10^{ 4} $ $ 1.76 \times 10^{ 4} $ F20 标准差 $ 5.09 \times 10^{ 3} $ $ 4.31\times10^{ 3} $ $ 3.17 \times 10^{ 2} $ $ 1.29 \times 10^{ 4} $ $ 1.77 \times 10^{2} $ $ 2.20 \times 10^{4} $ $ 1.56 \times 10^{4} $ $ 9.12 \times 10^{3} $ 排名 3 4 2 8 1 7 6 5 平均误差 $ 5.27 \times 10^{ 5} $ $ 4.39\times10^{ 5} $ $ {\bf{2.12 \times 10}}^{\bf{4}} $ $ 7.30\times 10^{ 6} $ $ 2.20 \times 10^{ 4} $ $ 3.54 \times 10^{ 5} $ $ 1.11 \times 10^{6} $ $ 3.27 \times 10^{ 5} $ F21 标准差 $ 3.59 \times 10^{ 5} $ $ 3.40\times10^{ 5} $ $ 1.61 \times 10^{ 4} $ $ 4.36 \times 10^{ 6} $ $ 2.22\times 10^{ 4} $ $ 3.48\times 10^{ 5} $ $ 7.95\times 10^{ 5} $ $ 2.86\times 10^{ 5} $ 排名 6 5 1 8 2 4 7 3 平均误差 $ 4.88 \times 10^{2} $ $ 2.53\times10^{ 3} $ $ 1.44 \times 10^{ 3} $ $ 1.14\times 10^{ 3} $ $ {\bf{3.14 \times 10}}^{\bf{2}} $ $ 9.47 \times 10^{ 2} $ $ 1.88 \times 10^{ 3} $ $ 1.69 \times 10^{ 3} $ F22 标准差 $ 9.15 \times 10^{ 1} $ $ 1.08\times10^{ 2} $ $ 1.59 \times 10^{ 2} $ $ 1.89 \times 10^{2} $ $ 1.41 \times 10^{ 2} $ $ 3.31 \times 10^{ 2} $ $ 2.04 \times 10^{ 2} $ $ 2.13 \times 10^{ 2} $ 排名 2 8 5 4 1 3 7 6 平均误差 $ 3.16 \times 10^{ 2} $ $2.60\times 10^{ 3} $ $ 3.55 \times 10^{ 2} $ $ 3.57\times 10^{ 2} $ $ 3.15 \times 10^{ 2} $ $ 3.29 \times 10^{ 2} $ $ 4.11 \times 10^{ 2} $ $ {\bf{2.00 \times 10}}^{\bf{2}} $ F23 标准差 $ 5.74 \times 10^{ - 1} $ $ 3.88\times10^{ 1} $ $ 1.77 \times 10^{ - 1} $ $ 7.30 \times 10^{ 0} $ $ 4.43 \times 10^{ - 1} $ $ 7.51 \times 10^{ 0} $ $ 6.43 \times 10^{ 1} $ 0 排名 3 8 5 6 2 4 7 1 平均误差 $ 2.31 \times 10^{ 2} $ $2.61\times 10^{ 3} $ $ 2.83 \times 10^{ 2} $ $ 2.71\times 10^{ 2} $ $ {\bf{2.00 \times 10}}^{\bf{2}} $ $ 2.78 \times 10^{ 2} $ $ 1.48 \times 10^{ 4} $ $ {\bf{2.00 \times 10}}^{\bf{2}} $ F24 标准差 $ 5.17 \times 10^{ 0} $ $ 3.98\times10^{ 0} $ $ 1.80 \times 10^{ 0} $ $ 1.78 \times 10^{ 0} $ $ 9.68 \times 10^{ - 4} $ $ 3.11 \times 10^{ 1} $ $ 8.37 \times 10^{ 3} $ 0 排名 3 7 6 4 1 5 8 1 平均误差 $ 2.05 \times 10^{ 2} $ $ 2.70\times10^{ 3} $ $ 2.18 \times 10^{ 2} $ $ 2.22\times 10^{ 2} $ $ 2.02 \times 10^{ 2} $ $ 2.23 \times 10^{ 2} $ $ 5.29 \times 10^{ 2} $ $ {\bf{2.00 \times 10}}^{\bf{2}} $ F25 标准差 $ 1.51 \times 10^{ 0} $ $ 1.41\times10^{ 0} $ $ 1.94 \times 10^{ 0} $ $ 2.80 \times 10^{ 0} $ $ 3.62 \times 10^{ 2} $ $ 9.39 \times 10^{ 0} $ $ 4.37 \times 10^{ 1} $ 0 排名 3 8 6 4 5 7 2 1 平均误差 $ 1.38 \times 10^{2} $ $ 2.70\times10^{ 3} $ $ 1.04 \times 10^{ 2} $ $ 1.01\times 10^{ 2} $ $ 1.10 \times 10^{ 2} $ $ 1.00 \times 10^{ 2} $ $ {\bf{2.13 \times 10}}^{\bf{0}} $ $ 1.00 \times 10^{ 2} $ F26 标准差 $ 4.84 \times 10^{ 1} $ $ 1.93\times10^{ 1} $ $ 1.82 \times 10^{ 1} $ $ 6.75 \times 10^{ - 2} $ $ 3.15 \times 10^{ 1} $ $ 1.63 \times 10^{ - 1} $ $ 3.46 \times 10^{ 0 } $ 0 排名 5 8 7 6 3 4 2 1 平均误差 $ 6.69 \times 10^{ 2} $ $ 3.14\times10^{ 3} $ $ 1.28 \times 10^{ 3} $ $ 1.08\times 10^{ 3} $ $ 7.94 \times 10^{ 2} $ $ 4.27 \times 10^{ 2} $ $ {\bf{1.96 \times 10}}^{\bf{2}} $ $ 2.00 \times 10^{ 2} $ F27 标准差 $ 1.63 \times 10^{ 2} $ $ 6.53\times10^{ 1} $ $ 1.47 \times 10^{ 2} $ $ 3.78 \times 10^{ 2} $ $ 2.15 \times 10^{ 2} $ $ 1.96 \times 10^{ 1} $ $ 1.04 \times 10^{ 2} $ 0 排名 4 8 7 6 5 3 1 2 平均误差 $ 1.03 \times 10^{ 3} $ $ 3.90\times10^{ 3} $ $ 1.92 \times 10^{ 3} $ $ 2.15 \times 10^{ 3} $ $ 1.43 \times 10^{ 3} $ $ 3.49 \times 10^{ 3} $ $ 1.94 \times 10^{ 3} $ $ {\bf{2.00 \times 10}}^{\bf{2}} $ F28 标准差 $ 1.21 \times 10^{ 2} $ $ 2.16\times10^{ 2} $ $ 1.26 \times 10^{ 2} $ $ 3.42 \times 10^{ 2} $ $ 4.37 \times 10^{ 2} $ $ 5.48 \times 10^{ 2} $ $ 5.49 \times 10^{ 2} $ 0 排名 2 8 4 6 3 7 5 1 平均误差 $ 1.40 \times 10^{ 3} $ $ 3.59\times10^{ 4} $ $ 2.00 \times 10^{ 4} $ $ 3.32\times 10^{ 3} $ $ 3.08 \times 10^{ 6} $ $ 5.44 \times 10^{ 5} $ $ 1.98 \times 10^{ 7} $ $ {\bf{2.00 \times 10}}^{\bf{2}} $ F29 标准差 $ 4.27 \times 10^{ 2} $ $ 1.64\times10^{ 5} $ $ 7.15 \times 10^{ 3} $ $ 1.46 \times 10^{ 3} $ $ 4.99 \times 10^{ 6} $ $ 2.61 \times 10^{ 6} $ $ 3.96 \times 10^{ 6} $ 0 排名 2 5 4 3 7 6 8 1 平均误差 $ 4.63 \times 10^{ 3} $ $ 1.55\times10^{ 4} $ $ 1.97 \times 10^{ 4} $ $ 1.61\times 10^{ 4} $ $ 6.47 \times 10^{ 3} $ $ 2.49 \times 10^{ 4} $ $ 6.96 \times 10^{ 6} $ $ {\bf{2.00 \times 10}}^{\bf{2}} $ F30 标准差 $ 2.32 \times 10^{3} $ $ 4.24\times10^{ 3} $ $ 2.00 \times 10^{ 3} $ $ 4.10 \times 10^{ 3} $ $ 3.43 \times 10^{3} $ $ 2.26 \times 10^{4} $ $ 1.03 \times 10^{7} $ 0 排名 2 4 6 5 3 7 8 1 平均排名 2.9333 7.0333 5.0333 4.7333 3.2667 5.1667 4.6333 3.0000 最终排名 1 8 6 5 3 7 4 2 表 7 不同算法对单二极管模型的最优辨识参数比较
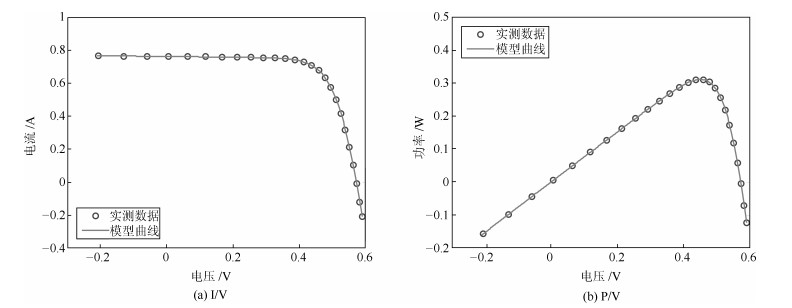
Table 7 Comparison among different algorithms on single diode model
算法 $ I_{ph} $ (A) $ I_{sd}\, (\mu$A) $R_S\, (\Omega)$ $R_{sh}\, (\Omega)$ $n$ RMSE BSA 0.7609 0.37749 0.0358 56.5266 1.4970 $ 1.0398 \times 10^{ - 3}$ IBSA 0.7607 0.35502 0.0361 58.2012 1.4907 $ 1.0092 \times 10^{ - 3}$ LBSA 0.7606 0.34618 0.0362 59.0978 1.4881 $ 1.0143 \times 10^{ - 3}$ CLPSO 0.7608 0.34302 0.0361 54.1965 1.4873 $ 9.9633 \times 10^{ - 3}$ BLPSO 0.7607 0.36620 0.0359 60.2845 1.4939 $ 1.0272 \times 10^{ - 3}$ DE-BBO 0.7605 0.32477 0.0364 55.2627 1.4817 $ 9.9922 \times 10^{ - 4}$ GOTLBO 0.7608 0.32970 0.0363 53.3664 1.4833 $ 9.8856 \times 10^{ - 3}$ LIL-GWO 0.7608 0.32363 0.0364 53.7967 1.4814 $ 9.8604 \times 10^{ - 4}$ -
[1] 吕柏权, 张静静, 李占培, 刘廷章.基于变换函数与填充函数的模糊粒子群优化算法.自动化学报, 2018, 44(1): 74-86 doi: 10.16383/j.aas.2018.c160547Lv Bai-Quan, Zhang Jing-Jing, Li Zhan-Pei, Liu Ting-Zhang. Fuzzy partical swarm optimization based on filled function and transformation function. Acta Automatica Sinica, 2018, 44(1): 74-86 doi: 10.16383/j.aas.2018.c160547 [2] Gao W F, Liu S Y, Huang L L. A novel artificial bee colony algorithm based on modified search equation and orthogonal learning. IEEE Transactions on Cybernetics, 2013, 43(3): 1011-1024 doi: 10.1109/TSMCB.2012.2222373 [3] 肖辉辉, 万常选, 段艳明, 谭黔林.基于引力搜索机制的花朵授粉算法.自动化学报, 2017, 43(4): 576-594 doi: 10.16383/j.aas.2017.c160146Xiao Hui-Hui, Wan Chang-Xuan, Duan Yan-Ming, Tan Qian-Lin. Flower pollination algorithm based on gravity search mechanism. Acta Automatica Sinica, 2017, 43(4): 576-594 doi: 10.16383/j.aas.2017.c160146 [4] 周晓根, 张贵军, 郝小虎.局部抽象凸区域剖分差分进化算法.自动化学报, 2015, 41(7): 1315-1327 doi: 10.16383/j.aas.2015.c140680Zhou Xiao-Gen, Zhang Gui-Jun, Hao Xiao-Hu. Differential evolution algorithm with local abstract convex region partition. Acta Automatica Sinica, 2015, 41(7): 1315-1327 doi: 10.16383/j.aas.2015.c140680 [5] Rakhshani H, Rahati A. Snap-drift cuckoo search: A novel cuckoo search optimization algorithm. Applied Soft Computing, 2017, 52: 771-794 doi: 10.1016/j.asoc.2016.09.048 [6] Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67 doi: 10.1016/j.advengsoft.2016.01.008 [7] Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61 doi: 10.1016/j.advengsoft.2013.12.007 [8] Nuaekaew K, Artrit P, Pholdee N, Bureerat S. Optimal reactive power dispatch problem using a two-archive multi-objective grey wolf optimizer. Expert Systems with Applications, 2017, 87: 79-89 doi: 10.1016/j.eswa.2017.06.009 [9] Precup R E, David R C, Petriu E M. Grey wolf optimizer algorithm-based tuning of fuzzy control systems with reduced parametric sensitivity. IEEE Transactions on Industrial Electronics, 2017, 64(1): 527-534 doi: 10.1109/TIE.2016.2607698 [10] Martin B, Marot J, Bourennane S. Mixed grey wolf optimizer for the joint denoising and unmixing of multispectral images. Applied Soft Computing, 2019, 74: 385-410 doi: 10.1016/j.asoc.2018.10.019 [11] Saxena A, Kumar R, Das S. β-chaotic map enabled grey wolf optimizer. Applied Soft Computing, 2019, 75: 84-105 doi: 10.1016/j.asoc.2018.10.044 [12] Medjahed S A, Ait Saadi T, Benyettou A, Ouali M. Gray wolf optimizer for hyperspectral band selection. Applied Soft Computing, 2016, 40: 178-186 doi: 10.1016/j.asoc.2015.09.045 [13] 姚鹏, 王宏伦.基于改进流体扰动算法与灰狼优化的无人机三维航路规划.控制与决策, 2016, 31(4): 701-708 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzyjc201604019Yao Peng, Wang Hong-Lun. Three-dimensional path planning for UAV based on improved interfered fluid dynamical system and grey wolf optimizer. Control and Decision, 2016, 31(4): 701-708 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzyjc201604019 [14] Mittal N, Singh U, Sohi B S. Modified grey wolf optimizer for global engineering optimization. Applied Computational Intelligence and Soft Computing, 2016, 2016: 7950348 http://smartsearch.nstl.gov.cn/paper_detail.html?id=800e2270dd2a1b4fd9717838002592b1 [15] Rodríguez L, Castillo O, Soria J. Grey wolf optimizer with dynamic adaptation of parameters using fuzzy logic. In: Proceedings of the 2016 IEEE Congress on Evolutionary Computation. Vancouver, Canada: IEEE, 2016. 3116-3123 [16] Long W, Jiao J J, Liang X M, Tang M Z. Inspired grey wolf optimizer for solving large-scale function optimization problems. Applied Mathematical Modelling, 2018, 60: 112-126 doi: 10.1016/j.apm.2018.03.005 [17] 魏政磊, 赵辉, 李牧东, 王渊, 柯益明.控制参数值非线性调整策略的灰狼优化算法.空军工程大学学报(自然科学版), 2016, 17(3): 68-72 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kjgcdxxb201603013Wei Zheng-Lei, Zhao Hui, Li Mu-Dong, Wang Yuan, Ke Yi-Ming. A grey wolf optimization algorithm based on nonlinear adjustment strategy of control parameter. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(3): 68-72 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kjgcdxxb201603013 [18] Long W, Jiao J J, Liang X M, Tang M Z. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Engineering Applications of Artificial Intelligence, 2018, 68: 63-80 doi: 10.1016/j.engappai.2017.10.024 [19] Rodríguez L, Castillo O, Soria J, Melin P, Valdez F, Gonzalez C I, et al. A fuzzy hierarchical operator in the grey wolf optimizer algorithm. Applied Soft Computing, 2017, 57: 315-328 doi: 10.1016/j.asoc.2017.03.048 [20] Jaiswal K, Mittal H, Kukreja S. Randomized grey wolf optimizer (RGWO) with randomly weighted coefficients. In: Proceedings of the 10th International Conference on Contemporary Computing. Noida, India: IEEE, 2017. 1-3 [21] Malik M R S, Mohideen E R, Ali L. Weighted distance grey wolf optimizer for global optimization problems. In: Proceedings of the 2015 IEEE International Conference on Computational Intelligence and Computing Research. Madurai, India: IEEE, 2015. 1-6 [22] 魏政磊, 赵辉, 韩邦杰, 孙楚, 李牧东.具有自适应搜索策略的灰狼优化算法.计算机科学, 2017, 44(3): 259-263 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjkx201703053Wei Zheng-Lei, Zhao Hui, Han Bang-Jie, Sun Chu, Li Mu-Dong. Grey wolf optimization algorithm with self-adaptive searching strategy. Computer Science, 2017, 44(3): 259-263 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjkx201703053 [23] Tawhid M A, Ali A F. A hybrid grey wolf optimizer and genetic algorithm for minimizing potential energy function. Memetic Computing, 2017, 9(4): 347-359 doi: 10.1007/s12293-017-0234-5 [24] Kamboj V K. A novel hybrid PSO-GWO approach for unit commitment problem. Neural Computing and Applications, 2016, 27(6): 1643-1655 doi: 10.1007/s00521-015-1962-4 [25] Arora S, Singh H, Sharma M, Sharma S, Anand P. A new hybrid algorithm based on grey wolf optimization and crow search algorithm for unconstrained function optimization and feature selection. IEEE Access, 2019, 7: 26343-26361 doi: 10.1109/ACCESS.2019.2897325 [26] Daniel E, Anitha J, Gnanaraj J. Optimum Laplacian wavelet mask based medical image using hybrid cuckoo search-grey wolf optimization algorithm. Knowledge-based Systems, 2017, 131: 58-69 doi: 10.1016/j.knosys.2017.05.017 [27] Zhang X M, Kang Q, Cheng J F, Wang X. A novel hybrid algorithm based on biogeography-based optimization and grey wolf optimizer. Applied Soft Computing, 2018, 67: 197-214 doi: 10.1016/j.asoc.2018.02.049 [28] 龙文, 赵东泉, 徐松金.求解约束优化问题的改进灰狼优化算法.计算机应用, 2015, 35(9): 2590-2595 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyy201509035Long Wen, Zhao Dong-Quan, Xu Song-Jin. Improved grey wolf optimization algorithm for constrained optimization problem. Journal of Computer Applications, 2015, 35(9): 2590-2595 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyy201509035 [29] Mahdad B, Srairi K. Blackout risk prevention in a smart grid based flexible optimal strategy using grey wolf-pattern search algorithms. Energy Conversion and Management, 2015, 98: 411-429 doi: 10.1016/j.enconman.2015.04.005 [30] Lu C, Gao L, Yi J. Grey wolf optimizer with cellular topological structure. Expert Systems with Applications, 2018, 107: 89-114 doi: 10.1016/j.eswa.2018.04.012 [31] Heidari A A, Pahlavani P. An efficient modified grey wolf optimizer with Lévy flight for optimization tasks. Applied Soft Computing, 2017, 60: 115-134 doi: 10.1016/j.asoc.2017.06.044 [32] Gupta S, Deep K. A novel random walk grey wolf optimizer. Swarm and Evolutionary Computation, 2019, 44: 101-112 doi: 10.1016/j.swevo.2018.01.001 [33] Wolpert D H, Macready W G. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82 doi: 10.1109/4235.585893 [34] Kumar V, Kumar D. An astrophysics-inspired grey wolf algorithm for numerical optimization and its application to engineering design problems. Advances in Engineering Software, 2017, 112: 231-254 doi: 10.1016/j.advengsoft.2017.05.008 [35] Rahnamayan S, Tizhoosh H R, Salama M M A. Opposition-based differential evolution. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 64-79 doi: 10.1109/TEVC.2007.894200 [36] 喻飞, 李元香, 魏波, 徐星, 赵志勇.透镜成像反学习策略在粒子群算法中的应用.电子学报, 2014, 42(2): 230-235 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201402004Yu Fei, Li Yuan-Xiang, Wei Bo, Xu Xing, Zhao Zhi-Yong. The application of a novel OBL based on lens imaging principle in PSO. Acta Electronica Sinica, 2014, 42(2): 230-235 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201402004 [37] 王晖.区域变换搜索的智能算法研究.[博士学位论文], 武汉大学, 中国, 2011Wang Hui. Research on intelligent algorithms based on region transformation search and its applications[Ph. D. dissertation], Wuhan University, China, 2011 [38] Hansen N, Müller S D, Koumoutsakos P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evolutionary Computation, 2004, 11(1): 1-18 http://ieeexplore.ieee.org/document/6790790 [39] Chatterjee A, Siarry P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Computer & Operations Research, 2006, 33(3): 859-871 [40] Zhu G P, Kwong S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Applied Mathematics and Computation, 2010, 217(7): 3166-3173 doi: 10.1016/j.amc.2010.08.049 [41] Rao R V, Patel V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems. Journal of Industrial Engineering Computations, 2012, 3(4): 535-560 doi: 10.5267/j.ijiec.2012.03.007 [42] Hu H, Bai Y, Xu T. Improved whale optimization algorithm based on inertia weights and theirs applications. International Journal of Circuits, Systems and Signal Processing, 2017, 11: 12-26 [43] 徐松金, 龙文.求解高维优化问题的改进正弦余弦算法.计算机应用研究, 2018, 35(9): 2574-2577 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyyyj201809003Xu Song-Jin, Long Wen. Improved sine cosine algorithm for solving high-dimensional optimization problems. Application Research of Computers, 2018, 35(9): 2574-2577 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyyyj201809003 [44] Liang J J, Qu B Y, Suganthan P N. Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization, Technical Report 201311, Nanyang Technological University, Singapore, 2014. [45] Assad A, Deep K. A hybrid harmony search and simulated annealing algorithm for continuous optimization. Information Sciences, 2018, 450: 246-266 doi: 10.1016/j.ins.2018.03.042 [46] Kallioras N A, Lagaros N D, Avtzis D N. Pity beetle algorithm - a new metaheuristic inspired by the behavior of bark beetles. Advances in Engineering Software, 2018, 121: 147-166 doi: 10.1016/j.advengsoft.2018.04.007 [47] Wang Y, Cai Z X, Zhang Q F. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 55-66 doi: 10.1109/TEVC.2010.2087271 [48] Akbari R, Hedayatzadeh R, Ziarati K, Hassanizadeh B. A multi-objective artificial bee colony algorithm. Swarm and Evolutionary Computation, 2012, 2: 39-52 doi: 10.1016/j.swevo.2011.08.001 [49] Zou F, Wang L, Hei X H, Chen D B, Yang D D. Teaching-learning-based optimization with dynamic group strategy for global optimization. Information Sciences, 2014, 273: 112-131 doi: 10.1016/j.ins.2014.03.038 [50] Mlakar U, Fister Jr I, Fister I. Hybrid self-adaptive cuckoo search for global optimization. Swarm and Evolutionary Computation, 2016, 29: 47-72 doi: 10.1016/j.swevo.2016.03.001 [51] Garg V, Deep K. Performance of Laplacian biogeography-based optimization algorithm on CEC 2014 continuous optimization benchmarks and camera calibration problem. Swarm and Evolutionary Computation, 2016, 27: 132-144 doi: 10.1016/j.swevo.2015.10.006 [52] Yu K J, Liang J J, Qu B Y, Cheng Z P, Wang H S. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Applied Energy, 2018, 226: 408-422 doi: 10.1016/j.apenergy.2018.06.010 [53] Easwarakhanthan T, Bottin J, Bouhouch I, Boutrit C. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. International Journal of Solar Energy, 1986, 4: 1-12 doi: 10.1080/01425918608909835 -




 下载:
下载: