Research on High Precision Flux Observer of Induction Motor Based on Neutral System Theory
-
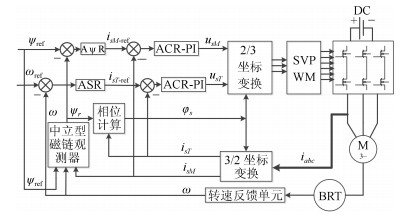
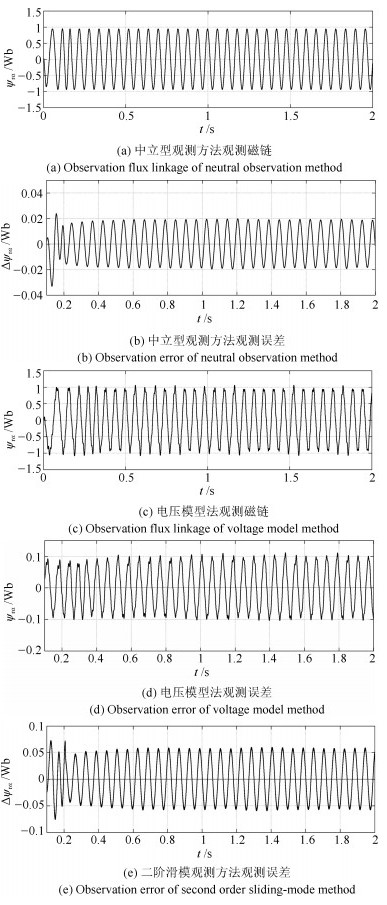
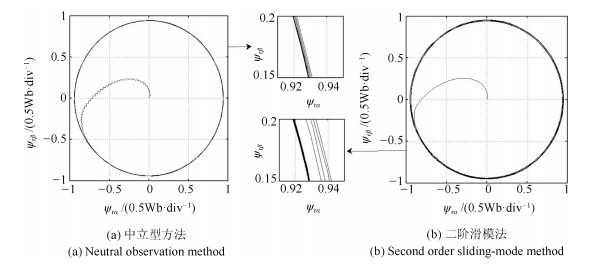
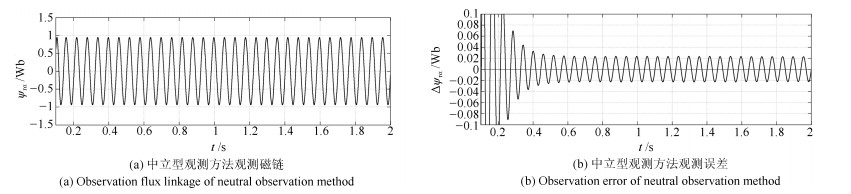
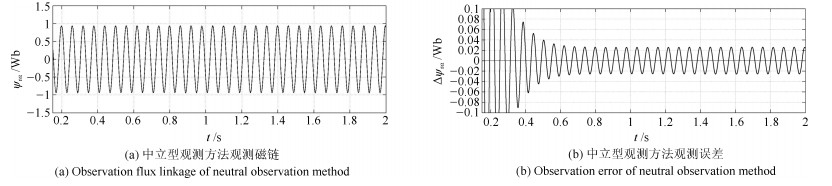
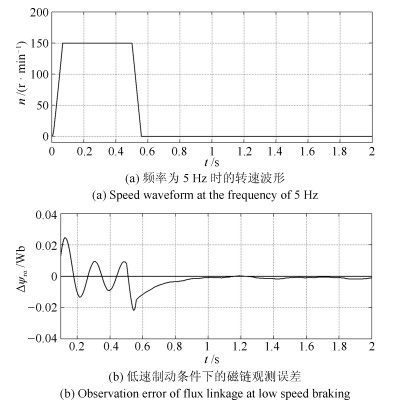
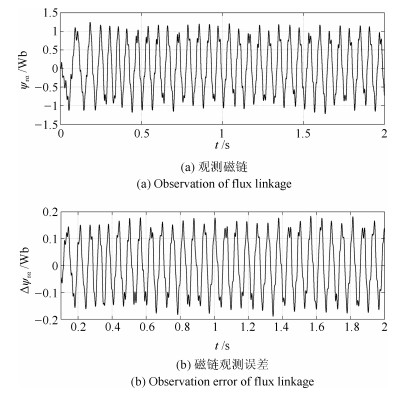
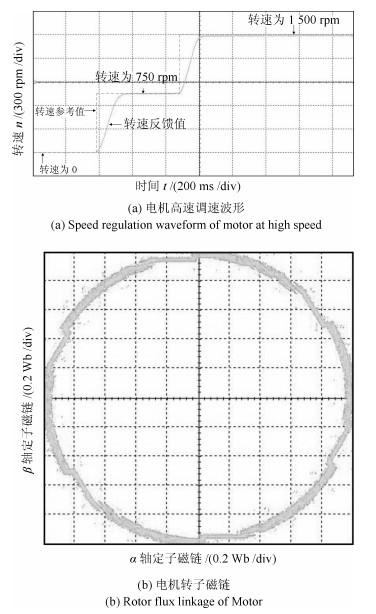
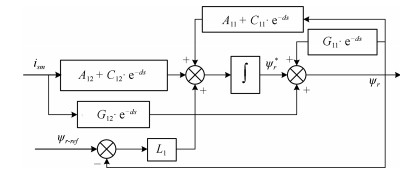
摘要: 针对感应电机交流传动控制系统磁链观测模型不精确, 忽略控制中的延时问题, 转子磁链观测一般具有观测精度不高、易受电机参数变化影响等问题, 运用中立型理论, 建立中立型感应电机观测模型, 提出一种基于中立型的转子磁链观测方法, 设计了中立型转子磁链观测器.该磁链观测器具有观测精度高、受电机参数变化影响小、鲁棒性好的优点, 通过建立精确的观测模型, 解决控制中延时问题对磁链观测精度的影响.对感应电机中立型磁链观测模型进行了稳定性分析.仿真和实验结果证明了所设计中立型转子磁链观测器的可行性和有效性.Abstract: For AC drive control system of the inductive motor, the model of flux observation is inaccurate, ignoring the delay problem in the control. The rotor flux observation generally has problems such as low observation accuracy and vulnerability to motor parameter variation. Neutral theory is used to establish neutral type observation model of induction motor, a neutral rotor flux observation method is proposed to design a neutral rotor flux observer. The flux observer has the advantages of high observation precision, small influence on motor parameter variation and good robustness. By establishing an accurate observation model, the influence of delay time in control on the accuracy of flux observation is solved. The stability analysis of the neutral flux observation model of the induction motor was carried out. Simulation and experimental results demonstrate the feasibility and effectiveness of the designed neutral rotor flux observer.
-
Key words:
- Induction motor /
- neutral theory /
- linear matrix inequality (LMI) /
- flux linkage observation /
- observation accuracy
1) 本文责任编委 梅生伟 -
表 1 电机参数
Table 1 Motor parameters
参数 数值 额定功率$P_N$ /kW 4 额定电压$U_N$/V 380 额定频率$f_N$/Hz 50 额定电流$I_N$/A 8.8 定子电阻$R_s/{\rm \Omega}$ 1.405 定子电感$L_s$/mH 178 转子电阻$R_r/{\rm \Omega}$ 1.395 转子电感$L_r/$mH 178 定转子互感$L_m/$mH 172.2 极对数$n_p$ 2 额定转速$n/{\rm r}\cdot {\rm min}_{-1}$ 1 440 表 2 磁链观测误差
Table 2 Observation error of flux linkage
参数变化量 $-0.5R_r$ $+0.5R_r$ $-0.5L_r$ $+0.5L_r$ $\Delta\Psi_{r\alpha}$变化量$10^{-3}$/kW + 0.9 + 1.0 +1.5 +1.6 $\Delta\Psi_{r\alpha}$变化率 $\leq 5 %$ $\leq 8 %$ -
[1] 任志斌, 许斌, 王喆, 温路佳.转子磁链角在线校正的异步电机矢量控制系统研究与实现.电机与控制应用, 2018, 45(6): 12-16 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201806003Ren Zhi-Bin, Xu Bin, Wang Zhe, Wen Lu-Jia. Research and realization of induction motor vector control system for online correction of rotor flux angle. Motor and Control Applications. 2018, 45(6): 12-16 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201806003 [2] 张兴, 张雨薇, 曹朋朋, 杨淑英.基于定子电流和转子磁链点乘的异步电机转子时间常数在线辨识算法稳定性分析.中国电机工程学报, 2018, 38(16): 4863-4873, 4992 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdjgcxb201816025Zhang Xing, Zhang Yu-Wei, Cao Peng-Peng, Yang Shu-Ying. Stability analysis of a dot product of stator currents and rotor flux based online rotor time constant updating algorithm in induction motor drives. Proceedings of the CSEE, 2018, 38(16): 4863-4873, 4992 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdjgcxb201816025 [3] 王铁军, 单潮龙, 赵镜红, 张俊洪.异步电机矢量控制中转子磁链的直接观测方法.海军工程大学学报, 2002(05): 19-21, 30 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hjgcdxxb200205005Wang Tie-Jun, Shan Chao-Long, Zhao Jing-Hong, Zhang Jun-Hong. Direct observation method of rotor flux in vector control of asynchronous motor. Journal of Naval University of Engineering, 2002(05): 19-21, 30 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hjgcdxxb200205005 [4] 刘燕, 邵晓强.异步电机矢量控制系统转子磁链间接检测方法.微电机(伺服技术), 2001(2): 27-29 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wdj200102007Liu Yan, Shao Xiao-Qiang. accuracy analysis and design of rotor flux observer for asynchronous motor. Micromotors (Servotechnology), 2001(2): 27-29 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wdj200102007 [5] 韦汉培, 朱保鹏, 魏海峰, 张懿.考虑效率最大化的新型感应电机转子磁链给定.电机与控制应用, 2018, 45(2): 81-85 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201802015Wei Han-Pei, Zhu Bao-Peng, Wei Hai-Feng, Zhang Yi. New rotor flux reference of induction motor considering efficiency maximization. Motor and Control Applications. 2018, 45(2): 81-85 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201802015 [6] 刘培刚.异步电机转子磁链两种电流观测模型的仿真研究.电气开关, 2009, 47(5): 42-44 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqkg200905014Liu Pei-Gang. Simulation research on two current observation models of rotor flux of asynchronous motor. Electric Switch, 2009, 47(5): 42-44 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqkg200905014 [7] 张春朋, 林飞, 陈寿孙.改进U-I法感应电机转子磁链估计器.中国电机工程学报, 2004 (5): 130-133 http://d.wanfangdata.com.cn/Periodical/zgdjgcxb200405024Zhang Chun-Peng, Lin Fei, Chen Shou-Sun. Improved U-I method induction motor rotor flux estimator. Proceedings of the CSEE, 2004(5): 130-133 http://d.wanfangdata.com.cn/Periodical/zgdjgcxb200405024 [8] 赵雷廷, 刁利军, 董侃, 刘志刚.基于状态空间拆分重组的牵引异步电机闭环离散全阶转子磁链观测器.电工技术学报, 2013, 28(10): 103-112 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dgjsxb201310014Zhao Lei-Ting, Diao Li-Jun, Dong Kang, Liu Zhi-Gang. Closed-loop discrete full-order rotor flux observer of traction tnduction motor based on state space splitting and recombination. Transactions of China Electrotechnical Society, 2013, 28(10): 103-112 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dgjsxb201310014 [9] Barut M. Bi input-extended Kalman filter based estimation technique for speed-sensorless control of induction motors. Energy Conversion and Management, Elsevier, 2010: 2032-2040 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=097d75d4a05fce7f9379dc457dabfdb8 [10] 黄亚欣, 张星慧, 蒋蒙蒙.带有输入和状态时滞的高阶非线性前馈系统的自适应控制.自动化学报, 2017, 43(7): 1273-1279 doi: 10.16383/j.aas.2017.e140146Huang Ya-Xin, Zhang Xing-Hui, Jiang Meng-Meng. Adaptive control for high-order nonlinear feedforward systems with input and state delays. Acta Automatica Sinica, 2017, 43(7): 1273-1279 doi: 10.16383/j.aas.2017.e140146 [11] 储建华, 于霜, 魏海峰.考虑参数摄动的感应电机新型滑模观测器.电气传动, 2018, 48(3): 3-8 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqcd201803001Chu Jian-Hua, Yu Shuang, Wei Hai-Feng. New sliding mode observer design for induction motor considering parameter perturbation. Electric Drive, 2018, 48(3): 3-8 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqcd201803001 [12] 文传博, 邓露, 吴兰.基于滑模观测器和广义观测器的故障估计方法.自动化学报, 2018, 44(9): 1698-1705 doi: 10.16383/j.aas.2017.c160730Wen Chuan-Bo, Deng Lu, Wu Lan. Fault estimation approaches with sliding mode observer and descriptor observer. Acta Automatica Sinica, 2018, 44(9): 1698-1705 doi: 10.16383/j.aas.2017.c160730 [13] 潘月斗, 陈涛, 郭映维.异步电机反馈线性化二阶滑模定子磁链观测器设计.控制理论与应用, 2016, 33(11): 1474-1482 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzllyyy201611008Pan Yue-Dou, Chen Tao, Guo Ying-Wei. Design of feedback linearized second-order sliding mode stator flux observer for asynchronous motor. Control Theory & Applications, 2016, 33(11): 1474-1482 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzllyyy201611008 [14] 孟庆硕, 许鸣珠, 李玲瑞.基于自适应PID的异步电机电流控制.电机与控制应用, 2018, 45(4): 39-43 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201804007Meng Qing-Shuo, Xu Ming-Zhu, Li Ling-Rui. Asynchronous motor current control based on adaptive PID. Motor and Control Applications. 2018, 45(4): 39-43 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201804007 [15] Park J H, Won R. Stability analysis for neutral delay differential systems. Journal of Franklin Institute, 2000, 337: 1-9 doi: 10.1016/S0016-0032(99)00040-X [16] 马会贤.基于转子磁场定向矢量控制的感应电机改进磁链观测方法.电机与控制应用, 2017, 44(8): 65-68 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201708012Ma Hui-Xian. Improved flux linkage observation method for induction motor based on rotor field oriented vector control. Motor and Control Applications, 2017, 44(8): 65-68 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj201708012 [17] Meng J M. Robust stabilization of induction neutral delay systems with uncertainty. Journal of Shandong Vocational and Technical College of Commerce, 2014, 14(2): 115-118 [18] Wang Z D, Lam J, Burnham K J. Stability analysis and observer design for neutral delay systems. IEEE Transactions on Automatic Control, 2002, 47(3): 478-483 doi: 10.1109/9.989144 [19] Wu M, He Y, She J H, Liu G P. Parameter-dependent Lyapunov functional for stability of time-delay systems with polytopic type uncertainties. IEEE: Transactions on Automatic Control, 2004, 49(5): 828-832 doi: 10.1109/TAC.2004.828317 [20] 王景成, 邵惠鹤.不确定时滞系统的基于Razumikhin定理的鲁棒H∞可靠控制.自动化学报, 28(2): 262-266 http://www.aas.net.cn/article/id/15528Wang Jing-Cheng, Shao Hui-He. Robust H∞ reliable control based on razumikhin theorem for uncertain time-delay systems. Acta Automatica Sinica, 28(2): 262-266 http://www.aas.net.cn/article/id/15528 [21] 徐君, 张国良, 曾静, 杜柏阳, 贾枭.高阶离散多智能体系统在参数不确定和带外部干扰下的鲁棒H∞一致性控制.自动化学报, 2017, 43(10): 1850-1857 doi: 10.16383/j.aas.2017.e160115Xu Jun, Zhang Guo-Liang, Zeng Jing, Du Bo-Yang, Jia Xiao. Robust H∞ consensus control for high-order discrete-time multi-agent systems with parameter uncertainties and external disturbances. Acta Automatica Sinica, 2017, 43(10): 1850-1857 doi: 10.16383/j.aas.2017.e160115 [22] 周笔锋, 罗毅平.时滞分布参数系统中和控制器设计.自动化学报, 2018, 44(12): 2222-2227 doi: 10.16383/j.aas.2018.c170084Zhou Bi-Feng, Luo Yi-Ping. Neutralization control of distributed parameter systems with delay. Acta Automatica Sinica, 2018, 44(12): 2222-2227 doi: 10.16383/j.aas.2018.c170084 -




 下载:
下载: