Fault Detection Strategy Based on Principal Component Score Difference of $ \pmb k $ Nearest Neighbors
-
摘要: 针对具有非线性和多模态特征过程的故障检测问题, 本文提出一种基于k近邻主元得分差分的故障检测策略.首先, 通过主元分析(Principal component analysis, PCA)方法计算样本的真实得分.然后, 应用样本的k近邻均值计算样本估计得分.接下来, 通过上述两种得分计算样本的得分差分矩阵和残差矩阵, 其中残差矩阵由样本的估计得分计算得到,这区别于传统方法.最后, 在差分子空间和残差子空间中分别建立新的统计指标进行故障检测.值得注意的是本文的得分差分方法能够消除数据结构对过程故障检测的影响, 同时, 新的统计量能够提高过程的故障检测率.将本文方法在两个模拟例子和Tennessee Eastman (TE)过程中进行测试, 并与传统方法如PCA、KPCA、DPCA和~FD-kNN等进行对比分析, 测试结果证明了本文方法的有效性.Abstract: In order to monitor a process with nonlinear and multimode characteristics effectively, this paper presents a novel fault detection method using principal component score difference based on k nearest neighbors. In the proposed method, firstly, real scores of samples are calculated through principal component analysis (PCA) method. Next, estimated scores of samples are calculated using the mean of k nearest neighbors through a linear transformation. After that a score difference matrix can be obtained through calculating the difference between the real scores and the estimated scores; meanwhile, a residual matrix can be also obtained by reconstructing a sample using the estimated scores. At last, two new statistics are built to monitor the variability of a sample in the score difference subspace (SDS) and residual subspace (RS), respectively. It should be noted that the proposed difference method is able to eliminate the impact of data structure on process monitoring and the new statistics can improve fault detection rate of a process. The efficiency of the proposed method in this paper is tested in two simulated cases and in the Tennessee Eastman (TE) processes. The experimental results indicate that the proposed method outperforms the conventional methods, such as PCA, KPCA, DPCA, and FD-kNN.
-
Key words:
- Principal component analysis (PCA) /
- difference of scores /
- k nearest neighbors (kNN) /
- multimode process /
- Tennessee Eastman (TE) processes /
- fault detection
1) 本文责任编委 刘允刚 -
表 1 参数设置, 故障检测率和误报率
Table 1 Setting of parameters, FDR and FAR
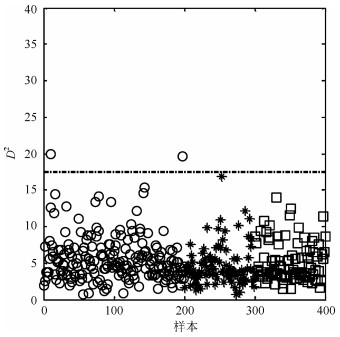
方法 PCs k FDR FAR PCA 2 - 0 0 PC-kNN 2 3 85 0 本文方法 2 5 100 0 表 2 各种方法的故障检测率
Table 2 FDRs using different methods
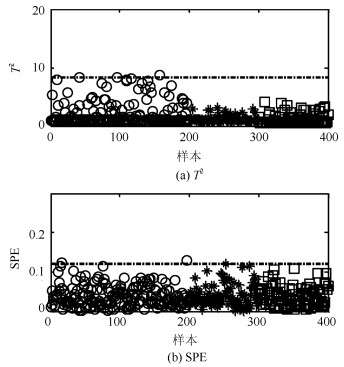
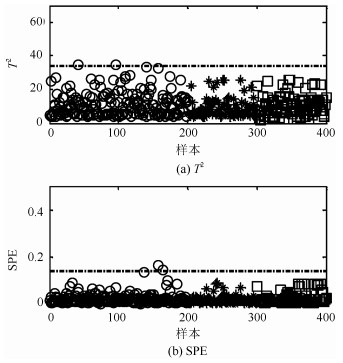
方法 F1 F2 F3 F4 F5 PCA-T2 54.6 0.1 89.4 67.8 3.4 PCA-SPE 79.8 0.6 98.8 76.5 1.4 KPCA-T2 69.6 1.4 6.1 67.6 0.5 KPCA-SPE 83.5 1.4 65.5 83.5 2 DPCA-T2 84.1 0 93.5 75.9 4.5 DPCA-SPE 65.8 0.1 88.1 76.6 1.5 Tdiff2 87.3 1.5 92.5 72.5 4.8 qdiff 92.5 90.3 100 92.5 95.1 表 3 各种方法的故障误报率
Table 3 FARs using different methods
方法 F1 F2 F3 F4 F5 PCA-T2 0 0 1.5 1.5 1.5 PCA-SPE 0 0 2.5 2.5 2.5 KPCA-T2 0.5 0.5 2 2 2 KPCA-SPE 0 0 2.5 2.5 2.5 DPCA-T2 0 0 3 3 3 DPCA-SPE 0 0 2.5 2.5 2.5 Tdiff2 0 0 0.5 0.5 0.5 qdiff 0 0 1 1 1 -
[1] 彭开香, 马亮, 张凯.复杂工业过程质量相关的故障检测与诊断技术综述.自动化学报, 2017, 43(3): 349-365 doi: 10.16383/j.aas.2017.c160427Peng Kai-Xiang, Ma Liang, Zhang Kai. Review of quality-related fault detection and diagnosis techniques for complex industrial processes. Acta Automatica Sinica, 2017, 43(3): 349-365 doi: 10.16383/j.aas.2017.c160427 [2] Su Q L, Chiu M S. Monitoring ph-shift reactive crystallization of l-glutamic acid using moving window MPCA. Journal of Chemical Engineering of Japan, 2016, 49(7): 680-688 doi: 10.1252/jcej.15we138 [3] Bakdi A, Kouadri A. A new adaptive PCA based thresholding scheme for fault detection in complex systems. Chemometrics & Intelligent Laboratory Systems, 2017, 49(7): 680-688 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=18caa3e40ea91cb132179eaed93bb60f [4] Zhang C, Gao X, Xu T, Li Y, Pang Y. Fault detection and diagnosis strategy based on a weighted and combined index in the residual subspace associated with PCA. Journal of Chemometrics.[Online], available: https://onlinelibrary.wiley.com/doi/abs/10.1002/cem.2981, July 1, 2018. [5] Xu Y, Liu Y, Zhu Q. Multivariate time delay analysis based local KPCA fault prognosis approach for nonlinear processes. sl Chinese Journal of Chemical Engineering, 2016, 24(10): 1413-1422 doi: 10.1016/j.cjche.2016.06.011 [6] Ammiche M, Kouadri A, Bensmail A. A modified moving window dynamic PCA with fuzzy logic filter and application to fault detection. Chemometrics & Intelligent Laboratory Systems, 2018, 177(1): 100-113 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=28270950996e2f1e2a84cf2b1a5f8537 [7] Taouali O, Jaffel I, Lahdhiri H. New fault detection method based on reduced kernel principal component analysis (RKPCA). International Journal of Advanced Manufacturing Technology, 2016, 85(5-8): 1-6 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=fdbecdaac5f91938f6325a6b35d0066d [8] Zhang Y, Li S, Hu Z. Improved multi-scale kernel principal component analysis and its application for fault detection. Chemical Engineering Research & Design, 2012, 90(9): 1271-1280 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=66297bcf0efe0a73fd60c255729309ce [9] Rato T J, Reis M S. Fault detection in the Tennessee Eastman benchmark process using dynamic principal components analysis based on decorrelated residuals (DPCA-DR). Chemometrics & Intelligent Laboratory Systems, 2013, 125(7): 101-108 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=9579abc7bcb7af5465b9609fe339c82b [10] Wang G, Liu J, Zhang Y. A novel multimode data processing method and its application in industrial process monitoring. Journal of Chemometrics, 2015, 29(2): 126-138 doi: 10.1002/cem.2686 [11] Rato T J, Reis M S. Advantage of using decorrelated residuals in dynamic principal component analysis for monitoring large-scale systems. Industrial & Engineering Chemistry Research, 2013, 52(38): 13685-13698 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=56e7f0c3c6ef194c12b6c1fbbbdb9e1d [12] He Q P, Wang J. Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes. IEEE Transactions on Semiconductor Manufacturing, 2007, 20(4): 345-354 doi: 10.1109/TSM.2007.907607 [13] Zhao S J, Zhang J, Xu Y M. Monitoring of processes with multiple operating modes through multiple principle component analysis models. Industrial & Engineering Chemistry Research, 2004, 43(22): 7025-7035 doi: 10.1021/ie0497893 [14] Zhao S J, Zhang J, Xu Y M. Performance monitoring of processes with multiple operating modes through multiple PLS models. Journal of Process Control, 2006, 16(7): 763-772 doi: 10.1016/j.jprocont.2005.12.002 [15] He Q P, Wang J. Large-scale semiconductor process fault detection using a fast pattern recognition-based method. IEEE Transactions on Semiconductor Manufacturing, 2010, 23(2): 194-200 doi: 10.1109/TSM.2010.2041289 [16] Ma H, Hu Y, Shi H. A novel local neighborhood standardization strategy and its application in fault detection of multimode processes. Chemometrics & Intelligent Laboratory Systems, 2012, 118(7): 287-300 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d1515317f0e05097065ba2a2b21a9833 [17] Ma H, Hu Y, Shi H. Nonlinear process monitoring using kernel principal component analysis. Chemical Engineering Science, 2004, 59(1): 223-234 doi: 10.1016/j.ces.2003.09.012 [18] Samuel R T, Cao Y. Nonlinear process fault detection and identification using kernel PCA and kernel density estimation. sl Systems Science & Control Engineering, 2016, 4(1): 1-9 doi: 10.1080/21642583.2016.1198940 [19] Kano M, Sakata T, Hasebe S. Just-in-time statistical process control: adaptive monitoring of vinyl acetate monomer process. World Congress, 2011, 18(1): 13157-13162 doi: 10.3182/20110828-6-it-1002.01756 [20] Wang G, Liu J, Li Y. Fault detection based on diffusion maps and k nearest neighbour diffusion distance of feature space. Journal of Chemical Engineering of Japan, 2015, 48(9): 756-765 doi: 10.1252/jcej.14we227 [21] Wang J, He Q P. Multivariate statistical process monitoring based on statistics pattern analysis. Industrial & Engineering Chemistry Research, 2010, 49(17): 7858-7869 doi: 10.1021/ie901911p [22] 张成, 郭青秀, 李元, 高宪文.基于主元分析得分重构差分的故障检测策略.控制理论与应用, 2019, 36(5): 774-782 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzllyyy201905014Zhang Cheng, Guo Qing-Xiu, Li Yuan, Gao Xian-Wen. Fault detection strategy based on difference of score reconstruction associated with principal component analysis. Control Theory & Applications, 2019, 36(5): 774-782 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kzllyyy201905014 [23] Cheng C Y, Hsu C C, Chen M C. Adaptive kernel principal component analysis (KPCA) for monitoring small disturbances of nonlinear processes. Industrial & Engineering Chemistry Research, 2011, 49(5): 2254-2262 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=2840c2e816144dca2eed0b388b4e62a3 [24] Yu H, Khan F. Improved latent variable models for nonlinear and dynamic process monitoring. Chemical Engineering Science, 2017, 168: 325-338 doi: 10.1016/j.ces.2017.04.048 -





 下载:
下载: