Relative Neighborhood and Pruning Strategy Optimized Density Peaks Clustering Algorithm
-
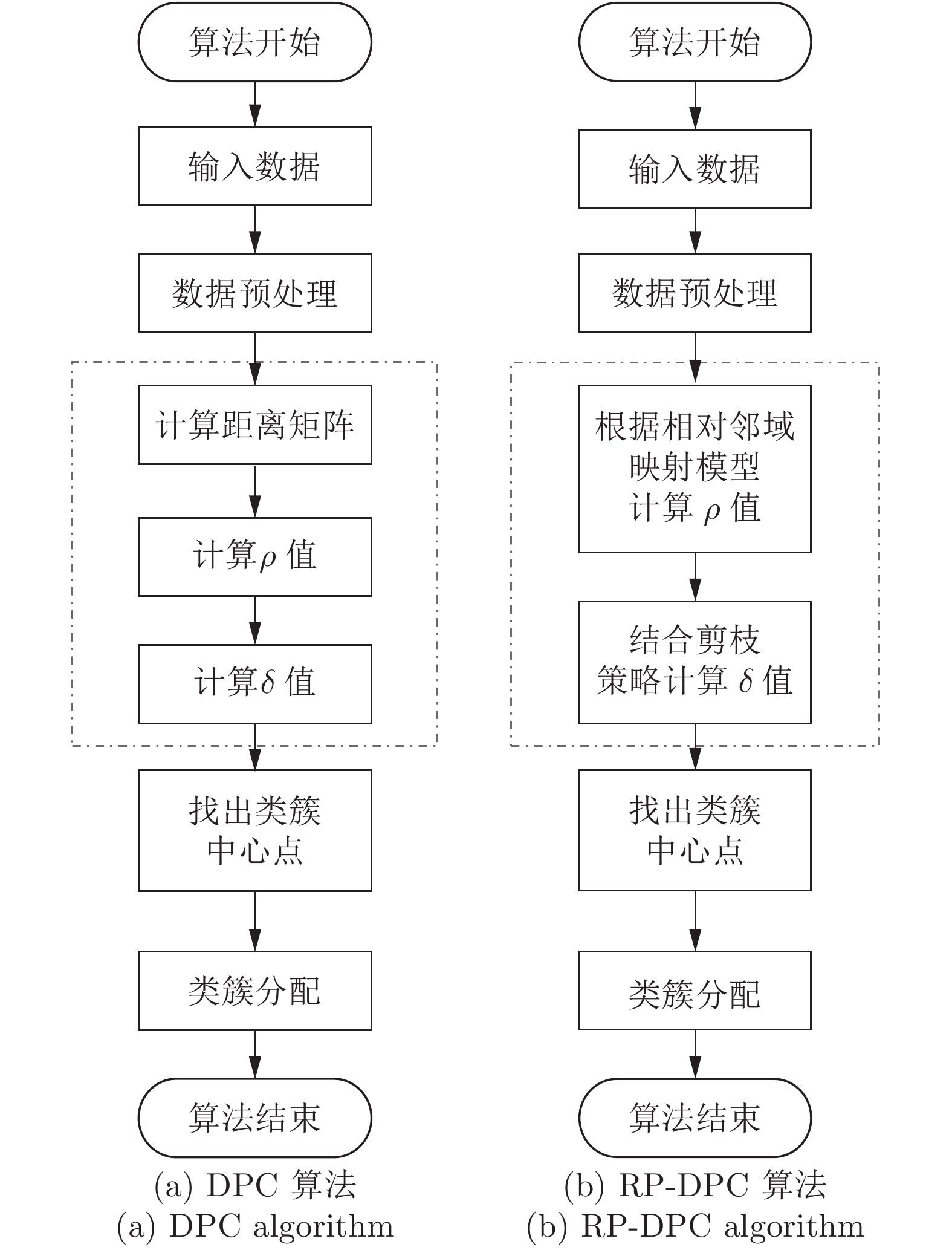
摘要: 针对Science发表的密度峰值聚类(Density peaks clustering, DPC)算法及其改进算法效率不高的缺陷, 提出一种相对邻域和剪枝策略优化的密度峰值聚类(Relative neighborhood and pruning strategy optimized DPC, RP-DPC)算法. DPC聚类算法主要有两个阶段: 聚类中心点的确定和非聚类中心点样本的类簇分配, 并且时间复杂度集中在第1个阶段, 因此RP-DPC算法针对该阶段做出改进研究. RP-DPC算法去掉了DPC算法预先计算距离矩阵的步骤, 首先利用相对距离将样本映射到相对邻域中, 再从相对邻域来计算各样本的密度, 从而缩小各样本距离计算及密度统计的范围; 然后在计算各样本的δ值时加入剪枝策略, 将大量被剪枝样本δ值的计算范围从样本集缩小至邻域以内, 极大地提高了算法的效率. 理论分析和在人工数据集及UCI数据集的对比实验均表明, 与DPC算法及其改进算法相比, RP-DPC算法在保证聚类质量的同时可以实现有效的时间性能提升.Abstract: In order to overcome the low efficiency defect of density peaks clustering (DPC) algorithm published in Science and its improvement algorithms, a new relative neighborhood and pruning strategy optimized DPC (RP-DPC) algorithm is proposed in this paper. There are two main phases in DPC: determination of cluster centers and cluster assignation for remaining samples. The time complexity of DPC is determined by the first phase, so the improvements for the determination of cluster centers are proposed in this paper. Firstly, the RP-DPC algorithm maps samples to their relative neighborhoods, then computes the local density of every sample on the basis of relative neighborhood. This method shrinks the range of distance computing and density counting of every sample, thus avoiding a lot of unnecessary distance calculations. Secondly, the pruning strategy is led into the δ value computing of every sample, which restricts the δ computing of massive pruned samples to within their own neighborhoods, so as to greatly improve the efficiency. We demonstrate that: our RP-DPC algorithm can improve the time performance significantly on the basis of having same clustering quality compared with the DPC algorithm and its improvement algorithms through the theory analysis and the experiments on several popular test cases that include both synthetic and real-world data sets from the UCI machine learning repository.
-
Key words:
- Clustering algorithm /
- density peaks /
- relative neighborhood /
- pruning strategy
1) 收稿日期 2017-11-06 录用日期 2018-08-28 Manuscript received November 6, 2017; accepted August 28, 2018 国家自然科学基金 (61602004, 61672034), 安徽省重点研究与开发计划 (1804d8020309), 安徽省自然科学基金 (1708085MF160, 1908085MF188), 安徽省高等学校自然科学研究重点项目 (KJ2016A041, KJ2017A011), 安徽大学信息保障技术协同创新中心公开招标课题 (ADXXBZ201605)资助 Supported by National Natural Science Foundation of China (61402004, 61672034), Key Research and Development Program of Anhui Province (1804d8020309), Natural Science Foundation of Anhui Province (1708085MF160, 1908085MF188), Natural Science Foundation of Anhui Higher Education Institutions (KJ2016A041, KJ2017A011), and Public Bidding Project of Co-Innovation Center for Information Supply and Assurance Technology of Anhui University (ADXXBZ201605) 本文责任编委 辛景民2) Recommended by Associate Editor XIN Jing-Min 1. 安徽大学计算机科学与技术学院 合肥 230601 2. 安徽大学计算智能与信号处理教育部重点实验室 合肥 230601 1. School of Computer Science and Technology, Anhui University, Hefei 230601 2. Key Laboratory of Intelligent Computing and Signal Processing of the Ministry of Education, Anhui University, Hefei 230601 -
表 1 实验数据集
Table 1 Data sets used in experiments
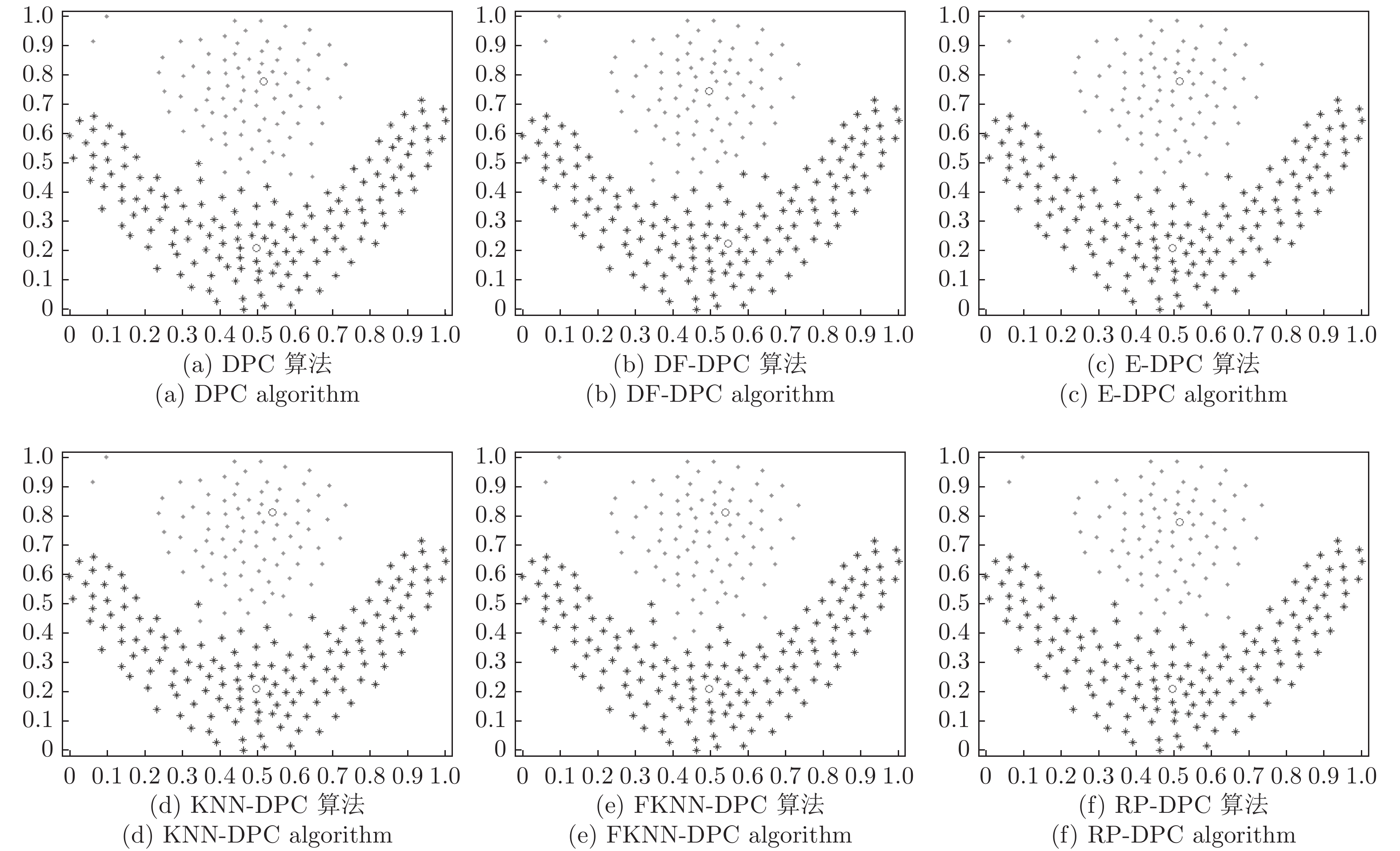
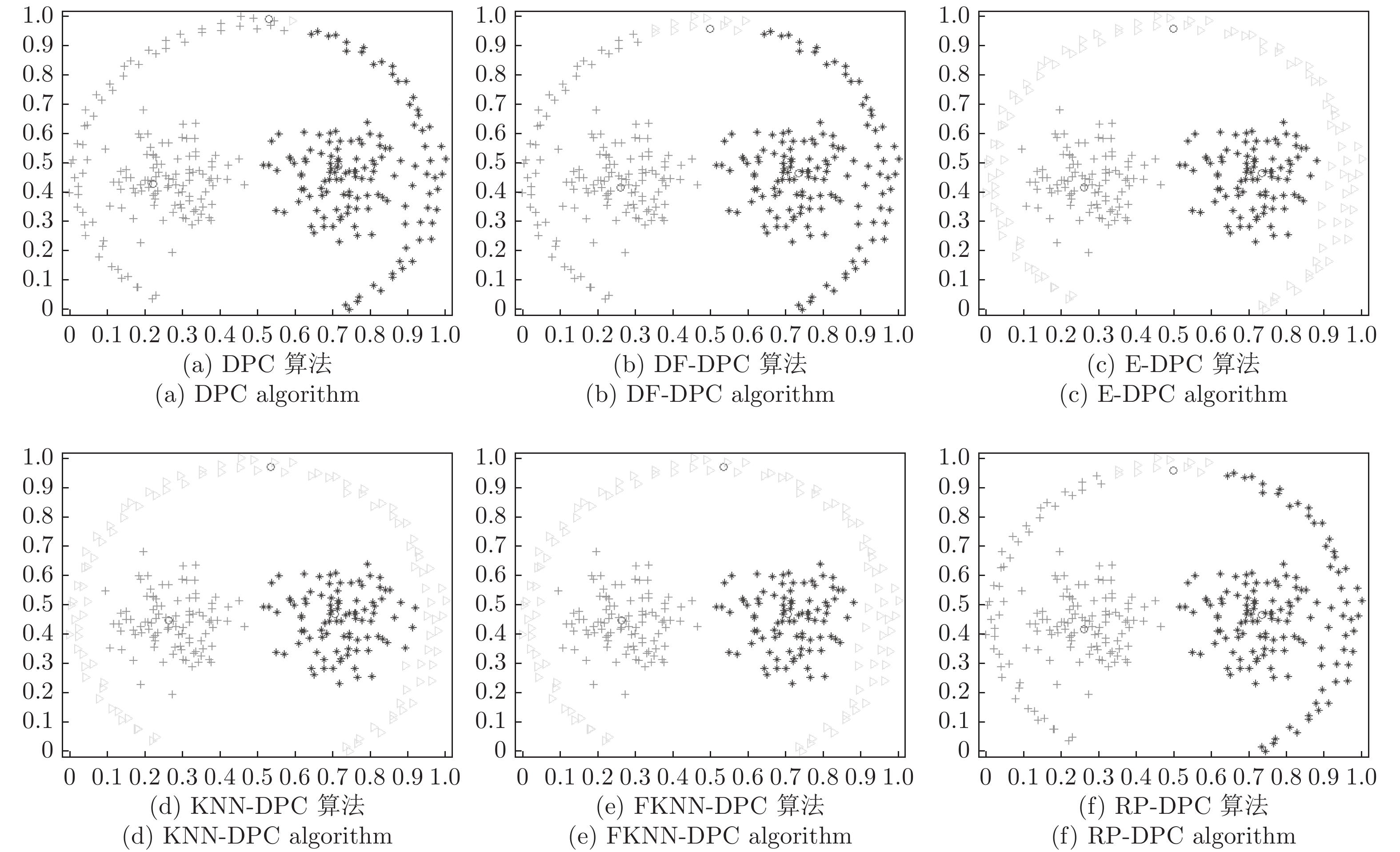
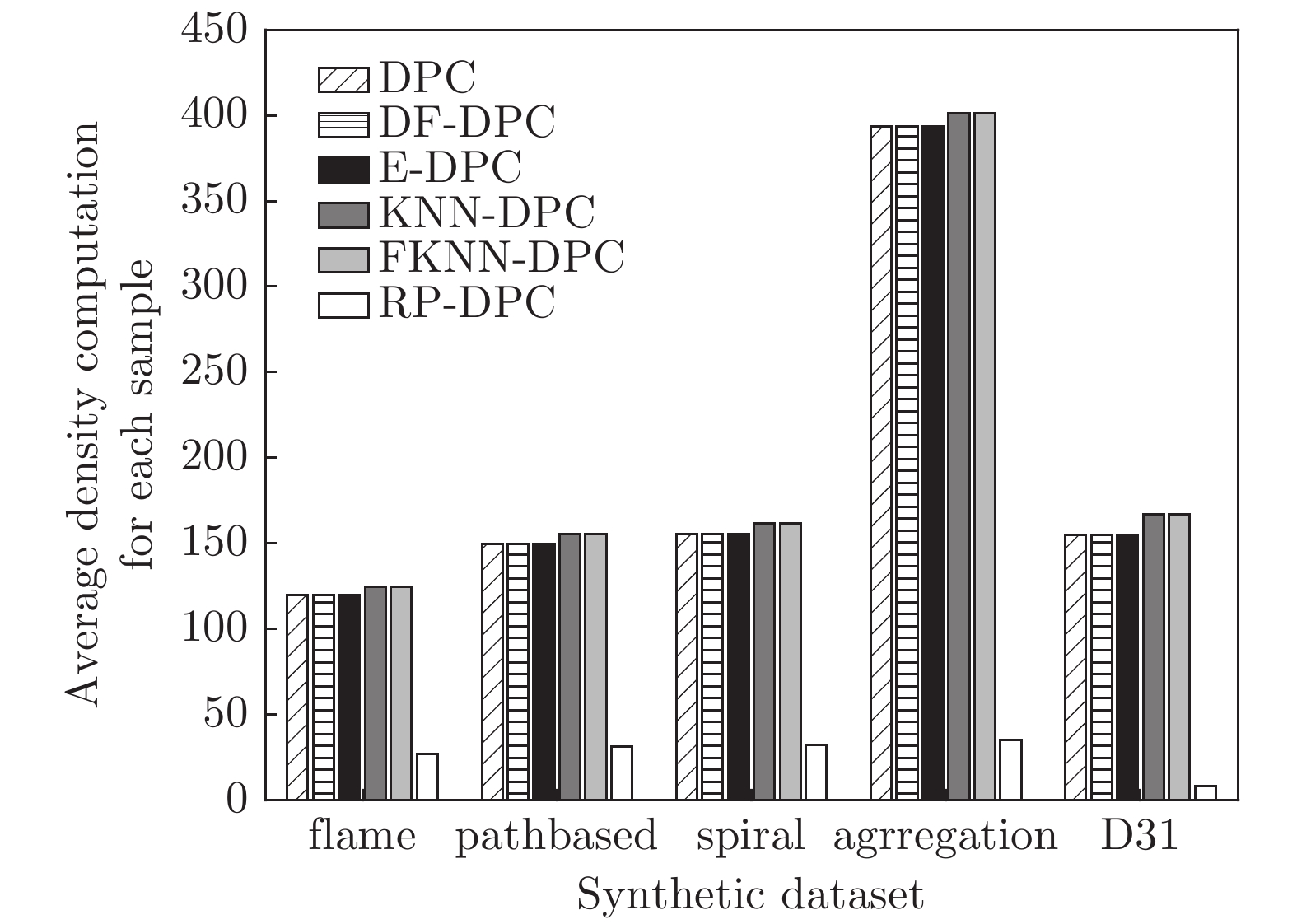
表 2 6种算法在人工数据集上的聚类结果
Table 2 Clustering results of six algorithms on synthetic datasets
数据集 算法 F/P Par Acc AMI ARI 算法 F/P Par Acc AMI ARI flame DPC 2/2 5 1.000 1.000 1.000 KNN-DPC 2/2 5 0.992 0.978 0.962 DF-DPC 2/2 0.157 1.000 1.000 1.000 FKNN-DPC 2/2 5 1.000 1.000 1.000 E-DPC 2/2 5 1.000 1.000 1.000 RP-DPC 2/2 5 1.000 1.000 1.000 pathbased DPC 3/3 2 0.752 0.578 0.517 KNN-DPC 3/3 6 0.983 0.951 0.924 DF-DPC 3/3 0.027 0.493 0.402 0.399 FKNN-DPC 3/3 6 0.983 0.951 0.924 E-DPC 3/3 5 0.987 0.941 0.960 RP-DPC 3/3 2 0.752 0.578 0.517 spiral DPC 3/3 2 1.000 1.000 1.000 KNN-DPC 3/3 6 1.000 1.000 1.000 DF-DPC 3/3 0.148 1.000 1.000 1.000 FKNN-DPC 3/3 6 1.000 1.000 1.000 E-DPC 3/3 5 1.000 1.000 1.000 RP-DPC 3/3 2 1.000 1.000 1.000 aggregation DPC 7/7 4 0.999 0.998 0.996 KNN-DPC 3/3 6 0.999 0.997 0.995 DF-DPC 7/7 0.084 0.999 0.998 0.996 FKNN-DPC 3/3 6 0.999 0.997 0.995 E-DPC 7/7 4 0.999 0.998 0.996 RP-DPC 3/3 2 0.999 0.998 0.996 D31 DPC 31/31 1 0.968 0.937 0.956 KNN-DPC 31/31 12 0.954 0.903 0.939 DF-DPC 31/31 0.039 0.968 0.937 0.956 FKNN-DPC 31/31 12 0.954 0.903 0.939 E-DPC 31/31 1 0.968 0.937 0.956 RP-DPC 31/31 1 0.968 0.937 0.956 表 3 6种算法在真实数据集上的聚类结果
Table 3 Clustering results of six algorithms on real datasets
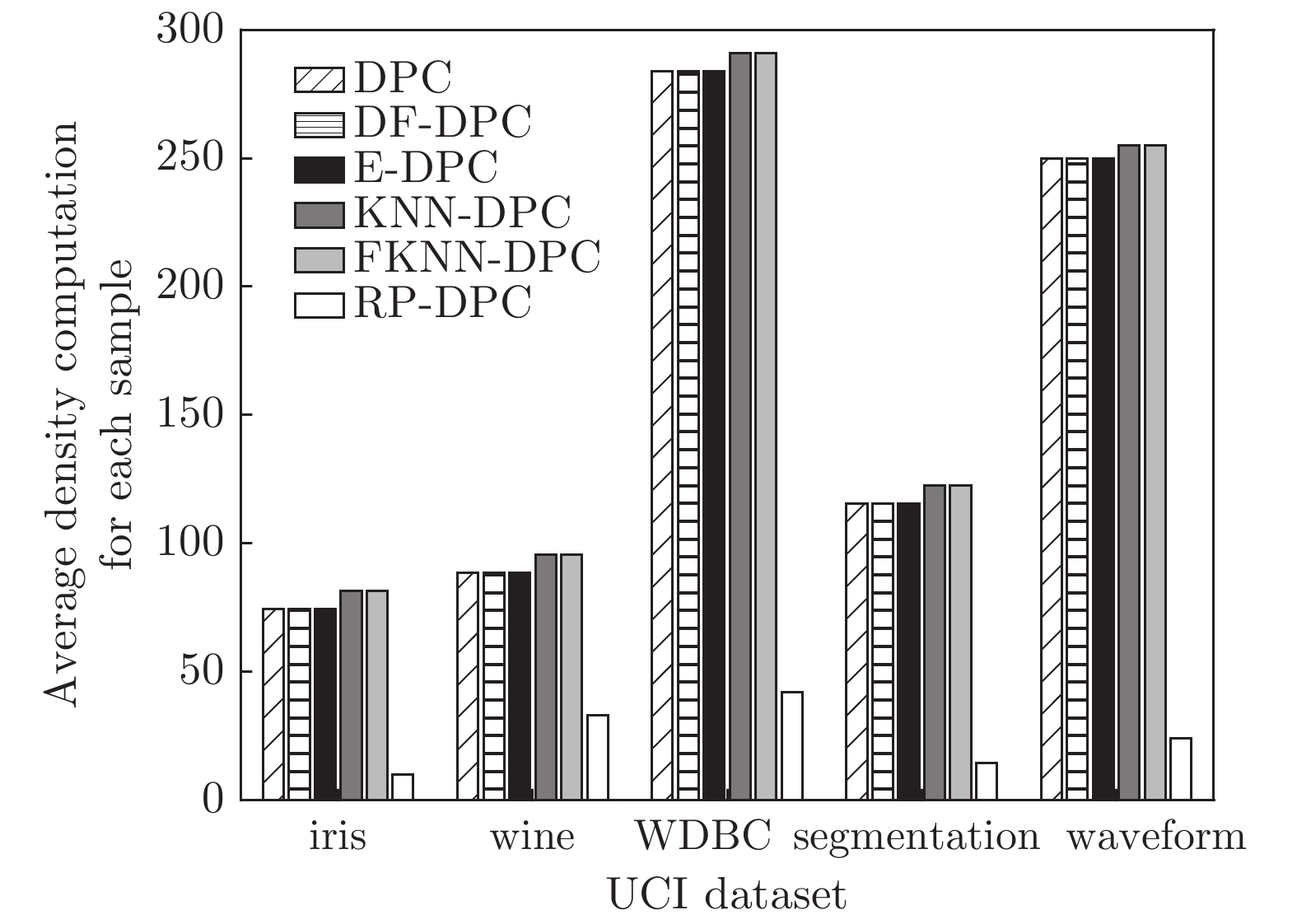
数据集 算法 F/P Par Acc AMI ARI 算法 F/P Par Acc AMI ARI iris DPC 3/3 2 0.887 0.767 0.720 KNN-DPC 3/3 7 0.960 0.902 0.860 DF-DPC 3/3 0.126 0.727 0.615 0.561 FKNN-DPC 3/3 7 0.973 0.912 0.922 E-DPC 3/3 2 0.933 0.887 0.862 RP-DPC 3/3 2 0.887 0.767 0.720 wine DPC 3/3 2 0.882 0.706 0.672 KNN-DPC 3/3 7 0.921 0.769 0.737 DF-DPC 3/3 0.473 0.916 0.757 0.756 FKNN-DPC 3/3 7 0.949 0.831 0.852 E-DPC 3/3 2 0.882 0.706 0.672 RP-DPC 3/3 2 0.882 0.706 0.672 WDBC DPC 2/2 0.85 0.845 0.415 0.471 KNN-DPC 2/2 7 0.944 0.679 0.786 DF-DPC 2/2 0.407 0.838 0.374 0.451 FKNN-DPC 2/2 7 0.944 0.679 0.786 E-DPC 2/2 0.85 0.845 0.415 0.471 RP-DPC 2/2 0.85 0.845 0.415 0.471 segmentation DPC 6/5 3 0.684 0.651 0.550 KNN-DPC 6/5 7 0.718 0.539 0.632 DF-DPC 6/5 0.337 0.746 0.703 0.607 FKNN-DPC 6/5 7 0.716 0.655 0.555 E-DPC 6/5 3 0.684 0.651 0.550 RP-DPC 6/5 3 0.684 0.651 0.550 waveform DPC 3/3 0.5 0.586 0.318 0.268 KNN-DPC 3/3 5 0.696 0.338 0.313 DF-DPC 3/3 0.604 0.492 0.325 0.276 FKNN-DPC 3/3 5 0.703 0.324 0.350 E-DPC 3/3 2 0.716 0.368 0.338 RP-DPC 3/3 0.5 0.586 0.318 0.268 表 4 6种算法在数据集上的运行时间 (s)
Table 4 Running time of six algorithms on several datasets (s)
数据集 DPC DF-DPC E-DPC KNN-DPC FKNN-DPC RP-DPC 人工数据集 flame 0.103 0.185 0.142 0.179 0.188 0.054 pathbased 0.137 0.265 0.201 0.193 0.260 0.036 spiral 0.132 0.313 0.211 0.221 0.311 0.027 aggregation 0.354 0.567 0.524 0.717 0.764 0.035 D31 1.825 3.603 3.592 4.382 4.671 0.221 真实数据集 iris 0.088 0.142 0.131 0.137 0.156 0.020 wine 0.108 0.172 0.131 0.141 0.165 0.032 WDBC 0.372 0.836 0.482 0.705 0.904 0.058 segmentation 1.836 2.763 2.013 4.220 4.918 0.191 waveform 9.551 16.381 13.106 22.528 24.741 0.537 表 5 RP-DPC算法在10个数据集上的剪枝率
Table 5 Pruning ratio of RP-DPC algorithm on ten data sets
数据集 数据集规模 RP-DPC 剪枝率(%) 数据集 数据集规模 RP-DPC 剪枝率(%) flame 240 5 97.9 iris 150 15 90 pathbased 300 8 97.3 wine 178 9 94.9 spiral 312 10 96.8 WDBC 569 21 96.3 aggregation 788 23 97.1 segmentation 2 310 55 97.6 D31 3 100 49 98.4 waveform 5 000 89 98.2 -
[1] 1 Xu R, Wunsch D C. Survey of clustering algorithms. IEEE Transactions on Neural Networks, 2005, 16(3): 645−678 doi: 10.1109/TNN.2005.845141 [2] 2 Frey B J, Dueck D. Clustering by passing messages between data points. Science, 2007, 315: 972−976 doi: 10.1126/science.1136800 [3] 3 Jain A K. Data clustering: 50 years beyond K-means. Pattern Recognition Letters, 2010, 31: 651−666 doi: 10.1016/j.patrec.2009.09.011 [4] Williamson B, Guyon I. Clustering: science or art? Journal of Machine Learning Research, 2012, 27: 65−80 [5] Kaufman L, Peter R. Clustering by means of medoids. Statistical Data Analysis Based on the L1 Norm and Related Methods, North-Holland: North-Holland Press, 1987. 405−416 [6] MacQueen J. Some methods for classification and analysis of multivariate observation. In: Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Los Angelas, University of California, USA: 1967. 281−297 [7] Zhang W, Wang X G, Zhao D L, Tang X O. Graph Degree Linkage: Agglomerative Clustering on a Directed Graph. Berlin: Springer, 2012. 428−441 [8] Wang W, Yang J, Muntz R. Sting: a statistical information grid approach to spatial data mining. In: Proceedings of International Comferenceon Very Large Date Bases (VLDB’97). San Francisco, CA, USA: Morgan Kaufman, 1997. 186−195 [9] Ester M, Kriegel H P, Sander J, Xu X W. A density-based algorithm for discovering clusters in large spatial databases with noise. In: Proceedings of ACM KDD’96. New York, USA: ACM, 1996. 226−231 [10] 10 Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science, 2014, 344(6191): 1492−1496 doi: 10.1126/science.1242072 [11] 11 Wang S L, Wang D K, Li C Y, Li Y, Ding G Y. Clustering by fast search and flnd of density peaks with data fleld. Chinese Journal of Electronics, 2016, 3(25): 397−402 [12] Zhang W K, Li J. Extended fast search clustering algorithm:widely density clusters, no density peaks. Computer Science andTechnology, 2015. [13] 谢娟英, 高红超, 谢维信. K 近邻优化的密度峰值快速搜索聚类算 法. 中国科学: 信息科学, 2016, 46(2): 258−28013 Xie Juan-Ying, Gao Hong-Chao, Xie Wei-Xin. K-nearest neighbors optimized clustering algorithm by fast search and flnding the density peaks of a data set. SCIENTIA SINICA Informationis, 2016, 46(2): 258−280 [14] 14 Xie J Y, Gao H C, Xie W X. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors. Information Science, 2016, 354: 19−40 doi: 10.1016/j.ins.2016.03.011 [15] 巩树凤, 张岩峰. EDDPC: 一种高效的分布式密度中心聚类算法. 计算机研究与发展, 2016, 53(6): 1400−1409 doi: 10.7544/issn1000-1239.2016.2015061615 Gong Shu-Feng, Zhang Yan-Feng. EDDPC: an efficient distributed density peaks clustering algorithm. Journal of Computer Research and Developmnet, 2016, 53(6): 1400−1409 doi: 10.7544/issn1000-1239.2016.20150616 [16] 16 Liu Y, Huang W L, Jiang Y L, Zeng Z Y. Quick attribute reduction algorithm for neighborhood rough set model. Information Sciences, 2014, 271: 65−81 doi: 10.1016/j.ins.2014.02.093 [17] 17 Gionis A, Mannila H, Tsaparas P. Clustering aggregation. ACM Transactions on Knowledge Discovery from Data, 2007, 1(1): 1−30 doi: 10.1145/1217299 [18] 18 Fu L M, Medico E. Flame, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioininformatics, 2007, 8(1): 3−17 doi: 10.1186/1471-2105-8-3 [19] 19 Chang H, Yeung D Y. Robust path-based spectral clustering. Pattern Recognition, 2008, 41(1): 191−203 doi: 10.1016/j.patcog.2007.04.010 [20] 20 Veenman C J, Reinders M J T, Baker E. A maximum variance cluster algorithm. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(9): 1273−1280 doi: 10.1109/TPAMI.2002.1033218 [21] Lichman M. UCI machine learning repository. http://archive.ics.uci.edu/ml. Irvine: University of California, March 21, 2017 -




 下载:
下载: