密度敏感鲁棒模糊核主成分分析算法

陶新民; 常瑞; 沈微; 李晨曦; 王若彤; 刘艳超

doi:10.16383/j.aas.2018.c170590

密度敏感鲁棒模糊核主成分分析算法

doi: 10.16383/j.aas.2018.c170590

陶新民^1, ,,
常瑞^1,,
沈微^1,,
李晨曦^1,,
王若彤^1,,
刘艳超^1,

1.
东北林业大学工程技术学院哈尔滨 150040

基金项目:

中央高校基本科研业务费专项资金 2572017EB02

中央高校基本科研业务费专项资金 2572017CB07

东北林业大学双一流科研启动基金 411112438

哈尔滨市科技局创新人才基金 2017RAXXJ018

国家自然基金 31570547

详细信息

作者简介:
常瑞  东北林业大学工程技术学院硕士研究生.主要研究方向为模式识别与信号处理. E-mail: m15765549429@163.com

沈微  东北林业大学工程技术学院讲师.主要研究方向为数据分析, 物流系统规划与管理咨询, 系统建模与优化. E-mail: Shenwei@nefu.edu.cn

李晨曦  东北林业大学工程技术学院硕士研究生.主要研究方向为不均衡数据分类和故障诊断. E-mail: chenxili@nefu.edu.cn

王若彤  东北林业大学工程技术学院硕士研究生.主要研究方向为人工智能和聚类分析. E-mail: celia wangrt@163.com

刘艳超  东北林业大学工程技术学院硕士研究生.主要研究方向为物联网技术应用, 模式识别与信号处理. E-mail: liuyanchao@nefu.edu.cn

通讯作者:
陶新民东北林业大学工程技术学院教授. 2005年获哈尔滨工业大学博士学位.主要研究方向为智能信号处理, 软计算方法, 模式识别.本文通信作者. E-mail: taoxinmin@nefu.edu.cn

计量
- 文章访问数: 1816
- HTML全文浏览量: 414
- PDF下载量: 184
- 被引次数: 0
出版历程
- 收稿日期: 2017-10-19
- 录用日期: 2018-01-29
- 刊出日期: 2020-03-06

Density-sensitive Robust Fuzzy Kernel Principal Component Analysis Algorithm

TAO Xin-Min^{1
, ,},
CHANG Rui^1
,,
SHEN Wei^1
,,
LI Chen-Xi^1
,,
WANG Ruo-Tong^1
,,
LIU Yan-Chao^1
,

1.
College of Engineering & Technology, Northeast Forestry University, Harbin 150040

Funds:

the Fundamental Research Funds for the Central Universities 2572017EB02

the Fundamental Research Funds for the Central Universities 2572017CB07

Two first-class scientific research foundation of Northeast Forestry University 411112438

Innovative talent fund of Harbin science and technology Bureau 2017RAXXJ018

National Natural Foundation of China 31570547

More Information

Author Bio:
CHANG Rui  Master student at the College of Engineering & Technology, Northeast Forestry University. Her research interest covers pattern recognition and signal processing

SHEN Wei  Lecturer at the College of Engineering & Technology, Northeast Forestry University. His research interest covers data analysis, logistics system planning and management consulting, and system modeling and optimization

LI Chen-Xi  Master student at the College of Engineering & Technology, Northeast Forestry University. Her research interest covers imbalanced data classification and fault diagnosis

WANG Ruo-Tong  Master student at the College of Engineering & Technology, Northeast Forestry University. Her research interest covers artificial intelligence and cluster analysis

LIU Yan-Chao  Master student at the College of Engineering & Technology, Northeast Forestry University. His research interest covers application of Internet of things technology, pattern recognition, and signal processing

Corresponding author: TAO Xin-Min Professor at the College of Engineering & Technology, Northeast Forestry University. He received his Ph. D. degree from Harbin Institute of Technology in 2005. His research interest covers intelligent signal processing, soft computing method, and pattern recognition. Corresponding author of this paper

摘要

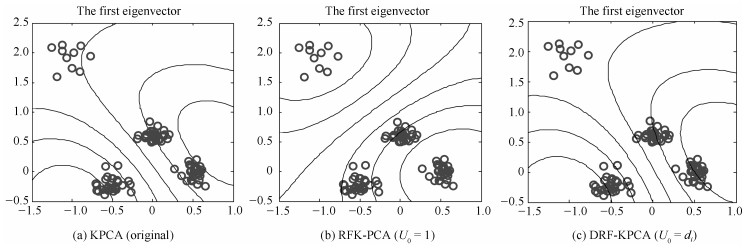
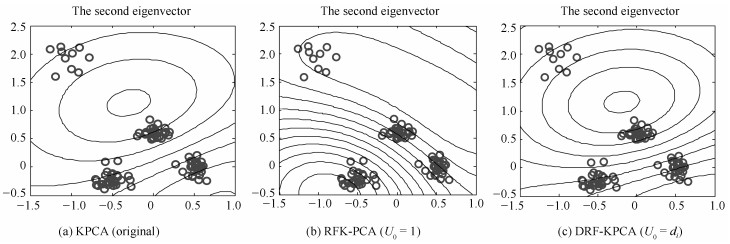
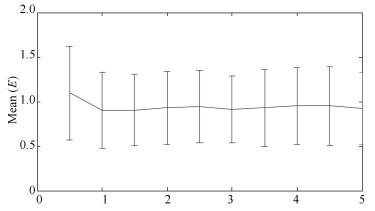
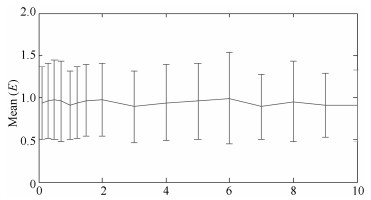
摘要: 针对传统核主成分分析算法(Kernel principal component analysis, KPCA)对野性样本点敏感等缺陷, 提出一种密度敏感鲁棒模糊核主成分分析算法(Density-Sensitive robust fuzzy kernel principal component analysis, DRF-KPCA).该算法首先通过引入相对密度确定样本初始隶属度, 并构建出基于重构误差的隶属度确定方法, 同时采用最优梯度下降法实现隶属度的更新, 有效解决了传统核主成分分析算法对野性样本点敏感导致的主成分偏移等问题.最后, 通过简化重构误差的计算公式, 大大降低了算法的计算复杂度和运行时间.实验部分, 利用有野性样本点和无野性样本点的数据集对本文算法、KPCA及其他改进算法的主成分分析性能进行测试, 结果表明DRF-KPCA能有效消除野性样本点对主元分布的影响.此外, 试验通过分析参数对算法性能的影响给出了合理的参数取值建议.最后将本文算法与其他算法应用到分类问题中进行对比, 实验表明本文算法的分类性能较其他算法有显著提高.
- 相对密度 /
- 核主成分分析算法 /
- 隶属度 /
- 分类性能
Abstract: In order to address the problem that the traditional kernel principal component analysis (KPCA) is sensitive to the sample points with large deviation and has higher computational complexity, a novel algorithm based on the density-sensitive robust fuzzy kernel principal component analysis algorithm (DRF-KPCA) is proposed. Firstly, the initial membership degree of the sample is determined by introducing the relative density. Secondly, the membership degree based on the reconstruction error is formulated and updated by the optimal gradient descent method, which can effectively solve the problem of the principal component skewing that is caused by the sensitivity of the traditional kernel principal component analysis algorithm to the data with outliers. Finally, the computational complexity and running time of the algorithm are significantly reduced by simplifying the calculation formula of the reconstruction error. In the experiments, compared with KPCA and other modified algorithms on both the datasets with large deviation samples and the datasets without large deviation samples, the DRF-KPCA is evaluated to effectively eliminate the impacts of the large deviation samples. In addition, the influence of parameters on the performance of the algorithm is analyzed and the suggestions of determination on the optimal parameters are given. Finally, the comparison results with other algorithms on classification problems demonstrate that the performance of the proposed algorithm is significantly improved.
- Relative density /
- kernel principal component analysis /
- membership degree /
- classification performance
Recommended by Associate Editor HU Qing-Hua
注释:

1) 本文责任编委胡清华

HTML全文

图 1 传统PCA算法对有无野性样本点数据集的主成分分布图

Fig. 1 The first principal component distribution using PCA algorithm on both the original data and the data with outliers

下载: 全尺寸图片幻灯片

图 2 不同KPCA算法的第一主元分布图

Fig. 2 The first principal component of different KPCA algorithms

下载: 全尺寸图片幻灯片

图 3 不同KPCA算法的第二主元分布图

Fig. 3 The second principal component of different KPCA algorithms

下载: 全尺寸图片幻灯片

图 4 三种算法的性能对比图

Fig. 4 Comparison of the statistics results of E evaluation indicator of three algorithms

下载: 全尺寸图片幻灯片

图 5 模糊化系数(p)对算法性能的影响

Fig. 5 Influence on the proposed algorithm performance of the fuzzy weight (p)

下载: 全尺寸图片幻灯片

图 6 不同正则化控制参数(σ²)对算法性能的影响

Fig. 6 Influence on the proposed algorithm performance of the regularization parameters (σ²)

下载: 全尺寸图片幻灯片

图 7 不同密度控制权重(ω)对算法性能的影响

Fig. 7 Influence on the proposed algorithm performance of the density control parameters (ω)

下载: 全尺寸图片幻灯片

图 8 不同平滑参数(s)对算法性能的影响

Fig. 8 Influence on the proposed algorithm performance of the smooth parameters (s)

下载: 全尺寸图片幻灯片

图 9 不同算法对不同数据的性能比较

Fig. 9 The performance comparison of different algorithms on different data

下载: 全尺寸图片幻灯片

图 10 不同算法对不同数据集的平均迭代时间比较

Fig. 10 Comparison of average iteration time for different data sets by different algorithms

下载: 全尺寸图片幻灯片

图 11 不同算法对SMK-CAN-187高维数据的降维性能对比

Fig. 11 Classification error rate of different algorithms with different reduced dimensions on SMK-CAN-187 dataset

下载: 全尺寸图片幻灯片

表 1 不同UCI数据的三种KPCA算法分类性能对比

Table 1 Classification performance of three kinds of KPCA algorithm for different UCI datasets

Dataset	Class (N) : Dimension	KPCA	GMM-PCA	RFK-PCA	DRF-KPCA
yeast	1 (463) : 2 (429) : 8	31.11±4.88	38.26±3.27	37.66±6.23	31.14±1.24
	1 (463) : 3 (244) : 8	23.94±3.22	30.24±4.21	26.79±5.15	24.01±0.98
	2 (429) : 3 (244) : 8	16.18±3.67	18.96±1.35	19.01±4.11	16.46±0.79
letter	H ((734) : R (758) : 16	10.67±2.15	9.17±3.66	7.16±2.35	5.48±0.07
	S (748) : Z (734) : 16	9.39±2.01	9.01±1.47	4.14 ± 1.97	2.13±0.09
	H (734) : O (753) : 16	10.74±2.46	12.01±3.53	9.45 ± 4.02	7.14±0.02
german	1 (700: 2 (300) : 24	23.12±3.48	24.44±4.87	25.38±5.96	22.24±1.01
haberman	1 (225) : 2 (81) : 3	17.46±3.16	17.32±2.55	16.73±4.98	15.12±0.49
ionophere	1 (225) : -1 (126) : 34	8.33±2.13	8.03±2.98	7.57±3.19	5.37±0.07
pima	1 (268) : 0 (500) : 8	25.71±4.01	29.63±4.76	31.88±6.23	25.33±1.11
phoneme	1 (1 586) : 0 (3 818) : 5	11.12±2.16	10.06±2.93	9.67±3.98	7.21±0.12
sonar	1 (111) : -1 (97) : 60	7.29±1.22	7.56±1.43	6.12 ± 2.79	5.32±0.02
	1 (1 528) : 2 (1 307) : 8	37.59±4.32	43.39±5.09	48.24±7.94	37.43±1.22
abalone	1 (1 528) : 3 (1 342) : 8	23.69±3.12	23.33±2.78	24.18 ± 5.12	20.59±1.03
	2 (1307) : 3 (1 342) : 8	12.83±1.22	10.74±1.07	11.24 ± 3.01	9.11±0.22

下载: 导出CSV

参考文献(25)

[1]	李春娜, 陈伟杰, 邵元海.鲁棒的稀疏L_p-模主成分分析.自动化学报, 2017, 43(1): 142-151 doi: 10.16383/j.aas.2017.c150512 Li Chun-Na, Chen Wei-Jie, Shao Yuan-Hai. Robust sparse L_p-norm principal component analysis. Acta Automatica Sinica, 2017, 43(1): 142-151 doi: 10.16383/j.aas.2017.c150512
[2]	张先鹏, 陈帆, 和红杰.结合多种特征的高分辨率遥感影像阴影检测.自动化学报, 2016, 42(2): 290-298 doi: 10.16383/j.aas.2016.c150196 Zhang Xian-Peng, Chen Fan, He Hong-Jie. Shadow detection in high resolution remote sensing images using multiple features. Acta Automatica Sinica, 2016, 42(2): 290-298 doi: 10.16383/j.aas.2016.c150196
[3]	董恩增, 魏魁祥, 于晓, 冯倩.一种融入PCA的LBP特征降维车型识别算法.计算机工程与科学, 2017, 39(2): 359-363 doi: 10.3969/j.issn.1007-130X.2017.02.021 Dong En-Zeng, Wei Kui-Xiang, Yu Xiao, Feng Qian. A model recognition algorithm integrating PCA into LBP feature dimension reduction. Computer Engineering and Science, 2017, 39(2): 359-363 doi: 10.3969/j.issn.1007-130X.2017.02.021
[4]	Wan M, Shang W L, Zeng P. Double behavior characteristics for one-class classification anomaly detection in networked control systems. IEEE Transactions on Information Forensics and Security, 2017, 12(12): 3011-3023 doi: 10.1109/TIFS.2017.2730581
[5]	Chen B J, Yang J H, Jeon B, Zhang X P. Kernel quaternion principal component analysis and its application in RGB-D object recognition. Neurocomputing, 2017, 266: 293-303 doi: 10.1016/j.neucom.2017.05.047
[6]	赵孝礼, 赵荣珍.全局与局部判别信息融合的转子故障数据集降维方法研究.自动化学报, 2017, 43(4): 560-567 doi: 10.16383/j.aas.2017.c160317 Zhao Xiao-Li, Zhao Rong-Zhen. A method of dimension reduction of rotor faults data set based on fusion of global and local discriminant information. Acta Automatica Sinica, 2017, 43(4): 560-567 doi: 10.16383/j.aas.2017.c160317
[7]	吴枫, 仲妍, 吴泉源.基于增量核主成分分析的数据流在线分类框架.自动化学报, 2010, 36(4): 534-542 doi: 10.3724/SP.J.1004.2010.00534 Wu Feng, Zhong Yan, Wu Quan-Yuan. Online classification framework for data stream based on incremental kernel principal component analysis. Acta Automatica Sinica, 2010, 36(4): 534-542 doi: 10.3724/SP.J.1004.2010.00534
[8]	吴广宁, 袁海满, 高波, 李帅兵.基于特征评估与核主元分析的电力变压器故障诊断.高电压技术, 2017, 43(8): 2533-2540 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdyjs201708013 Wu Guang-Ning, Yuan Hai-Man, Gao Bo, Li Shuai-Bing. Fault diagnosis of power transformer based on feature evaluation and kernel principal component analysis. High Voltage Engineering, 2017, 43(8): 2533-2540 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdyjs201708013
[9]	Huang J P, Yan X F. Quality relevant and independent two block monitoring based on mutual information and KPCA. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6518-6527 doi: 10.1109/TIE.2017.2682012
[10]	Xie H B, Zhou P, Guo T R, Sivakumar B, Zhang X, Dokos S. Multiscale two-directional two-dimensional principal component analysis and its application to high-dimensional biomedical signal classification. IEEE Transactions on Biomedical Engineering, 2016, 63(7): 1416-1425 doi: 10.1109/TBME.2015.2436375
[11]	Xia J S, Falco N, Benediktsson J A, Du P J, Chanussot J. Hyperspectral image classification with rotation random forest via KPCA. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(4): 1601-1609 doi: 10.1109/JSTARS.2016.2636877
[12]	阳同光, 桂卫华.基于KPCA与RVM感应电机故障诊断研究.电机与控制学报, 2016, 20(9): 89-95 http://d.old.wanfangdata.com.cn/Periodical/djykzxb201609013 Yang Tong-Guang, Gui Wei-Hua. Research on fault diagnosis of induction motor based KPCA and RVM. Electric Machines and Control, 2016, 20(9): 89-95 http://d.old.wanfangdata.com.cn/Periodical/djykzxb201609013
[13]	Wu X, Nie L, Xu M. Robust fuzzy quality function deployment based on the mean-end-chain concept: service station evaluation problem for rail catering services. European Journal of Operational Research, 2017, 263(3): 974-995 doi: 10.1016/j.ejor.2017.05.036
[14]	Gao X K, Lee H M, Gao S P. A robust parameter design of wide band DGS filter for common-mode noise mitigation in high-speed electronics. IEEE Transactions on Electromagnetic Compatibility, 2017, 59(6): 1735-1740 doi: 10.1109/TEMC.2017.2710202
[15]	Choi S W, Park J H, Lee I B. Process monitoring using a Gaussian mixture model via principal component analysis and discriminant analysis. Computers & Chemical Engineering, 2004, 28(8): 1377-1387 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=65dba41b16cab1ad18e6181b8673da19
[16]	Raveendran R, Huang B. Two layered mixture Bayesian probabilistic PCA for dynamic process monitoring. Journal of Process Control, 2017, 57: 148-163 doi: 10.1016/j.jprocont.2017.06.009
[17]	Huang S Y, Yen Y R, Eguchi S. Robust kernel principal component analysis. Neural Computation, 2009, 21(11): 3179-3213 doi: 10.1162/neco.2009.02-08-706
[18]	Huang H H, Yen Y R. An iterative algorithm for robust kernel principal component analysis. Neurocomputing, 2011, 74(18): 3921-3930 doi: 10.1016/j.neucom.2011.08.008
[19]	Heo G, Gader P, Frigui H. RKF-PCA: robust kernel fuzzy PCA. Neural Networks, 2009, 22(5-6): 642-650 doi: 10.1016/j.neunet.2009.06.013
[20]	陶新民, 刘福荣, 刘玉, 童智靖.一种多尺度协同变异的粒子群优化算法.软件学报, 2012, 23(7): 1805-1815 http://d.old.wanfangdata.com.cn/Periodical/rjxb201207013 Tao Xin-Min, Liu Fu-Rong, Liu Yu, Tong Zhi-Jing. Multi-scale cooperative mutation particle swarm optimization algorithm. Journal of Software, 2012, 23(7): 1805-1815 http://d.old.wanfangdata.com.cn/Periodical/rjxb201207013
[21]	张航, 叶东毅.一种基于多正则化参数的矩阵分解推荐算法.计算机工程与应用, 2017, 53(3): 74-79 http://d.old.wanfangdata.com.cn/Periodical/jsjgcyyy201703014 Zhang Hang, Ye Dong-Yi. Recommender algorithm based on matrix factorization with multiple regularization parameters. Computer Engineering and Application, 2017, 53(3): 74-79 http://d.old.wanfangdata.com.cn/Periodical/jsjgcyyy201703014
[22]	陶新民, 徐晶, 杨立标, 刘玉.一种改进的粒子群和K均值混合聚类算法.电子与信息学报, 2010, 32(1): 92-97 http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201001017 Tao Xin-Min, Xu Jing, Yang Li-Biao, Liu Yu. Improved cluster algorithm based on K-means and particle swarm optimization. Journal of Electronics & Information Technology, 2010, 32(1): 92-97 http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201001017
[23]	程昊翔, 王坚.基于快速聚类分析的支持向量数据描述算法.控制与决策, 2016, 31(3): 551-554 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201603025 Cheng Hao-Xiang, Wang Jian. Support vector data description based on fast clustering analysis. Control and Decision, 2016, 31(3): 551-554 http://d.old.wanfangdata.com.cn/Periodical/kzyjc201603025
[24]	郑祺, 黄德才.基于引力相似度和相对密度的不确定数据流聚类.上海交通大学学报, 2016, 50(6): 873-878 http://d.old.wanfangdata.com.cn/Periodical/shjtdxxb201606010 Zheng Qi, Huang De-Cai. Uncertain data stream clustering algorithm based on gravity similarity and relative density techniques. Journal of Shanghai Jiaotong University, 2016, 50(6): 873-878 http://d.old.wanfangdata.com.cn/Periodical/shjtdxxb201606010
[25]	Feature selection datasets[Online], availalde: http://featureselection.asu.edu/datasets.php, December 1, 2019