基于量子计算的粗糙集核属性求解算法

段隆振; 谢旭明; 邱桃荣; 杨舒晴

doi:10.16383/j.aas.2018.c170328

基于量子计算的粗糙集核属性求解算法

doi: 10.16383/j.aas.2018.c170328

段隆振^1,,
谢旭明^{1, 2,},
邱桃荣^1, ,,
杨舒晴^1,

1.
南昌大学信息工程学院南昌 330031
2.
南昌大学图书馆南昌 330031

基金项目:

国家自然科学基金 61070139

国家自然科学基金 81460769

国家自然科学基金 61762045

江西省科技化项目 20112BBG70087

详细信息

作者简介:
段隆振   南昌大学教授.主要研究方向为数据挖掘, 并行计算与大数据. E-mail:lzhduan@126.com

谢旭明   南昌大学博士研究生.主要研究方向为粗糙集与量子计算. E-mail: xiexuming@ncu.edu.cn

杨舒晴   南昌大学博士研究生.主要研究方向为粗糙集与量子计算. E-mail:ysqsinuo@163.com

通讯作者:
邱桃荣南昌大学教授.主要研究方向为粗糙集, 粒计算与量子计算.本文通信作者. E-mail: qiutaorong@ncu.edu.cn

计量
- 文章访问数: 1170
- HTML全文浏览量: 185
- PDF下载量: 96
- 被引次数: 0
出版历程
- 收稿日期: 2017-06-16
- 录用日期: 2018-01-01
- 刊出日期: 2020-08-26

A Quantum Algorithm of the Computation of Core in Rough Set

DUAN Long-Zhen^1
,,
XIE Xu-Ming^{1, 2
,},
QIU Tao-Rong^{1
, ,},
YANG Shu-Qing^1
,

1.
College of Information Engineering, Nanchang University, Nanchang 330031
2.
Library of Nanchang University, Nanchang 330031

Funds:

National Natural Science Foundation of China 61070139

National Natural Science Foundation of China 81460769

National Natural Science Foundation of China 61762045

Scientiflc and Technological Project of Jiangxi Province 20112BBG70087

More Information

Author Bio:
DUAN Long-Zhen    Professor at Nanchang University. His research interest covers data mining, parallel computing and big data

XIE Xu-Ming    Ph. D. candidate at Nanchang University. His research interest covers rough set and quantum computing

YANG Shu-Qing   Ph. D. candidate at Nanchang University. Her research interest covers rough set and quantum computing

Corresponding author: QIU Tao-Rong Professor at Nanchang University. His research interest covers rough set, granular computing and quantum computing. Corresponding author of this paper

摘要

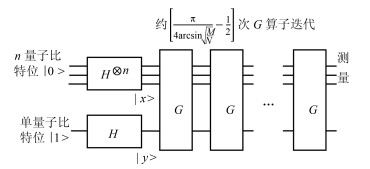
摘要: 粗糙集的核属性求解问题在经典计算中是一个NP问题.现有的方法中最优的时间复杂度也需要${\rm O}$$ \left(|C||U|\right)$($U$为论域、$C$为属性列数).由于量子计算的并行性特点, 本文致力于采用量子计算的方法来求解粗糙集的核属性, 拟提出了一种基于量子计算的粗糙集核属性求解算法.经过仿真实验, 在任何情况下, 该算法都能以1的总概率得到目标分量; 且通过理论分析证明了算法的时间复杂度不会高于${\rm O}$$\left(|\frac{{\rm{ \mathsf{ π}}}}{2\arcsin\sqrt {\frac{M}{C}}}+1||U|\right)$.
- 量子计算 /
- 粗糙集 /
- 核属性 /
- 算法设计
Abstract: The computation of core in rough set is an NP-hard problem in classic computing. The best time complexity of the existing algorithms is ${\rm O}$$\left(|C||U|\right)$ ($U$ stands for Universe, $C$ stands for the number of attributes). Due to its ability to compute in parallel, quantum computing, is adopted to find the core in rough set in this research. Thus, a quantum algorithm of the computation of core in rough set is proposed. Based on simulation experiment, the proposed algorithm is able to get one target out of the target set with the probability of 1. And the time complexity of the new algorithm is proved to be no more than ${\rm O}$$ \left(|\frac{{\rm{ \mathsf{ π}}}}{2\arcsin\sqrt {\frac{M}{C}}}+1||U|\right)$ by theoretical analysis.
- Quantum computing /
- rough set /
- core /
- algorithm design
Recommended by Associate Editor ZHANG Min-Ling
注释:

1) 本文责任编委张敏灵

HTML全文

图 1 $G$算子内部结构

Fig. 1 Inner structure of $G$

下载: 全尺寸图片幻灯片

图 2 Grover算法示意图

Fig. 2 Diagram of Grover algorithm

下载: 全尺寸图片幻灯片

图 3 核属性个数与目标分量概率的关系

Fig. 3 Comparing the number of core attributes and percentage of targets

下载: 全尺寸图片幻灯片

图 4 Comparing the number of core attributes and percentage of targets

Fig. 4 Comparing the number of core attributes and the number of iterations

下载: 全尺寸图片幻灯片

表 1 UCI数据集实验结果

Table 1 The test result of UCI sets

数据集	算法	迭代次数	概率
Iris数据集	Grover算法	失效	失效
Iris数据集	文献[15]算法	2	0.9686
Iris数据集	文献[16]算法	1	1.0000
Iris数据集	$\textbf{本文算法}$	$\textbf{1}$	$\textbf{1.0000}$
Soybean数据集	Grover算法	1	0.8815
Soybean数据集	文献[15]算法	3	0.9723
Soybean数据集	文献[16]算法	2	0.9766
Soybean数据集	$\textbf{本文算法}$	$\textbf{2}$	$\textbf{1.0000}$
Dermatology数据集	Grover算法	6	0.9983
Dermatology数据集	文献[15]算法	12	1.0000
Dermatology数据集	文献[16]算法	8	0.9978
Dermatology数据集	$\textbf{本文算法}$	$\textbf{6}$	$\textbf{1.0000}$
Balloons数据集	Grover算法	失效	失效
Balloons数据集	文献[15]算法	2	0.9686
Balloons数据集	文献[16]算法	1	1.0000
Balloons数据集	$\textbf{本文算法}$	$\textbf{1}$	$\textbf{1.0000}$
Breast Cancer数据集	Grover算法	1	1.0000
Breast Cancer数据集	文献[15]算法	3	0.9688
Breast Cancer数据集	文献[16]算法	2	0.9451
Breast Cancer数据集	$\textbf{本文算法}$	$\textbf{1}$	$\textbf{1.0000}$

下载: 导出CSV

参考文献(19)

[1]	Pawlak Z. Rough sets. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356
[2]	黎明, 张化光.基于粗糙集的神经网络建模方法研究.自动化学报, 2002, 28(1): 27-33 http://www.aas.net.cn/article/id/16371 Li Ming, Zhang Hua-Guang. Research on the method of neural network modeling based on rough sets theory. Acta Automatica Sinica, 2002, 28(1): 27-33 http://www.aas.net.cn/article/id/16371
[3]	张迎春, 郭禾.基于粗糙集和新能量公式的水平集图像分割.自动化学报, 2015, 41(11): 1913-1925 doi: 10.16383/j.aas.2015.c140823 Zhang Ying-Chun, Guo He. Level set image segmentation based on rough set and new energy formula. Acta Automatica Sinica, 2015, 41(11): 1913-1925 doi: 10.16383/j.aas.2015.c140823
[4]	Hu X H, Cercone N. Learning in relational databases: A rough set approach. Computational Intelligence, 1995, 11(2): 323-338 doi: 10.1111/j.1467-8640.1995.tb00035.x
[5]	叶东毅, 陈昭炯.一个新的差别矩阵及其求核方法.电子学报, 2002, 30(7): 1086-1088 doi: 10.3321/j.issn:0372-2112.2002.07.040 Ye Dong-Yi, Chen Zhao-Jiong. A new discernibility matrix and the computation of a core. Acta Electronica Sinica, 2002, 30(7): 1086-1088 doi: 10.3321/j.issn:0372-2112.2002.07.040
[6]	王国胤.决策表核属性的计算方法.计算机学报, 2003, 26(5): 611-615 doi: 10.3321/j.issn:0254-4164.2003.05.013 Wang Guo-Yin. Calculation methods for core attributes of decision table. Chinese Journal of Computers, 2003, 26(5): 611-615 doi: 10.3321/j.issn:0254-4164.2003.05.013
[7]	徐章艳, 杨炳儒, 蔡卫东, 崔巍, 谷冬元.一个基于正区域的快速求核算法.系统工程与电子技术, 2006, 28(12): 1902-1905, 1931 doi: 10.3321/j.issn:1001-506X.2006.12.032 Xu Zhang-Yan, Yang Bing-Ru, Cai Wei-Dong, Cui Wei, Gu Dong-Yuan. Quick algorithm for computing core based on the positive region. Systems Engineering and Electronics, 2006, 28(12): 1902-1905, 1931 doi: 10.3321/j.issn:1001-506X.2006.12.032
[8]	周江卫, 冯博琴, 刘洋.一种新的快速求核算法.西安交通大学学报, 2007, 41(6): 688-691 doi: 10.3321/j.issn:0253-987X.2007.06.013 Zhou Jiang-Wei, Feng Bo-Qin, Liu Yang. New algorithm for quick computing core. Journal of Xi'an Jiaotong University, 2007, 41(6): 688-691 doi: 10.3321/j.issn:0253-987X.2007.06.013
[9]	尹林子, 阳春华, 王晓丽, 桂卫华.基于标记可辨识矩阵的增量式属性约简算法.自动化学报, 2014, 40(3): 397-404 doi: 10.3724/SP.J.1004.2014.00397 Yin Lin-Zi, Yang Chun-Hua, Wang Xiao-Li, Gui Wei-Hua. An incremental algorithm for attribute reduction based on labeled discernibility matrix. Acta Automatica Sinica, 2014, 40(3): 397-404 doi: 10.3724/SP.J.1004.2014.00397
[10]	张靖, 李春文, 吴热冰.开放环境下多比特量子计算机的相干控制模型.自动化学报, 2005, 31(5): 759-764 http://www.aas.net.cn/article/id/15967 Zhang Jing, Li Chun-Wen, Wu Re-Bing. Coherent control modeling of quantum computers in open environments. Acta Automatica Sinica, 2005, 31(5): 759-764 http://www.aas.net.cn/article/id/15967
[11]	Deutsch D. Quantum theory, the church-turing principle and the universal quantum computer. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1985, 400(1818): 97-117
[12]	Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Journal on Computing, 1997, 26(5): 1484-1509 doi: 10.1137/S0097539795293172
[13]	Grover L. A fast quantum mechanical algorithm for database search. In: Proceedings of the 28th Annual ACM Symposium on the Theory of Computing. New York, USA: IEEE, 1996. 212-219
[14]	孙国栋, 苏胜辉, 徐茂智.求根问题的量子计算算法.北京工业大学学报, 2015, 41(3): 366-371 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjgydxxb201503007 Sun Guo-Dong, Su Sheng-Hui, Xu Mao-Zhi. Quantum mechanical algorithms for solving root finding problem. Journal of Beijing University of Technology, 2015, 41(3): 366-371 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjgydxxb201503007
[15]	Tulsi T, Grover L K, Patel A. A new algorithm for fixed point quantum search. Quantum Information & Computation, 2006, 6(6): 483-494 http://www.researchgate.net/publication/2195367_A_new_algorithm_for_fixed_point_quantum_search
[16]	张煜东, 韦耿, 吴乐南.一种改进的Grover量子搜索算法.信号处理, 2009, 25(2): 256-259 doi: 10.3969/j.issn.1003-0530.2009.02.017 Zhang Yu-Dong, Wei Geng, Wu Le-Nan. An improved Grover quantum searching algorithm. Signal Processing, 2009, 25(2): 256-259 doi: 10.3969/j.issn.1003-0530.2009.02.017
[17]	李盼池, 李士勇.基于自适应相位旋转的Grover量子搜索算法.系统仿真学报, 2009, 21(12): 3557-3560 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xtfzxb200912014 Li Pan-Chi, Li Shi-Yong. Grover$'$s quantum search algorithm based on adaptive phase rotation. Journal of System Simulation, 2009, 21(12): 3557-3560 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xtfzxb200912014
[18]	朱皖宁, 陈汉武.迭代次数自适应的Grover算法.电子学报, 2016, 44(12): 2975-2980 doi: 10.3969/j.issn.0372-2112.2016.12.023 Zhu Wan-Ning, Chen Han-Wu. Grover auto-control searching algorithm. Acta Electronica Sinica, 2016, 44(12): 2975-2980 doi: 10.3969/j.issn.0372-2112.2016.12.023
[19]	Brassard C H, Hoyer P, Tapp A. Quantum counting. In: Proceedings of the 25th International Colloquium Automata Language and Programming. Berlin, Germany: Springer-Verlag, 1998. 820-831